Розділ: Механіка
Тема: Динаміка: рівнодійна та закони Ньютона
Кількість завдань: 74
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Рух тіла під дією кількох сил.
Завдання скеровано на перевірку вміння розв’язувати комбіновані завдання ‒ описати коливальний рух за допомогою другого закону Ньютона і закону збереження механічної енергії.
Спочатку скористаймося законом збереження механічної енергії. У момент проходження кулькою положення рівноваги модуль швидкості
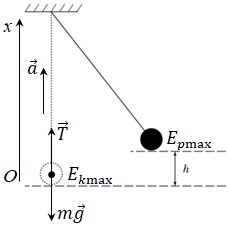
А коли кулька підіймається на максимальну висоту
Це формула для обчислення шуканої за умовою висоти. Але швидкість руху кульки невідома. Визначмо її, скориставшись другим законом Ньютона:
Тобто на кульку діє сила тяжіння
Оскільки, гойдаючись на нитці, кулька рухається по дузі кола, то прискорення
Знайдемо проєкції векторів усіх величин другого закону Ньютона на вісь
Виразимо звідси модуль швидкості руху
Підставимо це значення швидкості руху кульки у формулу для обчислення максимальної висоти її підйому:
Відповідь: 0,25.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на перевірку знання, розуміння і застосування другого закону Ньютона.
За другим законом Ньютона прискорення
Оскільки на тіло діє кілька сил, то сила
Знайдемо рівнодійну сил за допомогою додаткових побудов (див. рисунок). Побудуємо паралелограм спочатку на векторах
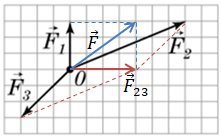
Обчислимо тепер модуль прискорення, набутого тілом під дією цих сил:
Відповідь: 2,5.
ТЕМА: Механіка. Основи динаміки. Момент сили. Умови рівноваги тіла.
Завдання скеровано на перевірку знання і розуміння умов рівноваги тіла на прикладі простого механізму ‒ важеля.
Якщо тіло може тільки обертатися (має нерухому вісь обертання), то за правилом моментів воно перебуває в рівновазі, якщо алгебраїчна сума моментів сил, що діють на тіло, дорівнює нулю:
Момент сили
Плече
Запишімо правило моментів відповідно до умови завдання, урахувавши знаки моментів сил. Для цього спочатку позначмо на рисунку сили і плечі цих сил.
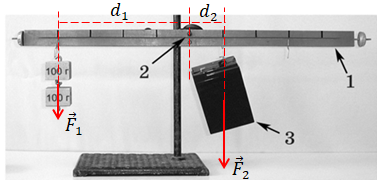
Сили
Відповідь: 0,8.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг.
Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі пов'язані з поверхневим натягом та законами Ньютона.
Дано:
Знайти:
Для розв’язання задачі необхідно розуміти, які сили заважають підняти тонку дротинку з поверхні.
Зокрема на дротинку діє сила тяжіння, що притискає її до поверхні рідини:
Крім того дротик виділяє на поверхні рідини дві області – праворуч та ліворуч від себе. Тому з обох боків на нього діятимуть сили поверхневого натягу.
Силу поверхневого натягу можна розрахувати за формулою
Тоді сила, що необхідна для того, щоб підняти кільце з поверхні має подолати силу тяжіння і сили поверхневого натягу праворуч і ліворуч від дротика:
Тож тепер можна виразити поверхневий натяг із формули:
Відповідь: 45.
ТЕМА: Енергія. Робота. Потужність. Сила.
Завдання скеровано на перевірку розуміння понять енергії, потужності, сили й прискорення.
Потужність
Енергія
Сила
Прискорення
Відповідь: 1В, 2Д, 3Б, 4А.
ТЕМА: Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.
Завдання скеровано на оцінювання розуміння постулатів спеціальної теорії відносності.
Швидкість світла є однаковою в усіх інерціальних системах відліку незалежно від того, із якою швидкістю рухається джерело. Тож попри те, що ракета з прожектором рухається зі швидкістю
Відповідь: Г.
Механіка. Елементи динаміки рідин i газів. Умова плавання тіл.
Завдання скеровано на перевірку розуміння поняття густини та вміння застосовувати закон Архімеда.
Силу Архімеда можна визначити за формулою
Силу тяжіння визначають за формулою
Густина речовини
Тоді масу тіла можна виразити як
Тоді силу тяжіння можна записати як:
Вважатимемо, що на тіло в рідині діє лише сила тяжіння, що напрямлена вниз, і виштовхувальна сила Архімеда, напрямлена вгору. За другим законом Ньютона
Тіло плаває в товщі рідини, а не спливає на поверхню чи тоне, тому прискорення
Якщо спрямувати вісь x у напрямку прискорення вільного падіння, можна спроєктувати векторне рівняння:
Відповідь: Б.
ТЕМА: Робота. Сила Архімеда.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про силу Архімеда.
Дано:
Знайти:
Для того, щоби перевернути блок, достатньо його центр мас підняти на висоту, на якій він у вертикальному положенні. Оскільки блок циліндричний, то в обох положеннях він на половині висоти блока (рис. 1).
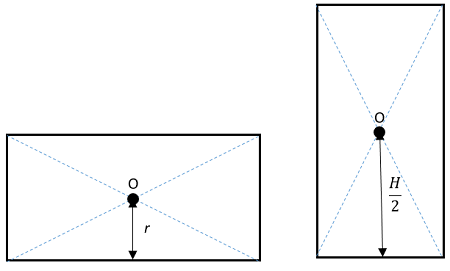
Рис. 1. Положення центра мас у вертикальному й горизонтальному положенні
Оскільки поперечні розміри стовпа за умовою враховувати не потрібно, то можна вважати, що під час перевертання центр мас піднімають на половину всієї висоти
Рівнодійну сил, що діють на блок, можна обчислити за формулою
Сила тяжіння діє вертикально вниз, притягуючи блок до землі, а сила Архімеда виштовхує блок вертикально вгору, інші сили на блок не діють. Якщо вважати напрямок «вертикально вниз» додатним,
Маса тіла пов’язана з його густиною формулою
Тоді
Оскільки об’єму блока невідомий, із дужок можна винести його густину:
Тоді робота, необхідна для підняття центра мас бетонного блока на половину його висоти, дорівнює
Відповідь: 6.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Закон всесвітнього тяжіння.
Завдання скеровано на перевірку розуміння законів Ньютона й закону всесвітнього тяжіння і їхнього застосування для описування реальних ситуацій.
Закони, про які йдеться в цьому завданні:
- перший закон Ньютона – існують такі системи відліку, відносно яких тіло зберігає стан спокою або рівномірного прямолінійного руху, якщо на нього не діють жодні сили або якщо ці сили скомпенсовані;
- другий закон Ньютона – прискорення, якого набуває тіло внаслідок дії сили, прямо пропорційне цій силі й обернено пропорційне масі тіла:
$$ \overrightarrow{a}=\frac{\overrightarrow{F}}{m}; $$ - третій закон Ньютона – тіла взаємодіють із силами, що мають одну природу, напрямлені вздовж однієї прямої, рівні за модулем і протилежні за напрямком:
$$ \overrightarrow{F_1}=-\overrightarrow{F_2}; $$ - закон всесвітнього тяжіння – будь-які два тіла притягуються одне до одного із силою, яка прямо пропорційна добутку мас цих тіл й обернено пропорційна квадрату відстані між ними:
$$ F=G\frac{m_1m_2}{r^2}. $$
А зменшення маси автомобіля, що привело до його прискорення, є прикладом другого закону Ньютона
Б нагрівання гальмівних колодок під час гальмування пов’язане зі зміною їхньої внутрішньої енергії внаслідок роботи сил тертя, отже цей приклад не пов’язаний із наведеними законами
В кинутий угору камінь притягається до Землі за законом всесвітнього тяжіння
Г якщо сила тертя компенсує силу тяжіння, то всі сили, що діють на дощову краплю під час її падіння, скомпенсовані. Тому те, що вона рухається рівномірно й прямолінійно – це приклад для першого закону Ньютона
Д сила удару, який комар завдав лобовому склу, і сила удару, яке скло завдало комарові, рівні за третім законом Ньютона
Відповідь: 1Г, 2А, 3Д, 4В.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням сили поверхневого натягу.
Дано:
Знайти:
На кільце на поверхні води діють сили поверхневого натягу, що утримують його на поверхні, і сила тяжіння. Силу тяжіння можна визначити за формулою
Окрім того, кільце обмежує на поверхні дві ділянки – усередині й зовні. Тому з обох боків на нього діятимуть сили поверхневого натягу.
Дріт, із якого зроблене кільце, – тонкий, тому можна вважати, що внутрішній радіус дорівнює зовнішньому радіусу кільця. Тож довжина кільця з боку зовнішньої і внутрішньої поверхні буде однаковою:
Тоді сила, що необхідна для того, щоби підняти кільце з поверхні, має подолати силу тяжіння і сили поверхневого натягу із зовнішнього і внутрішнього боку:
Відповідь: 56.
ТЕМА: Маса. Густина. Умова плавання тіл.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на використання умови плавання тіл.
Дано:
Знайти:
За умовою плавання тіл тіло перебуватиме в рівновазі, якщо
Силу тяжіння визначають за формулою
Масу й густину тіла пов’язує формула
Тому силу тяжіння можна записати як
Силу Архімеду визначають за формулою
Об’єм дошки можна визначити з її геометричних розмірів:
Дошка не повністю занурена під воду, а під час розрахунку сили Архімеда треба використовувати об’єм зануреної під воду частини. Цей об’єм можна розрахувати за формулою
Тоді умова плавання дошки матиме вигляд:
Відповідь: 750.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі про рух тіла під дією кількох сил.
Дано:
Знайти:
У такій конструкції всі три бруски рухатимуться як єдине ціле з однаковим прискоренням і масою
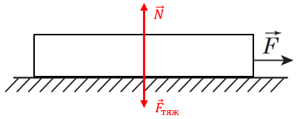
Рис. 1. Схематичне зображення дії сил на бруски як ціле
Для них можна записати 2 закон Ньютона:
Уздовж вертикальної осі бруски не рухаються, тому рівнодійна в цьому напрямку дорівнює 0. Спроєктувавши сили на цей напрямок, можна отримати вираз
Спроєктувавши другий закон Ньютона на горизонтальний напрямок, можна дійти висновку, що
Тож
Обмеження на максимальну силу, а отже й максимальне прискорення, створене міцністю ниток, якими зв’язано бруски.
Цю систему потрібно розглянути як два бруски масою
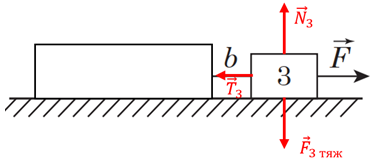
Рис. 2. Схематичне зображення сил, що діють на брусок 3
На брусок 3 діють усі зазначені вище сили й сила натягу нитки. Рухається цей брусок із тим самим прискоренням, яке використано в попередніх розрахунках. Тому можна записати рівнодійну сил, що діють на цей брусок:
Уздовж вертикальної осі брусок 3 не рухається, тому можна зробити той самий висновок, що й у попередніх розрахунках:
Проєкція другого закону Ньютона на горизонтальну вісь матиме вигляд:
Зважаючи на те, що
Значення максимальної сили натягу відоме з умови
Відповідь: 20
ТЕМА: Основи динаміки. Другий закон Ньютона. Основи електростатики. Закон Кулона.
Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі, пов’язані із силою Кулона.
1. Дано:
1. Знайти:
Спочатку на кульку діяли лише сили натягу підвісу й сила тяжіння (рис. 1, а). Кулька перебуває у стані спокою, тому рівнодійна цих сил дорівнює 0:
Цей векторний вираз можна спроєктувати на вертикальну вісь:
Після того, як до першої кульки наблизили другу, окрім сили натягу підвісу й сили тяжіння на кульку діє сила Кулона (рис. 1, б). Але навіть у такому разі тіло перебуває у стані спокою, тобто рівнодійна цих сил дорівнює нулю:
Цей векторний вираз можна спроєктувати на вертикальну вісь:
Зважаючи на те, що
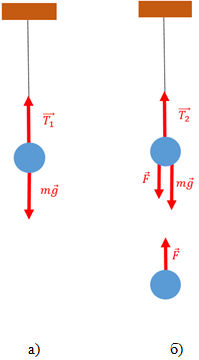
Рис. 1. Схематичне зображення сил: а) для одної кульки, б) для двох кульок
2. Дано:
2. Знайти:
Силу Кулона визначають за формулою
Тоді можна записати силу взаємодії до того, як кульки наблизили одну до одної:
Ця сила взаємодії дорівнює
Сила взаємодії після зближення дорівнюватиме
Як і до зближення, підвішена кулька перебуватиме у стані спокою, а рівнодійна всіх сил, що діють на неї, дорівнюватиме нулю:
Цей векторний вираз можна спроєктувати на вертикальну вісь:
Тож можна розрахувати силу натягу підвісу. Оскільки
Відповідь: 1. 0,5. 2. 3.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі з визначення роботи сил.
Якщо тіло зісковзує по площині рівномірно, то його прискорення
Рівнодійна сил, які діють на тіло, що рухається по похилій площині (рис. 1), дорівнює векторній сумі всіх цих сил:
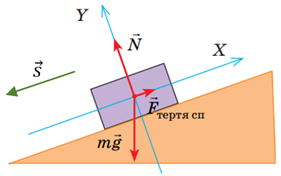
Рис. 1. Схематичне зображення сил, що діють на тіло на похилій площині
Це рівняння можна спроєктувати на осі
Тож
Силу тертя визначають за формулою
Тож
Роботу сили можна обчислити за формулою
Тоді можна записати роботу сили тяжіння і сили тертя. Кут
Кут між напрямком сили тертя і переміщенням
Оскільки модуль сили тяжіння і переміщення додатні, а
Відповідь: B.
ТЕМА: Механіка. Основа динаміки. Додавання сил.
Завдання скеровано на оцінювання розуміння поняття рівнодійної.
Якщо рівнодійна сил, що діють на тіло, дорівнює нулю, то тіло перебуває у стані спокою. Тіло у стані спокою має постійну швидкість.
Адже за другим законом Ньютона
Якщо тіло не рухається, можна вважати, що його швидкість постійна й дорівнює 0 м/с.
У варіанті відповіді А віз залишається на своєму місці, а в Б вода у склянці нерухома, тож їхні швидкості дорівнюють нулю. А отже й рівнодійна сил, що діють на них, – теж.
У варіанті відповіді В парашутист рухається рівномірно вниз, тобто його швидкість постійна, а отже й рівнодійна, що діє на нього, дорівнює нулю.
У варіанті відповіді Г літак щойно відірвався від злітно-посадкової смуги. Тобто він лише почав набирати швидкість і рухався із прискоренням. Тож рівнодійна сил, що діють на нього, не дорівнює нулю.
Відповідь: Г.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рух тіла під дією кількох сил.
Знайти:
Розв’язання цієї задачі доцільно розпочати зі створення схеми дії сил на брусок, який тягнуть по рейці (рис. 1). На нього діють сила тяжіння
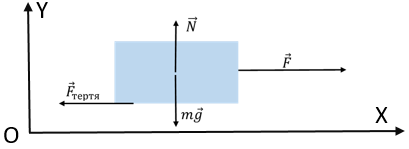
Рис. 1. Схема дії сил на брусок, що тягнуть по горизонтальній рейці
Другий закон Ньютона для бруска, що тягнуть по рейці, можна описати формулою
Оскільки брусок тягнуть рівномірно, то прискорення
Затим потрібно спроєктувати рівняння на осі
проєкція на вісь
проєкція на вісь
Тобто для осі
Величина сили тертя залежить від коефіцієнта тертя:
Тож
При цьому силу
Оскільки для тіла в стані спокою можна обчислити вагу
Тоді
Відповідь: 0,25.
ТЕМА: Механіка. Основи динаміки. Сили. Додавання сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з визначення рівнодійної кількох сил.
На кульку, що піднімається вгору в повітрі, діють три сили: сила Архімеда, що виштовхує її з товщі повітря вгору, сила тяжіння, яка притягує кульку до землі, і сила опору повітря, що заважає руху кульки (рис. 1). Оскільки сила Архімеда більша за значенням від сили тяжіння, кулька рухатиметься вгору, а сила опору повітря буде напрямлена вниз.
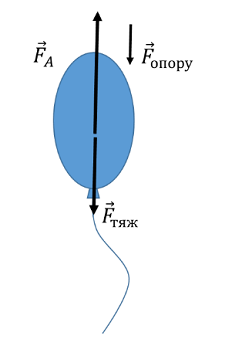
Рис. 1. Сили, що діють на кульку
Рівнодійна
Відповідь: A.
ТЕМА: Механіка. Основа динаміки. Додавання сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на визначення рівнодійної кількох сил.
Дано:
Знайти:
За умовою задачі схема дії сил на матеріальну точку така:
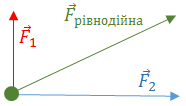
Для правильного розв’язання задачі потрібно визначити модуль рівнодійної сили, використавши теорему Піфагора й правило додавання векторів:
Відповідь: 5.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання вміння добирати вимірювальні прилади для проведення експериментів.
A. Оскільки період – це час, за який тіло робить одне повне коливання, то для його вимірювання використовують секундомір.
Б. Для визначення електрорушійної сили (ЕРС) і внутрішнього опору джерела потрібно скористатися законом Ома для повного кола. ЕРС в цьому разі є еквівалентом напруги в законі Ома для ділянки кола, тому її також вимірюють вольтметром.
В. Для визначення фокусної відстані й оптичної сили лінзи потрібно виміряти відстань від предмета до лінзи й від лінзи до зображення. Для цього використовують лінійку.
Г. Для визначення коефіцієнта корисної дії (ККД) похилої площини необхідно обчислити корисну роботу, яку розраховують як зміну потенціальної енергії початкового й кінцевого стану й витрачену роботу, що робчислюють за формулою
Д. Для вивчення теплового балансу під час змішування води різної температури потрібно зафіксувати початкові й кінцеву температури. Для цього використовують термометр.
Відповідь: 1Г, 2Б, 3А, 4Д.
ТЕМА: Механіка. Основи динаміки. Умови й види рівноваги.
Завдання скеровано на оцінювання розуміння поняття «рівновага».
Рівновага тіла – це збереження стану руху або стану спокою тіла з плином часу.
Тобто швидкості поступального й обертального рухів тіла в рівновазі залишаються незмінними.
Стан стійкої рівноваги – це стан, у якому за малих відхилень від положення рівноваги тіло довільно повертається в початкове положення.
Лише на рисунку Б зображено початкове положення кульки, у яке вона повертатиметься за будь-яких малих відхилень.
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Сили. Додавання сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на рух тіл під дією кількох сил.
Дано:
Знайти:
Корок у пляшці – нерухомий, тому можна зробити висновок, що рівнодійна сил, які діють на нього, дорівнює нулю. Оскільки масу корка не враховують, то дією сили тяжіння можна знехтувати. Тоді на корок діють лише сила атмосферного тиску
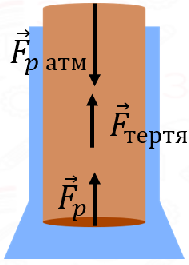
Рис. 1. Схематичне зображення сил, що діють на корок
Силу тиску можна знайти за формулою:
У випадку корка, який можна вважати циліндром, площею для розрахунку обох сил тиску можна вважати площу його основи. Сила тертя діє вздовж усієї площі контакту корка з пляшкою і протидіє його руху. Оскільки атмосферний тиск більший за тиск усередині пляшки, то й сила атмосферного тиску більша, а сила тертя діятиме в тому самому напрямку, що й сила тиску повітря в пляшці.
Тепер можна спроєктувати всі сили, що діють на корок, на одну пряму й записати другий закон Ньютона для корка:
Відповідь: 40.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона. Сила тертя.
Завдання скеровано на оцінювання розуміння впливу сили тертя в задачах на основі побутових прикладів.
Під час перетягування каната виграє той, хто може перетягнути стрічку посередині на свій бік. Чим більшою є сила тертя між учасником і підлогою, тим більшу силу треба прикласти, щоби зсунути його з місця. Тому для здобуття перемоги тягнути канат із більшою силою ніж опонент не достатньо, якщо сила тертя з боку підлоги в нього більша.
Сила тертя з боку каната важлива, але вона не визначає переможця, адже за дуже великої сили тертя між канатом й учасником він почне рухатися разом із канатом.
Маса учасників впливає лише на те, наскільки сила тяжіння діятиме на них. Притягування Землі може піти як на користь, так і на шкоду залежно від того в який бік нахилене тіло учасника.
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Система відліку. Швидкість.
Завдання скеровано на оцінювання розуміння понять швидкості світла й системи відліку.
Значення швидкості світла є сталим для будь-якої системи відліку незалежно від швидкості її руху.
Тому не залежно від того, яке тіло відліку вибрано (Земля, станція чи ракета), значення швидкості світла буде однаковим – 300 000 км/с.
Відповідь: A.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.
Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за збільшення температури і звужуються за її зменшення).
Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий вологою тканиною. Вода з тканини завжди випаровується, і швидкість випаровування залежить від вологості повітря навколо. Відповідно, для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.
Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд). На рисунку 1 зображено конструкцію такого приладу. Усередині анероїда є камера з гофрованою поверхнею (1), із якої відкачано повітря. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини кріпиться стрілка (2). Тому, коли кришка камери піднімається чи опускається, пружина деформується, і стрілка починає рухатись по шкалі (3).
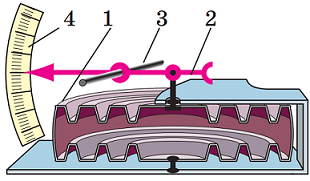
Рис. 1. Конструкція барометра-анероїда
Динамометр – це прилад для вимірювання сили. Зазвичай динамометр складається із пружини і шкали. Коли на кінець пружини діє сила, то за законом Гука пружина розтягується:
Тому, якщо відомий коефіцієнт жорсткості k пружини, то за значенням її видовження x можна визначити й силу, що його спричиняє.
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про рух тіла під дією кількох сил.
Сила, із якою тіло діє на опору чи підвіс – це вага
Сила тяжіння завжди діє в напрямку до центра Землі, тобто перпендикулярно до її поверхні. Тому, попри те, що тіло лежить на схилі під кутом до поверхі Землі, сила, із якою воно діятиме на опору, буде напрямлена вертикально вниз (рис. 1).
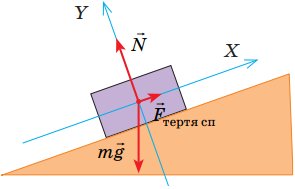
Рис. 1. Схема дії сил на тіло, що лежить на похилій поверхні
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Перший закон Ньютона. Механічна робота. Потужність.
Завдання скеровано на перевірку вміння розв'язувати комбіновані розрахункові задачі на закони Ньютона й механічну роботу, потужність.
Дано:
1. Знайти:
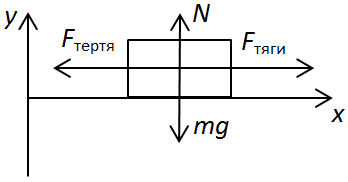
Спочатку треба записати перший закон Ньютона:
Після цього перейти до проєкцій:
за віссю
за віссю
Потужність
2. Знайти:
Робота
Відповідь: 1. 36. 2. 1,8.
ТЕМА: Механіка. Основи кінематики. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на перевірку знання законів кінематики й законів динаміки Ньютона, а також уміння розв'язувати комбіновані задачі, використовуючи поняття і закономірності з кількох розділів механіки.
Ураховуючи загальний вид рівняння руху
За II законом Ньютона
Відповідь: Б.
ТЕМА: Одиниці фізичних величин.
Завдання скеровано на перевірку вміння записувати одиниці фізичних величин через основні одиниці СІ.
1 Тесла (магнітна індукція)
Варто вибрати формулу, з якої можна виразити магнітну індукцію через величини, одиниці яких входять в СІ, або можуть бути легко вираженi через них. Для магнітної індукції можна використати вираз для сили Ампера:
Тоді можна записати рівність (1), використовуючи одиниці фізичних величин:
2 Генрі (індуктивність):
3 Ньютон (сила):
4 Джоуль (робота):
Відповідь: 1В, 2А, 3Д, 4Б.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.
Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за підвищення температури та звужуються за її зниження).
Динамометр – це прилад для вимірювання сили. Зазвичай складники динамометра – пружина та шкала. Коли на кінець пружини діє сила, то, за законом Гука, пружина розтягується.
Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд), усередині якого є вакуумна камера з гофрованою поверхнею. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини прикріплена стрілка. Тому, коли кришка камери піднімається чи опускається, пружина деформується і стрілка починає рухатися по шкалі.
Електрометр – це прилад для виявлення та вимірювання заряду. Його складники – металева куля, стержень і стрілки. Під дією електричного поля в стержні, стрілці й кулі відбувається перерозподіл зарядів. Оскільки вони з’єднані, то заряджаються однаково. Однойменно заряджені стрілка та стержень відштовхуються, тому рухома стрілка відхиляється.
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Додавання сил.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з визначення рівнодійної кількох сил.
За другим законом Ньютона рівнодійна всіх сил, що діють на тіло, пов’язана з його прискоренням формулою
Тож напрямок прискорення збігається з напрямком рівнодійної всіх сил.
Рівнодійну всіх зображених на рисунку сил можна визначити за методом паралелограма (методом графічного додавання векторів). Додавання трьох сил можна виконати покроково: спочатку додати сили
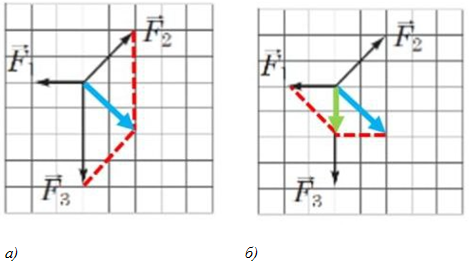
Рис. 1. Графічний спосіб визначення рівнодійної
Рівнодійна (позначена зеленим кольором на рис. 1, б), а отже й прискорення тіла спрямовані вниз.
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Другий і третій закон Ньютона.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням другого і третього законів Ньютона.
Дано:
Знайти:
Якщо поїзд рухався рівномірно по горизонтальній поверхні, то його прискорення в першому випадку дорівнювало нулю. Отже й рівнодійна всіх сил, що діють на цей потяг, також дорівнювала нулю:
Отже в початковому стані сила, що тягне вагони, дорівнювала силам, що протидіють рухові потяга (силі тертя, силі опору повітря, тощо).
Коли тягова сила збільшилась, то рівнодійна всіх сил, що діяли на потяг перестала дорівнювати 0 – сили, що тягнуть вагони перевищали сили, що протидіють їх руху.
Зважаючи на те, що в першому випадку тягові сили дорівнювали силам опору, можна обчислити рівнодійну після прискорення:
Тому можна обчислити прискорення:
Відповідь: 0,05.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання знання вимірювальних пристроїв і розуміння фізичних величин, для вимірювання яких їх використовують.
1. Фізична величина, що дорівнює відношенню шляху до часу – це швидкість:
Прилад, що вимірює швидкість – це спідометр.
2. Фізична величина, що дорівнює добутку густини, прискорення вільного падіння і висоти стовпчика рідини – це гідростатичний тиск (тиск нерухомого стовпчика рідини):
Прилад, що вимірює тиск рідини чи газу – це манометр.
3. Фізична величина, що дорівнює відношенню густини водяної пари до густини насиченої пари за певної температури й виражена у відсотках – це відносна вологість:
Прилад, що вимірює відносну вологість – це гігрометр.
4. Фізична величина, що дорівнює добутку маси на прискорення вільного падіння – це сила тяжіння:
Прилад, що вимірює силу – це динамометр.
Відповідь: 1В, 2А, 3Г, 4Б.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.
Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за збільшення температури і звужуються за її зменшення).
Психрометр – це прилад для вимірювання відносної вологості. Принцип його роботи такий: у корпусі приладу є два термометри. Кінець одного з них зазвичай обгорнутий у вологу тканину. Вода з тканини завжди випаровується, і швидкість випаровування залежить від того, яка вологість повітря навколо. Для вимірювання відносної вологості фіксують покази сухого й вологого термометрів і за допомогою спеціальних таблиць виконують необхідні розрахунки.
Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд), усередині якого є вакуумна камера з гофрованою поверхнею. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини прикріплено стрілку. Тому, коли кришка камери піднімається чи опускається, пружина деформується, а стрілка починає рухатися по шкалі.
Динамометр – це прилад для вимірювання сили. Зазвичай динамометр складається із пружини і шкали. Коли на кінець пружини діє сила, то за законом Гука пружина розтягується:
Тому, якщо відомий коефіцієнт жорсткості пружини, то за значенням її видовження можна визначити й силу, що його зумовлює.
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона.
Завдання скеровано на перевірку вміння розв’язувати задачі з динаміки з аналізом світлин експерименту.
За рисунком 1 легко визначити, що на лівій нитці блоку підчеплено п’ять тягарців із масою

Рис. 1. Сили, що діють на тягарці
1. Знайти:

Рис. 2. Сили, що діють на систему
Нерухомий блок – простий механізм, він не забезпечує виграшу ні в силі, ні у відстані, а лише змінює напрямок прикладання сили.
Оскільки сили
Запис другого закону Ньютона для тягарців із масою 5m і 3m відповідно:
Спроєктуймо рівняння на вертикальну вісь, спрямовану вниз. Для цього треба пригадати, що лівий вантаж рухається вниз, а правий – угору. Їхні прискорення мають такі самі напрямки:
Тож
Силу тяжіння можна розрахувати за формулою:
2. Знайти:
Маса одного тягарця дорівнює
З рівняння для другого закону Ньютона для вантажу масою
Відповідь: 1. 2,5. 2. 3,75.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух. Рівномірний рух по колу.
Завдання скеровано на перевірку розуміння зв’язку між силою, прискоренням і швидкістю руху тіла.
За другим законом Ньютона рівнодійна всіх сил, що діють на тіло, пов’язана з його прискоренням формулою
Тож напрямок прискорення збігається з напрямком дії сили.
1. Якщо сила весь час перпендикулярна до швидкості, то й прискорення перпендикулярне до неї. Прискорення, що перпендикулярне до швидкості, не змінює її модуля, але змінює її напрямок. Це відповідає рівномірному руху за криволінійною траєкторією, наприклад, руху по колу.
2. Якщо сила зберігає напрямок і величину незмінною, то й прискорення залишається незмінним. Оскільки напрямок швидкості відносно прискорення з умови невідомий, то визначити, збільшуватиметься чи зменшуватиметься модуль швидкості, неможливо. Тож це відповідає руху з постійним прискоренням.
3. Якщо напрямок сили, а отже й прискорення, збігається з напрямком швидкості, то модуль швидкості збільшується.
4. Якщо напрямок сили й прискорення протилежні до напрямку швидкості, то модуль швидкості зменшується.
Відповідь: 1В, 2Д, 3А, 4Г.
ТЕМА Механіка. Основи динаміки. Закони Ньютона.
Завдання скеровано на перевірку розуміння поняття інерціальної системи відліку та її складників.
Тіло відліку – це тіло, із яким в інерціальній системі відліку пов’язана система координат. Інерціальну систему відліку можна поєднати з тілом, що рухається без прискорення. В умові завдання єдиним тілом, яке рухається без прискорення, є шайба, що без тертя ковзає по льоду.
Відповідь: Г.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умови плавання тіл.
Завдання скеровано на перевірку розуміння умов плавання тіл і вміння математично описати їх.
У завданні тричі змінюються умови плавання дерев’яного бруска. Опишімо кожен із випадків.
1. На брусок діє сила тяжіння, яку врівноважує сила Архімеда:
2. Коли до бруска знизу прикріпили вантаж, то виштовхувальна сила діятиме і на занурену частину бруска, і на вантаж. Запишімо умову плавання бруска за цих умов:
3. Розгляньмо третій випадок, коли вантаж поклали на брусок зверху. Запишімо умову плавання:
Розв’яжімо систему трьох рівнянь:
Віднімімо від рівняння (2) рівняння (3):
Підставімо в рівняння (3) вираз замість
Розкриймо дужки й обчислімо
Відповідь: 15.
ТЕМА: Механічні коливання і хвилі. Коливання вантажу на пружині. Перетворення енергії під час гармонічних коливань.
Завдання скеровано на оцінку вміння розв’язувати комбіновані задачі, які передбачають обробку й аналіз результатів експерименту, зображених на рисунку, i використання законів збереження енергії в коливальному процесі.
Знайти:
З рисункa 1 можна визначити довжину гумки у двох крайніх положеннях коливання тягарця. У крайніх положеннях тягарець змінює напрямок руху на протилежний, а отже його швидкість
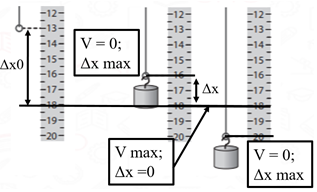
Рис. 1. Крайні положення тягарця
За цими значеннями можна обчислити амплітуду коливань:
Знаючи амплітуду коливань, можна визначити положення рівноваги – таке положення, у якому опиниться гумка під вагою тягарця, коли коливання повністю припиняться:
Під час коливань у положенні рівноваги швидкість найбільша, отже саме цю швидкість потрібно визначити.
Під час коливань зберігається повна механічна енергія системи
Кінетичну енергію можна визначити за формулою
Оскільки для гумової стрічки виконуваний закон Гука, можна обчислити потенціальну енергію за формулою, якою описують потенціальну енергію розтягнутої пружини:
Хоча повна механічна енергія системи зберігається, але значення кінетичної і потенціальної енергії постійно змінюється під час коливань.
У крайніх положеннях швидкість тягарця дорівнює нулю, а отже і його кінетична енергія теж. А от відхилення від положення рівноваги в цих положеннях найбільше, тому потенціальна енергія максимальна.
У положенні рівноваги все навпаки. Швидкість тягарця максимальна, а відхилення дорівнює нулю, отже кінетична енергія приймає найбільше значення, а потенціальна перетворюється на нуль.
Зважаючи на закон збереження енергії і спостереження, описані вище, можна записати таку рівність:
Тоді можна виразити максимальну швидкість:
Відношення
У стані спокою тягарець перебуватиме в положенні рівноваги. Тоді можна записати другий закон Ньютона:
Тоді
Після цього можна підставити отримане відношення у вираз для максимальної швидкості:
Відповідь: 28.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про рух тіла під дією кількох сил.
Дано:
Знайти:
На аеростат діють дві сили: сила тяжіння і сила Архімеда. Сила Архімеда не залежить від маси баласту, а силу тяжіння можна визначити за формулою
Тоді можна записати другий закон Ньютона для аеростата:
Сила тяжіння спрямована вниз, сила Архімеда – угору, до скидання балансу тіло аеростат опускається, тож прискорення також спрямоване вниз. Тоді векторне рівняння можна спроєктувати на вісь
Після скидання баласту проєкція другого закону Ньютона матиме інший вигляд:
Тоді з рівняння для руху аеростата до скидання баласту можна виразити силу Архімеда:
Тож:
Тоді маса скинутого баласту така:
Відповідь: 10.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота. Закон збереження енергії в механічних процесах.
Завдання скеровано на перевірку вміння застосовувати закон збереження механічної енергії під час розв’язування задач про рух тіла під дією кількох сил.
Якщо тілу надати певної швидкості, то воно матиме кінетичну енергію
Отже,
Відповідь: 6.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку вміння визначати напрямок рівнодійної сил і напрямок швидкості руху тіл під час різних видів руху.
Розгляньмо приклад A. Коли автобус гальмує, то рівнодійна

Коли футбольний м’яч, спрямований воротарем на іншу половину футбольного поля, піднімається, то рівнодійна
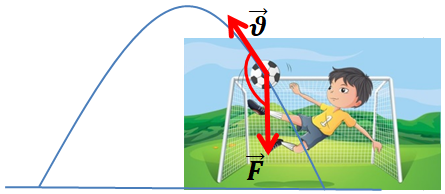
Напрямок рівнодійної
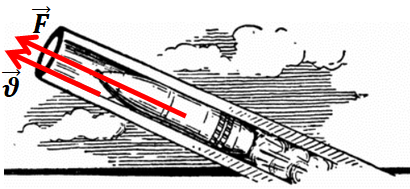
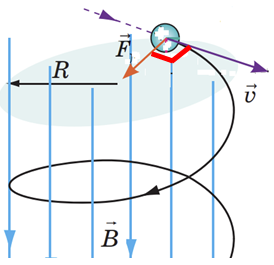
Коли електрон улітає в магнітне поле під певним кутом до ліній магнітної індукції, то траєкторією його руху є гвинтова лінія. Рівнодійна
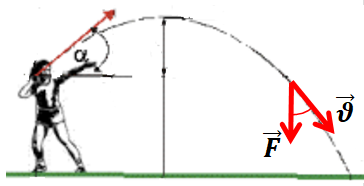
У прикладі з падінням камінця, кинутого під кутом до горизонту, рівнодійна
Відповідь: 1А, 2В, 3Г, 4Д.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на перевірку вміння застосовувати другий закон Ньютона.
Другий закон Ньютона: прискорення
Виразімо з формули шукану величину масу й запишімо її у проєкціях на горизонтальну вісь
Визначмо прискорення як відношення зміни швидкості руху тіла до інтервалу часу, за який ця зміна відбулася (теж у проєкціях на вісь
Відповідь: A.
ТЕМА: Механіка. Основи кінематики. Система відліку.
Завдання скеровано на перевірку знання поняття «система відліку» і розуміння відносності механічного руху.
Механічний рух ‒ зміна із часом положення тіла (або частин тіла) у просторі відносно інших тіл. Доки не вибрано систему відліку, неможливо стверджувати, рухається тіло чи перебуває в стані спокою.
Якщо людина підніматиметься по ескалатору зі швидкістю
Якщо людина стоятиме на ескалаторі, то відносно Землі вона рухатиметься з тією самою швидкістю, що й ескалатор, тобто
Якщо ж людина спускатиметься по ескалатору з такою самою швидкістю, із якою він піднімається, то відносно ескалатора людина рухатиметься зі швидкістю
Відповідь: Б.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна і його максимальне значення.
Завдання скеровано на перевірку розуміння принципу дії теплових двигунів і вміння визначати різними способами коефіцієнт корисної дії та фізичні величини, які на нього впливають.
Коефіцієнт корисної дії (ККД)
Корисна робота двигуна полягає в подоланні сили опору руху візка
Також коефіцієнт корисної дії такого двигуна можна визначити за формулою
Прирівняймо ці два вирази для обчислення коефіцієнта корисної дії:
Виразімо звідси модуль швидкості руху візка й обчислімо його:
Відповідь: 2.
ТЕМА: Механіка. Основи динаміки. Сила тертя.
Завдання скеровано на перевірку вміння визначати сили тертя і рівнодійну сил, прикладених до тіл.
Щоб натягнути нитку, якою зв’язано бруски, треба зрушити з місця другий брусок, подолати максимальну силу тертя спокою, протилежно напрямлену до прикладеної горизонтальної сили
Обчислімо силу натягу нитки
Перевірімо, чи рухатиметься за таких умов перший брусок і, відповідно, уся система тіл. Для цього обчислімо максимальну силу тертя спокою, яка мала б діяти на перший брусок, якби він зрушив із місця:
Нитку натягнуто із силою
Відповідь: 2.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з визначення маси тіла й виштовхувальної сили.
1. На рисунку 1 зображено тіло в повітрі, підвішене до динамометра. Динамометр показує значення ваги тіла в повітрі
З формули для визначення сили тяжіння визначмо масу
Відповідно
Відповідь: 3.
2. На рисунку 2 динамометр показує вагу тіла в рідині:
На тіло, занурене в рідину, діє виштовхувальна сила (сила Архімеда). У цій ситуації виштовхувальна сила дорівнюватиме різниці ваги тіла в повітрі й ваги тіла в рідині:
Відповідь: 10.
Відповідь: 1. 3. 2. 10.
ТЕМА: Механіка. Основи динаміки. Інерціальні системи відліку.
Завдання скеровано на перевірку розуміння руху тіла за інерцією і вміння читати графіки.
Тіло, на яке не діють інші тіла й поля, називають ізольованим (вільним), а рух ізольованого тіла – рухом за інерцією. У реальності практично неможливо створити умови, коли на тіло нічого не діє, тому рухом за інерцією називають рівномірний прямолінійний рух за відсутності або скомпенсованості дії на тіло інших тіл і полів.
Єдиний графік, який відповідає прямолінійному рівномірному руху ‒ це графік залежності координати
На рисунку Б зображено графік залежності прискорення
На рисунках В і Г зображено графіки прямолінійного рівноприскореного руху: графік залежності швидкості
Отже, правильна відповідь ‒ графік на рисунку А.
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги тіла.
Завдання скеровано на перевірку розуміння шарнірного з’єднання стержнів і скомпенсованості сил, уміння позначати сили, що діють, шукати їхні проєкції.
За умовою стержні невагомі, один на одного не діють.
У точці
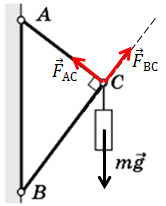
Побудуймо рівнодійну цих сил пружності. Вона буде компенсувати дію сили тяжіння.
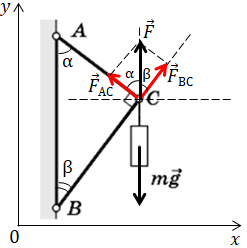
За другим законом Ньютона
Спроєктуймо вектори сил на вісь
Визначімо з прямокутного трикутника
Розв’яжімо систему рівнянь:
1) З другого рівняння системи визначімо силу пружності в стержні
Відповідь: 15.
2) Підставімо в перше рівняння системи значення сили пружності
Відповідь: 20.
Відповідь: 1. 15. 2. 20.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на перевірку другого закону Ньютона.
Відповідно до другого закону Ньютона тіло масою
Отже, під дією сили тіло буде рухатися рівноприскорено, із прискоренням
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Рух тіл під дією кількох сил.
Завдання скеровано на перевірку вміння розв’язувати задачі на рух тіла під дією кількох сил.
Запишімо рівняння другого закону Ньютона у векторному вигляді та в проєкціях на осі координат
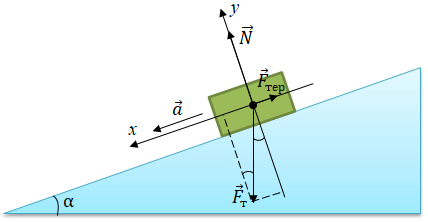
де
Виразімо силу нормальної реакції опори з рівняння (2) і підставимо в рівняння (1):
Обидві частини отриманого рівняння скоротімо на масу
Виразімо й обчислімо коефіцієнт тертя ковзання:
За умовою
Відповідно
Відповідь: 0,5.
ТЕМА: Механіка. Основи динаміки. Рух тіл під дією кількох сил.
Завдання скеровано на перевірку знання і розуміння дії простого механізму ‒ нерухомого блоку, і вміння аналітично описувати рух зв’язаних тіл за допомогою другого закону динаміки Ньютона.
Схематично зобразімо на рисунку сили тяжіння
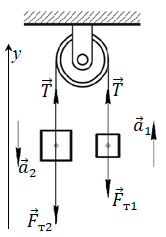
Запишімо для обох предметів другий закон динаміки Ньютона у векторному вигляді:
Запишімо систему рівнянь у проєкціях на вісь
Пояснімо, чому за модулем
Відповідно до умови кінематичного зв’язку, що випливає з нерозтяжності нитки, за будь-який інтервал часу ліва ділянка нитки подовжується саме на стільки, на скільки скорочується права. Таким чином, переміщення обох шматків жерсті весь час однакові за модулем. Звідси випливає, що в шматків однакові й модулі швидкостей, і модулі прискорень, тому
Якщо масами нитки та блока, а також тертям в осі блока можна знехтувати (а це можна зробити, тому що в умові завдання даних про це немає), то сила натягу нитки
Узявши до уваги попередні пояснення
і віднявши від першого рівняння системи друге, дістанемо:
В умові є інформація про матеріал і розміри шматків жерсті, тож виразімо їхні маси через густину
Шматки жерсті виготовлено з однакового матеріалу, тому
Товщина
Отже,
Підставимо отримані вирази для мас у формулу для прискорення:
Відповідь: Г.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота. Потенціальна енергія.
Завдання скеровано на перевірку розуміння закону збереження механічної енергії, уміння описати аналітично рух тіла під дією кількох сил.
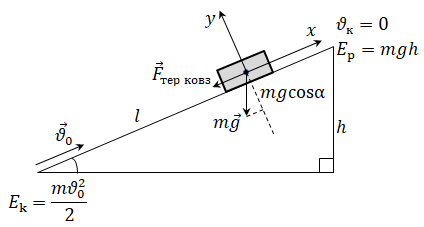
Перед початком руху тіло масою
Отже,
Ковзаючи по похилій площині довжиною
Сила тертя ковзання напрямлена проти руху тіла, а переміщається воно вздовж похилої площини, то ж зазначений кут становитиме
Схематично зобразимо на похилій площині й позначимо всі сили, що діють на тіло. Сила тяжіння
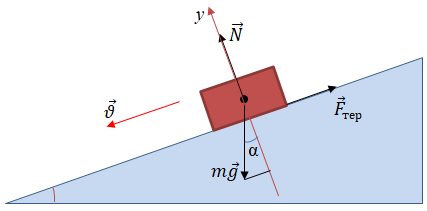
Запишімо другий закон Ньютона у векторній формі:
Сила тертя ковзання
Для того, щоб визначити
Отже,
Виразимо модуль переміщення тіла (довжину похилої площини) через дані в умові завдання:
Отже, остаточна формула для визначення роботи сили тертя ковзання набуває такого вигляду:
Відповідь: 2.
ТЕМА: Механіка. Закони збереження в механіці. Потужність.
Завдання скеровано на перевірку уміння визначати потужність.
Потужність
Робота рівнодійної всіх сил, які діють на тіло, дорівнює зміні кінетичної енергії
У результаті дії сил опору автомобіль зупиниться, тобто через час
Тобто
За умовою завдання автомобіль змінює швидкість, сповільнюється. Тому середня потужність двигуна ‒ це середнє арифметичне потужностей у певні моменти часу (так би мовити миттєвих потужностей), що дорівнюють добутку модуля сили тяги двигуна на модуль його миттєвої швидкості.
Оскільки всю енергію двигуна буде витрачено на подолання сил опору, то середня потужність двигуна дорівнюватиме середній потужності сил опору.
Отже, визначмо середню потужність сил опору:
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Система відліку.
Завдання скеровано на перевірку розуміння поняття системи відліку й відносності механічного руху.
Механічний рух ‒ зміна із часом положення тіла (або частин тіла) в просторі відносно інших тіл. Доки не вибрано систему відліку, неможливо стверджувати, рухається тіло чи перебуває в стані спокою.
Якщо людина підійматиметься ескалатором зі швидкістю
Якщо людина стоятиме нерухомо на ескалаторі, то відносно Землі вона рухатиметься з тією самою швидкістю, що й ескалатор, тобто
Якщо ж людина спускатиметься ескалатором із такою ж швидкістю, з якою він підійматиметься, то відносно ескалатора людина рухатиметься зі швидкістю
Відповідь: A.
Тема: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на перевірку розуміння другого закону Ньютона й уміння читати кінематичні рівняння.
Відповідно до другого закону Ньютона тіло масою
Для того щоб визначити модуль рівнодійної всіх сил, які діють на автомобіль, треба масу помножити на модуль прискорення:
Маса відома з умови. А прискорення визначімо з рівняння руху автомобіля, що наведене в умові.
Запишімо рівняння руху автомобіля в загальному вигляді:
Значення прискорення ‒ це множник біля
Обчислімо модуль рівнодійної:
Відповідь: Б.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умова плавання тіл.
Завдання скеровано на перевірку знання і розуміння повітроплавання тіл, уміння описувати його за допомогою формул.
Позначмо всі сили, що діють на систему тіл у повітрі: повітряна куля з гелієм ‒ вантаж. Це сила тяжіння

За другим законом Ньютона векторна сума всіх сил дорівнюватиме нулю, оскільки в умові зазначено, що система не рухається:
Запишімо це рівняння в проєкціях:
Розпишімо силу Архімеда:
Тобто
Запишімо рівняння Менделєєва ‒ Клапейрона для повітря:
Звідси визначімо густину повітря:
Підставімо вирази для густини повітря і для об’єму гелію у формулу виштовхувальної сили:
Повернімося до запису другого закону Ньютона в проєкціях і визначімо шукану величину ‒ масу гелію:
Відповідь: 100.
ТЕМА: Механіка. Основи динаміки. Рух тіл під дією кількох сил.
Завдання скеровано на перевірку розуміння того, які сили діють на тіло, уміння описати стан тіла за допомогою другого закону Ньютона.
Зображена система зв’язаних брусків не рухатиметься, якщо сили натягу нитки на обох її кінцях, створені кожним бруском, однакові.
Зобразімо на рисунку сили, що діють уздовж поверхонь похилих площин і які впливатимуть на стан системи брусків. Це проєкції сил тяжіння
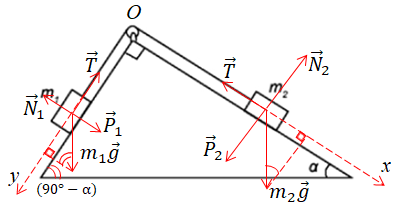
Запишімо другий закон Ньютона для обох брусків у проєкціях на осі вздовж поверхонь похилих площин:
Прирівняймо вирази для сили натягу нитки й визначімо співвідношення мас:
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Додавання сил. Другий закон Ньютона.
Завдання скеровано на перевірку знання і розуміння рівнодійної сил, прикладених до тіла, і вміння її знаходити за допомогою геометричної побудови.
Здебільшого (як в умові) на тіло діють кілька сил. Якщо тіло можна вважати матеріальною точкою, то всі ці сили можна замінити однією ‒ рівнодійною. Рівнодійна дорівнює геометричній сумі сил, які діють на тіло:
Суму двох векторів визначають за правилом паралелограма або за правилом трикутника.
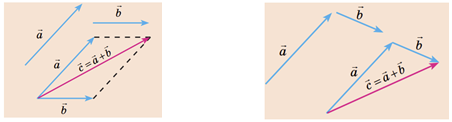
Візьмімо, наприклад, пару векторів
Діагональ, яка виходить із точки, у якій збігаються початки вибраних векторів, буде їхньою рівнодійною
З рисунка зрозуміло, що вектор сили
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку знання і розуміння рівнянь гармонічних коливань.
Коливання, під час яких координата
де
Коли координата тіла змінюється за гармонічним законом (за законом косинуса або синуса), швидкість і прискорення руху тіла теж змінюються гармонічно: перша похідна координати тіла за часом
В умові завдання маємо гармонічне рівняння прискорення руху тіла. Підставивши в це рівняння значення часу
Проєкцію сили на вісь
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
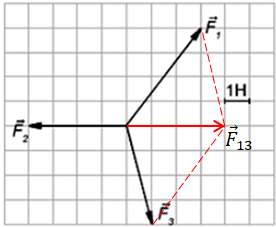
Завдання скеровано на перевірку знання і розуміння поняття рівнодійної сил, а також вміння графічно пов’язати динаміку й кінематику процесу.
Сформулюймо другий закон Ньютона: прискорення
Здебільшого на тіло діють кілька сил. Якщо тіло можна вважати матеріальною точкою, то всі ці сили можна замінити однією – рівнодійною. Рівнодійна дорівнює геометричній сумі сил, які діють на тіло:
Якщо сили, що діють на тіло, скомпенсовано, тобто рівнодійна дорівнює нулю
Графіком проєкції швидкості
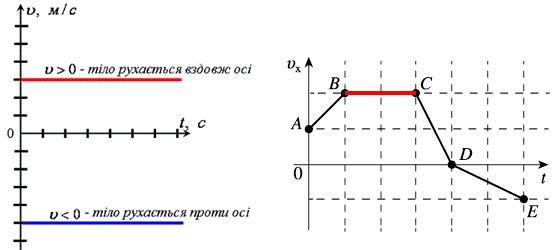
Відповідь: Б.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг рідин. Сила поверхневого натягу.
Завдання скеровано на перевірку знання і розуміння дії сили поверхневого натягу і вміння застосовувати другий закон Ньютона у відповідній ситуації.
Зобразимо на рисунку всі сили, що діють на дротинку: вертикально вниз ‒ сила тяжіння
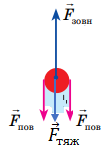
Щоб можна було відірвати дротинку від поверхні рідини, зовнішня сила, напрямлена вгору, повинна дорівнювати сумі сил, що напрямлені вертикально вниз:
Запишімо вирази для зазначених сил і визначімо шукану величину ‒ поверхневий натяг рідини
де
Відповідь: 45.
ТЕМА: Механіка. Основи динаміки. Інерціальні системи відліку.
Завдання скеровано на перевірку знання і розуміння поняття інерціальних систем відліку, а також фізичних величин у цих системах.
Інерціальною системою відліку називають систему відліку, відносно якої спостерігають явище інерції.
Інерцією називають явище збереження тілом стану спокою або рівномірного прямолінійного руху за умови, що на нього не діють інші тіла й поля або їхні дії скомпенсовані.
Систему відліку утворюють тіло відліку, пов’язана з ним система координат і прилад для відліку часу.
Швидкість руху досліджуваного тіла, його переміщення і напрямок руху залежатимуть від того, що буде вибрано за тіло відліку, з якою сталою швидкістю воно рухатиметься, як будуть зорієнтовані осі координат. Наприклад, якщо розглядати рух автомобіля в потоці відносно інших машин, то його швидкість може дорівнювати нулю, а відносно дерева на тротуарі автомобіль рухатиметься з певною швидкістю. Або якщо змінимо напрямок осі на протилежний, то напрямок руху автомобіля відносно до напрямку осі теж зміниться на зворотний.
Натомість прискорення залишиться незмінною величиною в будь-якій інерціальній системі відліку. Зміна швидкості руху тіла буде однаковою відносно систем відліку, що зберігають стан спокою або рухаються з певною сталою швидкістю.
Відповідь: Б.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умова плавання тіл.
Завдання скеровано на перевірку знання і розуміння повітроплавання тіл, уміння описувати його за допомогою формул.
Позначмо всі сили, що діють на систему тіл у повітрі: повітряна куля з газом ‒ вантаж. Це сила тяжіння
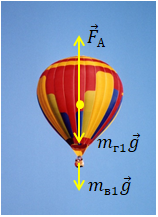
За другим законом Ньютона векторна сума всіх сил дорівнюватиме нулю, оскільки в умові не зазначено, що повітряна куля разом з вантажем піднімається вгору, отже, зупинимося на крайньому випадку, коли система не рухається ‒ куля просто утримує вантаж на певній висоті:
Запишімо це рівняння в проєкціях:
Розпишімо силу Архімеда:
Підставімо вираз для виштовхувальної сили в рівняння другого закону Ньютона:
‒ до нагрівання газу в кулі:
Урахуємо співвідношення густин повітря і газу:
‒ до нагрівання:
Визначимо відношення мас вантажу після і до нагрівання:
Отже, після нагрівання газу, яким заповнена повітряна куля, допустима маса вантажу, який зможе підняти куля, збільшиться в
Відповідь: 1,1.