Розділ: Коливання та хвилі. Оптика
Тема: Електромагнітні коливання та хвилі
Кількість завдань: 84
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на перевірку розуміння і вміння застосувати формулу Томсона до різних електричних схем з різними з’єднаннями пристроїв.
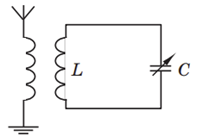
Період \(T\) вільних електромагнітних коливань у коливальному контурі визначаємо за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора (батареї конденсаторів).
Запишімо формулу для обчислення періоду коливань, коли ключ \(K\) розімкнутий, і коли його замкнули.
Коли ключ розімкнутий, то струм проходитиме лише через конденсатор з електроємністю \(C_1\) і котушку: $$ T_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1}. $$
Коли ж ключ замкнути, то струм піде і через конденсатор з електроємністю \(C_2,\) і через конденсатор з електроємністю \(C_3.\) У цьому разі треба визначити загальну електроємність \(C_\text{заг}\) батареї конденсаторів, що з’єднані на поданій в умові схемі паралельно:
Формула для періоду коливань матиме вигляд: $$ T_2=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_\text{заг}}. $$
Запишімо відношення періодів коливань для визначення, у скільки разів збільшився період коливань після того, як ключ замкнули:
\(T_2=3T_1\) ‒ після замикання ключа період коливань збільшився в \(3\) рази.
Відповідь: 3.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку розуміння особливостей роботи навантаженого трансформатора й співвідношення величин, якими описують його роботу.
Якщо вторинну обмотку трансформатора замкнути на навантаження (підімкнути споживача ‒ наприклад, лампу), то в обмотці виникне електричний струм (див. рисунок).
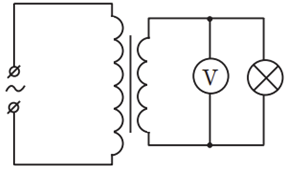
Цей струм спричинить зменшення магнітного потоку в осерді і, як наслідок, зменшення ЕРС (електрорушійної сили) самоіндукції в первинній обмотці. Унаслідок цього сила струму в первинній обмотці збільшиться і магнітний потік зросте до попереднього значення. Що більшими є сила струму у вторинній обмотці й потужність, яку трансформатор віддає споживачеві, то більшими є струм у первинній обмотці й потужність, яка надходить у трансформатор від джерела.
Під час роботи навантаженого трансформатора для відповідних значень напруги і сили струму справджується приблизна рівність: $$ \frac{U_1}{U_2}\approx\frac{I_2}{I_1}. $$
Це означає, що в підвищувальному трансформаторі сила струму більша в первинній обмотці \((U_1\lt U_2\Rightarrow I_1\gt I_2),\) а в понижувальному трансформаторі сила струму більша у вторинній обмотці \((U_1\gt U_2\Rightarrow I_1\lt I_2).\)
Якщо трансформатор ідеальний (утрати енергії дорівнюють нулю), то в скільки разів він збільшує напругу, у стільки ж разів він зменшує силу струму, і навпаки.
За умовою трансформатор знижувальний ‒ у вторинній обмотці менше витків, ніж у первинній, отже, правильними є співвідношення \(U_1\gt U_2,\ I_1\lt I_2.\)
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку знання і розуміння співвідношень між фізичними величинами, що характеризують трансформатор.
У режимі холостого ходу трансформатора (без навантаження, тобто вторинна обмотка розімкнена, до неї не підключено споживача) справджується рівність: $$ \frac{U_1}{U_2}=\frac{N_1}{N_2}, $$ де \(U_1\) ‒ напруга на первинній обмотці і \(N_1\) ‒ кількість витків у первинній обмотці, \(U_2\) ‒ напруга на вторинній обмотці і \(N_2\) ‒ кількість витків у вторинній обмотці.
Із цієї рівності визначимо напругу на вторинній обмотці:
\begin{gather*} U_2=\frac{U_1\cdot N_2}{N_1},\\[6pt] U_2=\frac{220\ \text{В}\cdot 2000}{500}=880\ \text{В}. \end{gather*}Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона. Електромагнітні хвилі та швидкість поширення їх. Електродинаміка. Основи електростатики. З’єднання конденсаторів.
Завдання скеровано на перевірку розуміння принципу роботи коливального контуру.
Радіохвилі ‒ це електромагнітні хвилі, які поширюються із швидкістю світла \(c.\)
Довжину хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) визначмо за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=cT, $$ де \(T\) ‒ період власних електромагнітних коливань у коливальному контурі. Його можна визначити за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки контуру, \(C\) ‒ електроємність конденсатора контуру.
Отже, довжину хвилі, на яку налаштовано радіоприймач, обчислімо за формулою: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_1=c\cdot 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1}. $$
Після приєднання паралельно до конденсатора ще одного, утричі більшої ємності, загальна електроємність дорівнюватиме: \begin{gather*} C_2=C_1+3C_1=4C_1, \end{gather*} бо за паралельного з’єднання конденсаторів їхні електроємності додають одну до одної.
Тепер радіоприймач буде налаштований на довжину хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2=c\cdot 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{L4C_1}. $$
Поділімо ліві і праві частини формул для довжин хвиль:
\begin{gather*} \frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_1}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2}=\frac{c\cdot 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1}}{c\cdot 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{L4C_1}}=\sqrt{\frac 14}=\frac 12,\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2=2\cdot \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_1=2\cdot 4\ \text{м}=8\ \text{м}. \end{gather*}Відповідь: 8.
ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру.
Дано:
\(W_{\text{конденсатора}\ max}=60\ \text{мДж}\)
\(W_\text{конденсатора}=2W_\text{котушки}\)
Знайти:
\(W_\text{конденсатора}(\text{мДж})\ -\ ?\)
У коливальному контурі під час незгасних коливань енергія переходить від конденсатора до котушки. Повна енергія системи є сталою, її визначають за формулою $$ W=W_\text{конденсатора}+W_\text{котушки} $$
Енергія конденсатора визначають за формулою $$ W_\text{конденсатора}=\frac{q^2}{2C}, $$ де \(q\) – заряд на обкладинках конденсатора, а \(C\) – ємність конденсатора.
Енергію котушки можна визначити за формулою $$ W_\text{котушки}=\frac{LI^2}{2}, $$ де \(L\) – індуктивність котушки, \(I\) – сила струму в ній.
Максимальною енергія конденсатора буде в момент, коли він повністю заряджений. Цієї миті в котушці немає струму, тож її енергія дорівнює нулю.
Оскільки енергія в коливальному контурі за незгасних коливань зберігається, то $$ W=W_{\text{конденсатора}\ max} $$
Тоді для моменту, коли енергія електричного поля вдвічі більша за енергію магнітного поля котушки
Відповідь: 40.
ТЕМА: Оптика. Оптика. Світло як електромагнітна хвиля.
Завдання скеровано на перевірку розуміння принципів поширення світла.
Природне світло утворене багатьма хвилями, випроміненими різними атомами. Через це в пучку природного світла є безліч напрямків коливання вектора напруженості електричного поля.
Унаслідок поляризації в пучку світла залишаються тільки хвилі певного напрямку (або напрямків).
Для поляризації використовують спеціальні фільтри – поляроїди (або поляризатори).

Рис. 1. Принцип роботи поляризатора
Поляризатор (рис. 1) працює як щілина, яка пропускає коливання, здійснювані лише в певному напрямку. Якби електромагнітні хвилі були поздовжніми, то поляризатор не вносив би ніяких змін, але зміни інтенсивності зафіксовано експериментально (адже значну частину променів відбиває поляризатор). Тому світло може бути лише поперечною хвилею.
Відповідь: Б.
ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру.
Коливальний контур – це фізичний пристрій, який складається з послідовно з’єднаних конденсатора й котушки індуктивності (рис. 1).
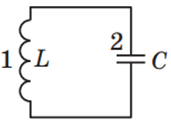
Рис. 1. Електрична схема коливального контуру:
1 – котушка індуктивності, 2 – конденсатор
В ідеальному коливальному контурі вся енергія під час коливань перетікає від конденсатора до котушки без утрат: $$ W_\text{конденсатора}=\frac{CU^2}{2}, $$ де \(U\) – напруга на обкладинках конденсатора, а \(C\) – його ємність.
За умовою (рис. 2) спостереження розпочато тоді, коли напруга на конденсаторі максимальна. У цей момент енергія конденсатора також буде максимальною.
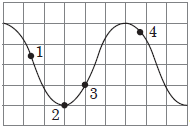
Рис. 2. Показники осцилографа
Під час коливань у контурі енергія повністю зарядженого конденсатора перетікатиме в енергію котушки, яку можна визначити за формулою: $$ W_\text{котушки}=\frac{LI^2}{2}, $$ де \(L\) – індуктивність котушки, \(I\) – сила струму в ній.
У контурі електрони, що накопичилися на одній з обкладинок конденсатора, рухатимуться в напрямку до іншої його обкладинки, утворюючи струм у колі. У результаті цього конденсатор почне розряджатися, напруга на його обкладинках зменшується, а отже зменшуватиметься і його енергія.
У котушці ж сила струму поступово збільшуватиметься, а разом із нею збільшуватиметься й енергія магнітного поля, яке вона створює. Коли конденсатор розрядиться повністю, струм у котушці стане максимальним.
Після того, як конденсатор повністю розрядиться, електрони продовжать свій рух, адже просто зупинитися вони не можуть. Тож тепер на вже нейтральну обкладинку конденсатора починають потрапляти електрони. У результаті цього вона заряджається, а струм у котушці поступово зменшується.
Унаслідок цього процесу заряд з однієї обкладинки конденсатора опиниться на іншій обкладинці. Тож тепер конденсатор заряджений протилежно до початкового стану, і напруга на ньому за модулем дорівнює початковій напрузі, але має протилежний знак (точка 2 на рисунку 2).
Отже і в початковій точці, і в точці 2 (рис. 2) енергія конденсатора максимальна, а енергія котушки дорівнює нулю. Енергія конденсатора дорівнює нулю тоді (енергія котушки максимальна), коли напруга на конденсаторі дорівнює нулю. На рисунку, наведеному в умові, цей стан відповідає лінії посередині, як це зображено на рисунку 3:
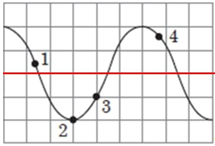
Рис. 3. Нульовий рівень напруги на конденсаторі
Що ближче точка до нульового рівня по вертикалі, то менша напруга на конденсаторі за модулем, і то більша енергія котушки. Тож у точці 1 енергія котушки буде найбільшою з усіх відмічених точок.
Відповідь: A.
ТЕМА: Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на перевірку вміння за графіком аналізувати коливання за допомогою формули Томсона.
Дано:
\(L=50\ \text{мГн}\)
1. Знайти:
\(T\ (\text{мс})\ -\ ?\)
Період коливань сили струму в контурі можна визначити за графіком. За один період система повертається в те саме положення, у якому вона перебувала. У разі залежності сили струму й від часу \(t\) система повертається у початкове положення (\(i = 0\) і продовжує спадання) за \(4\ \text{мс}\). Тому \(T=4\ \text{мс}\).
2. Знайти:
\(C\ (\text{мкФ})\ -\ ?\)
Період коливання коливального контуру пов’язаний з електроємністю конденсатора й індуктивністю котушки формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.
З неї можемо визначити вираз для електроємності:
Відповідь: 1. 4. 2. 8.
ТЕМА: Електромагнітні коливання і хвилі. Електромагнітні хвилі.
Завдання скеровано на перевірку розуміння поняття електромагнітної хвилі.
Для поширення електромагнітних хвиль не потрібне пружне середовище. В іншому разі випромінювання від Сонця не могло би поширюватися крізь космос і досягати Землі.
Відповідь: Б.
ТЕМА: Електромагнітні коливання і хвилі. Властивості електромагнітного випромінювання різних діапазонів. Радіолокація.
Завдання скеровано на перевірку розуміння принципів радіолокації й уміння розв’язувати відповідні розрахункові задачі.
Дано:
\(t=800\ \text{с}\)
\(v=3\cdot 10^8\ \text{м/с}\)
Знайти:
\(s\ -\ ?\)
Радіолокатори посилають короткі імпульси в напрямку, у якому проводять дослідження. Радіохвилі відбиваються від об’єктів, які трапляються на їхньому шляху, і повертаються до локатора. Локатор фіксує час, за який хвиля повернулася, а отже подолала дві відстані до об’єкта (від локатора до об’єкта й від об’єкта знову до локатора).
Тому відстань до об’єкта можна розрахувати за формулою
де \(v\) – швидкість поширення електромагнітних хвиль у середовищі, у якому проводили дослідження.
Відповідь: 120.
ТЕМА: Електромагнітні коливання і хвилі. Власна частота й період електромагнітних коливань. Формула Томсона. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).
Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі на використання формули Томсона й зв’язок між періодом і частотою електромагнітних коливань.
Дано:
\(C_1=26\ \text{нФ}\)
\(L_1=16\ \text{мГн}\)
\(C_2=24\ \text{нФ}\)
\(v_1=v_2\)
Знайти:
\(L_2\ (\text{мГн})\ -\ ?\)
Період коливань \(T\) пов’язаний із їхньою частотою ν формулою $$ T=\frac 1v. $$
Тож, якщо частоти двох коливальних контурів однакові, то однакові і їхні періоди коливань.
Період електромагнітних коливань в електричному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.
Оскільки періоди коливань для двох контурів однакові, \begin{gather*} 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{L_1C_1}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{L_2C_2};\\[7pt] L_1C_1=L_2C_2. \end{gather*}
Тоді можна визначити індуктивність котушки у другому контурі:
Відповідь: 24.
ТЕМА: Електромагнітні коливання і хвилі. Власна частота та період електромагнітних коливань. Формула Томсона. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).
Завдання скеровано на оцінювання вміння розв’язувати комбіновані задачі з використанням формули Томсона й на зв’язок між періодом, швидкістю поширення і довжиною хвилі.
Дано:
\(L=25\ \text{мкГн}\)
\(C=3600\ \text{пФ}\)
\(c=3\cdot 10^8\ \text{м/с}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}=3,1\)
Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\ (\text{м})-?\)
За ємністю конденсатора й індуктивністю котушки коливального контуру можна визначити період \(T\) коливань, які виникають під час роботи конденсатора: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}. $$
Період коливань – це час, за який коливання повністю повторюється.
Довжина хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) – це відстань між двома найближчими точками, які коливаються синхронно.
Тобто за один період частинка переміститься на довжину хвилі, тому можна записати таке співвідношення для цих величин: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=Tv, $$ де \(v\) – швидкість поширення хвилі.
Електромагнітні хвилі поширюються зі швидкістю світла, тому можемо уточнити цей вираз:
Відповідь: 558.
ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на оцінювання вміння аналізувати рівняння і графік гармонічних коливань, визначати основні фізичні величини, пов’язані з ними.
На рисунку зображено графік гармонічних коливань величини електрорушійної сили (ЕРС) залежно від часу.
Загальний вигляд рівняння гармонічних коливань такий: \begin{gather*} x=A\mathrm{cos}(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0)\\[7pt] \text{або}\ x=A\mathrm{sin}(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0), \end{gather*} де \(x\) – координата, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\) – циклічна частота коливань, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0\) – початкова фаза коливань, \(t\) – час.
Обидва варіанти цього рівняння можуть описувати будь-які гармонічні коливання, і єдине, що зміниться внаслідок переходу від рівняння із функцією синус до рівняння з функцією косинус, – це початкова фаза коливань.
Початкова фаза коливань – фаза коливань у момент початку відліку часу.
На рисунку до завдання в точці \(t = 0\) – відхилення від положення рівновагидорівнює 0. Таку криву в загальному випадку описують рівняннями \begin{gather*} x=A\mathrm{sin}(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0)\\[7pt] \text{або}\ x=A\mathrm{cos}(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}), \end{gather*} де \(\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}\) – початкова фаза.
Амплітуда коливань – це максимальне відхилення від положення рівноваги. Його можна визначити за рисунком – це відстань від осі \(x\) (рівня рівноваги) до максимуму або мінімуму синусоїди. \(A = 40\ \text{B}\).
Циклічну частоту \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\) можна визначити з рівності \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{2\pi}}{T}\), де \(T\) – період коливань.
Період коливань – це час, за який коливання повністю повторюється.
Можна визначити період коливань за рисунком. Це відстань між двома максимумами синусоїди: $$ T = 0,5\ \text{c} - 0,1\ \text{c}=0,4\ \text{c}. $$ Тоді \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{0,4}=5\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\).
Далі потрібно підставити всі визначені величини в рівняння гармонічних коливань: $$ x=40\mathrm{sin}(5\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}t)\ \text{або}\ x=40\mathrm{cos}(5\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}t+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}). $$
Відповідь: Б.
ТЕМА: Механіка. Кінематика. Рух тіла, кинутого горизонтально.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на характеристики коливального контуру.
Дано:
\(\triangle I=1,2\ \text{А}\)
\(\triangle t=0,6\ \text{c}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_{\text{с.і.}}=0,2\ \text{мВ}=0,0002\ \text{В}\)
\(C=0,2\ \text{пФ}=10\cdot 10^{-12}\ \text{Ф}=10^{-11}\ \text{Ф}\)
\(c=3\cdot 10^8\ \text{м/с}\)
Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}-?\)
Якщо вважати, що швидкість електромагнітної хвилі в повітрі дорівнює швидкості світла у вакуумі, то довжина радіохвилі, випромінюваної антеною, пов’язана з періодом коливань цієї антени і її контуру співвідношенням \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=cT\) (1).
Період коливання коливального контуру обчислюють за формулою Томсона \(T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}\) (2), де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.
Тож для обчислення періоду потрібно визначити індуктивність котушки в коливальному контурі.
Індуктивність \(L\) – фізична величина, якою характеризують провідник. Вона чисельно дорівнює ЕРС самоіндукції, що виникає в провіднику за зміни сили струму на 1 ампер за 1 секунду.
Тож індуктивність обчислюють за формулою $$ L=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_{\text{с.і.}}\triangle t}{\triangle I}=\frac{0,0002\cdot 0,6\ \text{с}}{1,2\ \text{А}}=0,0001\ \text{Гн}. $$ Тоді частота коливань антени й отриманої в результаті радіохвилі з виразу (2) дорівнює:
Відповідь: 60.
ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру і його повну енергію.
Коливальний контур – це схематично зображений на рисунку 1 фізичний пристрій із послідовно з’єднаних котушки індуктивності 1 і конденсатора 2.
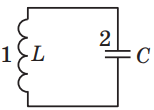
Рис. 1. Електрична схема коливального контуру
В ідеальному коливальному контурі вся енергія під час коливань перетікає від конденсатора до котушки без утрат. Якщо вважати, що в початковий момент часу конденсатор заряджений на повну, то його енергія перетікатиме в енергію котушки з максимальним струмом індукції під час коливань у такому електромагнітному контурі.
Тож можна обчислити зміну повної енергії контуру за зміною енергії зарядженого конденсатора: $$ W_{\text{конденсатора}}= \frac{q^2}{2C}, $$ де \(q\) – це максимальний заряд на обкладинці, а \(C\) – ємність конденсатора. Після збільшення максимального заряду енергія конденсатора
Відповідь: Г.
ТЕМА: Коливання і хвилі.
Завдання скеровано на оцінювання знання формул для обчислення циклічної частоти коливань різної природи.
За результатами аналізування ситуацій, описаних у завданні, можна дійти таких висновків:
А Вираз містить коефіцієнт жорсткості й масу, що є характеристиками пружинного маятника.
Б Вираз містить прискорення вільного падіння і довжину, які характеризують математичний маятник.
В Вираз містить індуктивність й електроємність, які характеризують коливальний контур.
Г Вираз описує загальний зв’язок частоти й циклічної частоти коливань.
Відповідь: B.
ТЕМА: Електромагнітні коливання і хвилі. Електромагнітні хвилі.
Завдання скеровано на оцінювання розуміння поняття електромагнітної хвилі.
Електромагнітна хвиля – це поширення в просторі коливань електромагнітного поля.
Така хвиля – поперечна, отже коливання векторів напруженості електричного поля \(\overrightarrow{E}\) та магнітної індукції \(\overrightarrow{B}\) в ній відбуваються перпендикулярно до напрямку її поширення \(\overrightarrow{c}\) (рис. 1).
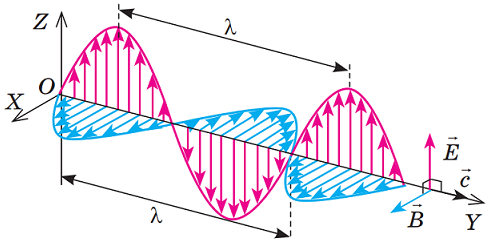
Рис. 1. Періодичні зміни вектора напруженості \(\overrightarrow{E}\) електричного поля і вектора магнітної індукції \(\overrightarrow{B}\) магнітного поля під час поширення електромагнітної хвилі в напрямку осі \(OY\)
Відповідь: Г.
ТЕМА: Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на оцінювання вміння аналізувати схеми електричного кола й розв’язувати розрахункові задачі з послідовного й паралельного підключення конденсаторів.
Дано:
\(C_1 = 0,5\ \text{мкФ}\)
\(C_2 = 1,5\ \text{мкФ}\)
\(C_3 = 2,5\ \text{мкФ}\)
1. Знайти:
\(C_{\text{заг}}\ -\ ?\)
Якщо ключ K закрити, то конденсатори \(C_2\) і \(C_3\) також будуть уключені в коло. Тоді конденсатори \(C_1,\ C_2\) і \(C_3\) будуть підключені паралельно. Ємність такої батареї конденсаторів дорівнює сумі ємностей окремих конденсаторів: $$ C_{\text{заг}}=C_1+C_2+C_3=0,5\ \text{мкФ}+1,5\ \text{мкФ}+2,5\ \text{мкФ}=4,5\ \text{мкФ}. $$
2. Знайти:
\(\frac{T_2}{T_1}\ -\ ?\)
Період коливання коливального контуру можна обчислити за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.
До того, як ключ K закрили, у коло було підключено лише конденсатор \(C_1\). Тому можна записати період електромагнітних коливань для випадків до та після закривання ключа: \begin{gather*} T_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1};\\[7pt] T_2=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_{\text{заг}}}. \end{gather*}
Тоді можна розрахувати, у скільки разів збільшився період електромагнітних коливань: $$ \frac{T_2}{T_1}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_{\text{заг}}}}{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1}}=\frac{C_{\text{заг}}}{C_1}=\sqrt{9}=3. $$
Відповідь: 1. 4,5. 2. 3.
ТЕМА: Коливання і хвилі. Шкала електромагнітних коливань.
Завдання скеровано на оцінювання вміння визначити область застосування електромагнітних коливань певного типу.
Щодо варіантів відповіді:
1 тепло, яке ми відчуваємо від тіл навколо – це інфрачервоне випромінювання, і саме його фіксують прилади нічного бачення
2 ультрафіолетове випромінювання спричиняє опіки й пришвидшує розвиток ракових клітин. Одним з основних способів захисту людського тіла від цього випромінювання є виділення меланіну в шкірі, що може поглинути УФ-промені. Меланін – це пігмент, що відповідає за колір шкіри й очей. Що більше меланіну у шкірі, то темніша вона. Тож ультрафіолетове випромінювання є причиною засмаги
3 Рентгенівське випромінювання може бути отримане в рентгенівській трубці. Її складники – два електроди в скляній вакуумній трубці. Електрони, що вилітають з катода під дією високої напруги, потрапляють на анод, де вповільнюються. У такому разі електрони рухаються з пришвидшенням \((a \lt 0)\), а отже випромінюються електромагнітні хвилі – рентгенівське випромінювання
4 Гамма-випромінювання утворюється під час самовільного розпаду ядер атомів
Відповідь: 1Б, 2А, 3Г, 4Д.
ТЕМА: Електромагнітні коливання і хвилі. Властивості електромагнітного випромінювання різних діапазонів. Радіолокація.
Завдання скеровано на оцінювання розуміння принципів радіолокації та вміння розв’язувати відповідні розрахункові задачі.
Радіолокатори посилають короткі імпульси в напрямку, у якому проводиться дослідження. Радіохвиля, як і інші елекромагнітні хвилі, відбивається від провідників. Тому радіохвилі відбиваються від об’єктів, які вони зустрічають на своєму шляху і повертаються до локатора. Локатор фіксує час, за який хвиля повернулась, а отже подолала дві відстані до об’єкта (від локатора до об’єкта і від об’єкта знову до локатора).
Тому відстань до об’єкта можна розрахувати за формулою $$ s=\frac{vt}{2}, $$ де \(v\) – швидкість поширення електромагнітних хвиль у середовищі, у якому здійснюють дослідження. У повітрі ця швидкість дуже близька до швидкості світла в вакуумі \(c.\)
Якщо максимальна відстань виявлення об’єкта – 150 км, можна визначити час, який знадобиться імпульсу, щоби зареєструвати сигнал від об’єкта з такої відстані: $$ t=\frac{2s}{v}=\frac{2\cdot 150\ \text{км}}{3\cdot 10^8\ \text{м}/\text{с}^2} =\frac{3\cdot 10^5\ \text{м}}{3\cdot 10^8\ \text{м}/\text{с}^2}=0,001\ \text{с}. $$
Саме з таким інтервалом радіолокатор може випускати імпульси. Тоді частота випускання імпульсів дорівнюватиме $$ v=\frac{1\ c}{t}=1000\ \text{(імпульсів)}. $$
Відповідь: A.
ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі. Явище й закони електромагнітної індукції.
Завдання скеровано на оцінювання вміння розв’язувати комплексні задачі, пов’язані з коливальними процесами в коливальному контурі і їхнім впливом на магнітне поле, а також ваше вміння складати схеми електричного кола.
Після того, як перемикачем П конденсатор приєднують до котушки, утворюється коливальний контур. У ньому електрони, що накопичилися на одній із обкладинок конденсатора, рухатимуться в напрямку до іншої його обкладинки, утворюючи струм в колі. Так конденсатор починає розряджатись.
Сила струму в котушці поступово збільшуватиметься. У котушці зі змінним струмом завжди утворюється магнітне поле. Саме воно й заряджає предмет усередині.
Після того, як конденсатор повністю розрядиться, електрони продовжать свій рух, адже просто зупинитися вони не можуть. Тож тепер на вже нейтральну обкладинку конденсатора починають потрапляти електрони. У результаті цього вона заряджається.
Унаслідок цього процесу заряд, що був на одній обкладинці конденсатора, опинився на іншій обкладинці, тож тепер усі кроки повторяться у зворотному напрямку. У цій частині процесу струм тектиме в протилежний бік, а отже й лінії магнітної індукції також матимуть протилежний напрямок. Це почне розряджати тіло всередині.
Такі коливання заряду й енергії в коливальному контурі не можуть тривати одвічно. Частина енергії з кожним коливанням розсіюється на дротах і контактах. Тож сила струму, що проходитиме крізь котушку, щоразу буде меншою і меншою, а отже й тіло всередині перемагнічуватиметься не до кінця.
Тож коли всі коливання закінчаться, тіло, яке намагалися зарядити, матиме невеликий заряд через те, що сила струму в обох напрямках відрізнялася. Проте неможливо визначити, у якому саме напрямку буде намагнічено тіло.
Для того, щоби намагнітити тіло всередині котушки сильніше, треба примусити струм у контурі рухатися лише в одному напрямку. Тоді розмагнічування тіла не відбудеться. Пристрій, що вможливлює одностороннє пропускання струму, – це діод.
Умовні позначення для схем електричних кіл:
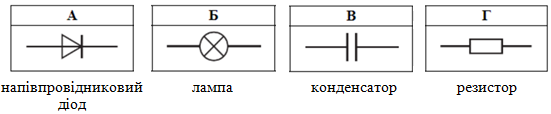
Відповідь: A.
ТЕМА: Оптика. Світло, як електромагнітна хвиля.
Завдання скеровано на оцінювання розуміння принципів поширення світла крізь різні середовища й оптичні прилади.
1 Природне світло складається з багатьох хвиль, випромінених різними атомами. Через це в пучку природного світла існує безліч напрямків коливання вектора напруженості електричного поля. Під час поляризації замість хаотичного розподілу напрямків у пучку світла залишається лише той напрямок (або напрямки), які потрібні. Для поляризації використовують спеціальні фільтри – поляроїди (або поляризатори, рис. 1).
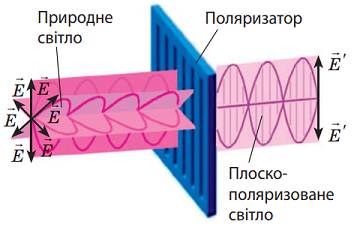
Рис. 1. Принцип роботи поляризатора
Поляризатор працює як щілина, що пропускає лише коливання певного напрямку. Якби електромагнітні хвилі були поздовжніми, то поляризатор не вносив би ніяких змін, але зафіксовано зміни в інтенсивності в експериментах (адже велика частина променів відбивається поляризатором). Тому світло може бути лише поперечною хвилею.
2 Світло, що падає на більшість предметів навколо, відбивається від них. Відбиті промені потрапляють на око, фокусуються кришталиком на сітківку, звідки сигнали через зоровий нерв передаються на обробку в мозок.
3 Принцип роботи лінзи полягає в заломленні променів на двох вигнутих поверхнях. Залежно від типу лінзи й початкової форми променя після проходження лінзи пучок може сфокусуватися в певній точці, розсіятися чи навіть стати паралельним. На рисунку 2 схематично зображено принцип роботи збиральної лінзи, на яку падає паралельний пучок.
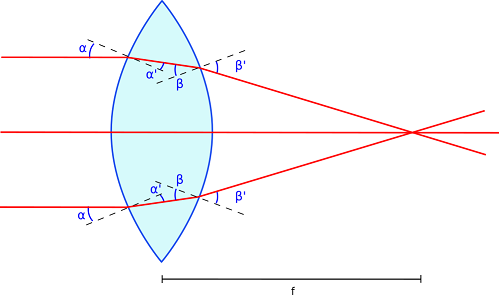
Рис. 2. Принцип роботи збиральної лінзи
4 Сонце – це одне з найбільш широкочастотних джерел випромінювання. Воно випромінює всі електромагнітні хвилі – від радіохвиль і до γ-випромінювання. Через це спектр сонця неперервний. Проте деякі гази поглинають кванти світла з дуже специфічними частотами. Тоді в неперервному спектрі утворюються темні смуги на місці цих поглинутих квантів (рис. 3).

Рис. 3. Вигляд лінійчастих спектрів поглинання
Відповідь: 1В, 2Г, 3Д, 4Б.
ТЕМА: Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на оцінювання вміння застосовувати формулу Томсона.
Період електромагнітних коливань у контурі можна визначити за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.
Тоді в положенні 1 період дорівнюватиме: $$ T_1=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{4LC}=4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}. $$
А в положенні 2: $$ T_2=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}. $$
Тобто: $$ T_1=2T_2. $$
Відповідь: A.
ТЕМА: Коливання і хвилі. Електромагнитні коливання і хвилі. Змінний електричний струм.
Завдання скеровано на перевірку вміння розв'язувати розрахункові комбіновані задачі, для розв'язування яких використовуються поняття і закономірності із різних розділів фізики.
Дано:
\(u=50\cos100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}t\)
\(C = 2\ \text{мкФ}\)
\(t = \frac 34 T\)
\(V_2 = 9\ \text{В}\)
1. Знайти:
\(T(\text{с})\ -\ ?\)
Періодична зміна напруги на конденсаторі $$ u=U_{max}\cos(wt). $$
За положенням у формулі \begin{gather*} U_{max}=50\ \text{В}\\[7pt] w=100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}, \end{gather*} тому \begin{gather*} w=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}=100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\\[6pt] T=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}=0,02\ \text{с}. \end{gather*}
2. Знайти:
\(q(\text{Кл})\ -\ ?\)
Заряд на обкладках конденсатора змінюється за законом
Відповідь: 1. 0,02. 2. 0.
ТЕМА: Коливання і хвилі. Власна частота й період електромагнітних коливань.
Завдання скеровано на перевірку вміння розв'язувати розрахункові задачі на залежність періоду власних коливань від параметрів системи й визначати довжину хвилі.
Дано:
\(С=50\ \text{пФ}=50\cdot 10^{-12}\ \text{Ф}\)
\(L=2\ \text{мкГн}=2\cdot 10^{-6}\ \text{Гн}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}=3\)
\(c=3\cdot 10^8\ \text{м/с}\)
Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\ -\ ?\)
Відповідь: B.
ТЕМА: Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням формули Томсона.
Дано:
\(L=10\ \text{мГн}\)
\(C=40\ \text{мФ}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}=3,14\)
1. Знайти:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\ -\ ?\)
Знаючи ємність конденсатора й індуктивність котушки коливального контуру можна визначити період коливань T, які виникають під час його роботи: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, \(C\) – електрємність конденсатора.
Циклічна частота пов’язана з періодом коливань формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}. $$
Тоді
2. Знайти:
\(t (\text{мс})\ -\ ?\)
Енергію конденсатора в коливальному контурі можна визначити за формулою $$ W_{\text{кон}}=\frac{CU^2}{2}, $$ де \(U\) – напруга, а \(C\) – електроємність.
Енергію котушки обчислюють за формулою \begin{gather*} W_{\text{кот}}=\frac{LI^2}{2}, \end{gather*} де \(L\) – індуктивність, \(I\) – сила струму.
Енергія в коливальному контурі змінюється періодично. За один період у коливальному контурі заряд з одної обкладинки конденсатора протікає через котушку на іншу обкладинку, а потім назад. Тож за один період сила струму в котушці (а отже й енергія) дорівнює нулю двічі: на початку періоду та в момент \(T/2\). Нульова енергія на котушці відповідає максимальній енергії на конденсаторі.
Тоді в момент \(T/4\) енергія на котушці буде максимальною, а на конденсаторі дорівнюватиме нулю.
Перший раз енергія котушки й конденсатора зрівняється між моментами максимуму енергії конденсатора \((t=0)\) і котушки \((t=T/4)\), тобто в момент \(t=T/8\).
Цей час можна обчислити:
Відповідь: 1. 50. 2. 16.
ТЕМА: Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на оцінювання вміння розраховувати енергію елементів коливального контуру.
Коливальний контур – це фізичний пристрій, який складено з послідовно з’єднаних конденсатора й котушки індуктивності (рис. 1).
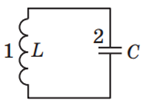
Рис. 1. Електрична схема коливального контуру: 1 – котушка індуктивності, 2 – конденсатор
В ідеальному коливальному контурі вся енергія під час коливань перетікає від конденсатора до котушки без утрат. Цей процес описують за допомогою формули $$ W_{\text{конденсатора}}=\frac{CU^2}{2}, $$ де \(U\) – напруга на обкладинках конденсатора, а \(C\) – його ємність.
Під час коливань у контурі енергія повністю зарядженого конденсатора перетікатиме в енергію котушки, яку можна визначити за формулою $$ W_{\text{котушки}}=\frac{LI^2}{2}, $$ де \(L\) – індуктивність котушки, \(I\) – сила струму в ній.
У контурі електрони, що накопичилися на одній з обкладинок конденсатора, рухатимуться в напрямку до іншої його обкладинки, утворюючи струм у колі. У результаті цього конденсатор почне розряджатися, напруга на його обкладинках зменшується, а отже зменшуватиметься і його енергія.
У котушці ж сила струму поступово збільшуватиметься, а разом із нею збільшуватиметься й енергія магнітного поля, яке вона створює. Коли конденсатор розрядиться повністю, струм у котушці стане максимальним.
Після того, як конденсатор повністю розрядиться, електрони продовжать свій рух, адже просто зупинитися вони не можуть. Тож тепер на вже нейтральну обкладинку конденсатора починають потрапляти електрони. У результаті цього вона заряджається, а струм у котушці поступово зменшується.
Унаслідок цього процесу заряд з однієї обкладинки конденсатора опиниться на іншій обкладинці. Тож тепер конденсатор заряджений протилежно до початкового стану, і напруга на ньому за модулем дорівнює початковій напрузі, але має протилежний знак.
Після цього струм почне текти в протилежному напрямку. Одне повне коливання закінчиться тоді, коли заряд повністю повернеться на першу обкладинку.
Тож за одне коливання потенціальна енергія конденсатора двічі досягає максимуму (коли весь заряд опиняється на одній з обкладинок) і двічі досягає \(0\) (коли струм у котушці максимальний).
Відповідь: Г.
ТЕМА: Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на оцінювання розуміння принципів роботи коливального контуру й уміння розв’язувати розрахункові задачі на зв’язок періоду й частоти коливань.
Дано:
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}= 1\ \text{кГц}\)
1. Знайти:
\(T(\text{с})\ -\ ?\)
Між періодом і частотою коливань існує зв’язок: $$ T=\frac{1}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}}=\frac{1}{1\ \text{кГц}}=\frac{1}{1\ 000\ \text{с}^{-1}}=0,001\ \text{с}. $$
2. Знайти:
\(N\ (\text{разів за секунду}\ I=0)\ -\ ?\)
За один період у коливальному контурі заряд з одної обкладинки конденсатора протікає через котушку на іншу обкладинку, а потім назад. Тож за один період сила струму в котушці дорівнює нулю двічі: на початку періоду й у момент \(T/2\). Якщо за один період сила струму в котушці дорівнює нулю двічі, то кількість таких ситуацій за секунду дорівнює подвоєній частоті коливань: $$ N=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}=2\cdot 1\ 000=2\ 000. $$
Відповідь: 1. 0,001. 2. 2000.
ТЕМА: Оптика. Інтерференція світла. Дисперсія світла. Поляризація світла.
Завдання скеровано на оцінювання вміння розпізнавати оптичні явища у природних явищах і сучасній техніці.
1. Бензин на асфальті утворює тонку прозору плівку, коефіцієнт заломлення у якої відрізняється від коефіцієнту заломлення повітря. Тож частина сонячних променів відбивається на межі бензин – повітря, а частина заломлюється і відбивається вже від поверхні бензин – асфальт (рисунок 1). Так між цими частинами проміння утворюється різниця ходу. Обидві частини мають одне джерело, тож вони є когерентними й відбувається інтерференція.
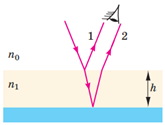
Рис. 1. Схема ходу променів під час інтерференції у плівці бензину
2. Туман виникає тоді, коли водяна пара в повітрі конденсується й утворюється багато водяних крапель. На кожній із них світло розсіюється й утворюється ореол.
3. Біле (сонячне) світло складається із хвиль із різними частотами. Показник заломлення для кожної з таких хвиль трохи відрізняється, тож кут заломлення після проходження крізь поверхню призми для них теж відрізнятимуться. У такий спосіб утворюється кольоровий спектр, як це зображено на рисунку 2.
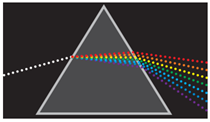
Рис. 2. Утворення дисперсійного спектра
4. Під час перегляду стереофільмів одночасно транслюють дві версії фільму, зняті під невеликим кутом одна до одної. Версії для кожного ока мають різну поляризацію, тому окуляри з поляризаторами дають змогу блокувати зображення, зняте для лівого ока на правому, і навпаки. Після цього, мозок обробляє два різнi зображення, отримані з двох очей, і «збирає» об’ємну картину.
Відповідь: 1В, 2А, 3Д, 4Б.
ТЕМА: Електромагнітні коливання та хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням формули Томсона.
Дано:
\(C=1\ \text{нФ}\)
\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=180\ \text{м}\)
Знайти:
\(L\ (\text{мкГн})\ -\ ?\)
Якщо вважати, що швидкість електромагнітної хвилі в повітрі дорівнює швидкості світла у вакуумі, то довжина випроміненої контуром хвилі пов’язана з періодом коливань цього контуру: $$ T=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{c}, $$ де \(c\) – швидкість світла у вакуумі, \(T\) – період коливань контуру.
Період електромагнітних коливань в електричному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{Lc}, $$ де \(L\) – індуктивність котушки, а \(C\) – електроємність конденсатора.
Тоді індуктивність котушки можна визначити за формулою:
Відповідь: 9.
ТЕМА: Електромагнітні коливання і хвилі. Електромагнітні хвилі.
Завдання скеровано на перевірку розуміння джерел електромагнітних хвиль.
Джерелом електромагнітної хвилі може бути заряджене тіло, що рухається з прискоренням, або провідник зі змінним струмом.
Тож рівномірний рух частинок не може бути причиною виникнення електромагнітної хвилі.
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Шкала електромагнітних хвиль. Властивості електромагнітного випромінювання різних діапазонів.
Завдання скеровано на перевірку знань про різні види електромагнітного випромінювання і їхні джерела.
Під час розпаду радіонуклідів у ядерному реакторі виникає радіоактивне випромінювання, один із видів якого – гамма-промені.
Будь-які тіла, температура яких вища від абсолютного нуля, випромінюють інфрачервоні промені. Саме на цьому ґрунтується застосування їх у тепловізорах – приладах нічного бачення. Тому гарячий чай є джерелом інфрачервоного (теплового) випромінювання.
Радіохвилі – від наддовгих із довжиною понад \(10\ \text{км}\) до ультракоротких і мікрохвиль із довжиною менш ніж \(0,1 \ \text{мм}\) – породжує змінний електричний струм. Електромагнітні хвилі радіодіапазону породжені високочастотним змінним струмом, який створюють генератори високочастотних електромагнітних коливань. У цьому завданні джерелом радіохвиль є супутник зв’язку.
Люмінофор – речовина, яка здатна світитися за збудження, тобто люмінесціювати. Люмінофори широко використовують в електроніці, наприклад, ними вкривають екран телевізора, електропроменевої трубки, де їхнє світіння за бомбардування електронами формує зображення, у сцинтиляційних лічильниках тощо. Людське око сприймає це світіння, отже це діапазон видимого світла.
Відповідь: 1В, 2А, 3Г, 4Д.
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння коливального процесу в коливальному контурі, а також уміння описувати цей процес відповідним рівнянням.
Коливання в коливальному контурі відбуваються за гармонічним законом: $$ \chi(t)=A\cos(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega} t+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0), $$ де \(\chi\) ‒ значення змінної величини в даний момент часу \(t,\) \(A\) ‒ амплітудне значення змінної величини, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\) – циклічна частота, \(t\) – час, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0\) ‒ початкова фаза коливань.
У даному випадку за гармонічним законом змінюється напруга \(u\) на конденсаторі: $$ u=U_{\mathrm{max}}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega} t, $$ де \(U_{\mathrm{max}}\) – амплітудне значення напруги.
За активного опору \(R\) у коливальному контурі коливання згасні́, оскільки частина енергії електромагнітного поля під час кожного коливання перетворюється на внутрішню (теплову) енергію.
Однак у будь-якій реальній коливальній системі завжди є втрати енергії: під час механічних коливань енергія витрачається на долання сил тертя, деформацію; під час електромагнітних коливань – на нагрівання провідників, випромінювання електромагнітних хвиль тощо. Унаслідок цього амплітуда коливань із часом зменшується. А через певний інтервал часу, якщо немає надходжень енергії від зовнішнього джерела, коливання припиняються (згасають). Тому вільні коливання завжди є згасними.
В умові не задано амплітудне значення напруги. Тому обчислимо циклічну частоту \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}=3,14,\ T\) – період коливань; $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}}=\frac{1}{\sqrt{LC}}, $$ де \(L\) – індуктивність котушки, \(C\) – електроємність конденсатора;
Отже, рівняння, що відповідає умові завдання, $$ u=0,5\cos 2000 t. $$
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Електрорушійна сила.
Завдання скеровано на перевірку вміння аналізувати графіки тригонометричних залежностей фізичних величин.
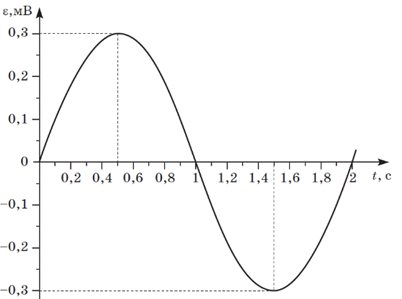
Рис. 1. Умова завдання
Знайти:
\(\text{ЕРС}\ (\text{мВ})\ -\ ?\)
Графік, зображений на рисунку 1, – це графік синусоїдальної залежності, тож електрорушійна сила (ЕРС) залежить від часу: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=A\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t, $$ де \(A\) – амплітуда коливань, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\) – циклічна частота коливань, \(t\) – момент часу.
Циклічна частота пов’язана з періодом формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}. $$
За графіком можна також визначити амплітуду коливань, яка дорівнює максимальному відхиленню від положення рівноваги: $$ A=0,3\ \text{мВ}, $$ тож $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,3\sin\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}t. $$
Тоді можна обчислити ЕРС в момент часу \(t=\frac{T}{12}\):
\begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,3\sin\left(\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}\ \frac{T}{12}\right);\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,3\sin\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{6};\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,3\cdot \frac 12;\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}=0,15\ (\text{мВ}). \end{gather*}Відповідь: 0,15.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Власна частота й період електромагнітних коливань. Формула Томсона.
Завдання скеровано на перевірку розуміння принципу дії коливального контуру.
Електромагнітну хвилю характеризують довжиною \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda},\) частотою \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) (періодом \(T\)) і швидкістю \(c\) поширення у вакуумі: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}}=cT. $$
Для того, щоб коливальний контур міг уловити випромінювані хвилі, його треба настроїти на частоту коливань випромінювача. Період власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки контуру, \(C\) ‒ електроємність конденсатора контуру.
Ураховуючи, що коливальний контур настроєний на таку саму частоту, із якою поширюється хвиля, і що частота і період взаємно обернені величини, дістанемо формулу для обчислення електроємності: \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=cT=c2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC},\\[6pt] C=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}^2}{c^2 4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}^2\cdot L}. \end{gather*}
Оскільки електроємність прямо пропорційна квадрату довжини хвилі, то електроємність конденсатора буде максимальною за максимального значення довжини хвилі, на яку може налаштуватися коливальний контур: \begin{gather*} C=\frac{540^2}{9\cdot 10^{16}\ \left(\frac{\text{м}}{\text{с}}\right)^2\cdot 4\cdot 10\cdot 0,27\cdot 10^{-3}\ \text{Гн}}=\\[6pt] =\frac{3}{10^{10}}\ \text{Ф}=300\cdot 10^{-12}\ \text{Ф}=300\ \text{пФ}. \end{gather*}
Відповідь: 300.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку знання і розуміння явищ геометричної і хвильової оптики.
Заломлення ‒ це явище зміни напрямку поширення хвилі під час її проходження через плоску межу двох однорідних середовищ.
Дифракція ‒ це явище потрапляння світлових хвиль в область геометричної тіні, тобто відхилення їх від прямолінійного поширення.
Дисперсія ‒ це явище залежності показника заломлення середовища від довжини електромагнітної хвилі.
Інтерференція ‒ це явище накладання когерентних хвиль, унаслідок якого спостерігається стійка в часі картина посилення їх та послаблення в різних точках простору.
Відповідь: 1Б, 2Д, 3А, 4Г.
ТЕМА: Коливання і хвилі. Оптика. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку розуміння перетворень у коливальному контурі під час вільних електромагнітних коливань.
За час одного коливання (період) у коливальному контурі конденсатор перезаряджається двічі. Протягом першої чверті періоду заряд на обкладках конденсатора зменшується до нуля \((q=0).\)
Після проходження котушки заряджені частинки продовжують рух у тому самому напрямку, а конденсатор перезаряджається ‒ заряд на його обкладках змінюється на протилежний. Отже, протягом другої чверті періоду конденсатор повністю заряджається \((q=q_{max}).\)
Наступну (третю) чверть періоду конденсатор знову розряджатиметься, однак уже в зворотному напрямку. Коли мине три чверті періоду, конденсатор повністю розрядиться, заряд дорівнюватиме нулю \((q=0).\)
За останню чверть періоду конденсатор зарядиться до максимального значення \((q=q_{max})\) з тими ж знаками електричного заряду на його обкладках, які були на початок коливання.
Отже, тієї миті, коли від початку коливання минуло три чверті періоду коливання, заряд на пластинах конденсатора дорівнюватиме нулю \((q=0).\)
Відповідь: Г.
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Електромагнітні хвилі та швидкість поширення їх.
Завдання скеровано на перевірку розуміння поширення електромагнітної хвилі через її характеристики.
Електромагнітну хвилю як процес поширення електромагнітного поля насамперед характеризують векторами напруженості \(\overrightarrow{E}\) і магнітної індукції \(\overrightarrow{B}.\) Будь-яка хвиля періодична і в часі, і в просторі, тому зазначені величини періодично змінюються і з часом, і зі зміною відстані від джерела хвилі. За теорією Максвелла вектори \(\overrightarrow{E}\) і \(\overrightarrow{B}\) одночасно сягають максимального значення й одночасно перетворюються на нуль, під час цього вони перпендикулярні як один до одного, так і до напрямку поширення хвилі (див. рисунок). Отже, електромагнітна хвиля ‒ це поперечна хвиля:
$$ \overrightarrow{E}\perp \overrightarrow{B},\ \ \overrightarrow{c}\perp \overrightarrow{E},\ \ \overrightarrow{c}\perp \overrightarrow{B}. $$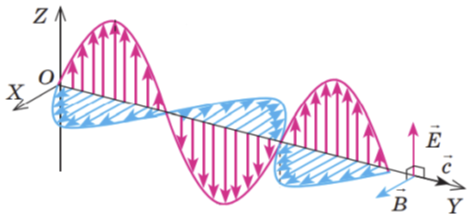
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння принципу роботи коливального контуру й особливостей перетворення енергії в ньому.
Під час розрядження конденсатора його заряд зменшуватиметься, а сила струму \(I\) в контурі ростиме. Відповідно енергія магнітного поля і модуль магнітної індукції поля котушки також збільшуватимуться: $$ W_\text{маг}=\frac{LI^2}{2}; $$ \(B\sim I\) (магнітна індукція прямо пропорційна до сили струму).
Енергію електричного поля \(W_\text{ел}\) зарядженого до напруги \(U\) конденсатора з електроємністю \(C\) і зарядом \(q,\) обчислюють за формулою $$ W_\text{ел}=\frac{qU}{2}, $$ тобто енергія електричного поля прямо пропорційна до заряду конденсатора \(W_\text{ел}\sim q,\) який під час розряджання зменшується. Унаслідок зменшення заряду зменшується енергія електричного поля конденсатора.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку розуміння перетворення енергії в коливальному контурі, уміння обчислювати необхідну фізичну характеристику електромагнітних коливань у будь-який момент часу.
Якщо на обкладках конденсатора накопичиться максимальний електричний заряд \(q_{\mathrm{max}},\) то повна енергія \(W\) коливального контуру дорівнюватиме максимальній енергії електричного поля \(W_{\text{ел}}\) між обкладками конденсатора: $$ W=W_{\text{ел}\ \mathrm{max}}=\frac{q^2_{\mathrm{max}}}{2C}, $$ де \(C\) ‒ електроємність конденсатора.
У той момент, коли конденсатор повністю розрядиться, енергія електричного поля дорівнюватиме нулю \((W_\text{ел}=0),\) сила струму сягне максимального значення \(I_\mathrm{max},\) а повна енергія \(W\) коливального контуру дорівнюватиме максимальній енергії \(W_\text{маг}\) магнітного поля: \begin{gather*} W=W_{\text{маг.}\ \mathrm{max}}=\frac{LI^2_\mathrm{max}}{2}, \end{gather*} де \(L\) ‒ індуктивність котушки.
Повну енергію \(W\) коливального контуру в довільний момент часу \(t\) можна обчислити за формулою $$ W=W_{\text{ел}}+W_{\text{маг}}=\frac{q^2}{2C}+\frac{LI^2}{2}. $$
Виконаймо необхідні математичні перетворення, щоб визначити шукану силу струму: $$ \frac{q^2_\mathrm{max}}{2C}=\frac{LI^2_\mathrm{max}}{2}=\frac{q^2}{2C}+\frac{LI^2}{2}. $$
Помножмо всі вирази на \(2\) й поділімо на \(L:\) $$ \frac{q^2_\mathrm{max}}{LC}=I^2_\mathrm{max}=\frac{q^2}{LC}+I^2. $$
Обчислімо добуток \(LC\) в одиницях СІ:
Підставмо це значення добутку \(LC\) у формулу із шуканою величиною:
Відповідь: 4.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку розуміння і застосування механічних й електромагнітних явищ.
Виникнення вихрового електричного поля або електричної поляризації провідника під час зміни магнітного поля або під час руху провідника в магнітному полі називають електромагнітною індукцією. Важливим наслідком електромагнітної індукції для генерування електричного струму є виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється.
Період \(T\) коливань математичного маятника не залежить від маси маятника, а лише від довжини \(l\) нитки та прискорення \(g\) вільного падіння в тому місці, де розташований цей маятник: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}=\sqrt{\frac lg}. $$
Тому, вимірявши довжину нитки й період коливань маятника, можна визначити прискорення вільного падіння в певній місцевості.
У радіолокації використовують ультракороткі електромагнітні хвилі частотою від \(100\) до \(1000\ \text{МГц}.\) У радіолокаційному пристрої радарі є передавальна та приймальна частини. Імпульс гостронапрямленої радіохвилі від потужного радіопередавача пересилають за допомогою параболічної антени. Досягнувши цілі, радіохвиля відбивається від неї та повертається назад. Відбиту хвилю, уловлену тією самою антеною, реєструє приймач.
Просвітлення оптики ‒ збільшення прозорості деталей оптичних систем (лінз, оптичних призм) нанесенням на їхні поверхні тонкого шару діелектрика (або кількох шарів) із показником заломлення, меншим, ніж у матеріалу оптичної деталі. Просвітлення оптики ‒ результат інтерференції світла, яке відбивається від передньої та задньої границь цього шару (просвітлювальної плівки). За належного добору речовини й товщини плівки для певного кута падіння відбиті світлові хвилі певної довжини можуть повністю погасити одна одну.
Відповідь: 1В, 2Б, 3Д, 4Г.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Електромагнітні хвилі та швидкість поширення їх.
Завдання скеровано на перевірку вміння визначати довжину електромагнітної хвилі через характеристики коливального контуру.
Довжину електромагнітної хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) можна визначити за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=cT, $$ де \(c\) ‒ швидкість світла у вакуумі, \(T\) ‒ період поширення електромагнітної хвилі.
Світло є електромагнітною хвилею, тож швидкість поширення електромагнітної хвилі також дорівнює \(3\cdot 10^8\ \text{м/с.}\)
Період поширення електромагнітної хвилі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора.
Обчислімо довжину електромагнітної хвилі:
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку розуміння перетворення енергії в коливальному контурі.
Коливальний контур – фізичний пристрій, який є коливальною системою, тобто в ньому можуть виникати вільні електромагнітні коливання. Коливальний контур можна створити, послідовно з’єднавши конденсатор і котушку індуктивності.
Якщо після зарядження конденсатор замкнути на котушку індуктивності, то під дією електричного поля конденсатора вільні заряджені частинки в контурі почнуть рухатися напрямлено. У контурі виникне електричний струм, а конденсатор почне розряджатися.
Заряд на обкладках конденсатора поступово зменшується, а сила струму в котушці зростає, тому магнітна індукція створеного струмом магнітного поля зростає теж. Отже, протягом першої чверті періоду енергія електричного поля \(W_\text{ел}\) конденсатора перетворюється на енергію магнітного поля котушки.
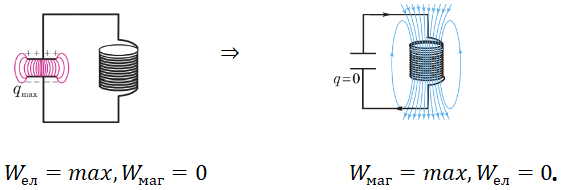
Конденсатор перезаряджається – заряд на його обкладках змінюється на протилежний. Отже, протягом другої чверті періоду енергія магнітного поля котушки перетворюється на енергію електричного поля конденсатора.
Наступну половину періоду характер зміни електричного заряду на обкладках конденсатора й характер зміни сили струму в контурі будуть такими самими, тільки у зворотному напрямку. Коли заряд на обкладках конденсатора досягне максимального значення, то завершиться одне повне коливання.
Час одного повного коливання ‒ це період. Період власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора.
Тоді можна визначити чверть періоду: $$ \frac 14 T=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}}{4}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}\sqrt{LC}. $$
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Інтерференція світла, її практичне застосування.
Завдання скеровано на перевірку знання і розуміння явища інтерференції.
Хвилі, які відповідають умовам когерентності, називають когерентними хвилями.
Умови когерентності хвиль:
1) хвилі повинні мати однакову частоту (відповідно й довжину);
2) різниця \(\Delta \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}\) початкових фаз хвиль має бути незмінною (хвилі, що накладаються, повинні мати незмінний у часі зсув фаз).
Ідеальними джерелами когерентних світлових хвиль є лазери ‒ оптичні квантові генератори.
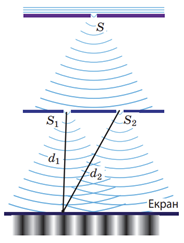
Коли хвилі надходять у точку \(P\) в протилежних фазах, вони гаситимуть одна одну (див. рисунок) ‒ у точці \(P\) спостерігають інтерференційний мінімум.
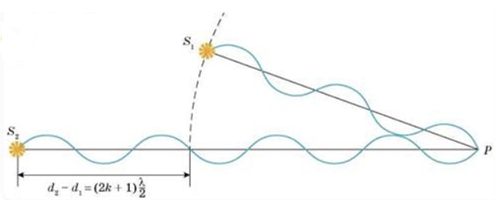
Це відбудеться за умови, що на відрізку \(\Delta d\) укладатиметься непарна кількість півхвиль. Умова інтерференційного мінімуму: у точці простору відбувається послаблення результувальних світлових коливань, якщо різниця ходу двох світлових хвиль, що надходять у цю точку, дорівнює непарному числу півхвиль: \begin{gather*} \Delta d=d_2-d_1=(2k+1)\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{2}\\[6pt] \text{або}\\[6pt] \Delta d=k\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{2}, \end{gather*} де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) ‒ довжина хвилі; \(k\) ‒ ціле число.
За умовою довжина хвилі випромінювання \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=600\ \text{нм.}\) Розгляньмо кожен із запропонованих варіантів відповіді.
A \(\Delta d=400\ \text{нм}=\frac 23\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=\frac 16\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{2}\) – за умовою \(k\) ‒ ціле число, а за такої різниці ходу \(k=\frac 16;\)
Б \(\Delta d=600\ \text{нм}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=\frac 12\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{2}\) – знову отримали \(k=\frac 12\) ‒ дробове число;
B \(\Delta d=1200\ \text{нм}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=\frac 32\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{2}-k=\frac 32\) – дробове число;
Г \(\Delta d=1500\ \text{нм}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}{2}-k=2\) – ціле число, що задовольняє умову інтерференційного мінімуму.
Отже, правильна відповідь Г ‒ \(1500\ \text{нм:}\) це дві цілі довжини хвилі і ще пів хвилі ‒ непарне число півхвиль ‒ п᾽ять.
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку знання і розуміння будови й роботи трансформатора.
У режимі холостого ходу трансформатора (в умові йдеться про розімкнену вторинну обмотку, тобто трансформатор не навантажений) справджується рівність: $$ \frac{U_1}{U_2}\approx\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_1}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_2}=\frac{N_1}{N_2}=k. $$
Відношення значень ЕРС \((\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_1\ \text{i}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_2)\) у дії, індукованих у первинній і вторинній обмотках трансформатора, дорівнює відношенню кількості витків \((N_1\ \text{i}\ N_2)\) в обмотках. Величину \(k\) називають коефіцієнтом трансформації. Первинна обмотка трансформатора підключена до джерела змінного струму, напруга на виході якого \(U_1.\) У вторинній обмотці струм не йде (вона розімкнена), тому напруга на кінцях вторинної обмотки за модулем дорівнює ЕРС індукції \((N_2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_2).\)
За умовою кількість витків первинної обмотки не змінювалася, і змінний струм у первинній обмотці протікав той самий. На кінцях вторинної обмотки напруга підвищилася, тож і кількість витків у ній збільшилася. Визначімо, на скільки збільшилася кількість витків у вторинній обмотці:
\begin{gather*} \frac{U_1}{U_2}=\frac{N_1}{N_2},\\[6pt] \frac{6\ \text{В}}{9\ \text{В}}=\frac{80}{N_2},\\[6pt] N_2=\frac{80\cdot 9\ \text{В}}{6\ \text{В}}=120. \end{gather*}Отже, \(N_2-N_1=120-80=40\) ‒ кількість витків у вторинній обмотці трансформатора збільшилася на \(40\) витків, щоб напруга підвищилася до \(9\ \text{В}.\)
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння перетворення енергії в коливальному контурі.
Коли конденсатор максимально заряджений, то на обкладках конденсатора накопичений максимальний електричний заряд \(q_\text{max},\) а між обкладками виникне електричне поле, енергія якого дорівнює \(W_\text{ел. max}:\) $$ W_\text{ел. max}=\frac{q^2_\text{max}}{2C}, $$ де \(C\) ‒ електроємність конденсатора, його незмінна характеристика.
У той момент, коли конденсатор повністю розрядиться, енергія електричного поля дорівнюватиме нулю, сила струму сягне максимального значення \(I_\text{max},\) а повна енергія контуру дорівнюватиме максимальній енергії магнітного поля \(W_\text{маг. max}:\) $$ W_\text{маг. max}=\frac{LI^2_\text{max}}{2}, $$ де \(L\) ‒ індуктивність котушки, її незмінна характеристика.
Запишімо закон збереження енергії контуру: $$ W_\text{ел. max}=W_\text{ел.}+W_\text{маг.}=W_\text{маг. max}. $$
Якщо за умовою струм, що проходить крізь котушку, становить \(80\ \text{%}\) від максимально можливого, то формула для визначення енергії магнітного поля матиме вигляд:
Тоді енергія електричного поля конденсатора становитиме
Відповідно до закону збереження енергії
Відповідь: 0,6.
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Змінний електричний струм.
Завдання скеровано на перевірку розуміння виникнення змінного електричного струму й законів, яким він підпорядкований.
У рамці, яка обертається в магнітному полі зі сталою кутовою швидкістю, індукуватиметься змінна електрорушійна сила (ЕРС), що змінюватиметься за гармонічним законом – за законом синуса або косинуса. Кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) між нормаллю до площини рамки й вектором магнітної індукції під час обертання змінюватиметься за законом $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\cdot t. $$
Тому й магнітний потік через площину рамки змінюватиметься: $$ \mathrm{Ф}=BS\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t. $$
Відповідно ЕРС індукції, що виникає в рамці за законом Фарадея, змінюватиметься за законом $$ e(t)=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_{max}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t, $$ оскільки $$ e(t)=-\mathrm{Ф}'(t), $$ де \(\mathrm{Ф}'(t)\) – похідна магнітного потоку за часом.
Сила струму в рамці, згідно із законом Ома, змінюватиметься так:
Отже, сила струму пропорційна часу, але під тригонометричною функцією. Тому із часом сила струму, як і ЕРС індукції, змінюватиметься за законом синуса (або косинуса за певних умов).
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на перевірку вміння застосовувати формули для визначення довжини хвилі й періоду коливань коливального контуру.
Довжину \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) радіохвилі визначімо за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=c\cdot T, $$ де \(c\) ‒ швидкість поширення світла у вакуумі (також швидкість поширення всіх електромагнітних хвиль, якими є радіохвилі), \(T\) ‒ період поширення хвилі.
Період поширення електромагнітної хвилі визначімо за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки коливального контуру, що є джерелом електромагнітних хвиль, \(C\) ‒ електроємність конденсатора, що також є складником коливального контуру.
Запишімо формули для обчислення обох зазначених в умові довжин радіохвиль:
\begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda_1}=c\cdot T_1=c\cdot 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1},\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda_2}=c\cdot T_2=c\cdot 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_2}. \end{gather*}Поділімо ліві і праві частини цих формул і визначімо шукану величину:
Отже, електроємність конденсатора \(C_2\) треба збільшити в \(9\) разів, щоб налаштувати радіоприймач на довжину хвилі, утричі більшу за початкову.
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Власна частота і період електромагнітних коливань. Формула Томсона. Електричний резонанс.
Завдання скеровано на перевірку знання і розуміння власної частоти, періоду коливань коливального контуру і поняття електричного резонансу.
Електромагнітні хвилі, досягши приймальної антени, збуджують у ній коливання тієї самої частоти, що й частота хвиль.
Частота зовнішньої хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{хв}\) дорівнює: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{хв}=\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) ‒ довжина хвилі, \(c=3\cdot 10^8\ \text{м/с}\) ‒ швидкість поширення електромагнітної хвилі.
Але в антену надходять коливання від різних радіостанцій, і кожна радіостанція працює на своїй частоті. Щоб із безлічі коливань виділити коливання потрібної частоти, використовують електричний резонанс. Для цього індуктивно з антеною пов’язують коливальний контур (див. рисунок). Змінюючи електроємність конденсатора (настроюючи радіоприймач), змінюють власну частоту \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{к}\) коливань контуру ‒ величину, обернену до періоду \(T\) коливань, що визначається за формулою Томсона: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{к}=\frac 1T=\frac{1}{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора.
Коли власна частота коливань коливального контуру збігається із частотою електромагнітної хвилі, на яку настроєно радіоприймач, настає резонанс: амплітуда вимушених коливань сили струму в контурі різко збільшується. Отже, з безлічі сигналів, що збуджують коливання в приймальній антені, виділений один високочастотний модульований сигнал.
Прирівняємо вирази для частоти: \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{хв}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}_\text{к},\\[6pt] \frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}=\frac 1T=\frac{1}{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}}. \end{gather*}
Виразімо й обчислімо шукану величину ‒ електроємність конденсатора:
Відповідь: 2.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Шкала електромагнітних хвиль.
Завдання скеровано на перевірку знання і розуміння видів електромагнітного випромінювання.
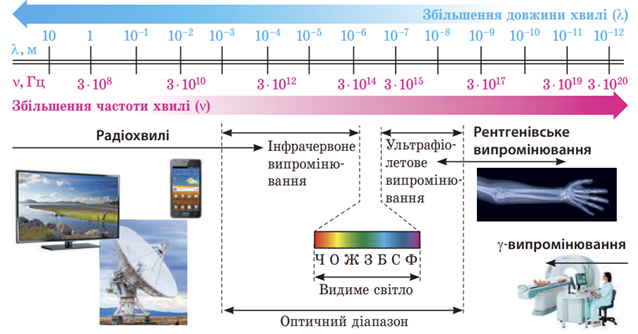
Шкала (спектр) електромагнітних хвиль ‒ безперервна послідовність частот і довжин електромагнітних хвиль, що існують у природі.
Довжина хвилі й частота випромінювання пов’язані формулою: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=\frac{c}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}}\Rightarrow \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\sim \frac{1}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}}. $$
Залежність між довжиною хвилі і частотою є оберненою: що більша частота, то менша довжина хвилі, і навпаки, що менша частота, то більша довжина хвилі (див. рисунок).
Найбільші довжини хвиль відповідають радіохвилям ‒ електромагнітним хвилям довжиною від \(100\ \text{км}\) до \(0,1\ \text{мм.}\) Відповідно діапазон частот є найменшим ‒ від \(3\ \text{кГц}\) до \(3\ \text{ТГц.}\)
Оптичний діапазон включає в себе інфрачервоне (теплове, довжина хвилі від \(1–2\ \text{мм}\) до \(760\ \text{нм}\)), видиме (довжина хвилі від \(760\) до \(400\ \text{нм}\)) і ультрафіолетове випромінювання (довжина хвилі від \(400\) до \(10\ \text{нм}\)). Відповідно у такому ж порядку зростає частота:
‒ інфрачервоне ‒ порядку \(10^{12}‒10^{14}\ \text{Гц,}\)
‒ видиме ‒ порядку \(10^{14}\ \text{Гц,}\)
‒ ультрафіолетове ‒ порядку \(10^{14}‒10^{16}\ \text{Гц.}\)
Рентгенівське випромінювання (\(X\text{-випромінювання}\)) ‒ електромагнітні хвилі довжиною від \(100\ \text{нм}\) до \(0,001\ \text{нм.}\) Відповідно частота буде порядку \(10^{15}‒10^{20}\ \text{Гц.}\)
Гамма \((\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma})\text{-випромінювання}\) ‒ електромагнітні хвилі довжиною менш ніж \(0,05\ \text{нм.}\) Частота ‒ порядку \(10^{20}\ \text{Гц}\) і вище.
Отже, з названих у варіантах відповіді видів електромагнітного випромінювання найбільшу частоту мають рентгенівські хвилі.
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння закону збереження енергії під час електромагнітних коливань в коливальному контурі і вміння його застосовувати.
Під час електромагнітних коливань в коливальному контурі відбувається періодичне перетворення енергії: енергія електричного поля конденсатора переходить в енергію магнітного поля, і навпаки.
Запишімо закон збереження енергії для ідеального (вважаємо, що енергія не витрачається на нагрівання підвідних проводів, обмотки котушки, на поляризацію діелектрика, тощо) коливального контуру відповідно до умови завдання: $$ \frac{CU^2_{max}}{2}=\frac{CU^2}{2}+\frac{Li^2}{2}=\frac{LI^2_{max}}{2}, $$ де \(C\) ‒ електроємність конденсатора, \(U\) ‒ напруга на конденсаторі, \(L\) ‒ індуктивність котушки, \(I\) ‒ сила струму в котушці.
Помножмо цю рівність на \(2\) й визначмо модуль напруги на конденсаторі після зменшення сили струму в котушці:
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.
Завдання скеровано на перевірку знання і розуміння фізичного змісту відносного показника заломлення.
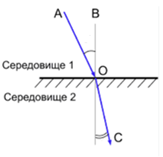
$$ n_{21}=\frac{n_2}{n_1}, $$ де \(n_{21}\) ‒ це фізична величина, яку називають відносним показником заломлення середовища \(2\) (середовища, в якому світло поширюється після заломлення) відносно середовища \(1\) (середовища, із якого світло падає).
Відносний показник заломлення \(n_{21}\) показує, у скільки разів швидкість \(v_1\) поширення світла в середовищі \(1\) більша (або менша), ніж швидкість \(v_2\) поширення світла в середовищі \(2:\) $$ n_{21}=\frac{v_1}{v_2}. $$
Отже, обчислімо відношення швидкостей світла в середовищах з різними показниками заломлення відповідно до умови: $$ \frac{v_1}{v_2}=\frac{n_2}{n_1}=\frac{1,65}{1,5}=1,1. $$
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання. Власна частота й період електромагнітних коливань. Формула Томсона.
Завдання скеровано на перевірку знання формули Томсона й розуміння її фізичного змісту.
Період \(T\) власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора.
Коливання в ідеальній коливальній системі називають власними коливаннями, період власних коливань визначений параметрами коливальної системи і не залежить від амплітуди коливань, тобто від енергії, яку передано системі під час виведення її з положення рівноваги. Оскільки конденсатор і котушка після зміни сили струму залишилися ті самі, то і період коливань контуру не зміниться.
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку розуміння будови трансформатора й уміння описувати його роботу аналітично, через відношення фізичних величин.
Первинна обмотка трансформатора підключена до джерела змінного струму, напруга на виході якого \(u_1.\) Під час проходження струму в обмотці виникає ЕРС (електрорушійна сила) самоіндукції \(e_1.\) Опір обмотки вважатимемо нехтовно малим. І в будь-який момент часу для діючих значень напруги й ЕРС правильною є рівність $$ U_1\approx \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_1. $$
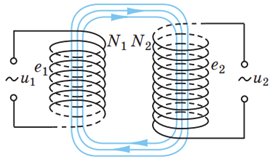
У вторинній обмотці струм не йде (вона розімкнена), тому напруга на кінцях вторинної обмотки за модулем дорівнює ЕРС індукції, отже, відповідно маємо рівність: $$ U_2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_2. $$
Отже, у режимі холостого ходу справджується рівність \begin{gather*} \frac{U_2}{U_1}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_2}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_1}=\frac{N_2}{N_1}=k, \end{gather*} де \(N_1\) і \(N_2\) ‒ кількість витків у першій і другій обмотках відповідно, \(k\) ‒ коефіцієнт трансформації.
У разі підключення обмоток першим способом ЕРС індукції в першій обмотці дорівнює фактично напрузі на джерелі: \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_1=U. \end{gather*}
А ЕРС індукції у вторинній обмотці за умовою дорівнює \(16\ \text{В}:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_2=16\ \text{В}. $$
Якщо ж поміняти місцями обмотки й підключити вторинну обмотку до джерела, то \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_2=U. \end{gather*}
А ЕРС індукції в первинній обмотці, яка тепер стала вторинною, за умовою дорівнює \(4\ \text{В}:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_1=4\ \text{В}. $$
Коефіцієнт трансформації для першого способу підключення $$ k=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_2}{U}=\frac{16}{U}. $$
А для другого способу з’єднання коефіцієнт трансформації буде такий самий: $$ k=\frac{U}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_1}=\frac U4. $$
Прирівняємо праві частини цих рівностей: $$ \frac{16}{U}=\frac U4. $$
Обчислимо напругу джерела:
\begin{gather*} U^2=16\cdot 4=64,\\[7pt] U=8\ \text{В}. \end{gather*}Відповідь: 8.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на перевірку знання і розуміння формули Томсона ‒ формули для визначення періоду власних коливань контуру.
Період \(T\) власних електромагнітних коливань у коливальному контурі, складниками якого є котушка і конденсатор, визначають за формулою Томсона $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора.
Запишімо формулу для визначення періоду до змін і після них:
Отже, після змін параметрів котушки і конденсатора період власних коливань контуру збільшиться вдвічі.
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння перетворення енергії в коливальному контурі.
У той момент, коли конденсатор повністю розрядиться, енергія електричного поля дорівнюватиме нулю \(W_\text{ел}=0,\) сила струму сягне максимального значення \(I_\text{max},\) а повна енергія контуру становитиме:
За законом збереження енергії для ідеального коливального контуру максимальна енергія електричного поля дорівнює максимальній енергії магнітного поля: $$ W_\text{ел max}=W_\text{маг max}=45\ \text{мДж}. $$
Відповідь: \(45.\)
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння того, як змінюються фізичні величини під час електромагнітних коливань у коливальному контурі.
У коливальному контурі виникають електромагнітні коливання, якщо зарядити конденсатор. На обкладках конденсатора накопичиться деякий електричний заряд \(q,\) а між обкладками виникне електричне поле, енергія \(W_\text{ел}\) якого дорівнює (\(C\) ‒ електроємність конденсатора): $$ W_\text{ел}=\frac{q^2}{2C}. $$
Якщо після зарядки конденсатор замкнути на котушку індуктивності, то під дією електричного поля конденсатора вільні заряджені частинки в контурі почнуть рухатися напрямлено. У контурі виникне електричний струм \(i,\) а конденсатор почне розряджатися. Тобто заряд конденсатора зменшуватиметься, а отже й енергія електричного поля конденсатора меншатиме, оскільки вона прямо пропорційна квадрату заряду.
Під час того як конденсатор розряджатиметься, сила струму в контурі збільшуватиметься, а магнітне поле посилюватиметься, зростатиме його силова характеристика ‒ модуль магнітної індукції магнітного поля котушки. Оскільки енергія магнітного поля \(W_\text{маг}\) котушки (\(L\) ‒ індуктивність котушки) $$ W_\text{маг}=\frac{Li^2}{2} $$ прямо пропорційна силі струму \(i\) в ній, збільшуватиметься й енергія магнітного поля.
Тож єдина з поданих фізична величина, яка зменшуватиметься під час розрядження конденсатора, ‒ це енергія електричного поля.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку знання суті і розуміння закономірностей коливального процесу в коливальному контурі, а також уміння описувати цей процес відповідним рівнянням.
Коливання (зміна значень напруги) у коливальному контурі відбуваються за гармонічним законом (законом косинуса або синуса): \begin{gather*} u=U_{max}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t,\\[7pt] \text{або}\\[7pt] u=U_{max}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t, \end{gather*} де \(u\) – миттєве значення напруги, \(U_{max}\) – амплітудне значення напруги, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\) – циклічна частота напруги, \(t\) – час.
В умові не задано амплітудне значення напруги, тож зосередимося на визначенні циклічної частоти \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}, $$ де \(T\) – період коливань.
Період власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, \(C\) – електроємність конденсатора.
Отже, за цих умов єдиним рівнянням, що описує залежність напруги \(u\) в котушці від часу \(t,\) може бути рівняння $$ u=0,5\cos2000t. $$
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Шкала електромагнітних хвиль. Властивості електромагнітного випромінювання різних діапазонів.
Завдання скеровано на перевірку знань про різні види електромагнітного випромінювання і їхні джерела.
Під час розпаду радіонуклідів у ядерному реакторі виникає радіоактивне випромінювання, один із видів якого – гамма-промені.
Будь-які тіла, температура яких вища від абсолютного нуля, випромінюють інфрачервоні промені. Саме на цьому ґрунтується застосування їх у тепловізорах – приладах нічного бачення. Тому гарячий чай є джерелом інфрачервоного (теплового) випромінювання.
Радіохвилі – від наддовгих із довжиною понад \(10\ \text{км}\) до ультракоротких і мікрохвиль із довжиною менш ніж \(0,1\ \text{мм}\) – породжує змінний електричний струм. Електромагнітні хвилі радіодіапазону породжені високочастотним змінним струмом, який створюють генератори високочастотних електромагнітних коливань. У цьому завданні джерелом радіохвиль є супутник зв’язку.
Люмінофор – речовина, яка здатна світитися за збудження, тобто люмінесціювати. Люмінофори широко використовують в електроніці, наприклад, ними вкривають екран телевізора, електропроменевої трубки, де їхнє світіння за бомбардування електронами формує зображення, у сцинтиляційних лічильниках тощо. Людське око сприймає це світіння, отже це діапазон видимого світла.
Відповідь: 1В, 2А, 3Г, 4Д.
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку знання суті і розуміння закономірностей коливального процесу в коливальному контурі, а також уміння описувати цей процес відповідним рівнянням.
Коливання в коливальному контурі (у котушці зокрема) відбуваються за гармонічним законом (законом косинуса або синуса): \begin{gather*} i=I_{max}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t,\\[7pt] \text{або}\\[7pt] i=I_{max}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t, \end{gather*} де \(i\) – миттєве значення сили струму, \(I_{max}\) – амплітудне значення сили струму, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\) – циклічна частота змінного струму, \(t\) – час.
У будь-якій реальній коливальній системі завжди є втрати енергії. Під час електромагнітних коливань – на нагрівання провідників, випромінювання електромагнітних хвиль. Частина енергії електромагнітного поля під час кожного коливання перетворюється на внутрішню (теплову) енергію тощо. Унаслідок цього амплітуда коливань із часом зменшується. А через певний інтервал часу, якщо немає надходжень енергії від зовнішнього джерела, коливання припиняються (згасають). Тому вільні коливання завжди є згасними. Але в умові зазначено, що амплітуда коливань не змінюється, отже, вважатимемо коливання незгасними.
В умові не задано амплітудне значення сили струму, тож зосередимося на визначенні циклічної частоти \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}, $$ де \(T\) – період коливань.
Період власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, \(C\) – електроємність конденсатора.
Отже, за цих умов єдиним рівнянням, що описує залежність сили струму \(i\) в котушці від часу \(t,\) може бути рівняння $$ i=0,15\sin250t. $$
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на перевірку знання і розуміння формули Томсона, уміння визначати довжину електромагнітної хвилі.
За час, що дорівнює періоду \(T,\) хвиля зі швидкістю \(v\) поширюється на відстань, яку називають довжиною \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) хвилі: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=vT. $$
За умовою цієї задачі хвиля поширюється зі швидкістю світла: $$ v=c=3\cdot 10^8\ \text{м/с}. $$
Період \(T\) коливань коливального контуру радіоприймача визначімо за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора.
Дістанемо загальну формулу для визначення довжини хвилі, на яку настроєний радіоприймач:
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння електромагнітного коливання і його частоти.
За умовою частота вільних електромагнітних коливань $$ 1\ \text{кГц}=1000\ \text{Гц}. $$
Це означає, що за секунду відбувається \(1000\) коливань. Тобто за кожне з \(1000\) коливань конденсатор коливального контуру встигає двічі перезарядитися, тож струм у котушці двічі набуває максимального значення і двічі він дорівнює нулю. У той момент, коли конденсатор повністю розряджений (рисунок в і ж), сила струму сягне максимального значення. А коли конденсатор повністю заряджений, то сила струму в котушці дорівнює нулю (рисунок а і д).
Отже, щосекунди сила струму в котушці індуктивності дорівнюватиме нулю \(2000\) разів. Щодо рисунка и, де пластини конденсатора вже знову повністю заряджені так само, як і на початку коливання (рисунок а), а струм в котушці дорівнює нулю: це вже початок наступного повного коливання, як на рисунку а. Коли відбулося пів коливання ‒ пройшло пів періоду (рисунок д) ‒ конденсатор повністю заряджений, він перезарядився, тобто заряд на його обкладках змінився на протилежний.
Схематичне зображення повного електромагнітного коливання:
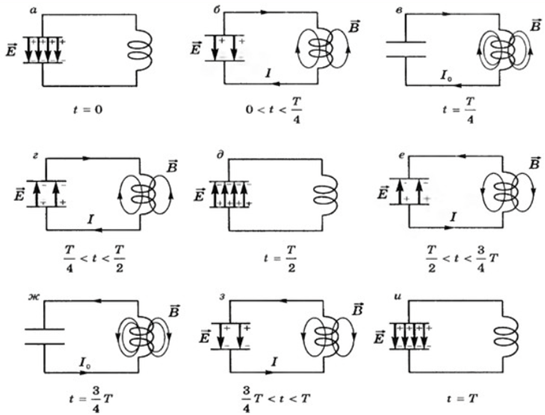
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку знання і розуміння принципу будови й дії трансформатора.
Основною причиною шуму трансформаторів є фізичне явище – магнітострикція. Коротко це означає: якщо на лист електротехнічної сталі діяти магнітним полем, цей лист згинатиметься сам собою.
Найпростіший трансформатор складається із замкненого осердя (магнітопроводу) і двох обмоток (див. рисунок). Осердя (сердечник) виготовлено з тонких пластин трансформаторної сталі.
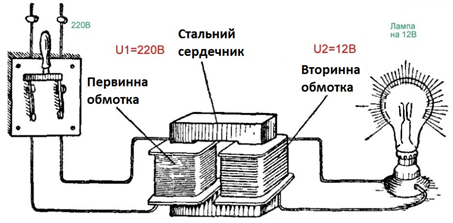
Явища зміни форми й розмірів феромагнітних тіл досліджували ще у ХІХ столітті. Англійський дослідник Джеймс Джоуль 1842 року помітив, що під дією магнітного поля тонкий залізний об’єкт подовжується в одному напрямку й скорочується в іншому, зберігаючи колишній об’єм. Таку деформацію супроводжують звуки: уявімо собі, що ми почуємо, якщо спробуємо зігнути лист металу або навіть звичайної фольги.
В умовах дії електромагнітного поля подібний процес набуває стабільної частоти. Частота гулу досить низька, що й дає змогу людському вуху його вловлювати. Оскільки йдеться про змінний струм, магнітне поле встигає двічі за фазу змінити свій напрямок, розгойдуючи усі мікрообласті металу сердечника. В Україні побутова електрична мережа з напругою \(220\ \text{В}\) працює за частоти \(50\ \text{Гц}.\) Це означає, що трансформаторні обмотки коливаються вдвічі частіше – із частотою \(100\ \text{Гц}.\) Для порівняння в США, де загальні мережі видають \(110\ \text{В}\) за \(60\ \text{Гц},\) трансформатори звучать вище – із частотою \(120\ \text{Гц}.\)
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона. Електромагнітні хвилі та швидкість поширення їх. Електродинаміка. Основи електростатики. З’єднання конденсаторів.
Завдання скеровано на перевірку розуміння принципу роботи коливального контуру.
Радіохвилі ‒ це електромагнітні хвилі, які поширюються зі швидкістю світла \(c.\)
Довжину хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) визначімо за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}=cT, $$ де \(T\) ‒ період власних електромагнітних коливань у коливальному контурі. Його можна визначити за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки контуру, \(C\) ‒ електроємність конденсатора контуру.
Отже, довжину хвилі, на яку налаштовано радіоприймач, обчислімо за формулою $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_1=c\cdot 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1}. $$
Після приєднання паралельно до конденсатора ще одного, утричі більшої ємності, загальна електроємність $$ C_2=C_1+3C_1=4C_1, $$ бо за паралельного з’єднання конденсаторів їхні електроємності додають одну до одної.
Тепер радіоприймач буде налаштований на довжину хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2:\) \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2=c\cdot 2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{L4C_1}. \end{gather*}
Поділімо ліві і праві частини формул для довжин хвиль:
\begin{gather*} \frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_1}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2}=\frac{c2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC_1}}{c2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{L4C_1}}=\sqrt{\frac 14}=\frac 12,\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2=2\cdot \style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_1=2\cdot 4\ \text{м}=8\ \text{м}. \end{gather*}Відповідь: 8.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Властивості електромагнітного випромінювання різних діапазонів.
Завдання скеровано на перевірку знання і розуміння властивостей електромагнітного випромінювання різних діапазонів.
1. Інфрачервоне (теплове) випромінювання (довжина хвилі від \(760\ \text{нм}\) до \(1–2\) мм) ‒ застосовують у приладах нічного бачення (Б).
Інфрачервоні промені випромінюють будь-які тіла, що мають температуру, вищу за абсолютний нуль. Саме на цьому ґрунтується їхнє застосування в тепловізорах ‒ приладах нічного бачення. Людське око не здатне бачити інфрачервоне випромінювання, адже енергії квантів недостатньо, щоб збудити нервові клітинки в оці. Але багато представників фауни мають пристосування ‒ своєрідні прилади нічного бачення, які здатні сприймати ці промені. Інфрачервоне випромінювання зазвичай є корисним для людини, але у великих дозах може спричинити запаморочення, знепритомніння ‒ тепловий і сонячний удари.
2. Ультрафіолетове випромінювання (довжина хвилі від \(10\) до \(400\) нм) ‒ спричиняє засмагу (А).
Ультрафіолет випромінюють Сонце й інші зорі, електричні дуги, спеціальні кварцові лампи. Людське око не реагує на ультрафіолетове випромінювання. Найімовірніше, це пов’язано з еволюцією, адже ці промені добре поглинає вода в рогівці ока. Ультрафіолет має високу хімічну активність, тому у великих дозах негативно впливає на людину. Саме тому не варто перебувати на сонці, коли сонячне випромінювання найінтенсивніше. Проте в невеликих дозах ультрафіолет є корисним: він сприяє виробленню вітаміну D, зміцнює імунну систему, стимулює низку важливих життєвих функцій в організмі.
3. Рентгенівське випромінювання (\(X\)-випромінювання) ‒ електромагнітні хвилі довжиною від \(0,001\ \text{нм}\) до \(100\ \text{нм}\) ‒ виникає в результаті гальмування швидких електронів на аноді (Г).
Рентгенівське випромінювання виникає внаслідок взаємодії швидких електронів з атомами катода в рентгенівській трубці – вакуумній скляній колбі з двома електродами. Між електродами створюється висока напруга \((10–500\ \text{кВ}),\) а катодом пропускають електричний струм; коли катод нагрівається, то з його поверхні починають вилітати (емітувати) електрони. Електрони, які випромінює катод, розганяє до величезних швидкостей електричне поле. Рентгенівське випромінювання найширше застосовують у медицині, адже воно має властивість проходити крізь непрозорі предмети (наприклад, тіло людини). Кісткові тканини менш прозорі для рентгенівського випромінювання, ніж інші тканини організму людини, тому кістки чітко видно на рентгенограмі. Рентгенівське випромінювання чинить руйнівну дію на клітини організму, тому застосовувати його потрібно надзвичайно обережно. Рентгенівську зйомку використовують також у промисловості (для виявлення дефектів), хімії (для аналізу сполук), фізиці (для дослідження структури кристалів).
4. Гамма \((\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma})\)-випромінювання ‒ електромагнітні хвилі довжиною менш ніж \(0,05\ \text{нм}\) ‒ виникає в результаті самочинного розпаду атомних ядер (Д).
Гамма-випромінювання випускають збуджені атомні ядра під час ядерних реакцій, радіоактивних перетворень атомних ядер і перетворень елементарних частинок. Гамма-випромінювання використовують у дефектоскопії (виявлення дефектів усередині деталей); радіаційній хімії (наприклад, у процесі полімеризації); сільському господарстві й харчовій промисловості (стерилізація харчів); медицині (стерилізація приміщень, променева терапія). На організми гамма-випромінювання чинить мутагенний (стійкі спадкові зміни) і канцерогенний (здатність викликати злоякісні пухлини) вплив. Разом із тим чітко спрямоване й дозоване гамма-випромінювання застосовують для знищення ракових клітин (променева терапія).
Відповідь: 1Б, 2А, 3Г, 4Д.