Розділ: Механіка
Тема: Елементи механіки рідин та газів
Кількість завдань: 52
ТЕМА: Механіка. Елементи механіки рідин і газів. Гідростатичний тиск. Атмосферний тиск.
Завдання скеровано на перевірку знання і розуміння атмосферного й гідростатичного тисків і їхніх властивостей.
На повітря під ртуттю тисне повітря (позначмо цей тиск як
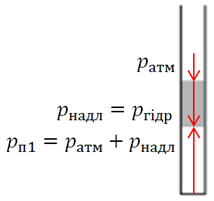
Повітря під ртуттю за умовою має надлишковий тиск
Обчислімо тиск повітря під ртуттю:
Коли ж повернути трубку у вертикальній площині на
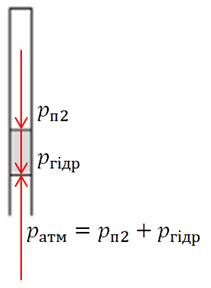
Отже, визначимо тиск повітря в трубці після її перевертання:
Відповідь:
ТЕМА: Механіка. Елементи механіки рідин і газів. Тиск нерухомої рідини на дно й стінки посудини.
Завдання скеровано на перевірку знання і розуміння закону Паскаля і формули гідростатичного тиску.
Із закону Паскаля (тиск, створюваний на нерухому рідину, передається рідиною однаково в усіх напрямках) і формули гідростатичного тиску
Отже, робимо висновок, що тиск усередині нерухомої однорідної рідини ‒ у воді (див. рисунок) ‒ у точках
На рівні точок
Це одна з властивостей сполучених посудин (у завданні ‒
Тиск у точках
На рівні точки
А на рівні точки
Відповідь: B.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.
Завдання скеровано на перевірку знання і вміння застосувати закон Архімеда.
Скористаймося законом Архімеда. На тіло, занурене в рідину або газ, діє виштовхувальна сила
Обчислимо значення сили Архімеда:
Відповідь: 20.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.
Завдання скеровано на перевірку знання і застосування закону Архімеда.
Для того, щоб пліт із вантажем утримувався на плаву (пліт буде максимально навантажений так, щоб вантаж на намокав), потрібно, щоб силу тяжіння
Відповідь: 2000.
Механіка. Елементи динаміки рідин i газів. Умова плавання тіл.
Завдання скеровано на перевірку розуміння поняття густини та вміння застосовувати закон Архімеда.
Силу Архімеда можна визначити за формулою
Силу тяжіння визначають за формулою
Густина речовини
Тоді масу тіла можна виразити як
Тоді силу тяжіння можна записати як:
Вважатимемо, що на тіло в рідині діє лише сила тяжіння, що напрямлена вниз, і виштовхувальна сила Архімеда, напрямлена вгору. За другим законом Ньютона
Тіло плаває в товщі рідини, а не спливає на поверхню чи тоне, тому прискорення
Якщо спрямувати вісь x у напрямку прискорення вільного падіння, можна спроєктувати векторне рівняння:
Відповідь: Б.
ТЕМА: Робота. Сила Архімеда.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про силу Архімеда.
Дано:
Знайти:
Для того, щоби перевернути блок, достатньо його центр мас підняти на висоту, на якій він у вертикальному положенні. Оскільки блок циліндричний, то в обох положеннях він на половині висоти блока (рис. 1).
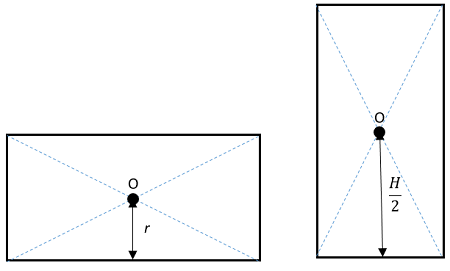
Рис. 1. Положення центра мас у вертикальному й горизонтальному положенні
Оскільки поперечні розміри стовпа за умовою враховувати не потрібно, то можна вважати, що під час перевертання центр мас піднімають на половину всієї висоти
Рівнодійну сил, що діють на блок, можна обчислити за формулою
Сила тяжіння діє вертикально вниз, притягуючи блок до землі, а сила Архімеда виштовхує блок вертикально вгору, інші сили на блок не діють. Якщо вважати напрямок «вертикально вниз» додатним,
Маса тіла пов’язана з його густиною формулою
Тоді
Оскільки об’єму блока невідомий, із дужок можна винести його густину:
Тоді робота, необхідна для підняття центра мас бетонного блока на половину його висоти, дорівнює
Відповідь: 6.
ТЕМА: Елементи механіки рідин і газів. Гідростатичний тиск.
Завдання скеровано на розуміння понять тиску й сили тиску та вміння визначати гідростатичний тиск.
Якщо всю воду з ширшої посудини перелили у вужчу, то об’єм води не змінився, площа дна посудини зменшилася, а рівень води збільшився, як показано на рисунку 1.
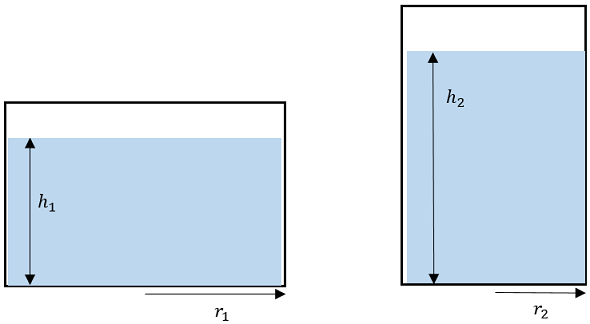
Рис. 1. Рівень води в широкій і високій посудинах
Тиск на дно в обох посудинах є сумою гідростатичного тиску стовпчика води й атмосферного тиску. Гідростатичний тиск
Тиск на дно в першій (широкій) посудині дорівнює:
Вирази для тиску відрізняються лише висотою стовпчика, тож у посудині, де вона більша, тиск на дно також буде більшим.
Сила, що діє на дно обох посудин і створює тиск, – це вага рідини в посудині:
Маса води після переливання не змінилася, посудини перебувають у стані спокою, а отже й вага не змінилася. Тож сила тиску під час такого переливання не зміниться.
Відповідь: Б.
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням сили поверхневого натягу.
Дано:
Знайти:
На кільце на поверхні води діють сили поверхневого натягу, що утримують його на поверхні, і сила тяжіння. Силу тяжіння можна визначити за формулою
Окрім того, кільце обмежує на поверхні дві ділянки – усередині й зовні. Тому з обох боків на нього діятимуть сили поверхневого натягу.
Дріт, із якого зроблене кільце, – тонкий, тому можна вважати, що внутрішній радіус дорівнює зовнішньому радіусу кільця. Тож довжина кільця з боку зовнішньої і внутрішньої поверхні буде однаковою:
Тоді сила, що необхідна для того, щоби підняти кільце з поверхні, має подолати силу тяжіння і сили поверхневого натягу із зовнішнього і внутрішнього боку:
Відповідь: 56.
ТЕМА: Маса. Густина. Умова плавання тіл.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на використання умови плавання тіл.
Дано:
Знайти:
За умовою плавання тіл тіло перебуватиме в рівновазі, якщо
Силу тяжіння визначають за формулою
Масу й густину тіла пов’язує формула
Тому силу тяжіння можна записати як
Силу Архімеду визначають за формулою
Об’єм дошки можна визначити з її геометричних розмірів:
Дошка не повністю занурена під воду, а під час розрахунку сили Архімеда треба використовувати об’єм зануреної під воду частини. Цей об’єм можна розрахувати за формулою
Тоді умова плавання дошки матиме вигляд:
Відповідь: 750.
ТЕМА: Гідростатичний тиск.
Завдання скеровано на оцінювання розуміння поняття гідростатичного тиску й уміння застосовувати його під час розв’язування розрахункових задач.
Гідростатичний тиск
Якщо вважати, що тиск у повітряних кишенях запаяних трубок однаковий, то тиск у точці B дорівнює тиску в точці Вʹ, а тиск у точці С дорівнює тиску в точці Сʹ. Тиск однорідної рідини на однаковій висоті однаковий, тому можна визначити рівень у воді за межами трубок, який відповідає точкам В і С (рис. 1).
Тиск в точці А дорівнює атмосферному
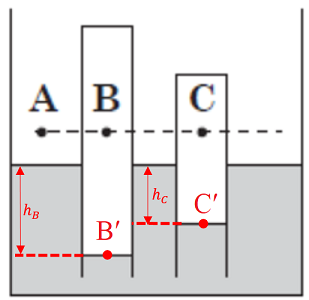
Рис. 1. Визначення гідростатичного тиску
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Сили. Додавання сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з визначення рівнодійної кількох сил.
На кульку, що піднімається вгору в повітрі, діють три сили: сила Архімеда, що виштовхує її з товщі повітря вгору, сила тяжіння, яка притягує кульку до землі, і сила опору повітря, що заважає руху кульки (рис. 1). Оскільки сила Архімеда більша за значенням від сили тяжіння, кулька рухатиметься вгору, а сила опору повітря буде напрямлена вниз.
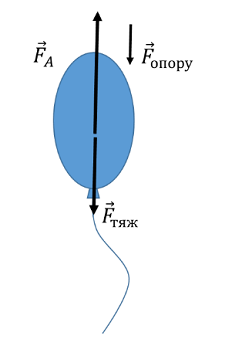
Рис. 1. Сили, що діють на кульку
Рівнодійна
Відповідь: A.
ТЕМА: Механіка. Елементи динаміки рідин і газів. Умова плавання тіл.
Завдання скеровано на оцінювання розуміння поняття «густина» і вміння застосовувати закон Архімеда.
Густина речовини
Для правильного розв’язання завдання потрібно пригадати умови плавання тіл:
Густину зубної пасти, укинутої в посудину з водою, обчислюють за формулою:
Відповідь: A.
ТЕМА: Сполучені посудини.
Завдання скеровано на оцінювання розуміння поняття «гідростатичний тиск».
У сполучених посудинах у кожній трубці рівень рідин установлюється так, що гідростатичний тиск стовпчика рідини в них однаковий.
Гідростатичний тиск
Якщо рідини в трубках однорідні, то тиск на однаковій висоті в усіх трубках однаковий. За умовою завдання в лівій трубці посудини рівень гасу вищий за рівень води в правій трубці. Це відбувається тому, що густина гасу менша порівняно з водою, і щоби створити такий самий гідростатичний тиск, як і в стовпчика води в правій трубці, висота стовпчика гасу має бути більшою.
У точці B (див. рисунок) тиск дорівнює атмосферному
Тобто
Оскільки точка C лежить на межі розділу двох рідин, то тиск стовпця гасу над нею дорівнює тиску стовпця води над точкою D на такій самій висоті, але в трубці із водою. Тож
Точки E і F на однаковій висоті у воді, тому тиск у них однаковий, а
Відповідь: B.
ТЕМА: Механіка. Елементи механіки рідин і газів. Умова неперервності течії рідини.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання умови неперервності течії.
Дано:
Знайти:
Незалежно від зміни форми труби течія всередині повинна залишатись неперервною, тобто кількість води, що проходить за секунду через переріз труби в будь-якому місці має залишатись однаковою. Тоді чим вужча труба, тим швидшою має бути течія на цій ділянці й навпаки. Тоді умову неперервності течії для труби, у якої є дві ділянки – широка й вузька, можна записати так:
Площу перерізу циліндричної труби можна обчислити за такою формулою:
Тоді
Відповідь: 1,6.
ТЕМА: Сполучені посудини.
Завдання скеровано на оцінювання розуміння принципів роботи сполучених посудин.
У сполучених посудинах у кожній трубці однорідні рідини встановлюються на однаковому рівні, адже стовпчик рідини в кожній із посудин має створювати однаковий гідростатичний тиск.
Гідростатичний тиск p визначають за формулою
Відповідь: Г.
ТЕМА: Гідростатичний тиск
Завдання скеровано на оцінювання розуміння понять атмосферного й гідростатичного тиску, уміння розв’язувати розрахункові задачі, пов’язані з ними.
Дано:
Знайти:
Атмосферний тиск – це тиск повітря над рівнем, де його вимірюють. Тому тиск на першому поверсі буде більшим від тиску на 101-му поверсі саме на значення тиску стовпа повітря висотою 100 поверхів. Тиск нерухомого повітряного стовпа – це гідростатичний тиск. Його визначають за формулою:
Тоді висота повітряного стовпа, утвореного 100 поверхами дорівнюватиме:
І гідростатичний тиск цього повітряного стовпа:
Відповідь: 3,9.
ТЕМА: Маса. Густина. Умова плавання тіл.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про умови плавання тіл, розуміння понять густини й маси.
На шматочок льоду у воді діє виштовхувальна сила Архімеда. Тож об’єм, зафіксований до того, як лід розтанув, – це сума об’єму води й об’єму частини кубика льоду, що перебувала під водою.
Щоби шматочок льоду плавав, сила Архімеда, яка діє на його занурену частину, має дорівнювати силі тяжіння, що діє на нього:
Силу тяжіння, що діє на шматочок льоду, можна розрахувати за формулою:
Тоді можемо знайти об’єм води, витіснений цим шматком льоду, знаючи вираз для розрахунку сили Архімеда:
Тоді можна виразити об’єм з (3):
Тож певний рівень води в мензурці, що встановився на позначці 50 мл, зумовлений водою об’ємом 40 мл і льодом об’ємом 10 мл (він перебуває під водою і витісняє рідину).
Після того, як лід розтане, до води об’ємом 40 мл буде додано об’єм води, що утвориться з кубика льоду після його розтавання. Цей об’єм можна обчислити, знаючи, що під час танення маса речовини не змінюється, тож маса льоду дорівнюватиме масі води, що утвориться.
Вираз для густини води:
Тож, виразивши об’єм талої води з (5), дістанемо:
Тобто після танення льоду об’єм речовини в мензурці складається з об’єму води, що була там від початку (40 мл) і талої води об’ємом 10 мл, разом – 50 мл.
Відповідь: Б.
ТЕМА: Динаміка рідин і газів. Потужність.
Завдання скеровано на перевірку розуміння поняття потужності та динаміки потоку рідини в трубі.
Дано:
Знайти:
Роботу сили можна визначити за формулою
На якір у воді діє сила тяжіння, сила Архімеда й зовнішня сила, що піднімає якір (рис. 1).
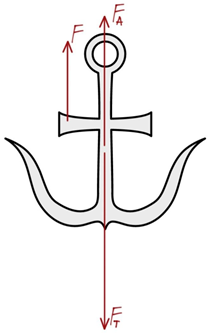
Рис. 1. Сили, що діють на якір
Формула, якою описують другий закон термодинаміки, така:
Оскільки якір піднімають повільно, можна вважати, що прискорення дорівнює нулю, тоді в проєкції на вісь OY другий закон Ньютона можна записати так:
Силу тяжіння визначають за формулою
Маса тіла, його густина й об’єм пов’язані формулою
Тож
Тоді, зважаючи на те, що напрямок сили та переміщення однакові,
Відповідь: 2.
ТЕМА: Сполучені посудини.
Завдання скеровано на перевірку вміння розв’язувати задачі зі сполученими посудинами.
У сполучених посудинах у кожній трубці рівень рідин установлюється так, що гідростатичний тиск стовпчика однакової рідини у них рівний.
Гідростатичний тиск
Якщо рідини в трубках однорідні, то тиск на однаковій висоті в усіх трубках буде однаковим. Але в лівій трубці посудини рівень олії вищий, ніж рівень води в правій трубці, адже олія має меншу густину. Щоби створити такий самий гідростатичний тиск, як і в правій трубці, висота стовпчика рідини має бути більшою.
Порівняймо точки, позначені на рисунку.
У точці В тиск дорівнює атмосферному
Точка С в правій трубці на тому ж рівні, що межа розділу двох рідин у лівій трубці, тому тиск у ній дорівнює тиску всього стовпчика олії. Висота всього стовпчика олії більша за висоту стовпчика над точкою А, тому
Точка D перебуває найглибше з усіх точок у воді, тому тиск на неї найбільший.
Відповідь: A.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання знання вимірювальних пристроїв і розуміння фізичних величин, для вимірювання яких їх використовують.
1. Фізична величина, що дорівнює відношенню шляху до часу – це швидкість:
Прилад, що вимірює швидкість – це спідометр.
2. Фізична величина, що дорівнює добутку густини, прискорення вільного падіння і висоти стовпчика рідини – це гідростатичний тиск (тиск нерухомого стовпчика рідини):
Прилад, що вимірює тиск рідини чи газу – це манометр.
3. Фізична величина, що дорівнює відношенню густини водяної пари до густини насиченої пари за певної температури й виражена у відсотках – це відносна вологість:
Прилад, що вимірює відносну вологість – це гігрометр.
4. Фізична величина, що дорівнює добутку маси на прискорення вільного падіння – це сила тяжіння:
Прилад, що вимірює силу – це динамометр.
Відповідь: 1В, 2А, 3Г, 4Б.
ТЕМА: Гідростатичний тиск.
Завдання скеровано на оцінювання розуміння поняття гідростатичного тиску
У кожній із посудин, зображених на рисунку, рідина встановилася на однаковому рівні. Тиск на дно рідини складатиметься з атмосферного тиску, який буде однаковим для трьох посудин, що розташовані в тій самій кімнаті і тиску стовпчика рідини в посудині. Тиск нерухомого стовпчика рідини або газу називають гідростатичним.
Гідростатичний тиск
Оскільки висота стовпчика рідини в усіх посудинах однакова, то і їхній гідростатичний тиск також буде однаковим. А отже й загальний тиск на дно посудини буде однаковим.
Відповідь: A.
ТЕМА: Динаміка рідин і газів. Потужність.
Завдання скеровано на перевірку розуміння поняття потужності й динаміки потоку рідини в трубі.
Дано:
Знайти:
Водний насос, що перекачує воду, виконує роботу над нею. Оскільки труба горизонтальна, то під час руху нею потенціальна енергія води не змінюється. Робота, виконана над водою в трубі, переходить у її кінетичну енергію.
Тоді потужність водяного насоса
Маса й об’єм пов’язані між собою формулою
Маса води, що протікає крізь трубу, дорівнює добутку її густини на об’єм:
За умовою кількість води, що протікає по трубі, і, відповідно, її маса мають збільшитися вдвічі
Об’єм води, що протікає крізь трубу за час
Тоді потужність
Оскільки переріз труби не змінюється, то для збільшення об’єму води вдвічі має збільшитися вдвічі швидкість потоку:
Тоді відношення потужності до і після зміни таке:
Відповідь: 8.
ТЕМА: Механіка. Основи динаміки. Умова плавання тіл.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням закону Архімеда.
Дано:
Знайти:
На камінь у воді діють дві сили – сила тяжіння, що притягує його до дна, і виштовхувальна сила Архімеда (рис. 1).
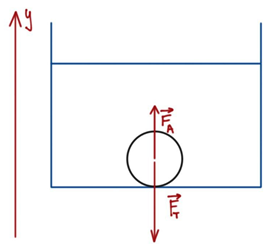
Рис. 1. Схема дії сил на камінь
Пригадаймо, що силу тяжіння можна визначити за формулою
Силу Архімеда можна визначити за формулою
Тоді можна записати другий закон Ньютона для каменя:
Спроєктуймо сили на вісь
Оскільки проєкція рівнодійної в цьому разі від’ємна, то сила тяжіння більша за виштовхувальну силу, що діє на камінь, тож камінь лежить у воді на дні.
Роботу сили можна визначити за формулою
За умови, що кут між напрямком сили й переміщенням каменя дорівнює нулю, а переміщення тіла дорівнює висоті його підйому
Робота, яку людина має виконати для піднімання тіла, – це робота проти рівнодійної сил, що діють на нього. Тому модуль піднімальної сили має дорівнювати модулю рівнодійної сил, що діють на камінь. Тоді роботу людини можна розрахувати за формулою:
Відповідь: 180
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умови плавання тіл.
Завдання скеровано на перевірку розуміння умов плавання тіл і вміння математично описати їх.
У завданні тричі змінюються умови плавання дерев’яного бруска. Опишімо кожен із випадків.
1. На брусок діє сила тяжіння, яку врівноважує сила Архімеда:
2. Коли до бруска знизу прикріпили вантаж, то виштовхувальна сила діятиме і на занурену частину бруска, і на вантаж. Запишімо умову плавання бруска за цих умов:
3. Розгляньмо третій випадок, коли вантаж поклали на брусок зверху. Запишімо умову плавання:
Розв’яжімо систему трьох рівнянь:
Віднімімо від рівняння (2) рівняння (3):
Підставімо в рівняння (3) вираз замість
Розкриймо дужки й обчислімо
Відповідь: 15.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про рух тіла під дією кількох сил.
Дано:
Знайти:
На аеростат діють дві сили: сила тяжіння і сила Архімеда. Сила Архімеда не залежить від маси баласту, а силу тяжіння можна визначити за формулою
Тоді можна записати другий закон Ньютона для аеростата:
Сила тяжіння спрямована вниз, сила Архімеда – угору, до скидання балансу тіло аеростат опускається, тож прискорення також спрямоване вниз. Тоді векторне рівняння можна спроєктувати на вісь
Після скидання баласту проєкція другого закону Ньютона матиме інший вигляд:
Тоді з рівняння для руху аеростата до скидання баласту можна виразити силу Архімеда:
Тож:
Тоді маса скинутого баласту така:
Відповідь: 10.
ТЕМА: Механіка. Динаміка. Капілярні явища. Сила Архімеда. Сила пружності. Невагомість.
Завдання скеровано на перевірку розуміння природи фізичних явищ і сил.
1 Капілярні явища зумовлені тим, що рідини в тонких трубках мають велику площу контактування з твердою речовиною. Увігнутий або опуклий меніск утворюється залежно від того, чи змочує рідина поверхню чи не змочує. Унаслідок дії сил поверхневого натягу під деформованою поверхнею виникне надлишковий тиск (тиск Лапласа), який приведе до підняття або опускання стовпчика рідини.
2 Архімедова сила виникає завдяки тому, що в однорідних рідинах на різних рівнях установлюється різний гідростатичний тиск. Що більша глибина, то більший гідростатичний тиск. За законом Паскаля тиск у рідинах і газах поширюється однаково в усіх напрямках. Тоді на верхню поверхню тіла діє менший порівняно з нижньою його поверхнею тиск. Унаслідок такої різниці тисків утворюється сила, що завжди спрямована на виштовхування тіла з рідини – сила Архімеда.
3 Сила пружності – це сила, яка виникає під час деформації тіла й намагається повернути тіло в недеформований стан.
4 Невагомість – це стан тіла, у якому його вага дорівнює нулю. Для тіл на поверхні Землі або поруч із її поверхнею це свідчить про те, що на тіло діє лише сила тяжіння. У такому разі всі тіла рухаються з однаковим прискорення – прискоренням вільного падіння.
Відповідь: 1Г, 2Б, 3А, 4В.
ТЕМА: Елементи механіки рідин і газів. Гідростатичний тиск.
Завдання скеровано на перевірку вміння визначати гідростатичний тиск.
Рівень рідини в трубці встановлюється так, що тиск у рідині на кожному рівні дорівнює тиску в рідині в широкій посудині.
Тиск у широкій посудині на кожному рівні можна визначити за формулою
Гідростатичний тиск – тиск нерухомого стовпчика рідини або газу.
Гідростатичний тиск визначають за формулою
Тиск повітря в трубці можна вважати однаковим у кожній точці, уключно із тиском на межі повітря – рідина. Тиск на цій межі можна визначити за формулою
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона. Механіка. Основи динаміки. Рух тіл під дією кількох сил.
Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі з різних розділів фізики.
Запишімо рівняння другого закону Ньютона у векторному вигляді та в проєкціях на осі координат для початкового стану:
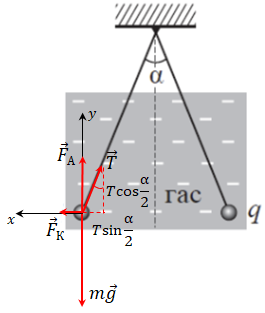
Дістаємо систему рівнянь:
Звідси
Запишімо рівняння другого закону Ньютона у векторному вигляді та в проєкціях на осі координат, коли кульки занурили в гас:
Сила Кулона в гасі зміниться від того, що в іншого середовища інша діелектрична проникність. За умовою кут між нитками не змінився після занурення в гас. Тож відстань між кульками не змінилася. Але на кульки в гасі діє сила Архімеда. Узявши до уваги всі ці умови, дістаємо систему рівнянь:
Звідси
Складімо систему з отриманих для обох ситуацій рівнянь і розв’яжімо її:
де
Тобто
Відповідь: 1600.
ТЕМА: Механіка. Елементи механіки рідин та газів. Тиск. Закон Паскаля для рідин та газів.
Завдання скеровано на перевірку розуміння принципу роботи гідравлічного преса.
Гідравлічний прес ‒ це найпростіша гідравлічна машина, яку використовують для створення великих сил тиску (див. рисунок).
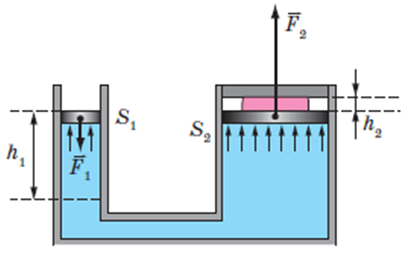
Якщо до поршня меншого циліндра прикласти силу
За законом Паскаля цей тиск передаватиметься в усі точки рідини, якою заповнені сполучені циліндри. Тож рідина почне тиснути з певною силою
Отже, сила, що діє з боку рідини на великий поршень, більша від сили, що діє на малий поршень, у стільки разів, у скільки разів площа великого поршня більша за площу малого:
Використанням гідравлічного преса забезпечено виграш у силі й, водночас, програш у відстані та, відповідно, швидкості. Час опускання меншого поршня такий самий, як і час піднімання більшого поршня. А відстань
Відповідь: Г.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.
Завдання скеровано на перевірку вміння розв᾽язувати задачі, коли на тіло діє кілька сил.
Позначмо сили, які діють на тіло, занурене в олію, а потім – у воду.
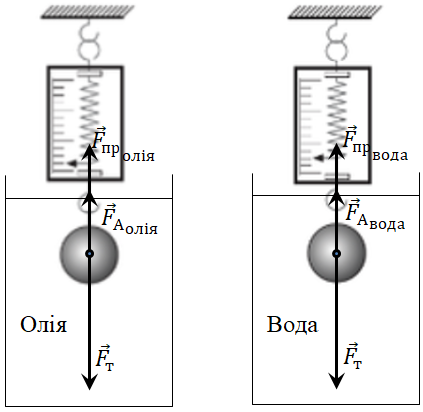
Запишімо рівняння другого закону Ньютона в проєкціях на вертикальну вісь, напрямлену вниз:
Усі тіла внаслідок гравітаційного притягання стискають або прогинають опору або розтягують підвіс. Силу, яка характеризує таку дію тіл, називають вагою і позначають
Прирівняємо праві частини цих формул:
Запишімо, чому дорівнює сила Архімеда у воді та олії:
Відповідь: B.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з визначення маси тіла й виштовхувальної сили.
1. На рисунку 1 зображено тіло в повітрі, підвішене до динамометра. Динамометр показує значення ваги тіла в повітрі
З формули для визначення сили тяжіння визначмо масу
Відповідно
Відповідь: 3.
2. На рисунку 2 динамометр показує вагу тіла в рідині:
На тіло, занурене в рідину, діє виштовхувальна сила (сила Архімеда). У цій ситуації виштовхувальна сила дорівнюватиме різниці ваги тіла в повітрі й ваги тіла в рідині:
Відповідь: 10.
Відповідь: 1. 3. 2. 10.
ТЕМА: Механіка. Елементи механіки рідин і газів. Умови плавання тіл.
Завдання скеровано на перевірку розуміння умов плавання тіл.
Розгляньмо два варіанти плавання бруска: у гасі й у воді. Силу тяжіння
Варіант перший – брусок плаває у гасі:
Після перетворень дістанемо вираз:
Варіант другий – брусок плаває у воді:
Після перетворень дістанемо вираз:
Прирівняймо вирази для визначення маси
Визначмо й обчислімо шукану величину
Відповідь: Б.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умова плавання тіл.
Завдання скеровано на перевірку знання і розуміння умови плавання тіл і закону Архімеда.
Прирівняймо сили, що діють на кубик:
Розпишімо ці сили:
Маса тіла дорівнює добутку густини й об’єму тіла:
Кубик лише на
Відповідно до таблиці, у якій наведено густини металів, кубик виготовлено з алюмінію
Відповідь: Б.
ТЕМА: Фізичні величини. Вимірювання фізичних величин.
Завдання скеровано на перевірку розуміння побудови шкали приладів і вміння визначати за показами шкали приладів певні фізичні величини, зокрема об’єм.
Поділка ‒ це відстань між рисками (горизонтальними позначками, лініями) на вимірювальній шкалі.
Кількість поділок, на яку заповнено рідиною мірний циліндр, дорівнює
Відповідь: B.
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.
Завдання скеровано на перевірку розуміння і вміння застосовувати рівняння стану газу.
Запишімо рівняння стану газу до накачування і після:
Запишімо формули для маси повітря як добуток густини
Підставімо в рівняння стану газу замість мас відповідні вирази й поділімо ліві і праві частини цих рівнянь:
Обчислімо шукану величину ‒ кількість накачувань:
Відповідь: 10.
ТЕМА: Механіка. Елементи механіки рідин та газів. Гідростатичний тиск. Атмосферний тиск.
Завдання скеровано на перевірку знання і розуміння атмосферного і гідростатичного тисків та їхніх властивостей.
На повітря під ртуттю тисне повітря (позначмо цей тиск як
Повітря під ртуттю за умовою має надлишковий тиск
Обчислімо тиск повітря під ртуттю:
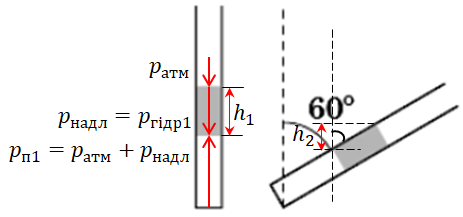
Коли ж нахилити трубку, зміниться гідростатичний тиск ртуті, який залежить від висоти (див. рисунок) стовпчика рідини в посудині:
Тоді тиск повітря під стовпчиком ртуті дорівнюватиме:
Відповідь: Б.
ТЕМА: Механіка. Елементи механіки рідин та газів. Закон Паскаля для рідин та газів. Атмосферний тиск. Тиск нерухомої рідини на дно і стінки посудини.
Завдання скеровано на перевірку знання і розуміння атмосферного і гідростатичного тисків, а також вміння визначати тиск у будь-якій точці сполучених посудин.
У точці
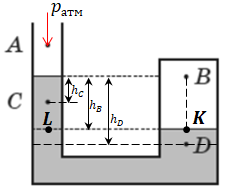
Точка
У точці
У точці
Найменшим буде тиск у точці
Відповідь: A.
ТЕМА: Механіка. Елементи механіки рідин і газів. Сполучені посудини.
Завдання скеровано на перевірку знання, розуміння і вміння застосовувати властивості сполучених посудин.
Відповідно до основної властивості сполучених посудин у відкритих сполучених посудинах вільні поверхні однорідної нерухомої рідини (за умовою – води) встановлюються на одному рівні. Тож поки в посудинах була лише вода, її рівень в обох посудинах однаковий.
Після того, як обережно (не змішуючи) в одну з посудин (праворуч) долили важчу за воду рідину (густина
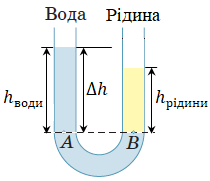
В однорідній рідині (тут – у воді) тиск на одному горизонтальному рівні є однаковим. На рівні
Визначімо висоту стовпчика води
Оскільки
або
Звідси дізнаймося висоту стовпчика води:
Якщо нульовим рівнем уважати рівень води в посудині праворуч, різниця рівнів води дорівнюватиме висоті стовпчика води в посудині ліворуч:
Відповідь: Г.
ТЕМА: Механіка. Елементи механіки рідин і газів. Атмосферний тиск. Тиск нерухомої рідини на дно та стінки посудини.
Завдання скеровано на перевірку знання і розуміння поняття тиску ‒ атмосферного й гідростатичного.
Тиск на поверхні води дорівнює атмосферному тиску ‒
А тиск
Запишімо відношення тисків:
Отже, тиск на глибині більший за тиск на поверхні води в
Відповідь: Г.
Тема: Фізичні величини. Вимірювання фізичних величин.
Завдання скеровано на перевірку розуміння побудови шкали приладів і вміння визначати за показами шкали приладів певні фізичні величини, зокрема об’єм.
Поділка ‒ це відстань між рисками (горизонтальними позначками, лініями) на вимірювальній шкалі.
Кількість поділок, на яку заповнено рідиною мірний циліндр, дорівнює
Відповідь: B.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умова плавання тіл.
Завдання скеровано на перевірку знання і розуміння повітроплавання тіл, уміння описувати його за допомогою формул.
Позначмо всі сили, що діють на систему тіл у повітрі: повітряна куля з гелієм ‒ вантаж. Це сила тяжіння

За другим законом Ньютона векторна сума всіх сил дорівнюватиме нулю, оскільки в умові зазначено, що система не рухається:
Запишімо це рівняння в проєкціях:
Розпишімо силу Архімеда:
Тобто
Запишімо рівняння Менделєєва ‒ Клапейрона для повітря:
Звідси визначімо густину повітря:
Підставімо вирази для густини повітря і для об’єму гелію у формулу виштовхувальної сили:
Повернімося до запису другого закону Ньютона в проєкціях і визначімо шукану величину ‒ масу гелію:
Відповідь: 100.
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу. Механіка. Елементи механіки рідин і газів. Тиск нерухомої рідини на дно й стінки посудини.
Завдання скеровано на перевірку знання і розуміння зв’язку між макроскопічними параметрами газу, а також на розуміння атмосферного й гідростатичного тиску.
Виразімо зв’язок між макроскопічними параметрами повітря (тиском
За умовою температура стала, отже,
Тиск
А тиск біля поверхні дорівнює атмосферному тиску:
Запишімо відношення об’ємів, підставивши вирази для тисків:
Отже, об’єм бульбашки збільшиться у 2,5 раза.
Відповідь: B.
ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умова плавання тіл.
Завдання скеровано на перевірку знання і розуміння повітроплавання тіл, уміння описувати його за допомогою формул.
Позначмо всі сили, що діють на систему тіл у повітрі: повітряна куля з газом ‒ вантаж. Це сила тяжіння
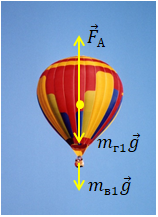
За другим законом Ньютона векторна сума всіх сил дорівнюватиме нулю, оскільки в умові не зазначено, що повітряна куля разом з вантажем піднімається вгору, отже, зупинимося на крайньому випадку, коли система не рухається ‒ куля просто утримує вантаж на певній висоті:
Запишімо це рівняння в проєкціях:
Розпишімо силу Архімеда:
Підставімо вираз для виштовхувальної сили в рівняння другого закону Ньютона:
‒ до нагрівання газу в кулі:
Урахуємо співвідношення густин повітря і газу:
‒ до нагрівання:
Визначимо відношення мас вантажу після і до нагрівання:
Отже, після нагрівання газу, яким заповнена повітряна куля, допустима маса вантажу, який зможе підняти куля, збільшиться в
Відповідь: 1,1.