Квантова фізика. Елементи теорії відносності – Елементи теорії відносності

ТЕМА: Квантова фізика. Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на перевірку знання і розуміння наслідків постулатів спеціальної теорії відносності, зокрема того, який зв’язок між масою та енергією.

Будь-яке тіло (будь-яка частинка) масою \(m\) несе із собою запас енергії \(E.\)

Дійсно, навіть якщо швидкість руху тіла (частинки) зменшується до нуля \((v=0),\) то тіло все одно має енергію:

За умовою газ унаслідок конвекції отримав ще кількість теплоти \(Q,\) а потім утратив унаслідок теплопровідності кількість теплоти \(0,2Q\) і виконав під час розширення роботу \(0,5Q\) (тобто теж втратив), то загалом ще отримав

Якщо тіло, навіть не рухаючись, має енергію \(E,\) то його маса $$ m=\frac{E}{c^2}. $$

Отримавши ще енергію \(\Delta Q\) внаслідок перебігу процесів, зазначених в умові завдання, тіло матиме енергію \((\Delta Q+E).\) Його масу можна обчислити так: \begin{gather*} \Delta Q+E=mc^2,\\[7pt] m=\frac{E}{c^2}+\frac{\Delta Q}{c^2},\\[6pt] m=\frac{E}{c^2}+\frac{0,3Q}{c^2}. \end{gather*}

Тобто маса тіла збільшилася на \(\frac{0,3Q}{c^2}.\)

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на перевірку розуміння закону додавання швидкостей у класичній і релятивістській механіці.

Швидкість світла \(c\) – це найбільша швидкість, яка може бути досягнута в космічному вакуумі. Тому електрон не може набути швидкості, більшої за швидкість світла, тобто варіант відповіді, у якій швидкість руху електрона дорівнюватиме \(1,08c,\) неправильний.

Також швидкість руху електрона в системі відліку, пов’язаній із космічним кораблем, що за умовою віддаляється в протилежний від електрона бік, не може бути менша за \(0,72c,\) оскільки космічний корабель віддаляється від Землі зі швидкістю \(0,72c.\) Отже, варіанти відповіді, що менші за \(0,72c,\) теж неправильні.

Залишається єдина можлива із запропонованих швидкість руху електрона – \(0,90c.\)

Відповідь: B.

ТЕМА: Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на оцінювання розуміння постулатів спеціальної теорії відносності.

Швидкість світла є однаковою в усіх інерціальних системах відліку незалежно від того, із якою швидкістю рухається джерело. Тож попри те, що ракета з прожектором рухається зі швидкістю \(\frac 45c\), швидкість світла, яку зафіксують на Землі, все одно дорівнюватиме \(c\).

Відповідь: Г.

ТЕМА: Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на оцінку розуміння постулатів спеціальної теорії відносності.

Щоби порівняти час, виміряний у рухомій і нерухомій системах, потрібно пригадати, як їх визначають.

Рухома система координат прив’язана до тіла, що рухається. У ній спостерігач рухається разом із тілом, як, наприклад, пасажир усередині ракети. Для такого спостерігача тіло і світловий годинник, який вимірює час, не рухається.

У нерухомій системі координат спостерігач стежить за рухомим тілом, як, наприклад, людина, що залишається на Землі, коли ракета пролітає в небі. У такому разі світловий годинник рухається.

За спеціальною теорією відносності швидкість світла у вакуумі має однакові значення в усіх системах відліку. Тож, щоби швидкість світла в рухомій і нерухомій системі відліку могла бути однаковою, час у них має текти по-різному. Час, виміряний у рухомій системі координат, має бути меншим, ніж виміряний у нерухомій системі: $$ \mathbf{\tau}=\frac{\mathbf{\tau}_0}{\sqrt{1-\frac{v^2}{c^2}}}, $$ де \(\mathbf{\tau}_0\) – час, виміряний у рухомій системі координат, \(\mathbf{\tau}\) – час, виміряний у нерухомій систем координат (у цій системі координат спостерігач бачить рух тіла ззовні).

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом й атомне ядро. Квантові постулати Бора.

Завдання скеровано на оцінювання розуміння практичного застосування лінійчастих спектрів у техніці.

Лінійчасті спектри утворюються тоді, коли електрони в атомах поглинають (для спектрів поглинання) або випромінюють (для спектрів випромінювання) кванти світла. Це відбувається завдяки тому, що електрони перебувають в особливих стаціонарних станах і перехід між цими станами потребує певної кількості енергії \(h\mathbf{\nu}\), де \(\mathbf{\nu}\) – це частота кванта світла. Перехід між станами \(n\) і \(k\) описано виразом $$ h\mathbf{\nu}=|E_k-E_n|. $$

Для кожного елемента переходи можуть відбуватися лише на певних енергетичних рівнях. У результаті цих переходів утворюється унікальний набір ліній у спектрах поглинання і випромінювання, що дає змогу використати їх для визначення хімічного складу речовин.

Відповідь:Г.

ТЕМА: Інерціальні системи відліку. Постулати спеціальної теорії відносності.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі для тіл, що рухаються зі швидкостями, близькими до швидкості світла.

Дано:
\(\mathbf{\tau}=2,2\ \text{мкс}\)
\(\mathbf{\nu}=0,8\ \text{с}\)
\(c=3\cdot 10^8\ \text{м/с}\)

1. Знайти:
\(l\ -\ ?\)

Час життя мюона на Землі можна розрахувати за формулою: $$ \mathbf{\tau}=\frac{\mathbf{\tau}_0}{\sqrt{1-\frac{\mathbf{\nu}^2}{c^2}}}= \frac{2,2\ \text{мкс}}{\sqrt{1-\frac{(0,8\ \text{с})^2}{c^2}}}=\frac{2,2\ \text{мкс}}{0,6}\approx 3,67\ \text{мкс}. $$

Тоді відстань, яку мюон пройде відносно Землі, дорівнюватиме: $$ l=\mathbf{\tau}\mathbf{\nu}=3,67\ \text{мкс}\cdot 0,8\cdot 10^8\frac{\text{м}}{\text{с}}=3,67\cdot 10^{-6}\ \text{с}\cdot 0,8\cdot 3\cdot 10^8\frac{\text{м}}{\text{с}}\approx 880\ \text{м}. $$

Відповідь: 880.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.

Завдання скеровано на оцінювання розуміння постулатів Бора і їхнього застосування для опису процесів випромінювання і поглинання.

Модель атома Бора є вдосконаленням планетарної моделі. Один із головних недоліків планетарної моделі такий:
якщо описувати рух електронів навколо ядра законами класичної механіки, то вони б постійно наближались до ядра і з часом упали б на нього. Такий атом не може існувати.

Тому Бор сформулював постулати:

1) атомна система може перебувати лише в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії; у стаціонарному стані атом не випромінює енергію;

2) під час переходу з одного стаціонарного енергетичного стану (з енергією \(E_k\)) в інший (з енергією \(E_n\)) атом випромінює або поглинає квант електромагнітної енергії: $$ hv=|E_k-E_n|. $$

Квант електромагнітної хвилі має специфічну частоту, для видимого випромінювання це означає, що випромінений квант на спектрах випромінювання виглядає як вузька кольорова смужка. У спектрі поглинання поглинутий квант виглядає як вузька темна смужка (рис. 1).

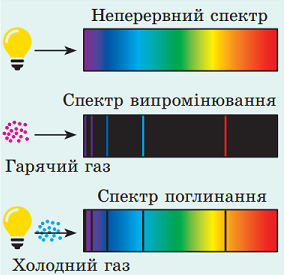
Рис. 1. Вигляд лінійчастих спектрів поглинання і випромінювання

Відповідь: Б.

ТЕМА: Оптіка. Спектральній аналіз.

Завдання скеровано на перевірку вміння розв'язувати задачі, які передбачають оброблення й аналіз результатів експерименту, поданих на фото або схематичному рисунку.

Усі спектральні лінії \(\mathrm{Na}\) є у спектрі суміші.

Спектральні лінії \(\mathrm{H}\) теж є у спектрі суміші (рис. Б).

Натомість ліній із довжинами хвиль як у \(\mathrm{He}\) в суміші немає.

Відповідь: B.

ТЕМА: Квантова фізика.

Завдання скеровано на перевірку розуміння зв’язку маси та енергії.

Дано:
\(E=200\ \text{кВт}\cdot \text{год}\)

1. Знайти:
\(m\ (\text{мкг})\ -\ ?\)

Енергію, спожиту родиною, необхідно перевести в Дж:

Енергія пов’язана з масою формулою $$ E=mc^2. $$

Тоді

Відповідь: 8.

ТЕМА: Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням релятивістського закону додавання швидкостей.

Обидві частинки рухаються зі швидкістю, порівнюваною зі швидкістю світла. Тому в цьому разі для додавання швидкостей необхідно використовувати релятивістський закон: $$ v=\frac{v_1+v_2}{1+\frac{v_1v_2}{c^2}}, $$ де \(v\) – швидкість руху тіла відносно нерухомої системи відліку (К), \(v_1\) – швидкість руху тіла відносно рухомої системи відліку, \(v_2\) – швидкість рухомої системи відліку К'.

У цьому випадку нерухома система відліку К – це адронний колайдер (на рисунку 1 позначено чорним кольором). Рухому систему координат К' варто «прив’язати» до одного з ядер (на рисунку 1 позначено синім кольором). Інше ядро тоді можна вважати рухомим тілом у цих системах координат (на рисунку 1 позначено червоним кольором).

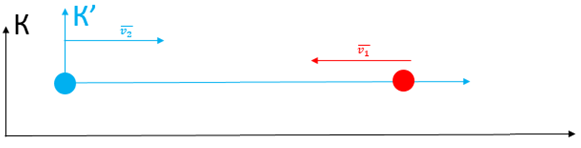
Рис. 1. Схема руху протонів в адронному колайдері

За умовою відомі швидкості руху ядер в адронному колайдері, тобто це швидкість v руху тіла відносно нерухомої системи координат і швидкість \(v_2\) рухомої системи координат К' відносно нерухомої.

Тоді, щоби знайти швидкість руху одного ядра відносно іншого, необхідно знайти швидкість руху тіла відносно рухомої системи координат (\(v_1\)). Виразимо швидкість \(v_1\) із виразу для релятивістського додавання швидкостей:

Тож одне з ядер рухалось назустріч іншому зі швидкістю \(0,8c\).

Відповідь: B.

ТЕМА: Елементи теорії відносності.

Завдання скеровано на перевірку розуміння постулатів спеціальної теорії відносності.

Постулати спеціальної теорії відносності:

1. В інерціальних системах відліку всі закони природи однакові.

2. Швидкість поширення світла у вакуумі однакова в усіх інерціальних системах відліку.

Відповідь: A.

ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси й енергії.

Завдання скеровано на перевірку розуміння потужності й уміння визначати її.

Потужність випромінювання \(P\) – це повна енергія \(E,\) яку переносить світло за одиницю часу \(t:\) $$ P=\frac Et. $$

Виділення тілом енергії (випромінювання) супроводжується зменшенням його маси. Зміна енергії тіла прямо пропорційна зміні його маси: $$ \Delta E=\Delta mc^2, $$ де \(m\) – маса тіла, \(c\) – швидкість поширення випромінювання.

Відповідно \begin{gather*} P=\frac{\Delta E}{t}=\frac{\Delta mc^2}{t};\\[6pt] \Delta m=\frac{Pt}{c^2}. \end{gather*}

Перед обчисленням потрібно перевести значення часу в систему СІ: \(3\ \text{хв} = 180\ \text{с.}\)

Відповідь: B.

ТЕМА: Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням релятивістського закону додавання швидкостей.

Дано:
\(v_\text{рух}=0,5\ \text{с}\)
\(v_\text{кат}=0,5\ \text{с}\)

Знайти:
\(\frac{c}{v_\text{нерух}}\ -\ ?\)

Усі тіла рухаються зі швидкістю, порівнюваною зі швидкістю світла. Тому в цьому разі для додавання швидкостей необхідно використовувати релятивістський закон: $$ v_\text{нерух}=\frac{v_\text{рух}+v_\text{кат}}{1+\frac{v_\text{рух}v_\text{кат}}{c^2}} $$ де \(v\) – швидкість руху тіла відносно нерухомої системи відліку (Землі), \(v_\text{кат}\) – швидкість руху тіла відносно рухомої системи відліку (ракети), \(v_\text{рух}\) – швидкість рухомої системи відліку (ракети).

Тож

\begin{gather*} \frac{c}{v_\text{нерух}}=c:\frac{v_\text{рух}+v_\text{кат}}{1+\frac{v_\text{рух}v_\text{кат}}{c^2}};\\[6pt] \frac{c}{v_\text{нерух}}=c\cdot\frac{1+\frac{v_\text{рух}v_\text{кат}}{c^2}}{v_\text{рух}+v_\text{кат}};\\[6pt] \frac{c}{v_\text{нерух}}=c\cdot\frac{1+\frac{0,5\ \text{с}\cdot 0,5\ \text{с}}{c^2}}{0,5\ \text{с}+0,5\ \text{с}};\\[6pt] \frac{c}{v_\text{нерух}}=c\cdot\frac{1+\frac{0,25\ \text{с}^2}{c^2}}{c};\\[6pt] \frac{c}{v_\text{нерух}}=1,25. \end{gather*}

Відповідь: 1,25.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Кванти світла (фотони).

Завдання скеровано на перевірку вміння розв’язувати задачі, використовуючи формули, що описують кванти світла (фотони).

За умовою завдання імпульс електрона \(p_\text{е}\) дорівнює імпульсу фотона \(p_\text{ф}\) світла, від якого електрон отримує енергію: $$ p_\text{е}=p_\text{ф}. $$

Імпульс фотона дорівнює відношенню сталої Планка \(h\) до довжині хвилі \(\mathbf{\lambda}\) фотона: $$ p_\text{ф}=\frac{h}{\mathbf{\lambda}}. $$

Імпульс електрона дорівнює добутку маси \(m_\text{е}\) електрона і швидкості \(v_\text{е}\) його руху: $$ p_\text{е}=m_\text{е}\cdot v_\text{е}. $$

Обчислімо швидкість руху електрона:

Відповідь: 1,1.

ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на перевірку розуміння законів релятивістської механіки.

Відповідно до другого постулату спеціальної теорії відносності (СТВ) швидкість поширення світла у вакуумі є незмінною і не залежить від швидкості руху джерела або приймача світла. Це означає, що класичний закон додавання швидкостей у релятивістській механіці застосовувати не можна. У СТВ застосовують релятивістський закон додавання швидкостей. Запишімо цей закон для ситуації, описаній в умові завдання: $$ v_\text{З}=\frac{v_\text{Р-С}+v_\text{С-З}}{1+\frac{v_\text{Р-С}\cdot v_\text{С-З}}{c^2}}, $$ де \(v_\text{З}\) ‒ проєкція швидкості руху ракети відносно Землі як нерухомої системи відліку, \(v_\text{Р-С}\) ‒ проєкція швидкості руху ракети відносно космічної станції як рухомої системи відліку, \(v_\text{С-З}\) ‒ проєкція швидкості руху рухомої системи відліку відносно нерухомої ‒ космічної станції відносно Землі, \(c\) ‒ швидкість поширення світла у вакуумі.

Відповідно до другого постулату СТВ швидкість поширення світла ‒ максимально можлива швидкість поширення будь-якої взаємодії. Матеріальні об’єкти не можуть мати швидкість більшу за швидкість світла. Отже, варіант відповіді Г \((1,7c)\) суперечить другому постулату СТВ і є неправильним.

Підставмо у формулу вирази, що відповідають швидкостям руху космічної станції відносно Землі і ракети відносно цієї станції. Звернімо увагу, що ця формула записана для випадку додавання швидкостей, напрямлених уздовж однієї прямої \((\text{осі}\ Ox),\) як це зображено на рисунку в умові завдання. Оскільки і ракета, і станція рухаються в один бік, то у формулі в чисельнику швидкості додаємо \((0,9c+0,8c).\)

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на перевірку знання постулатів теорії відносності Ейнштейна й розуміння відмінностей між класичною механікою і релятивістською.

Відповідно до другого постулату спеціальної теорії відносності швидкість поширення світла у вакуумі однакова в усіх інерціальних системах відліку. Це означає, що швидкість поширення світла у вакуумі інваріантна ‒ вона не залежить від швидкості руху джерела або приймача світла.

Час у класичній механіці І. Ньютона однаковий у будь-якій інерціальній системі відліку (СВ), тобто такі поняття, як зараз, раніше, пізніше, одночасно, не залежать від вибору СВ.

У релятивістській механіці час залежить від вибору СВ. Події, що відбулися в одній СВ одночасно, в іншій СВ можуть бути розділені часовим проміжком, тобто одночасність двох подій відносна.

Отже, згідно зі спеціальною теорією відносності в рухомій і нерухомій системах час плине по-різному, а швидкість світла у вакуумі однакова.

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси й енергії.

Завдання скеровано на перевірку вміння визначати потужність випромінювання.

Потужність випромінювання \(P\) – це повна енергія \(E,\) яку переносить світло за одиницю часу \(t:\) $$ P=\frac Et. $$

Енергію світлових променів, про які йдеться, визначають за формулою \(E=mc^2.\) Запишімо формулу для визначення маси:

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на перевірку знання і розуміння постулатів теорії відносності.

Перший постулат спеціальної теорії відносності (СТВ): в інерціальних системах відліку (СВ) усі закони природи однакові.

Другий постулат СТВ: швидкість поширення світла у вакуумі однакова в усіх інерціальних СВ.

Це означає, що швидкість поширення світла у вакуумі інваріантна ‒ вона не залежить від швидкості руху джерела або приймача світла. Відповідно до цього постулату швидкість поширення світла ‒ максимально можлива швидкість поширення будь-якої взаємодії.

Отже, варіанти відповіді А і В суперечать другому постулату СТВ.

У релятивістській механіці час залежить від вибору СВ. Події, що відбулися в одній СВ одночасно, в іншій СВ можуть бути розділені часовим проміжком. Одночасність двох подій відносна: події, одночасні в одній інерціальній СВ, не є одночасними в інерціальних СВ, що рухаються відносно першої СВ. Математично це підтверджено формулою: \begin{gather*} \mathbf{\tau}=\frac{\mathbf{\tau}_0}{\sqrt{1-\frac{v^2}{c^2}}} \end{gather*} (якщо поділити значення часу на десятковий дріб із-під кореня квадратного, то отримаємо більше значення часу).

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Кванти світла (фотони).

Завдання скеровано на перевірку знання і розуміння імпульсу тіла та імпульсу фотона.

Імпульс тіла \(\overrightarrow{p}\) ‒ це векторна фізична величина, яка дорівнює добутку маси \(m\) тіла на швидкість \(\overrightarrow{v}\) його руху: $$ \overrightarrow{p}=m\overrightarrow{v}. $$

Отже, в проєкціях на вісь \(Ox\) імпульс електрона \(p_e\) дорівнюватиме: $$ p_e=mv. $$

Імпульс фотона \(p_\text{ф}\) дорівнює відношенню його енергії \(E\) до швидкості руху \(c\) та обернено пропорційний довжині хвилі \(\mathbf{\lambda}\) фотона: $$ p_\text{ф}=\frac Ec=\frac{h\mathbf{\nu}}{c}=\frac{h}{\mathbf{\lambda}}. $$

За умовою імпульс електрона дорівнює імпульсу фотона: $$ mv=\frac{h}{\mathbf{\lambda}}. $$

З цієї рівності виразімо й обчислімо шукану величину ‒ швидкість руху електрона:

Відповідь: 1,1.

ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси та енергії.

Завдання скеровано на перевірку знання і розуміння зв’язку маси та енергії як важливого результату спеціальної теорії відносності, коли тіла (частинки) рухаються зі швидкістю порядку швидкості світла у вакуумі.

З погляду спеціальної теорії відносності, якщо тіло масою \(m\) рухається зі швидкістю \(v\) відносно якоїсь системи відліку, то енергія \(E\) тіла в цій системі відліку становить: $$ E=\frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}, $$ де \(c\) ‒ швидкість світла у вакуумі.

Будь-яке тіло (будь-яка частинка), що має масу, несе із собою запас енергії. Дійсно, навіть якщо швидкість руху тіла (частинки) зменшується до нуля \((v=0),\) то згідно із цією формулою тіло все одно має енергію \(E_0:\) $$ E_0=mc^2. $$

Цю енергію називають енергією спокою.

Тоді формула для повної енергії матиме такий вигляд: $$ E=\frac{E_0}{\sqrt{1-\frac{v^2}{c^2}}}. $$

Підставімо значення відповідних величин з умови завдання й обчислімо повну енергію електрона:

Відповідь: 136.

ТЕМА: Квантова фізика. Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на перевірку розуміння наслідків постулатів теорії відносності.

Оскільки в умові завдання йдеться про релятивістський ефект скорочення довжини тіла, а це стає помітним тільки в разі руху тіла зі швидкістю \(v,\) яка порівнянна зі швидкістю поширення світла \(c,\) тож скористаймося наслідком постулатів теорії відносності: $$ l=l_0\sqrt{1-\frac{v^2}{c^2}}, $$ де \(l_0\) ‒ довжина тіла в системі відліку, відносно якої тіло перебуває у спокої; \(l\) ‒ довжина тіла в системі відліку, відносно якої тіло рухається (відносно спостерігача в лабораторії).

Якщо за умовою поздовжні розміри тіла зменшилися на \(20\ \text{%},\) то $$ l=0,8l_0. $$

Підставімо це відношення у формулу й визначмо швидкість руху тіла:

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на перевірку розуміння релятивістського закону додавання швидкостей та умов його застосування.

Можна одразу відкинути варіанти відповіді Б і Г як неможливі. Адже в них швидкість електрона або досягла максимального значення ‒ швидкості світла у вакуумі, або перевищила його.

У завданні необхідно визначити максимально можливу швидкість руху електрона відносно Землі. Ідеться про ситуацію, коли ядро й електрон, який з нього вилітає, рухатимуться в одному напрямку.

Оскільки йдеться про швидкості руху порядку швидкості світла, то треба скористатися релятивістським законом додавання швидкостей:

де \(v\) ‒ швидкість руху електрона відносно Землі, \(v_1\) ‒ швидкість руху електрона відносно ядра, \(v_2\) ‒ швидкість руху ядра відносно Землі.

Отже,

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності.

Завдання скеровано на перевірку знання і розуміння дослідів або спостережень, що сприяли відкриттям із розділів «Елементи теорії відносності», «Світлові кванти» й «Атом та атомне ядро».

1. Явище радіоактивності – засвічення фотопластинки солями Урану (Г).

Анрі Антуан Беккерель (1852–1908) − французький фізик, знаючи, що рентгенівські промені, на відміну від світлових, проходять крізь чорний папір, узяв загорнуту в чорний папір фотопластинку, поклав на неї крупинки уранової солі й на кілька годин виніс фотопластинку на яскраве сонячне світло. Після проявлення на фотопластинці виявилися темні плями саме в тих місцях, де лежала уранова сіль. Таким чином було з’ясовано, що уранова сіль дійсно випускає випромінювання, яке має велику проникну здатність і діє на фотопластинку. Беккерель вирішив продовжити дослідження і підготував дослід, який дещо відрізнявся від попереднього. Проте науковцю завадила похмура погода, і він із жалем поклав готову до досліду фотопластинку з урановою сіллю та мідним хрестом між ними в шухляду стола. Через кілька днів, так і не дочекавшись появи сонця, Беккерель вирішив про всяк випадок проявити фотопластинку. Результат був несподіваним: на пластинці з’явився контур хреста. Тож сонячне світло тут ні до чого, і сіль Урану сама, без впливу зовнішніх чинників, випускає невидиме випромінювання, якому не є перешкодою навіть шар міді! Пізніше таке випромінювання назвали радіоактивним випромінюванням (від латин. radio − випромінюю, activus − дієвий); здатність речовин до радіоактивного випромінювання – радіоактивністю. Це був 1896 рік.

2. Планетарна модель атома − бомбардування альфа-частинками золотої фольги (А).

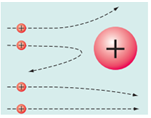
Вузький пучок \(\mathbf{\alpha}\text{-частинок}\) зі свинцевого контейнера спрямовувався на тонку золоту фольгу, а далі потрапляв в екран, покритий шаром кристалів цинк сульфіду. Якщо в такий екран улучала \(\mathbf{\alpha}\text{-частинка},\) то в місці її влучання відбувався слабкий спалах світла. Переважна більшість \(\mathbf{\alpha}\text{-частинок}\) проходила крізь золоту фольгу, не змінюючи напрямку руху, деякі відхиляються від початкової траєкторії. Приблизно одна з \(20000\) частинок відскакувала від фольги, начебто натикаючись на якусь перешкоду. Після зазначених дослідів Ернест Резерфорд (1871–1937), видатний англійський фізик, у 1911 р. запропонував ядерну модель будови атома: атом складається з позитивно зарядженого ядра, оточеного негативно зарядженими частинками − електронами; саме в ядрі зосереджена мало не вся маса атома.

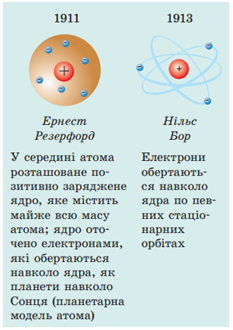
Ядерна (планетарна) модель атома, запропонована Резерфордом, була розвинена в роботах видатного данського фізика Нільса Бора (1885–1962). Саме на ядерній моделі ґрунтується сучасне уявлення про будову атома.

3. Закони фотоефекту – опромінювання металів світлом (В).

Розрізняють зовнішній фотоефект, за якого фотоелектрони вилітають за межі тіла, і внутрішній фотоефект, за якого електрони, «вирвані» світлом із молекул і атомів, залишаються всередині тіла.

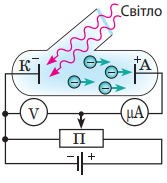
Зовнішній фотоефект відкрив німецький фізик Г. Герц 1887 р., а детально дослідив О. Столєтов (1839–1896) у 1888–1890 рр. Для вивчення фотоефекту О. Столєтов використав пристрій, сучасне зображення якого схематично наведено на рисунку. Усередині камери, з якої викачано повітря, розташовані два електроди (катод К і анод А), на які подається напруга від джерела постійного струму.

4. Три типи радіоактивних променів – дія магнітного поля на випромінювання урану (Б).

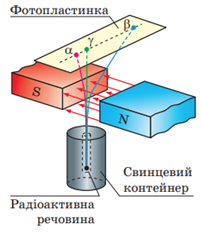
Досліди з вивчення природи радіоактивного випромінювання показали, що радіоактивні речовини можуть випромінювати промені трьох видів: позитивно заряджені частинки (\(\mathbf{\alpha}\) (альфа)-випромінювання), негативно заряджені частинки (\(\mathbf{\beta}\) (бета)-випромінювання) і нейтральні промені (\(\mathbf{\gamma}\) (гамма)-випромінювання). На рисунку зображено схему одного з таких дослідів: пучок радіоактивного випромінювання потрапляє спочатку в сильне магнітне поле постійного магніту, а потім на фотопластинку. Після проявлення фотопластинки на ній чітко видно три темні плями. Найбільший внесок у вивчення \(\mathbf{\alpha}\text{-випромінювання}\) зробив Е. Резерфорд. Він одним із перших з’ясував, що \(\mathbf{\alpha}\text{-випромінювання}\) − це потік ядер атомів Гелію. \(\mathbf{\beta}\text{-випромінювання},\) як і \(\mathbf{\alpha}\text{-випромінювання},\) відхиляється магнітним полем, але в протилежний бік. Виявлено, що \(\mathbf{\beta}\text{-випромінювання}\) − це потік електронів, які летять із величезною швидкістю (наближеною до швидкості поширення світла). Вивчення \(\mathbf{\gamma}\text{-випромінювання}\) показало, що це електромагнітні хвилі надзвичайно високої частоти (понад \(10^{18}\) Гц).

Відповідь: 1Г, 2А, 3В, 4Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на перевірку знання і розуміння коли і як треба застосовувати формули релятивістської і класичної механіки.

Рух тіл зі швидкостями, порівнюваними зі швидкістю світла, розглядають у розділі фізики «Релятивістська механіка» й описують спеціальними формулами.

В умові завдання треба визначити вираз, за яким можна обчислити відстань між електронами через певний час. Тут достатньо скористатися формулою класичної механіки для обчислення відстані під час прямолінійного рівномірного руху: $$ l=vt. $$

Електрони рухаються в протилежних напрямках. Один із них відносно ядра за час \(t\) пролетить відстань: $$ l_1=v_1t=0\mathord{,}8c\cdot t. $$

Другий електрон за час \(t\) пролетить відносно ядра ту саму відстань, однак у протилежному напрямку: $$ l_2=v_2t=0\mathord{,}8c\cdot t. $$

Загальна відстань між ними через час \(t\) становитиме: $$ l=l_1+l_2=0\mathord{,}8ct+0\mathord{,}8ct=1\mathord{,}6ct. $$

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності.

Завдання скеровано на перевірку знання досягнень фізичної науки й авторів цих відкриттів.

1. Вимірювання тиску світла ‒ Лебедєв П. (А).

Тиском світла називається тиск, який чинять електромагнітні світлові хвилі, які падають на поверхню будь-якого тіла. Гіпотезу про існування тиску висунув Дж. Максвел у своїй електромагнітній теорії світла.

Експериментально існування світлового тиску вперше встановив 1900 р. фізик П.М. Лебедєв. Для вимірювання світлового тиску він спрямував інтенсивний світловий потік на легкі металеві пластинки, підвішені на тонкій нитці в балоні, з якого було викачано повітря. Пластинки лівого ряду підвісу були чорними, а пластинки правого ‒ блискучими. Тому тиск світла на пластинки лівого ряду був меншим, ніж на пластинки правого ряду. Унаслідок цього під впливом світла підвіс повертався на певний кут, за значенням якого можна було визначити силу закручування і, отже, світловий тиск.

2. Створення планетарної моделі атома ‒ Резерфорд Е. (Б).

У 1908–1911 рр. під керівництвом Ернеста Резерфорда науковці досліджували будову атома. Вони спрямовували на тонку золоту фольгу вузький пучок \(\mathbf{\alpha}\text{-частинок}\) зі свинцевого контейнера. Виявили, що переважна більшість \(\mathbf{\alpha}\text{-частинок}\) проходить крізь фольгу, не змінюючи напрямку руху, лише деякі відхиляються від початкової траєкторії. Приблизно одна з \(20 000\) частинок відскакувала від фольги, начебто натикаючись на якусь перешкоду. І Резерфорд висунув гіпотезу про існування ядра в атомі. За результатами дослідів Резерфорд запропонував ядерну (планетарну) модель будови атома:

• в атомі позитивно заряджене ядро оточене негативно зарядженими частинками ‒ електронами, які обертаються навколо ядра, як планети навколо Сонця;
• саме в ядрі зосереджена мало не вся маса атома.

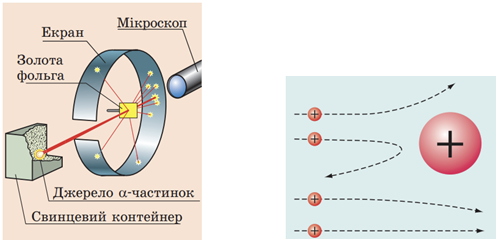
3. Створення теорії фотоефекту ‒ Ейнштейн А. (В).

Зовнішній фотоефект відкрив 1887 року німецький фізик Генріх Герц. Детальніше це явище дослідив Олександр Столєтов. У досліді він використав вакуумну камеру з двома електродами (катод і анод) усередині, на які подається напруга від джерела постійного струму. Під дією світла, яке потрапляє в камеру через спеціальне віконце, катод випромінює електрони. Рухаючись від катода до анода в електричному полі, електрони створюють фотострум. Якщо збільшувати напругу на електродах, сила фотоструму теж зросте. Змінюючи почергово інтенсивність і частоту світла, що падає на катод, а також матеріал катода, О. Столєтов сформулював три закони зовнішнього фотоефекту. Але лише більш як через \(20\) років завдяки своєму рівнянню для зовнішнього фотоефекту А. Ейнштейн зміг пояснити всі закони фотоефекту. Саме ідею М. Планка про кванти використав Ейнштейн для пояснення законів фотоефекту. За пояснення явища фотоефекту А. Ейнштейн одержав найвищу наукову нагороду ‒ Нобелівську премію (1921 р.).

4. Створення першого ядерного реактора ‒ Фермі Е. (Г).

Фермі 1938 року одержав Нобелівську премію за «демонстрацію існування нових радіоактивних елементів, утворених під час опромінення нейтронами, і за пов’язані відкриття ядерних реакцій, викликані повільними нейтронами». До весни 1941 року розробляв теорію ланцюгової реакції в урано-графітовій системі, а вже влітку розпочав серію експериментів, головним завданням яких було вимірювання нейтронного потоку. Разом з Г. Андерсоном провів близько тридцяти дослідів. У червні 1942 року було досягнуто значення коефіцієнта розмноження нейтронів, більшого за одиницю. Це означало можливість отримання ланцюгової реакції у достатньо великій ґратці з урану й графіту й послужило початком розроблення конструкції водно-графітового реактора. Фермі також спроєктував гігантський намет із тканини для оболонок аеростатів навколо конструкції реактора. Так з’явилася можливість підтримувати відповідний склад середовища, що оточувало реактор. Будівництво реактора розпочалося в Металургійній лабораторії Чиказького університету в жовтні, а завершилося 2 грудня 1942 року. У лабораторії під стадіоном англ. Stagg Field Stadium на цьому реакторі під назвою англ. Chicago Pile-1 (CP-1) було проведено експеримент, що продемонстрував першу самопідтримну ланцюгову ядерну реакцію.

Відповідь: 1А, 2Б, 3В, 4Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Кванти світла (фотони).

Завдання скеровано на перевірку знання і розуміння гіпотези Планка й формули для визначення енергії фотона.

За гіпотезою Планка випромінювання електромагнітних хвиль атомами й молекулами речовини відбувається не безперервно, а дискретно, тобто окремими порціями, енергія \(E\) кожної з яких прямо пропорційна частоті \(\mathbf{\nu}\) випромінювання: $$ E=h\mathbf{\nu}=\frac{hc}{\mathbf{\lambda}}, $$ де \(h\) ‒ стала Планка, \(\mathbf{\lambda}\) ‒ довжина хвилі фотона, \(c\) ‒ швидкість руху фотона, що дорівнює швидкості поширення світла у вакуумі. Згодом порції енергії стали називати квантами енергії, а потім фотонами.

Визначімо співвідношення енергій \(E_1\) і \(E_2\) фотонів з різними довжинами хвиль

Відповідь: B.