Розділ: Механіка
Тема: Кінематика: основні поняття кінематики
Кількість завдань: 38
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку вміння і розуміння, як знаходити напрямок швидкості руху тіла і напрямок прискорення тіл під час різних видів руху.
Напрямок руху тіла визначений напрямком швидкості руху тіла. А напрямок прискорення збігається з напрямком рівнодійної всіх сил, що діють на тіло.
1) Розгляньмо рух снаряда перед падінням на землю. На рисунку зображена відповідна частина траєкторії. Як бачимо, вектор швидкості
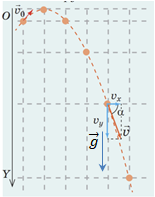
Отже, прискорення напрямлене під гострим кутом до напрямку швидкості руху (див. рисунок) ‒ варіант відповіді Г.
2) Кінець годинникової стрілки рухається по колу. Швидкість
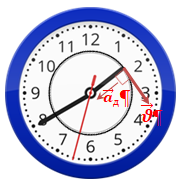
Отже, у цьому разі доцентрове прискорення буде напрямлене під прямим кутом до напрямку швидкості руху ‒ варіант відповіді Д.
3) Напрямок рівнодійної
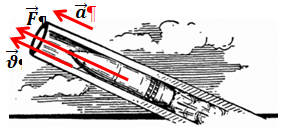
4) Після вимикання двигуна катер продовжить рухатися в попередньому напрямку і так само буде напрямлений вектор швидкості
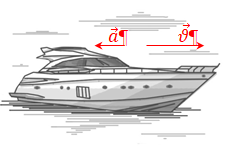
Отже, прискорення буде напрямлене протилежно до напрямку швидкості руху – варіант відповіді А.
Відповідь: 1Г, 2Д, 3В, 4А.
ТЕМА: Механіка. Основи кінематики. Шлях і переміщення.
Завдання скеровано на перевірку знання і розуміння базових понять кінематики ‒ шлях і переміщення.
Шлях ‒ це фізична величина, яка дорівнює довжині траєкторії або довжині її ділянки.
Переміщення ‒ це векторна величина, яку графічно подають у вигляді напрямленого відрізка прямої, який з’єднує початкове і кінцеве положення матеріальної точки.
В автобусі лічильник, на якому зафіксували збільшення пробігу, ‒ це одометр (дав. грец. ‒ шлях, дорога й міра, мірило) ‒ пристрій для вимірювання відстані, яку подолав транспортний засіб.
Отже, пройдений шлях становитиме
А модуль переміщення дорівнюватиме нулю, оскільки автобус після рейсу повернувся в гараж, тобто його початкове і кінцеве положення збіглися.
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку вміння описувати рух аналітично.
За умовою швидкість під час прямолінійного руху тіла протягом усього часу збільшується, тобто тіло рухається прискорено.
Запишімо рівняння залежності координати
Варіанти відповіді
Розгляньмо рівняння
Розгляньмо рівняння
Відповідь: A.
ТЕМА: Механіка. Основи кінематики. Траєкторія. Шлях і переміщення.
Завдання скеровано на перевірку знання і розуміння змісту понять шляху й переміщення.
Шлях
Переміщення
Згідно з умовою шлях утричі більший за модуль переміщення:
Розгляньмо кожен варіант відповіді.
A півколо
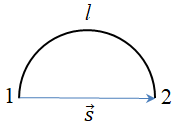
Шлях у цьому разі дорівнюватиме довжині півкола радіуса
Модуль переміщення дорівнюватиме подвійному радіусу ‒ діаметру цього кола:
Б дві сторони квадрата
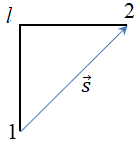
Шлях у цьому разі дорівнюватиме сумі довжин двох сторін
Модуль переміщення дорівнюватиме довжині діагоналі квадрата зі стороною
B відрізок
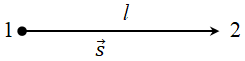
Шлях у цьому разі дорівнює модулю переміщення:
Г три сторони квадрата
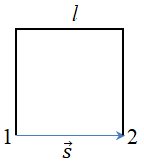
Шлях у цьому разі дорівнюватиме сумі довжин трьох сторін
Модуль переміщення дорівнюватиме довжині сторони квадрата зі стороною
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Закони збереження в механіці. Потенціальна і кінетична енергія.
Завдання скеровано на перевірку розуміння характеру прямолінійного рівноприскореного руху тіла, кинутого вертикально вгору, а також під час цього руху перехід механічної енергії з одного виду в інший.
Рух тіла, кинутого вертикально вгору, − це прямолінійний рівноприскорений рух.
Прискорення, із яким рухається тіло, − це прискорення вільного падіння
Розглянемо кожний момент часу.
1)
Потенціальна енергія дорівнює нулю, оскільки тіло ще не встигло піднятися на хоч якусь висоту від нульового рівня:
Отже, моменту часу
2)
Кінетичну енергію в цей момент часу обчислюють за формулою:
Тоді потенціальна енергія тіла за законом збереження механічної енергії дорівнюватиме різниці максимальної кінетичної енергії (під час старту тіла в момент часу
Отже, моменту часу
3)
Кінетична енергія в цей момент часу дорівнює нулю:
Тоді потенціальна енергія тіла за законом збереження механічної енергії дорівнює максимальній кінетичній енергії під час старту тіла в момент часу
Отже, моменту часу
4)
Кінетична енергія в цей момент часу дорівнює:
Тоді потенціальна енергія тіла за законом збереження механічної енергії дорівнює різниці максимальної кінетичної енергії (під час старту тіла в момент часу
Отже, моменту часу
Відповідь: 1А, 2Г, 3Д, 4В.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.
Завдання скеровано на перевірку розуміння рівномірного руху по колу та його характеристик.
Період
Тоді час
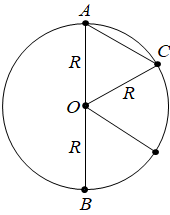
Час руху
Визначімо, у скільки разів модуль переміщення за
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на перевірку знання і розуміння однієї з фізичних моделей ‒ матеріальної точки.
Матеріальна точка ‒ це фізична модель тіла, розмірами якого в умові задачі можна знехтувати. Те саме тіло в умовах однієї задачі можна вважати матеріальною точкою, а в умовах іншої ‒ ні.
Під час сонячного затемнення не можна нехтувати розмірами Місяця, оскільки від цього залежить тривалість затемнення та розміри тіні й півтіні, які спостерігають на поверхні Землі.
Напевне не можна вважати супутник Землі матеріальною точкою під час вибору місця посадки космічного корабля на Місяць, а також у ситуації вивчення рельєфу поверхні Місяця.
Добираючи місце посадки космічного корабля на Місяць, вибирають місцевість, задають певні координати на поверхні. Тому знехтувати розмірами Місяця і вважати його матеріальною точкою не можна.
Вивчаючи рельєф поверхні Місяця, описують просторові закономірності його будови й розвитку, нескінченні западини і височини, розмірами яких не можна знехтувати. Тобто вважати Місяць матеріальною точкою під час дослідження його рельєфу не можна.
Гравітаційну силу між Місяцем і Сонцем визначають за законом всесвітнього тяжіння, у якому йдеться про притягування будь-яких двох тіл одне до одного із силою, що прямо пропорційна добутку мас цих тіл й обернено пропорційна квадрату відстані між ними. Цей закон справджується, якщо обидва тіла є матеріальними точками (розмірами тіл нехтують, а маса матеріальної точки дорівнює масі даного тіла). Отже, у цій ситуації Місяць можна вважати матеріальною точкою.
Відповідь: B.
ТЕМА: Механіка. Основи кінематики.
Завдання скеровано на перевірку розуміння понять швидкості та прискорення.
Краплі з піпетки падають через однакові проміжки часу
Тоді швидкість на кожному проміжку можна визначити за формулою:
Якщо смужку протягували зі збільшенням швидкості, то відстань між краплями праворуч має бути меншою, ніж між краплями ліворуч. Такий вигляд має смужка Б.
Відповідь: Б.
ТЕМА: Енергія. Робота. Потужність. Сила.
Завдання скеровано на перевірку розуміння понять енергії, потужності, сили й прискорення.
Потужність
Енергія
Сила
Прискорення
Відповідь: 1В, 2Д, 3Б, 4А.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на перевірку вміння визначати ціну поділки шкали.
Оскільки шкала динамометра розрахована на
Між двома великими поділками є

Рис. 1. Визначення ціни поділки
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики.
Завдання скеровано на перевірку розуміння поняття рівномірного руху.
Рівномірний рух – рух, під час якого матеріальна точка за будь-які рівні інтервали часу долає однаковий шлях.
Тобто проміжки 1, 2 й 3 мають бути рівними. Однакові проміжки 1, 2 й 3 зображені у варіанті відповіді А.
Відповідь: A.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на перевірку вміння працювати зі шкалами вимірювальних пристроїв і визначати ціну поділки шкали.
Для того щоби визначити ціну поділки секундоміра, потрібно вибрати дві поділки, значення яких відомі. Шкала секундоміра розрахована на 60 с. Тож цифри, зображені на шкалі поруч із великими поділками, відповідають часу, виміряному в секундах (5 с, 10 с, 15 с тощо).
Ціна великої поділки дорівнює різниці між двома послідовними великими поділками (позначено червоним кольором на рисунку 1):

Рис. 1. Дві послідовні великі поділки на шкалі та п’ять середніх поділок між ними
Між двома послідовними великими поділками є п’ять середніх поділок (позначено синім кольором на рис. 1). Між двома сусідніми середніми поділками є п’ять поділок, ціну яких потрібно визначити. Тобто між двома великими поділками розташовано 25 маленьких. Ціну маленької поділки можна обчислити як частку від ділення ціни великої поділки на кількість маленьких поділок на ній:
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Поступальний і обертальний рух.
Завдання скеровано на перевірку розуміння понять поступального й обертального рухів.
За визначенням поступальний рух – це такий рух тіла, за якого всі його точки рухаються однаково.
Обертальний рух – це такий рух тіла, за якого його точки рухаються по колах, центри яких лежать на одній прямій – осі обертання.
Сходи ескалатора в метро, курсор на моніторі й потяг на прямолінійній ділянці дороги рухаються поступально, тобто всі їхні точки рухаються з однаковою швидкістю і в однаковому напрямку.
Точки дзиґи під час її обертання описують кола різного радіуса навколо осі її обертання. Тобто дзиґа рухається непоступально.
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на оцінювання розуміння межі застосовуваності моделі матеріальної точки.
Матеріальна точка – це фізична модель тіла, розмірами якого в умовах задачі можна знехтувати.
Лише розраховуючи час польоту літака ми можемо знехтувати його розмірами. Адже вони не впливають на швидкість польоту, а літак є набагато меншим за відстань, яку він долає.
Натомість розмір деталі, закріпленої у верстаті, важливий для роботи всієї системи. Вивчення рельєфу потребує знання висоти й протяжності гір. А під час виступу фігуриста важливо стежити не лише за шляхом спортсмена на льоду, а й за рухом як його кінцівок, так і тіла в цілому.
Відповідь: Г.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання вміння добирати вимірювальні прилади для проведення експериментів.
A. Оскільки період – це час, за який тіло робить одне повне коливання, то для його вимірювання використовують секундомір.
Б. Для визначення електрорушійної сили (ЕРС) і внутрішнього опору джерела потрібно скористатися законом Ома для повного кола. ЕРС в цьому разі є еквівалентом напруги в законі Ома для ділянки кола, тому її також вимірюють вольтметром.
В. Для визначення фокусної відстані й оптичної сили лінзи потрібно виміряти відстань від предмета до лінзи й від лінзи до зображення. Для цього використовують лінійку.
Г. Для визначення коефіцієнта корисної дії (ККД) похилої площини необхідно обчислити корисну роботу, яку розраховують як зміну потенціальної енергії початкового й кінцевого стану й витрачену роботу, що робчислюють за формулою
Д. Для вивчення теплового балансу під час змішування води різної температури потрібно зафіксувати початкові й кінцеву температури. Для цього використовують термометр.
Відповідь: 1Г, 2Б, 3А, 4Д.
ТЕМА: Механіка. Основи кінематики. Система відліку. Траєкторія.
Завдання скеровано на оцінювання знання понять «система відліку», «траєкторія» і розуміння відносності руху.
Траєкторія руху – це уявна лінія, у кожній точці якої послідовно перебувала матеріальна точка під час руху.
Система відліку – це сукупність тіла відліку, системи координат, пов’язаної з ним, і приладу для вимірювання часу.
Відносність механічного руху полягає в тому, що траєкторія, шлях, переміщення і швидкість залежать від вибору системи відліку.
За умовою завдання необхідно визначити траєкторію руху лопатей у системі відліку, яка пов’язана з панеллю приладів літака. У такій системі відліку тілом відліку є панель приладів, тож її вважають нерухомою.
Для визначення траєкторії руху лопатей потрібно уявити себе в кабіні біля панелі приладів. Оскільки лопаті закріплено в конструкції літака, то поступального руху відносно кабіни вони не роблять, а виконують лише обертання навколо своєї осі. Траєкторія такого руху – коло.
Відповідь: B.
ТЕМА: Вимірювання фізичних величин. Усереднення.
Завдання скеровано на оцінювання вміння аналізувати результати експерименту, зображені на фото.
Визначити середній діаметр
Відповідь: 7.
ТЕМА: Фізичні явища й фізичні величини.
Завдання скеровано на оцінювання розуміння поняття фізичного явища й фізичної величини.
Фізичне явище – це зміни в природі, які можна описати за допомогою відповідних фізичних законів.
Фізична величина – це кількісно виражена характеристика тіла або фізичного явища.
Проаналізуймо поняття, наведені в кожному варіанті відповіді.
У варіанті А теплопровідність, остигання і горіння – це фізичні явища, а площа – це фізична величина.
У варіанті Б падіння, електроліз і нагрівання – це фізичні явища, а ньютон – це одиниця вимірювання сили.
У варіанті В гальмування – це фізичне явище, кілограм і діоптрія – це одиниці вимірювання маси й оптичної сили лінзи відповідно, а густина – це фізична величина.
У варіанті Г всі поняття є фізичними явищами.
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка. Шлях і переміщення.
Завдання скеровано на оцінювання розуміння понять шляху й переміщення, відмінності між ними.
Матеріальна точка – це фізична модель тіла, розмірами якого в умовах задачі можна знехтувати.
Переміщення
Період обертання
За один період матеріальна точка зробить один повний оберт, і початкове положення руху збігатиметься із кінцевим положенням. Тоді модуль переміщення дорівнюватиме 0.
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка. Шлях і переміщення.
Завдання скеровано на оцінювання розуміння понять шляху й переміщення і відмінності між ними.
Для правильного розв’язання завдання потрібно пригадати визначення шляху й переміщення.
Переміщення
Шлях
Тож для автобуса, про який ідеться в завданні, відстань між початковою і кінцевою точками (обидві – у гаражі), дорівнює нулю.
Водночас лічильником, установленим в автобусі, вимірюють відстань, пройдену цим транспортним засобом, тобто шлях. Тож шлях автобуса дорівнює 150 км.
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на перевірку поняття «матеріальна точка» і вміння застосовувати основні поняття механіки.
Матеріальною точкою називають будь-яке тіло, розмірами якого за певних умов можна знехтувати, тому поняття «матеріальна точка» можна застосувати і до ведмедя, і до бджоли залежно від умов задачі.
Відповідь: В.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух. Рівномірний рух по колу.
Завдання скеровано на перевірку розуміння зв’язку між силою, прискоренням і швидкістю руху тіла.
А Важок математичного маятника здійснює коливальний рух, під час якого швидкість тіла змінюється від 0 в найвищій точці його траєкторії до максимального значення в найнижчій. Окрім того напрямок руху важка змінюється двічі за коливання, тож і швидкість також змінює свій напрямок постійно.
Б Швидкість літака, що гальмує на посадковій смузі, зменшується за модулем, але її напрямок не змінюється.
В Швидкість, автомобіля, що рухається по прямій дорозі рівномірно, не змінюється.
Г Горіх, що падає на Землю з дерева, рухається лише під дією її сили тяжіння, тобто з прискоренням вільного падіння. Модуль швидкості тіла в такому разі збільшується, а напрямок не змінюється.
Д Стрілка годинника рухається по колу з однаковою лінійною швидкістю, проте будь-який рух по колу супроводжуваний доцентровим прискоренням, що змушує напрямок миттєвої швидкості безперервно змінюватися.
Відповідь: 1Б, 2Г, 3Д, 4А.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на перевірку розуміння поняття матеріальної точки.
Матеріальна точка – це фізична модель тіла, розмірами якого в умовах задачі можна знехтувати.
Диспетчер не може знехтувати розмірами Землі, адже літаки набагато менші за планету та рухаються близько до її поверхні. Відстані, що проходять літаки, є лише невеликими відрізками на поверхні Землі.
З тієї самої причини космонавт не може знехтувати розміром Землі під час посадки корабля.
Геолог не може знехтувати розміром планети, адже корисні копалини закладені в її корі.
Під час обчислення сили тяжіння розмірами тіла можна знехтувати.
Відповідь: B.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання знання вимірювальних пристроїв і розуміння фізичних величин, для вимірювання яких їх використовують.
1. Фізична величина, що дорівнює відношенню шляху до часу – це швидкість:
Прилад, що вимірює швидкість – це спідометр.
2. Фізична величина, що дорівнює добутку густини, прискорення вільного падіння і висоти стовпчика рідини – це гідростатичний тиск (тиск нерухомого стовпчика рідини):
Прилад, що вимірює тиск рідини чи газу – це манометр.
3. Фізична величина, що дорівнює відношенню густини водяної пари до густини насиченої пари за певної температури й виражена у відсотках – це відносна вологість:
Прилад, що вимірює відносну вологість – це гігрометр.
4. Фізична величина, що дорівнює добутку маси на прискорення вільного падіння – це сила тяжіння:
Прилад, що вимірює силу – це динамометр.
Відповідь: 1В, 2А, 3Г, 4Б.
ТЕМА: Механіка. Основи кінематики.
Завдання скеровано на перевірку розуміння понять швидкості та прискорення.
Краплі з піпетки падають через однакові проміжки часу
Тоді швидкість на кожному проміжку можна визначити за формулою:
Тож що більша відстань між краплями, то більша швидкість руху на проміжку.
Рівномірний рух – рух, під час якого матеріальна точка за будь-які рівні інтервали часу долає однаковий шлях.
Якщо смужку протягували рівномірно, то відстань між краплями має бути однаковою. Такий вигляд має смужка B.
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу рівномірного й рівноприскореного рухів.
Завдання скеровано на перевірку вміння читати графіки й описувати їх кінематичними рівняннями.
Оскільки графіками залежності координати
Розгляньмо кожен момент часу, коли змінюються графіки.
Запишімо рівняння координати для ділянок від
Отже, у момент часу
Розгляньмо ділянки від
Отже, у момент часу
Розгляньмо ділянки від
Отже, у моменти часу
Можна, не обчислюючи значення швидкості для кожного моменту часу, визначити, які ділянки графіків відповідатимуть однаковим швидкостям.
Рівняння координати
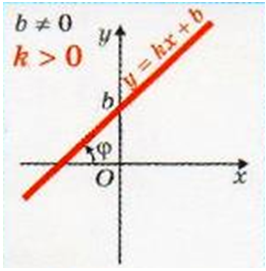
Рис. 1. Графік лінійної функції, яка зростає
Від коефіцієнта
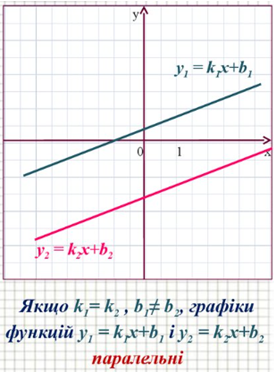
Рис. 2. Прямі з однаковим кутовим коефіцієнтом
Отже, використавши геометричний зміст графіків, наведених в умові, можна без обчислень дійти висновку, що швидкості руху будуть однакові, якщо ділянки графіків нахилені під однаковим кутом до осі
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на перевірку знання і розуміння однієї з фізичних моделей ‒ матеріальної точки.
Матеріальна точка ‒ це фізична модель тіла, розмірами якого в умові задачі можна знехтувати. Те саме тіло в умовах однієї задачі можна вважати матеріальною точкою, а в умовах іншої ‒ ні.
Це визначення можна застосувати до ведмедя і бджоли. Наприклад, розглядаючи будову тіла бджоли, не можна знехтувати розмірами її тіла. А під час вивчення її руху – можна.
Те саме стосується і ведмедя. Коли вивчають анатомію тварини, розміри важливі. Коли ж спостерігають за міграцією ведмедя, розмірами можна знехтувати.
Отже, чи можна знехтувати розмірами тіла, чи ні, визначають умови, за яких це тіло розглядаємо.
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу за рівномірного й рівноприскореного рухів.
Завдання скеровано на перевірку вміння інтерпретувати графіки, переходити від однієї до другої залежності величин.
Розгляньмо щосекунди наведений в умові завдання графік залежності координати
Ділянка графіка від початку відліку часу до першої секунди: це графік прямолінійного рівноприскореного руху. Адже графіком є частина параболи (вітки вниз), початкова координата
Оскільки
Знаючи прискорення руху тіла, знайдімо кінцеву швидкість руху тіла наприкінці першої секунди:
Знак «мінус» указує на те, що тіло рухалося в напрямку, протилежному до напрямку осі
Значення початкової і кінцевої швидкості руху тіла за першу секунду відповідають лише варіанту відповіді A. Щоб упевнитися в правильності варіанта відповіді A, проаналізуймо рух тіла в наступні секунди.
Від 1-ї до 2-ї секунди: ділянка графіка залежності координати тіла від часу прямолінійна, отже, рух рівномірний, швидкість стала.
Від 2-ї до 3-ї секунди: це графік прямолінійного рівноприскореного руху, оскільки графіком є частина параболи (вітки вгору), тіло гальмує, швидкість руху тіла зменшується до нуля, тіло зупиняється.
Від 3-ї до 4-ї секунди: координата тіла не змінюється, отже, швидкість тіла дорівнює нулю ‒ тіло не рухається.
Відповідь: A.
ТЕМА: Механіка. Основи кінематики. Шлях і переміщення.
Завдання скеровано на перевірку знання і розуміння фізичної величини переміщення.
Якщо спочатку турист рухався на захід, а потім ‒ на північ, це означає, що він, пройшовши
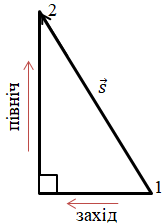
Якщо з’єднаємо початкову точку
Визначмо модуль цього переміщення ‒ довжину відрізка, що з’єднує точки
Отже, модуль переміщення дорівнюватиме
А можна без обчислень одразу сказати, чому дорівнюватиме гіпотенуза (модуль переміщення) цього прямокутного трикутника. Якщо сторони прямокутного трикутника співвідносяться як
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на перевірку знання і розуміння фізичної моделі ‒ матеріальної точки.
Матеріальна точка ‒ це фізична модель тіла, розмірами якого в умові задачі можна знехтувати. Те саме тіло в умовах однієї задачі можна вважати матеріальною точкою, а в умовах іншої ‒ ні.
Це визначення можна застосувати до ведмедя і бджоли. Наприклад, розглядаючи будову тіла бджоли, не можна знехтувати розмірами її тіла. А під час вивчення її руху – можна.
Те саме стосується і ведмедя. Коли вивчають анатомію тварини, розміри важливі. Коли ж спостерігають за міграцією ведмедя, розмірами можна знехтувати.
Отже, чи можна знехтувати розмірами тіла, чи ні, визначають умови, за яких це тіло розглядаємо.
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на перевірку знання і розуміння однієї з фізичних моделей ‒ матеріальної точки.
Матеріальна точка ‒ це фізична модель тіла, розмірами якого в умові задачі можна знехтувати. Те саме тіло в умовах однієї задачі можна вважати матеріальною точкою, а в умовах іншої ‒ ні.
Під час сонячного затемнення не можна нехтувати розмірами Місяця, оскільки від цього залежить тривалість затемнення і розміри тіні й півтіні, які спостерігають на поверхні Землі.
Напевне не можна вважати супутник Землі матеріальною точкою під час вибору місця посадки космічного корабля на Місяць, а також у ситуації вивчення рельєфу поверхні Місяця.
Добираючи місце посадки космічного корабля на Місяць, вибирають місцевість, задають певні координати на поверхні. Тому знехтувати розмірами Місяця і вважати його матеріальною точкою не можна.
Вивчаючи рельєф поверхні Місяця, описують просторові закономірності його будови й розвитку, нескінченні западини і височини, розмірами яких не можна знехтувати. Тобто вважати Місяць матеріальною точкою під час дослідження його рельєфу не можна.
Гравітаційну силу між Місяцем і Сонцем визначають за законом всесвітнього тяжіння, у якому йдеться про притягування будь-яких двох тіл одне до одного із силою, що прямо пропорційна добутку мас цих тіл й обернено пропорційна квадрату відстані між ними. Цей закон справджується, якщо обидва тіла є матеріальними точками (розмірами тіл нехтують, а маса матеріальної точки дорівнює масі того чи того тіла). Отже, у цій ситуації Місяць можна вважати матеріальною точкою.
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу в рівномірному й рівноприскореному рухах.
Завдання скеровано на перевірку знання і розуміння графічної інтерпретації шляху, пройденого тілом.
Шлях чисельно дорівнює площі фігури під графіком швидкості руху:
для прямолінійного рівномірного руху
|
для прямолінійного рівноприскореного руху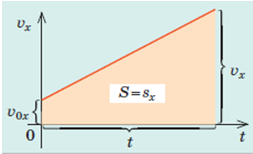
|
для будь-якого руху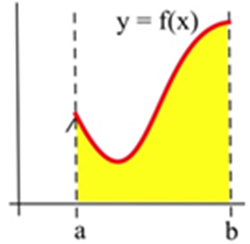
|
|
Отже, розгляньмо й порівняймо площі фігур під графіками швидкості руху тіл А, Б, В й Г. Відповідно до умови обмежмо праворуч ці фігури вертикальною прямою, що пройде через позначку
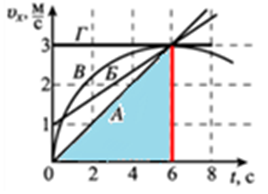 найменший шлях пройде тіло А |
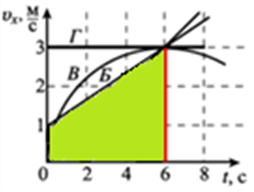 шлях, який пройшло тіло Б |
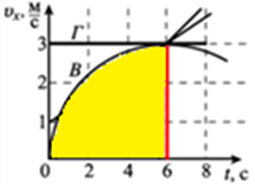 шлях, який пройшло тіло В |
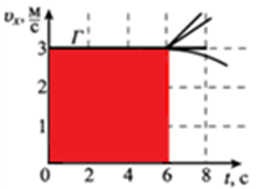 найбільший шлях пройде тіло Г |
Відповідь: Г.
ТЕМА: Фізичні величини. Вимірювання фізичних величин.
Завдання скеровано на перевірку розуміння побудови шкали приладів і вміння визначати за показами шкали приладів певні фізичні величини, зокрема час.
Поділка ‒ це відстань між рисками (позначками, лініями) на вимірювальній шкалі.
Ціна поділки шкали вимірювального приладу ‒ це значення фізичної величини, що відповідає найменшій поділці шкали цього приладу.
Щоб визначити ціну поділки шкали вимірювального приладу, треба:
1) вибрати два найближчі значення величини, які подано на шкалі, та обчислити їхню різницю;
2) визначити кількість поділок між рисками, поряд із якими вказано ці значення;
3) отриману різницю поділити на кількість поділок:
Візьмемо, наприклад, сусідні підписані поділки
Визначімо ціну поділки шкали секундоміра:
Відповідь: Б.
Тема: Механіка. Основи кінематики. Матеріальна точка.
Завдання скеровано на перевірку знання і розуміння поняття матеріальної точки.
Описуючи рух тіла, розміри якого набагато менші, ніж відстані, які воно долає, тіло замінюють на фізичну модель ‒ матеріальну точку. Матеріальна точка не має розмірів, а її маса дорівнює масі тіла, яке є нею. Тож все залежить від умов задачі.
Диспетчер ніяк не може вважати Землю матеріальною точкою, оскільки він повинен чітко знати, наприклад, якої довжини повинні бути злітно-посадкові смуги, де і як припаркувати літаки різних розмірів на території аеропорту тощо.
Космонавт, готуючись до посадки космічного корабля на Землю, може корегувати траєкторію і місце приземлення. Тож не може знехтувати розмірами, наприклад, прогнозованого майданчика для посадки.
Обчислити силу тяжіння між планетами можна за законом всесвітнього тяжіння. Однією з умов виконання цього закону є те, що обидва тіла можна вважати матеріальними точками. Отже, науковець, обчислюючи силу тяжіння між Землею і Марсом, має право припустити, що Земля ‒ матеріальна точка.
Для пошуку родовищ потрібно проводити пошукові виробки, аналізувати винесені частинки корисної копалини на земній поверхні, звертати увагу на особливий вигляд рослинності над покладом тощо, досліджуючи під час цього метр за метром земної поверхні. Тому в цій діяльності не можна знехтувати розмірами Землі.
Відповідь: B.