Механіка – Кінематика: прямолінійний рух

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку вміння описувати рух аналітично.

За умовою швидкість під час прямолінійного руху тіла протягом усього часу збільшується, тобто тіло рухається прискорено.

Запишімо рівняння залежності координати \(x\) від часу \(t\) в загальному вигляді для прямолінійного рівноприскореного руху: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) ‒ початкова координата, \(v_0\) ‒ початкова швидкість, \(a\) ‒ прискорення.

Варіанти відповіді \(x=5+3t\) і \(x=5-3t\) описують прямолінійний рівномірний рух, тому що немає доданку \(\frac{at^2}{2},\) тобто прискорення дорівнює нулю.

Розгляньмо рівняння \(x=5t-2t^2:\) початкова координата \(x_0=0,\) початкова швидкість \(v_0=5\ \text{м/с},\) прискорення \(a=-4\ \text{м/с}^2\) (знак мінус тут означає, що тіло гальмує, вектори швидкості й прискорення напрямлені протилежно, що суперечить умові завдання).

Розгляньмо рівняння \(x=5-2t^2:\) початкова координата \(x_0=5\ \text{м},\) початкова швидкість \(v_0=0,\) прискорення \(a=-4\ \text{м/с}^2.\) Тобто тіло розганяється зі стану спокою, але в напрямку, протилежному до напрямку осі \(Ox,\) тому прискорення від’ємне. Це правильна відповідь.

Відповідь: A.

ТЕМА: Механіка. Основи кінематики. Прямолінійний рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку розуміння закономірностей прямолінійного рівномірного і рівноприскореного рухів.

Розгляньмо рух парашутиста й монети.

За умовою завдання парашутист опускається зі сталою швидкістю \(v=5\ \text{м/с},\) оскільки дія сили тяжіння скомпенсована дією сили опору повітря. Отже, відстань \(h=100\ \text{м}\) він пройде за \(20\ \text{с}:\) $$ t_\text{пар} =\frac hv=\frac{100}{5}=20\ \text{с}. $$

Монета пройде той самий шлях \(h=100\ \text{м},\) але рухатиметься рівноприскорено. Початкова швидкість монети відносно парашутиста дорівнює нулю, оскільки вона просто випала з кишені. Оскільки монета випала з кишені парашутиста, який рухався зі швидкістю \(5\ \text{м/с},\) початкова швидкість монети відносно поверхні землі дорівнює \(v_0=5\ \text{м/с}.\) Вплив опору повітря на монету за умовою не враховуємо, тож знайдімо час її падіння з кінематичного рівняння: $$ h=v_0t+\frac{>^2}{2}, $$ (\(g\) ‒ прискорення вільного падіння; усі векторні величини записані у проекціях на вісь \(Oy,\) яка напрямлена вертикально вниз, так само, як і вектор прискорення вільного падіння).

Підставмо значення величин у рівняння: $$ h=v_0t+\frac{>^2}{2}\Rightarrow 100=5t+\frac{10t^2}{2}. $$

Поділімо ліву і праву частини рівняння на \(5\) й отримаємо зведене квадратне рівняння: $$ t^2+t-20=0. $$

За теоремою Вієтта визначмо корені рівняння: \(t_1=-5,\ \ t_2=4.\)

Час не може бути від’ємним, умову завдання задовольняє корінь \(t_2=4\ \text{с},\) тобто монета впала за \(4\ \text{с},\) а парашутист, відповідно, приземлився на \(16\ \text{с}\) пізніше: $$ \Delta t=t_\text{пар}-t_2=20\ \text{с}-4\ \text{с}=16\ \text{с}. $$

Відповідь: 16.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.

Завдання скеровано на перевірку вміння використовувати закон збереження імпульсу й уміння визначати швидкість у різних системах відліку.

Дано:
\(m_2=45\ \text{т}\)
\(m_1=55\ \text{т}\)
\(v_1=3\ \text{м/с}\)
\(v=3,9\ \text{м/с}\)
\(t=26\ \text{с}\)

1. Знайти:
\(v_2\ \left(\frac{\text{м}}{\text{с}}\right)\ -\ ?\)

За законом збереження імпульсу сума імпульсів тіл до зіткнення дорівнюватиме сумі імпульсів тіл після.

Імпульс розраховують за формулою $$ \overrightarrow{p}=m\overrightarrow{v}, $$ де \(m\) – маса тіла, а \(\overrightarrow{v}\) – його швидкість.

До зіткнення вагони рухаються незалежно й мають власні імпульси, а після зіткнення вони рухаються як одне тіло з єдиним імпульсом, спільною швидкістю і масою, яка дорівнює сумі мас двох вагонів. Тобто

2. Знайти:
\(l_0\ (\text{м})\ -\ ?\)

Для того, щоби визначити відстань, яку вагони пройшли до зіткнення, потрібно визначити їхню швидкість один відносно одного. Вагони рухаються в одному напрямку, тому їхня швидкість один відносно одного буде меншою, ніж відносно землі. Швидкість другого вагона відносно першого можна обчислити за формулою $$ v_{2(1)}=v_2-v_1=5\ \frac{\text{м}}{\text{с}}-3\ \frac{\text{м}}{\text{с}}=2\ \frac{\text{м}}{\text{с}}. $$

Початкова відстань, яку другий вагон скоротив до \(0\) за \(26\ \text{с}\), дорівнює $$ l_0= v_{2(1)}t=2\ \frac{\text{м}}{\text{с}}\cdot 26\ \text{с}=52\ \text{м}. $$

Відповідь: 1. 5. 2. 52.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на перевірку розуміння поняття лінійної швидкості обертання і вміння визначати характеристики складного руху.

Велосипед складено з різних частин, чий рух принципово відрізняється: рами, яка під час прямолінійного руху всього велосипеда також рухається поступально, і коліс та педалей, які, крім поступального руху разом з усім велосипедом, здійснюють обертальний.

Позначмо швидкість прямолінійного руху велосипеда як \(v\). Тоді кожна його частина, що рухається поступально, матиме таку саму швидкість. Тому швидкість у точці \(A\) також дорівнюватиме \(v\).

Якщо колесо рухається без проковзування, то лінійна швидкість під час руху по колу будь-якої його точки на зовнішній поверхні має дорівнювати швидкості поступального руху його центра. Тому для точок, зображених на рис. 1 \(V_O = V_K\).

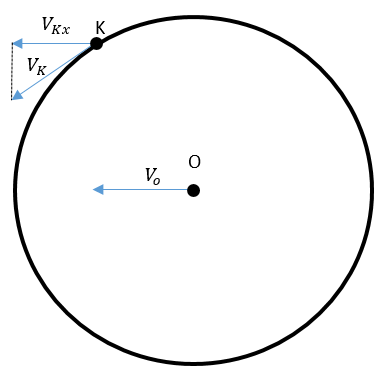
Рис. 1. Лінійна швидкість \(V_O\) обертального руху точки на колі та швидкість \(V_K\) поступального руху центра кола (коло обертається проти годинникової стрілки)

Тоді швидкість руху для будь-якої точки на поверхні кола можна визначити як суму швидкості поступального руху його центра й проєкції на вісь х його лінійної швидкості руху по колу: $$ V=V_{K_x}+V_O $$

Така рівність дійсна для всіх точок зовнішньої поверхні колеса. Тож проекції лінійної швидкості обертального руху за модулем найбільші в найнижчій (Г) і найвищій (Б) точці колеса. У найвищій точці лінійна швидкість обертального руху співнапрямлена зі швидкістю поступального руху всього колеса, а в найнижчій точці – напрямлена протилежно до неї.

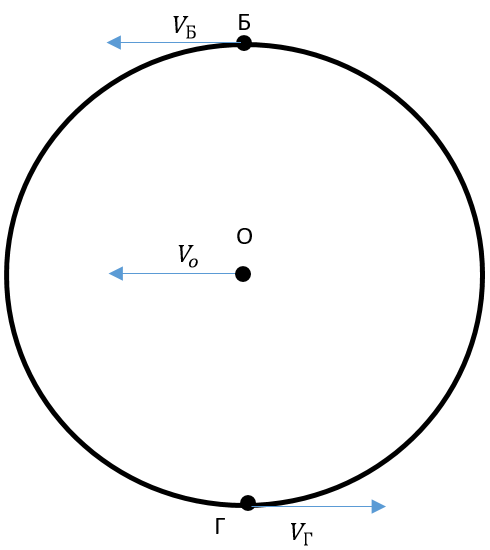
Рис. 2. Напрямок лінійної швидкості обертального руху для точок Б й Г

Тоді загальна швидкість у точці Г дорівнює нулю: $$ V_O-V_{Г}=V_O-V_O=0. $$

А в точці Б: $$ V_O-V_{Б}=V_O+V_O=2V_O. $$ Одна найвища точка колеса матиме найбільшу швидкість, будь-яка інша його точка матиме меншу швидкість.

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на визначення основних кінематичних величин за рівномірного руху.

Дано:
\(\triangle t=2,25\ \text{c}\)
\(v_{\text{звуку}}=340\ \text{м/с}\)
\(v_{\text{кулі}}=680\ \text{м/с}\)

1. Знайти:
\(\frac{t_{\text{кулі}}}{t_{\text{звуку}}}-?\)

Нехай \(t_{\text{кулі}}\) – це час, який знадобився кулі, щоби пройти шлях \(l\) від спортсмена до мішені, а \(t_{\text{звуку}}\) – це час, який знадобився, аби звук удару кулі об мішень дійшов до спортсмена.

З огляду на те, що відстані, яку подолали куля і звукова хвиля, рівні, а швидкості руху кулі й поширення звуку відомі, можна виразити обидва проміжки часу: $$ t_{\text{кулі}}=\frac{l}{v_{\text{кулі}}},\ \ t_{\text{звуку}}=\frac{l}{v_{\text{звуку}}}. $$

Тоді справедливим буде таке співвідношення: \begin{gather*} \frac{t_{\text{кулі}}}{t_{\text{звуку}}}=\frac{\frac{l}{v_{\text{кулі}}}}{\frac{l}{v_{\text{звуку}}}}=\frac{v_{\text{звуку}}}{v_{\text{кулі}}}=\frac{340\ \text{м/с}}{680\ \text{м/с}}=0,5. \end{gather*}

2. Знайти::
\(l\ \text{(м)} - ?\)

Куля пройшла шлях від спортсмена до мішені, а потім звук від удару кулі об мішень повернувся назад до спортсмена. Тоді час від вистрілу до моменту, коли спортсмен почув звук цього удару, можна записати як суму цих двох проміжків часу: $$ \triangle t=t_{\text{кулі}}+t_{\text{звуку}}. $$

Потім потрібно виконати підстановки й здійснити перетворення: \begin{gather*} \triangle t=0,5t_{\text{звуку}}+t_{\text{звуку}}=1,5t_{\text{звуку}},\\[6pt] t_{\text{звуку}}=\frac{2,25\ \text{c}}{1,5}=1,5\ \text{c}; \end{gather*}

Після цього можна обчислити шукану відстань \(l\): $$ l=t_{\text{звуку}}v_{\text{звуку}}=1,5\ \text{c}\cdot 340\frac{\text{м}}{\text{c}}=510\ \text{м}. $$

Відповідь: 1. 0,5. 2. 510.

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу в рівноприскореному русі.

Завдання скеровано на оцінювання вміння аналізувати графіки руху тіл і визначати за ними параметри руху.

У графіку, наведеному в завданні, виокремлено п’ять частин, на кожній із яких відображено різні режими руху тіла. Швидкість руху тіла, відкладену на осі \(y\), визначають за формулою \(v_x=v_0+a_x t\) (1), де \(v_0\) – значення початкової швидкості, \(a_x\) – прискорення, \(t\) – час руху.

Вираз (1) – це рівняння прямої з кутовим коефіцієнтом \(a_x\). Тоді проміжку часу, коли тіло рухається рівноприскорено зі збільшенням модуля швидкості, на графіку відповідає вгорубіжна пряма \((a_x\gt 0)\).

Відповідь: Б.

ТЕМА: Механіка. Кінематика. Швидкість. Додавання швидкостей.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі із додавання швидкостей.

1. Дано:
\(L=60\ \text{км}\)
\(t_{\text{за течією}}=3\ \text{год}\)
\(t_{\text{проти течії}}=6\ \text{год}\)

Знайти:
\(v_{\text{течії}}-?\)

Сумарна швидкість руху човна \((\overrightarrow{v}_{\text{сум}})\) є векторною сумою швидкості човна \((\overrightarrow{v}_{\text{човна}})\) і швидкості течії \((\overrightarrow{v}_{\text{течії}})\): \(\overrightarrow{v}_{\text{сум}}= \overrightarrow{v}_{\text{човна}}+\overrightarrow{v}_{\text{течії}}\) (1).

Якщо човен пливе за течією і проти неї: \(v_{\text{сум за}}= v_{\text{човна}}+v_{\text{течії}}\) (2), \(v_{\text{сум проти}}= v_{\text{човна}}-v_{\text{течії}}\) (3).

Також можна обчислити швидкості за формулами (2) і (3) з урахуванням пройденого човном шляху: \(v_{\text{сум за}}=\frac{L}{t_{\text{за течією}}}\) (4), \(v_{\text{сум проти}}=\frac{L}{t_{\text{проти течії}}}\) (5).

Підставивши (4) і (5) у (2) і (3) відповідно, можна дістати систему з двох рівнянь: \begin{gather*} \begin{cases} \frac{L}{t_{\text{за течією}}}=v_{\text{човна}}+v_{\text{течії}}\\ \frac{L}{t_{\text{проти течії}}}=v_{\text{човна}}-v_{\text{течії}} \end{cases} \ \boldsymbol (6). \end{gather*} Далі, розв’язавши систему рівнянь (6), потрібно визначити швидкість течії:

2. Знайти:
\(t_{\text{без течії}} - ?\)

Дізнатися \(t_{\text{без течії}}\) можна зі співвідношення \(v_{\text{човна}}=\frac{L}{t_{\text{без течії}}}\), із нього випливає, що \(t_{\text{без течії}}=\frac{L}{v_{\text{човна}}}\) (8).

Затим, використавши систему рівнянь (6), можна визначити \(v_{\text{човна}}\):

Тоді за формулою (8) можна обчислити \(t_{\text{без течії}}=\frac{60\ \text{км}}{15\ \text{км/год}}=4\ \text{год}\).

Відповідь: 1. 5. 2. 4.

ТЕМА: Механіка. Основи кінематики. Середня швидкість.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, пов’язані із середньою і миттєвою швидкостями тіла.

Дано:
\(v_1=20\ \frac{\text{м}}{\text{с}}\)
\(v_{\text{сер}}=24\ \frac{\text{м}}{\text{с}}\)
\(l_1=l_2\)

Знайти:
\(v_2\ -\ ?\)

Середню швидкість можна визначити за формулою: $$ v_{\text{сер}}=\frac <, $$ де \(l\) – шлях між двома містами, а \(t\) – час, за який автомобіль його подолав.

Зважаючи на те, що \begin{gather*} l=l_1+l_2,\\[7pt] t=t_1+t_2, \end{gather*} можна дійти висновку: $$ v_{\text{сер}}=\frac{l_1+l_2}{t_1+t_2}. $$

Оскільки немає інформації про час руху автомобіля на проміжку або на його половині, потрібно виразити ці величини через швидкості й шлях: \begin{gather*} t=\frac{l}{v_{\text{сер}}},\\[6pt] t=t_1+t_2=\frac{l_1}{v_1}+\frac{l_2}{v_2}. \end{gather*}

Зважаючи на те, що шлях пройдений із першою швидкістю, дорівнює шляху, пройденому з другою швидкістю, можна записати: $$ t_1+t_2=\frac{l}{2v_1}+\frac{l}{2v_2}. $$

Отже \begin{gather*} \frac{l}{v_{\text{сер}}}=\frac{l}{2v_1}+\frac{l}{2v_2};\\[6pt] \frac{l}{v_{\text{сер}}}=\frac{2v_2l+2v_1l}{4v_1v_2}=\frac{2l(v_2+v_1)}{4v_1v_2}. \end{gather*}

Тоді \begin{gather*} 4lv_1v_2=2l(v_2+v_1)v_{\text{сер}};\\[6pt] 4\cdot 20\ \frac{\text{м}}{\text{с}}\cdot v_2=2\left(v_2+20\ \frac{\text{м}}{\text{с}}\right)\cdot 24\ \frac{\text{м}}{\text{с}};\\[6pt] 80\ \frac{\text{м}}{\text{с}}\cdot v_2=\left(2v_2+40\ \frac{\text{м}}{\text{с}}\right)\cdot 24\ \frac{\text{м}}{\text{с}};\\[6pt] 80\ \frac{\text{м}}{\text{с}}\cdot v_2=48\ \frac{\text{м}}{\text{с}}\cdot v_2+960\ \frac{\text{м}}{\text{с}}\cdot \ \frac{\text{м}}{\text{с}};\\[6pt] 80\ \frac{\text{м}}{\text{с}}\cdot v_2-48\ \frac{\text{м}}{\text{с}}\cdot v_2=960\ \frac{\text{м}}{\text{с}}\cdot \ \frac{\text{м}}{\text{с}};\\[6pt] 32\ \frac{\text{м}}{\text{с}}\cdot v_2=960\ \frac{\text{м}}{\text{с}}\cdot\ \frac{\text{м}}{\text{с}};\\[6pt] v_2\frac{960\ \frac{\text{м}}{\text{с}}\cdot\ \frac{\text{м}}{\text{с}}}{32\ \frac{\text{м}}{\text{с}}}=30\ \frac{\text{м}}{\text{с}}. \end{gather*}

Відповідь: 30.

ТЕМА: Механіка. Кінематика. Швидкість. Додавання швидкостей.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з додавання швидкостей і розуміння поняття відносності руху.

За умовою завдання швидкості поїзда й людини співнапрямлені, а швидкість вітру направлена в протилежний бік. Це схематично зображено на рисунку 1.

Рис. 1. Швидкості руху поїзда, людини й вітру

Тоді перш за все знайдемо швидкість людини відносно землі, щоби порівняти її зі швидкістю вітру, яку визначаємо саме відносно землі.

Швидкість людини відносно землі згідно з умовою завдання дорівнює: $$ \overrightarrow{v_{\text{л.в.з.}}}=\overrightarrow{v_{\text{людини}}}+ \overrightarrow{v_{\text{поїзда}}} $$

У проєкції на вісь \(OX\) швидкість людини відносно землі дорівнює: $$ v_{\text{л.в.з.}}=-v_{\text{людини}}-v_{\text{поїзда}}=-2\ \frac{\text{м}}{\text{с}}-10\ \frac{\text{м}}{\text{с}}=-12\ \frac{\text{м}}{\text{с}}. $$

Тоді швидкість вітру відносно людини дорівнює різниці векторів швидкості людини й вітру відносно землі: $$ \overrightarrow{v_{\text{в.в.л.}}}=\overrightarrow{v_{\text{вітру}}}+ \overrightarrow{v_{\text{л.в.з.}}} $$

У проєкції на вісь \(OX\) швидкість вітру відносно людини дорівнює: $$ v_{\text{л.в.з.}}=v_{\text{вітру}}-v_{\text{людини}}=3\ \frac{\text{м}}{\text{с}}-\left(-12\ \frac{\text{м}}{\text{с}}\right)=15\ \frac{\text{м}}{\text{с}}. $$

Відповідь: Г.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Сила тертя

Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі на використання принципів рвномірного руху по колу.

Дано:
\(\mathbf{\mu}_1=0,72\)
\(\mathbf{\mu}_2=0,18\)

Знайти:
\(\frac{v_1}{v_2}\ -\ ?\)

Можна вважати, що під час повертання машина рухається по ділянці кола (рис. 1).

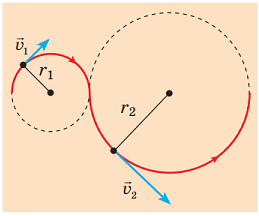
Рис. 1. Зображення поворотів як елементів кола під час криволінійного руху

Під час такого руху швидкість автомобіля спрямовано по дотичній до кола. Оскільки під час руху по колу швидкість постійно змінює свій напрямок, виникне доцентрове пришвидшення.

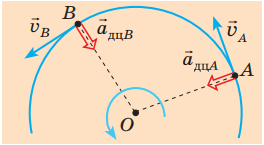
Рис. 2. Напрямок пришвидшення і швидкості під час руху по колу

За другим законом Ньютона рівнодійна сил дорівнює добутку маси тіла на пришвидшення, набуте під час взаємодії, тобто $$ \overrightarrow{F}=m\overrightarrow{a}. $$

Єдиною силою, що діє на автомобіль у площині напрямку руху є сила тертя, тому другий закон Ньютона в цьому разі можна записати так: $$ \overrightarrow{F_{\text{тер}}}=m\overrightarrow{a_{\text{доц}}}. $$

Силу тертя визначають за формулою $$ \overrightarrow{F_{\text{тер}}}=\mathbf{\mu}\overrightarrow{N}, $$ де \(\overrightarrow{N}\) – сила реакції опори.

Її можна визначити, записавши другий закон Ньютона для осі OY. Уздовж цієї осі на машину діє сила тяжіння і сила реакції опори, але рух не відбувається, а отже рівнодійна дорівнює нулю: \begin{gather*} \overrightarrow{F_{\text{тяж}}}+\overrightarrow{N}=0;\\[7pt] F_{\text{тяж}}-N=0;\\[7pt] F_{\text{тяж}}=N=mg. \end{gather*}

Тоді сила тертя дорівнюватиме: $$ F_{\text{тер}}=\mathbf{\mu}mg. $$

Сила тертя завжди заважає рухові. Оскільки швидкість автомобіля спрямована з кола, то сила тертя буде спрямована до його центра. Крім сили тертя, можна також обчислити доцентрове пришвидшення, виразивши його за допомогою швидкості руху автомобіля і радіуса повороту: $$ a_{\text{доц}}=\frac{v^2}{R}. $$

Тоді можна перетворити рівняння: \begin{gather*} F_{\text{тер}}=ma_{\text{доц}};\\[7pt] \mathbf{\mu}mg=m\frac{v^2}{R}. \end{gather*}

Тож можна виразити швидкість руху: $$ v=\sqrt{\mathbf{\mu}gR}. $$

Відношення швидкостей до і після зміни коефіцієнта тертя тоді можна записати так: $$ \frac{v_1}{v_2}=\frac{\sqrt{\mathbf{\mu}_1gR}}{\sqrt{\mathbf{\mu}_2gR}} =\sqrt{\frac{\mathbf{\mu}_1}{\mathbf{\mu}_2}}=\sqrt{\frac{0,72}{0,18}} =2. $$

Відповідь: 2.

ТЕМА: Механіка. Основи кінематики. Система відліку. Швидкість.

Завдання скеровано на оцінювання розуміння понять швидкості світла й системи відліку.

Значення швидкості світла є сталим для будь-якої системи відліку незалежно від швидкості її руху.

Тому не залежно від того, яке тіло відліку вибрано (Земля, станція чи ракета), значення швидкості світла буде однаковим – 300 000 км/с.

Відповідь: A.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на оцінювання вміння застосовувати формулу залежності координат від часу для рівноприскореного руху.

Загальний вигляд залежності координати від часу за прямолінійного рівноприскореного руху виражено формулою: $$ x=x_0+v_{0x}t+\frac{a_x}{2}t^2\ \ (1), $$ де \(x_0\) – початкова координата, \(v_{0x}\) – початкова швидкість, \(a_x\) – прискорення тіла, \(t\) – час руху.

За умовою початкова швидкість \(v_{0x}=6\ \text{м/с}\), прискорення \(a_x=1\ \text{м/с}^2.\) Тож рівняння координати таке: $$ x=x_0+6t+\frac 12 t^2\ \ (2). $$

Хоча значення початкової координати невідоме, однак можна з-поміж наведених вибрати відповідь, що не суперечить виразу (2).

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Прискорення. Графіки залежності кінематичних величин від часу.

Завдання скеровано на перевірку вміння розв'язувати задачі на аналіз графіків руху тіл і визначення за ними його параметрів.

Спочатку потрібно записати залежність координати від часу: $$ x=x_0+V_{Ox}t+\frac{a_xt^2}{2} $$

З графіка \begin{gather*} x=20\ \text{за}\ t=2\ \text{с},\ x_0=-10\ \text{м}\\[7pt] V_0=3\ \text{м/с}\\[6pt] 20=-10+3\cdot 2+\frac{a_x2^2}{2}\\[6pt] a=12\ \text{м/с}^2. \end{gather*}

Відповідь: 12.

ТЕМА: Механіка. Основи кінематики. Основи динаміки. Другий закон Ньютона.

Завдання скеровано на перевірку знання законів кінематики й законів динаміки Ньютона, а також уміння розв'язувати комбіновані задачі, використовуючи поняття і закономірності з кількох розділів механіки.

Ураховуючи загальний вид рівняння руху $$ x=x_0+V_{0x}t-\frac{a_xt^2}{2} $$ і розташуванням коефіцієнтів у рівнянні руху в умові, можна визначити, що $$ \frac{a_x}{2}=4, $$ тоді $$ a=a_x=8\ \text{м/с}^2. $$

За II законом Ньютона $$ R=ma= 800\ \text{кг} \cdot 8\ \text{м/с}^2=6\ 400\ \text{Н}. $$

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на рівноприскорений рух.

Дано:
\(t=5\ \text{с}\)
\(v_0=0\ \frac{\text{м}}{\text{с}}\)
\(v=10\ \frac{\text{м}}{\text{с}}\)
\(t_1=4\ \text{с}\)

1. Знайти:
\(a\ \left(\frac{\text{м}}{\text{с}^2}\right)\ -\ ?\)

Швидкість за рівноприскореного руху можна визначити за формулою $$ v=v_0+at, $$ де \(v_0\) – початкова швидкість, \(a\) – прискорення, \(t\) – час руху тіла.

Оскільки тіло рухається зі стану спокою, то початкова швидкість тіла дорівнює нулю, тоді $$ v=at. $$

Тож з формули можна виразити прискорення: \begin{gather*} a=\frac vt=\frac{10\ \frac{\text{м}}{\text{с}}}{5\ \text{с}}=2\ \frac{\text{м}}{\text{с}^2} \end{gather*}

2. Знайти:
\(l\ (\text{м})\ -\ ?\)

Шлях, пройденим тілом, під час рівноприскореного руху можна визначити за формулою $$ l=v_0t+\frac{at^2}{2}, $$ де \(v_0\) – початкова швидкість тіла, \(a\) – прискорення тіла, \(t\) – час руху тіла.

Початкова швидкість тіла дорівнює нулю, тож шлях, який тіло пройшло за \(4\ \text{с}\), можна обчислити за формулою \begin{gather*} l=\frac{at^2}{2}=2\ \frac{\text{м}}{\text{с}^2}\cdot\frac{(4\ \text{с})^2}{2}=16\ \text{м}. \end{gather*}

Відповідь: 1. 2. 2. 16.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух. Рівномірний рух по колу.

Завдання скеровано на оцінювання вміння визначати напрямок прискорення і швидкості в різних процесах.

А Снаряд, випущений гарматою чи будь-яким іншим способом, рухатиметься під дією сили тяжіння після вистрілу. У такому разі прискорення, що діє на тіло, – це прискорення вільного падіння, що завжди напрямлене до центра Землі. Тобто якщо поверхня горизонтальна, то прискорення вільного падіння спрямоване перпендикулярно до поверхні. Тіло в такому разі рухається по параболі. Схематичне зображення руху тіла, кинутого під кутом до горизонту, тобто руху снаряду, зображено на рисунку 1. Стрілкою червоного кольору позначено прискорення тіла, зеленого – напрямок швидкості тіла (напрямок руху). Кут між цими напрямками гострий.

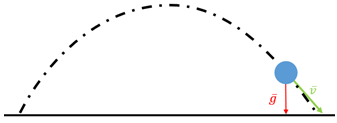
Рис. 1. Схематичне зображення руху снаряду перед падінням

Б Кінець годинникової стрілки рівномірно рухається по колу. За визначенням рівномірний рух тіла по колу – це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється із часом.

Під час руху по колу швидкість тіла постійно напрямлена по дотичній до кола. Це значить, що напрямок швидкості руху тіла постійно змінюється, але оскільки рух рівномірний, то модуль швидкості має залишатися постійним. Це можливо лише якщо прискорення напрямлене перпендикулярно до швидкості тіла. На рисунку 2 схематично зображено рух кінця годинної стрілки (позначеного синім кругом на рисунку). Тож кут між напрямком руху тіла й прискоренням у цьому разі завжди прямий.

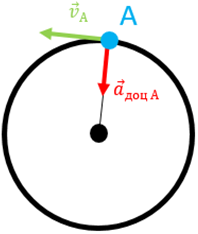
Рис. 2. Схематичне зображення руху кінця годинникової стрілки

В Під час руху снаряда в каналі ствола гармати його швидкість збільшується. Тобто прискорення співнапрямлене зі швидкістю тіла.

Г Після вимикання двигуна катера його швидкість починає зменшуватися. Тобто прискорення протилежно напрямлене до швидкості тіла.

Відповідь: 1Г, 2Д, 3В, 4А.

ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух. Кінетична енергія.

Завдання скеровано на оцінювання вміння розраховувати кінетичну енергію для різних типів руху, зокрема рівноприскореного.

Кінетична енергія \(T\) – це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси m тіла на квадрат швидкості v його руху: $$ T=\frac{mv^2}{2}, $$ де \(m\) – маса тіла, а \(v\) – швидкість його руху.

Під час рівноприскореного руху залежність швидкості тіла від часу можна записати так: $$ v=v_0+at, $$ де \(v_0\) – початкова швидкість, а \(a\) – прискорення тіла.

Після підставлення виразу для швидкості рівноприскореного руху у вираз для кінетичної енергії можна дістати залежність кінетичної енергії від часу: $$ T=\frac{m(v_0+at)^2}{2}=\frac m2 (v^2_0+2v_0at+a^2t^2). $$

У виразі є \(t^2\) – час у квадраті. Тобто залежність має вигляд параболи. На рисунку єдиний проміжок, що не є прямою – це проміжок 2–3.

Відповідь: Б.

ТЕМА: Механіка. Кінематика. Швидкість. Додавання швидкостей.

Завдання скеровано на оцінювання розуміння поняття відносності руху й уміння розв’язувати розрахункові задачі з додавання швидкостей.

Оскільки винищувач злітає з носа авіаносця, то їхні швидкості співнапрямлені. Тоді швидкість літака відносно берега дорівнює сумі швидкості авіаносця відносно берега й швидкості літака відносно корабля:

Тож можна розрахувати швидкість літака відносно корабля:

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики.

Завдання скеровано на перевірку вміння аналізувати графіки, що описують рух тіла.

Прямолінійний рух – це рух, траєкторію якого є пряма.

Щодо графіків у завданні:

А Це графік залежності проєкції швидкості \(v\) на вісь \(x\) від часу \(t\). Якщо проєкція швидкості на вісь незмінна, як на графіку, то рух рівномірний уздовж цієї осі. Проте рух за умовою відбувається в площині, а не вздовж осі. Інформації про рух уздовж іншої осі на цьому графіку немає, а без неї не можна зробити висновок про прямолінійність руху. Прикладом непрямолінійного руху з таким графіком залежності \(v_x(t)\) є рух тіла, кинутого під кутом до горизонту. Траєкторія такого руху – парабола.

Б Це графік залежності координати \(y\) від часу \(t\). Координата y за цим графіком залишається незмінною, проте інформації про зміну координати \(x\) на графіку немає. Тіло може як рухатися вздовж осі \(x\), так і залишатися на місці.

В Це графік залежності координати \(y\) від координати \(x\). У таких координатах графік зображує траєкторію руху тіла. У цьому разі траєкторія є прямою, тож рух прямолінійний.

Г Це графік залежності проекції швидкості \(v\) на вісь \(x\) від координати \(x\). Цей графік не надає інформації про рух тіла вздовж осі \(x\) чи \(y\), тож висновок про прямолінійність руху зробити не можна.

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух.

Завдання скеровано на перевірку вміння визначати основні кінематичні характеристики, якими описують рівноприскорений рух, а саме проєкцію швидкості й прискорення.

1. За умовою рух є рівноприскореним, підтвердженням цього також є наведений графік залежності координати від часу. Графіком є частина параболи, вершина якої відповідає точці розвороту. Це саме момент часу \(4\ \text{с}.\) Наближаючись до цієї точки тіло гальмує, у цій точці воно зупиняється на мить і починає рухатися у зворотному напрямку. Отже, швидкість руху тіла в момент часу \(4\ \text{с}\) дорівнюватиме \(0\ \text{м/с}.\)
Відповідь: 0.

2. Рівняння координати для прямолінійного рівноприскореного руху в загальному вигляді таке: $$ x=x_0+v_0t+\frac{at^2}{2}\ (\text{у проєкціях на вісь } Ox), $$ де \(x\) – координата тіла, \(x_0\) – початкова координата тіла, \(v_0\) – початкова швидкість руху тіла, \(t\) – час руху тіла, \(a\) – прискорення руху тіла.

Розгляньмо проміжок часу від \(4\) до \(5\) секунд. Зручно взяти саме цей проміжок, бо за ним можна визначити всі необхідні дані для обчислення прискорення руху тіла. Візьмемо дані для рівняння з графіка: \begin{gather*} x=10,5\ \text{м},\\[7pt] x_0=11\ \text{м},\\[7pt] v_0=0\ \text{м/с},\\[7pt] t=1\ \text{с}. \end{gather*}

Спростімо рівняння: $$ x-x_0=\frac{at^2}{2}. $$

Виразімо й обчислімо прискорення руху тіла: $$ a=\frac{2\Delta x}{t^2}=\frac{2\cdot(-0,5)\ \text{м}}{1\ \text{с}^2}=-1\ \text{м/с}^2. $$

Знак «мінус» вказує на те, що тіло рухається у протилежному до осі \(Ox\) напрямку.
Відповідь: –1.

Відповідь: 1. 0. 2. –1.

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.

Завдання скеровано на перевірку вміння застосовувати закон додавання швидкостей.

Закон додавання швидкостей полягає в тому, що швидкість \(\overrightarrow{v}_2\) руху тіла в нерухомій системі відліку дорівнює геометричній сумі швидкості \(\overrightarrow{v}_{23}\) руху тіла в рухомій системі відліку та швидкості \(\overrightarrow{v}_3\) руху рухомої системи відліку відносно нерухомої: $$ \overrightarrow{v}_{2}=\overrightarrow{v}_{23}+\overrightarrow{v}_{3}. $$

Якщо відома швидкість руху другої мурахи відносно землі \((\overrightarrow{v}_2)\) і швидкість руху третьої мурахи відносно землі \((\overrightarrow{v}_3)\), то можна обчислити швидкість руху другої мурахи відносно третьої \((\overrightarrow{v}_{23}).\)

Спочатку потрібно вибрати напрямок (зліва направо) горизонтальної oсі Ох, уздовж якої рухаються всі мурахи:

Якщо перша мураха біжить у напрямку осі, то модуль її швидкості дорівнює \(4\ \text{мм/с}\) за умовою.

Швидкість руху другої мурахи відносно землі дорівнює \(5\ \text{мм/с},\) але біжить вона назустріч першій, отже, проєкція її швидкості на вісь від’ємна: $$ v_{2x}=-5\ \frac{\text{мм}}{\text{с}}. $$

Третя мураха рухається в тому самому напрямку, що й перша, зі швидкістю \(3\ \text{мм/с}\) відносно неї. Тому швидкість третьої мурахи відносно землі дорівнює \(7\ \text{мм/с}:\) $$ v_{3x}=4\ \text{мм/с}+3\ \text{мм/с}=7\ \text{мм/с}. $$

Тож можна обчислити швидкість руху другої мурахи відносно третьої: $$ v_{23x}=v_{2x}-v_{3x}=-5-7=-12\ \frac{\text{мм}}{\text{с}}. $$

Відповідь: Б.

ТЕМА: Механіка. Кінематика. Швидкість. Додавання швидкостей.

Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з додавання швидкостей.

Вважатимемо першу систему відліку нерухомою, а другу – рухомою. Швидкість тіла в рухомій системі відліку можна визначити за формулою: $$ \overrightarrow{V_{\text{тіла рух}}}=\overrightarrow{V_{\text{тіла нерух}}}+\overrightarrow{V_{\text{рух}}}, $$ де \(\overrightarrow{V_{\text{тіла рух}}}\) – швидкість тіла в рухомій системі відліку, \(\overrightarrow{V_{\text{тіла нерух}}}\) – швидкість тіла в нерухомій системі відліку, \(\overrightarrow{V_{\text{рух}}}\) – швидкість рухомої системи відліку.

Тоді швидкість рухомої системи можна визначити за формулою $$ \overrightarrow{V_{\text{рух}}}=\overrightarrow{V_{\text{тіла рух}}}-\overrightarrow{V_{\text{тіла нерух}}}. $$

Найменшою буде швидкість рухомої системи відліку, якщо напрямок її руху збігається з напрямком руху самого тіла. Тоді векторне рівняння можна спроєктувати на вісь \(OX\):

Відповідь: A.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку розуміння характеру руху тіл.

Позначимо сталу – модуль швидкості руху потягу – \(v.\) Тоді відстань \(s_\text{п},\) яку пройшов потяг за час \(t\) від моменту відчеплення до моменту зупинки вагона, можна визначити за формулою для обчислення відстані під час прямолінійного рівномірного руху: $$ s_\text{п}=v\cdot t. $$

Час руху потяга на цьому відрізку шляху такий самий, як і час руху відчепленого останнього вагона до зупинки. Вагон рівномірно сповільнюватиметься. Його початковою швидкістю \(v_0\) буде швидкість руху потягу \(v,\) а кінцева швидкість \(v_\text{к}\) дорівнюватиме нулю.

Отже, $$ s_\text{в}=\frac{v_0+v_\text{к}}{2}\cdot t=\frac v2\cdot t, $$ де \(s_\text{в}\) ‒ відстань, яку пройшов вагон до зупинки.

Виразімо із цієї формули час руху вагона \(t\) і підставімо цей вираз у формулу для відстані, яку пройшов потяг:

Відповідь: 400.

ТЕМА: Механіка. Основи кінематики. Нерівномірний рух. Середня і миттєва швидкості.

Завдання скеровано на перевірку розуміння фізичного змісту середньої швидкості.

Середня швидкість \(v_\text{сер}\) дорівнює відношенню всього шляху \(l\) до інтервалу часу \(t,\) за який цей шлях подолано:

Перша частина шляху \(l_1=900\ \text{м}\), її велосипедист подолав зі швидкістю \(v_1=15\ \text{м/с.}\) Обчислімо час $$ t_1=\frac{l_1}{v_1}=\frac{900\ \text{м}}{15\ \text{м/с}}=60\ \text{с.} $$

Друга частина шляху \(l_2=400\ \text{м}.\) Її велосипедист подолав зі швидкістю \(v_2=36\ \text{км/год}=10\ \text{м/с}.\) Обчислимо час

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух.

Завдання скеровано на перевірку знання і вміння застосовувати кінематичні характеристики прямолінійного рівномірного руху.

Проаналізуймо наведені в умові кінематичні рівняння руху велосипедиста і мотоцикліста. Як бачимо, це залежність координати \(x\) від часу \(t\) в першому степені. Загальний вигляд рівняння координати для прямолінійного рівномірного руху такий: $$ x=x_0+vt, $$ де \(x_0\) ‒ початкова координата; \(v\) ‒ проєкція швидкості на горизонтальну вісь \(Ox,\) уздовж якої рухається тіло.

Для велосипедиста: початкова координата \(x_{01}=150\ \text{м,}\) проєкція швидкості \(v_1=-5\ \text{м/с.}\) Знак мінус означає, що велосипедист рухається в протилежному до вибраного напрямку горизонтальної осі \(Ox\) (див. рисунок).

Для мотоцикліста: початкова координата \(x_{02}=-50\ \text{м,}\) проєкція швидкості \(v_2=20\ \text{м/с.}\) Початкова координата зі знаком мінус означає, що мотоцикліст на початку руху перебував лівіше від початку відліку, вибраного на осі \(Ox\) (див. рисунок).

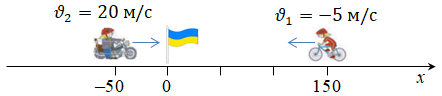
1. Час, через який зустрінуться велосипедист і мотоцикліст, однаковий для них, бо час плине однаково для всіх. Велосипедист зустрінеться з мотоциклістом ‒ це означає, що вони перебуватимуть у точці з однаковою координатою. Тож прирівняймо їхні координати \(x_1=x_2:\)

Велосипедист і мотоцикліст зустрінуться через \(8\ \text{с.}\)

Відповідь: 8.

2. Оскільки до зустрічі велосипедист рухався \(8\ \text{с}\) зі швидкістю \(5\ \text{м/с,}\) шлях визначімо за формулою: \begin{gather*} s_1=v_1t,\\[6pt] s_1=5\ \frac{\text{м}}{\text{с}}\cdot 8\ \text{с}=40\ \text{м}. \end{gather*}

Можна визначити координату велосипедиста через \(8\ \text{с}\) руху й обчислити його шлях до зустрічі з мотоциклістом, як різницю між початковою і кінцевою координатами велосипедиста:

Відповідь: 40.

Відповідь: 1. 8. 2. 40.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку розуміння і вміння описувати рух тіл за допомогою кінематичних рівнянь, знаходити потрібні фізичні величини.

1). Опишімо рух кота і мишеняти за допомогою кінематичних рівнянь координат (у проєкціях на вісь \(Ox\)).

Для кота ‒ прямолінійний рівноприскорений рух: \begin{gather*} X=x_\text{0к}+v_\text{0к}t+\frac{at^2}{2},\\[6pt] X=x_\text{0к}+\frac{at^2}{2}, \end{gather*} де \(X\) ‒ кінцева координата кота (точка \(X,\) у якій кіт наздожене мишеня (див. рисунок)), \(x_\text{0к}=-4,5\ \text{м}\) ‒ початкова координата кота, \(v_\text{0к}=0\) (за умовою) ‒ проєкція початкової швидкості руху кота, \(t\) ‒ час руху кота (поки наздожене мишеня), \(a=2\ \text{м/с}^2\) ‒ проєкція прискорення руху кота.

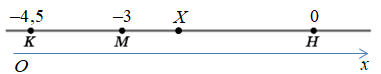
Для мишеняти ‒ прямолінійний рівномірний рух: $$ X=x_\text{0м}+v_\text{м}t, $$ де \(X\) ‒ кінцева координата мишеняти (співпадає з кінцевою координатою кота (див. рисунок)), \(x_\text{0м}=-3\ \text{м}\) ‒ початкова координата мишеняти, \(v_\text{м}=0,5\ \text{м/с}\) (за умовою) ‒ проєкція швидкості руху мишеняти, \(t\) ‒ час руху мишеняти (такий самий, як для кота).

Оскільки час руху кота і мишеняти однаковий, прирівняймо його, щоб визначити спільну кінцеву координату \(X:\)

Підставімо числові значення величин (в умові всі значення величин подано в системі SI):

Координата \(X_2=-3,5\) не задовольняє умову завдання, оскільки мишеня біжить до нірки і його кінцева координата має бути більша за \(‒3\) (див. рисунок).

Отже, координата точки, у якій кіт наздожене мишеня, дорівнює $$ X=-2,25\ \text{м}, $$ тобто кіт упіймає мишеня на відстані \(2,25\ \text{м}\) від нори.

Відповідь: 2,25.

2). Для визначення часу, за який кіт наздожене мишеня скористаймося формулами, отриманими у першій частині завдання: \begin{gather*} t^2=\frac{2(X-x_\text{0к})}{a},\\[6pt] t=\frac{X-x_\text{0м}}{v_\text{м}}. \end{gather*}

Можна підставити значення в одну із формул і обчислити час:

Перевірка за іншою формулою:

Відповідь: 1,5.

Відповідь: 1. 2,25. 2. 1,5.

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу у рівномірному і рівноприскореному рухах.

Завдання скеровано на перевірку знання і розуміння характеристик прямолінійного рівномірного і рівноприскореного рухів.

Проаналізуймо всі ділянки й точки графіка залежності проєкції швидкості прямолінійного руху тіла від часу.

У точці А тіло має певну початкову швидкість, відмінну від нуля, а далі продовжує рухатися прямолінійно рівноприскорено (ділянка АБ).

Від моменту часу, що відповідає точці Б, тіло сповільнює свій рух (ділянка БB), потім зупиняється (точка B).

Після зупинки в точці В тіло набирає швидкість, рухаючись у протилежному напрямку (ділянка BГ).

Продовжуючи рух з моменту часу, що відповідає точці Г, тіло рухається зі сталою швидкістю – прямолінійний рівномірний рух.

Отже, зміна напрямку руху відбувається в момент часу, що відповідає точці В.

Відповідь: В.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку знання і розуміння рівноприскореного руху і вміння застосовувати кінематичні рівняння для його описання.

1. Кінематичне рівняння, що описує прямолінійний рівноприскорений рух, \(x=-8+8t-2t^2\) має загальний вигляд $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x\) ‒ кінцева координата для відповідного часу спостереження, \(x_0\) ‒ початкова координата; \(v_0\) ‒ проєкція початкової швидкості руху тіла; \(t\) ‒ час спостереження руху, \(a\) ‒ проєкція прискорення руху тіла.

Початкова координата тіла дорівнювала $$ x_0=-8\ \text{м}. $$

Визначмо, через скільки секунд тіло опиниться в початку координат ‒ \(x=0:\)

За теоремою Вієта для зведеного рівняння (коефіцієнт біля \(t^2\) дорівнює \(1\)) визначмо корені рівняння: $$ \left\{ \begin{array}{l} t_1\cdot t_2=4,\\ t_1+t_2=4, \end{array} \right. $$ звідси $$ t_1=t_2=2. $$

Отже, через \(2\ \text{с}\) від початку відліку часу тіло опиниться в початку координат.

Відповідь: 2.

2. Рівняння проєкції швидкості для прямолінійного рівноприскореного руху має вигляд \begin{gather*} v=v_0+at. \end{gather*}

З рівняння $$ x=-8+8t-2t^2, $$ що дане в умові, можемо визначити потрібні для обчислення швидкості руху значення:
‒ початкової швидкості $$ v_0=8\ \text{м/с}, $$ ‒ прискорення $$ a=-4\ \text{м/с}^2 $$ (знак мінус означає, що тіло сповільнює свій рух, гальмує).

Час, через який тіло опиниться в початку координат, ми визначили, відповідаючи на перше питання: $$ t=2\ \text{с}. $$

Обчислімо значення швидкості руху тіла під час проходження точки з координатою \(x=0\) ‒ початку координат:

Отже, в початку координат тіло зупиниться.

Відповідь: 0.

Відповідь: 1. 2. 2. 0.

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу під час рівномірного і рівноприскореного руху.

Завдання скеровано на перевірку вміння читати графіки залежності кінематичних величин від часу під час рівномірного і рівноприскореного рухів.

Залежність проєкції швидкості \(v\) тіла від часу \(t\) для прямолінійного рівноприскореного руху $$ v=v_0+at $$ є лінійною, тому графік проєкції швидкості ‒ це відрізок прямої, нахиленої під певним кутом до осі часу (\(v_0\) ‒ проєкція початкової швидкості руху тіла, \(a\) ‒ проєкція прискорення).

Що більше прискорення руху тіла, то більший кут нахилу графіка проєкції швидкості до осі часу.

Розгляньмо рисунок. Найменший кут нахилу графіка ‒ на ділянці від \(10\) до \(20\ \text{с.}\)

Перевірити правильність відповіді можна за допомогою розрахунків, скориставшись формулою для прискорення $$ a=\frac{v-v_0}{t}. $$

Інтервал часу від \(0\) до \(10\ \textbf{с:}\) $$ a_{0-10}=\frac{15-0}{10}\ \text{м/с}^2=1,5\ \text{м/с}^2. $$

Інтервал часу від від \(10\) до \(20\ \textbf{с:}\) $$ a_{10-20}=\frac{20-15}{10}\ \text{м/с}^2=0,5\ \text{м/с}^2. $$

Інтервал часу від від \(20\) до \(30\ \textbf{с:}\) $$ a_{20-30}=\frac{0-20}{10}\ \text{м/с}^2=-2\ \text{м/с}^2. $$ (знак мінус указує на гальмування тіла, але модуль прискорення дорівнює \(2\ \text{м/с}^2\)).

Інтервал часу від від \(30\) до \(40\ \textbf{с:}\) $$ a_{30-40}=\frac{10-0}{10}\ \text{м/с}^2=1\ \text{м/с}^2. $$

Як бачимо, мінімальне прискорення відповідає інтервалу часу від \(10\) до \(20\ \text{с.}\)

Відповідь: Г.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку знання і розуміння кінематичних характеристик прямолінійного рівномірного і рівноприскореного рухів, що є складниками рівняння руху.

1. Рівнянням координати \(x\) $$ x=5+2t $$ описують прямолінійний рівномірний рух: $$ x=x_0+vt, $$ де \(x_0\) – початкова координата, \(v\) – проєкція швидкості руху, \(t\) – час спостереження.

Відповідно до цього рівняння початкова координата \(x_0=5\ \text{м},\) швидкість руху тіла \(v=2\ \text{м/с},\) а прискорення \(a=0\ \text{м/с}^2,\) оскільки рух рівномірний – варіант відповіді Г.

2. Рівнянням координати \(x\) $$ x=5t+2t^2 $$ описують прямолінійний рівноприскорений рух: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) – початкова координата, \(v_0\) – проєкція початкової швидкості руху, \(t\) – час спостереження, \(a\) – проєкція прискорення.

Відповідно до цього рівняння початкова координата \(x_0=0\ \text{м},\) початкова швидкість руху тіла \(v_0=5\ \text{м/с},\) а прискорення \(a=4\ \text{м/с}^2\) – варіант відповіді А.

3. Рівнянням координати \(x\) $$ x=2t+5t^2 $$ описують прямолінійний рівноприскорений рух: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) – початкова координата, \(v_0\) – проєкція початкової швидкості руху, \(t\) – час спостереження, \(a\) – проєкція прискорення.

Відповідно до цього рівняння початкова координата \(x_0=0\ \text{м},\) початкова швидкість руху тіла \(v_0=2\ \text{м/с},\) а прискорення \(a=10\ \text{м/с}^2\) – варіант відповіді Б.

4. Рівнянням координати \(x\) $$ x=5+t^2 $$ описують прямолінійний рівноприскорений рух: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) – початкова координата, \(v_0\) – проєкція початкової швидкості руху, \(t\) – час спостереження, \(a\) – проєкція прискорення.

Відповідно до цього рівняння початкова координата \(x_0=5\ \text{м},\) початкова швидкість руху тіла \(v_0=0\ \text{м/с},\) а прискорення \(a=2\ \text{м/с}^2\) – варіант відповіді Д.

Відповідь: 1Г, 2А, 3Б, 4Д.

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.

Завдання скеровано на перевірку вміння застосовувати закон додавання швидкостей.

Закон додавання швидкостей полягає в тому, що швидкість \(\overrightarrow{v}_\text{м(З)}\) руху м’ячика в нерухомій системі відліку (відносно Землі) дорівнює геометричній сумі швидкості \(\overrightarrow{v}_\text{м(a)}\) руху м’ячика в рухомій системі відліку (відносно автомобіля) та швидкості \(\overrightarrow{v}_\text{a(З)}\) руху рухомої системи відліку (автомобіля) відносно нерухомої (Землі): $$ \overrightarrow{v}_\text{м(З)}=\overrightarrow{v}_\text{м(a)}+\overrightarrow{v}_\text{a(З)}. $$

Визначімо знаки проєкцій цих векторів у відповідних системах відліку (див. рисунок).

Напрямок вектора швидкості \(\overrightarrow{v}_\text{м(З)}\) руху м’ячика в нерухомій системі відліку (відносно Землі) збігається з напрямком побудованої осі \(Ox.\)

Напрямок вектора швидкості \(\overrightarrow{v}_\text{a(З)}\) руху автомобіля відносно нерухомої системи відліку (Земля) є протилежним до напрямку осі \(Ox,\) отже, проєкція цієї швидкості від’ємна:

Напрямок вектора швидкості \(\overrightarrow{v}_\text{м(a)}\) руху м’ячика в рухомій системі відліку (відносно автомобіля) протилежний до напрямку руху автомобіля, отже, напрямок вектора \(\overrightarrow{v}_\text{м(a)}\) співпадає з напрямком осі \(Ox,\) відповідно проєкція швидкості руху м᾽ячика дорівнюватиме: $$ v_\text{м(a)}=5\ \text{м/с}. $$

Визначімо за законом додавання швидкостей модуль швидкості м’ячика відносно Землі:

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.

Завдання скеровано на перевірку знання і розуміння закону додавання швидкостей у класичній механіці.

Для визначення часу, який знадобиться автомобілю, щоб проїхати від останнього до першого вагона, необхідно знати швидкість руху автомобіля відносно поїзда. Відстань, яку треба проїхати автомобілю, ‒ це довжина \(l\) поїзда. Виберемо поїзд як систему відліку. Тоді

де \(v_{\text{А(П)}}\) – швидкість руху автомобіля відносно поїзда

Тепер можна обчислити час \(t,\) за який автомобіль випередить поїзд:

Відповідь: 20.

ТЕМА: Механіка. Основи кінематики. Прямолінійний рівноприскорений рух.

Завдання скеровано на перевірку вміння застосовувати кінематичні рівняння для прямолінійного рівноприскореного руху.

1. Векторну фізичну величину, яка характеризує швидкість зміни швидкості руху тіла й дорівнює відношенню зміни швидкості руху тіла до інтервалу часу, за який ця зміна відбулася, називають прискоренням руху тіла.

Користуючись тим, що в умові дана відстань \(l,\) яку долає кулька, і час \(t\) руху кульки, можна визначити прискорення \(a\) з формули $$ l=v_0t+\frac{at^2}{2}. $$

За умовою початкова швидкість руху кульки дорівнює нулю \((v_0=0)\) ‒ кулька вільно скочується. Тому формулу можна спростити: $$ l=\frac{at^2}{2}. $$

Учень п’ять разів виміряв час, тому необхідно визначити середнє значення часу як середнє арифметичне значення:

Виразімо й обчислимо прискорення:

Відповідь: 2.

2. Формула для визначення модуля прискорення така: \begin{gather*} a=\frac{v-v_0}{t_\text{сер}}. \end{gather*}

Тож для рівноприскореного прямолінійного руху маємо рівняння, із якого можна визначити швидкість кульки в нижній точці \(B\) похилої площини: $$ v=v_0+at_\text{сер}. $$ Оскільки \(v_0=0,\)

Відповідь: 2.

Відповідь: 1. 2. 2. 2.

ТЕМА: Механіка. Основи кінематики. Шлях і переміщення.

Завдання скеровано на перевірку знання і розуміння фізичної величини переміщення.

Якщо спочатку турист рухався на захід, а потім ‒ на північ, це означає, що він, пройшовши \(3\ \text{км},\) повернув на \(90^\circ\) і далі рухався під прямим кутом до попереднього напрямку ще \(4\ \text{км}\) (див. рисунок).

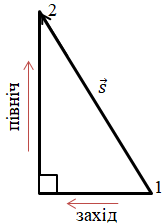
Якщо з’єднаємо початкову точку \(1,\) з якої турист стартував, і кінцеву точку \(2\) його маршруту, то вектор \(\overrightarrow{s}\) ‒ це і є переміщення, яке здійснив турист.

Визначмо модуль цього переміщення ‒ довжину відрізка, що з’єднує точки \(1\) і \(2.\) Цей відрізок ‒ це гіпотенуза утвореного прямокутного трикутника з катетами \(3\) і \(4\ \text{км}.\) За теоремою Піфагора обчислімо гіпотенузу:

Отже, модуль переміщення дорівнюватиме \(5\ \text{км}.\)

А можна без обчислень одразу сказати, чому дорівнюватиме гіпотенуза (модуль переміщення) цього прямокутного трикутника. Якщо сторони прямокутного трикутника співвідносяться як \(3 : 4 : 5,\) то такий трикутник називають єгипетським. Катети утвореного туристом маршруту дорівнюють \(3\) і \(4\ \text{км},\) відповідно гіпотенуза становитиме \(5\ \text{км}.\)

Відповідь: Г.

ТЕМА: Механіка. Основи кінематики. Лінійна і кутова швидкості.

Завдання скеровано на перевірку знання і розуміння поступально-обертального руху.

Визначаючи лінійну швидкість верхнього кінця стержня, треба врахувати те, що сам стержень у той момент, коли його кінці ковзають із певними лінійними швидкостями відносно взаємно перпендикулярних поверхонь підлоги й стіни, здійснює обертальний рух із певною кутовою швидкістю.

Кутова швидкість \(\mathbf{\omega}\) ‒ це фізична величина, яка чисельно дорівнює куту \(\mathbf{\varphi}\) повороту радіуса за одиницю часу \(t:\) $$ \mathbf{\omega}=\frac{\mathbf{\varphi}}{t}. $$

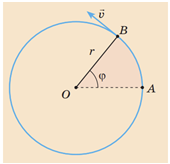
За час, що дорівнює періоду \((t=T),\) радіус виконує один оберт \((\mathbf{\varphi}=2\mathbf{\pi}),\) тому кутову швидкість можна обчислити за формулою: $$ \mathbf{\omega}=\frac{2\mathbf{\pi}}{T}. $$

Стержень довжиною \(l\) у заданий момент часу обертатиметься навколо певної миттєвої осі обертання \(O\) ‒ навколо якої стержень у цей момент часу обертається. Побудуємо її. Для цього проведемо перпендикуляри до векторів лінійних швидкостей руху \(\overrightarrow{v}_\text{н}\) і \(\overrightarrow{v}_\text{в}\) обох кінців стержня – нижнього і верхнього, і на їхньому перетині отримаємо місце розташування миттєвої осі обертання, яку позначимо точкою \(O.\)

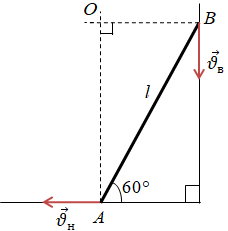
Лінійну швидкість \(\overrightarrow{v}\) рівномірного руху тіла по колу визначаємо за періодом \(T\) обертання та радіусом \(R\) колової траєкторії: $$ v=\frac{2\mathbf{\pi}R}{T} - $$ за час оберту \(t=T\) тіло долає відстань, що дорівнює довжині кола $$ L=2\mathbf{\pi}R. $$

Кутова і лінійна швидкості пов’язані співвідношенням: $$ v=\mathbf{\omega}R. $$

Кутова швидкість кожної точки стержня буде та сама. Тому виразімо кутову швидкість для верхнього і нижнього кінців стержня через їхні відповідні лінійні швидкості й радіуси та прирівняємо ці вирази:

Виразімо \(OA\) і \(OB\) з прямокутного трикутника \(AOB:\)

Визначмо швидкість руху верхнього кінця стержня:

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку знання і розуміння фізичних величин, що визначають прямолінійний рівноприскорений рух і вміння їх визначати.

1. В умові дано прискорення, отже, розглядається прямолінійний рівноприскорений рух.

З формули (записаної в проєкціях на горизонтальну вісь \(Ox\)) для прискорення \(a\) прямолінійного рівноприскореного руху визначімо час \(t,\) затрачений велосипедистом для досягнення вказаної швидкості \(v:\) $$ a=\frac{v-v_0}{t}, $$ де \(v_0=0\) (за умовою) − швидкість руху тіла в момент початку відліку часу (початкова швидкість); \(v\) − швидкість руху тіла через деякий інтервал часу \(t.\)

Відповідь: 5.

2. Для визначення шляху, подоланого велосипедистом за час \(t=5\ \text{с},\) скористаймося одним із рівнянь залежності проєкції переміщення \(s\) від часу для прямолінійного рівноприскореного руху (проєкції шляху і переміщення співпадають під час прямолінійного руху): \begin{gather*} s=v_0t+\frac{at^2}{2},\\[6pt] s=0\cdot 5\ \text{с}+\frac{1\ \text{м/с}^2\cdot (5\ \text{с})^2}{2}=12,5\ \text{м}. \end{gather*}

Відповідь: 12,5.

Відповідь: 1. 5. 2. 12,5.

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу в рівномірному й рівноприскореному рухах.

Завдання скеровано на перевірку знання і розуміння кінематичних величин, уміння користуватися графіком.

Для рівноприскореного прямолінійного руху рівняння координати має вигляд: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) і \(x\) ‒ початкова і кінцева координата тіла відповідно через деякий інтервал часу \(t,\) \(v_0\) ‒ модуль швидкості руху тіла в момент початку відліку часу (початкова швидкість); \(a\) ‒ модуль прискорення руху тіла.

Із цього рівняння прискорення дорівнюватиме: $$ a=(x-x_0-v_0t)\cdot \frac{2}{t^2}. $$

Значення всіх величин візьмемо з графіка в умові: \begin{gather*} x_0=-10\ \text{м},\\[7pt] x=20\ \text{м},\\[7pt] t=2\ \text{с}. \end{gather*}

Початкова швидкість руху матеріальної точки дорівнює $$ v_0=3\ \text{м/c}. $$

Обчислімо прискорення цієї точки:

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей. Рівномірний рух.

Завдання скеровано на перевірку знання і розуміння прямолінійного рівномірного руху, а також вміння додавати швидкості.

Щоб визначити швидкість руху товарного потяга, треба зрозуміти, як було визначено час \(t,\) протягом якого пасажирський потяг проходив повз зустрічний товарний потяг. Рух потягів прямолінійний рівномірний, тож скористаймося відповідною формулою: $$ t=\frac lv. $$

Уявімо, як голови потягів порівнялися, й із цього моменту пішов відлік часу.

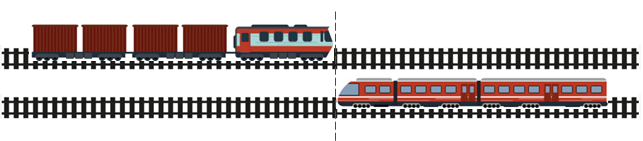
Щоб потяги повністю розминулися, голова пасажирського потяга повинна пройти вздовж усього товарного, а потім ще весь пасажирський потяг повинен пройти повз хвіст товарного потяга.

Тож загальний шлях \(l,\) який пройде голова пасажирського потяга з моменту, коли голови потягів порівнялися і до моменту, коли порівняються їхні хвости, становитиме суму довжин обох потягів ‒ пасажирського \(l_\text{п}\) і товарного \(l_\text{т}:\) $$ l= l_\text{п}+l_\text{т}. $$

Якщо потяги рухалися один відносно одного, то й швидкість їхнього руху треба розглядати не відносно землі, а відносно один одного.

Скористаймося законом додавання швидкостей: швидкість \(\overrightarrow{v}\) руху тіла в нерухомій системі відліку (пасажирського потяга відносно товарного) дорівнює геометричній сумі швидкості \(\overrightarrow{v}_\text{п}\) руху тіла в рухомій системі відліку (пасажирського потяга відносно землі) і швидкості \(\overrightarrow{v}_\text{т}\) руху рухомої системи відліку відносно нерухомої (наче землі відносно товарного потяга, що те саме ‒ товарного потяга відносно землі): $$ v=v_\text{п}+v_\text{т}. $$

Запишімо ще раз формулу для часу й визначмо швидкість товарного потяга:

Відповідь: А.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку знання і розуміння кінематичних рівнянь, що описують рух тіл.

Проаналізуймо рівняння з умови завдання: $$ x=12-5t. $$

Координата \(x\) лінійно залежить від часу \(t\) (змінна \(t\) в першому степені). Отже, цим рівнянням описано прямолінійний рівномірний рух.

Запишімо це рівняння в загальному вигляді: $$ x=x_0+vt, $$ де \(x_0\) ‒ початкова координата тіла, \(v\) ‒ швидкість руху тіла.

Отже, \(x_0=12\ \text{м}, v=-5\ \text{м/с}\) ‒ знак мінус указує на те, що тіло рухається в протилежному напрямку до напрямку горизонтальної осі, уздовж якої рухається тіло.

Визначмо координату тіла через \(4\ \text{с}\) після початку руху: $$ x(4)=12-5\cdot 4=12-20=-8\ \text{м}. $$

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей. Рівномірний рух.

Завдання скеровано на перевірку знання і розуміння прямолінійного рівномірного руху, а також вміння додавати швидкості.

Для того щоб визначити час \(t,\) протягом якого пасажир бачитиме зустрічний поїзд, треба знати довжину \(l\) (дана в умові) і швидкість \(v\) руху цього поїзда відносно пасажира. Визначмо її.

Скористаймося законом додавання швидкостей: швидкість \(\overrightarrow{v}\) руху тіла в нерухомій системі відліку дорівнює геометричній сумі швидкості \(\overrightarrow{v}_\text{рух}\) руху тіла в рухомій системі відліку й швидкості \(\overrightarrow{v}_\text{нерух}\) руху рухомої системи відліку відносно нерухомої: \begin{gather*} \overrightarrow{v}=\overrightarrow{v}_\text{рух}+\overrightarrow{v}_\text{нерух}. \end{gather*}

Оскільки рух і спокій є відносними, то відповідно до умови завдання як нерухому систему відліку можна вибрати й систему відліку, пов’язану з пасажиром, що сидить біля вікна у вагоні поїзда 1. У такому разі земля буде рухомою системою відліку, напрямок її руху буде протилежним до напрямку руху поїзда 1, а швидкість руху землі відносно поїзда 1 (із пасажиром) за модулем дорівнюватиме швидкості руху цього поїзда.

Введемо позначення: швидкість руху \(\overrightarrow{v}_{21}\) ‒ це буде швидкість руху поїзда 2 відносно поїзда 1 (пасажира) ‒ нерухомої системи відліку; швидкість руху \(\overrightarrow{v}_2\) ‒ це швидкість руху поїзда 2 в рухомій системі відліку, тобто відносно землі (та, яку дано в умові, \(45\ \text{км/год}\)); швидкість руху \(\overrightarrow{v}_1\) ‒ це швидкість рухомої системи відліку (землі) відносно нерухомої \((63\ \text{км/год}),\) тобто відносно поїзда 1:

Рух поїздів прямолінійний рівномірний, тож скористаймося відповідною формулою:

Відповідь: 10.

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.

Завдання скеровано на перевірку знання і розуміння додавання швидкостей і вміння застосовувати цей закон до будь-яких ситуацій.

Скористаймося законом додавання швидкостей:
швидкість \(\overrightarrow{v}_{12}\) руху першого човна в нерухомій системі відліку (відносно другого човна) дорівнює геометричній сумі швидкості \(\overrightarrow{v}_{1 \text{бер}}\) руху першого човна в рухомій системі відліку (відносно берега) й швидкості \(\overrightarrow{v}_{\text{бер} 2}\) руху рухомої системи відліку відносно нерухомої (ніби берега відносно другого човна): $$ \overrightarrow{v}_{12}=\overrightarrow{v}_{1 \text{бер}}+\overrightarrow{v}_{\text{бер} 2} $$ (рух і спокій є відносними, тож в наведеному в умові прикладі як нерухому систему відліку ми обрали систему відліку, пов’язану з другим човном. У такому разі система відліку, пов’язана з берегом, буде рухомою, а напрямок її руху буде протилежним напрямку руху першого човна).

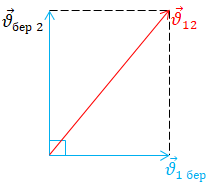
Модуль швидкості \(\overrightarrow{v}_{12}\) руху першого човна відносно другого човна знайдемо за теоремою Піфагора:

Відповідь: 5.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи. Рух по колу.

Завдання скеровано на перевірку вміння визначати напрямок швидкості руху тіла й напрямок прискорення тіл під час різних видів руху.

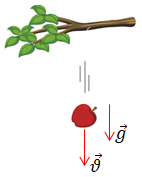
1. Яблуко в безвітряну погоду падатиме вертикально, тож і напрямок швидкості \(\overrightarrow{v}\) його руху теж буде напрямлений вертикально вниз (див. рисунок).

Падіння тіл у безповітряному просторі, тобто падіння лише під дією сили тяжіння, називають вільним падінням. У разі вільного падіння всі тіла падають на Землю з однаковим прискоренням ‒ прискоренням вільного падіння \(\overrightarrow{g}.\) Вектор прискорення вільного падіння завжди напрямлений вертикально вниз.

Отже, кут між напрямком швидкості руху яблука й напрямком прискорення становитиме нуль, тобто прискорення напрямлене в напрямку швидкості руху ‒ варіант відповіді В.

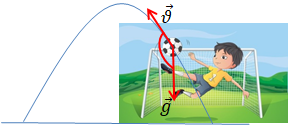
2. Коли футбольний м’яч піднімається, спрямований під кутом до горизонту (див. рисунок), то швидкість \(\overrightarrow{v}\) руху м’яча буде напрямлена по дотичній до траєкторії руху вгору ‒ до параболи. А прискорення \(\overrightarrow{g}\) вільного падіння під час руху м’яча по параболі буде напрямлене завжди вертикально вниз.

Отже, кут між векторами \(\overrightarrow{v}\) і \(\overrightarrow{g}\) буде тупий ‒ варіант відповіді Б.

3. Коли автомобіль гальмує, рухаючись прямолінійно, то напрямок прискорення \(\overrightarrow{a}\) буде протилежним до напрямку руху, тобто до напрямку швидкості \(\overrightarrow{v}\) руху автомобіля (див. рисунок) ‒ варіант відповіді А.

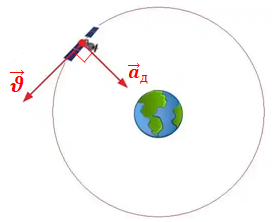
4. Штучний супутник рухається навколо Землі по коловій орбіті. Швидкість \(\overrightarrow{v}\) його руху в кожній точці кола напрямлена по дотичній до кола. А доцентрове прискорення \(\overrightarrow{a}_\text{д}\) спрямоване до центра кола (див. рисунок).

Отже, у цьому разі доцентрове прискорення буде напрямлене під прямим кутом до напрямку швидкості руху ‒ варіант відповіді Д.

Відповідь: 1В, 2Б, 3А, 4Д.