Розділ: Механіка
Тема: Кінематика: рух під дією сили тяжіння
Кількість завдань: 23
ТЕМА: Механіка. Рух під дією сили тяжіння.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про рух тіла під дією сили тяжіння.
Дано:
1. Знайти:
Оберімо вісь для обчислень і намалюймо схему руху тіла.
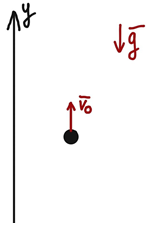
Рис. 1. Схема руху тіла
Рух тіла під дією сили тяжіння можна описати рівняннями для рівноприскореного руху. Замінимо прискорення в цьому рівнянні на прискорення вільного падіння. Тіло кинуте вертикально вгору, а прискорення вільного падіння спрямоване вниз. Тож початкова швидкість на прискорення вільного падіння матимуть різні знаки:
Тоді в момент часу 3 швидкість тіла
За умовою задачі потрібно визначити модуль швидкості на третій секунді руху, тож
2. Знайти:
Шлях тіла, кинутого вгору, складатиметься з двох частин: підйому й падіння. Вважатимемо, що тіло кинули з рівня землі, оскільки це не суперечить умові задачі. Тоді шлях підйому та шлях падіння будуть рівні.
Обчислімо шлях підйому. Для цього оцінимо його час. У момент, коли тіло перестає підніматися і починає падати, його швидкість дорівнює нулю. Тоді маємо рівняння, з якого можемо визначити час падіння:
Шлях також можемо визначити за формулою для рівноприскореного руху, з урахуванням того, що початкова швидкість і прискорення мають різні значення:
Тоді повний шлях тіла до падіння дорівнюватиме:
Відповідь: 1. 10. 2. 40.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична й потенціальна енергія.
Завдання скеровано на перевірку вміння обчислювати потенціальну енергію тіла, що перебуває під дією сили тяжіння.
Потенціальна енергія тіла, яке рухається під дією сили тяжіння, можна визначити за формулою
Прискорення вільного падіння вважаємо постійним на Землі, маса кульки під час її руху не змінюється, тому найвищу потенціальну енергію кулька матиме в найвищій точці своєї траєкторії – точці Б.
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на визначення основних кінематичних величин за рівноприскореного руху.
Дано:
Знайти:
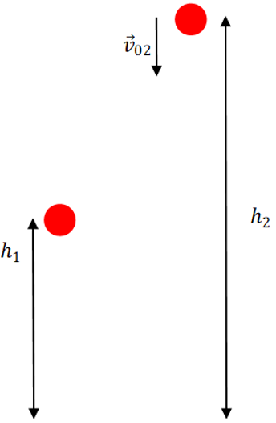
Рис. 1. Схема руху двох тіл
Обидва тіла рухаються лише під дією сили тяжіння, тож їхній рух – рівноприскорений. Оскільки переміщення
Тож можна записати переміщення для тіл, про які йдеться в завданні, узявши до уваги, що переміщення
Оскільки приземлитись тіла мають одночасно, то
Із першого рівняння системи можна виразити час падіння
Тоді з другого рівняння системи можна виразити початкову швидкість другого тіла:
Відповідь: 5.
2
ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.
Завдання скеровано на оцінювання розуміння процесу руху кинутого горизонтально тіла, на яке діє сила тяжіння.
Тіло, кинуте під кутом до горизонту, рухається під дією сили тяжіння. Сила тяжіння не змінюється протягом усього руху, й не залежить від того, у якій точці траєкторії перебуває тіло. Не залежить ця сила й від напрямку руху тіла. Тож і прискорення, якого сила тяжіння надає тілу, залишається сталим.
Це прискорення – прискорення вільного падіння
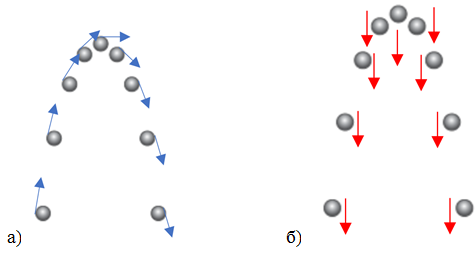
Рис. 1. Схематичне зображення напрямку в різні моменти часу
векторів: а) швидкості
Відповідь: A.
ТЕМА: Механіка. Кінематика. Рух тіла, кинутого горизонтально.
Завдання скеровано на перевірку розуміння закономірностей руху під діє сили тяжіння кинутого горизонтально тіла.
У тіла, кинутого горизонтально, є два складники руху – вертикальний і горизонтальний. Ці складники незалежні, тобто рух по вертикалі не впливає на рух по горизонталі.
По горизонталі точка рухається із такою самою швидкістю, що й у початковий момент часу, адже немає жодної сили, яка діє на тіло в цьому напрямку.
По вертикалі тіло рухається під дією сили тяжіння. Під дією сили тяжіння всі тіла рухаються із прискоренням вільного падіння.
Тож оскільки прискорення вздовж осі x дорівнює 0, загальне прискорення тіла збігається із прискоренням уздовж осі y, тобто прискоренням вільного падіння.
Прискорення вільного падіння завжди напрямлене перпендикулярно до поверхні Землі.
Відповідь: A.
ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання формул рівноприскореного руху.
1. Дано:
1. Знайти:
Тіло, що вільно падає, рухається лише під дією сили тяжіння. Усі тіла під час вільного падіння рухаються з однаковим прискоренням – прискоренням вільного падіння.
Рух тіла, про яке йдеться в завданні, закінчиться тоді, коли воно зустрінеться із землею, тому можна вважати, що висота падіння тіла дорівнює пройденому ним шляху.
Тіло за умовою кинуто без початкової швидкості. Тож можна скористатися модифікованою формулою для тіла, що рухається рівноприскорено:
Тоді час падіння тіла
2. Знайти:
Оскільки швидкість тіла, що падає, має постійно збільшуватись аж до моменту зіткнення з поверхнею, можна вважати, що максимальною є швидкість за момент до падіння, тому можна використати для її розрахунку час падіння тіла:
Відповідь: 1. 8. 2. 80.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух. Рівномірний рух по колу.
Завдання скеровано на оцінювання вміння визначати напрямок прискорення і швидкості в різних процесах.
А Снаряд, випущений гарматою чи будь-яким іншим способом, рухатиметься під дією сили тяжіння після вистрілу. У такому разі прискорення, що діє на тіло, – це прискорення вільного падіння, що завжди напрямлене до центра Землі. Тобто якщо поверхня горизонтальна, то прискорення вільного падіння спрямоване перпендикулярно до поверхні. Тіло в такому разі рухається по параболі. Схематичне зображення руху тіла, кинутого під кутом до горизонту, тобто руху снаряду, зображено на рисунку 1. Стрілкою червоного кольору позначено прискорення тіла, зеленого – напрямок швидкості тіла (напрямок руху). Кут між цими напрямками гострий.
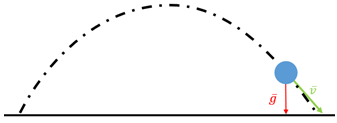
Рис. 1. Схематичне зображення руху снаряду перед падінням
Б Кінець годинникової стрілки рівномірно рухається по колу. За визначенням рівномірний рух тіла по колу – це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється із часом.
Під час руху по колу швидкість тіла постійно напрямлена по дотичній до кола. Це значить, що напрямок швидкості руху тіла постійно змінюється, але оскільки рух рівномірний, то модуль швидкості має залишатися постійним. Це можливо лише якщо прискорення напрямлене перпендикулярно до швидкості тіла. На рисунку 2 схематично зображено рух кінця годинної стрілки (позначеного синім кругом на рисунку). Тож кут між напрямком руху тіла й прискоренням у цьому разі завжди прямий.
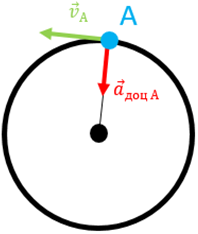
Рис. 2. Схематичне зображення руху кінця годинникової стрілки
В Під час руху снаряда в каналі ствола гармати його швидкість збільшується. Тобто прискорення співнапрямлене зі швидкістю тіла.
Г Після вимикання двигуна катера його швидкість починає зменшуватися. Тобто прискорення протилежно напрямлене до швидкості тіла.
Відповідь: 1Г, 2Д, 3В, 4А.
ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.
Завдання скеровано на перевірку розуміння поняття кінетичної енергії та її зміни під час руху тіла унаслідок дії сили тяжіння.
Кінетичну енергію тіла визначають за формулою
Тіло, кинуте під кутом до горизонту, рухається внаслідок дії сили тяжіння, тобто з прискоренням, що дорівнює прискоренню вільного падіння.
Прискорення спрямоване вздовж осі
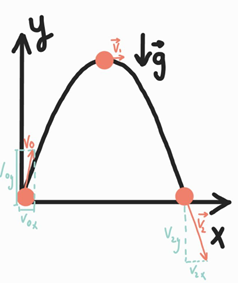
Рис. 1. Рух тіла, кинутого під кутом до горизонту
Модуль швидкості V в будь-який момент часу можна визначити за теоремою Піфагора:
Тож модуль швидкості й кінетична енергія тіла будуть найменшими тоді, коли проекція
У найвищій точці траєкторії тіло змінює напрямок свого руху: до цієї точки тіло піднімається і модуль
Відповідь: A.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку вміння визначати кінематичні характеристики (швидкість руху) під час вільного падіння.
Спосіб 1. Для визначення швидкості руху м᾽яча на певній висоті скористаймося кінематичним рівнянням, яким описують вільне падіння вздовж вертикальної осі
Спосіб 2. Для визначення швидкості руху м᾽яча на певній висоті можна також скористатися законом збереження механічної енергії: сума потенціальної і кінетичної енергій на висоті
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Прямолінійний рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку розуміння закономірностей прямолінійного рівномірного і рівноприскореного рухів.
Розгляньмо рух парашутиста і рух монети.
За умовою завдання парашутист опускався зі сталою швидкістю
Монета пройшла той самий шлях
Підставмо значення величин у рівняння:
Поділімо ліву і праву частину рівняння на
За теоремою Вієта визначмо корені рівняння:
Час не може бути від’ємним, тому умову задовольняє корінь
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку знання і розуміння кінематичних рівнянь, що описують прямолінійний рівноприскорений рух і вміння застосовувати їх.
Обчислімо модуль переміщення
Можна також спочатку визначити проміжок часу, за який швидкість руху зміниться від
Знаючи проміжок часу, за який відбулася зазначена в умові зміна швидкості, можна визначити модуль переміщення:
Відповідь: 27.
ТЕМА: Механіка. Основи кінематики. Прямолінійний рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку розуміння закономірностей прямолінійного рівномірного й рівноприскореного рухів.
Розгляньмо рух парашутиста й монети.
Парашутист за умовою опускається зі сталою швидкістю
Монета пройде той самий шлях
Вплив опору повітря на монету за умовою до уваги не беремо, тож знайдемо час її падіння з кінематичного рівняння:
Підставімо значення величин у рівняння:
Поділімо ліву і праву частину рівняння на
За теоремою Вієтта знайдімо корені рівняння:
Час не може бути від’ємним, тому умову задовольняє корінь
Відповідь: 1.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку знання і розуміння закону збереження імпульсу і руху під дією сили тяжіння.
У горизонтальному напрямку на систему осколків зовнішні сили не діють, хоча вертикально на них діє сила тяжіння (тобто система незамкнена). Отже, горизонтальна складова імпульсу не повинна змінюватися. Тому в горизонтальному напрямку виконуватиметься закон збереження імпульсу:
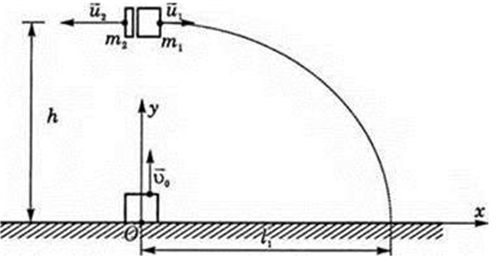
Запишемо проєкцію на вісь
Відстань
Визначмо час падіння, скориставшись тим, що з умови можна знайти час підйому. У верхній точці снаряд спочатку зупинився, а потім вже розірвався.
Запишімо рівняння для швидкості
Отже,
Підставмо вирази для швидкості і часу у формулу для відстані, яку пролетить перший (більший) осколок (
Виконаймо обчислення:
Відповідь:
ТЕМА: Механіка. Закони збереження в механіці. Імпульс тіла.
Завдання скеровано на перевірку знання і розуміння поняття імпульсу тіла, його напрямку й напрямку швидкості під час руху тіла, кинутого під кутом до горизонту.
Імпульс тіла
У ході криволінійного руху напрямок швидкості руху весь час змінюється. Оскільки рівняння траєкторії руху тіла, кинутого з деякої висоти зі швидкістю під кутом до горизонту, має вигляд квадратичної функції (з виведенням формули можна ознайомитися в параграфах підручника з відповідної теми), то траєкторія руху тіла, якому поблизу поверхні Землі надано початкової швидкості, є параболічною (як в умові завдання).
Напрямок вектора імпульсу збігається з напрямком вектора швидкості:
У точці
Дотична ‒ це пряма, яка торкається кривої або поверхні в одній точці, не перетинаючи її. Якщо розглянути рисунок і візуально продовжити зображені промені в обидва боки, то дотична збігатиметься з напрямком
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Рух тіла під дією сили тяжіння.
Завдання скеровано на перевірку знання і розуміння руху тіла під дією сили тяжіння, а також вміння застосувати їх до нестандартного руху тіла, описаного в завданні.
Зробимо схематичний рисунок.
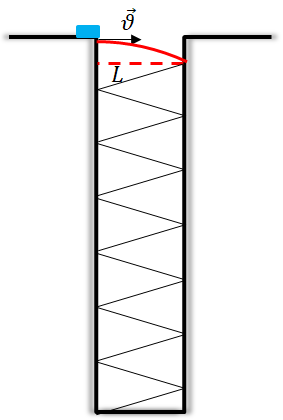
Діставшись краю щілини, тіло рухається далі, як ніби його кинули горизонтально зі швидкістю
Визначімо спочатку час
Під час такого руху швидкість зберігатиметься сталою, оскільки за умовою удари тіла об стінки щілини абсолютно пружні. Отже, і всі наступні проміжки часу між ударами зі стінками щілини будуть теж
Одночасно з рівномірним прямолінійним рухом тіло падатиме вертикально рівноприскорено без початкової швидкості.
Тіло вдариться об стінки щілини
Обчислімо час руху тіла від верхньої точки щілини до дна, якщо тіло падатиме вертикально рівноприскорено:
Отже, якщо на один переліт від стінки до стінки витрачається
Відповідь: 40.
ТЕМА: Механіка. Основи динаміки. Рух тіла під дією сили тяжіння.
Завдання скеровано на перевірку знання і розуміння руху тіла під дією сили тяжіння, кинутого горизонтально, і вміння застосовувати відповідні рисунки і формули.
Розглянемо рух камінця, кинутого горизонтально зі скелі, скориставшись принципом незалежності рухів. Опором повітря нехтуємо (за умовою), тобто рух відбувається лише під дією сили тяжіння з прискоренням
Зобразімо схематично рух камінця. Нехай через
З рисунка бачимо, що переміщення
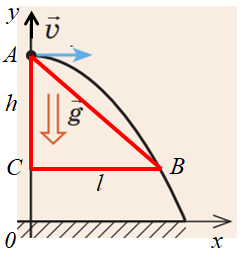
Дальність польоту
Відстань
Тепер за теоремою Піфагора визначімо модуль переміщення камінця:
Відповідь: 25.
ТЕМА: Механіка. Основи кінематики. Вільне падіння.
Завдання скеровано на перевірку розуміння вільного падіння тіл.
Якщо б у трубці було повітря, то найважче тіло (дробинка) впало б на дно трубки найшвидше. Однак за умовою завдання повітря з трубки відкачано. Тіла падають вільно й з однакової висоти.
Вільним називають падіння тіл у безповітряному просторі, тобто це падіння лише під дією сили тяжіння.
Експериментально доведено, що швидкість будь-якого тіла, яке вільно падає, щосекунди збільшується приблизно на
Без повітря всі тіла ‒ дробинка, корок і пташине перо ‒ незалежно від їхньої маси, об’єму, форми ‒ впадуть на дно трубки одночасно.
Отже, правильна відповідь ‒ Г.
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Рух тіла під дією сили тяжіння.
Завдання скеровано на перевірку знання і розуміння поняття відносності руху, додавання швидкостей і знання властивостей зображення, що дає плоске дзеркало.
Намалюємо пояснювальний рисунок: початок координат пов’яжемо з точкою
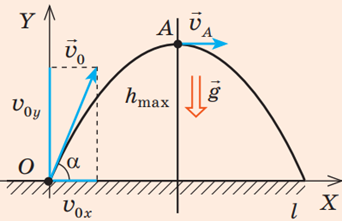
У вибраній системі відліку рух уздовж осі
У найвищій точці своєї траєкторії ‒ точці
Зображення камінця в дзеркальній поверхні озера рухатиметься з тією ж швидкістю
Один відносно одного камінець і зображення в ту мить, коли камінець перебуває на максимальній висоті підйому і ще не почав падати, але перестав підійматися, не рухатимуться. Тобто вони й не наближаються і не віддаляються, а швидкість руху камінця відносно його зображення в цю мить дорівнюватиме нулю.
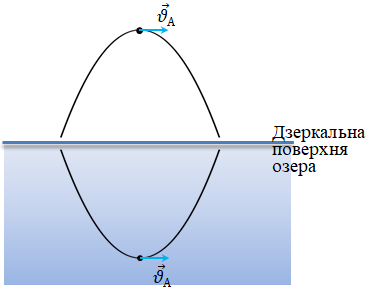
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи. Рух по колу.
Завдання скеровано на перевірку вміння визначати напрямок швидкості руху тіла й напрямок прискорення тіл під час різних видів руху.
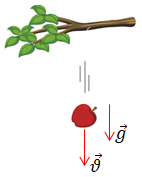
1. Яблуко в безвітряну погоду падатиме вертикально, тож і напрямок швидкості
Падіння тіл у безповітряному просторі, тобто падіння лише під дією сили тяжіння, називають вільним падінням. У разі вільного падіння всі тіла падають на Землю з однаковим прискоренням ‒ прискоренням вільного падіння
Отже, кут між напрямком швидкості руху яблука й напрямком прискорення становитиме нуль, тобто прискорення напрямлене в напрямку швидкості руху ‒ варіант відповіді В.
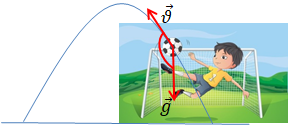
2. Коли футбольний м’яч піднімається, спрямований під кутом до горизонту (див. рисунок), то швидкість
Отже, кут між векторами
3. Коли автомобіль гальмує, рухаючись прямолінійно, то напрямок прискорення

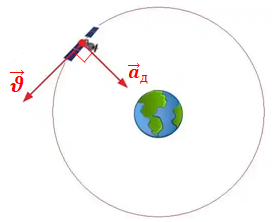
4. Штучний супутник рухається навколо Землі по коловій орбіті. Швидкість
Отже, у цьому разі доцентрове прискорення буде напрямлене під прямим кутом до напрямку швидкості руху ‒ варіант відповіді Д.
Відповідь: 1В, 2Б, 3А, 4Д.