Розділ: Механіка
Тема: Кінематика: рух по колу
Кількість завдань: 36
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.
Завдання скеровано на перевірку знання і розуміння поняття обертової частоти, і вміння її визначати.
Обертова частота
Одиниця обертової частоти в SІ ‒ оберт за секунду:
Обчислимо частоту обертання барабана пральної машини:
Відповідь:
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.
Завдання скеровано на перевірку розуміння рівномірного руху по колу та його характеристик.
Період
Тоді час
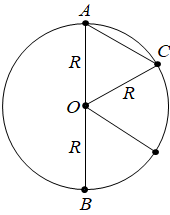
Час руху
Визначімо, у скільки разів модуль переміщення за
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку вміння визначати доцентрове прискорення на криволінійній траєкторії.
Криволінійна траєкторія утворена елементами двох кіл із різними радіусами (рис. 1).
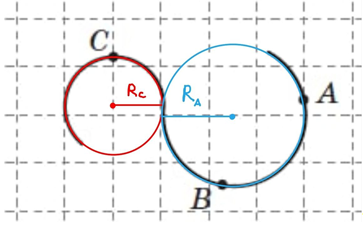
Рис. 1. Радіуси криволінійної траєкторії
Точки А і В лежать на більшому колі, а точка С – на меншому, тож
Доцентрове прискорення можна обчислити з виразу:
Оскільки модуль лінійної швидкості не змінюється, то можна записати прискорення в кожній із точок:
Оскільки
Цей вираз можна записати в іншому вигляді:
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Сила тяжіння. Рівномірний рух по колу. Кінетична енергія.
Завдання скеровано на перевірку вміння розв’язувати комплексні задачі про рівномірний рух по колу.
Дано:
Знайти:
Кінетичну енергію тіла можна обчислити за формулою
Під час руху супутника навколо Землі його швидкість спрямована по дотичній до кола, а прискорення – до центру.
Доцентрове прискорення можна обчислити з виразу
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії:
Єдиною силою, що діє на частинки в площині напрямку руху є сила тяжіння Землі:
Тобто
Із цього рівняння можна виразити добуток маси й квадрату швидкості та підставити його у формулу для кінетичної енергії:
Відповідь: 20
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку розуміння поняття лінійної швидкості обертання і вміння визначати характеристики складного руху.
Велосипед складено з різних частин, чий рух принципово відрізняється: рами, яка під час прямолінійного руху всього велосипеда також рухається поступально, і коліс та педалей, які, крім поступального руху разом з усім велосипедом, здійснюють обертальний.
Позначмо швидкість прямолінійного руху велосипеда як
Якщо колесо рухається без проковзування, то лінійна швидкість під час руху по колу будь-якої його точки на зовнішній поверхні має дорівнювати швидкості поступального руху його центра. Тому для точок, зображених на рис. 1
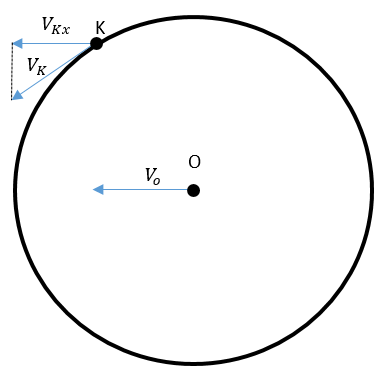
Рис. 1. Лінійна швидкість
Тоді швидкість руху для будь-якої точки на поверхні кола можна визначити як суму швидкості поступального руху його центра й проєкції на вісь х його лінійної швидкості руху по колу:
Така рівність дійсна для всіх точок зовнішньої поверхні колеса. Тож проекції лінійної швидкості обертального руху за модулем найбільші в найнижчій (Г) і найвищій (Б) точці колеса. У найвищій точці лінійна швидкість обертального руху співнапрямлена зі швидкістю поступального руху всього колеса, а в найнижчій точці – напрямлена протилежно до неї.
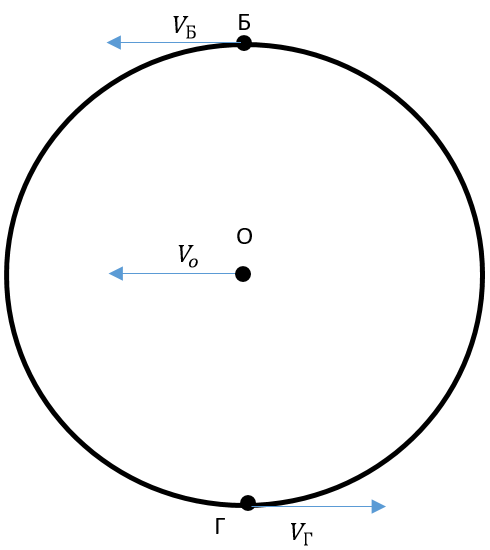
Рис. 2. Напрямок лінійної швидкості обертального руху для точок Б й Г
Тоді загальна швидкість у точці Г дорівнює нулю:
А в точці Б:
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.
Завдання скеровано на оцінку вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.
Дано:
Знайти:
У рівняннях ядерних реакцій поруч із символом елемента лівим верхнім індексом позначають кількість нуклонів у ядрі (сумарна кількість протонів і нейтронів), а лівим підрядковим – кількість протонів. Тож у цього нукліда Берилію 9 нуклонів, 4 з яких – протони. Маса нейтрона приблизно дорівнює масі протона, тому маса нукліда Берилію у 9 разів більша, ніж маса протона:
Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центру.
Доцентрове прискорення можна знайти з виразу
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто
Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца:
Зважаючи на те, що частинки рухаються в полі по колу, то
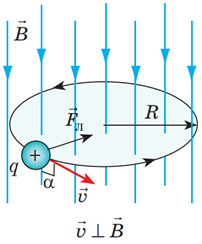
Рис. 1. Схема руху позитивно зарядженої частинки по колу
Тоді можна записати, що
Оскільки в нукліда Берилію є чотири позитивно заряджені протони й п’ять нейтральних нейтронів, його заряд у чотири рази більший, ніж заряд протона:
Записи другого закону Ньютона для обох частинок такі:
Після цього потрібно виразити радіуси кола, уздовж якого здійснюється рух, для обох частинок:
Далі треба підставити всі відомі співвідношення між фізичними величинами, що відповідають протону й α-частинці:
Тобто
Відповідь: 2,25.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на оцінку розуміння фізичних понять, що стосуються рівномірного руху по колу.
Переміщення – це векторна величина, яку графічно подають у вигляді напрямленого відрізка прямої, який з’єднує початкове й кінцеве положення матеріальної точки.
Шлях – це фізична величина, що чисельно дорівнює довжині траєкторії руху матеріальної точки за певний інтервал часу.
Швидкість – це векторна фізична величина, яка дорівнює відношенню переміщення
Кутова швидкість – це фізична величина, яка чисельно дорівнює куту повороту
Під час переміщення з точки 1 у точку 2 тіло пройшло півкола, тобто
Шлях у цьому випадку – це довжина дуги, яку пройшло тіло. Її можна розрахувати за формулою:
Модуль швидкості можна розрахувати, якщо модуль переміщення
Кутову швидкість можна розрахувати за формулою
Відповідь: 1Г, 2В, 3Б, 4А.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на зв’язок основних фізичних величин, що описують рівномірний рух по колу, зокрема кутової швидкості.
Дано:
1. Знайти:
Знаючи зв’язок між циклічною частотою і періодом, можна знайти період обертання:
2. Знайти::
Період – це проміжок часу, за який тіло робить повний оберт.
Тоді за один період тіло пройде шлях, що дорівнює довжині кола, яке воно описує:
Відповідь: 1. 4. 2. 125,6.
ТЕМА: Механіка. Основи кінематики. Матеріальна точка. Шлях і переміщення.
Завдання скеровано на оцінювання розуміння понять шляху й переміщення, відмінності між ними.
Матеріальна точка – це фізична модель тіла, розмірами якого в умовах задачі можна знехтувати.
Переміщення
Період обертання
За один період матеріальна точка зробить один повний оберт, і початкове положення руху збігатиметься із кінцевим положенням. Тоді модуль переміщення дорівнюватиме 0.
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.
Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.
Дано:
1. Знайти:
Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центра.
Доцентрове прискорення можна обчислити з виразу
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто
Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца:
З огляду на те, що частинки рухаються в полі по колу,
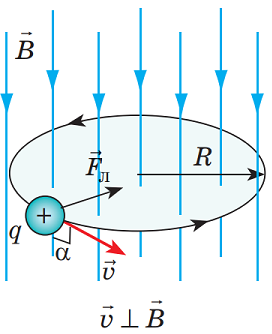
Рис. 1. Схема руху позитивно зарядженої частинки по колу
Тоді можна записати:
Оскільки складники
Запис другого закону Ньютона для обох частинок такий:
Після цього потрібно записати вирази для радіусів кола, уздовж якого здійснюється рух, для обох частинок:
Далі потрібно підставити всі відомі співвідношення між фізичними величинами, що відповідають протону й
Тому
Відповідь: 2.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку розуміння фізичних засад рівномірного руху по колу й уміння розв’язувати розрахункові задачі на основні фізичні величини, пов’язані з рівномірним рухом по колу (доцентрове прискорення, лінійна швидкість).
Пригадаймо, що за визначенням рівномірний рух тіла по колу – це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється із часом.
Для правильного розв’язання задачі потрібно вибрати дві точки твердого тіла, що обертається навколо осі
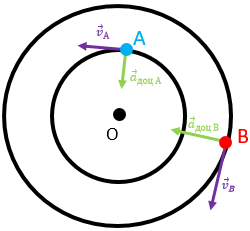
Рис. 1. Точки А і В твердого тіла
Нехай точка
Після цього можна обчислити лінійну швидкість кожної точки:
Отже:
Кутову швидкість
Оскільки за період
Те саме можна зробити і для будь-якої іншої пари точок твердого тіла, отже кутова швидкість буде однаковою для всіх його точок.
Доцентрове прискорення для всіх точок напрямлене до центра, тому його напрямок відрізняється для точок у різних частинах тіла, як зображено на рисунку 1.
Модуль доцентрового прискорення можна обчислити за формулою:
Потім потрібно порівняти модулі доцентрового прискорення для точок A і B:
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на оцінювання розуміння фізичних понять, що стосуються рівномірного руху по колу, зокрема доцентрового прискорення.
Під час рівномірного руху по колу лінійна швидкість не змінюється. Проте лінійна швидкість – це скалярна величина, яку розраховують як середню шляхову швидкість криволінійного руху. Тобто твердження «лінійна швидкість не змінюється» означає, що модуль вектора швидкості під час рівномірного руху по колу залишається незмінним, натомість напрямок швидкості постійно змінюється, щоби підтримувати траєкторію руху (коло).
Вектор швидкості в кожен момент напрямлений по дотичній до кола, тож має змінювати свій напрямок під дією певного прискорення (адже дотична в кожній точці кола відрізнятиметься від дотичної в іншій точці).
Це прискорення може бути напрямлене лише перпендикулярно до вектора швидкості, адже в будь-якому іншому разі воно змінюватиме не лише напрямок, а й модуль вектора.
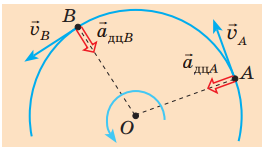
Рис. 1. Напрямок прискорення і швидкості під час руху по колу
Тож вектор прискорення під час рівномірного руху по колу завжди напрямлений до центра кола, а тому змушений змінювати свій напрямок щоразу, коли його змінює вектор швидкості. Доцентрове прискорення має постійний модуль, який можна обчислити за формулою
Відповідь: B.
ТЕМА: Механіка. Ріномірний рух по колу. Період і частота. Лінійна і кутова швидкості.
Завдання скеровано на перевірку вміння розв'язувати розрахункові задачі, застосовуючи функціональні залежності між основними фізичними величинами, на рівномірний рух по колу.
1.
2.
3.
4.
Відповідь: 1Г, 2B, 3Б, 4A.
ТЕМА: Основи кінематики. Ріномірний рух по колу. Доцентрове прискорення.
Завдання скеровано на перевірку вміння розрізняти різні види руху за його параметрами й розв'язувати розрахункові задачі на рівномірний рух по колу.
Модуль доцентрового прискорення
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.
Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.
У камері Вільсона частинки рухаються по дугах – елементах кола, отже камера перебуває в магнітному полі (рис. 1).

Рис. 1. Треки заряджених частинок у камері Вільсона
Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центра.
Доцентрове прискорення можна обчислити з виразу:
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто
Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца:
Зважаючи на те, що частинки рухаються в полі по колу, то
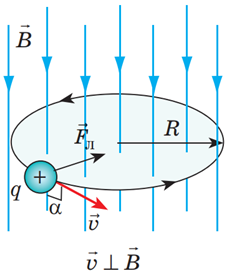
Рис. 2. Схема руху позитивно зарядженої частинки по колу
Тоді для випадку, описаного в задачі, можна записати:
Вираз для кінетичної енергії тіла:
Тож можна виразити швидкість руху частинки з другого закону Ньютона для випадків до і після проходження крізь фольгу й обчислити кінетичні енергії для обох випадків:
Співвідношення радіусів треків до і після проходження крізь фольгу таке:
А кінетичні енергії матимуть вигляд:
Можна обчислити різницю кінетичних енергій до i після проходження крізь фольгу:
Тоді, знайшовши відношення цієї різниці до початкової кінетичної енергії, можна визначити, на скільки зменшилася кінетична енергія:
Ця різниця становитиме 75 %.
Відповідь: 75.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух. Рівномірний рух по колу.
Завдання скеровано на оцінювання вміння визначати напрямок прискорення і швидкості в різних процесах.
А Снаряд, випущений гарматою чи будь-яким іншим способом, рухатиметься під дією сили тяжіння після вистрілу. У такому разі прискорення, що діє на тіло, – це прискорення вільного падіння, що завжди напрямлене до центра Землі. Тобто якщо поверхня горизонтальна, то прискорення вільного падіння спрямоване перпендикулярно до поверхні. Тіло в такому разі рухається по параболі. Схематичне зображення руху тіла, кинутого під кутом до горизонту, тобто руху снаряду, зображено на рисунку 1. Стрілкою червоного кольору позначено прискорення тіла, зеленого – напрямок швидкості тіла (напрямок руху). Кут між цими напрямками гострий.
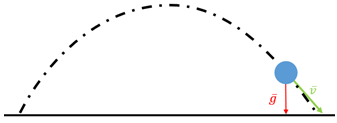
Рис. 1. Схематичне зображення руху снаряду перед падінням
Б Кінець годинникової стрілки рівномірно рухається по колу. За визначенням рівномірний рух тіла по колу – це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється із часом.
Під час руху по колу швидкість тіла постійно напрямлена по дотичній до кола. Це значить, що напрямок швидкості руху тіла постійно змінюється, але оскільки рух рівномірний, то модуль швидкості має залишатися постійним. Це можливо лише якщо прискорення напрямлене перпендикулярно до швидкості тіла. На рисунку 2 схематично зображено рух кінця годинної стрілки (позначеного синім кругом на рисунку). Тож кут між напрямком руху тіла й прискоренням у цьому разі завжди прямий.
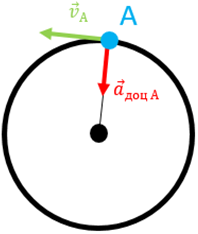
Рис. 2. Схематичне зображення руху кінця годинникової стрілки
В Під час руху снаряда в каналі ствола гармати його швидкість збільшується. Тобто прискорення співнапрямлене зі швидкістю тіла.
Г Після вимикання двигуна катера його швидкість починає зменшуватися. Тобто прискорення протилежно напрямлене до швидкості тіла.
Відповідь: 1Г, 2Д, 3В, 4А.
ТЕМА: Механіка. Кінематика. Основи кінематики. Шлях і переміщення.
Завдання скеровано на перевірку розуміння поняття переміщення.
Переміщення
Літак, який рухається вздовж меридіану від полюса до екватора, має траєкторію, що є чвертю великого кола Землі (рис. 1). Велике коло – це коло на поверхні Землі, центр якого збігається із центром Землі. Його радіус дорівнює радіусу Землі
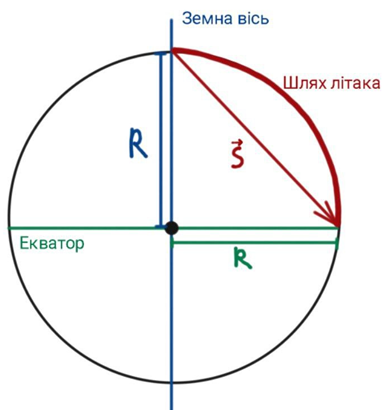
Рис. 1. Схема руху літака вздовж меридіана
Переміщення літака за цих умов – це хорда великого кола Землі. Її довжину можна дістати з теореми Піфагора:
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Шлях і переміщення.
Завдання скеровано на перевірку розуміння поняття «переміщення».
Переміщення – це векторна величина, яку графічно зображують як напрямлений відрізок прямої, що з’єднує початкове і кінцеве положення матеріальної точки.
Земля за рік робить повний оберт навколо Сонця – проходить повне коло. Відповідно за пів року Земля пройде половину кола (рис. 1).
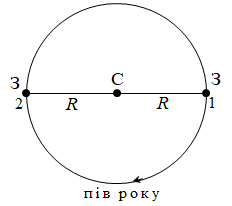
Рис. 1. Рух Землі навколо Сонця: 1 – початкове положення Землі; 2 ‑ кінцеве положення Землі (через пів року);
Якщо з’єднати початкове положення Землі (точка 1) із кінцевим (точка 2), де вона опиниться через пів року, то відрізок 1–2 буде діаметром орбіти, якою рухається планета. Оскільки радіус орбіти за умовою дорівнює
Інші варіанти відповіді можна отримати, якщо сплутати переміщення зі шляхом й обчислювати не довжину відрізка, яким з’єднані початкове і кінцеве положення тіла, а визначати довжину траєкторії руху тіла. Також до неправильної відповіді може призвести нерозуміння закономірностей руху Землі навколо Сонця.
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Закон всесвітнього тяжіння. Сила тяжіння. Рух штучних супутників. Перша космічна швидкість.
Завдання скеровано на перевірку розуміння і застосування закону всесвітнього тяжіння, а також розуміння руху штучних супутників.
1. Для того, щоб об’єкт рухався біля планети коловою орбітою, йому необхідно надати швидкість, яку називають першою космічною швидкістю.
Візьмемо до уваги, що саме сила тяжіння
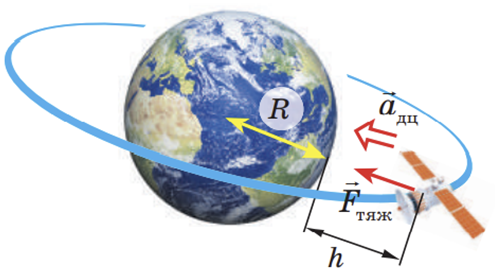
За другим законом Ньютона
Обчислімо, у скільки разів прискорення руху першого супутника більше за прискорення руху другого супутника, урахувавши співвідношення їхніх радіусів:
Отже,
Відповідь: 16.
2. Формули для обчислення перших космічних швидкостей руху супутників виведемо з формул для їхніх доцентрових прискорень:
Обчислімо, у скільки разів швидкість
Отже,
Відповідь: 2.
Відповідь: 1. 16. 2. 2.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Лінійна і кутова швидкості.
Завдання скеровано на перевірку знання і розуміння характеристик рівномірного руху по колу.
За періодом
Оскільки
Запишімо відповідні формули для визначення лінійних швидкостей стрілок годинника:
За умовою хвилинна стрілка вдвічі довша за годинну. Оскільки йдеться про рух кінців цих стрілок, то довжини стрілок – це радіуси обертання кінців стрілок – хвилинної
Тоді період обертання хвилинної стрілки становитиме
А період обертання годинної стрілки –
Запишімо відношення лінійних швидкостей стрілок годинника і обчислімо його:
Отже, лінійна швидкість хвилинної стрілки
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку знання і розуміння фізичних величин, що описують рух тіла по колу, і вміння їх визначати.
1. Модуль переміщення
2. Шлях
3. Швидкість руху
4. Кутову швидкість визначмо з формули, яка зв’язує кутову швидкість і швидкість:
Відповідь: 1Г, 2В, 3Б, 4А.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку знання і розуміння фізичних характеристик рівномірного руху по колу – доцентрового прискорення, лінійної швидкості, кутової швидкості.
1. Запишімо формулу для визначення доцентрового прискорення
За умовою кутова швидкість для всіх точок стала й однакова, а модуль доцентрового прискорення прямо пропорційний радіусу кола. Отже, модуль доцентрового прискорення
Визначімо відношення максимального і мінімального модулів доцентрових прискорень:
Відповідь: 8.
2. Формула для визначення лінійної швидкості ϑ рівномірного руху тіла по колу:
За умовою кутова швидкість для всіх точок стала й однакова, а лінійна швидкість прямо пропорційна радіусу кола. Отже, найбільшою буде лінійна швидкість
Визначімо, у скільки разів максимальна швидкість записування / зчитування інформації більша за мінімальну:
Відповідь: 3.
Відповідь: 1. 8. 2. 3.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку знання і розуміння фізичних величин, що описують рух тіла по колу, і вміння їх визначати.
1. Модуль переміщення
2. Шлях
3. Швидкість руху
4. Кутову швидкість визначмо з формули, яка пов’язує кутову і лінійну швидкості:
Відповідь: 1Г, 2В, 3Б, 4А.
ТЕМА: Механіка. Основи кінематики. Доцентрове прискорення.
Завдання скеровано на перевірку знання і розуміння, від яких фізичних величин і як залежить доцентрове прискорення.
У разі рівномірного руху тіла по колу вектор прискорення напрямлений до центра кола ‒ саме тому прискорення рівномірного руху тіла по колу називають доцентровим прискоренням
Позначмо на рисунку центри
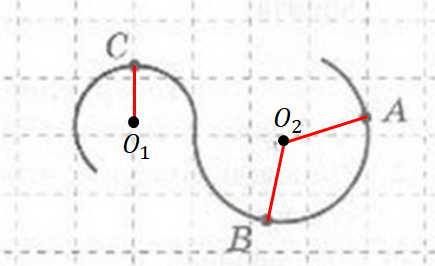
Запишімо формули для доцентрового прискорення в кожній точці:
За умовою модуль швидкості тіла не змінюється. А за побудовою бачимо, що
Оскільки прискорення обернено пропорційне до радіуса кола
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Доцентрове прискорення.
Завдання скеровано на перевірку знання і розуміння рівномірного руху матеріальної точки по колу і доцентрового прискорення.
Рівномірний рух тіла по колу ‒ це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється із часом.
У разі рівномірного руху тіла по колу вектор прискорення напрямлений до центра кола ‒ саме тому прискорення рівномірного руху тіла по колу називають доцентровим прискоренням
Переведімо значення швидкості в систему SI:
Обчислимо шукану величину ‒ доцентрове прискорення:
Відповідь: В.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.
Завдання скеровано на перевірку знання і розуміння періоду обертання і його залежності від певних характеристик руху, а також застосування другого закону Ньютона для визначення його.
На супутник, що рухається коловою орбітою навколо планети, діє лише сила тяжіння
Запишімо рівняння другого закону Ньютона (
де
Масу в рівнянні можна скоротити, а для доцентрового прискорення і прискорення вільного падіння запишімо відповідні формули:
Як отримуємо формулу для прискорення вільного падіння:
‒ за законом всесвітнього тяжіння
‒ за формулою для сили тяжіння
Прирівняймо праві частини цих формул й отримаємо формулу для прискорення вільного падіння:
Повернімося до другого закону Ньютона:
Лінійну швидкість
Дійсно, за час
Отже,
Звідси період обертання
Визначмо співвідношення періодів обертання штучних супутників планет
Отже, період обертання супутника навколо планети
Відповідь:
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку знання і розуміння поступального й обертального руху; а також уміння визначати суму векторів за правилом паралелограма й формулою діагоналі.
Розгляньмо рух кожної точки колеса машини одночасно як рівномірний поступальний рух і рівномірний обертальний рух відносно центра колеса з лінійною швидкістю
Напрямок вектора швидкості
Поступальна швидкість завжди напрямлена горизонтально вправо, як зображено на рисунку.
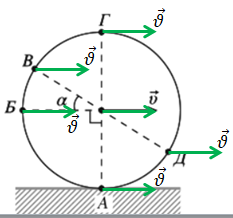
А вектор лінійної швидкості обертального руху
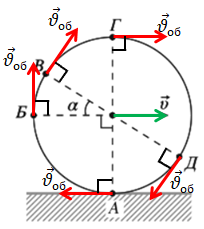
Скористаймося законом додавання швидкостей для визначення швидкості будь-якої точки колеса відносно Землі:
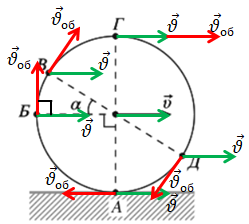
За умовою колесо машини рухається без проковзування, тож швидкість точки
Отже, швидкість поступального руху дорівнює лінійній швидкості обертального руху за модулем. Дійсно, для точки A швидкості руху
Точка Б: як видно з рисунка, вектори швидкостей розміщені під прямим кутом. На цих векторах можна добудувати квадрат, тобто скористатися правилом паралелограма. І тоді діагональ квадрата це сума векторів за цим правилом. Скористаймося теоремою Піфагора:
Точка Г: вектори лежать на одній прямій і напрямлені в один бік:
Для точок В й Д скористаймося і правилом паралелограма, і формулою визначення довжини діагоналі
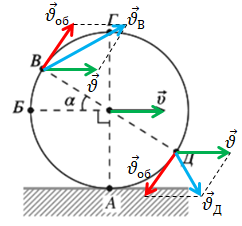
(кут між векторами визначмо з рисунка за побудовою;
Підставімо відповідно до умови значення кута й визначмо швидкість точки В:
Точка Д:
Відповідь: 1А, 2Д, 3Б, 4В.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рухому заряджену частинку.
На рухому заряджену частинку в магнітному полі діє сила Лоренца
За умовою частинка рухається перпендикулярно до ліній магнітної індукції.

У цьому разі
За другим законом Ньютона:
Ми виразили з рівняння швидкість, тому що кінетична енергія
За умовою після проходження частинки крізь фольгу радіус треку зменшився вдвічі, тож формула для швидкості матиме вигляд:
Тоді можемо визначити, яку частину кінетичної енергії втратила частинка під час проходження крізь фольгу:
тобто частинка втратила три чверті кінетичної енергії.
Відповідь: 0,75.
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи. Рух по колу.
Завдання скеровано на перевірку вміння визначати напрямок швидкості руху тіла й напрямок прискорення тіл під час різних видів руху.
1. Яблуко в безвітряну погоду падатиме вертикально, тож і напрямок швидкості
Падіння тіл у безповітряному просторі, тобто падіння лише під дією сили тяжіння, називають вільним падінням. У разі вільного падіння всі тіла падають на Землю з однаковим прискоренням ‒ прискоренням вільного падіння
Отже, кут між напрямком швидкості руху яблука й напрямком прискорення становитиме нуль, тобто прискорення напрямлене в напрямку швидкості руху ‒ варіант відповіді В.
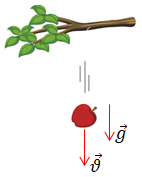
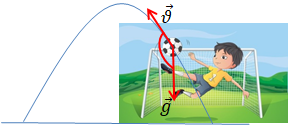
2. Коли футбольний м’яч піднімається, спрямований під кутом до горизонту (див. рисунок), то швидкість
Отже, кут між векторами
3. Коли автомобіль гальмує, рухаючись прямолінійно, то напрямок прискорення

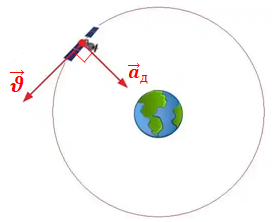
4. Штучний супутник рухається навколо Землі по коловій орбіті. Швидкість
Отже, у цьому разі доцентрове прискорення буде напрямлене під прямим кутом до напрямку швидкості руху ‒ варіант відповіді Д.
Відповідь: 1В, 2Б, 3А, 4Д.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку знання і розуміння фізичних величин, що характеризують рівномірний рух тіла по колу, і їхнього графічного зображення.
Рух по колу ‒ це криволінійний рух. Під час прямолінійного руху напрямок вектора швидкості
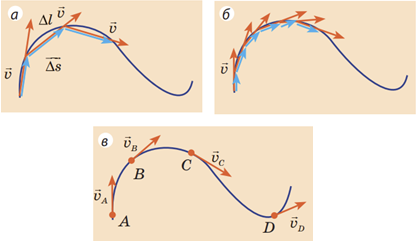
Вектор прискорення
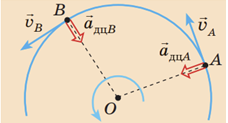
(Докладне доведення напрямку доцентрового прискорення наведено в підручнику: Фізика (рівень стандарту, за навчальною програмою авторського колективу під керівництвом Локтєва В. М.) : підруч. для 10 кл. закл. загал. серед. освіти / [В. Г. Бар’яхтар, С. О. Довгий, Ф. Я. Божинова, О. О. Кірюхіна] ; за ред. В. Г. Бар’яхтара, С. О. Довгого. ‒ Харків: Вид-во «Ранок», 2018. ‒ c. 49‒50.)
Отже, правильне розташування векторів миттєвої швидкості і прискорення для рівномірного руху по колу зображено на рисунку В.
На рисунку А напрямки швидкості і прискорення збігаються ‒ це випадок прямолінійного рівноприскореного руху (тіло розганяється). На рисунку Б напрямки швидкості і прискорення протилежні ‒ це випадок прямолінійного рівноприскореного руху (тіло гальмує). На рисунку Г зображено випадок, ідентичний випадку А, але тіло рухається не горизонтально праворуч (рисунок А), а в тому напрямку, що на рисунку Г.
Відповідь: B.