Розділ: Електродинаміка
Тема: Магнітне поле, електромагнітна індукція
Кількість завдань: 96
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Досліди Фарадея. Явище електромагнітної індукції. Правило Ленца.
Завдання скеровано на перевірку знання і розуміння дослідів Фарадея, а також уміння застосовувати правило Ленца для визначення напрямку індукційного струму.
Пригадаймо висновок, який зробив Майкл Фарадей на основі своїх дослідів. Ці досліди доводили, що за допомогою магнітного поля можна отримати електричний струм: у замкненому провідному контурі виникає електричний струм, якщо кількість ліній магнітної індукції, що пронизують поверхню, обмежену контуром, змінюється.
Це явище назвали електромагнітною індукцією, а електричний струм, який при цьому виникає, ‒ індукційним (наведеним) струмом.
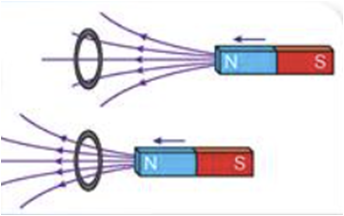
Якщо змінювати магнітне поле, що пронизує котушку (наприклад, наближати або віддаляти магніт, як сказано в умові завдання), то в котушці виникає індукційний струм. Унаслідок цього котушка сама стає магнітом.
Як свідчать досліди, якщо магніт наближати до котушки (за умовою північним полюсом), то кількість ліній магнітної індукції, що пронизують котушку, збільшується (магнітне поле всередині котушки посилюється), і в ній виникає індукційний струм такого напрямку, що котушка буде обернена до магніту однойменним полюсом
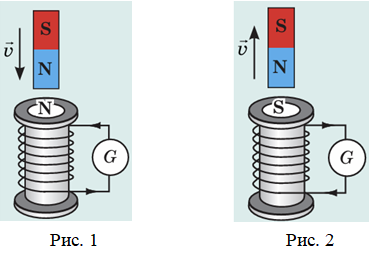
Якщо ж магніт віддаляти від котушки, то кількість ліній магнітної індукції, що пронизують котушку, зменшується, і в котушці виникає індукційний струм такого напрямку, що котушка буде обернена до магніту різнойменним полюсом
Знаючи полюси котушки та скориставшись правилом правої руки (див. рисунок),
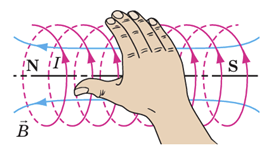
можна визначити напрямок індукційного струму (на обох рисунках 1 і 2 напрямок струму позначено стрілками на обмотках котушок, з’єднаних із гальванометром
Отже, у першій ситуації (унаслідок наближення магніту) котушка й магніт відштовхуватимуться, а в другій (унаслідок віддалення магніту) ‒ притягуватимуться.
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Правило Ленца.
Завдання скеровано на перевірку знання і розуміння природи індукційного струму, а також вміння застосовувати правило Ленца для визначення напрямку індукційного струму.
Правило для визначення напрямку індукційного струму (правило Ленца): індукційний струм, який виникає в замкненому провідному контурі, має такий напрямок, що створений цим струмом магнітний потік перешкоджає зміні магнітного потоку, який спричинив появу індукційного струму.
Щоб з’ясувати, у якому з прикладів А ‒ Г правильно показано напрямок індукційного струму
1. Визначаємо напрямок ліній магнітної індукції
2. З’ясовуємо, посилюється чи послаблюється зовнішнє магнітне поле (тобто збільшується чи зменшується кількість ліній магнітної індукції, що пронизують контур).
3. Визначаємо напрямок магнітної індукції магнітного поля, створеного індукційним струмом
4. Визначаємо напрямок індукційного струму.
Розгляньмо рисунок А.
1. Магніт повернутий до кільця північним полюсом. А магнітні лінії поза магнітом виходять із північного полюса
2. Вертикальна стрілка на рисунку вказує, що магніт рухається до кільця, наближається, тобто зовнішнє магнітне поле посилюється (збільшується кількість ліній магнітної індукції, що пронизують кільце).
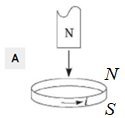
3. Це означає, що в кільці виникає індукційний струм такого напрямку, що кільце буде обернене до магніту однойменним полюсом (кільце відштовхуватиметься від магніту), тобто північним
4. За правилом правої руки визначаємо напрямок індукційного струму в кільці:
орієнтуємо праву руку так, що відігнутий на
Проаналізуймо інші варіанти відповіді, з’ясуймо помилки на рисунках.
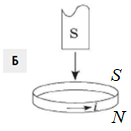
Рисунок Б. Магніт наближається до кільця південним полюсом
За правилом правої руки визначімо напрямок індукційного струму в кільці:
орієнтуємо праву руку так, що відігнутий на
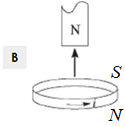
Рисунок В. Магніт віддаляється від кільця північним полюсом
За правилом правої руки визначаємо напрямок індукційного струму в кільці:
орієнтуємо праву руку так, що відігнутий на
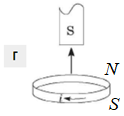
Рисунок Г. Магніт віддаляється від кільця південним полюсом
За правилом правої руки визначаємо напрямок індукційного струму в кільці:
орієнтуємо праву руку так, що відігнутий на
Відповідь: A.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння визначення напрямку дії сили Лоренца.
Силу, з якою магнітне поле діє на рухому заряджену частинку, називають силою Лоренца.
Напрямок сили Лоренца визначають за правилом лівої руки: лінії магнітної індукції
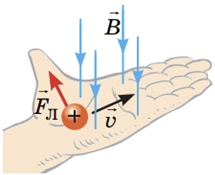
Отже, якщо людина розмістить долоню лівої руки відповідно до правила, великий палець буде напрямлений до неї перпендикулярно до площини рисунка. Це варіант відповіді B.
Відповідь: B.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік.
Завдання скеровано на перевірку розуміння суті магнітного потоку й параметрів, від яких він залежить.
Кількість ліній магнітної індукції, що пронизують певну поверхню (у цьому завданні – поверхню, обмежену плоским дротяним кільцем), називають потоком магнітної індукції або магнітним потоком.
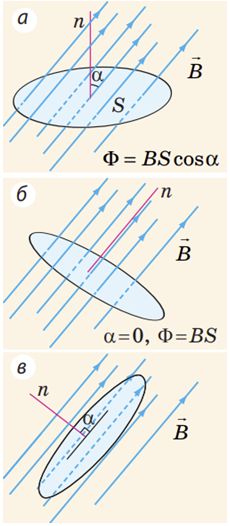
Розгляньмо плоский замкнений контур у магнітному полі. Нормаль
Потік магнітної індукції (магнітний потік)
Магнітний потік буде максимальним, якщо поверхня перпендикулярна до ліній магнітної індукції (рис. б), і дорівнюватиме нулю, якщо поверхня паралельна цим лініям (рис. в).
Залізо ‒ феромагнетик, намагнічується під дією зовнішнього магнітного поля, створює власне сильне магнітне поле, напрямлене в бік зовнішнього магнітного поля. Залізне осердя, розташоване в кільці, що проводить струм, значно посилить магнітну дію дротяного кільця. Отже, осердя впливатиме на зміну магнітного потоку.
Зминання кільця приводить до зміни площі поверхні, через яку проходить магнітний потік, прямо пропорційний цій площі.
Якщо повернемо кільце навколо осі, перпендикулярної до площини кільця (ця вісь збігається з нормаллю або паралельна їй, як показано на рис. a), то на зовнішнє магнітне поле це не вплине, площа поверхні, обмеженої кільцем, кут між нормаллю і вектором магнітної індукції не зміняться. Отже, такою дією магнітний потік змінити не можна.
Якщо ж повернути кільце навколо осі, що проходить у його площині, зміниться кут між нормаллю і вектором магнітної індукції, і, відповідно, магнітний потік.
Відповідь: B.
ТЕМА: Перетворення енергії в коливальному контурі. Закон Джоуля – Ленца. Рівняння теплового балансу.
Завдання скеровано на оцінювання знання формул для визначення енергії коливального контуру, кількості теплоти, що виділяється під час згоряння палива, і закону Джоуля – Ленца.
Відповідь: 1В, 2А, 3Г, 4Д.
ТЕМА: Електродинаміка. Магнітне поле та явище магнітної індукції.
Завдання скеровано на перевірку вміння визначати напрямок ліній магнітної індукції за допомогою правила правої руки.
За правилом правої руки можна визначити напрямок ліній магнітної індукції навколо провідника зі струмом.
Якщо спрямувати великий палець уздовж напрямку протікання струму, то загнуті пальці правої руки вкажуть напрямок ліній магнітної індукції магнітного поля провідника зі струмом.
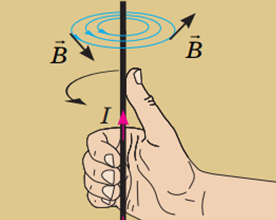
Рис. 1. Правило правої руки
Для провідника, про який ідеться в задачі, можна визначити напрямок ліній індукції магнітного поля (рис. 2).
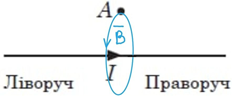
Рис. 2. Лінії індукції магнітного поля
Тож у точці
Напрямок ліній магнітної індукції – це і є напрямок, в якому зорієнтований північний полюс магнітної стрілки в даній точці.
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле та явище магнітної індукції.
Завдання скеровано на перевірку розуміння впливу магнітного поля на провідники зі струмом, уміння використовувати правило правої руки й знань про магнітне поле Землі.
Гальванічний елемент із провідником, що з’єднує його краї, утворюють виток зі струмом. Уважаємо, що струм у провіднику рухається від плюса до мінуса, тобто в цьому разі – проти годинникової стрілки. На цей виток діє сила Ампера. Напрямок сили Ампера залежить від кута між напрямком ліній магнітної індукції та напрямком протікання струму.
У витку в різних його частинах напрямок протікання струму різний. У крайній лівій його частині струм напрямлений вертикально вниз, а в крайній правій точці – вертикально вгору (рис. 1).
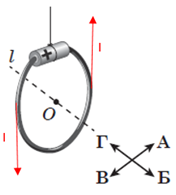
Рис. 1. Напрямок протікання струму в крайніх лівій і правій точках витка зі струмом
Тоді в цих точках сила Ампера матиме протилежний напрямок. Це створює обертальний момент, який можна обчислити за формулою
Рамка зупинилася, коли обертальний момент сил Ампера, що на неї діють, зменшився до нуля. Це можливо, якщо
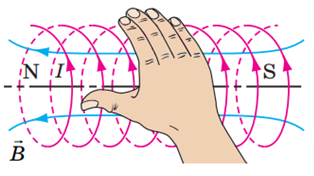
Рис. 2. Правило правої руки
Якщо чотири пальці правої руки обгорнути за напрямком струму в контурі, то великий палець укаже на напрямок Б, тобто північний полюс витка попереду (рис. 3).
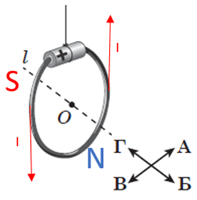
Рис. 3. Застосування правила правої руки
Географічний напрямок північ – це напрямок, на який указує північний полюс магнітної стрілки компаса, тобто з погляду фізики він є південним магнітним полюсом. Тому напрямок Б вказує на географічний напрямок північ.
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.
Завдання скеровано на оцінку вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.
Дано:
Знайти:
У рівняннях ядерних реакцій поруч із символом елемента лівим верхнім індексом позначають кількість нуклонів у ядрі (сумарна кількість протонів і нейтронів), а лівим підрядковим – кількість протонів. Тож у цього нукліда Берилію 9 нуклонів, 4 з яких – протони. Маса нейтрона приблизно дорівнює масі протона, тому маса нукліда Берилію у 9 разів більша, ніж маса протона:
Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центру.
Доцентрове прискорення можна знайти з виразу
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто
Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца:
Зважаючи на те, що частинки рухаються в полі по колу, то
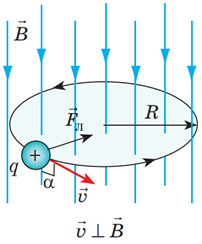
Рис. 1. Схема руху позитивно зарядженої частинки по колу
Тоді можна записати, що
Оскільки в нукліда Берилію є чотири позитивно заряджені протони й п’ять нейтральних нейтронів, його заряд у чотири рази більший, ніж заряд протона:
Записи другого закону Ньютона для обох частинок такі:
Після цього потрібно виразити радіуси кола, уздовж якого здійснюється рух, для обох частинок:
Далі треба підставити всі відомі співвідношення між фізичними величинами, що відповідають протону й α-частинці:
Тобто
Відповідь: 2,25.
ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції.
Завдання скеровано на оцінку вміння визначати напрямок ліній магнітної індукції за допомогою правила правої руки.
За правилом правої руки можна визначити напрямок ліній магнітної індукції.
Якщо спрямувати великий палець уздовж напрямку протікання струму, то загнуті пальці правої руки вкажуть напрямок ліній магнітної індукції магнітного поля провідника зі струмом.
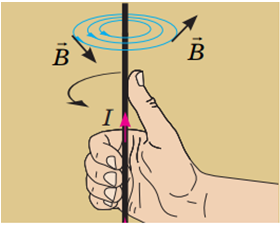
Рис. 1. Правило правої руки
Тож, як зображено на рисунку, якщо сила струму напрямлена вгору, то лінії магнітної індукції утворюють коло навколо провідника, і вектор магнітної індукції спрямований праворуч у точці кола, найближчій до спостерігача.
Відповідь: B.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція, Закон електромагнітної індукції.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на застосування закону електромагнітної індукції.
Дано:
Знайти:
Заряд проходить через виток під час зміни магнітного потоку, бо за законами електромагнітної індукції в такому разі утвориться струм. Цей струм сприятиме виникненню власного магнітного поля витка, що протидіятиме зміні потоку крізь нього. Такий струм називають індукційним. Силу індукційного струму визначають за формулою
За законом електромагнітної індукції ЕРС індукції дорівнює швидкості зміни магнітного потоку, який пронизує поверхню, обмежену контуром. Тобто
За визначенням сила струму – це фізична величина, яка характеризує електричний струм. Її описують формулою
Тоді
Відповідь: 0,5.
ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції. Сила Ампера.
Завдання скеровано на оцінювання вміння розраховувати модуль сили Ампера для провідників зі струмом під дією магнітного поля.
Сила Ампера – це сила, що діє на провідник зі струмом в магнітному полі. Її напрямок визначають за правилом лівої руки, а модуль – за формулою
Оскільки сила струмі
У цьому разі напрямок сили струму й напрямок ліній магнітної індукції є або паралельними
Лінії магнітної індукції проводять від північного полюса до південного, тож у випадках A, B і Г
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Енергія магнітного поля.
Завдання скеровано на оцінювання вміння обчислювати енергію магнітного поля провідника зі струмом.
Дано:
Знайти:
Для визначення енергії магнітного поля котушки потрібно скористатися формулою
Відповідь: 5.
ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції.
Завдання скеровано на оцінювання вміння визначати напрямок ліній магнітної індукції за допомогою правила правої руки.
За правилом правої руки можна визначити напрямок ліній магнітної індукції: якщо спрямувати великий палець уздовж напрямку протікання струму, то загнуті пальці правої руки вкажуть напрямок ліній магнітної індукції магнітного поля провідника зі струмом (рис. 1).
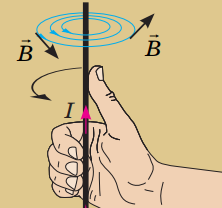
Рис. 1. Правило правої руки
Магнітна стрілка в магнітному полі повернеться вздовж ліній магнітної індукції так, що лінії входитимуть у її південний полюс і виходитимуть із її північного полюса.
Відповідь: Б.
ТЕМА: Електродинаміка. Явище й закони електромагнітної індукції.
Завдання скеровано на оцінювання знання поняття «електромагнітна індукція» і вміння застосовувати закони електромагнітної індукції.
Гальванометр у досліді, описаному в завданні, фіксує індукційний струм у котушці.
Для правильного розв’язання завдання потрібно пригадати закони електромагнітної індукції.
1. Електричний струм у замкненому провідному контурі виникає лише тоді, коли змінюється магнітний потік через поверхню, обмежену контуром.
2. Чим швидше змінюється магнітний потік, тим більшою є сила індукційного струму в контурі.
3. Напрямок індукційного струму в контурі залежить від того, збільшується чи зменшується магнітний потік через поверхню, обмежену контуром.
За першим законом електромагнітної індукції в котушці виникає струм, бо за наближення або введення магніту змінюється магнітний потік, що через неї протікає.
Чим швидше змінюватиметься магнітний потік, тим більшою, відповідно до другого закону електромагнітної індукції, буде сила струму. Щоби швидше змінювати магнітний потік від магніту, його треба рухати швидше.
Якщо тримати магніт нерухомо, то струм індукції в котушці не виникне, бо магнітний потік, який протікає через контур котушки, не змінюватиметься. А якщо змінити напрямок руху магніту, то, за правилом Ленца, зміниться лише напрямок індукованого струму.
Відповідь: Б.
ТЕМА: Одиниці фізичних величин.
Завдання скеровано на оцінювання вміння виражати одиниці фізичних величин через основні одиниці SI.
Для запису одиниць фізичних величин через основні одиниці СІ використовують метод розмірностей.
А Тесла (магнітна індукція). Потрібно вибрати формулу, із якої можна виразити магнітну індукцію через величини, одиниці яких входять у СІ або можуть бути виражені через них. Для магнітної індукції можна використати вираз для сили Ампера:
Аналогічні дії потрібно виконати й для варіантів Б – Г.
Б Генрі (індуктивність).
B Ньютон (сила).
Г Джоуль (робота).
Відповідь: 1В, 2А, 3Д, 4Б.
ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції. Сила Ампера.
Завдання скеровано на оцінювання вміння визначати за правилом лівої руки напрямок сили Ампера.
Якщо ліву руку розташувати так, щоби лінії магнітної індукції входили в долоню, а чотири витягнуті пальці вказували напрямок струму в провіднику, то відігнутий на 90° великий палець укаже напрямок сили Ампера (рис. 1).
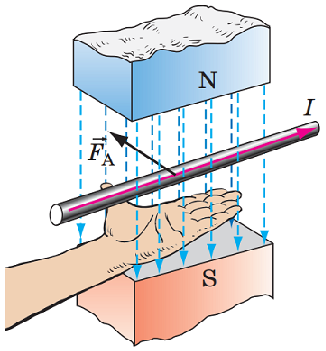
Рис. 1. Правило лівої руки
За рисунком 2 можна визначити напрямок струму I в провіднику й напрямок ліній магнітної індукції
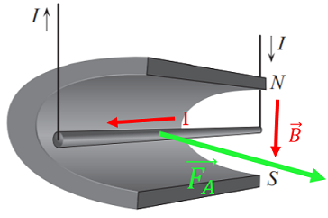
Рис. 2. Напрямок струму, ліній магнітної індукції та сили Ампера
Відповідь: A.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.
Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.
Дано:
1. Знайти:
Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центра.
Доцентрове прискорення можна обчислити з виразу
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто
Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца:
З огляду на те, що частинки рухаються в полі по колу,
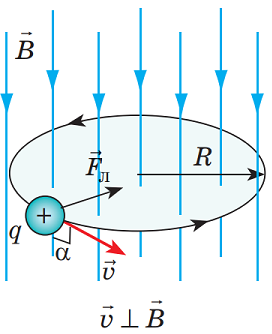
Рис. 1. Схема руху позитивно зарядженої частинки по колу
Тоді можна записати:
Оскільки складники
Запис другого закону Ньютона для обох частинок такий:
Після цього потрібно записати вирази для радіусів кола, уздовж якого здійснюється рух, для обох частинок:
Далі потрібно підставити всі відомі співвідношення між фізичними величинами, що відповідають протону й
Тому
Відповідь: 2.
ТЕМА: Магнітне поле, електромагнітна індукція. Індуктивність. Енергія магнітного поля.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, пов’язані з енергією магнітного поля і її перетворенням на інші види енергії.
Дано:
Знайти:
Робота сторонніх сил акумулятора витрачається на збільшення енергії котушки. Максимальна енергія котушки може бути визначена за формулою
Проте коло за умовою не ідеальне – частина роботи акумулятора втрачається у вигляді виділеної теплоти. Тоді разом робота сторонніх сил акумулятора має дорівнювати сумі енергії котушки й кількості виділеної теплоти:
Відповідь: 95.
ТЕМА: Електродинаміка. Явище й закони електромагнітної індукції. Сила Ампера. Сила Лоренца.
Завдання скеровано на оцінювання знання розрахункових формул сили Ампера, сили Лоренца, індуктивності й потоку магнітної індукції.
Щодо варіантів відповіді:
A
Б
B
Г
Д
Відповідь: 1Г, 2А, 3В, 4Д.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.
Завдання скеровано на оцінювання розуміння природи магнітної індукції і вміння аналізувати результати експерименту за його схематичним рисунком.
Лінії індукції магнітного поля, утвореного провідником зі струмом, мають вигляд кола. Чим далі від провідника точка, тим менше в ній значення індукції магнітного поля.
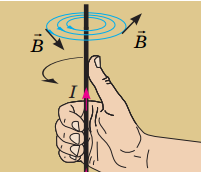
Рис. 1. Лінії магнітної індукції навколо провідника зі струмом
Коли провідник скручують у петлі, утворюється котушка. Лінії магнітної індукції всередині котушки набагато густіші (рис. 2), тож і значення індукції більше. Чим більше витків у котушці, тим більшим може бути значення індукції всередині неї.
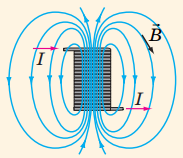
Рис. 2. Напрямок магнітної індукції в котушці
Тож, оскільки провідник поруч з усіма точками відрізняється лише тим, якої форми він набуває (петля, дві петлі чи пряма). То найбільшим буде значення індукції в центрі котушки з найбільшою кількістю петель. Тобто в точці 3.
Відповідь: B.
ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням законів для рухомих провідників у магнітному полі.
Дано:
Знайти:
Два крила літака – це один суцільний провідник, що рухається в магнітному полі. Оскільки рух літака відбувається вздовж магнітного меридіана Землі, то напрямок його швидкості збігається із горизонтальним складником напруженості магнітного поля і перпендикулярний до її вертикального складника.
Під час руху провідника перпендикулярно до ліній напруженості магнітного поля в тому самому напрямку рухаються і всі його вільні електрони. На кожен із цих вільних електронів діє сила Лоренца. За правилом лівої руки, якщо долоню повернути так, щоби чотири пальці показували напрямок, протилежний до напрямку швидкості негативно заряджених частинок, а лінії магнітної індукції входили в долоню, то великий палець лівої руки вкаже напрямок дії сили Лоренца.
У результаті цього вільні електрони змістяться в одне крило, тому крила поляризуються. Тоді для рухомого провідника в магнітному полі можна обчислити електрорушійну силу (ЕРС), що дорівнює різниці потенціалів між двома кінцями провідника:
Тоді
Відповідь: 0,15.
ТЕМА: Магнітне поле, електромагнітна індукція. Трансформатор.
Завдання скеровано на оцінювання розуміння принципів роботи трансформатора й уміння розв’язувати розрахункові задачі відповідного змісту.
Дано:
1. Знайти:
Описаний в умові трансформатор – підвищувальний, отже коефіцієнт трансформації
Якщо розімкнути іншу обмотку трансформатора, то первинною вважатимуть обмотку з напругою
Такий трансформатор знижуватиме напругу, а за умовою напруга має підвищуватися, тому для подальшого розв’язку потрібно використати коефіцієнт трансформації
2. Знайти:
Також коефіцієнт трансформації можна обчислити як відношення кількості мотків у первинній обмотці до кількості мотків у вторинній:
Тоді
Відповідь: 1. 0,02 або 50. 2. 2000.
ТЕМА: Електричне коло.
Завдання скеровано на оцінювання знання умовних позначень для створення схем електричних кіл:
A – котушка індуктивності, соленоїд

Б – конденсатор

B – напівпровідниковий діод
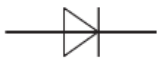
Г – батарея гальванічних елементів
 або
або
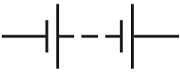
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле. Закон Ампера.
Завдання скеровано на перевірку знання закону Ампера й уміння розв'язувати задачі на визначення напрямку сили Ампера.
За правилом «лівої руки» долоня вказує на північний полюс, а чотири пальці лівої руки направлені до нас із площини рисунка. Тоді відведений на 90° великий палець лівої руки вкаже напрямок дії сили Ампера вниз.
Відповідь: Г.
ТЕМА: Одиниці фізичних величин.
Завдання скеровано на перевірку вміння записувати одиниці фізичних величин через основні одиниці СІ.
1 Тесла (магнітна індукція)
Варто вибрати формулу, з якої можна виразити магнітну індукцію через величини, одиниці яких входять в СІ, або можуть бути легко вираженi через них. Для магнітної індукції можна використати вираз для сили Ампера:
Тоді можна записати рівність (1), використовуючи одиниці фізичних величин:
2 Генрі (індуктивність):
3 Ньютон (сила):
4 Джоуль (робота):
Відповідь: 1В, 2А, 3Д, 4Б.
ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку розуміння природи сили Лоренца.
У магнітному полі на заряджену частинку діє сила Лоренца, яку можна розрахувати за формулою
Частинка продовжуватиме свій рух по прямій без змін, якщо
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку розуміння залежності магнітного потоку від зовнішніх чинників.
Магнітний потік
Тож магнітний потік, що пронизує плоске дротяне кільце, зміниться, якщо змінити його площу (зім’яти його), змінити напруженість магнітного поля, що проходить крізь кільце (помістити всередину кільця залізне осердя) чи якщо змінити кут між вектором магнітної індукції та нормаллю до поверхні (повернути кільце навколо осі, що проходить у його площині).
Відповідь: B.
ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку розуміння поняття роботи сили.
Роботу сили можна обчислити за формулою:
Поле не виконує роботу над зарядженою частинкою, якщо
Відповідно на електрично заряджену частинку діє лише сила Лоренца в сталому магнітному полі.
Відповідь: Г.
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Електродинаміка. Сила Лоренца.
Завдання скеровано на оцінювання вміння розв’язувати комплексні розрахункові задачі на використання принципів рівномірного руху по колу.
У камері Вільсона частинки рухаються по дугах – елементах кола, отже камера перебуває в магнітному полі (рис. 1).

Рис. 1. Треки заряджених частинок у камері Вільсона
Під час руху по колу швидкість руху частинки буде спрямована по дотичній до кола, а прискорення – до центра.
Доцентрове прискорення можна обчислити з виразу:
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії, тобто
Єдиною силою, що діє на частинки в площині напрямку руху, є сила Лоренца:
Зважаючи на те, що частинки рухаються в полі по колу, то
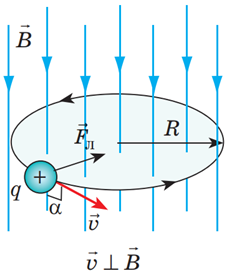
Рис. 2. Схема руху позитивно зарядженої частинки по колу
Тоді для випадку, описаного в задачі, можна записати:
Вираз для кінетичної енергії тіла:
Тож можна виразити швидкість руху частинки з другого закону Ньютона для випадків до і після проходження крізь фольгу й обчислити кінетичні енергії для обох випадків:
Співвідношення радіусів треків до і після проходження крізь фольгу таке:
А кінетичні енергії матимуть вигляд:
Можна обчислити різницю кінетичних енергій до i після проходження крізь фольгу:
Тоді, знайшовши відношення цієї різниці до початкової кінетичної енергії, можна визначити, на скільки зменшилася кінетична енергія:
Ця різниця становитиме 75 %.
Відповідь: 75.
ТЕМА: Магнітне поле, електромагнітна індукція. Трансформатор.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, що ґрунтується на розумінні принципів роботи трансформатора.
Трансформатор – електромагнітний пристрій, що перетворює змінний струм однієї напруги на змінний струм іншої напруги за незмінної частоти.
Тож збільшується саме значення напруги змінного струму.
Відношення кількості витків у первинній обмотці до кількості витків у вторинній обмотці – це коефіцієнт трансформації. За умовою кількість витків у вторинній обмотці в
Так само коефіцієнт трансформації можна визначити як відношення початкової напруги змінного струму до кінцевої:
Тоді
Відповідь: A.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.
Завдання скеровано на оцінювання розуміння понять магнітної індукції, індуктивності, магнітного потоку й магнітної проникності середовища.
Магнітна індукція
Індуктивність
Магнітний потік
Магнітна проникність середовища
Відповідь: A.
ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на оцінювання розуміння законів руху заряджених частинок в електричному полі.
На рухому заряджену частинку в полі діє сила Лоренца. Саме вона й зумовить зміну напрямку руху електрона, що рухається в однорідному магнітному полі. Сила Лоренца залежить від заряду частинки, її швидкості, індукції магнітного поля і кута, який утворюють напрямок швидкості й лінії магнітної індукції:
Якщо траєкторія електрона прямолінійна, то сила Лоренца не впливає на його рух, а отже має дорівнювати 0. Сила Лоренца дорівнюватиме нулю, коли
Тому, якщо лінії магнітної індукції напрямлені вертикально, то й електрон має рухатися в такому напрямку.
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле та явище магнітної індукції.
Завдання скеровано на перевірку знання одиниць виміру для фізичних величин, пов’язаних із магнітним полем.
А Магнітну індукцію
Б Індуктивність
В Магнітний потік
Г Електроємність
Відповідь: A.
ТЕМА: Магнітне поле, електромагнітна індукція.
Завдання скеровано на оцінку вміння визначати напрямок ліній магнітної індукції за допомогою правила правої руки.
Після замикання ключа
Права частина котушки підключена до негативного полюса джерела, а ліва – до позитивного. Струм у колі тече від + до –, тож він буде спрямований униз у ближній до спостерігача частині рисунка й угору в дальній частині.
Напрямок магнітного поля в котушці можна визначити за правилом правої руки (рис. 1):
якщо чотири зігнуті пальці правої руки спрямувати за напрямком струму в контурі, то відігнутий на
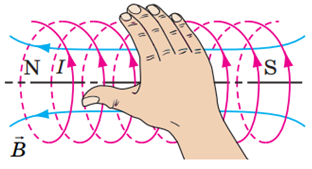
Рис. 1. Правило правої руки
Тобто для котушки в завданні також можна визначити напрямок ліній магнітної індукції, а отже і її магнітні полюси (рис. 2).
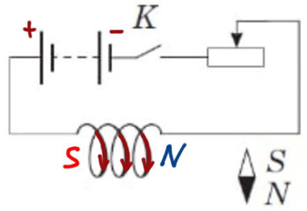
Рис. 2. Результат застосування правила правої руки
Магнітна стрілка на рисунку поруч із північним магнітним полюсом, тож вона повернеться до нього своїм південним полюсом.
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера.
Завдання скеровано на перевірку розуміння дії магнітного поля на провідник з електричним струмом.
Силу, із якою магнітне поле діє на провідник зі струмом, називають силою Ампера
Напрямок дії сили Ампера визначають за правилом лівої руки: якщо ліву руку розташувати так, щоб лінії магнітної індукції
Розгляньмо кожний зображений варіант. Ліву руку орієнтуватимемо відносно сторінки з рисунком.
На рисунку 1 вектор магнітної індукції напрямлений перпендикулярно до площини рисунка від вас (позначено хрестиком). Отже, орієнтуємо ліву руку долонею до себе (лінії магнітної індукції входять в долоню), чотири пальці напрямлені вертикально вгору за напрямком струму, тоді великий палець, відігнутий на
На рисунку 2 вектор магнітної індукції напрямлений вертикально вниз, отже долоню орієнтуємо торцем (перпендикулярно) до площини рисунка, а чотири пальці руки спрямовуємо праворуч за напрямком сили струму. Тоді великий палець, відігнутий на
На рисунку 3 сила Ампера не діятиме, оскільки напрямок сили струму збігається з напрямком вектора магнітної індукції і неможливо зорієнтувати ліву руку відповідно до правила визначення сили Ампера. За формулою сила Ампера також дорівнює нулю. Оскільки кут
На рисунку 4 вектор магнітної індукції напрямлений перпендикулярно до площини рисунка до вас (позначено точками). Отже, орієнтуємо ліву руку долонею від себе (лінії магнітної індукції входять в долоню), чотири пальці напрямлені вертикально вгору за напрямком струму, тоді великий палець, відігнутий на
Відповідь: 1А, 2В, 3Д, 4Б.
ТЕМА: Механіка. Молекулярна фізика і термодинаміка. Електродинаміка.
Завдання скеровано на перевірку знань і розуміння принципів дії пристроїв і механізмів із різних розділів фізики.
Гальмівні механізми (дискові або барабанні) не дають обертатися колесам, унаслідок чого автомобіль зменшує швидкість. Принцип дії гальмівного механізму заснований на використанні сили тертя. Під час гальмування кінетична енергія переходить у внутрішню.
Тепловий двигун – це машина, яка працює циклічно й перетворює енергію палива на механічну роботу. Робоче тіло (газ, який виконує роботу під час свого розширення) отримує певну кількість теплоти від нагрівника. Ця теплота частково перетворюється на механічну енергію (робоче тіло виконує роботу), а частково передається холодильнику.
Індукційні генератори струму перетворюють механічну енергію на електричний струм. Складені з металевого осердя, у пази якого поміщено обмотку. Кінці обмотки з’єднані з кільцями, до кожного з яких притиснуто щітку для відведення напруги до споживача. Осердя з обмоткою (ротор) обертається в магнітному полі нерухомого постійного магніту або електромагніту.
Електричний двигун є пристроєм для перетворення електричної енергії на механічну та приведення до руху машин і механізмів. Робота електродвигуна основана на втягуванні або виштовхуванні провідника з електричним струмом у магнітному полі й дії на провідник зі струмом сили Ампера. Під час роботи двигуна рух ротора (рухомої частини двигуна) передається валу, а з нього – безпосередньо до споживача.
Відповідь: 1А, 2Б, 3В, 4Г.
ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Змінний електричний струм.
Завдання скеровано на перевірку розуміння умов виникнення змінного електричного струму й законів, якими описують його.
У рамці, яка зі сталою кутовою швидкістю обертається в магнітному полі, індукуватиметься змінна електрорушійна сила (ЕРС), яка змінюватиметься за гармонічним законом – із часом за законом синуса або косинуса.
Кут
Тому й магнітний потік
Відповідно ЕРС індукції
Згідно із законом Ома миттєве значення сили струму
Отже, сила струму пропорційна часу, але під тригонометричною функцією. Тому із часом сила струму так само, як ЕРС індукції, змінюватиметься за законом синуса (або косинуса за певних умов).
Відповідь: B.
ТЕМА: Електродинаміка. Магнітне поле і явище магнітної індукції.
Завдання скеровано на перевірку розуміння явища магнітної індукції.
Рух магніту крізь кільце викликає в ньому появу індукційного струму. Індукційний струм у кільці виникає такий, щоб утворене навколо нього магнітне поле протидіяло рухові магніту. Тобто якщо магніт наближається до кільця, то навколо кільця утвориться поле, що примушуватиме його віддалятись і навпаки.
Напрямок магнітного поля можна визначити за правилом правої руки (рис. 1):
якщо чотири зігнуті пальці правої руки спрямувати за напрямком струму в контурі, то відігнутий на
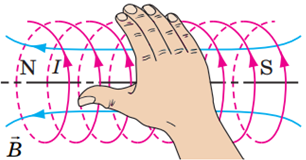
Рис. 1. Правило правої руки
Тоді для варіантів відповіді А – В північний полюс кільця буде розташований над ним, а південний – під ним. У варіанті Г навпаки – північний полюс котушки відштовхуватиме північний полюс магніту або притягувати його південний полюс. Ці дії спрямовані на те, щоби не дати північному полюсу магніту наблизитися або південному – віддалитися. Цю умову задовольняє лише варіант А.
Відповідь: A.
ТЕМА: Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку вміння визначати напрямок дії сили Лоренца на заряджену частинку в магнітному полі.
Силу Лоренца визначають за правилом лівої руки: якщо ліву руку розташувати так, щоби лінії магнітної індукції входили в долоню, а чотири витягнуті пальці вказували напрямок швидкості руху позитивно зарядженої частинки, то відігнутий на
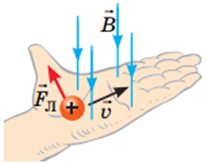
Рис. 1. Правило лівої руки
Якщо перевірити напрямок сили Лоренца на рисунку за правилом лівої руки, то великий палець вказуватиме праворуч, хоча на рисунку напрямок сили Лоренца вказаний ліворуч. Це свідчить про те, що частинка заряджена негативно.
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Закон електромагнітної індукції.
Завдання скеровано на перевірку розуміння закону електромагнітної індукції.
Силу індукційного струму
Закон залежності електрорушійної сили
Оскільки за умовою змінюється площа, обмежена контуром, маємо:
За умовою завдання провідник постійно перебуває в горизонтальній площині перпендикулярно до ліній індукції магнітного поля. Це означає, що лінії індукції магнітного поля паралельні з нормаллю до площини поверхні контуру, тобто кут
Розпишімо, чому дорівнює сила струму й опір, і підставимо всі вирази в першу формулу:
де
Визначмо зміну площі
Довжина кола
Якщо з провідника довжиною
Обчислімо шукану величину:
Відповідь: 62,5.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку вміння застосовувати теоретичні знання з електродинаміки для пояснення принципу дії відповідних технічних пристроїв.
На взаємодії магнітного поля постійних магнітів компаса з горизонтальним складником магнітного поля Землі заснований принцип дії цього приладу. Вільно обертова магнітна стрілка повертається навколо осі, розташовуючись уздовж силових ліній магнітного поля. Тож стрілка завжди вказує одним кінцем у напрямку ліній магнітної індукції, що йдуть до Південного магнітного (Північного географічного) полюса.
Посудину з високою стійкістю до впливів кислот, лугів і розчинників, у якій відбувається електроліз, називають електролітичною ванною (електролізером). Проходження електричного струму крізь розчин або розплав електроліту зумовлює хімічні реакції на поверхні поділу електрод ‒ розчин (розплав електроліту). Отже, хімічну дію електричного струму спостерігають під час проходження його крізь розчин електроліту в електролітичній ванні.
Електромагнітна індукція ‒ явище створення в просторі вихрового електричного поля змінним магнітним потоком. Один із наслідків електромагнітної індукції, практично важливий для генерації електричного струму, ‒ виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється. Саме генератори змінного струму (ГЗС) ‒ це джерела електричної енергії, які створюють електрорушійну силу (ЕРС), що періодично змінюється.
Робота всіх електричних нагрівачів ґрунтується на тепловій дії струму: у таких пристроях енергія електричного струму перетворюється на внутрішню енергію нагрівача. Під час проходження електричного струму спіраль лампи розжарювання сильно нагрівається завдяки тепловій дії струму.
Будь-який напівпровідниковий діод складений із двох контактних напівпровідникових ділянок із різними типами провідності ‒ електронною і дірковою; до кожної ділянки приєднано виводи. Основна властивість напівпровідникового діода ‒ пропускати електричний струм переважно в одному напрямку.
Відповідь: 1Б, 2Г, 3А, 4В.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Явище електромагнітної індукції.
Завдання скеровано на перевірку розуміння виникнення індукційного струму.
Розглянутий у завданні дослід є одним із сучасних варіантів дослідів Майкла Фарадея, завдяки яким він дійшов висновку: у замкненому провідному контурі (котушці) виникає електричний струм, якщо кількість ліній магнітної індукції, що пронизують поверхню, обмежену контуром, змінюється. Це явище було названо електромагнітною індукцією, а електричний струм, який під час цього виникає, ‒ індукційним (наведеним) струмом.
У цьому досліді, як зображено на схематичному рисунку, ліву котушку через вимикач приєднано до джерела струму, а праву котушку замкнено на гальванометр. Якщо розмикати чи замикати коло лівої котушки, то в правій котушці виникне індукційний струм.
Кількість ліній магнітної індукції, що пронизують певну поверхню, характеризують фізичною величиною – потоком магнітної індукції або магнітним потоком. Магнітний потік максимальний, якщо поверхня, яку пронизують лінії магнітної індукції, перпендикулярна до цих ліній.
Лінії магнітної індукції магнітного поля найщільніше розташовані біля полюсів котушки і проходять перпендикулярно до площини перерізу котушки (див. рисунок). Тобто найбільша кількість ліній магнітної індукції пройде крізь котушку з гальванометром, коли осі котушок збігатимуться, як це зображено на рисунку у варіанті відповіді Г.
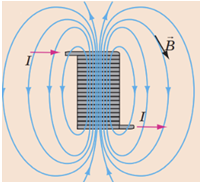
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Енергія магнітного поля.
Завдання скеровано на перевірку розуміння чинників, від яких залежить енергія магнітного поля.
Енергія магнітного поля
Енергія магнітного поля прямо пропорційна до квадрату сили струму:
Отже, якщо сила струму зросте втричі, то енергія магнітного поля збільшиться в
Відповідь: B.
Електродинаміка. Магнітне поле, електромагнітна індукція. Енергія магнітного поля.
Завдання скеровано на перевірку вміння розрахувати енергію магнітного поля.
Енергію
Відповідь: 0,375.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік. Закон електромагнітної індукції.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з визначення магнітного потоку й електрорушійної сили індукції.
1. Зміна потоку магнітної індукції (магнітного потоку)
За умовою вектор магнітної індукції перпендикулярний до площини рамки
Обчислімо зміну магнітного потоку:
Відповідь: 0,1.
2. За законом електромагнітної індукції електрорушійна сила індукції
(Знак «мінус» відображає правило Ленца для визначення напрямку індукційного струму.)
Обчислімо ЕРС індукції:
Відповідь:
Відповідь: 1. 0,1. 2. 0,05.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку розуміння і застосування механічних й електромагнітних явищ.
Виникнення вихрового електричного поля або електричної поляризації провідника під час зміни магнітного поля або під час руху провідника в магнітному полі називають електромагнітною індукцією. Важливим наслідком електромагнітної індукції для генерування електричного струму є виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється.
Період
Тому, вимірявши довжину нитки й період коливань маятника, можна визначити прискорення вільного падіння в певній місцевості.
У радіолокації використовують ультракороткі електромагнітні хвилі частотою від
Просвітлення оптики ‒ збільшення прозорості деталей оптичних систем (лінз, оптичних призм) нанесенням на їхні поверхні тонкого шару діелектрика (або кількох шарів) із показником заломлення, меншим, ніж у матеріалу оптичної деталі. Просвітлення оптики ‒ результат інтерференції світла, яке відбивається від передньої та задньої границь цього шару (просвітлювальної плівки). За належного добору речовини й товщини плівки для певного кута падіння відбиті світлові хвилі певної довжини можуть повністю погасити одна одну.
Відповідь: 1В, 2Б, 3Д, 4Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку знання формул, за якими визначають фізичні величини.
Електрорушійну силу індукції, що виникає в провіднику внаслідок зміни його власного магнітного поля, називають ектрорушійною силою (ЕРС) самоіндукції
ЕРС самоіндукції
Коефіцієнт пропорційності
Потік магнітної індукції (магнітний потік)
Силу, із якою магнітне поле діє на рухому заряджену частинку, називають силою Лоренца:
Сила Ампера
Відповідь: 1Г, 2А, 3Д, 4В.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку розуміння руху зарядженої частинки під дією магнітного поля.
Силу, з якою магнітне поле діє на рухому заряджену частинку, називають силою Лоренца
За умовою магнітне поле є однорідним. Частинка влітає в магнітне поле під деяким кутом
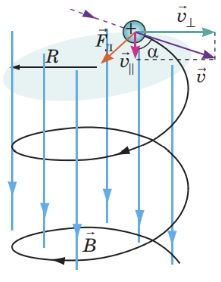
У цьому разі швидкість
Відповідь: B.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік. Закон електромагнітної індукції.
Завдання скеровано на перевірку знання і розуміння поняття індукційного струму, електрорушійної сили (ЕРС) індукції, магнітного потоку й уміння застосувати аналітичні зв'язки між цими поняттями.
Силу індукційного струму
За законом електромагнітної індукції визначімо електрорушійну силу (ЕРС) індукції
Знак мінус відображає правило Ленца: індукційний струм, який виникає в замкненому провідному контурі, має такий напрямок, що створений цим струмом магнітний потік перешкоджає зміні магнітного потоку, який спричинив появу індукційного струму.
Потік магнітної індукції (магнітний потік)
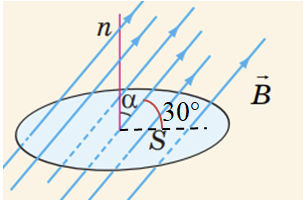
В умові кут між вектором магнітної індукції й горизонтом
За умовою завдання магнітне поле, у якому перебуває контур (горизонтальне кільце), змінюється, тому маємо:
Тоді силу індукційного струму
Відповідь: 0,6.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік.
Завдання скеровано на перевірку знання і розуміння фізичного змісту фізичних величин, які визначають магнітний потік.
Потік магнітної індукції (магнітний потік)
Одиниця магнітного потоку в SІ ‒ вебер (названо на честь В. Вебера (1804‒1891), німецького фізика):
Одиниця магнітної індукції в SІ ‒ тесла (названо на честь Ніколи Тесли (1856–1943), сербського фізика).
Отже,
Метр і ампер ‒ це основні одиниці SI. Виразімо ще ньютон через основні одиниці SI.
Ньютон ‒ одиниця сили в SІ:
Кілограм і секунда ‒ теж основні одиниці SI. Тож тепер остаточно запишімо одиницю магнітного потоку через основні одиниці SI:
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку знання одиниць фізичних величин із розділу «Магнітне поле, електромагнітна індукція».
Одиниця магнітної індукції
1 тесла − це магнітна індукція такого однорідного магнітного поля, яке діє з максимальною силою
Одиниця магнітного потоку
1 вебер − це максимальний магнітний потік, який створюється магнітним полем індукцією
Одиниця індуктивності
Індуктивність провідника дорівнює 1 генрі, якщо в ньому виникає ЕРС самоіндукції
Одиниця електрорушійної сили (ЕРС) індукції
Електрорушійна сила індукції (ЕРС індукції) дорівнює
Відповідь: 1Б, 2В, 3Д, 4Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рух зарядженої частинки в магнітному полі.
Сила Лоренца завжди перпендикулярна до швидкості руху частинки, тому вона не виконує роботу і не змінює кінетичну енергію частинки, бо під дією сили Лоренца заряджена частинка рухається рівномірно. Проте траєкторія руху частинки буде різною ‒ залежно від того, під яким кутом частинка влетіла в магнітне поле і чи є магнітне поле однорідним.
За умовою електрон влітає в однорідне магнітне поле зі швидкістю, паралельною до вектора магнітної індукції (див. рисунок).
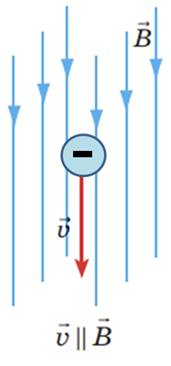
У цьому разі кут
Отже, магнітне поле не діє на електрон, тому, якщо немає інших сил, електрон рухатиметься рівномірно прямолінійно вздовж ліній магнітної індукції і траєкторією руху електрона буде пряма лінія.
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння руху зарядженої частинки в електромагнітному полі і вміння застосувати відповідні формули.
На частинку, яка має заряд
За умовою електрон рухається прямолінійно рівномірно. Це відбудеться у разі, коли сили, що діють на частинку, будуть скомпенсовані (
Зобразімо електрон і позначмо сили, що діють на нього.
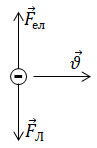
Тепер впевнімося, що електричне і магнітне поля дійсно взаємно перпендикулярні. Поля характеризує вектор напруженості
Якщо ми зобразили вектор сили Лоренца
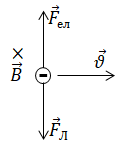
Сила
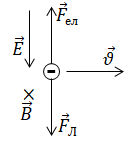
Отже, вектори полів дійсно взаємно перпендикулярні:
Повернімося до рівності сил:
Виразімо й обчислімо шукану величину ‒ швидкість руху електрона:
Відповідь: 1000.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Індуктивність.
Завдання скеровано на перевірку знання і розуміння фізичного змісту індуктивності.
Індуктивність
Одиниця індуктивності в SІ ‒ генрі:
Одиниця сили струму ампер (А) і одиниця часу секунда (с) є одиницями SI.
Розпишімо одиницю електрорушійної сили самоіндукції ‒ вольт (В) ‒ через одиниці SI:
Виразимо одиницю індуктивності через основні одиниці SI:
Відповідь: A.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку знання і розуміння фізичних величин, що характеризують магнітне поле.
1. За визначенням кількість ліній магнітної індукції, що пронизують виділену в магнітному полі рамку, характеризує фізична величина, яку називають потік магнітної індукції або магнітний потік − В.
2. Фізичну величину, яка характеризує магнітні властивості середовища і дорівнює відношенню магнітної індукції магнітного поля в середовищі до магнітної індукції магнітного поля у вакуумі, називають відносною магнітною проникністю середовища – Г.
3. Фізична величина, яка характеризує провідник і чисельно дорівнює ЕРС (електрорушійній силі) самоіндукції, що виникає в провіднику в разі зміни сили струму на
4. Моментом сили, яка діє на рамку площею
Відповідь: 1В, 2Г, 3А, 4Б.
ТЕМА: Електромагнетизм. Магнітне поле, електромагнітна індукція. Магнітний потік.
Завдання скеровано на перевірку знання і розуміння фізичного змісту магнітного потоку і фізичних величин, від яких він залежить.
Потік магнітної індукції (магнітний потік)
За умовою магнітне поле є однорідним і незмінним, тому його силова характеристика магнітна індукція також залишається незмінною під час повороту контуру навколо його сторони. І площа поверхні, обмежена контуром, також не змінюється під час повороту.
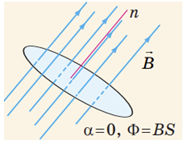
Магнітний потік буде максимальним, якщо поверхня перпендикулярна до ліній магнітної індукції:
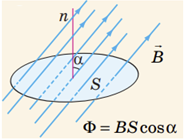
Нормаль
Отже, для того, щоб магнітний потік зменшився вдвоє, треба контур повернути навколо його сторони на кут
Відповідь: B.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Правило Ленца.
Завдання скеровано на перевірку розуміння індукційного струму, взаємодії створеного ним магнітного поля з магнітним полем, що викликало цей струм.
Модель із кільцями, використана в завданні, дуже схожа на пристрій, сконструйований Емілем Ленцем для демонстрації однойменного правила. Але в пристрої «Кільця Ленца» одне кільце розрізане.
Якщо наближати магніт до суцільного кільця, то в кільці виникне індукційний струм
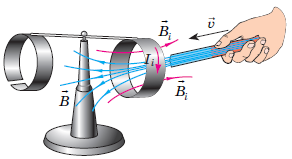
Якщо магніт віддаляти від суцільного кільця, то кільце притягуватиметься до магніту.
У розрізаному кільці індукційний струм не міг виникнути, бо кільце не замкнене. А в моделі, про яку йдеться в умові завдання, друге кільце суцільне. Але в ньому також не може виникнути індукційний струм. Адже до другого кільця магніт не наближають, із першим кільцем воно з’єднане дерев’яним стержнем, а дерево – це діелектрик.
Отже, унаслідок унесення в кільце штабового магніту (тобто наближення магніту) кільце рухатиметься за напрямком стрілки – відштовхуватиметься від магніту.
Відповідь: Б.
ТЕМА: Електродинаміка. Робота поля з переміщення заряду.
Завдання скеровано на перевірку знання і розуміння загального поняття роботи у фізиці, а також вміння визначати, від яких параметрів залежить робота різних полів.
Робота у фізиці – характеристика дії сили на тіло, що залежить від величини й напрямку цієї сили та переміщення точки її прикладання.
Запишімо загальну формулу роботи сили. Робота сили дорівнює добутку модуля сили
1. Вихрове електричне поле. Змінне магнітне поле завжди супроводжується появою вихрового електричного поля. Саме вихрове електричне поле діє на вільні заряджені частинки в провіднику й надає їм напрямленого руху, створюючи індукційний струм.
Робота вихрового електричного поля на замкненій траєкторії зазвичай не дорівнює нулю.
Робота вихрового електричного поля з переміщення одиничного позитивного заряду по замкнутому нерухомому провіднику чисельно дорівнює ЕРС індукції в цьому провіднику.
2. Електричне поле – форма матерії, яка існує навколо заряджених тіл і виявляється в дії з деякою силою на заряджене тіло, що перебуває в цьому полі.
Електричне поле є складником єдиного електромагнітного поля. Джерелами електричного поля можуть бути рухомі й нерухомі електричні заряди та змінні магнітні поля.
Електричне поле, створене лише нерухомими зарядами, є незмінним у часі (статичним). Таке поле називають електростатичним.
Нехай в однорідному електричному полі напруженістю
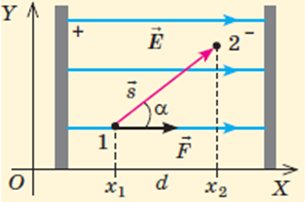
За означенням роботи:
Поле однорідне, тому сила
Отже, робота сил однорідного електростатичного поля в ході переміщення електричного заряду
Формула
3. Гравітаційне поле існує навколо будь-якого тіла і виявляється у взаємному притяганні тіл одне до одного. Визначити силу
Отже, сила, а значить, і робота гравітаційного поля залежатиме від маси частинки, не залежатиме від форми траєкторії, але від відстані (переміщення) залежатиме, тобто від положення початкової та кінцевої точок руху частинки (Г).
4. Магнітне поле – складник електромагнітного поля, основною властивістю якої є дія на рухомі заряджені частинки. Силова характеристика магнітного поля – вектор магнітної індукції

Тобто, ця сила напрямлена перпендикулярно до швидкості руху заряду й напрямку магнітного поля. А напрямок швидкості руху тіла збігається з напрямком його переміщення. Через це робота, що її виконує магнітне поле над частинкою, дорівнює нулю:
Відповідь: 1Д, 2Б, 3Г, 4А.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік. Закон електромагнітної індукції.
Завдання скеровано на перевірку знання і розуміння виникнення індукційного струму в рамці під дією магнітного поля, уміння чисельно його описати.
Під час обертання замкнутої рамки в магнітному полі у ній збуджується індукційне електричне поле, електрорушійна сила
Зміна магнітного потоку
де
За умовою
З іншого боку, сила індукційного струму
Звідси
Отже, зваживши ще й на закон Ома (
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рух зарядженої частинки в магнітному полі.
Сила Лоренца завжди перпендикулярна до швидкості руху частинки, тому вона не виконує роботу і не змінює кінетичну енергію частинки, бо під дією сили Лоренца заряджена частинка рухається рівномірно. Проте траєкторія руху частинки буде різною ‒ залежно від того, під яким кутом частинка влетіла в магнітне поле і чи є магнітне поле однорідним.
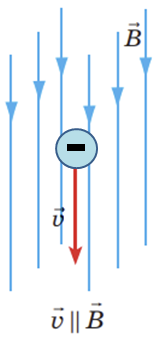
За умовою електрон влітає в однорідне магнітне поле зі швидкістю, паралельною до вектора магнітної індукції (див. рисунок).
У цьому разі кут
Отже, магнітне поле не діє на електрон, тому, якщо немає інших сил, електрон рухатиметься рівномірно прямолінійно вздовж ліній магнітної індукції і траєкторією руху електрона буде пряма лінія.
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння принципу будови коливального контуру, і вміння проаналізувати перетворення енергії в цьому контурі.
Після замикання ключа конденсатор заряджатиметься. У той момент, коли його заряд стане максимальним, струм на цій ділянці припиниться. Отже, коли ключ замкнуто, то електричний струм тече через котушку й резистор, а на конденсаторі буде тільки спад напруги (струм крізь нього не тече). На котушці не буде спаду напруги, а струм, що тече через котушку, дорівнюватиме струму, що тече через резистор. Обчислімо силу струму
Обчислімо спад напруги на конденсаторі до розмикання ключа:
Отже,
Після розмикання ключа конденсатор розряджатиметься на котушці й резисторі. Тобто виникнуть згасні (бо є резистор) електромагнітні коливання.
У початковий момент, після розмикання ключа, енергія коливань ‒ це накопичена енергія конденсатором і котушкою. Із закону збереження енергії очевидно, що вся енергія, яку має коливальний контур до розмикання ключа, перетвориться на тепло.
Визначмо кількість теплоти, яка виділяється на резисторі за час існування змінного струму в колі
Обчислімо шукану кількість теплоти:
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку знання одиниць фізичних величин із розділу «Магнітне поле, електромагнітна індукція».
1. Генрі (Гн) ‒ одиниця індуктивності
Індуктивність провідника дорівнює
Варіант відповіді ‒ Д.
2. Ват (Вт) ‒ одиниця потужності струму
Варіант відповіді ‒ А.
3. Тесла (Тл) ‒ одиниця магнітної індукції
Варіант відповіді ‒ Б.
4. Фарад (Ф) ‒ одиниця електроємності у Міжнародній системі одиниць SI, названа на честь англійського фізика і хіміка Майкла Фарадея (1791‒1867):
Варіант відповіді ‒ В.
Відповідь: 1Д, 2А, 3Б, 4В.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння сил електромагнітної природи.
Магнітне поле діє на провідник зі струмом із певною силою ‒ силою Ампера.
Оскільки електричний струм ‒ це напрямлений рух заряджених частинок, виникнення сили Ампера є результатом дії магнітного поля на окремі заряджені частинки, що рухаються в провіднику. Силу, з якою магнітне поле діє на одну рухому заряджену частинку, називають силою Лоренца. Тобто, на електрон, що влітає в магнітне поле, діятиме сила Лоренца.
Стала Фарадея ‒ фізична стала, заряд електронів кількістю речовини
Сила Кулона ‒ це сила взаємодії між нерухомими точковими зарядами.
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Енергія магнітного поля.
Завдання скеровано на перевірку знання і розуміння того, якими величинами визначається енергія магнітного поля.
Енергія магнітного поля
Магнітний потік
Звідси
Підставімо вираз для індуктивності у формулу енергії магнітного поля й обчислімо її:
Відповідь: 5.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера.
Завдання скеровано на перевірку знання і розуміння сили, що діє на провідник із струмом із боку магнітного поля – сили Ампера, уміння визначати її напрямок.
Сила Ампера − це сила, із якою магнітне поле діє на провідник зі струмом.
Напрямок сили Ампера визначають за правилом лівої руки (див. рисунок): якщо ліву руку розташувати так, щоб лінії магнітної індукції
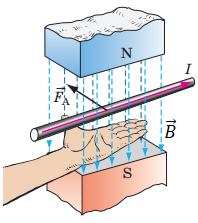
Розгляньмо кожний зображений варіант. Ліву руку орієнтуватимемо відносно сторінки з рисунком. Пригадаймо позначення:
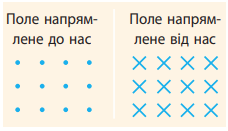
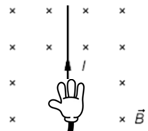
На рисунку 1 вектор магнітної індукції напрямлений перпендикулярно до площини рисунка від вас (позначено хрестиком). Отже, зорієнтуймо ліву руку долонею до себе (лінії магнітної індукції входять в долоню), чотири пальці напрямлені вертикально вгору за напрямком струму, тоді великий палець, відігнутий на
На рисунку 2 вектор магнітної індукції напрямлений вертикально вниз, отже долоню зорієнтуймо торцем (перпендикулярно) до площини рисунка, а чотири пальці руки спрямуймо праворуч за напрямком сили струму. Тоді великий палець, відігнутий на
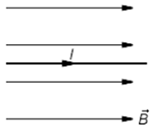
На рисунку 3 сила Ампера не діятиме, оскільки напрямок сили струму збігається з напрямком вектора магнітної індукції та неможливо зорієнтувати ліву руку відповідно до правила визначення сили Ампера. За формулою сила Ампера також дорівнює нулю. Оскільки кут
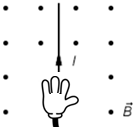
На рисунку 4 вектор магнітної індукції напрямлений перпендикулярно до площини рисунка до вас (позначено точками). Отже, зорієнтуймо ліву руку долонею від себе (лінії магнітної індукції входять в долоню), чотири пальці напрямлені вертикально вгору за напрямком струму, тоді великий палець, відігнутий на
Відповідь: 1А, 2В, 3Д, 4Б.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітне поле. Магнітна індукція.
Завдання скеровано на перевірку знання і розуміння магнітної індукції, уміння визначати полюси котушки за правилом правої руки.
Алюмінієвий дріт, намотаний на каркас, називають котушкою. Якщо цим дротом пропустити електричний струм, котушка стане штучним магнітом. Треба визначити полюси такого магніту, тоді зможемо визначити, як поводитимуться магніти, підвішені з ним поруч на нитках.
За напрямок струму в замкненому електричному колі прийнято напрямок, у якому частинки, що мають позитивний заряд, рухаються по колу, тобто напрямок від позитивного полюса джерела струму до негативного (див. рисунок).
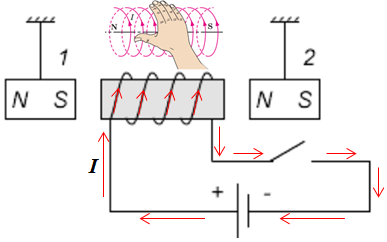
Котушка зі струмом має два полюси ‒ південний
якщо чотири зігнуті пальці правої руки спрямувати за напрямком струму
Отже, ліворуч у котушки північний полюс, а праворуч ‒ південний. Підвішені магніти зорієнтовані різнойменними полюсами до полюсів котушки, тому притягуватимуться і зліва, і справа до котушки.
Відповідь: A.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Закон електромагнітної індукції.
Завдання скеровано на перевірку знання і розуміння закону електромагнітної індукції.
Скористаймося законом електромагнітної індукції: електрорушійна сила індукції
Знак мінус відображає правило Ленца: індукційний струм, який виникає в замкненому провідному контурі, має такий напрямок, що створений цим струмом магнітний потік перешкоджає зміні магнітного потоку, який спричинив появу індукційного струму.
Відповідно до рисунка, за
Відповідь:
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку вміння застосовувати теоретичні знання з електродинаміки для пояснення принципу дії відповідних технічних пристроїв.
1. Лампа розжарювання є прикладом прояву теплової дії струму (Д): унаслідок проходження електричного струму спіраль лампи дуже сильно нагрівається. Узагалі робота всіх електричних нагрівачів ґрунтується на тепловій дії струму: у таких пристроях енергія електричного струму перетворюється на внутрішню енергію нагрівача.
2. В основі принципу дії генератора змінного струму лежить явище електромагнітної індукції (В). Це явище полягає в тому, що внаслідок зміни магнітного потоку, який пронизує провідник, у провіднику виникає електричний струм. У генераторі змінного струму обертається котушка (ротор) у магнітному полі. Завдяки цьому відбувається зміна магнітного потоку, що пронизує котушку, і, як наслідок, виникає змінна електрорушійна сила (ЕРС) і змінний струм. Виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється, ‒ це наслідок електромагнітної індукції, практично важливий для генерації електричного струму.
3. Посудину з високою стійкістю до впливів кислот, лугів і розчинників, у якій відбувається електроліз, називають електролітичною ванною (електролізером). Проходження електричного струму крізь розчин або розплав електроліту зумовлює хімічні реакції на поверхні поділу електрод ‒ розчин (розплав електроліту). Отже, хімічна дія струму (Г) проявляється під час його проходження крізь розчин електроліту, який міститься в електролітичній ванні.
4. Принцип дії компаса заснований на взаємодії магнітного поля постійних магнітів (А) компаса з горизонтальною складовою магнітного поля Землі. Обертова магнітна стрілка вільно повертається навколо осі, розташовуючись уздовж силових ліній магнітного поля. Тож стрілка завжди вказує одним кінцем у напрямку ліній магнітної індукції, що йдуть до Південного магнітного полюса (Північного географічного полюса).
Відповідь: 1Д, 2В, 3Г, 4А.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера. Електродвигун.
Завдання скеровано на перевірку знання і розуміння принципу дії електроприладів.
Силу, з якою магнітне поле діє на провідник зі струмом називають силою Ампера.
На плоский замкнений контур зі струмом, розташований в однорідному магнітному полі, сили Ампера створюють обертальний момент. Обертання рамки зі струмом у магнітному полі використовують в електричних двигунах ‒ пристроях, у яких електрична енергія перетворюється на механічну.
На рисунку зображено модель електричного двигуна.
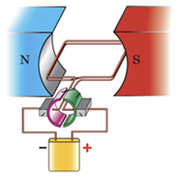
Реостат ‒ це пристрій зі змінним опором, призначений для регулювання сили струму в електричному колі. Змінюючи довжину провідника в реостаті, можна змінити його опір.

Лампа розжарювання ‒ це тип лампи, у якій світло випромінюється внаслідок нагрівання нитки розжарювання електричним струмом до високої температури.

Електрочайник ‒ це побутовий електричний прилад, призначений для швидкого нагрівання і кип’ятіння води за допомогою електричного нагрівального елемента (спіралі або диска), який розміщено всередині корпусу (теплова дія струму).

Відповідь: B.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рухому заряджену частинку.
Силу, з якою магнітне поле діє на рухому заряджену частинку, називають силою Лоренца.
Сила Лоренца завжди перпендикулярна до швидкості руху частинки, тому вона не виконує роботу і не змінює кінетичну енергію частинки, ‒ під дією сили Лоренца заряджена частинка рухається рівномірно. Проте траєкторія руху частинки буде різною ‒ залежно від того, під яким кутом частинка влетіла в магнітне поле і чи є магнітне поле однорідним.
За умовою протон влітає в магнітне поле перпендикулярно до ліній магнітної індукції. У цьому разі
Протон рухатиметься рівномірно по колу перпендикулярно до ліній магнітної індукції
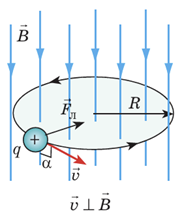
Відповідь: Б.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рухому заряджену частинку.
На рухому заряджену частинку в магнітному полі діє сила Лоренца
За умовою частинка рухається перпендикулярно до ліній магнітної індукції.

У цьому разі
За другим законом Ньютона:
Ми виразили з рівняння швидкість, тому що кінетична енергія
За умовою після проходження частинки крізь фольгу радіус треку зменшився вдвічі, тож формула для швидкості матиме вигляд:
Тоді можемо визначити, яку частину кінетичної енергії втратила частинка під час проходження крізь фольгу:
тобто частинка втратила три чверті кінетичної енергії.
Відповідь: 0,75.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Явище електромагнітної індукції (генератор змінного струму).
Завдання скеровано на перевірку знання і розуміння будови й принципу дії генератора змінного струму.
Генератор змінного струму ‒ це пристрій, який перетворює механічну енергію в електричну на основі явища електромагнітної індукції.
Електромагнітна індукція ‒ явище створення в просторі вихрового електричного поля змінним магнітним потоком (за допомогою руху (обертання) котушки (ротора) в магнітному полі нерухомого електромагніту (статора)). Одним із наслідків електромагнітної індукції є виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється. Саме вихрове електричне поле діє на вільні заряджені частинки в провіднику та надає їм напрямленого руху, створюючи індукційний струм. Тому є ще одне означення генератора змінного струму ‒ це джерело електричної енергії, яке створює електрорушійну силу (ЕРС), що періодично змінюється.
Відповідь: A.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Явище самоіндукції. Індуктивність.
Завдання скеровано на перевірку знання і розуміння закону самоіндукції.
Відразу після розімкнення кола сила струму
Явище виникнення вихрового електричного поля в провіднику, у якому тече змінний електричний струм, називають явищем самоіндукції.
Скористаймося законом самоіндукції: електрорушійна сила самоіндукції
Визначімо час існування струму в котушці після розмикання кола:
Відповідь: 0,01.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння сили Лоренца, уміння застосувати правило визначення напрямку її дії в конкретній ситуації.
Електронний пучок ‒ це потік електронів, що рухаються за близькими траєкторіями в одному напрямку, має розміри, значно більші в напрямку руху, ніж у поперечній площині.
Коли над центром екрана осцилографа розмістили магніт, то на електрони подіяло магнітне поле. А магнітне поле діє на рухомі заряджені частинки із силою Лоренца, напрямок дії якої визначається за правилом лівої руки: лінії магнітної індукції
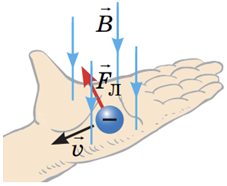
Якщо ми дивимося на екран осцилографа, то пучок електронів напрямлений до нас, тобто чотири витягнуті пальці направляємо протилежно до напрямку руху електронів ‒ перпендикулярно до екрану від нас).
За умовою завдання магніт піднесли зверху екрана північним полюсом донизу, отже, лінії магнітної індукції магнітного поля будуть напрямлені вертикально вниз, входити в долоню.
Тоді відігнутий на
Відповідь: A.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Досліди Фарадея. Явище електромагнітної індукції.
Завдання скеровано на перевірку знання і розуміння дослідів Фарадея, причин виникнення індукційного струму й уміння застосувати ці знання до конкретної практичної ситуації.
Судячи з рисунка, струм пропускають по котушці, що міститься ліворуч на феромагнітному осерді. На кінцях котушки є клеми, за допомогою яких котушку можна приєднати до джерела струму, реостата, вимикача тощо. Котушка зі струмом є штучним електромагнітом, навколо якого існує магнітне поле.
Котушка праворуч, яка замкнена на амперметр, є нерухомим провідним контуром, розташованим у магнітному полі електромагніту (котушки ліворуч).
За означенням явища електромагнітної індукції індукційний (наведений) електричний струм буде виникати в котушці праворуч у разі зміни сили струму в котушці ліворуч. Змінити силу струму в котушці можна, наприклад, замикаючи і розмикаючи електричне коло котушки ліворуч, або, наприклад, рухаючи повзунок реостата, якщо приєднати його послідовно з котушкою (відповідно до осучаснених дослідів Фарадея). Що швидше змінюватиметься значення сили струму, то сильніше мінятиметься магнітне поле котушки ліворуч.
Але в цьому разі сили, що діють з боку змінного магнітного поля, не можуть зробити хаотичний рух заряджених частинок всередині котушки праворуч напрямленим. Чому ж у цій котушці виникає індукційний струм? Річ у тім, що змінне магнітне поле завжди супроводжує поява в навколишньому просторі вихрового електричного поля (силові лінії такого поля є замкненими). Саме електричне поле, а не магнітне, діє на вільні заряджені частинки в котушці праворуч та надає їм напрямленого руху, створюючи в такий спосіб індукційний струм.
Тепер проаналізуймо графік з умови. Є ділянки графіка, де струм має стале значення. Це інтервали часу від
За проміжок часу від
Відповідь: A.