Розділ: Коливання та хвилі. Оптика
Тема: Механічні коливання та хвилі
Кількість завдань: 95
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.
Завдання скеровано на перевірку знання і розуміння залежності періоду коливань нитяного маятника від його параметрів, і вміння визначати їх.
Запишімо формулу для обчислення періоду
З умови нам відомий період коливань іншого маятника –
Його довжина
Поділімо ліві і праві частини цих рівностей:
Отже, довжина шуканого маятника
Відповідь: Б.
ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння процесу коливань тіла на пружині й характеру зміни фізичних величин, які описують ці коливання.
Розгляньмо ту частину періоду незатухаючих горизонтальних коливань тіла (наприклад, візка) на пружині, коли пружина починає стискатися.
У момент, коли візок доходить до положення рівноваги, сила пружності й прискорення дорівнюють нулю, а швидкість руху візка сягає максимального значення.
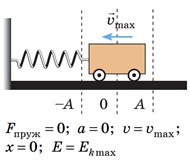
Потенціальна енергія пружини дорівнює нулю:
Кінетична енергія візка максимальна й дорівнює повній енергії системи:
Досягнувши положення рівноваги, візок не зупиняється, а внаслідок інертності продовжує рух ліворуч. Пружина починає стискатися, і щораз більша сила пружності гальмує рух візка. Видовження
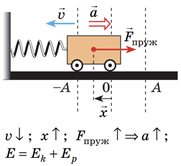
Кінетична енергія візка зменшується:
Потенціальна енергія пружини зростає:
Повна енергія системи дорівнює сумі кінетичної і потенціальної енергій.
Отже, з усіх наведених у варіантах відповіді фізичних величин меншатиме кінетична енергія тіла ‒ варіант відповіді А.
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку вміння застосовувати рівняння гармонічних коливань і знання відповідних фізичних величин.
Коливання, під час яких координата
За умовою амплітуда коливань
Отже, із чотирьох рівнянь у варіантах відповіді умову задовольняють лише ті два, у яких множник біля функції синуса дорівнює
За умовою період коливань тіла
Тобто циклічна частота
Циклічна частота в рівнянні, записаному в загальному вигляді, є множником біля часу
Отже, усім параметрам відповідає рівняння
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку розуміння гармонічних коливань і знання базового поняття механічного руху ‒ переміщення.
Запишімо рівняння гармонічних коливань у загальному вигляді:
Модуль переміщення
На початку відліку часу, коли
Через
Відповідь: 8.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Довжина хвилі.
Завдання скеровано на перевірку знання і розуміння поняття довжини хвилі й уміння визначати її за графіком.
Довжина хвилі
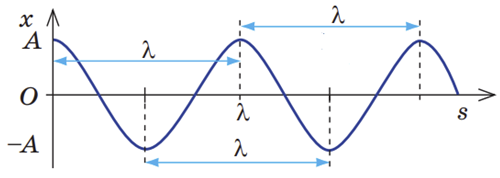
Розгляньмо рисунок в умові завдання. Виберімо точки, що рухаються синхронно.
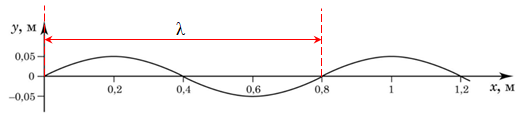
Отже, довжина хвилі, як видно з графіка, дорівнює
Відповідь: B.
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на пошук частоти коливань.
Дано:
Знайти:
Частоту коливання тіла можна обчислити за формулою
Переведімо частоту в герци, для цього пригадаймо, що:
Тобто
Відповідь: 4.
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань. Довжина хвилі.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на зв’язок різних параметрів коливальної системи.
Дано:
1. Знайти:
Період коливань поверхні води збігається з періодом хвилі. Період хвилі – це час, за який хвиля проходить відстань, що дорівнює одній її довжині. Період хвилі можна обчислити за формулою
Кількість довжин хвиль можна визначити, порахувавши кількість гребнів хвиль, що вдаряються об берег, тобто сплесків. За умовою
2. Знайти:
Відстань між двома сусідніми гребнями хвиль – це довжина хвилі. Вона пов’язана з періодом за формулою:
Швидкість хвилі можна обчислити за формулою
Тобто
Відповідь: 1. 0,5. 2. 2,5.
ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку вміння пов’язувати поняття з теми «Механічні коливання і хвилі» та їхні приклади в реальному житті.
Вільні гармонічні коливання – це коливання, які відбуваються під дією внутрішніх сил системи після того, як її було виведено з положення рівноваги, а координата
Так можна описати рух пружинного маятника.
Вимушені коливання – це коливання, які відбуваються в системі внаслідок дії зовнішньої сили, що періодично змінюється.
Шари повітря поруч із гучномовцем постійно зазнають впливу від мембрани, що їх штовхає, тобто вони коливаються під дією зовнішньої сили.
Затухаючі (згасні) коливання – це коливання, амплітуда яких із часом зменшується.
Прикладом такого руху є рух тонкої гілки дерева, з якої злетів птах.
Автоколивання – незатухаючі (незгасні) коливання, які відбуваються в системі за рахунок надходження енергії від постійного джерела, що регулює сама система. Тобто в самій системі є механізм, який дає їй змогу перерозподіляти енергію під час коливань.
У маятниковому годиннику є храпове колесо (3 на рис. 1), що має зазублини. У процесі коливання маятник (1 на рис. 1) відхиляється і чіпляється то за ту, то за ту зазублину двостороннім кріпленням у верхній його частині (4 на рис. 1). Як наслідок, коли кріплення чіпляється за зазублину, маятник отримує додатковий поштовх.
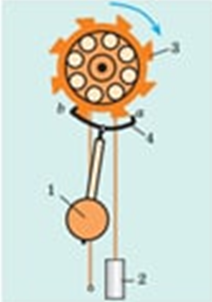
Рис. 1. Схема роботи маятникового годинника
Відповідь: 1Д, 2В, 3Г, 4Б.
ТЕМА: Механічні коливання і хвилі.
Завдання скеровано на перевірку розуміння закономірностей зміни енергії під час коливального руху.
Якщо маятник настінного годинника має частоту коливань 2 Гц, то він виконує 2 коливання за секунду. Тоді за хвилину він робить 120 коливань.
Потенціальну енергію маятника можна визначити за формулою
На найбільшій висоті маятник перебуває в крайніх точках своєї траєкторії (рис. 1).
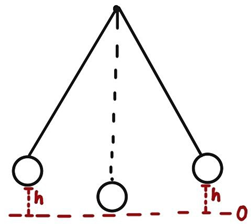
Рис. 1. Крайні положення коливання маятника
Тож за одне коливання маятник двічі опиняється в точках, де його потенціальна енергія максимальна. Тоді за 120 коливань його потенціальна енергія буде максимальною 240 разів.
Відповідь: Г.
ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.
Завдання скеровано на перевірку розуміння основних фізичних величин, пов’язаних із механічними коливаннями.
Амплітуда коливань – це максимальне відхилення від положення рівноваги.
Якщо коливання гармонічні, і на рисунку 1 зображено крайнє ліве положення, на рисунку 2 – крайнє праве, то посередині між ними положення рівноваги. Амплітуда – це і є відстань від положення рівноваги до будь-якого крайнього положення. Тож відстань між двома крайніми положеннями відповідає двом амплітудам.
На рисунку 1 лівий край візка стоїть на відмітці
Відповідь: 15.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага. Рівномірний рух по колу.
Завдання скеровано на перевірку вміння розв’язувати комплексні задачі про рівномірний рух по колу.
Дано:
Знайти:
Гойдалка рухається за траєкторією, що є частиною кола. Тож вона матиме доцентрове прискорення, напрямлене в бік кріплення підвісу гойдалки. У найнижчій точці це прискорення буде напрямлене вертикально вгору. Вага тіл, що рухаються із прискоренням, що напрямлене вертикально вгору, може бути розрахована за формулою:
Доцентрове прискорення можна обчислити з виразу
Тоді
Відповідь: 5
ТЕМА: Механічні коливання і хвилі. Звукові хвилі. Ехолокація.
Завдання скеровано на оцінку розуміння принципів ехолокації і вміння розв’язувати відповідні розрахункові задачі.
Дано:
1. Знайти:
Звук – це механічна хвиля, що має частоту
2. Знайти:
Нехай кажан отримає зворотний сигнал на відстані
Кажан пройде відстань, що дорівнює різниці початкової і кінцевої відстані до перепони:

Кажан і звукова хвиля долають відповідні відстані за однаковий час, тому:
Відповідь: 1. 0,5. 2. 151.
ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.
Завдання скеровано на перевірку розуміння фізичних величин, пов’язаних із механічними коливаннями.
1. Потенціальна енергія тіла, що здійснює коливання на пружині (зокрема горизонтальні), залежить від жорсткості пружини і її абсолютного видовження:
2. Період коливань математичного маятника залежить лише від його довжини й прискорення вільного падіння:
3. Кінетична енергія тіла (зокрема того, що коливається), залежить від його швидкості й маси:
4. Період коливання тіла, що здійснює коливання на пружин, і залежить від жорсткості пружини й маси тіла:
Відповідь: 1А, 2Д, 3Г, 4Б.
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.
Завдання скеровано на перевірку розуміння базових понять, що стосуються механічних коливань.
А Швидкість світла в повітрі близька до швидкості світла у вакуумі
Б Вимушені коливання – це коливання, які відбуваються в системі внаслідок дії зовнішньої сили, що періодично змінюється. Між двома торканнями на струни не діє жодна зовнішня сила, тому в цьому разі коливання є вільними.
В Звук – це поздовжня механічна хвиля. Механічні хвилі можуть поширюватися лише в середовищі. У відкритому космосі немає атмосфери, у якій би міг поширюватися звук, тому єдиний спосіб комунікації – це електромагнітні хвилі, які можуть поширюватись у вакуумі. Радіохвилі – це електромагнітні хвилі із частотою меншою, ніж
Г Збіг власної частоти коливання крил і частоти коливання повітряних потоків приведе до резонансу. Резонанс – це явище різкого збільшення амплітуди, яке виникає, якщо частота зовнішньої сили, що періодично змінюється, збігається із власною частотою коливань системи. Кріплення крил літака можуть не витримати різкого збільшення амплітуди коливань і зруйнуватися.
Тож твердження Г – правильне.
Відповідь: Г.
ТЕМА: Механічні коливання і хвилі. Нитяний маятник, період коливання нитяного маятника.
Завдання скеровано на оцінювання вміння розв’язувати задачі на залежність періоду власних коливань системи від її параметрів.
Знайти:
Математичний маятник – це фізична модель коливальної системи, яка складається з матеріальної точки, підвішеної на невагомій і нерозтяжній нитці, і гравітаційного поля.
Характеристики коливань математичного маятника залежать від його довжини. Зокрема, можна визначити період коливань математичного маятника:
Період коливань – це час, за який коливання повністю повторюється.
За графіком коливань математичного маятника можна визначити період, вимірявши відстань між двома точками з однаковим положенням. Найпростіше визначити період між двома максимумами або мінімумами графіка. У цій задачі період коливань
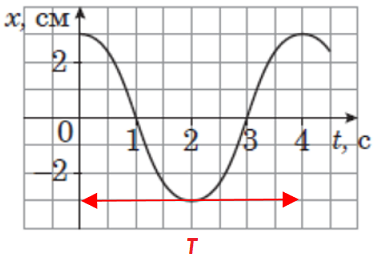
Рис. 1. Визначення періоду коливань
За допомогою періоду коливань можна виразити довжину маятника:
Оскільки за умовою
Відповідь: 4.
ТЕМА: Механічні коливання і хвилі. Частота й період коливань.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження параметрів коливань частинок хвилі.
Паперовий кораблик на гребені хвилі коливається так само, як і частинки води у хвилі.
Під час коливань за один період тіло повертається в початкове положення. Якщо вважати, що в початковий момент часу кораблик був у точці максимального відхилення рівноваги, то за чверть періоду він опиниться на рівні спокійної води, а за наступну чверть – у точці максимального відхилення від положення рівноваги з іншого боку від рівня рівноваги, тобто в найнижчому положенні.
Якщо частота коливань
Тоді, оскільки кораблик опиниться в найнижчій точці за половину періоду, можна обчислити цей час:
Відповідь: A.
ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на оцінювання вміння аналізувати рівняння і графік гармонічних коливань, визначати основні фізичні величини, пов’язані з ними.
На рисунку зображено графік гармонічних коливань величини електрорушійної сили (ЕРС) залежно від часу.
Загальний вигляд рівняння гармонічних коливань такий:
Обидва варіанти цього рівняння можуть описувати будь-які гармонічні коливання, і єдине, що зміниться внаслідок переходу від рівняння із функцією синус до рівняння з функцією косинус, – це початкова фаза коливань.
Початкова фаза коливань – фаза коливань у момент початку відліку часу.
На рисунку до завдання в точці
Амплітуда коливань – це максимальне відхилення від положення рівноваги. Його можна визначити за рисунком – це відстань від осі
Циклічну частоту
Період коливань – це час, за який коливання повністю повторюється.
Можна визначити період коливань за рисунком. Це відстань між двома максимумами синусоїди:
Далі потрібно підставити всі визначені величини в рівняння гармонічних коливань:
Відповідь: Б.
ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з виявлення зв’язку між періодом коливання і параметрами коливальної системи.
Період коливання
Якщо вдвоє скласти гумову нитку, яка виконує функцію пружини, то утвориться маятник, що коливається на двох удвічі менших пружинах, з’єднаних паралельно. Тоді до складання велику пружину (гумову нитку) можемо вважати двома половинками, що з’єднані послідовно.
Якщо є дві пружини із жорсткістю
Для паралельного з’єднання пружин їхня жорсткість
Для послідовного з’єднання жорсткість
Половинки пружини мають однакову жорсткість і
Оскільки
Якщо з’єднати ці дві половинки паралельно, то отримана пружина матиме жорсткість
Тоді період такої пружини дорівнюватиме
Порівняння його з періодом коливання
Відповідь: Б.
ТЕМА: Сила пружності. Механічні коливання. Коливання вантажу на пружині.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на виявлення зв’язку між періодом коливання і параметрами коливальної системи.
Дано:
Знайти:
Період коливань пружинного маятника визначають за формулою
За умовою
Нехай ціла пружина мала коефіцієнт жорсткості
Закон Гука описують формулами
а
Тоді, підставивши (7) і (8) у (6) і прирівнявши вирази для сили пружності з виразів (6) і (5), можна дістати
Під час розрізання пружини на дві коротші площа перерізу й модуль Юнга не змінюються, тому:
Відповідь: 2.
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі про зв’язок частоти й амплітуди коливань із параметрами системи.
1. Дано:
1. Знайти:
Тому 300 Гц – це 300 коливань за секунду.
2. Знайти:
За бджолою спостерігають протягом часу
За цей час вона зробить
За той самий час бджола пролетить відстань
Тоді
Відповідь: 1. 300. 2. 0,75.
ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на оцінювання вміння аналізувати рівняння і графік гармонічних коливань і визначати основні фізичні величини, пов’язані з ними.
Загальний вигляд рівняння гармонічних коливань
Обома варіантами цього рівняння можна описати будь-які гармонічні коливання, і єдине, що зміниться внаслідок переходу від рівняння, що використовує
Початкова фаза коливань – фаза коливань у момент початку відліку часу.
На рисунку до завдання в точці
Амплітуда коливань – це максимальне відхилення від положення рівноваги. Його можна визначити за рисунком – це відстань від осі
Циклічну частоту
Період коливань також можна визначити за рисунком як відстань між двома максимумами синусоїди –
Затим потрібно підставити всі визначені величини в рівняння гармонічних коливань:
Відповідь: Г.
ТЕМА: Механічні коливання і хвилі. Коливання вантажу на пружині. Перетворення енергії за гармонічних коливань.
Завдання скеровано на оцінювання вміння розв’язувати комплексні задачі, що передбачає оброблення й аналізування результатів експерименту, зображених на рисунку, і використання законів збереження енергії в коливальному процесі.
За рисунком 1 можна визначити довжину гумки в двох крайніх положеннях коливання тягарця. У крайніх положеннях тягарець змінює напрямок руху на протилежний, тож його швидкість
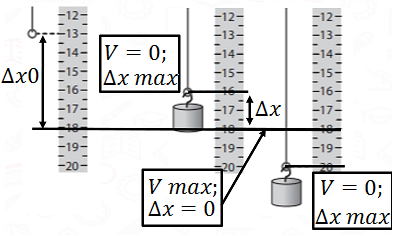
Рис. 1. Крайні положення тягарця
Також можна обчислити амплітуду коливань:
Оскільки амплітуда – це відхилення від положення рівноваги, то можна обчислити саме його. Це положення, у якому опиниться гумка під вагою тягарця, коли коливання повністю стихнуть:
Під час коливань у положенні рівноваги швидкість найбільша, отже саме цю швидкість потрібно визначити.
Під час коливань зберігається повна механічна енергія системи
Кінетичну енергію визначають за формулою
Оскільки для гумової стрічки виконуваний закон Гука, то можна обчислити потенціальну енергію за формулою, що описує потенціальну енергію розтягнутої пружини:
Хоча повна механічна енергія системи зберігається, але значення кінетичної та потенціальної енергії постійно змінюється під час коливань.
У крайніх положеннях швидкість тягарця дорівнює нулю, тож і його кінетична енергія також дорівнює нулю. А відхилення від положення рівноваги в цій ситуації найбільше, а отже й потенціальна енергія також максимальна.
У положенні рівноваги все навпаки. Швидкість тягарця максимальна, а відхилення дорівнює нулю, тож кінетична енергія приймає найбільше значення, а потенціальна стає рівною нулю.
Зважаючи на закон збереження енергії й спостереження, описані вище, можна записати рівність:
Тоді максимальна швидкість
Відношення
Тоді
Відповідь: 28.
ТЕМА: Коливання і хвилі. Поперечні й поздовжні хвилі. Довжина хвилі.
Завдання скеровано на оцінювання вміння розв'язувати задачі на аналіз графічного зображення хвиль.
Довжина хвилі
Потрібно вибрати дві точки, для яких легко визначити синхронність їхнього руху, наприклад, максимуми хвилі, й обчислити відстань на ними (рис. 1).
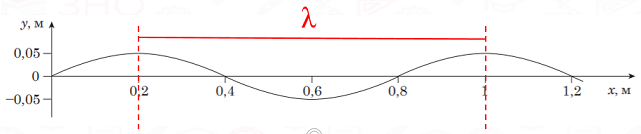
Рис. 1. Визначення довжини хвилі
Тоді
Відповідь: 0,8.
ТЕМА: Коливання і хвилі.
Завдання скеровано на оцінювання знання формул для обчислення циклічної частоти коливань різної природи.
За результатами аналізування ситуацій, описаних у завданні, можна дійти таких висновків:
А Вираз містить коефіцієнт жорсткості й масу, що є характеристиками пружинного маятника.
Б Вираз містить прискорення вільного падіння і довжину, які характеризують математичний маятник.
В Вираз містить індуктивність й електроємність, які характеризують коливальний контур.
Г Вираз описує загальний зв’язок частоти й циклічної частоти коливань.
Відповідь: B.
ТЕМА: Механічні коливання і хвилі. Частота гармонічних коливань.
Завдання скеровано на оцінювання розуміння зв’язку між частотою коливань і їхньою кількістю.
Частота коливань – це фізична величина, що дорівнює кількості коливань за одиницю часу.
За частотою
Оскільки 1 Гц дорівнює 1 коливанню за секунду,
Відповідь: Г.
ТЕМА: Механічні коливання і хвилі. Частота й період коливань. Вимушені коливання і явище резонансу.
Завдання скеровано на оцінювання розуміння понять вимушених коливань і резонансу й уміння розв’язувати пов’язані з ними розрахункові задачі.
Дано:
Знайти:
Гойдалка розгойдуватиметься сильніше, якщо частота її власних коливань збігатиметься із частотою прикладання зовнішньої сили (підштовхування), тобто під час резонансу.
Оскільки між періодом і частотою існує зв’язок, який відображає формула
Період власних коливань гойдалки можна обчислити за виразом
А отже й інтервал між підштовхуваннями дорівнює
Відповідь: 2,5.
ТЕМА: Механічні коливання і хвилі. Нитяний маятник, період коливання нитяного маятника. Пружне зіткнення.
Завдання скеровано на оцінювання розуміння поняття періоду коливань і природи пружних зіткнень.
Кулька, яку відвели на невеликий кут, перебуває на найбільшій відстані від положення рівноваги. Після того, як її відпустили, за 0,6 с вона зустрілася з другою кулькою, що була нерухомою. Тобто за 0,6 с перша кулька подолала відстань від найбільшого відхилення до положення рівноваги, тобто амплітуду. За один період тіло долає 4 амплітуди, тому період коливання цієї кульки 2,4 с.
За законом збереження імпульсу, після удару нерухому кульку також виводять із положення рівноваги, тож вона також почне коливатись. Кульку на довгій нитці, що відхиляється на невеликий кут від положення рівноваги, можна вважати математичним маятником. Період коливань математичного маятника визначають за формулою
Оскільки нитки обох маятників однакової довжини, то й період їхніх коливань буде однаковим.
Унаслідок пружного удару кульки почнуть рухатись у протилежні боки. Тоді вони одночасно почнуть рух із положення рівноваги, отже наступного разу зустрінуться, коли знову повернуться туди. Кожна з кульок пройде одну амплітуду до точки з найбільшим відхиленням, а потім ще одну – до точки рівноваги. Дві амплітуди кульки проходять за 1,2 с.
Відповідь: B.
ТЕМА: Механічні коливання і хвилі. Частота й період коливань.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на визначення параметрів коливань частинок хвилі.
Паперовий кораблик на гребені хвилі коливається так само, як і частинки води у хвилі.
Під час коливань за один період тіло повертається в початкове положення. Нехай у початковий момент часу кораблик перебуває в точці максимального відхилення рівноваги. Тоді за чверть періоду кораблик опиниться на рівні спокійної води. А за наступну чверть періоду – у точці максимального відхилення від положення рівноваги з іншого боку від рівня рівноваги, тобто в найнижчому положенні.
Якщо частота коливань
Тоді, оскільки кораблик опиниться в найнижчій точці за половину періоду, можна обчислити цей час:
Відповідь: 0,25.
ТЕМА: Механіка. Механічні коливання. Закони збереження в механиці. Коливання вантажу на пружині. Математичний маятник. Прості механізми.
Завдання скеровано на перевірку вміння застосовувати основні поняття i закони механіки, формули для визначення фізичних величин, математичні вирази законів.
1. Малі коливання на нитці можна вважати коливаннями математичного маятника. Отже, 1 – A.
2. Закручування гайки гайковим ключем – це важіль. Отже, 2 – Б.
3. Дві кульки пружно зіткнулися і їхній рух після взаємодії визначено законом збереження імпульсу. Отже, 3 – Г.
4. Період коливання тіла на пружині визначають за формулою В.
Відповідь: 1A, 2Б, 3Г, 4В.
ТЕМА: Механічні коливання і хвилі. Поперечні і поздовжні хвилі.
Завдання скеровано на перевірку вміння розпізнавати напрямки векторів швидкості і прискорення під час поширення поперечних хвиль.
Хвиля поширюється вправо. Якщо дорисувати нову хвилю так, як вона виглядатиме через малий проміжок часу, то стане очевидним, що тільки точка Б рухається вгору й розганяється.
Тому вектори швидкості і прискорення направлені вгору.
Відповідь: Б.
ТЕМА: Механічні коливання та хвилі. Частота й період коливань. Вимушені коливання та явище резонансу.
Завдання скеровано на перевірку розуміння поняття резонансу.
Резонанс – це явище різкого збільшення амплітуди, яке виникає, якщо частота зовнішньої сили, що періодично змінюється, збігається з власною частотою коливань системи.
Відповідь: A.
ТЕМА: Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку розуміння зв’язку між частотою хвилі, її довжиною та швидкістю поширення.
Частота хвилі, її довжина та швидкість поширення пов’язані формулою
Частота не змінюється під час переходу з одного середовища в інше.
За умовою завдання відомо, що швидкість поширення хвилі під час переходу збільшилася. Якщо частота не змінюється, то лише зміна довжини хвилі може привести до зміни швидкості поширення. Якщо швидкість збільшилася, то й довжина хвилі також збільшилася.
Відповідь: B.
ТЕМА: Механічні коливання і хвилі. Звукові хвилі. Ехолокація.
Завдання скеровано на оцінювання розуміння принципів ехолокації і вміння розв’язувати відповідні розрахункові задачі.
Ехолоти посилають короткі ультразвукові імпульси в напрямку, у якому проводять дослідження. Ультразвукова хвиля відбивається від морського дна й повертається до ехолота. Ехолот фіксує час, за який хвиля повернулась, а отже подолала дві відстані – від ехолота до об’єкта й від об’єкта знову до ехолота.
Тому відстань до об’єкта можна розрахувати за формулою
Відповідь: Г.
ТЕМА: Коливання і хвилі. Поперечні та поздовжні хвилі. Довжина хвилі.
Завдання скеровано на перевірку вміння аналізувати графічні зображення хвиль.
1. Знайти:
Довжина хвилі
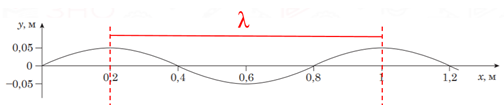
Рис. 1. Визначення довжини хвилі
Тоді
2. Знайти:
Період коливань поплавка збігається з періодом коливань частинок води у хвилі. Період коливання частинок і період хвилі також збігаються для будь-якої хвилі.
За один період гребінь хвилі переміститься на одну довжину хвилі, тож
Тоді період можна визначити за формулою
Відповідь: 1. 0,8. 2. 1,6.
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.
Завдання скеровано на перевірку розуміння основних величин, пов’язаних із коливаннями математичного маятника.
Тіло на довгій нитці можна вважати математичним маятником (рис. 1).
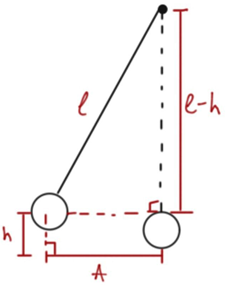
Рис. 1. Математичний маятник у положеннi максимального відхилення
1. Період коливань математичного маятника
2, 3. Енергію коливань можна визначити за формулою
У точці з найбільшим відхиленням потенціальна енергія тіла на підвісі максимальна, а кінетична енергія дорівнює
Максимальну висоту
За теоремою Піфагора
Якщо коливання малі, то й висота підйому
Тобто максимальна висота тягарця над нижньою точкою траєкторії залежить від
Енергія коливань
Тож енергія коливань пропорційна до
4. У найнижчій точці траєкторії потенціальна енергія тягарця дорівнює нулю, а його кінетична енергія, а отже й модуль швидкості, максимальні:
Тобто максимальна швидкість пропорційна до
Відповідь: 1В, 2А, 3Д, 4Г.
ТЕМА: Механічні коливання і хвилі. Звукові хвилі.
Завдання скеровано на перевірку розуміння поняття звукової хвилі.
Звукові хвилі – це поздовжні механічні хвилі. Вони можуть поширюватися в будь-якому пружному середовищі (у газах, рідинах і твердих тілах).
Відповідь: B.
ТЕМА: Механічні коливання і хвилі. Нитяний маятник, період коливання нитяного маятника.
Завдання скеровано на перевірку вміння розв’язувати задачі про залежність періоду власних коливань системи від її параметрів.
Математичний маятник – це фізична модель коливальної системи з матеріальної точки, підвішеної на невагомій і нерозтяжній нитці, і гравітаційного поля.
Характеристики коливань математичного маятника напряму залежать від його довжини. Зокрема, можна визначити період коливань математичного маятника
Нехай довжина маятника до укорочення дорівнювала
Після укорочення період
Частоту коливань маятника можна визначити за формулою
За умовою відомо, що до укорочення нитки частота коливань маятника
Тож період коливань після укорочення
А частота цих коливань
Тобто вкорочений маятник виконує 200 коливань за той самий інтервал часу.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).
Завдання скеровано на перевірку вміння розв’язувати задачі про поширення механічних хвиль.
На рисунку позначмо період.
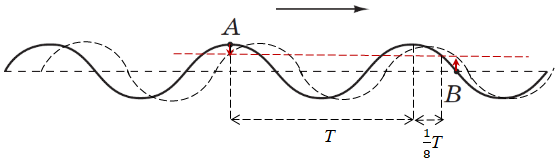
Через шуканий час
Відповідь: 0,2.
ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Вільні механічні коливання.
Завдання скеровано на розпізнання вільних механічних коливань у реальних прикладах.
Вільними є коливання, які відбуваються під дією внутрішніх сил системи після того, як її було виведено з положення рівноваги. Тобто певна зовнішня сила один раз подіяла на систему й після цього система сама виконує коливання.
На голку діє періодична зовнішня сила від обертання ручним чи ножним механічним або електроприводом. Ця сила, передана через усі необхідні для цього складники швейної машинки, змушує голку підніматися й опускатися.
Коливання буйка під дією хвиль і штори під дією протягу підтримуються нехай не періодичною зовнішньою силою, але силою, що діє постійно.
Пташка, коли злітала з гілочки, один раз відштовхнулася від неї, а після цього гілочка сама продовжила коливання, тому саме ці коливання є вільними.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку розуміння особливостей коливання на пружині, фізичних величин, якими ці коливання описують, і закономірностей переходу одного виду енергії в інший.
Причиною коливань за умовою є сила пружності, що виникла в деформованій пружині. Оскільки ця пружина спільна для обох тягарців, то однаковою для них буде саме частота коливань пружини (пружина буде одночасно скорочуватися і видовжуватися для обох тіл, а частота – це кількість коливань за певний проміжок часу).
Потенціальна енергія пружини переходитиме в кінетичну енергію тягарця і навпаки. За умовою механічна енергія зберігається (утрати на тертя не враховуємо). Кінетична енергія прямо пропорційна масі, а маси тягарців різняться у 2 рази. Тому максимальна швидкість і, відповідно, максимальна кінетична енергія також різні. Оскільки потенціальна енергія теж різна, то й максимальне видовження пружини ‒ амплітуда ‒ різнитиметься для різних за масою тягарців.
Відповідь: A.
ТЕМА: Механічні коливання і хвилі. Коливання вантажу на пружині. Перетворення енергії під час гармонічних коливань.
Завдання скеровано на оцінку вміння розв’язувати комбіновані задачі, які передбачають обробку й аналіз результатів експерименту, зображених на рисунку, i використання законів збереження енергії в коливальному процесі.
Знайти:
З рисункa 1 можна визначити довжину гумки у двох крайніх положеннях коливання тягарця. У крайніх положеннях тягарець змінює напрямок руху на протилежний, а отже його швидкість
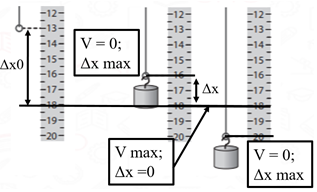
Рис. 1. Крайні положення тягарця
За цими значеннями можна обчислити амплітуду коливань:
Знаючи амплітуду коливань, можна визначити положення рівноваги – таке положення, у якому опиниться гумка під вагою тягарця, коли коливання повністю припиняться:
Під час коливань у положенні рівноваги швидкість найбільша, отже саме цю швидкість потрібно визначити.
Під час коливань зберігається повна механічна енергія системи
Кінетичну енергію можна визначити за формулою
Оскільки для гумової стрічки виконуваний закон Гука, можна обчислити потенціальну енергію за формулою, якою описують потенціальну енергію розтягнутої пружини:
Хоча повна механічна енергія системи зберігається, але значення кінетичної і потенціальної енергії постійно змінюється під час коливань.
У крайніх положеннях швидкість тягарця дорівнює нулю, а отже і його кінетична енергія теж. А от відхилення від положення рівноваги в цих положеннях найбільше, тому потенціальна енергія максимальна.
У положенні рівноваги все навпаки. Швидкість тягарця максимальна, а відхилення дорівнює нулю, отже кінетична енергія приймає найбільше значення, а потенціальна перетворюється на нуль.
Зважаючи на закон збереження енергії і спостереження, описані вище, можна записати таку рівність:
Тоді можна виразити максимальну швидкість:
Відношення
У стані спокою тягарець перебуватиме в положенні рівноваги. Тоді можна записати другий закон Ньютона:
Тоді
Після цього можна підставити отримане відношення у вираз для максимальної швидкості:
Відповідь: 28.
ТЕМА: Коливання і хвилі. Поперечні та поздовжні хвилі. Довжина хвилі.
Завдання скеровано на оцінювання вміння розв’язувати задачі на основі аналізування графічного зображення хвиль.
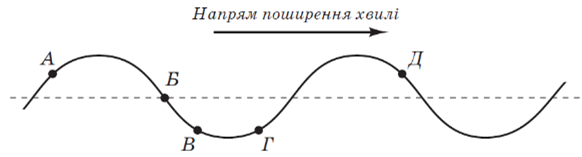
Рис. 1. Умова завдання
Поперечна хвиля – хвиля, у якій частинки середовища коливаються перпендикулярно до напрямку поширення хвилі. Хвиля, зображена в завданні, є поперечною.
У поперечній хвилі швидкість частинок у точках найбільшого відхилення від положення рівноваги дорівнює нулю.
Для точок перед найближчим гребнем (точки Б, В та Д) швидкість спрямована вгору, а для точок після гребня (точки А, Г) – униз (рис. 2). Точка перебуває перед найближчим гребнем, якщо гребінь рухається до неї.
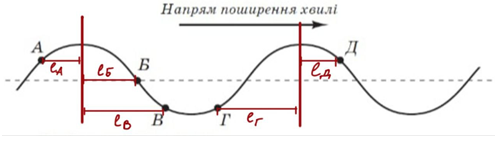
Рис. 2. Відстань від точок до гребенів хвиль
Якщо швидкість частинки зменшується, то її прискорення має протилежний напрямок до напрямку швидкості й навпаки. Прискорення частинок у поперечній хвилі завжди спрямоване до положення рівноваги, тож:
Точка А: швидкість спрямована вниз, прискорення – вниз.
Точка Б: швидкість спрямована вгору, прискорення дорівнює нулю.
Точка В: швидкість спрямована вгору, прискорення – вгору.
Точка Г: швидкість спрямована вниз, прискорення – вгору.
Точка Д: швидкість спрямована вгору, прискорення – вниз.
Відповідь: 1Г, 2В, 3А, 4Д.
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.
Завдання скеровано на перевірку розуміння поняття амплітуди коливань.
Амплітуда коливань – це максимальне відхилення від положення рівноваги. За одне коливання тіло проходить відстань, яка дорівнює чотирьом амплітудам (рис. 1).
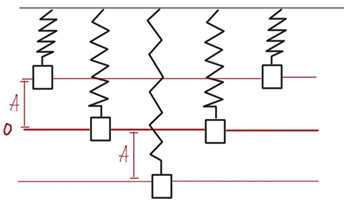
Рис. 1. Одне повне коливання пружинного маятника
Тоді за п’ять коливань тіло проходить
Відповідь: A.
ТЕМА: Механічні коливання і хвилі. Амплітуда, частота, період гармонічних коливань.
Завдання скеровано на перевірку розуміння основних величин, пов’язаних із коливаннями математичного маятника.
Відхилене на невелику відстань від вертикального положення масивне тіло на довгій нерозтяжній нитці можна вважати математичним маятником.
Оскільки радіуси сталевої та дерев’яної кульок однакові, то їхні об’єми рівні. Однак густина сталі більша за густину деревини, тому сталева кулька масивніша за дерев’яну.
Період коливань математичного маятника можна визначити за формулою
Від маси кульки період не залежить, тож він буде однаковим для обох маятників.
Коливання з більшою енергією згасатимуть повільніше. Енергію коливань можна визначити як потенціальну енергію в момент початку коливань. Потенціальну енергію тіла, піднятого над поверхнею Землі можна визначити за формулою
Оскільки обидві кульки відвели на однакову відстань, то й висота їхнього підйому теж буде однаковою. Тоді кулька з більшою масою – сталева – матиме більшу енергію порівняно з дерев’яною. Тому коливання сталевої кульки згасатимуть повільніше.
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.
Завдання скеровано на перевірку вміння застосовувати формулу для періоду нитяного маятника.
Період коливань
Запишімо формули періоду коливань для першого і другого маятників:
Виразімо довжини маятників через кількість клітинок, позначивши буквою
Поділімо ліві і праві частини формул для періодів обох маятників й обчислімо значення періоду коливань маятника
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.
Завдання скеровано на перевірку розуміння, від яких чинників залежить період коливань нитяного маятника.
Період коливань
Згідно з формулою для визначення періоду, він не залежить від маси тягарця. Довжина нитки у формулі – під квадратним коренем, тож її треба збільшити в
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку розуміння і застосування механічних й електромагнітних явищ.
Виникнення вихрового електричного поля або електричної поляризації провідника під час зміни магнітного поля або під час руху провідника в магнітному полі називають електромагнітною індукцією. Важливим наслідком електромагнітної індукції для генерування електричного струму є виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється.
Період
Тому, вимірявши довжину нитки й період коливань маятника, можна визначити прискорення вільного падіння в певній місцевості.
У радіолокації використовують ультракороткі електромагнітні хвилі частотою від
Просвітлення оптики ‒ збільшення прозорості деталей оптичних систем (лінз, оптичних призм) нанесенням на їхні поверхні тонкого шару діелектрика (або кількох шарів) із показником заломлення, меншим, ніж у матеріалу оптичної деталі. Просвітлення оптики ‒ результат інтерференції світла, яке відбивається від передньої та задньої границь цього шару (просвітлювальної плівки). За належного добору речовини й товщини плівки для певного кута падіння відбиті світлові хвилі певної довжини можуть повністю погасити одна одну.
Відповідь: 1В, 2Б, 3Д, 4Г.
ТЕМА: Механіка. Коливання і хвилі.
Завдання скеровано на перевірку розуміння фізичних процесів механіки і знання формул, якими описують ці процеси.
Усім тілам у Всесвіті властива гравітаційна взаємодія, виявом якої є їхнє взаємне притягання. Відповідно до закону всесвітнього тяжіння планети Венера й Марс притягуються одна до одної із силою
Якщо розтягнуту гумову нитку відпустити, то, скорочуючись, вона виконає роботу. Робота сили пружності визначена лише початковим і кінцевим станами гумової нитки, тобто сила пружності ‒ консервативна або потенціальна сила. Величину
Між дотичними поверхнями стрічки транспортера й цеглини діє сила тертя спокою, яка перешкоджає виникненню відносного руху їх. Сила тертя спокою завжди дорівнює за модулем і протилежна за напрямком рівнодійній зовнішніх сил, які намагаються зрушити тіло з місця. Після того як рівнодійна зовнішніх сил зрівняється з максимальною силою тертя спокою, тіло починає ковзання, тобто починає діяти сила тертя ковзання. Отже, максимальна сила тертя спокою дорівнює силі тертя ковзання:
Маленька сталева кулька коливається на довгій нерозтяжній нитці ‒ це модель нитяного (математичного) маятника. Період коливань
Відповідь: 1А, 2Г, 3Д, 4Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Звукові хвилі.
Завдання скеровано на перевірку вміння визначати довжину хвилі через інші її характеристики.
Довжину хвилі
Оскільки в умові дано діапазон частот звукових хвиль у повітрі, можна обчислити діапазон відповідних їм довжин хвиль:
Тобто діапазон довжини хвиль такий:
Із наведених у варіантах відповіді у цей діапазон потрапляє лише хвиля довжиною
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку знання і розуміння характеристик механічних коливань, уміння читати рівняння гармонічних коливань і брати з них потрібну інформацію.
Кількість
Частоту
Циклічну частоту визначімо з рівняння в умові завдання ‒ це множник перед
Отже,
Визначімо тепер кількість коливань за
Відповідь: 20.
ТЕМА: Механіка. Основи динаміки (закон всесвітнього тяжіння.). Закони збереження в механіці (прості механізми, закон збереження імпульсу). Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння механічних процесів, уміння описати їх за допомогою формул і законів.
Взаємодію Землі і Місяця описуємо за допомогою закону всесвітнього тяжіння: будь-які два тіла притягуються одне до одного із силою
Відкручування гайки за допомогою гайкового ключа є прикладом застосування простого механізму ‒ важеля ‒ на практиці. Чим довшою буде ручка гайкового ключа, тим легше ми відкрутимо або сильніше закрутимо гайку, прикладаючи меншу силу. Описати цей процес можна відповідно до правила моментів:
Коливання тіла масою
Зіткнення більярдних куль, як приклад абсолютно пружного удару, опишімо за допомогою закону збереження імпульсу: у замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії. Зваживши на те, що імпульс тіла дорівнює добутку маси
Відповідь: 1Д, 2Б, 3В, 4Г.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливальний рух.
Завдання скеровано на перевірку знання і розуміння частоти коливань.
Частота коливань
Звідси знайдімо формулу для визначення кількості коливань:
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і застосування формули періоду коливань на пружині.
Формула для обчислення періоду
Маса тіла дорівнює добутку густини
До пружин підвішено кулі, об’єм кулі обчислюють за формулою
Запишімо формули періодів малих вертикальних коливань обох куль на пружинах, зваживши на те, що за умовою радіуси куль однакові, однакові й пружини, тобто однакова жорсткість пружин:
Визначімо співвідношення періодів:
Тобто
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. ‒ Механічні коливання і хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).
Завдання скеровано на перевірку знання і розуміння характеристик механічної хвилі.
1. Довжина хвилі
Довжина хвилі
2. Період
Період
3. Амплітуда
Амплітуда
4. Швидкістю поширення хвилі називають швидкість переміщення точок із однаковою фазою коливань (наприклад, швидкість переміщення гребеня хвилі). Швидкість поширення хвилі не збігається зі швидкістю руху частинок середовища: частинки коливаються біля положень рівноваги, а хвиля поширюється в певному напрямку.
Із означення довжини хвилі
Відповідь: 1Г, 2В, 3А, 4Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.
Завдання скеровано на перевірку вміння застосовувати формули періоду коливань нитяного маятника, розуміння того, від яких фізичних величин залежить період коливань цього маятника.
Маленька мавпочка на довгій, нерозтяжній і невагомій ліані є фізичною моделлю нитяного маятника.
Період
Коли ж мавпочка піднялася по ліані вгору на відстань
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.
Завдання скеровано на перевірку знання і розуміння формули для періоду математичного маятника і вміння її застосовувати.
Фізична величина довжина
Виразімо
Період
Обчислімо довжину маятника:
Відповідь: 6,25.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Звукові хвилі. Висота тону і тембр звуку.
Завдання скеровано на перевірку знання і розуміння суб’єктивних (фізіологічних) характеристик звуку.
Висоту звуку визначає, переважно, частота звукової хвилі: що більша її частота, то вищий тон звуку. Наприклад, ноті ля першої октави відповідає частота
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання. Зміщення, амплітуда, період, частота і фаза гармонічних коливань.
Завдання скеровано на перевірку знання і розуміння періоду коливань.
За умовою завдання зміщення тіла фіксували протягом половини періоду:
Із наведених варіантів відповіді єдиний, який задовольняє умову, це варіант Б ‒ послідовність моментів часу від
Усі інші числові дані в завданні є зайвими за поданого формулювання умови.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння механічних коливань тіла на пружині.
Запишімо формулу для визначення періоду
Під час максимальної деформації пружини на тіло, прикріплене до неї, діятиме максимальна сила пружності
Отже,
Амплітудне значення відхилення тіла можна визначити, скориставшись повною енергією тіла. Оскільки в крайній точці тіло не рухатиметься, тобто кінетична енергія дорівнюватиме нулю, то повна (максимальна) енергія тіла ‒ це потенціальна енергія
Визначімо амплітуду
Тепер можемо визначити жорсткість пружини
Обчислімо період коливань тіла
Результат округлімо до сотих:
Відповідь: 1,26.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Перетворення енергії у гармонічних коливаннях.
Завдання скеровано на перевірку знання і розуміння закону збереження механічної енергії на прикладі математичного маятника.
Повна механічна енергія кульки, яка складається з кінетичної і потенціальної енергій, зберігатиметься: уважаємо, що опір повітря нехтовно малий, а сили, що діють у системі, є консервативними. Якщо значення одного виду енергії зменшується, то відповідно, значення іншого виду енергії збільшується.
За умовою завдання маятник рухається в бік положення рівноваги (вертикального положення). Це означає, що висота підняття кульки під час здійснення коливання зменшуватиметься, а швидкість руху кульки у напрямку положення рівноваги збільшуватиметься (див. рисунок).
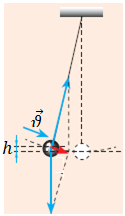
Потенціальна енергія
Отже, якщо висота зменшується, то потенціальна енергія теж зменшується.
Кінетична енергія
Отже, у разі збільшення швидкості руху кінетична енергія кульки теж збільшуватиметься.
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння того, від яких величин залежить період коливань тіла на пружині.
Застосуймо формулу для обчислення періоду
Зазначмо, що період коливань пружинного маятника не залежить ні від амплітуди коливань, ні від того, де відбуваються ці коливання (на поверхні Землі, у космічному кораблі чи на поверхні Місяця), ‒ він визначений тільки власними характеристиками коливальної системи «тіло ‒ пружина».
Відповідно до умови важок перебуває в спокої, отже, сила тяжіння і сила пружності зрівноважують одна одну:
Замінимо відношення величин
Обчислімо період вертикальних коливань важка на пружині:
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння перетворення механічної енергії під час коливального руху пружинного маятника.
У завданні описана ситуація, коли тягарець проходить якесь проміжне положення і не перебуває ні в положенні рівноваги, ні на максимальній відстані від нього, яку називають амплітудою.
Під час коливального руху тягарця потенціальна енергія деформованої пружини перетворюватиметься на кінетичну енергію руху тягарця, і навпаки. Тобто виконуватиметься закон збереження механічної енергії.
Запишімо розподіл енергії в цьому проміжному положенні. Тягарець володітиме кінетичною енергією
У крайньому положенні, тобто коли тягарець віддалений від положення рівноваги на максимальну відстань, його кінетична енергія дорівнюватиме нулю, тому що він на мить зупиняється, тобто швидкість його руху дорівнює нулю.
А потенціальна енергія розтягнутої пружини буде максимальною
Запишімо закон збереження механічної енергії:
Помножимо ліву і праву частини рівності на
Обчислимо значення амплітуди:
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку вміння визначати фізичні величини, які характеризують гармонічні коливання.
Гармонічними називають коливання, під час яких координата
Перша похідна від координати за часом
А друга похідна від координати за часом або перша похідна від швидкості ‒ це прискорення
Зробимо заміну в рівнянні для прискорення, скориставшись першим загальним рівнянням:
У будь-який момент часу руху тіла його прискорення прямо пропорційне зміщенню і напрямлене в бік, протилежний зміщенню (тому знак «мінус»).
Визначмо циклічну частоту коливань:
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення та періодом (частотою).
Завдання скеровано на перевірку знання і розуміння зв᾽язку між довжиною хвилі, швидкістю її поширення та періодом (частотою).
Відстань
Довжину ж хвилі можна визначити за формулою хвилі ‒ це формула взаємозв’язку довжини
Якщо поділимо відстань, яку пройде звук, на довжину хвилі, то дізнаємося, скільки довжин хвиль укладеться на цій відстані:
Відповідь:
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Поперечні та поздовжні хвилі.
Завдання скеровано на перевірку знання і розуміння руху точок хвилі.
Перш за все нагадаймо, що кожна точка шнура здійснює коливання. Коли зміщення від положення рівноваги максимальне за модулем, напрямок руху точки змінюється на протилежний, тобто в такі моменти швидкість руху точки дорівнює нулю. Але такі точки на шнурі не позначено.
На рисунку покажемо форму шнура через невеликий проміжок часу (точки на шнурі вже позначено штрихами).

Ми бачимо, що точки А та Г опустилися (найближчий гребінь хвилі віддалився від неї), а точки Б, В та Д піднялися (до кожної з них наблизився сусідній гребінь хвилі).
На кожну точку хвилі завжди діє сила, яка намагається повернути її до положення рівноваги, а згідно із другим законом Ньютона напрямок сили збігається з напрямком прискорення точки. Отже, прискорення кожної точки хвилі завжди напрямлене до положення рівноваги, коли шнур був у спокої.
Отже,
1 - швидкість напрямлена вниз, прискорення вгору ‒ точка Г,
2 - швидкість і прискорення напрямлені вгору ‒ точка В,
3 - швидкість і прискорення напрямлені вниз ‒ точка А,
4 - швидкість напрямлена вгору, прискорення вниз ‒ точка Д.
Відповідь: 1Г, 2В, 3А, 4Д.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Перетворення енергії при гармонічних коливаннях.
Завдання скеровано на перевірку знання і розуміння перетворення енергії під час гармонічних коливань, а також уміння читати рівняння гармонічних коливань і брати з нього необхідні дані для розв’язання.
Потенціальна енергія
Визначмо координату маятника в момент часу
Підставмо цей вираз для координати у формулу для потенціальної енергії:
Запишімо закон збереження енергії для двох різних моментів часу ‒ для
Отже,
Робімо висновок, що
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння поняття амплітуди, поняття одного повного коливання і шляху, що проходить тіло за один період коливання.
Амплітуда
Тоді за п’ять періодів коливань тіло, що здійснює коливання на пружині, пройде шлях
Відповідь: 10.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі.
Завдання скеровано на перевірку знання і розуміння формул розділу «Механічні коливання і хвилі».
1. Потенціальна енергія
2. Період
3. Кінетична енергія
4. Період
Відповідь: 1А, 2Д, 3Г, 4Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку знання і розуміння гармонічних коливань, а також уміння правильно їх описувати за допомогою графіків.
За умовою коливання є гармонічними, тож координата
де
Крива
Імпульс тіла
Коли координата тіла змінюється за гармонічним законом (за законом косинуса або синуса), швидкість і прискорення руху тіла теж змінюються гармонічно. Швидкість руху тіла ‒ це похідна від зміщення тіла за часом:
Функція залежності модуля імпульсу тіла від часу матиме вигляд
Графіком такої функції
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Вільні механічні коливання.
Завдання скеровано на перевірку знання і розуміння видів механічних коливань, і вміння розпізнавати їх у конкретних прикладах.
Вільні коливання ‒ це коливання, які відбуваються під дією внутрішніх сил системи після того, як її було виведено з положення рівноваги. Щоб у коливальній системі виникли вільні коливання, необхідне виконання двох умов: 1) системі має бути передано надлишкову енергію; 2) тертя в системі має бути досить малим, інакше коливання швидко затухнуть або навіть не виникнуть. Оскільки під час вільних коливань система не отримує енергію ззовні, то вільні коливання ‒ це завжди згасні коливання.
З усіх наведених ситуацій прикладом вільних коливань є коливання гілочки, з якої щойно злетіла пташка ‒ пташка вивела гілочку із стану рівноваги, один раз штовхнувши її лапками (передала енергію), поступово ці коливання затухнуть унаслідок дії сил пружності і опору повітря.
Коливання занавіски біля прочиненого вікна під дією протягу й коливання буйка під дією хвиль можна вважати вимушеними: на занавіски діє зовнішня сила, що періодично змінюється, ‒ протяг, а буйок піднімається й опускається разом із хвилями на поверхні води. Такі коливання зазвичай незгасні, їхня частота дорівнює частоті зміни зовнішньої сили, що змушує тіло коливатися.
Коливання голки швацької машинки, що працює, ‒ це автоколивання. Ці коливання є незгасними й відбуваються внаслідок здатності системи самостійно регулювати надходження енергії від постійного джерела.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання суті і розуміння закономірностей коливань тіла на пружині, сил, що діють на тіло в певній ситуації.
Позначмо на рисунку сили, які діють на кульку, що підвішена до пружини й поки не коливається на ній (див. рисунок ліворуч). На кульку діє сила тяжіння
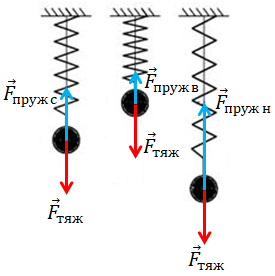
Коли кулька переміститься у верхню точку (див. рисунок посередині), сила пружності
У нижній точці навпаки: сила пружності
Отже, сили, що діють на кульку, будуть урівноважені лише в положенні рівноваги, тобто в середній точці.
Відповідь: Б.
Коливання і хвилі. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.
Завдання скеровано на перевірку знання і розуміння параметрів, від яких залежить період коливань нитяного маятника.
Період коливань
За умовою довжини обох ниток однакові:
У формулу також входить прискорення вільного падіння, але в умові не зазначено, що кульки в різних місцях, тому вважаємо, що прискорення вільного падіння однакове для обох кульок.
З формули зрозуміло, що період коливань нитяного маятника не залежить від маси тіла. Тож ні від густини (у металу й дерева значення густини різні), ні від об’єму (за умовою радіуси кульок однакові) період коливань також не залежить.
Період коливань математичного маятника не залежить від маси маятника, а визначається лише довжиною нитки та прискоренням вільного падіння в тому місці, де розташований цей маятник.
Отже, періоди малих коливань кульок із різних матеріалів на нитках однакової довжини будуть однакові:
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку знання і розуміння гармонічних коливань і їхніх характеристик, а також вміння визначати їх.
Коливання, під час яких координата
де
Тоді рівняння гармонічних коливань маятника автомобіля матиме загальний вигляд:
Робимо висновок, що іграшковий автомобіль рухається прямолінійно рівномірно вздовж осі
Період коливань
З графіка візьмемо дві синхронні точки по осі
Для математичного (нитяного) маятника період коливань
Обчислімо швидкість руху автомобіля:
Відповідь:
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку знання і розуміння рівнянь гармонічних коливань.
Коливання, під час яких координата
де
З умови відоме рівняння гармонічних коливань:
1. Амплітуда. Множник перед функцією косинуса ‒ це і є амплітудне (максимальне) значення координати
2. Початкова фаза. Це фаза коливань у момент початку відліку часу ‒ це доданок під знаком функції косинуса, який не помножено на час ‒
3. Період. Знаючи з рівняння циклічну частоту
4. Циклічна частота. Ми вже взяли з рівняння в умові значення циклічної частоти в попередньому пункті 3 ‒ це множник біля
Відповідь: 1Г, 2Б, 3А, 4Д.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Вимушені механічні коливання. Явище резонансу.
Завдання скеровано на перевірку знання і розуміння видів механічних коливань і їхніх характеристик.
Коливання ‒ це зміни стану системи біля певної точки рівноваги, які точно або приблизно повторюються із часом. За характером взаємодії з навколишніми тілами й полями розрізняють вільні коливання, вимушені коливання, автоколивання.
Вільні коливання ‒ це коливання, які відбуваються під дією внутрішніх сил системи й виникають після того, як систему виведено зі стану рівноваги. Амплітуда цих коливань із часом зменшується, і через певний інтервал часу, якщо немає надходжень енергії від зовнішнього джерела, коливання припиняються. Такі коливання називають згасними (затухаючими).
Вимушені коливання ‒ це коливання, які відбуваються в системі тільки під дією зовнішнього періодичного впливу. Під час вимушених коливань може виникнути явище резонансу ‒ різке збільшення амплітуди коливань у разі, якщо частота зовнішнього періодичного впливу збігається з власною частотою коливань системи. Амплітуда вимушених коливань визначається інтенсивністю зовнішнього періодичного впливу і з часом не змінюється. Такі коливання називають незгасними (незатухаючими).
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку знання і розуміння принципу будови й дії трансформатора.
Основною причиною шуму трансформаторів є фізичне явище – магнітострикція. Коротко це означає: якщо на лист електротехнічної сталі діяти магнітним полем, цей лист згинатиметься сам собою.
Найпростіший трансформатор складається із замкненого осердя (магнітопроводу) і двох обмоток (див. рисунок). Осердя (сердечник) виготовлено з тонких пластин трансформаторної сталі.
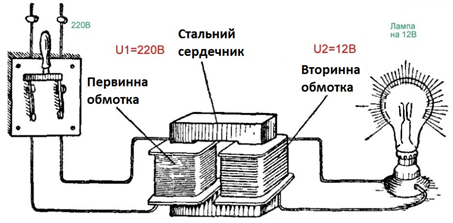
Явища зміни форми й розмірів феромагнітних тіл досліджували ще у ХІХ столітті. Англійський дослідник Джеймс Джоуль 1842 року помітив, що під дією магнітного поля тонкий залізний об’єкт подовжується в одному напрямку й скорочується в іншому, зберігаючи колишній об’єм. Таку деформацію супроводжують звуки: уявімо собі, що ми почуємо, якщо спробуємо зігнути лист металу або навіть звичайної фольги.
В умовах дії електромагнітного поля подібний процес набуває стабільної частоти. Частота гулу досить низька, що й дає змогу людському вуху його вловлювати. Оскільки йдеться про змінний струм, магнітне поле встигає двічі за фазу змінити свій напрямок, розгойдуючи усі мікрообласті металу сердечника. В Україні побутова електрична мережа з напругою
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Довжина хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).
Завдання скеровано на перевірку знання і розуміння поняття періоду коливань, довжини хвилі й уміння визначати її за графіком.
Поширення коливань у пружному середовищі називають механічною хвилею.
За час, що дорівнює періоду
Отже, період вертикальних коливань поплавка (чергове підняття поплавка на гребені хвилі) дорівнюватиме:
Визначімо за графіком з умови довжину хвилі. Довжина хвилі
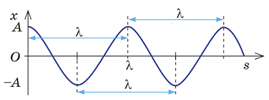
Розгляньмо рисунок в умові завдання. Виберімо точки, що рухаються синхронно.
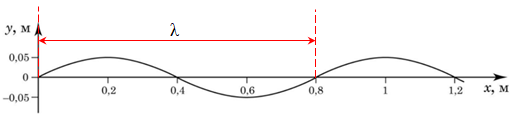
Отже, довжина хвилі, як видно з графіка, дорівнює
Обчислімо тепер значення періоду коливань поплавка:
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Звукові хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення та періодом (частотою).
Завдання скеровано на перевірку знання і розуміння поширення механічних хвиль і зміни під час цього їхніх характеристик.
Швидкість поширення хвилі в основному визначають пружні властивості середовища, у якому хвиля поширюється, тому, якщо хвиля переходить з одного середовища в інше, то швидкість
Але ще впевнимося в правильності варіанта А, довівши, що довжина
За умовою швидкість поширення звуку в повітрi дорівнює
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний (математичний) маятник.
Завдання скеровано на перевірку знання і розуміння фізичних величин, що характеризують коливання математичного маятника.
Математичний маятник ‒ це фізична модель коливальної системи, яка складається з матеріальної точки, підвішеної на невагомій і нерозтяжній нитці, і гравітаційного поля. Положення рівноваги маятника ‒ це положення, у якому маятник висить непорушно строго вертикально, сила тяжіння
Одразу можна сказати, що вага маятника за означенням буде максимальною у вертикальному положенні (положенні рівноваги). Отже, варіант відповіді Г ‒ неправильний.
Частота коливань маятника теж залишиться незмінною, оскільки в умові сказано, що коливання незгасні.
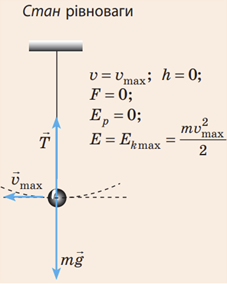
У ході коливань маятника його потенціальна та кінетична енергії безперервно змінюються. Потенціальна енергія є максимальною в точках повороту й дорівнює нулю в момент проходження маятником положення рівноваги. Кінетична енергія в точках повороту дорівнює нулю й сягає максимального значення в момент проходження маятником положення рівноваги. Отже, мінімальною в момент проходження маятником положення рівноваги буде потенціальна енергія.

Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Перетворення енергії під час гармонічних коливаннях.
Завдання скеровано на перевірку знання і розуміння суті повного коливання нитяного маятника й перетворень його енергії під час коливань.
Нитяний маятник є фізичною моделлю маятника настінного годинника.
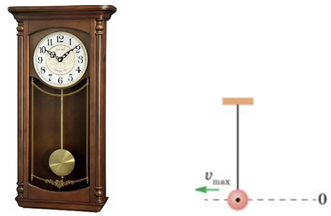
Виберімо положення рівноваги маятника за нульовий рівень, де потенціальна енергія дорівнюватиме нулю. Здійснюючи коливання, маятник відхиляється на певний кут, піднімаючись на певну максимальну висоту.
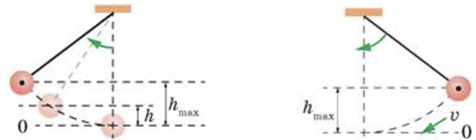
За одне повне коливання (маятник повинен повернутися в початкове положення), маятник два рази піднімається на максимальну висоту. Отже, за одне коливання потенціальна енергія маятника двічі набуває максимального значення.
Тепер обчислімо, скільки ж повних коливань здійснив маятник за хвилину, коливаючись із частотою
Визначімо час одного коливання ‒ період. Частота
За час
І, зваживши на те (як ми вже раніше довели), що за кожне коливання потенціальна енергія маятника двічі набуватиме максимального значення, то за хвилину потенціальна енергія буде максимальною
Відповідь: Г.