Розділ: Коливання та хвилі. Оптика
Тема: Оптика
Кількість завдань: 95
ТЕМА: Коливання і хвилі. Оптика. Оптична сила лінзи. Формула тонкої лінзи. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку знання і розуміння побудови зображень, які дає тонка лінза, уміння застосовувати формулу тонкої лінзи й формулу для визначення лінійного збільшення лінзи.
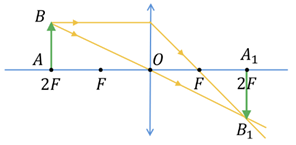
Опишімо зазначене в умові розміщення предмета й лінзи формулою тонкої лінзи:
Щодо знаків мінус у формулі: зауважмо, що відстань
Також скористаймося відношенням лінійного розміру
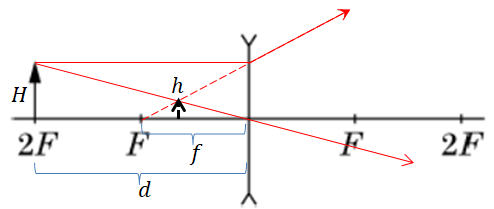
Виразімо висоту зображення
За умовою
Відстань
Підставмо всі значення і вирази у формулу для
Відповідь:
ТЕМА: Коливання і хвилі. Оптика. Прямолінійність поширення світла в однорідному середовищі.
Завдання скеровано на перевірку знання і розуміння закону прямолінійного поширення світла, а також понять повної тіні і півтіні.
Джерело світла, яке випромінює світло однаково в усіх напрямках і розмірами якого, зважаючи на відстань до місця спостереження, можна знехтувати, називають точковим джерелом світла.
Найкращим прикладом точкових джерел світла є зорі, адже ми спостерігаємо їх із Землі, тобто з відстані, що в мільйони разів перевищує розміри самих зір.
Джерела світла, що не є точковими, називають протяжними джерелами світла.
Повна тінь ‒ це область простору, в яку не потрапляє світло від джерела.
Якщо джерело світла є точковим, тінь від предмета буде чіткою. У цьому разі утворюється тільки повна тінь.

Якщо тіло освітлене протяжним джерелом світла, то утворюється тінь із нечіткими контурами, тобто утворюється не тільки повна тінь, а ще й півтінь.

Півтінь ‒ це область простору, освітлена деякими з наявних точкових джерел світла або частиною протяжного джерела.
Повну тінь і півтінь пояснюють відповідно до закону прямолінійного поширення світла.
Отже, правильна відповідь ‒ Б.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння будувати зображення в збиральній лінзі й уміння застосовувати формулу тонкої лінзи.
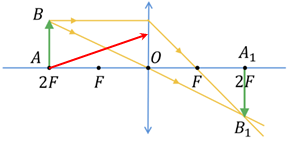
Побудуємо відповідно до умови завдання зображення, що дає збиральна лінза.
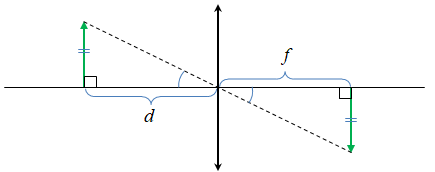
Побудувавши, отримуємо два рівні прямокутні трикутники – за катетом і гострим кутом: гострі кути рівні як вертикальні, катети рівні за умовою – предмет і його зображення однакового розміру.
Зваживши на це, запишімо формулу тонкої лінзи:
З рівності трикутників випливає, що
Обчислімо фокусну відстань лінзи:
Відповідь: 20.
ТЕМА: Коливання і хвилі. Оптика. Дисперсія світла.
Завдання скеровано на перевірку знання та розуміння хвильових явищ.
Дифракція ‒ це явище потрапляння світлових хвиль в область геометричної тіні, тобто відхилення їх від прямолінійного поширення.
Явище розкладання світла в спектр, зумовлене залежністю абсолютного показника заломлення середовища від частоти світлової хвилі, називають дисперсією світла.
Отже, різнокольоровий блиск каміння, освітленого білим світлом, пояснюють дисперсією.
Інтерференція ‒ це явище накладання когерентних хвиль, унаслідок якого спостерігають стійку в часі картину посилення їх і послаблення в різних точках простору.
Поляризація ‒ це властивість світлових і електромагнітних коливань відбуватися в одній площині. Максвелл припустив, що заряди не приходять ззовні, а утворюються завдяки поляризації всередині речовини. Поляризація світла ‒ перетворення пучків природного світла на світло з обмеженим напрямком коливань.
Отже, дисперсія є причиною утворення різних кольорів, спектру.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку розуміння явищ хвильової оптики й застосування їх у різних галузях.
1. Інтерференція ‒ явище накладання хвиль, унаслідок якого в деяких точках простору спостерігають стійке в часі посилення (або послаблення) результувальних коливань.
Світлова хвиля частково відбивається від зовнішньої поверхні плівки, частково проходить через плівку й відбивається від її внутрішньої поверхні. Між ними є різниця ходу. Обидві хвилі когерентні, адже створені одним джерелом, тому внаслідок накладання їх спостерігають стійку інтерференційну картину.
Саме інтерференцією світла зумовлений колір багатьох комах. Плівки різної товщини райдужно забарвлені – мильні бульбашки, оліїста плівка на поверхні води тощо (B).
2. Явище обгинання хвилями перешкод або будь-яке інше відхилення поширення хвилі від законів геометричної оптики називають дифракцією. Дифракція властива будь-яким хвилям незалежно від їхньої природи. Особливо помітна дифракція на перешкодах, розмір яких набагато менший від довжини хвилі. Саме це заважає побачити атом за допомогою оптичного мікроскопа: адже розмір атома приблизно у
3. Явище розкладання світла в спектр, зумовлене залежністю абсолютного показника заломлення середовища від частоти світлової хвилі, називають дисперсією світла. Веселка – це атмосферне оптичне явище, яке спостерігають унаслідок освітлення Сонцем безлічі водяних крапельок (дощу, туману тощо). Крапельки води по-різному відхиляють світло різних кольорів, тому біле світло розкладається на спектр (Г).
4. Світло ‒ поперечна хвиля. Поляризація світла ‒ це виділення у світловій хвилі коливань лише в одній площині або в кількох визначених. Поляризацію світла застосовують для створення об’ємного зображення в 3D-кінотеатрах. Цього досягають за допомогою окулярів із поляризаційними плівками. Поляризаційну плівку також наклеюють на екран, з якого транслюють зображення. Поляризаційна плівка на екрані розбиває цілісну картину на дві, формуючи стереопару. Унаслідок цього крізь спеціальні окуляри одне око бачить лише парні, а друге – тільки непарні рядки. Завдяки бінокулярності зору людський мозок може сумістити ці два зображення в одне. Невелика відстань між очима забезпечує незначну відмінність між обома картинками, тож цілісне зображення набуває об’ємності (А).
Відповідь: 1В, 2Б, 3Г, 4А.
ТЕМА: Коливання і хвилі. Оптика. Закони заломлення світла.
Завдання скеровано на перевірку знання і розуміння законів заломлення світла.
Світловий промінь 1 проходить через межу в середовище 2, змінюючи, зазвичай, напрямок (див. рисунок). Отже, твердження A – неправильне.
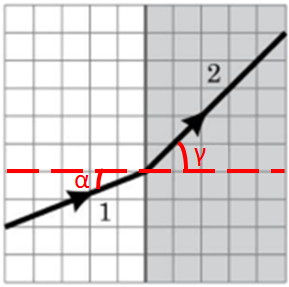
Зміну напрямку поширення світла в разі його проходження через межу поділу двох середовищ називають заломленням світла. Промінь 2, який задає напрямок заломленого пучка світла, називають заломленим променем. Кут
Оскільки кут падіння менший за кут заломлення, то це означає, що промінь переходить з оптично густішого середовища в оптично менш густе. І тоді швидкість світла в середовищі 1 менша, ніж у середовищі 2. Твердження В ‒ правильне.
Під час переходу з одного середовища в інше швидкість
Тобто твердження Г – неправильне.
Відповідь: B.
ТЕМА: Оптика. Лінза. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі із застосування законів геометричної оптики й формули тонкої лінзи.
Дано:
Знайти:
Оптична сила пов’язана з фокусною відстанню лінзи
Фокусну відстань лінзи та її положення відносно об’єкта і його зображення пов’язує формула тонкої лінзи
Тоді можна виразити з формули тонкої лінзи відстань між лінзою і зображенням:
Відповідь: 0,25.
ТЕМА: Оптика. Лінза. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі із застосування законів геометричної оптики й формули тонкої лінзи.
Дано:
Знайти:
Фокусну відстань лінзи та її положення відносно об’єкта і його зображення пов’язує формула тонкої лінзи:
Розміри зображення і предмета з їхніми відстанями від лінзи пов’язує лінійне збільшення лінзи Г:
З виразу для лінійного збільшення лінзи можемо обчислити відстань
Відповідь: 100.
ТЕМА: Оптика. Інтерференція світла та її практичне застосування.
Завдання скеровано на перевірку розуміння механізмів інтерференції та її проявів у природі.
На тонкій поверхні мильної бульбашки відбувається інтерференція (рис. 1).
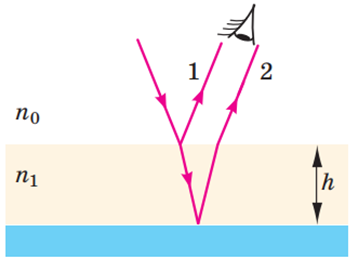
Рис. 1. Механізм інтерференції
Одна частина променю, що падає на зовнішню поверхню мильної плівки, відбивається від неї, а інша проходить у товщу плівки й заломлюється. Ця частина променю відбивається вже на другій поверхні плівки й заломлюється на шляху назад із плівки в повітря. Дві частини променю є когерентними, але вони пройшли різну відстань, тож мають певну різницю ходу. У результаті хвилі накладаються одна на одну, у певних місцях підсилюючи одна одну, а в інших ослаблюючи – утворюється інтерференційна картина.
Сонячне світло складається з багатьох хвиль різної довжини, тому інтерференційна картина для кожного кольору буде інша. Для підсилення якогось конкретного кольору товщину плівки треба дібрати так, щоби хвилі мали різницю ходу, кратну парній кількості півхвиль. Якщо товщина плівки різниться в різних місцях, як це часто буває в мильних бульбашках, то в різних її частинах підсилюватиметься хвиля іншого кольору й утворюватиметься кольоровий візерунок.
Відповідь: B.
ТЕМА: Оптика. Закони заломлення світла.
Завдання скеровано на оцінювання розуміння законів заломлення світла.
За законом заломлення променів
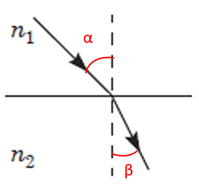
Рис. 1. Закон заломлення променів
Кут падіння і кут заломлення мають бути меншими за 90° (рис. 1).
За графіком функції
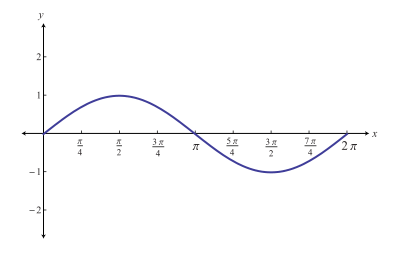
Рис. 2. Графік функції
Отже, якщо кут заломлення менший, ніж кут падіння, то і синус кута заломлення буде меншим за синус кута падіння. Тож, щоб закон заломлення виконувався, якщо кут падіння більший за кут відбивання, то показник заломлення в середовищі падаючого променю має бути меншим за показник заломлення і середовищі заломленого променю.
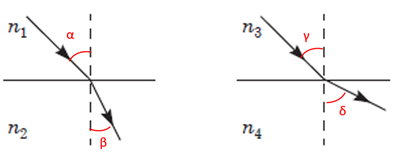
Рис. 3. Умова завдання
За умовою завдання для у першому випадку кут заломлення
У другому випадку кут падіння
Відповідь: Б.
ТЕМА: Оптика. Закони заломлення світла.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на закони заломлення світла, зокрема з використанням явища повного внутрішнього відбивання.
Дано:
1. Знайти:
Абсолютний показник заломлення
Тоді можна розрахувати швидкість поширення світла у склі:
2. Знайти:
Вираз закону заломлення світла на межі двох середовищ:
Промінь, що падає на призму, заломлюється двічі – на кожній поверхні призми.
Усі кути в законі заломлення відраховуються від перпендикуляр до поверхні. Оскільки падний промінь перпендикулярний до лівої поверхні призми, то кут між перпендикуляром і кутом падіння дорівнює
Оскільки
Тож заломлений промінь також перпендикулярний до поверхні призми. На другій поверхні призми кут
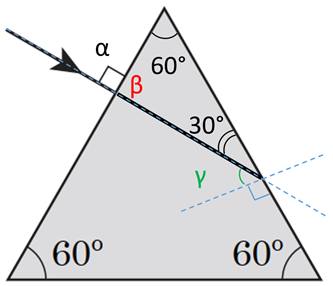
Рис. 1. Визначення кута
Зважаючи на те, що кути при основі призми дорівнюють
Кут
Перед тим, як застосовувати закон заломлення світла вдруге, потрібно перевірити, чи не відбувається в цьому разі повне внутрішнє відбивання. Повне внутрішнє відбивання – це явище відбивання світла на межі двох середовищ. Воно відбувається для всіх кутів, більших за критичний кут
У цьому разі
Це значення синуса не є табличним, тому визначити кут
Із таблиці можна дізнатися, що
Для порівняння
Тепер залишається порівняти чисельники цих дробів.
Якщо
Відомо, що
Оскільки кут падіння променю на другу поверхню призми більший, ніж кут повного внутрішнього відбивання, то заломлення не відбудеться, і промінь відбиватиметься від другої поверхні призми (рис. 2).
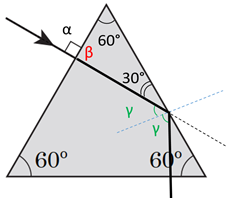
Рис. 2. Повне внутрішнє відбивання променю світла
Кут падіння завжди дорівнює куту відбивання і в цьому разі становить
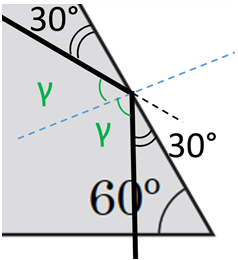
Рис. 3. Визначення кута падіння на нижню поверхню призми
Тоді кут, під яким відбитий промінь падає на нижню поверхню, дорівнює:
Тому кут відхилення від початкового ходу
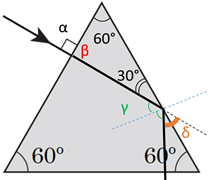
Рис. 4. Визначення відхилення променю від початкового напрямку
На рисунку кут падіння на другу поверхню призми, рівний до нього кут відбивання від цієї поверхні й шуканий кут
Відповідь: 1. 200. 2. 60.
ТЕМА: Оптика. Закони відбивання світла. Закони заломлення світла. Лінза.
Завдання скеровано на перевірку розуміння принципів роботи оптичних елементів.
Промені проходять крізь склянку з водою, адже в іншому разі неможливо було би побачити Гаррі, що розташований за нею. Тому склянка з водою не виконує функцію дзеркала. З тієї самої причини склянка не змінює хід променів на зворотний.
Після наповнення склянки водою утворюється дійсне перевернуте зображення Гаррі. Розсіювальна лінза утворює лише уявне пряме зменшене зображення. Збиральна ж лінза може утворювати дійсне перевернуте зображення, що має ті самі розміри, що і предмет, якщо він перебуває на відстані від лінзи, яка дорівнює її подвійному фокусу.
Відповідь: А.
ТЕМА: Оптика. Джерела світла.
Завдання скеровано на оцінку розуміння поняття джерела світла.
Місяць – це кам’яний супутник Землі. Подібно до інших планет і супутників він не може бути джерелом світла, тобто випромінювати частинки світла (фотони). Він лише відбиває сонячне випромінювання.
Відповідь: B.
ТЕМА: Оптика. Оптична сила лінзи. Формула тонкої лінзи.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на формулу тонкої лінзи.
Дано:
Знайти:
Оптичну силу лінзи і її положення відносно об’єкта і його зображення пов’язує формула тонкої лінзи:
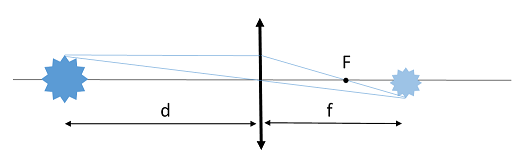
Рис. 1. Схема ходу променів крізь тонку лінзу
За умовою потрібно отримати зображення на відстані 3 м від світильника, тобто
Отже
Затим потрібно підставити всі відомі величини й розв’язати отримане внаслідок перетворень рівняння відносно
Дискримінант
Умову задачі задовольняє менше значення
Відповідь: 1.
ТЕМА: Оптика. Лінза. Плоске дзеркало.
Завдання скеровано на оцінювання розуміння принципів роботи оптичних елементів під час проходження крізь них паралельних променів.
Оптична сила лінзи
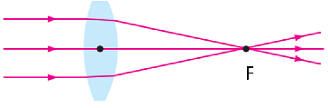
Рис. 1. Хід променів після проходження збиральної лінзи
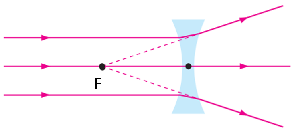
Рис. 2. Хід променів після проходження розсіювальної лінзи
Плоскопаралельна пластинка – це оптичний елемент, у якого дві заломлювальні поверхні паралельні одна одній. Тобто можна уявити шар скла для опису проходження променів.
За законом заломлення променів
Якщо встановити плоскопаралельну пластинку так само, як схематично зображено на рисунках 1 і 2, то кут
Оскільки кут заломлення дорівнює нулю, то напрямок променів не змінився. Цей розрахунок застосований для будь-якого променя з паралельного пучка. Оскільки жоден із них не змінить напрямку, то вони залишаться паралельними.
Унаслідок відбивання від плоского дзеркала напрямок променя зміниться, але за законами відбивання кут падіння дорівнюватиме куту відбивання. Якщо пучок складався з паралельних променів, то вони всі падали на поверхню дзеркала під однаковим кутом, а отже й відбиватимуться також під однаковим кутом, що не порушить їхньої взаємної паралельності, як показано на рисунку 3.
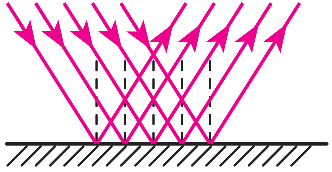
Рис. 3. Відбивання паралельних променів від плоского дзеркала
Відповідь: 1Б, 2А, 3В, 4Г.
ТЕМА: Оптика. Закони відбивання і заломлення світла. Лінза. Дифракційна ґратка.
Завдання скеровано на оцінювання розуміння принципів роботи оптичних елементів.
До оптичного елемента на рисунку, наведеному в умові завдання, пучок променів розширюється, а після – перетворюється на пучок паралельних променів.
Пучок не може стати паралельним після проходження через плоске дзеркало чи дифракційну ґратку за жодних обставин.
Щодо лінз: якщо пучок виходить із фокусу лінзи, після неї промені будуть паралельними, але ця умова набирає різних форм для розсіювальних і збиральних лінз. Для розсіювальної лінзи продовження напрямку променів до лінзи мають збиратись у фокусі за лінзою (рис. 1), тобто пучок до лінзи повинен звужуватись, а для збиральної лінзи пучок має виходити із фокусу перед лінзою, тобто пучок розширюватиметься (рис. 2).
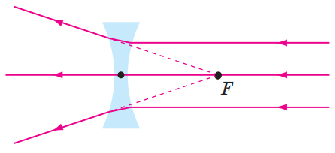
Рис. 1. Хід променів у розсіювальній лінзі
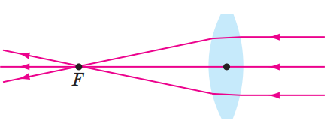
Рис. 2. Хід променів у збиральній лінзі
Відповідь: Б.
ТЕМА: Оптика. Лінза. Оптична сила лінзи.
Завдання скеровано на оцінювання вміння розв’язувати графічні задачі на зображення ходу світлових променів у системах із лінзами.
Оптична сила лінзи
Для визначення фокусної відстані лінзи потрібно проаналізувати рисунок.
Якщо вважати, що точка перетину променю з оптичною віссю зліва від лінзи – це об’єкт, а справа від лінзи – його зображення, то за формулою тонкої лінзи відстань від об’єкта до лінзи
На рисунку
Відповідь: 25.
ТЕМА: Оптика. Квантова фізика. Світлові кванти.
Завдання скеровано на оцінювання розуміння корпускулярно-хвильової природи світла і явищ інтерференції, дифракції, дисперсії і фотоефекту.
Інтерференція – явище накладання хвиль, унаслідок якого в деяких точках простору спостерігають стійке в часі посилення (або послаблення) результувальних коливань.
Дифракція – явище огинання хвилями перешкод або будь-яке інше відхилення поширення хвилі від законів геометричної оптики.
Дисперсія світла – явище розкладання світла у спектр, зумовлене залежністю абсолютного показника заломлення середовища (а отже, і швидкості поширення світла в цьому середовищі) від частоти світлової хвилі.
Фотоефект – це явище взаємодії світла з речовиною, супроводжуване випромінюванням (емісією) електронів.
Тобто інтерференція, дифракція і дисперсія – це явища, пов’язані з хвильовою природою світла.
Корпускулярна природа світла виявляється у фотоефекті, закони якого потрібно знати для правильного розв’язання завдання.
1. Кількість фотоелектронів, яку випромінює катод за одиницю часу, прямо пропорційна інтенсивності світла.
Цей закон фотоефекту можна пояснити й хвильовою теорією світла, адже чим більша інтенсивність світла, тим більше його частинок (фотонів) потрапляє на катод і може брати участь у взаємодії.
2. Максимальна початкова швидкість фотоелектронів збільшується зі збільшенням частоти падного світла й не залежить від його інтенсивності.
Цей закон можна пояснити, якщо розглядати фотоефект лише як явище «вибивання» фотонами електронів із поверхні катода.
Під час зіткнення у катоді з фотоном електрон поглинає енергію фотона, яку визначають за формулою
Ця енергія має бути витрачена на те, щоби вирвати електрон із поверхні катода (цю частку енергії називають роботою виходу
А вона залежить від частоти світла, а не від кількості фотонів, які потрапляють на катод (тобто інтенсивності).
3. Для кожної речовини є максимальна довжина світлової хвилі
Цей закон також пояснюють лише корпускулярною природою світла. Якщо
Відповідь: Г.
ТЕМА: Оптика. Закони заломлення світла. Відносний показник заломлення.
Завдання скеровано на оцінювання вміння визначати відносний показник заломлення речовини.
Для правильного розв’язання завдання потрібно визначити кут падіння
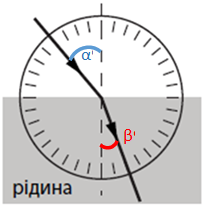
Рис. 1. Кут падіння і кут заломлення за проходження променю через межу повітря і рідини
За законом заломлення:
Абсолютний показник заломлення
За визначенням відносний показник заломлення показує, у скільки разів швидкість поширення світла в середовищі 1 більша (або менша) за швидкість поширення світла в середовищі 2.
У завданні необхідно визначити відносний показник заломлення рідини відносно повітря, тобто обчислити, у скільки разів швидкість світла в рідині менша за швидкість світла в повітрі:
За законом заломлення можна обчислити відносний показник заломлення:
Відповідь: Б.
ТЕМА: Оптика. Лінза. Формула тонкої лінзи.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на закони геометричної оптики й формулу тонкої лінзи.
Дано:
Знайти:
Спочатку потрібно намалювати схему ходу променів із завдання (рис. 1).
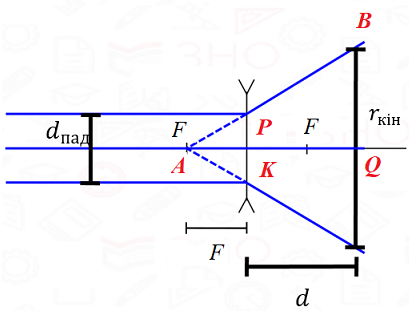
Рис. 1. Схема ходу променів
Затим необхідно перевести всі відстані з умови в одиниці СІ (метр):
Фокусну відстань можна визначити із співвідношень подібності для трикутників
Ці відрізки можна виразити через фізичні величини, пов’язані з ними:
Тепер можна зробити підстановку
Відповідь: 5.
ТЕМА: Оптика. Закони заломлення світла.
Завдання скеровано на оцінювання розуміння явища заломлення світла.
Око бачить межі різних матеріалів через те, що світло заломлюється на межі поділу середовищ.
Це одна з причин того, чому іноді складно зрозуміти чи є перед вами скло, якщо ваш погляд падає на нього перпендикулярно. Коли промінь падає на межу поділу перпендикулярно, його напрямок не змінюється.
Коли в більшій склянці стоїть менша, то промінь заломлюватиметься на межі повітря ззовні й скла зовнішньої склянки, на межі скла зовнішньої склянки й повітря між склянками, на межі повітря між склянками й скла внутрішньої склянки та на межі скла зовнішньої склянки й повітря всередині.
Коли олива заповнює порожнину меншої склянки, а згодом і порожнину між склянками, то промінь світла повинен заломлюватися стільки само разів, скільки й до заповнення. Єдине, що може «стерти» межі між склянками й оливою – це близькість їхніх показників заломлення. Якщо показники заломлення оливи й скла близькі між собою, то для світла всі ці матеріали еквівалентні еквівалентні одному суцільному шару речовини.
Відповідь: Б.
ТЕМА: Фізичні явища й фізичні величини.
Завдання скеровано на оцінювання розуміння поняття фізичного явища й фізичної величини.
Фізичне явище – це зміни в природі, які можна описати за допомогою відповідних фізичних законів.
Фізична величина – це кількісно виражена характеристика тіла або фізичного явища.
Проаналізуймо поняття, наведені в кожному варіанті відповіді.
У варіанті А теплопровідність, остигання і горіння – це фізичні явища, а площа – це фізична величина.
У варіанті Б падіння, електроліз і нагрівання – це фізичні явища, а ньютон – це одиниця вимірювання сили.
У варіанті В гальмування – це фізичне явище, кілограм і діоптрія – це одиниці вимірювання маси й оптичної сили лінзи відповідно, а густина – це фізична величина.
У варіанті Г всі поняття є фізичними явищами.
Відповідь: Г.
ТЕМА:. Оптика. Лінза. Плоске дзеркало.
Завдання скеровано на оцінювання вміння складати схеми ходу променів для розв’язання оптичних задач.
A – збиральна лінза
Б – розсіювальна лінза
В – плоске дзеркало
Г – світловод
Відповідь: B.
ТЕМА: Оптика. Світло, як електромагнітна хвиля.
Завдання скеровано на оцінювання розуміння принципів поширення світла крізь різні середовища й оптичні прилади.
1 Природне світло складається з багатьох хвиль, випромінених різними атомами. Через це в пучку природного світла існує безліч напрямків коливання вектора напруженості електричного поля. Під час поляризації замість хаотичного розподілу напрямків у пучку світла залишається лише той напрямок (або напрямки), які потрібні. Для поляризації використовують спеціальні фільтри – поляроїди (або поляризатори, рис. 1).
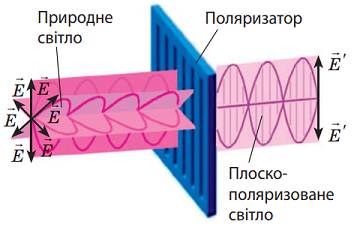
Рис. 1. Принцип роботи поляризатора
Поляризатор працює як щілина, що пропускає лише коливання певного напрямку. Якби електромагнітні хвилі були поздовжніми, то поляризатор не вносив би ніяких змін, але зафіксовано зміни в інтенсивності в експериментах (адже велика частина променів відбивається поляризатором). Тому світло може бути лише поперечною хвилею.
2 Світло, що падає на більшість предметів навколо, відбивається від них. Відбиті промені потрапляють на око, фокусуються кришталиком на сітківку, звідки сигнали через зоровий нерв передаються на обробку в мозок.
3 Принцип роботи лінзи полягає в заломленні променів на двох вигнутих поверхнях. Залежно від типу лінзи й початкової форми променя після проходження лінзи пучок може сфокусуватися в певній точці, розсіятися чи навіть стати паралельним. На рисунку 2 схематично зображено принцип роботи збиральної лінзи, на яку падає паралельний пучок.
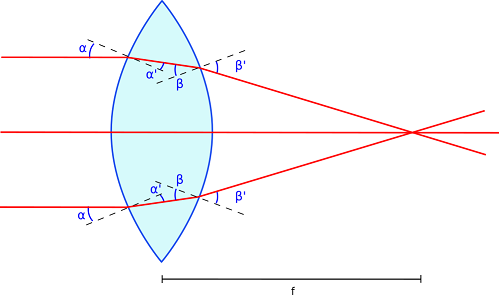
Рис. 2. Принцип роботи збиральної лінзи
4 Сонце – це одне з найбільш широкочастотних джерел випромінювання. Воно випромінює всі електромагнітні хвилі – від радіохвиль і до γ-випромінювання. Через це спектр сонця неперервний. Проте деякі гази поглинають кванти світла з дуже специфічними частотами. Тоді в неперервному спектрі утворюються темні смуги на місці цих поглинутих квантів (рис. 3).

Рис. 3. Вигляд лінійчастих спектрів поглинання
Відповідь: 1В, 2Г, 3Д, 4Б.
ТЕМА: Оптика. Закони відбивання заломлення і поглинання світла. Лінза. Дифракційна ґратка.
Завдання скеровано на оцінювання вміння застосовувати знання про дифракцію і закони геометричної оптики під час аналізу прикладів із життя.
Дифракція – це явище огинання хвилями перешкод.
У разі проходження крізь лінзу фотоапарата електромагнітна хвиля заломлюється, тобто всі процеси відбуваються за законами геометричної оптики. Натомість дифракція – це явище хвильової оптики.
Світлофільтр поглинає частину електромагнітних хвиль, які потрапляють на нього, у результаті чого він пропускає частоти лише певного діапазону. Огинання перешкод у цьому процесі не відбувається.
Під час рентгеноструктурного аналізу рентгенівський промінь падає на кристалічну ґратку. Її можна розглядати як природну дифракційну ґратку, у якій відстані між атомами є прозорими ділянками, а самі атоми – непрозорими. У цьому разі відбувається дифракція, і за утвореною дифракційною картиною аналізують досліджувану поверхню.
Під час перегляду стереофільмів одночасно транслюють дві версії фільму, зняті під невеликим кутом одна до одної. За допомогою окулярів зі спеціальними фільтрами зображення, зняте для лівого ока, блокують на правому й навпаки. Після чого мозок обробляє два різних зображення, отримані з двох очей, і збирає об’ємну картину. Дифракція при цьому не відбувається.
Відповідь: B.
ТЕМА: Оптика. Прямолінійність поширення світла в однорідному середовищі.
Завдання скеровано на оцінювання розуміння принципів освітлення точковими і протяжними джерелами.
Півтінь – це область простору, освітлена деякими з наявних точкових джерел світла або частиною протяжного джерела.
Якщо джерело світла точкове й випромінює в усіх напрямках, то та частина променів, що потрапляє на непрозоре тіло, ніяк не може потрапити у простір за ним (рис. 1).
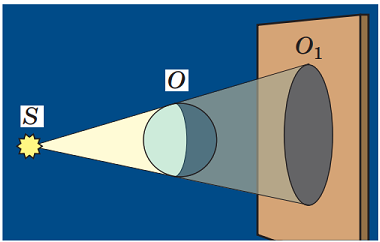
Рис. 1. Утворення повної тіні під час освітлювання точковим джерелом
Якщо тіло освічують кілька точкових джерел, то для кожного з них відбувається те саме. Але оскільки джерела розташовані на певній відстані одне від одного, то кути, під якими утворюватимуться конуси їхніх тіней, трохи відрізнятимуться. Там, де всі конуси перекриваються, утворюється тінь, а в усіх інших областях (де перекривається лише частина конусів або й узагалі лише один) утворюється півтінь (рис. 2).
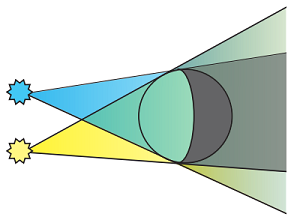
Рис. 2. Утворення півтіні під час освітлення кількома точковими джерелами
Коли джерело протяжне, то можна вважати кожну точку його площі окремим точковим джерелом, тому за такого освітлення також утворюватиметься півтінь (рис. 3).
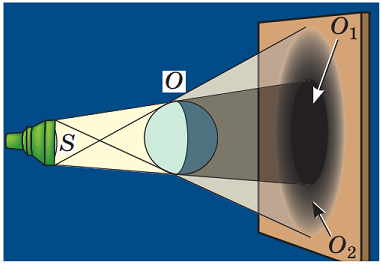
Рис. 3. Утворення півтіні під час освітлення протяжним джерелом
Відповідь: Б.
ТЕМА: Оптика. Закони заломлення світла. Абсолютний і відносний показники заломлення світла.
Завдання скеровано на перевірку вміння розв'язувати задачі, які передбачають оброблення й аналізування результатів експерименту, поданих на схематичному рисунку.
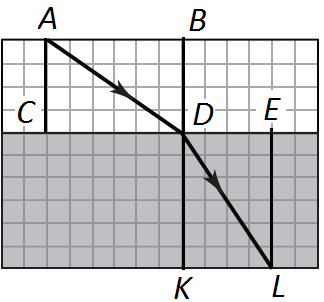
Прямокутники
Промінь падає з повітря, абсолютний показник заломлення якого
Нехай сторона однієї клітинки зошита дорівнює
Відповідь: 1,5.
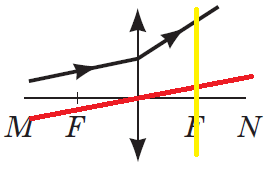
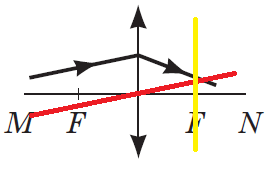
ТЕМА: Оптика. Лінза. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку вміння розв'язувати задачі на зображення ходу світлових променів через тонку лінзу.
З рисунків зрозуміло, що йдеться про збиральну лінзу. Тож після заломлення світловий промінь повинен перетнутися зі своєю пібічною віссю у фокальній площині.
Тому потрібно доповнити рисунок, накресливши побічну вісь і фокальну площину.
A |
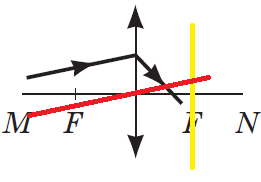
|
Б |
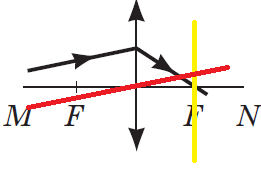
|
B |
|
Г |
|
Заданій умові відповідає тільки останній рисунок.
Відповідь: Г.
ТЕМА: Оптика. Закони відбивання світла.
Завдання скеровано на перевірку вміння розпізнавати прояви хвильових явищ, зокрема, явище дзеркального відбивання світла.
Металева поверхня не прозора, не чорна, тому заломлення і повне поглинання неможливі.
За умовою поверхня полірована, тому відбивання саме дзеркальне.
Відповідь: Б.
ТЕМА: Оптика. Закони заломлення світла.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі із застосуванням законів заломлення світла.
Дано:
Знайти:
Рис. 1. Умова освітлення дна колодязя
Для того, щоби промінь міг освітити дно вузького колодязя, він має бути паралельним до його стінок, тобто перпендикулярним до горизонтальної поверхні (див. рисунок 1).
Рис. 2. Позначення кута
Чорним пунктиром позначено горизонтальний напрямок. Горизонтальна поверхня паралельна до горизонту. Тож можна розглядати поверхню і чорний пунктир як дві паралельні прямі, а дзеркало як їхню січну. Тоді
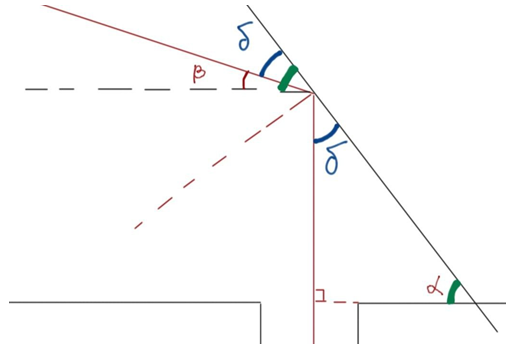
Рис. 3. Позначення кута
Тоді кут між падним променем і поверхнею дзеркала
За умовою відбивання кут падіння дорівнює куту відбивання. Тому кути між падним променем і поверхнею відбивання та відбитим променем і поверхнею відбивання також рівні.
Тож маємо прямокутний трикутник із гострими кутами
Відповідь: 55.
ТЕМА: Оптика. Інтерференція світла. Дисперсія світла. Поляризація світла.
Завдання скеровано на перевірку розуміння застосовності оптичних явищ у техніці.
А Рідкі кристали в дисплеї пропускають лише світло певної поляризації. Під час проходження струму, рідкий кристал змінює свою форму / положення, у результаті чого змінюється і поляризація, яку він пропускає. Саме так формується зображення.
Б Для виготовлення дзеркал скло високої якості вкривають тонким шаром металу, що відбиває світло.
В Для того, щоби зменшити вплив відбивання світла на границях лінз, на їхні поверхні наносять тонкі плівки. У результаті інтерференції для певних довжин хвиль відбиті промені накладаються та гасять одне одного.
Г Лазер є основним джерелом енергії, яка руйнує шар металу під час різання. Усю ця енергію поглинає метал, унаслідок чого підвищується температура в опроміненій ділянці, що й приводить до руйнування.
Д Світловий промінь залишається всередині довгого оптичного волокна завдяки тому, що він падає на стінки волокна під кутом повного внутрішнього відбивання (або більшим кутом), тож замість того, щоби заломлюватися на межі скла й повітря, промінь відбивається і продовжує свій рух усередині.
Відповідь: 1А, 2В, 3Г, 4Д.
ТЕМА: Оптика. Лінза. Плоске дзеркало.
Завдання скеровано на перевірку розуміння принципів роботи основних оптичних елементів.
Плоске дзеркало може створити зображення тіла, що має такий самий розмір, як і сам об’єкт.
Перископ, що складений із кількох дзеркал і дає змогу перенаправити промені від об’єкта до спостерігача, так само може створити лише зображення такого ж розміру, як і об’єкт.
Розсіювальна лінза завжди створює зменшене уявне зображення, а збиральна лінза може створити уявне збільшене зображення, якщо відстань від лінзи до тіла менша за її фокусну відстань.
Відповідь: Г.
ТЕМА: Оптика. Лінза. Оптична сила лінзи.
Завдання скеровано на оцінювання вміння розв’язувати графічні задачі на зображення ходу світлових променів у системах із лінзами.
Оптична сила лінзи
Тобто
За формулою тонкої лінзи відстань
Уважатимемо, що світло рухається зліва направо. Оскільки зображення уявне, то і зображення, і предмет будуть розташовані зліва від лінзи. У такому разі відстань від предмета до лінзи у формулі буде додатною, бо напрямок переміщення від предмета до лінзи збігається із напрямком ходу променів. Відстань від лінзи до зображення у формулі тонкої лінзи буде від’ємною, адже переміщення від лінзи до зображення в цьому разі протилежно направлене до напрямку ходу променю.
Тоді можемо обчислити відстань від лінзи до зображення:
Відповідь: 20.
ТЕМА: Оптика. Інтерференція світла. Дисперсія світла. Поляризація світла.
Завдання скеровано на оцінювання вміння розпізнавати оптичні явища у природних явищах і сучасній техніці.
1. Бензин на асфальті утворює тонку прозору плівку, коефіцієнт заломлення у якої відрізняється від коефіцієнту заломлення повітря. Тож частина сонячних променів відбивається на межі бензин – повітря, а частина заломлюється і відбивається вже від поверхні бензин – асфальт (рисунок 1). Так між цими частинами проміння утворюється різниця ходу. Обидві частини мають одне джерело, тож вони є когерентними й відбувається інтерференція.
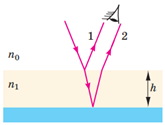
Рис. 1. Схема ходу променів під час інтерференції у плівці бензину
2. Туман виникає тоді, коли водяна пара в повітрі конденсується й утворюється багато водяних крапель. На кожній із них світло розсіюється й утворюється ореол.
3. Біле (сонячне) світло складається із хвиль із різними частотами. Показник заломлення для кожної з таких хвиль трохи відрізняється, тож кут заломлення після проходження крізь поверхню призми для них теж відрізнятимуться. У такий спосіб утворюється кольоровий спектр, як це зображено на рисунку 2.
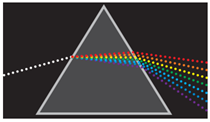
Рис. 2. Утворення дисперсійного спектра
4. Під час перегляду стереофільмів одночасно транслюють дві версії фільму, зняті під невеликим кутом одна до одної. Версії для кожного ока мають різну поляризацію, тому окуляри з поляризаторами дають змогу блокувати зображення, зняте для лівого ока на правому, і навпаки. Після цього, мозок обробляє два різнi зображення, отримані з двох очей, і «збирає» об’ємну картину.
Відповідь: 1В, 2А, 3Д, 4Б.
ТЕМА: Оптика. Прямолінійність поширення світла в однорідному середовищі.
Завдання скеровано на оцінювання розуміння принципів прямолінійного поширення світла і їхнього зв’язку з фазами Місяця.
Повний місяць спостерігають тоді, коли освітлену частину Місяця повністю видима на неосвітленій частині Землі. Освітлена частина Місяця на рисунку позначена світло-сірим, а неосвітлену – темно-сірим.
У випадках А і В лише половина освітленої частини Місяця видима на Землі. Це перша й остання чверть місячної фази відповідно. У випадку Б освітлену частину видно повністю – це повний місяць. У випадку Г видно менше половини освітленої частини Місяця – це також остання чверть місячної фази.
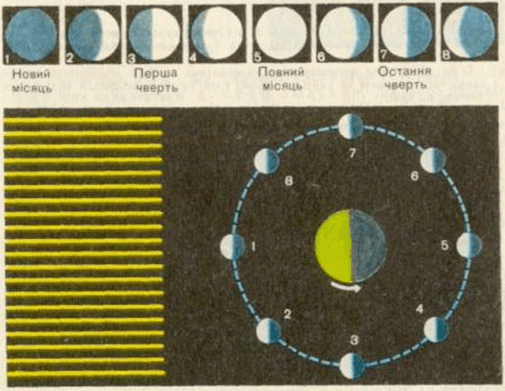
Рис. 1. Місячні фази залежно від положення Місяця (біло-синє коло) відносно Землі (жовто-синє коло) і Сонця (сонячні промені позначено жовтими лініями)
Відповідь: Б.
ТЕМА: Оптика. Побудова зображень, які дає плоске дзеркало.
Завдання скеровано на перевірку розуміння принципів побудови зображень у дзеркалі.
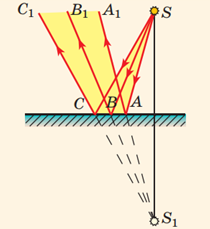
Рис. 1. Схема побудови зображення в дзеркалі
Відстань між дзеркалом й об’єктом дорівнює відстані між дзеркалом і зображенням.
Якщо тіло перебувало на відстані 15 см від дзеркала, то після того, як його відсунули, воно опинилося на відстані 30 см від дзеркала. На такій самій відстані буде і його зображення.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла.
Завдання скеровано на перевірку вміння застосовувати закони відбивання світла для розв’язування задач із геометричної оптики.
За законом відбивання світла падний промінь, відбитий промінь і перпендикуляр до поверхні відбивання, проведений із точки падіння променя, лежать в одній площині. А також кут відбивання
Зобразімо це на рисунку.
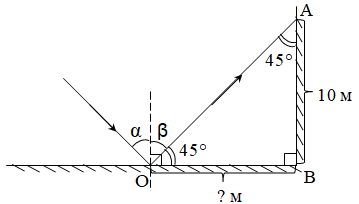
За умовою кут
Найкоротшою відстанню від точки падіння променя на калюжу до стіни школи є перпендикуляр, проведений від цієї точки до стіни школи. Тоді
Відповідь: 10.
ТЕМА: Коливання і хвилі. Оптика. Повне відбивання.
Завдання скеровано на перевірку розуміння явища повного відбивання і вміння бачити (виявляти) це явище в реальних прикладах.
Повне відбивання світла спостерігають, коли заломлення світла немає, тобто світло повністю відбивається від межі поділу із середовищем меншої оптичної густини.
Світловод – це волокно зі скла чи штучного матеріалу, а також трубка або плівка для передавання світла навіть на дуже великі відстані завдяки ефекту багаторазового повного внутрішнього відбивання. Світловоди використовують у телетрансляції, у медичних приладах для спостереження органів ізсередини (ендоскопія) тощо.
Коли світло поширюється в тумані, то воно розсіюється – багато разів невпорядковано змінює напрямок, відбиваючись від великої кількості маленьких крапельок води.
Якщо розмір отвору, крізь який проходить світло, такого ж порядку, як довжина світлової хвилі, то спостерігають дифракцію – огинання країв вузького отвору та проникнення світла в ділянку геометричної тіні. Наприклад, під час світіння ліхтаря промені відбиваються від його обмежувальної поверхні й на краях напрямленого пучка світла можна побачити дифракцію.
Отже, повне відбивання спостерігають під час поширення світла у світловоді.
Відповідь: Г.
ТЕМА: Оптика. Лінза. Оптична сила лінзи.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з оптики на основі аналізу оптичних схем.
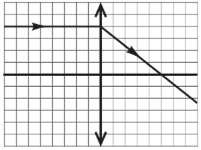
Рис. 1. Умова завдання
Промені, паралельні головній оптичній осі, збираються у фокусі збиральної лінзи. За рисунком 1 фокусна відстань
Оптичну силу лінзи можна визначити за формулою
Відповідь: Г.
ТЕМА: Природні явища.
Завдання скеровано на перевірку вміння поєднувати фізичні явища з їхніми проявами в природі й використанням у техніці.
Явище, коли заломлення світла немає, тобто світло повністю відбивається від межі поділу із середовищем меншої оптичної густини, називають явищем повного внутрішнього відбивання.
А Сонячне затемнення – це явище, під час якого Місяць відкидає повну тінь на поверхню Землі.
Б Крила метелика складені з хітинових лусочок, які утворюють дифракційну ґратку.
В Веселка – це наслідок дисперсії сонячного світла на краплинках води в повітрі.
Г Світло поширюється у світловоді завдяки повному внутрішньому відбиванню, адже оптична густина скла більша за оптичну густину повітря зовні.
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.
Завдання скеровано на перевірку розуміння поширення світла в різних середовищах.
Фізичну величину, якою характеризують оптичну густину середовища, і яка показує, у скільки разів швидкість
Звідси
За умовою завдання час
Відповідь: 16.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку знання і розуміння явищ геометричної і хвильової оптики.
Заломлення ‒ це явище зміни напрямку поширення хвилі під час її проходження через плоску межу двох однорідних середовищ.
Дифракція ‒ це явище потрапляння світлових хвиль в область геометричної тіні, тобто відхилення їх від прямолінійного поширення.
Дисперсія ‒ це явище залежності показника заломлення середовища від довжини електромагнітної хвилі.
Інтерференція ‒ це явище накладання когерентних хвиль, унаслідок якого спостерігається стійка в часі картина посилення їх та послаблення в різних точках простору.
Відповідь: 1Б, 2Д, 3А, 4Г.
ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає плоске дзеркало.
Завдання скеровано на перевірку розуміння побудови зображень у плоскому дзеркалі.
Загальні характеристики зображень у плоских дзеркалах
1. Плоске дзеркало дає уявне зображення предмета: частина відбитих від дзеркала променів потрапляє до вашого ока і вам здається, що відбиті за законом відбивання промені виходять із точки
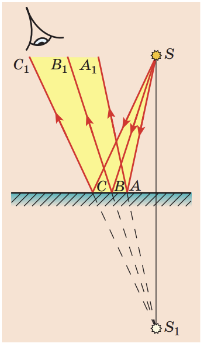
2. Зображення предмета в плоскому дзеркалі та власне предмет є симетричними відносно поверхні дзеркала:
1) зображення предмета дорівнює за розміром самому предмету;
2) зображення предмета розташоване на тій самій відстані від поверхні дзеркала, що й предмет;
3) відрізок, який сполучає точку на предметі з відповідною їй точкою на зображенні, є перпендикулярним до поверхні дзеркала.
Тому зображенням точки
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки й використання їх для визначення довжини світлової хвилі.
Завдання скеровано на перевірку знання принципу дії дифракційної ґратки й розуміння формули, що описує її.
Запишімо формулу дифракційної ґратки:
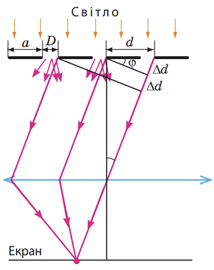
Обчислімо спочатку синус кута
Відповідь: 30.
ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку знання і вміння будувати зображення в тонкій лінзі і плоскому дзеркалі.
Побудуймо хід променів відповідно до умови завдання: після проходження крізь лінзу (один промінь паралельно головній оптичній осі і далі уявно через фокус лінзи, а другий промінь ‒ через оптичний центр лінзи не заломлюючись) промені за законами відбивання відбиваються від плоского дзеркала під тими самими кутами, що й упали на дзеркало, і знову проходять крізь лінзу (див. рисунок).
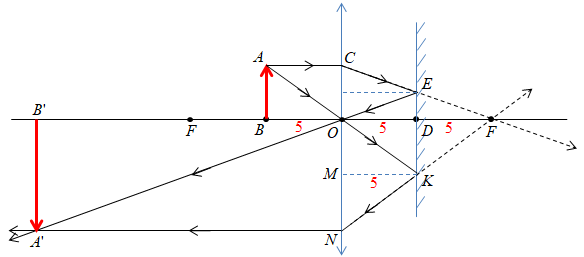
1. Розгляньмо прямокутні
Розгляньмо прямокутні
Розгляньмо прямокутні
Отже,
Відповідь: 20.
2. Як уже було доведено в пункті 1,
Відповідь: 2.
Відповідь: 1. 20. 2. 2.
ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.
Завдання скеровано на перевірку знання і розуміння понять абсолютний і відносний показники заломлення світла.
Фізичну величину, яка характеризує оптичну густину середовища й показує, у скільки разів швидкість
Звідси виразімо швидкість
Також показник заломлення можна визначити як відношення синуса кута падіння до синуса кута заломлення:
Підставімо значення показника заломлення у формулу для швидкості:
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Закони заломлення світла.
Завдання скеровано на перевірку знання, розуміння і застосування законів відбивання і заломлення світла.
Як зображено на рисунках А і Б, частина пучка зазнає дзеркального відбивання на верхній або нижній поверхні пластинки. У точках, де світло відбивається, уявно будуємо перпендикуляр до межі середовищ, і тоді за законами відбивання кут падіння дорівнює куту відбивання.
Також на рисунках Б і В заломлення показано правильно. Оскільки оптична густина скла більша за оптичну густину повітря, кут заломлення світла у склі має бути меншим від кута падіння світла з повітря.
На рисунку В на поверхнях плоскопаралельної пластинки світло двічі зазнає заломлення (після цього пучок поширюється в тому самому напрямку, але зміщується). Це правильно.
На рисунку Г не показано заломлення внаслідок перетинання світлом нижньої грані пластинки. Це неправильно.
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Лінза. Оптична сила лінзи. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння розрахувати оптичну силу лінзи, виконавши необхідні геометричні побудови.
Оберненою до фокусної відстані лінзи фізичну величину, якою характеризують лінзу, називають оптичною силою лінзи. Оптичну силу лінзи позначають символом
Отримане зображення (див. рисунок в умові) дійсне, зменшене й перевернуте. Таке зображення могла дати лише збиральна лінза. Оптична сила збиральної лінзи є додатною. Тому формула тонкої лінзи така:
Отже, потрібно дізнатися місцеположення лінзи. За правилами побудови зображень у тонкій лінзі з’єднаймо точку
З’єднаймо точку
Отже, на перетині променів
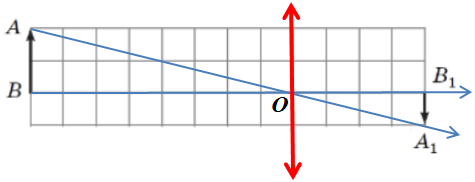
За рисунком можна визначити відстань
Визначмо відстань
Обчислімо оптичну силу лінзи:
Відповідь: 6,25.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку розуміння і застосування механічних й електромагнітних явищ.
Виникнення вихрового електричного поля або електричної поляризації провідника під час зміни магнітного поля або під час руху провідника в магнітному полі називають електромагнітною індукцією. Важливим наслідком електромагнітної індукції для генерування електричного струму є виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється.
Період
Тому, вимірявши довжину нитки й період коливань маятника, можна визначити прискорення вільного падіння в певній місцевості.
У радіолокації використовують ультракороткі електромагнітні хвилі частотою від
Просвітлення оптики ‒ збільшення прозорості деталей оптичних систем (лінз, оптичних призм) нанесенням на їхні поверхні тонкого шару діелектрика (або кількох шарів) із показником заломлення, меншим, ніж у матеріалу оптичної деталі. Просвітлення оптики ‒ результат інтерференції світла, яке відбивається від передньої та задньої границь цього шару (просвітлювальної плівки). За належного добору речовини й товщини плівки для певного кута падіння відбиті світлові хвилі певної довжини можуть повністю погасити одна одну.
Відповідь: 1В, 2Б, 3Д, 4Г.
ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку вміння будувати зображення в тонкій лінзі.
На рисунку зображено розсіювальну лінзу (зверніть увагу на позначення її кінців). Через оптичний центр лінзи точку
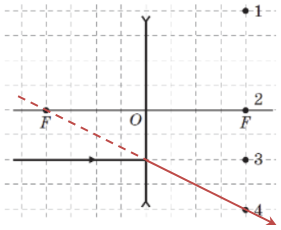
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.
Завдання скеровано на перевірку знання і розуміння формули тонкої лінзи й побудови зображень у тонкій лінзі.
Оптичну силу
Математична залежність між відстанню d від предмета до лінзи, відстанню f від зображення предмета до лінзи і фокусною відстанню F лінзи представлена формулою тонкої лінзи:
Розгляньмо схематичну побудову зображення
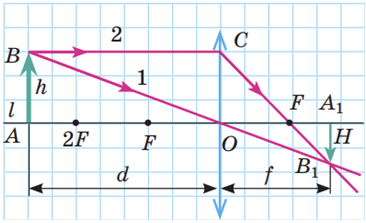
За умовою об᾽єктив фотоапарата дає зображення дерева, зменшене в
Відношення лінійного розміру
Відстань
Тепер можна визначити оптичну силу об᾽єктива фотоапарата:
Відповідь треба округлити до цілого числа (до одиниць), отже,
Відповідь: 40.
ТЕМА: Коливання і хвилі. Оптика. Інтерференція світла, її практичне застосування.
Завдання скеровано на перевірку знання і розуміння явища інтерференції.
Хвилі, які відповідають умовам когерентності, називають когерентними хвилями.
Умови когерентності хвиль:
1) хвилі повинні мати однакову частоту (відповідно й довжину);
2) різниця
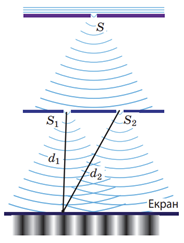
Ідеальними джерелами когерентних світлових хвиль є лазери ‒ оптичні квантові генератори.
Коли хвилі надходять у точку
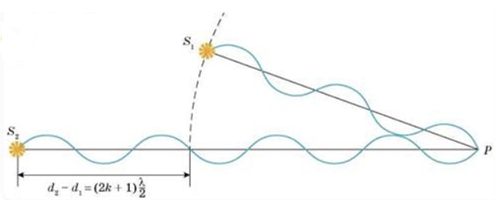
Це відбудеться за умови, що на відрізку
За умовою довжина хвилі випромінювання
A
Б
B
Г
Отже, правильна відповідь Г ‒
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку знання і застосування правил побудови зображень, які дає розсіювальна і збиральна лінзи.
Уявне зображення ‒ це оптичне зображення, утворене променями, які насправді не перетинаються, а перетинаються тільки їхні уявні продовження.
Розсіювальна лінза завжди дає уявне, зменшене, пряме зображення предмета.
А збиральна лінза дає уявне зображення лише в разі розміщення предмета між лінзою і фокусом.
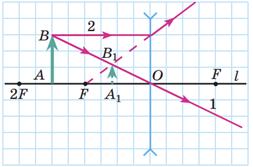
Приклад побудови зображення в розсіювальній лінзі
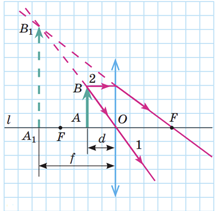
Приклад побудови уявного зображення в збиральній лінзі
Отже, обидві лінзи, і розсіювальна, і збиральна, можуть давати уявне зображення.
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки й використання їх для визначення довжини світлової хвилі.
Завдання скеровано на перевірку розуміння будови дифракційної ґратки.
Скористаймося формулою дифракційної ґратки (
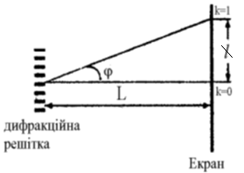
Скористаймося малокутовим наближенням (апроксимація малих кутів), яке зазначено в умові:
Отримаємо формулу для визначення
Відповідь: 30.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла.
Завдання скеровано на перевірку розуміння законів відбивання світла й уміння будувати промені, які падають і відбиваються від плоского дзеркала.
Закони відбивання світла:
1. Промінь, що падає, промінь відбитий і перпендикуляр до поверхні відбивання, проведений із точки падіння променя, лежать в одній площині.
2. Кут відбивання дорівнює куту падіння.
Зробімо додаткові побудови ‒ перпендикуляри в точках падіння променів на обох дзеркалах.
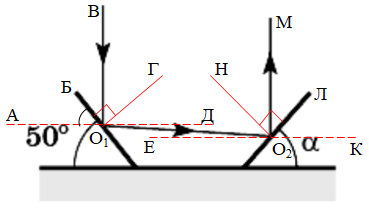
Перенесемо паралельним переносом горизонтальну поверхню в точки падіння променів
Тоді
Розгляньмо дві паралельні прямі
Тоді й
Перейдімо до другого дзеркала й розгляньмо кут падіння
Тоді обчислімо кут
Промінь
Тоді
Тобто друге дзеркало розташоване до поверхні столу під кутом
Відповідь: 40.
ТЕМА: Коливання і хвилі. Оптика. Оптика. Абсолютний і відносний показники заломлення.
Завдання скеровано на перевірку знання і застосування законів заломлення геометричної оптики.
Закони заломлення світла:
1. Промінь, що падає, промінь заломлений і перпендикуляр до межі поділу двох середовищ, установлений із точки падіння променя, лежать в одній площині.
2. Відношення синуса кута падіння до синуса кута заломлення для двох даних середовищ є величиною незмінною:
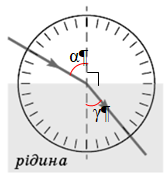
Повне коло становить
Показнику заломлення рідини дорівнюватиме значення виразу
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Оптика. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку вміння застосовувати знання про побудову зображень, які дає тонка лінза.
Розгляньмо спочатку побудову зображення предмета
На рисунку в умові завдання бачимо, що промінь, який пройшов крізь лінзу, перетинає головну оптичну вісь на такій самій відстані, що й промінь, який падає на лінзу. Тобто, можна зробити висновок, що це подвійна фокусна відстань.
Підтвердьмо це побудовою точки
А тепер побудуймо зображення точки
Далі через оптичний центр лінзи (точку
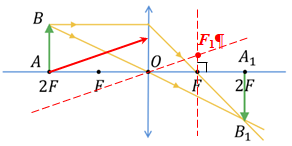
Після проходження крізь лінзу промінь пройде через побічний фокус
На рисунку в умові завдання зображено саме цей випадок побудови. Отже, відстань від лінзи до точок перетину променів з головною оптичною віссю ‒ це подвійна фокусна відстань
Оптична сила лінзи ‒ це фізична величина, яка характеризує лінзу та є оберненою до фокусної відстані лінзи:
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Оптика. Закони відбивання світла. Побудова зображень, які дає плоске дзеркало.
Завдання скеровано на перевірку знання і розуміння закону відбивання світла і вміння застосовувати його до побудови зображення світлового променя, які дає плоске дзеркало.
Закони відбивання світла:
1. Промінь, що падає, промінь відбитий і перпендикуляр до поверхні відбивання, проведений із точки падіння променя, лежать в одній площині.
2. Кут відбивання дорівнює куту падіння:
Як бачимо з рисунка, даного в умові, кут
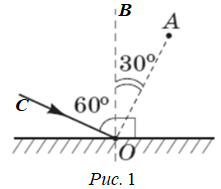
За другим законом кут відбивання
За означенням променя, що падає, і за першим законом відбивання
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння застосовувати формулу тонкої лінзи.
Якщо лінза дає дійсне зображення, то це збиральна лінза.
Запишімо формулу тонкої лінзи:
Скористаймося ще відношенням розмірів і відстаней. Відношення лінійного розміру
За умовою зображення предмета втричі більше за предмет:
Отже,
Визначімо відстань
Тоді відстань
Обчислімо фокусну відстань цієї лінзи:
Відповідь: 15.
ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.
Завдання скеровано на перевірку знання і розуміння фізичного змісту відносного показника заломлення.
Відносний показник заломлення
Отже, обчислімо відношення швидкостей світла в середовищах з різними показниками заломлення відповідно до умови:
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки та використання їх для визначення довжини світлової хвилі.
Завдання скеровано на перевірку розуміння будови дифракційної ґратки.
Скористаймося формулою дифракційної ґратки
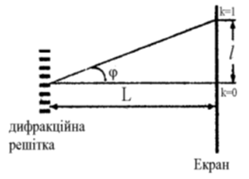
Скористаймося малокутовим наближенням (апроксимація малих кутів):
Отримаємо формулу для визначення
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Повне відбивання.
Завдання скеровано на перевірку знання і розуміння оптичного явища ‒ повного внутрішнього відбивання.
Явище, коли заломлення світла немає, тобто світло повністю відбивається від межі поділу із середовищем меншої оптичної густини, називають явищем повного внутрішнього відбивання.
Найменший кут падіння, починаючи з якого вся світлова енергія повністю відбивається від межі поділу двох прозорих середовищ, називають граничним кутом повного внутрішнього відбивання
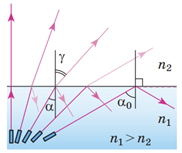
За умовою завдання світло переходитиме з речовини, яка оптично густіша за повітря. На рисунку нижче зображена ситуація, коли промінь йде по межі двох середовищ. Якщо далі збільшувати кут падіння, то промінь повністю відбиватиметься в речовині, не заломлюватиметься і не виходитиме в повітря.
Оскільки промені від точкового джерела розходяться в усі боки, то виберемо з них ті, які падають під кутом
Для двох середовищ відношення синуса кута падіння
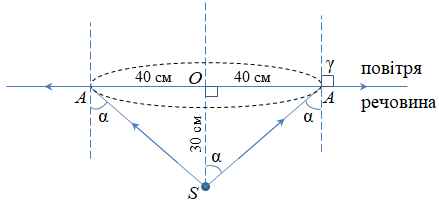
Показник заломлення повітря дорівнює
Щоб визначити
Якщо один катет
Тоді
Підставимо це значення в формулу для показника заломлення і обчислимо його:
Відповідь: 1,25.
ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння застосовувати формулу тонкої лінзи.
Зробимо схематичний збільшений рисунок відповідно до фотографії в умові завдання.
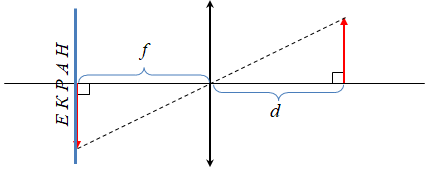
Лінза є збиральною, оскільки дає дійсне зображення: на екрані з іншого від предмета (нитки розжарення) боку лінзи зображення утворюють саме заломлені промені, що пройшли крізь лінзу, а не їхні продовження з того самого боку лінзи, що й предмет.
З фото видно, що відстань від предмета до лінзи
Зваживши на це, запишімо формулу тонкої лінзи:
де
Фізичну величину, яка характеризує заломні властивості лінзи й обернена до її фокусної відстані, називають оптичною силою
Отже, дістанемо формулу для визначення оптичної сили лінзи відповідно до умов завдання:
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки й використання їх для визначення довжини світлової хвилі.
Завдання скеровано на перевірку розуміння поняття дифракційної ґратки й утворення спектрів різних порядків.
Скористаймося формулою дифракційної ґратки
Вимірюючи кут
Ось приклад зображення дифракційного спектру. Інтерференційні максимуми

Запишімо формули для визначення довжин хвиль для максимумів
Дифракційна ґратка та сама, тож період однаковий. Оскільки спектри перекриваються, то
Поділимо ліві і праві частини формул:
Звідси визначмо довжину хвилі в спектрі
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика.
Завдання скеровано на перевірку знання і розуміння оптичних явищ геометричної і хвильової оптики.
1) Поширення світла в тумані ‒ А. Розсіювання світла туманом відбувається через взаємодію світлових променів з малими частинками води або інших речовин у тумані. Коли світло зустрічає ці частинки, воно розсіюється в усі напрямки, що дає змогу спостерігати туман як прозору або розсіяну масу, а не яскравий промінь.
2) Світіння ліхтаря ‒ Б. Ліхтар є джерелом світла, випромінювачем.
3) Проходження світла крізь вузький отвір ‒ Г. Дифракція ‒ явище обгинання хвилями перешкод або будь-яке інше відхилення поширення хвилі від законів геометричної оптики.
4) Поширення світла у світловоді ‒ В. Повіне відбивання світла ‒ явище, за якого заломлення світла відсутнє (світло повністю відбивається від середовища з меншою оптичною густиною).
Відповідь: 1А, 2Б, 3Г, 4В.
ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку знання і розуміння побудови зображень у різних оптичних пристроях.
Побудова зображень, одержаних за допомогою розсіювальної лінзи, показує, що розсіювальна лінза завжди дає уявне, зменшене, пряме зображення предмета.
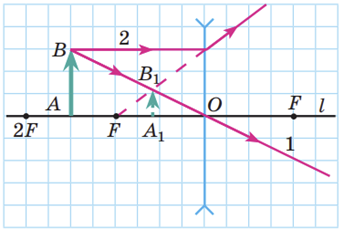
Зображення предмета в плоскому дзеркалі є уявним і прямим, дорівнює за розміром самому предмету й розташоване на тій самій відстані від дзеркала, що й предмет.
Перископ ‒ оптичний прилад, що дає змогу спостерігати за об’єктом, що перебуває в горизонтальній площині, яка не збігається з горизонтальною площиною ока спостерігача. Найпростіша конструкція пристрою ‒ це вертикальна труба з двома, нахиленими під кутом
Якщо ж предмет розташований за подвійним фокусом збиральної лінзи, його зображення, одержане за допомогою лінзи, є дійсним, зменшеним, перевернутим. Таке зображення, наприклад, на сітківці ока або на матриці фотоапарата.
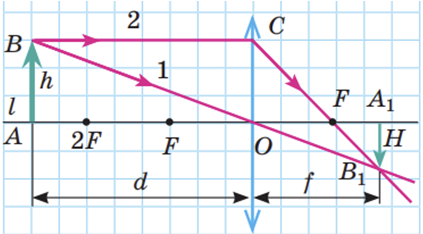
В усіх інших варіантах розташування предмета відносно лінзи орієнтуємося за таблицею.
| Місце розташування предмета | Характеристика зображення в лінзі | |
|---|---|---|
| збиральній | розсіювальній | |
| За подвійним фокусом лінзи |
дійсне, зменшене, обернене | уявне, зменшене, пряме |
| У подвійному фокусі |
дійсне, рівне, обернене | |
| Між фокусом і подвійним фокусом лінзи |
дійсне, збільшене, обернене | |
| У фокусі лінзи |
зображення не існує | |
| Між лінзою і фокусом |
уявне, збільшене, пряме | |
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки.
Завдання скеровано на перевірку знання і розуміння будови дифракційної ґратки й уміння визначати її період.
Періодом ґратки або сталою ґратки називають загальну ширину
Визначмо загальну довжину
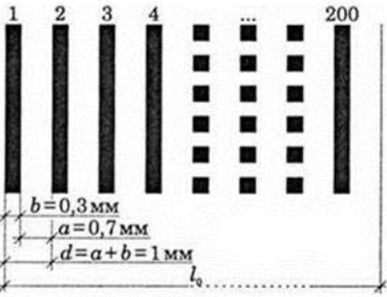
Відповідно до умови обчислімо довжину
Визначмо період дифракційної ґратки:
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Оптична сила лінзи. Формула тонкої лінзи. Побудова зображень, які дає тонка лінза.
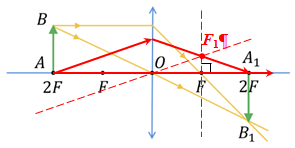
Завдання скеровано на перевірку знання і розуміння побудови зображень, які дає тонка лінза, уміння застосовувати формулу тонкої лінзи.
За умовою розміри предмета та його зображення збігаються. А це можливо тоді, коли предмет розташований у подвійному фокусі збиральної лінзи. Тоді зображення отримуємо теж у подвійному фокусі лінзи (за побудовою), дійсне, перевернуте, рівне за розмірами предмету (див. рисунок).
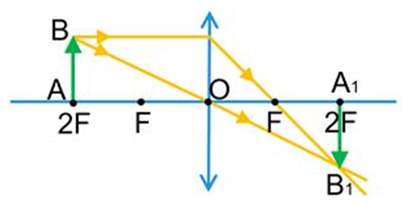
За умовою відома відстань між предметом
Скористаймося формулою тонкої лінзи, щоб визначити її оптичну силу
Обчислімо оптичну силу лінзи:
Відповідь: 2,5.
ТЕМА: Коливання і хвилі. Оптика. Закони заломлення світла.
Завдання скеровано на перевірку знання і розуміння законів заломлення світла.
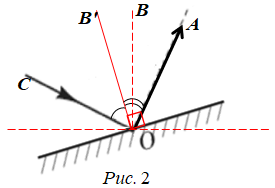
Світловий промінь
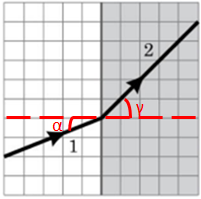
Зміну напрямку поширення світла в разі його проходження через межу поділу двох середовищ називають заломленням світла. Промінь
Оскільки кут падіння менший за кут заломлення, то це означає, що промінь переходить з оптично густішого середовища в оптично менш густе. І тоді швидкість світла в середовищі
Під час переходу з одного середовища в інше швидкість
Тобто твердження Г – неправильне.
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Побудова зображень, які дає плоске дзеркало.
Завдання скеровано на перевірку знання і розуміння законів відбивання, правил побудови зображень, які дає плоске дзеркало.
За умовою промінь
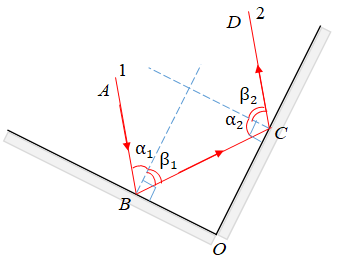
Отже,
За законами відбивання кут падіння дорівнює куту відбивання, отже,
Знайдімо суму кутів
Тепер розгляньмо
Отже,
Відповідь: 90.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання заломлення світла.
Завдання скеровано на перевірку знання і розуміння законів поширення світла.
Кут
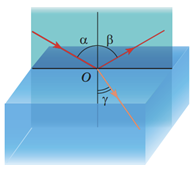
З огляду на визначення, кути
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Прямолінійність поширення світла в однорідному середовищі.
Завдання скеровано на перевірку знання і розуміння закону прямолінійного поширення світла, а також понять повної тіні й півтіні.
Джерело світла, яке випромінює світло однаково в усіх напрямках і розмірами якого, зважаючи на відстань до місця спостереження, можна знехтувати, називають точковим джерелом світла.
Найкращим прикладом точкових джерел світла є зорі, адже ми спостерігаємо їх із Землі, тобто з відстані, що в мільйони разів перевищує розміри самих зір.
Джерела світла, що не є точковими, називають протяжними джерелами світла.
Повна тінь ‒ це область простору, у яку не потрапляє світло від джерела.
Якщо джерело світла є точковим, тінь від предмета буде чіткою. У цьому разі утворюється тільки повна тінь.

Якщо тіло освітлене протяжним джерелом світла, то утворюється тінь із нечіткими контурами, тобто утворюється не тільки повна тінь, а ще й півтінь.

Півтінь ‒ це область простору, освітлена деякими з наявних точкових джерел світла або частиною протяжного джерела.
Повну тінь і півтінь пояснюють відповідно до закону прямолінійного поширення світла.
Отже, правильна відповідь ‒ Б.
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку знання і розуміння законів поширення променя в збиральній лінзі, уміння схематично зобразити його хід.
Спочатку добудуймо фокальну площину, яка проходить через фокус лінзи точку
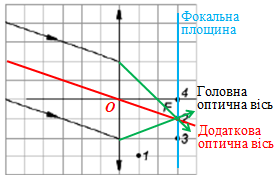
Далі побудуймо додаткову оптичну вісь, що проходить так само, як і головна, крізь оптичний центр лінзи точку
Отримуємо точку перетину додаткової оптичної осі і фокальної площини (див. схематичний рисунок). Ця точка збіглася з точкою
Будь-який пучок паралельних променів, навіть якщо ці промені не паралельні головній оптичній осі, після заломлення в збиральній лінзі завжди перетинаються в одній точці ‒ у головному фокусі
Тож після проходження крізь збиральну лінзу промені перетнуться в точці
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає плоске дзеркало.
Завдання скеровано на перевірку знання і розуміння побудови зображення в плоскому дзеркалі.
Загальні характеристики зображень у плоских дзеркалах:
1. Плоске дзеркало дає уявне зображення предмета.
2. Зображення предмета в плоскому дзеркалі й сам предмет є симетричними відносно поверхні дзеркала, і це означає:
1) зображення предмета дорівнює за розміром самому предмету;
2) зображення предмета розташоване на тій самій відстані від поверхні дзеркала, що й предмет;
3) відрізок, який сполучає точку на предметі з відповідною їй точкою на зображенні, є перпендикулярним до поверхні дзеркала.
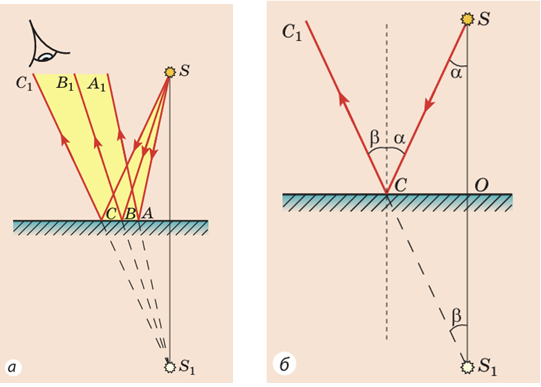
Отримання зображення точкового джерела світла
в плоскому дзеркалі:
Якщо між дзеркалами
Для побудови зображення в системі з двох дзеркал достатньо уявно продовжити їхні площини після перетину й будувати зображення відносно кожної площини дзеркал окремо, уважаючи, що утворене одним дзеркалом зображення можна вважати предметом для другого ‒ принцип Гюйгенса. Усього в дзеркалах, установлених під кутом
дзеркал
Відповідь:
ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.
Завдання скеровано на перевірку знання і розуміння абсолютного показника заломлення середовища.
Фізичну величину, яка характеризує оптичну густину середовища й показує, у скільки разів швидкість поширення світла в середовищі
Звідси можемо визначити швидкість поширення світла в середовищі
Формулу, що зв’язує довжину хвилі
Обчислімо добутки довжини хвилі
1)
2)
3)
1)
Відповідь: 1В, 2Б, 3А, 4Г.
ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.
Завдання скеровано на перевірку знання і розуміння побудови зображень предмета в тонкій збиральній лінзі, а також вміння визначати потрібні величини за допомогою формули тонкої лінзи.
Для визначення відстані між лінзою та зображенням предмета скористаймося формулою тонкої лінзи:
Фізичну величину, яка характеризує лінзу та є оберненою до фокусної відстані
Запишімо формулу тонкої лінзи в такому вигляді:
За умовою предмет розташовано в подвійному фокусі лінзи, оскільки
Оскільки зображення предмета дійсне, то відстань
Визначмо відстань
Отже, зображення отримаємо теж в подвійному фокусі лінзи, то
Відповідь: B.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла.
Завдання скеровано на перевірку знання і розуміння прямолінійного поширення світла, законів відбивання світлових променів від плоского дзеркала й уміння розв’язувати задачі, використовуючи комбінації кутів.
Промінь, що падає під кутом
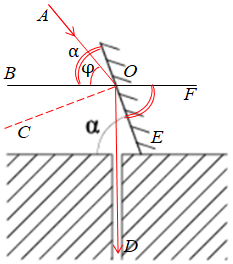
Складімо рівняння для визначення кута нахилу дзеркала до горизонту ‒ кута
Відповідь: 70.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Закони заломлення світла.
Завдання скеровано на перевірку знання, розуміння і застосування законів відбивання і заломлення світла.
Як зображено на рисунках А і Б, частина пучка зазнає дзеркального відбивання на верхній або нижній поверхні пластинки. У точках, де світло відбивається, уявно будуємо перпендикуляр до межі середовищ, і тоді за законами відбивання кут падіння дорівнює куту відбивання.
Також на рисунках Б і В заломлення показано правильно. Оскільки оптична густина скла більша за оптичну густину повітря, кут заломлення світла в склі має бути меншим від кута падіння світла з повітря.
На рисунку В на поверхнях плоскопаралельної пластинки світло двічі зазнає заломлення (після цього пучок поширюється в тому самому напрямку, але зміщується). Це правильно.
На рисунку Г не показано заломлення внаслідок перетинання світлом нижньої грані пластинки. Це неправильно.
Відповідь: Г.
ТЕМА: Коливання і хвилі. Оптика. Оптична сила лінзи. Формула тонкої лінзи.
Завдання скеровано на перевірку знання і розуміння будови ока й уміння застосовувати формулу тонкої лінзи.
Відстанню найкращого зору називають найменшу відстань, на якій око бачить предмет практично не напружуючись. Для людини з нормальним зором відстань найкращого зору становить приблизно
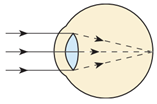
В умові завдання йдеться про далекозору людину. У разі далекозорості фокус оптичної системи ока в ненапруженому стані розташований за сітківкою (див. рисунок) і зображення предметів на сітківці також є нечітким, розмитим. Відстань найкращого зору в цьому разі більша за
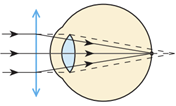
Запишімо формулу тонкої лінзи для випадку, коли людина читає без окулярів:
Якщо окуляри дібрано правильно, людині буде зручно читати, тримаючи книжку на відстані
Визначімо оптичну силу окулярів, розв’язавши систему рівнянь (від другого рівняння віднімемо перше):
Відповідь: 1,5.
ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Побудова зображень, які дає плоске дзеркало.
Завдання скеровано на перевірку знання і розуміння законів відбивання, правил побудови зображень, які дає плоске дзеркало.
Продовжмо спочатку відбитий промінь з точки
Визначімо кут, під яким промінь
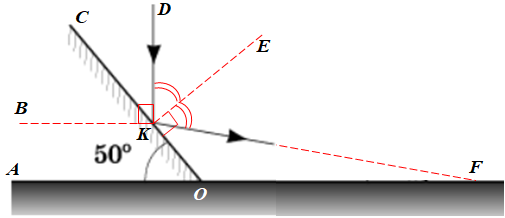
Оскільки за умовою промінь
Тепер можемо визначити кут падіння променя на дзеркало ‒
За законами відбивання кут відбивання променя дорівнюватиме куту падіння:
Тепер розгляньмо
А оскільки сума кутів трикутника дорівнює
Відповідь: 10.
ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.
Завдання скеровано на перевірку знання і розуміння законів поширення променя в збиральній лінзі, уміння схематично зобразити його хід.
Спочатку добудуймо фокальну площину, яка проходить через фокус лінзи точку
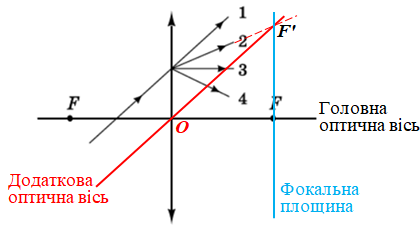
Далі побудуймо додаткову оптичну вісь, що проходить так само, як і головна, крізь оптичний центр лінзи точку
Отримуємо точку перетину додаткової оптичної осі і фокальної площини (див. схематичний рисунок). Це є додатковий фокус
Будь-який пучок паралельних променів (у цій умові це промінь, що падає на лінзу і промінь, що поширюється вздовж додаткової оптичної осі), навіть якщо ці промені не паралельні головній оптичній осі, після заломлення в збиральній лінзі завжди перетинаються в одній точці ‒ у головному фокусі
Тож після проходження крізь збиральну лінзу промінь поширюватиметься вздовж напрямку
Відповідь: Б.