Розділ: Електродинаміка
Тема: Основи електростатики
Кількість завдань: 101
ТЕМА: Електродинаміка. Основи електростатики. Робота електричного поля при переміщенні заряду.
Завдання скеровано на перевірку знання і розуміння поняття роботи електричного поля при переміщенні заряду.
За означенням робота
Поле однорідне, тому сила
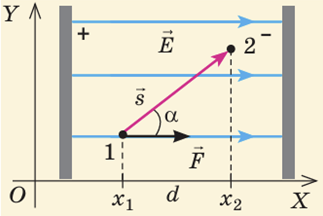
Тоді робота сил однорідного електростатичного поля напруженістю
Якби заряд переміщувався не з точки
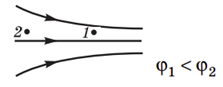
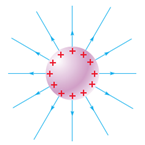
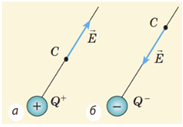
За умовою електричне поле створено негативним зарядом, отже, силові лінії будуть направлені до цього заряду (рис. 1). Відповідно й вектор напруженості теж буде направлений до джерела поля (рис. 2), тому що за напрямок вектора напруженості в даній точці
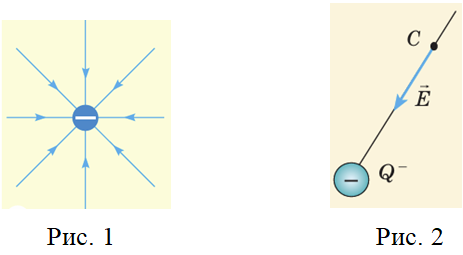
Якщо позитивний заряд
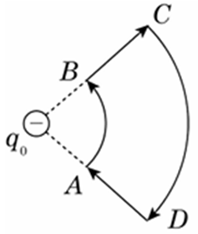
Це пов’язано з тим, що сила поля перпендикулярна до напрямку переміщення (і робота поля залежить лише від різниці потенціалів між початковою і кінцевою точками):
Якщо ж заряд
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Принцип суперпозиції полів.
Завдання скеровано на перевірку розуміння напруженості електричного поля і вміння застосовувати принцип суперпозиції полів.
Якщо електричне поле утворене кількома зарядами, то результувальна сила
Звідси випливає принцип суперпозиції (накладання) електричних полів: напруженість
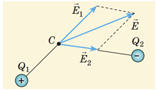
Модуль напруженості
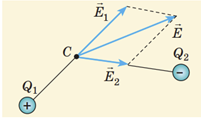
Визначімо модулі напруженості, які створюють заряди в точках
Той заряд, що ліворуч від точки
Заряд, що праворуч від точки
Однакові заряди розташовані по різні боки від точки
Відносно точки
Визначімо правильне співвідношення між модулями напруженості
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Енергія електричного поля.
Завдання скеровано на перевірку знання величин, від яких залежить енергія електричного поля конденсатора.
Енергію електричного поля
Якщо заряд конденсатора зменшили вдвічі, то
Отже, за незмінної електроємності (тому що зменшували заряд того самого конденсатора) енергія конденсатора залежить від зміни заряду.
Унаслідок зменшення заряду у
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля. Потенціал, різниця потенціалів.
Завдання скеровано на перевірку розуміння силової та енергетичної характеристик електростатичного поля.
Напруженість – це силова характеристика електричного поля. Якщо відстань між лініями напруженості в деякій області простору є однаковою, то так само однаковою є напруженість поля в цій області. Електричне поле, вектори напруженості якого однакові в усіх точках простору, називають однорідним. Оскільки з рисунка в умові випливає, що відстані між лініями напруженості електричного поля різні, то це поле неоднорідне. Напруженість поля більшає в міру наближення до заряду, силові лінії згущуються. Отже, напруженість у точці
Потенціал – це енергетична характеристика електростатичного поля. Силові лінії поля напрямлені в бік зменшення потенціалу. Що більша напруженість, то швидше зменшується потенціал під час переміщення вздовж силової лінії (напруженість характеризує швидкість зміни потенціалу). Отже, потенціал у точці
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона. Електромагнітні хвилі та швидкість поширення їх. Електродинаміка. Основи електростатики. З’єднання конденсаторів.
Завдання скеровано на перевірку розуміння принципу роботи коливального контуру.
Радіохвилі ‒ це електромагнітні хвилі, які поширюються із швидкістю світла
Довжину хвилі
Отже, довжину хвилі, на яку налаштовано радіоприймач, обчислімо за формулою:
Після приєднання паралельно до конденсатора ще одного, утричі більшої ємності, загальна електроємність дорівнюватиме:
Тепер радіоприймач буде налаштований на довжину хвилі
Поділімо ліві і праві частини формул для довжин хвиль:
Відповідь: 8.
ТЕМА: Електродинаміка. Основи електростатики. Потенціал і різниця потенціалів.
Завдання скеровано на перевірку знання і розуміння характеристик електричного поля ‒ напруженості, потенціалу.
Однорідне електричне поле спричиняє перерозподіл електричних зарядів у провіднику, унаслідок чого на поверхні провідника виникають електричні заряди. Це явище електростатичної індукції. Індуковані заряди, що виникли, створюють власне електричне поле, напруженість якого напрямлена в бік, протилежний напруженості зовнішнього поля.
Перерозподілення зарядів у провіднику триватиме до моменту, коли створюване індукованими зарядами поле всередині провідника повністю компенсує зовнішнє поле. За дуже малий інтервал часу напруженість результувального поля всередині провідника дорівнюватиме нулю.
Одна з електростатичних властивостей провідників постулює, що поверхня провідника є еквіпотенціальною (в усіх точках такої поверхні значення потенціалу електростатичного поля однакове). Це твердження є прямим наслідком зв’язку між напруженістю
Якщо напруженість поля всередині провідника дорівнює нулю, то різниця потенціалів також дорівнює нулю, тому потенціали в усіх точках провідника є однаковими.
Відповідь: A.
ТЕМА: Перетворення енергії в коливальному контурі. Закон Джоуля – Ленца. Рівняння теплового балансу.
Завдання скеровано на оцінювання знання формул для визначення енергії коливального контуру, кількості теплоти, що виділяється під час згоряння палива, і закону Джоуля – Ленца.
Відповідь: 1В, 2А, 3Г, 4Д.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на перевірку розуміння поняття електроємності.
Електроємність – це фізична величина, яка характеризує здатність провідника накопичувати заряд.
Відповідь: Г.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі, у яких ідеться про залежність опору провідника від його геометричних параметрів.
Дано:
Знайти:
Опір провідника залежить від його геометричних характеристик:
Якщо вважати форму перерізу провідника колом, його площу можна обчислити за формулою
Під час шліфування ні довжина, ні питомий опір провідника не змінювались, тобто
Відповідь: 4.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на перевірку знання законів послідовного й паралельного з’єднання конденсаторів.
Енергію конденсатора можна обчислити за формулою
Електроємність конденсатора визначають за формулою
У схемі, наведеній у завданні, конденсатор 1 послідовно підключений до конденсаторів 2 й 3, що підключені один до одного паралельно.
Напруга на паралельно підключених елементах однакова:
За умовою ємність усіх конденсаторів рівна, тож
Якщо конденсатори підключені паралельно, то максимальний заряд на їхніх котушках
Ємність таких конденсаторів можна обчислити за формулою
Якщо конденсатори підключено послідовно, то максимальні заряди на їхніх обкладинках рівні:
Тож
Тоді можна обчислити енергії конденсаторів:
Відповідь: 4.
ТЕМА: Сила тяжіння. Сила пружності. Сила кулона. Ядерні сили.
Завдання скеровано на перевірку розуміння впливу сил різної природи на природні явища.
1 електронейтральні нейтрони й позитивно заряджені протони утримуються в ядрах (й альфа-частинках, що є ядрами атомів Гелію, зокрема) завдяки дії ядерних сил
2 куля деформує броню в момент зіткнення. Залежно від величини цієї деформації броня повертається в попередній стан (зазнає пружної деформації), зберігає деформацію після зіткнення (зазнає пластичної деформації) або руйнується. Подальший рух кулі також від цього залежить, адже завдяки силі пружності, що виникає в броні, куля може зрикошетити й змінити напрямок руху чи його швидкість
3 причиною руху Місяця навколо Землі є її сила тяжіння
4 часто рух негативно зарядженого електрона в атомі зумовлений його кулонівською взаємодією з позитивно зарядженим ядром.
Відповідь: 1Г, 2Д, 3А, 4Б.
ТЕМА: Атом й атомне ядро. Основи електростатики. Електричний заряд.
Завдання скеровано на перевірку розуміння будови атома й уміння обчислювати електричний заряд тіл.
Атом – це нейтральна частинка, складниками якої є позитивно заряджене ядро й негативно заряджені електрони. Тому заряд увсіх електронів в атомі дорівнює заряду його ядра.
Ядро містить позитивно заряджені протони й електронейтральні нейтрони. Заряд усіх електронів в атомі дорівнює заряду всіх його протонів. Заряд електрона й заряд протона рівні за модулем, але протилежні за знаком, тому кількість електронів в атомі дорівнює кількості його протонів.
У ядерній фізиці використовують опис ядер, у якому поруч із символом хімічного елемента лівим надрядковим індексом позначають кількість нуклонів у ядрі
В атомі
У молекулі води два атоми Гідрогену, у кожного з яких по одному електрону, й один атом Оксигену, у якому вісім електронів. Разом у молекулі води десять електронів, їхній сумарний заряд
Відповідь: B.
ТЕМА: Основи електростатики. Закон Кулона.
Завдання скеровано на оцінювання розуміння взаємодії між електричними зарядами.
Тіла з однойменними електричними зарядами відштовхуються, а з різнойменними – притягаються. За таким законом змінили своє положення лише кульки на рисунку Б.
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на перевірку розуміння принципів паралельного і послідовного з’єднання конденсаторів.
Дано:
Знайти:
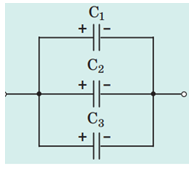
Рис. 1. Схема паралельного підключення конденсаторів
Ємність батареї конденсаторів, з’єднаних паралельно, визначають за формулою:
Відповідь: 35.
ТЕМА: Основи динаміки. Другий закон Ньютона. Основи електростатики. Закон Кулона.
Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі, пов’язані із силою Кулона.
1. Дано:
1. Знайти:
Спочатку на кульку діяли лише сили натягу підвісу й сила тяжіння (рис. 1, а). Кулька перебуває у стані спокою, тому рівнодійна цих сил дорівнює 0:
Цей векторний вираз можна спроєктувати на вертикальну вісь:
Після того, як до першої кульки наблизили другу, окрім сили натягу підвісу й сили тяжіння на кульку діє сила Кулона (рис. 1, б). Але навіть у такому разі тіло перебуває у стані спокою, тобто рівнодійна цих сил дорівнює нулю:
Цей векторний вираз можна спроєктувати на вертикальну вісь:
Зважаючи на те, що
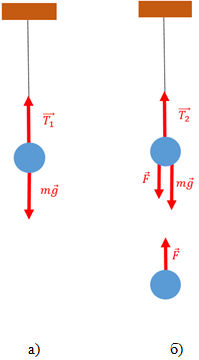
Рис. 1. Схематичне зображення сил: а) для одної кульки, б) для двох кульок
2. Дано:
2. Знайти:
Силу Кулона визначають за формулою
Тоді можна записати силу взаємодії до того, як кульки наблизили одну до одної:
Ця сила взаємодії дорівнює
Сила взаємодії після зближення дорівнюватиме
Як і до зближення, підвішена кулька перебуватиме у стані спокою, а рівнодійна всіх сил, що діють на неї, дорівнюватиме нулю:
Цей векторний вираз можна спроєктувати на вертикальну вісь:
Тож можна розрахувати силу натягу підвісу. Оскільки
Відповідь: 1. 0,5. 2. 3.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.
Завдання скеровано на оцінювання вміння визначати опір провідників за їхніми геометричними характеристиками.
Опір провідника залежить від його геометричних характеристик:
Опір провідника не зміниться, якщо не змінюється його довжина чи площа поперечного перерізу.
У варіанті відповіді А довжина провідника зменшиться вдвічі, а поперечний переріз збільшиться вдвічі, якщо розрізати його навпіл і з’єднати половинки паралельно. Тож опір провідника зменшиться:
У варіанті відповіді Б довжина провідника збільшиться. Під час видовження площа поперечного перерізу зменшиться. А тому опір провідника збільшиться.
У варіанті відповіді В під час нарізання різьби на провіднику зменшиться площа його поперечного перерізу, а опір, відповідно, збільшиться.
Лише у варіанті відповіді Г не змінюються геометричні характеристики провідника. Доданий зовні ізолювальний шар не впливає на його опір.
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Електростатичний потенціал.
Завдання скеровано на оцінювання розуміння понять електростатичного потенціалу, різниці потенціалів і роботи електричного поля з перенесення заряду й уміння розв’язувати розрахункові задачі, пов’язані із цими поняттями.
Потенціал
Для точкового заряду потенціал можна розрахувати за формулою
де
Різниця потенціалів – скалярна фізична величина, яка дорівнює відношенню роботи сил електростатичного поля з переміщення заряду з початкової точки в кінцеву до значення цього заряду:
Тож робота, виконувана полем під час перенесення заряду залежить від різниці потенціалів між початковою і кінцевою точкою: чим менша ця різниця, тим менша (за модулем) виконувана робота.
З огляду на те, що точки О і Г лежать на одній еквіпотенціальній поверхні, то
Інші точки лежать на інших еквіпотенціальних поверхнях, тому найменшу (за модулем) роботу
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.
Завдання скеровано на оцінювання розуміння поняття електричного заряду, вільних носіїв заряду і їхнього передавання під час електричної взаємодії.
Позитивно заряджені частинки всередині ядра атома – це протони, а негативно заряджені частинки, що рухаються навколо ядра, – електрони. Відокремити протон від ядра дуже складно, тому під час таких електричних явищ, як, наприклад, зарядження шерсті внаслідок тертя, зміни кількості протонів у ядрах не відбувається.
Атоми зберігають свою нейтральність за рахунок однакової кількості протонів й електронів. Відповідно, щоби зарядитися позитивно, атоми речовини повинні віддати частину своїх електронів, а щоби зарядитись негативно – захопити додаткові електрони.
Оскільки за умовою завдання шерсть набуває позитивного заряду, то саме вона віддає паличці свої електрони.
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.
Завдання скеровано на оцінювання розуміння поняття напруженості електричного поля і вміння порівнювати її значення в різних точках електричного поля.
На рисунку зображено позитивний заряд, який створює навколо себе електричне поле. Для порівняння напруженості електричного поля і потенціалу в точки А і В потрібно помістити пробний заряд
Напруженість електричного поля
На пробний заряд з боку поля діє сила Кулона, модуль якої
Відстань між лініями сітки в цій задачі не зазначено, тому можна вважати, що її вимірюють в умовних одиницях довжини (у. о. д.).
Тоді
Відповідь: A.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання вміння добирати вимірювальні прилади для проведення експериментів.
A. Оскільки період – це час, за який тіло робить одне повне коливання, то для його вимірювання використовують секундомір.
Б. Для визначення електрорушійної сили (ЕРС) і внутрішнього опору джерела потрібно скористатися законом Ома для повного кола. ЕРС в цьому разі є еквівалентом напруги в законі Ома для ділянки кола, тому її також вимірюють вольтметром.
В. Для визначення фокусної відстані й оптичної сили лінзи потрібно виміряти відстань від предмета до лінзи й від лінзи до зображення. Для цього використовують лінійку.
Г. Для визначення коефіцієнта корисної дії (ККД) похилої площини необхідно обчислити корисну роботу, яку розраховують як зміну потенціальної енергії початкового й кінцевого стану й витрачену роботу, що робчислюють за формулою
Д. Для вивчення теплового балансу під час змішування води різної температури потрібно зафіксувати початкові й кінцеву температури. Для цього використовують термометр.
Відповідь: 1Г, 2Б, 3А, 4Д.
ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.
Завдання скеровано на оцінювання розуміння понять потенціалу й напруженості й уміння порівнювати ці величини в різних точках електричного поля.
На рисунку схематично зображено позитивний заряд, який створює навколо себе електричне поле. Для правильного розв’язання завдання потрібно позначити його величину як
Напруженість
На пробний заряд з боку поля діє сила Кулона, модуль якої
Тоді
Потенціал
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на дію електричного поля на заряд.
Дано:
Знайти:
Напруженість електричного поля
Тобто
Тоді, перевівши значення заряду з нанокулонів у кулони й значення напруженості електричного поля з
Відповідь: 50.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на оцінювання вміння графічно зображувати залежності між фізичними величинами.
Залежність заряду
Її графік – це пряма, що проходить через початок координат.
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.
Завдання скеровано на оцінювання знання поняття електричного заряду й розуміння принципу роботи електрометра.
Електрометр – це прилад для виявлення і вимірювання заряду. Складники електрометра – металева куля, стержні й стрілки.
У металах вільними носіями є електрони. Під дією електричного поля завжди відбувається перерозподіл зарядів. Зокрема, паличка, яку дівчинка піднесла до електрометра, утворила електричне поле, яке й стало причиною подальшого руху зарядів.
Спершу дівчинка торкнулася металевої кулі пальцем. Так вона створила шлях відходу для електронів, адже людське тіло також є хорошим провідником електричного струму.
Оскільки дівчинка до іншої частини кулі піднесла негативно заряджену паличку, то електрони, які також заряджені негативно, «відштовхнулися» від палички, перемістилися на інший бік кулі й «стекли» по руці дівчинки.
Оскільки дівчинка спершу прибрала руку, а потім паличку, то електрони не встигли повернутися назад у металеву кулю. Тому в усій конструкції електрометра виник дефіцит електронів. Унаслідок цього металевий стержень і стрілка набули позитивного заряду. Оскільки стрілка й стержень стали однойменно зарядженими, то стрілка відхилилася.
Коли дівчинка піднесла позитивно заряджену паличку до кулі, то під дією електричного поля палички знову відбувся перерозподіл зарядів. Частина електронів, зокрема зі стержня і стрілки, перемістилися ближче до палички, тому й стрілка відхилилася ще більше.
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на енергію зарядженого конденсатора і її перетворення на інші види енергії.
Дано:
1. Знайти:
Енергію електричного поля зарядженого конденсатора можна визначити за формулою
2. Знайти:
Потужність спалаху
Відповідь: 1. 45. 2. 30.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на знаходження енергії зарядженого конденсатора.
Під час зарядження конденсатори набувають потенціальної енергії. Коли вони розряджаються, енергія, що накопичилась у них, розсіюється на резисторі. Розсіювання відбувається завдяки тому, що резистор нагрівається і віддає енергію в середовище. Тож резистор нагріється найбільше тоді, коли отримає найбільше енергії від конденсатора. Енергію зарядженого конденсатора обчислюють за формулою:
Далі потрібно обчислити величини енергій чотирьох конденсаторів:
Тож після підключення до третього конденсатора резистор нагріється найбільше.
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.
Завдання скеровано на оцінювання розуміння напруженості електричного поля і вміння порівнювати її різних точках електричного поля.
На рисунку зображено позитивний заряд
Напруженість електричного поля в точці
На пробний заряд із боку поля діє сила Кулона, яка за модулем дорівнює
Тоді модуль напруженості електричного поля дорівнюватиме
Оскільки
Тоді
Отже
або
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Електростатичний потенціал.
Завдання скеровано на оцінювання розуміння понять електростатичного потенціалу, різниці потенціалів і роботи електричного поля з перенесення заряду.
Поле не виконує роботу під час переміщення заряду, якщо воно відбувається по еквіпотенціальній поверхні.
Еквіпотенціальна поверхня – це поверхня, у всіх точках якої потенціал електростатичного поля має однакове значення (рис. 1).
Тому необхідно знайти точку на тій самій еквіпотенціальній поверхні, що й початкова точка. Еквіпотенціальні поверхні перпендикулярні до силових ліній поля. Тому, якщо провести перпендикулярну до силових ліній пряму через точку 1, то будь-яке переміщення вздовж неї не вимагатиме від поля виконання роботи.
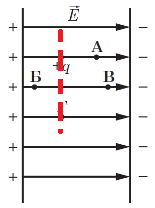
Рис. 1. Зображення еквіпотенціальної поверхні (червоним)
Відповідь: Г.
ТЕМА: Основи електростатики. Електричний заряд.
Завдання скеровано на оцінювання розуміння перерозподілення заряду під час контактування двох провідників.
Негативно заряджена кулька має надлишок електронів, а позитивно заряджена – дефіцит їх. Якщо з’єднати кульки провідником, то електрони рівномірно розподіляться по обох кульках, тому заряд двох з’єднаних кульок становитиме:
Після того як провідник приберуть, електрони нікуди не перемістяться і залишаться розподіленими рівномірно по всій системі. Оскільки кульки однакові, то заряд кожної кульки окремо дорівнюватиме половині всього заряду з’єднаних кульок:
Відповідь: Б.
ТЕМА: Квантова фізика. Світлові кванти. Фотоефект і його закони. Рівняння Ейнштейна для фотоефекту.
Завдання скеровано на перевірку вміння застосовувати основні поняття теорії фотоефекту й уміння розв'язувати розрахункові задічі на застосування рівняння Ейнштейна для фотоефекту.
Дано:
1. Знайти:
Кулька заряджається позитивно завдяки фотоефекту.
Рівняння Ейнштейна
Після того як кулька зарядиться максимально завдяки різниці потенціалу, електрони почнуть повертатися назад на кульку, тому максимальний потенціал дорівнює запірній напрузі
Відповідь: 0,36.
ТЕМА: Електродинаміка. Основи електростатики. Коденсатори.
Завдання скеровано на перевірку вміння аналізувати дію електричного поля на заряд і розв'язувати задачі із застосуванням функціональних залежностей між основними фізичними величинами.
Напруженість однорідного електричного поля плоского конденсатора
Сила iз якою це поле діє на електрон:
З другого закону Нютона прискорення електрона
Звідти
Електрон у вертикальному напрямку рухається без початкової швидкості, тому
Час руху обчислюють за формулою
Дано:
Знайти:
Відповідь: 8.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість однорідного електричного поля.
Завдання скеровано на перевірку знання понять «напруженість» i «діелектрична проникність речовини».
Напружність двох різнойменних нескінчених пластин з однаковою поверхневою густиною
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду.
Завдання скеровано на перевірку вміння застосовувати поняття електричний заряд, елементарний заряд та закон збереження електричного заряду.
Металева кулька, що має заряд
Якщо дві металеві кульки доторкнули, то електрони переросподілились і нескомпенсованим залишився заряд
За умовою розмір кульок однаковий, тому після роз'єднання заряд ділиться навпіл:
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики.
Завдання скеровано на перевірку знання явища електризації, уміння розпізнавати прояви електромагнітних явищ.
Електризація відбувається тоді, коли перерозподіляються електрони.
Електрони є носіями від'ємного заряду. Тому шерсть матиме позитивний заряд, якщо негативні електрони перейдуть із шерсті на паличку.
Відповідь: В.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на перевірку розуміння впливу зовнішніх чинників на електроємність конденсатора.
Знайти:
Електроємність конденсатора залежить від його геометричних характеристик:
Під час повороту обкладинок конденсатора змінюється площа їхнього перекриття. Нехай довжина пластини становить
Після повороту область перекриття перетворилася на квадрат зі стороною 3 клітинки, площа якої дорівнює:
Відповідь: 0,6.
ТЕМА: Молекулярна фізика і термодинаміка. Рівняння теплового балансу. Робота. Потужність. Коефіцієнт корисної дії (ККД).
Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі, пов’язані з електричною потужністю і рівнянням теплового балансу.
Дано:
1. Знайти:
Потужність пов’язана з роботою формулою
Потужність електричного нагрівача можна визначити за формулою
Тож
2. Знайти:
ККД нагрівача визначають як відношення корисної роботи, виконаної ним, до повної роботи:
Необхідну для нагрівання води кількість енергії можна визначити за формулою
Повна робота – це робота струму в електричному нагрівачі, тож
Відповідь: 1. 400. 2. 84.
ТЕМА: Основи електростатики. Закон Кулона.
Завдання скеровано на оцінювання розуміння взаємодії між електричними зарядами.
У металевому тілі багато вільних електронів, що рухаються під дією зовнішнього електричного поля. Негативно заряджені електрони в металевому тілі рухатимуться до позитивного заряду, тож ділянка 1 матиме надлишок електронів, а ділянка 2 – їхню нестачу.
Тобто ділянка 2 буде заряджена позитивно, а 1 – негативно.
Відповідь: Г.
ТЕМА: Вимірювальні пристрої.
Завдання скеровано на оцінювання розуміння фізичних принципів роботи вимірювальних пристроїв.
Термометр – це прилад для вимірювання температури. Він працює завдяки тому, що деякі речовини за сталого тиску суттєво змінюють свій об’єм за зміни температури (ртуть чи спирт розширюються за підвищення температури та звужуються за її зниження).
Динамометр – це прилад для вимірювання сили. Зазвичай складники динамометра – пружина та шкала. Коли на кінець пружини діє сила, то, за законом Гука, пружина розтягується.
Барометр – це прилад для вимірювання атмосферного тиску. У завданні зображено безводний барометр (анероїд), усередині якого є вакуумна камера з гофрованою поверхнею. За високого атмосферного тиску кришка коробки сильно опускається, а за низького – піднімається. До кришки за допомогою пружини прикріплена стрілка. Тому, коли кришка камери піднімається чи опускається, пружина деформується і стрілка починає рухатися по шкалі.
Електрометр – це прилад для виявлення та вимірювання заряду. Його складники – металева куля, стержень і стрілки. Під дією електричного поля в стержні, стрілці й кулі відбувається перерозподіл зарядів. Оскільки вони з’єднані, то заряджаються однаково. Однойменно заряджені стрілка та стержень відштовхуються, тому рухома стрілка відхиляється.
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на оцінювання розуміння залежності ємності конденсатора від його геометричних параметрів.
На рисунку зображено плоский конденсатор. Вираз для його електроємності такий:
Зміщення пластин одна відносно одної і їхній поворот не впливають на ємність конденсатора.
Зменшення відстані між пластинами її збільшить, а збільшення – зменшить.
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.
Завдання скеровано на оцінювання розуміння напруженості електричного поля і вміння порівнювати її в різних точках електричного поля.
Напруженість електричного поля в певній точці
На пробний заряд
Тоді модуль напруженості електричного поля дорівнюватиме
Оскільки масштаб рисунку невідомий, то можна вважати, що клітинка дорівнює умовній одиниці довжини (у. о. д.). Відстань до точки 1 становить 1 у. о. д. і 2 у. о. д. від кожного із зарядів відповідно. Відстань до точки 2 становить 6 у. о. д. і 3 у. о. д. від кожного із зарядів відповідно.
Напруженості електричного поля різних зарядів додають векторно, тому для точки 1 поле створене обома зарядами буде спрямоване у протилежні боки. Вважатимемо, що напрямок зліва направо – додатний, тоді загальна напруженість електричного поля в точці 1 становитиме:
А для точки 2 поля, створені обома зарядами, спрямовані в один бік, тому загальна напруженість становить
Тоді можемо знайти відношення напруженості електрично в кожній із точок:
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.
Завдання скеровано на перевірку розуміння понять потенціалу й еквіпотенціальних поверхонь.
Потенціал на поверхні провідника в усіх точках однаковий, тобто поверхня провідника є еквіпотенціальною.
Потенціал на поверхні металевої кулі визначають за формулою
Тож за однакових зарядів потенціал кулі з більшим радіусом є меншим за потенціал кулі з меншим радіусом.
З’єднані кулі утворюють один провідник, поверхня якого також має бути еквіпотенціальною, тож заряди перерозподіляться. Заряд від кулі з більшим потенціалом (малої кулі) перейде до кулі з меншим потенціалом (великої).
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Принцип суперпозиції полів.
Завдання скеровано на перевірку вміння геометрично інтерпретувати дію кількох електричних полів у точці простору.
Електричне поле можна зобразити графічно лініями напруженості.
Якщо в точці простору електричне поле створене системою зарядів, то напруженість цього результувального поля дорівнюватиме векторній сумі напруженостей полів цих зарядів.
За напрямок напруженості в точці електричного поля потрібно взяти напрямок сили, яка діяла б на пробний позитивний заряд, якби він був поміщений у цю точку поля.
На рисунку в умові завдання зображено два негативні заряди. Під час взаємодії з умовним позитивним зарядом в точці
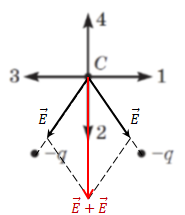
Якщо добудувати на цих векторах напруженості паралелограм, то за правилом додавання векторів можна визначити їхню векторну суму – більшу діагональ побудованого паралелограма. Вона збігатиметься з напрямком 2.
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду.
Завдання скеровано на розуміння закону збереження електричного заряду.
За законом збереження електричного заряду в замкненій системі тіл повний заряд залишається незмінним, заряд не може звідкись виникнути або кудись зникнути, заряди лише перерозподіляються між тілами системи, що контактують між собою.
Оскільки заряд накопичується на поверхні провідників, то не має значення, що одна з куль порожниста, як зазначено в умові. Головне, що зовнішні параметри в них однакові. У куль однакового радіуса площа зовнішньої поверхні та сама. Кулі виготовленого з одного матеріалу. Тому після дотику заряд перерозподілиться порівну між кулями, і заряд кульки 1 дорівнюватиме заряду кульки 2.
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на перевірку розуміння принципів паралельного і послідовного з’єднання конденсаторів.
Дано:
Знайти:
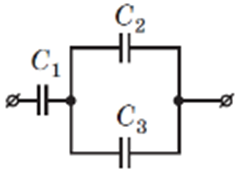
Рис. 1. Умова завдання
Енергію конденсатора можна визначити за формулою
Для визначення енергії системи конденсаторів необхідно визначити її сумарну ємність. Конденсатори 2 та 3 з’єднані паралельно, а до них послідовно підключений конденсатор 1.
Ємність батареї конденсаторів, з’єднаних паралельно, визначають за формулою
Ємність батареї конденсаторів, з’єднаних послідовно, визначають за формулою
Тоді енергію батареї конденсаторів обчислюємо за формулою
Відповідь: 21,6.
ТЕМА: Електродинаміка. Основи електростатики. Електричне поле. Напруженість електричного поля.
Завдання скеровано на оцінку вміння обчислювати напруженість електричного поля точкового заряду.
Напруженість поля точкового заряду можна визначити за формулою
Якщо
Відповідно
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона. Механіка. Основи динаміки. Рух тіл під дією кількох сил.
Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі з різних розділів фізики.
Запишімо рівняння другого закону Ньютона у векторному вигляді та в проєкціях на осі координат для початкового стану:
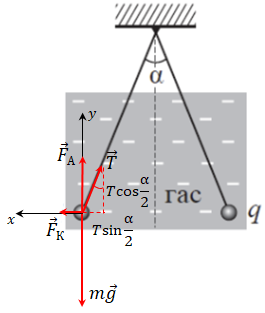
Дістаємо систему рівнянь:
Звідси
Запишімо рівняння другого закону Ньютона у векторному вигляді та в проєкціях на осі координат, коли кульки занурили в гас:
Сила Кулона в гасі зміниться від того, що в іншого середовища інша діелектрична проникність. За умовою кут між нитками не змінився після занурення в гас. Тож відстань між кульками не змінилася. Але на кульки в гасі діє сила Архімеда. Узявши до уваги всі ці умови, дістаємо систему рівнянь:
Звідси
Складімо систему з отриманих для обох ситуацій рівнянь і розв’яжімо її:
де
Тобто
Відповідь: 1600.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора. Енергія електричного поля.
Завдання скеровано на перевірку знання і застосування формул для обчислення електроємності плоского конденсатора й енергії електричного поля конденсатора.
1. Конденсатор, складений із двох паралельних металевих пластин (обкладок), розділених шаром діелектрика, називають плоским. Електроємність
Підставмо у формулу значення величин, виражених у системі СІ, й обчислімо електроємність конденсатора:
Відповідь: 45.
2. Заряджений конденсатор має енергію. Цю енергію точніше було б назвати енергією електростатичного поля, яке існує між обкладками зарядженого конденсатора, оскільки енергія будь-яких заряджених тіл зосереджена в електричному полі, створюваному цими тілами.
Отже, обчислімо енергію
Відповідь: 36.
Відповідь: 1. 45. 2. 36.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Магнітне поле, електромагнітна індукція.
Завдання скеровано на перевірку вміння застосовувати теоретичні знання з електродинаміки для пояснення принципу дії відповідних технічних пристроїв.
На взаємодії магнітного поля постійних магнітів компаса з горизонтальним складником магнітного поля Землі заснований принцип дії цього приладу. Вільно обертова магнітна стрілка повертається навколо осі, розташовуючись уздовж силових ліній магнітного поля. Тож стрілка завжди вказує одним кінцем у напрямку ліній магнітної індукції, що йдуть до Південного магнітного (Північного географічного) полюса.
Посудину з високою стійкістю до впливів кислот, лугів і розчинників, у якій відбувається електроліз, називають електролітичною ванною (електролізером). Проходження електричного струму крізь розчин або розплав електроліту зумовлює хімічні реакції на поверхні поділу електрод ‒ розчин (розплав електроліту). Отже, хімічну дію електричного струму спостерігають під час проходження його крізь розчин електроліту в електролітичній ванні.
Електромагнітна індукція ‒ явище створення в просторі вихрового електричного поля змінним магнітним потоком. Один із наслідків електромагнітної індукції, практично важливий для генерації електричного струму, ‒ виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється. Саме генератори змінного струму (ГЗС) ‒ це джерела електричної енергії, які створюють електрорушійну силу (ЕРС), що періодично змінюється.
Робота всіх електричних нагрівачів ґрунтується на тепловій дії струму: у таких пристроях енергія електричного струму перетворюється на внутрішню енергію нагрівача. Під час проходження електричного струму спіраль лампи розжарювання сильно нагрівається завдяки тепловій дії струму.
Будь-який напівпровідниковий діод складений із двох контактних напівпровідникових ділянок із різними типами провідності ‒ електронною і дірковою; до кожної ділянки приєднано виводи. Основна властивість напівпровідникового діода ‒ пропускати електричний струм переважно в одному напрямку.
Відповідь: 1Б, 2Г, 3А, 4В.
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку вміння обчислювати потужність струму за послідовного з’єднання провідників.
Визначмо спочатку загальну потужність
Якщо ж замінити один резистор опором
Для визначення загального опору ділянки кола за послідовного з’єднання провідників (резисторів) їхні опори додають.
Обчислімо, у скільки разів змінилася потужність струму в резисторах:
Отже, потужність струму
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.
Завдання скеровано на перевірку знання і розуміння принципу суперпозиції електричних полів.
Модуль напруженості
Оскільки за умовою є два електричні заряди, то діятиме принцип суперпозиції (накладання) електричних полів: напруженість електричного поля системи зарядів у даній точці простору дорівнює векторній сумі напруженостей полів, які створюються цими зарядами в точці (див. рисунок).
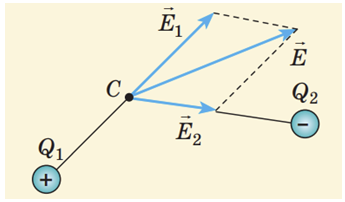
Розглянувши на рисунку в умові завдання взаємне розташування кульок і точок і взявши до уваги, що в кульок
В усіх інших ситуаціях вектор суми напруженостей відмінний від нуля, тож правильною відповіддю є точка симетрії – точка
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Потенціал, різниця потенціалів.
Завдання скеровано на перевірку знання і розуміння руху зарядженої частинки в електричному полі.
Силові лінії поля напрямлені завжди в бік зменшення потенціалу, а порошинка рухається в напрямку, протилежному до напрямку силових ліній електричного поля, отже, потенціал
Скористаймося законом збереження енергії порошинки в електричному полі:
Візьмемо до уваги, що
Відповідно
Відповідь: 200.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання чинників, від яких залежить електроємність конденсатора, і вміння читати графіки.
Електроємність
З наведеної формули зрозуміло, що електроємність обернено пропорційна відстані між пластинами конденсатора:
Зі збільшенням відстані між пластинами електроємність конденсатора зменшуватиметься. Треба зауважити, що ця формула для визначення електроємності конденсатора справедлива лише за малих значень
Розгляньмо, як вплине діелектрик між пластинами конденсатора на його електроємність. Візьмемо до уваги, що в ізоляції конденсаторів використовують тонкі шари діелектрика.
Проаналізуймо зображені графіки. Якщо розглядати конденсатор без діелектрика, то його електроємність відмінна від нуля (як це зображено у варіанті відповіді Б) і має якесь початкове значення
Якщо ж заповнити простір між пластинами (обкладками) конденсатора діелектриком, то на електроємність конденсатора шар діелектрика впливає так: що більша його діелектрична проникність, то більшу електроємність має конденсатор порівняно з електроємністю такого самого конденсатора, діелектриком у якому є повітря.
Тому вміщення діелектрика між пластинами приведе до збільшення електроємності в
Отже, варіанти відповіді В і Г не задовольняють умову завдання, оскільки зі збільшенням відстані між обкладками конденсатора для заповнення діелектриком електроємність за цими графіками зменшується.
Правильною відповіддю є варіант A (див. рисунок).
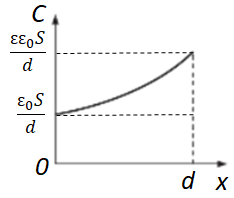
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду. Напруженість електричного поля.
Завдання скеровано на перевірку розуміння закону збереження електричного заряду й силової характеристики електричного поля ‒ напруженості.
Модуль напруженості
Запишімо формулу для визначення модуля напруженості електричного поля дощової краплі із зарядом
Визначмо заряд
За законом збереження електричного заряду повний заряд електрично замкненої системи тіл залишається незмінним під час усіх узаємодій, які відбуваються в цій системі:
Тобто
Запишімо формулу для визначення модуля напруженості електричного поля на тій самій відстані
Визначмо відношення модулів напруженості:
Отже, напруженість
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Зв’язок між напругою і напруженістю однорідного електричного поля.
Завдання скеровано на перевірку розуміння зв’язку між напругою і напруженістю однорідного електричного поля, уміння визначати напругу між точками поля.
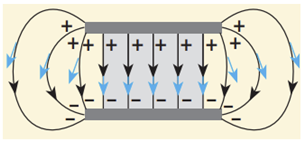
Картину силових ліній електричного поля, створеного системою двох пластин, заряди яких рівні за модулем і протилежні за знаком, зображено на рисунку. Синіми стрілками позначено напрямки векторів напруженості. Між пластинами поле однорідне, тому що вектори напруженості між ними однакові.
Повернімо на
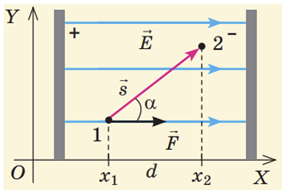
За умовою напруга між пластинами дорівнює
Якщо з’єднати букву Б з буквою А вектором й визначити в уяві його проєкцію на вертикально напрямлену вниз силову лінію, то проєкція дорівнюватиме стороні однієї клітинки, отже, напруга між точками Б і А становитиме
Точки А і Г лежать на одній горизонтальній прямій, тому вектор, яким можна з’єднати їх, проєктується в точку, тобто його проєкція дорівнює нулю. Тому, з огляду на формулу, напруга між точками А і Г теж дорівнюватиме нулю:
Проєкція вектора, яким можна з’єднати точки Б і В, відповідає трьом одиничним відрізкам, тож напруга між цими точками дорівнює
Проєкція вектора, яким можна з’єднати точки Г і В, відповідає двом одиничним відрізкам, тож напруга між цими точками дорівнює
Відповідь: 1Б, 2А, 3Г, 4В.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність.
Завдання скеровано на перевірку розуміння поняття електроємності провідника.
Електроємність характеризує здатність провідників або системи з кількох провідників накопичувати електричний заряд.
Електроємність провідника – це властивість провідного тіла, яка залежить від його розмірів, форми, навколишнього середовища, розташування інших провідників і характеризує пряму пропорційну залежність між зарядом тіла та потенціалом його поверхні.
Отже, правильна відповідь ‒ А.
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.
Завдання скеровано на перевірку знання і розуміння залежності між зарядом конденсатора й напругою на його обкладках.
Зарядом конденсатора називають модуль заряду однієї з його обкладок. Відношення заряду q конденсатора до різниці потенціалів
Електроємність конденсатора визначають за формулами:
Отже, заряд конденсатора прямо пропорційний напрузі, прикладеній до його пластин:
Графіком такої залежності є пряма ‒ графік А.
Наприклад, під час розряджання конденсатора напруга між його обкладками спадатиме прямо пропорційно заряду
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду.
Завдання скеровано на перевірку вміння застосовувати закон збереження електричного заряду.
Закон збереження електричного заряду: повний заряд електрично замкненої системи тіл залишається незмінним під час усіх взаємодій, які відбуваються в цій системі:
За умовою
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики.
Завдання скеровано на перевірку знання і розуміння основних фізичних величин електростатики.
1. Потенціал
Варіант відповіді – Г.
2. Напруженість електричного поля
Варіант відповіді – А.
3. Електроємність – це характеристика конденсатора, яку визначають як відношення заряду
Варіант відповіді – Д.
4. Густина енергії − енергія речовини або поля віднесена до одиниці об’єму. Густину енергії електричного поля визначмо за формулою
Варіант відповіді – Б.
Відповідь: 1Г, 2А, 3Д, 4Б.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання і розуміння характеристики конденсатора ‒ електроємності, а також від яких параметрів і як вона залежить.
Електроємність
З формули видно, що електроємність прямо пропорційна діелектричній проникності діелектрика:
Оскільки в умові питають, як зміниться електроємність системи конденсаторів, то йдеться про загальну електроємність. Отже, після того, як повітряні конденсатори (діелектрична проникність повітря дорівнює практично
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.
Завдання скеровано на перевірку знання і розуміння напруженості електричного поля.
Напруженість електричного поля
Визначмо модуль сили, з якою діє електричне поле Землі на краплю води:
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Енергія електричного поля.
Завдання скеровано на перевірку вміння визначати характеристики батарей конденсаторів у разі їхнього паралельного і послідовного з’єднання, а також уміння визначати енергію електричного поля конденсаторів.
Енергію електричного поля
Конденсатор
Оскільки в разі паралельного з’єднання конденсаторів напруга на них однакова й за умовою електроємність конденсаторів однакова, то й заряди конденсаторів
Отже,
Запишімо формулу для енергії електричного поля конденсатора
Визначімо, у скільки разів енергія електричного поля конденсатора
Відповідь: 4.
ТЕМА: Електродинаміка. Основи електростатики. Потенціал і різниця потенціалів.
Завдання скеровано на перевірку знання і розуміння потенціалу.
Потенціал
Ця формула справджується і для потенціалу поля рівномірно зарядженої сфери (або кулі) на відстанях, які більші за її радіус або дорівнюють йому.
Обчислімо загальний заряд восьми крапель ртуті відповідно до закону збереження заряду:
Обчислімо об’єм однієї краплі ртуті:
Загальний об’єм великої краплі дорівнюватиме
Тоді радіус утвореної великої краплі становитиме
Визначімо загальний потенціал краплі, утвореної з восьми крапель ртуті, підставивши визначені значення загального заряду
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.
Завдання скеровано на перевірку знання і розуміння поняття силової характеристики електричного поля ‒ напруженості.
Розгляньмо поле зарядженої сфери за умови рівномірного розподілу заряду
Біля поверхні сфери напруженість буде максимальною (на відстані радіуса R від центру сфери), про що говорить стрибок значення напруженості на графіку
Залишається визначити поле ззовні від сфери.
Напруженість є силовою характеристикою електричного поля. Напруженість
За законом Кулона модуль сили дорівнює
Маємо
Тобто напруженість поля точкового заряду
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання і розуміння параметрів, від яких залежить електроємність конденсатора.
Електроємність
Виразімо з формули шукану величину – діелектричну проникність
Площу пластини конденсатора визначимо за формулою
Обчислімо діелектричну проникність текстоліту:
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля. Принцип суперпозиції полів.
Завдання скеровано на перевірку розуміння напруженості електричного поля, уміння застосовувати принцип суперпозиції електричних полів.
Напруженість електричного поля
За напрямок вектора напруженості в точці електричного поля беруть напрямок сили, яка діяла б на пробний позитивний заряд, якби він був поміщений у цю точку поля. На рисунку це точка C: поле створив позитивний точковий заряд
Якщо ж поле утворено кількома зарядами, то результувальна сила, яка діє на пробний заряд із боку системи зарядів, є геометричною сумою сил, із якими діють ці заряди на пробний заряд:
Звідси випливає принцип суперпозиції (накладання) електричних полів: напруженість електричного поля системи зарядів у певній точці простору дорівнює векторній сумі напруженостей полів, створених цими зарядами в цій точці:
Якщо ж точка

За умовою заряд рівномірно розподілений по всій довжині дротин, із яких виготовлені рамки. Дротяні фігури є симетричними, тому можна в кожній із них знайти симетричні пари точок, відносно яких за принципом суперпозиції електричних полів напруженість дорівнюватиме нулю. І таких пар точок нескінченно багато.
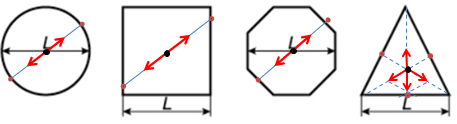
У рівносторонньому трикутнику, наприклад, три рівновіддалені від його центра точки. Центр рівностороннього трикутника є центром описаного і вписаного кіл. Визначаємо геометрично за правилом паралелограма суму двох векторів напруженостей (на рисунку ‒ вектор, що позначає їхню суму, напрямлений вертикально вниз). Якщо додати геометрично вектори, що на рисунку напрямлені вертикально, їхня сума дорівнюватиме нулю. І так для безлічі рівновіддалених точок.
Отже, напруженість дорівнюватиме нулю в геометричному центрі кожної дротяної фігури, про яку йдеться в умові.
Відповідь: Б.
ТЕМА: Електродинаміка. Робота поля з переміщення заряду.
Завдання скеровано на перевірку знання і розуміння загального поняття роботи у фізиці, а також вміння визначати, від яких параметрів залежить робота різних полів.
Робота у фізиці – характеристика дії сили на тіло, що залежить від величини й напрямку цієї сили та переміщення точки її прикладання.
Запишімо загальну формулу роботи сили. Робота сили дорівнює добутку модуля сили
1. Вихрове електричне поле. Змінне магнітне поле завжди супроводжується появою вихрового електричного поля. Саме вихрове електричне поле діє на вільні заряджені частинки в провіднику й надає їм напрямленого руху, створюючи індукційний струм.
Робота вихрового електричного поля на замкненій траєкторії зазвичай не дорівнює нулю.
Робота вихрового електричного поля з переміщення одиничного позитивного заряду по замкнутому нерухомому провіднику чисельно дорівнює ЕРС індукції в цьому провіднику.
2. Електричне поле – форма матерії, яка існує навколо заряджених тіл і виявляється в дії з деякою силою на заряджене тіло, що перебуває в цьому полі.
Електричне поле є складником єдиного електромагнітного поля. Джерелами електричного поля можуть бути рухомі й нерухомі електричні заряди та змінні магнітні поля.
Електричне поле, створене лише нерухомими зарядами, є незмінним у часі (статичним). Таке поле називають електростатичним.
Нехай в однорідному електричному полі напруженістю
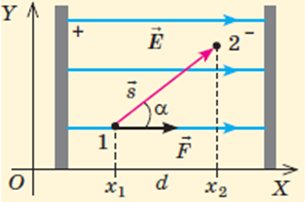
За означенням роботи:
Поле однорідне, тому сила
Отже, робота сил однорідного електростатичного поля в ході переміщення електричного заряду
Формула
3. Гравітаційне поле існує навколо будь-якого тіла і виявляється у взаємному притяганні тіл одне до одного. Визначити силу
Отже, сила, а значить, і робота гравітаційного поля залежатиме від маси частинки, не залежатиме від форми траєкторії, але від відстані (переміщення) залежатиме, тобто від положення початкової та кінцевої точок руху частинки (Г).
4. Магнітне поле – складник електромагнітного поля, основною властивістю якої є дія на рухомі заряджені частинки. Силова характеристика магнітного поля – вектор магнітної індукції

Тобто, ця сила напрямлена перпендикулярно до швидкості руху заряду й напрямку магнітного поля. А напрямок швидкості руху тіла збігається з напрямком його переміщення. Через це робота, що її виконує магнітне поле над частинкою, дорівнює нулю:
Відповідь: 1Д, 2Б, 3Г, 4А.
ТЕМА: Електродинаміка. Основи електростатики. Робота електричного поля при переміщеннi заряду. Потенціал і різниця потенціалу.
Завдання скеровано на перевірку знання і розуміння закону збереження енергії під час переміщення заряду електричним полем.
Найдоцільніше скористатися законом збереження енергії:
Візьмімо до уваги, що за умовою
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Зв᾽язок між напругою і напруженістю однорідного електричного поля. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання і розуміння зв᾽язку електростатичних величин ‒ напруги, напруженості, електроємності і характеристик конденсатора.
Напруженість
Оскільки конденсатор зарядили і відключили від батарейки, то його заряд
Електроємність плоского конденсатора обчислюємо за формулою:
Підставимо вирази для напруги і електроємності у формулу для напруженості:
Виходячи з даних умови, що діелектрична проникність слюди вшестеро більша за діелектричну проникність повітря, робимо висновок, що якщо у простір між пластинами конденсатора помістити слюдяну пластинку, то напруженість такого конденсатора зменшиться в
У другому ж випадку, коли пластини конденсатора розсовують, не заповнюючи простір між ними діелектриком, легко бачити, що напруженість залишиться незмінною, оскільки за формулою вона не залежить від відстані між пластинами:
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики.
Завдання скеровано на перевірку знання і розуміння властивостей розміщення статичного заряду, принципу суперпозиції полів.
Електрон рухається рівномірно там, де електричне поле не діє. На інших ділянках швидкість електрона змінюватиметься. Рівномірно заряджена сфера, заряд якої дорівнює
У цій ситуації поля в точці немає, якщо сумарний заряд усіх внутрішніх для заданої точки сфер дорівнює нулю. Отже, електричного поля немає лише всередині найменшої сфери.
Ззовні найменшої сфери діє поле із зарядом
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона.
Завдання скеровано на перевірку знання і розуміння того, від яких фізичних величин і як залежить сила Кулона.
Закон Кулона: сила
Отже, правильне твердження: «Сила кулонівської взаємодії двох нерухомих точкових заряджених тіл обернено пропорційна квадрату відстані між ними».
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.
Завдання скеровано на перевірку знання і розуміння основ утворення позитивно і негативно заряджених тіл.
Існують два роди електричних зарядів ‒ позитивні і негативні. Електричний заряд такого роду, як заряд, отриманий на бурштині або ебонітовій паличці, потертих об вовну, заведено називати негативним, а такого роду, як заряд, отриманий на паличці зі скла, потертій об шовк або папір, ‒ позитивним.
Вовна втримує свої електрони менш міцно, ніж ебоніт, тому під час контакту електрони переважно переходять із вовни на ебонітову паличку, а не навпаки. Отже, після роз’єднання паличка стає негативно зарядженим фізичним тілом, а вовна ‒ позитивно зарядженим.
Отже, електрони під час електризації тертям переходять із шерсті на ебонітову паличку.
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Дія електричного поля на заряд.
Завдання скеровано на перевірку знання і розуміння руху зарядженої частинки (електрона) в однорідному електричному полі конденсатора.
Електрон, який влітає між пластинами конденсатора, рухатиметься до позитивно зарядженої пластини. За час
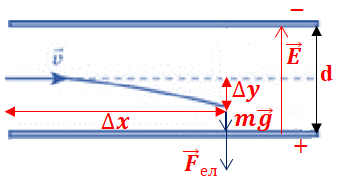
Електрон рухається горизонтально, відстань
Відстань
Щоб визначити прискорення, запишімо другий закон Ньютона для електрона, що рухається в однорідному електричному полі напруженістю
(прискоренням вільного падіння можна знехтувати ‒ сила тяжіння набагато менша за силу електричного поля).
Визначімо вертикальне зміщення електрона:
Відповідь: 8.
ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона.
Завдання скеровано на перевірку знання і розуміння закону Кулона, а також вміння шукати рівнодійну сил.
Закон Кулона: сила
Сили, з якими взаємодіють точкові заряди, називають силами Кулона. Сили Кулона напрямлені вздовж умовної прямої, яка з’єднує точкові заряди, що взаємодіють.
З боку кульки
З боку кульки
Парні сили взаємодії до вже позначених сил не позначено на рисунку, щоб його не захаращувати, але зрозуміло, що кулька
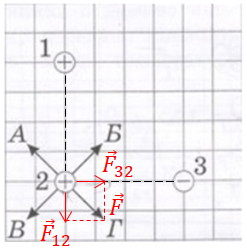
Відповідно до закону Кулона сила, що діє з боку кульки
Тож рівнодійну
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання і розуміння будови конденсатора, а також розуміння зв’язку його технічних характеристик.
Для зарядження конденсатора обидві його обкладки (пластини) з’єднують із полюсами джерела струму: на внутрішніх (унаслідок притягання різнойменних зарядів) поверхнях обкладок накопичуються рівні за модулем, але протилежні за знаком заряди.
За умовою конденсатор зарядили й від’єднали від джерела струму. Це означає, що незмінним залишиться накопичений заряд. Зарядом
Електроємність плоского конденсатора обчислюють за формулою
Для однорідного електричного поля між обкладками плоского конденсатора зв’язок між напруженістю
Запишімо тепер формулу для визначення заряду конденсатора:
звідки
З формули випливає, що напруженість електричного поля всередині конденсатора не залежить від відстані між обкладками (пластинами) конденсатора. А всі інші фізичні величини
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність. Конденсатори.
Завдання скеровано на перевірку знання і розуміння будови конденсатора та його технічних характеристик.
Годинник зможе працювати від цього конденсатора, поки напруга на ньому буде не нижчою за
Отже, за певний час заряд конденсатора зменшиться на
Сила струму
За нижчої напруги годинник не працюватиме.
Визначімо проміжок часу, у який працюватиме годинник:
Відповідь: 25.
ТЕМА: Електродинаміка. Основи електростатики. З’єднання конденсаторів.
Завдання скеровано на перевірку знання і розуміння з’єднання конденсаторів, уміння визначати їхні характеристики.
Енергію
Визначімо загальний заряд
У разі паралельного з’єднання конденсаторів позитивно заряджені обкладки всіх конденсаторів з’єднують в один вузол, а негативно заряджені ‒ в інший вузол (див. рисунок).
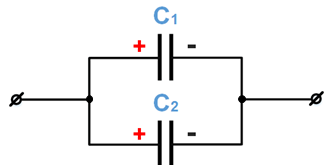
У такому разі загальний заряд
За умовою заряд першого конденсатора дорівнює
З’єднані в один вузол обкладки є одним провідником, тому потенціали обкладок і різниця потенціалів (напруга
Отже, за паралельного з’єднання конденсаторів допустима робоча напруга батареї визначена робочою напругою одного конденсатора. Візьмемо до уваги, що
Тому
А загальна електроємність
Зважаючи, що електроємності конденсаторів рівні
Визначімо енергію електричного поля утвореної системи конденсаторів:
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду.
Завдання скеровано на перевірку вміння застосовувати закон збереження електричного заряду.
Закон збереження електричного заряду: повний заряд електрично замкненої системи тіл залишається незмінним під час усіх взаємодій, які відбуваються в цій системі:
За умовою
Отже, після з’єднання кульок тонким провідником заряд перерозподілиться порівну між кульками, і заряд кульки
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання і розуміння електроємності конденсатора, того, від яких фізичних величин вона залежить.
Відношення заряду
Електроємність конденсатора визначають за формулами:
Значення заряду й напруги візьмімо з графіка в умові завдання:
Обчислімо шукану величину ‒ електроємність конденсатора:
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Робота електричного поля з переміщення заряду. Потенціал і різниця потенціалу.
Завдання скеровано на перевірку знання і розуміння закону збереження енергії під час переміщення заряду електричним полем.
Позитивно заряджена порошинка за умовою розганяється, тобто її кінетична енергія
Скористаймося законом збереження енергії, щоб довести це розрахунками:
Візьмімо до уваги, що за умовою
Відповідь: A.
ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона.
Завдання скеровано на перевірку знання і розуміння того, від яких фізичних величин і як залежить сила Кулона.
Закон Кулона: сила
Отже, якщо відстань між точковими зарядженими тілами зменшити в
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Закони постійного струму.
Завдання скеровано на перевірку знання і розуміння одиниць електродинамічних величин і їхнього фізичного змісту.
Одиниця електричного заряду
Одиниця напруженості
Напруженість електричного поля
Одиниця потенціалу
Потенціал
Одиниця електричного опору
Відповідь: 1Д, 2Б, 3А, 4В.
ТЕМА: Електродинаміка. Основи електростатики. Потенціал і різниця потенціалів.
Завдання скеровано на перевірку розуміння енергетичної характеристики електростатичного поля.
Силовою характеристикою електричного поля є напруженість. Електричне поле, вектори напруженості якого однакові в усіх точках простору, називають однорідним. Напруженість поля більшає в міру наближення до заряду (на наближення вказують стрілочки на рисунку). Отже, напруженість у точці
Якщо відстань між лініями напруженості в деякій області простору є однаковою (див. рисунок), то так само однаковою є напруженість поля в цій області:
Потенціал – це енергетична характеристика електростатичного поля. Силові лінії поля напрямлені в бік зменшення потенціалу. Що більша напруженість, то швидше зменшується потенціал під час переміщення вздовж силової лінії (напруженість характеризує швидкість зміни потенціалу). Отже, потенціал у точці
І відповідно в точках
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.
Завдання скеровано на перевірку знання і розуміння зв’язку між напруженістю електричного поля і напругою на пластинах конденсатора, а також залежності напруженості від відстані між його пластинами.
Поле між пластинами плоского конденсатора є однорідним, тому зв’язок між напруженістю
За умовою напруженість електричного поля зменшиться вдвічі:
Визначімо відношення відстаней між пластинами конденсатора:
Отже, відстань між пластинами конденсатора треба збільшити вдвічі.
Відповідь: B.
ТЕМА: Електродинаміка. Основи електростатики. З’єднання конденсаторів.
Завдання скеровано на перевірку знання і розуміння, що таке конденсатор, і вміння визначати параметри з’єднань конденсаторів.
Якщо відповідно до умови замкнути вимикач, то конденсатори будуть з’єднані послідовно. А в разі послідовного з’єднання заряди обох конденсаторів будуть однаковими та дорівнюватимуть заряду батареї:
Напруга на батареї послідовно з’єднаних конденсаторів дорівнює сумі напруг на окремих конденсаторах, що й зазначено в умові (варіант Г ‒ неправильний):
Енергія зарядженого конденсатора
Однакові конденсатори (за умовою) мають однакову електроємність:
Між пластинами конденсатора електричне поле однорідне. Для однорідного електричного поля між напруженістю
Напруга на другому конденсаторі змінилася, отже, змінилася і напруженість.
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.
Завдання скеровано на перевірку знання видів електричних зарядів і розуміння, як може змінюватися заряд тіла.
За умовою крапля є електрично нейтральною, отже, кількість позитивно заряджених частинок дорівнює кількості негативно заряджених частинок. Носієм найменшого негативного заряду є електрон. Цей заряд зазвичай позначають символом e; його значення:
Носій найменшого позитивного заряду ‒ протон
Відповідно до умови спочатку з поверхні краплі вилетів електрон. Це означає, що негативно заряджених частинок стало на одну менше, тобто позитивно заряджених частинок залишилося на одну більше ‒ заряд краплі став позитивним і дорівнюватиме заряду одного протона:
Потім крапля поглинула протон, тож заряд краплі збільшився на заряд ще одного протона:
Відповідь: Г.