Розділ: Електродинаміка
Тема: Закони постійного струму
Кількість завдань: 106
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.
Завдання скеровано на перевірку знання і розуміння послідовного та паралельного з’єднання провідників, уміння визначати характеристики електричного струму.
Резистори
Це буде струм, який проходить крізь резистор
Відповідь:
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку знання і розуміння законів постійного струму, і вміння визначати залежність фізичних величин, що характеризують електричний струм.
Потужність струму
Узявши до уваги, що
Зауважмо, що за умовою напруга стала.
А якщо вкоротити спіраль (тобто меншою стане довжина
Згідно із законом Ома
Висновок: якщо напруга залишається сталою, а опір зменшується (залежність обернена
Відповідь: A.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.
Завдання скеровано на перевірку знання і розуміння поняття електричний опір провідника.
Опір провідника
Запишімо, яким був опір мідного дроту до шліфування і після нього (зауважимо, що питомий опір матеріалу, з якого виготовлений дріт, і його довжина під час цього процесу не змінилися):
Обчислімо опір дроту після шліфування:
Відповідь: 4.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.
Завдання скеровано на перевірку знання закону Ома для ділянки кола й параметрів, від яких залежить електричний опір.
Електричний опір
Якщо не замінювати дріт, а брати лише його частину, то у формулі зміниться лише значення довжини дроту, а питомий опір і площа поперечного перерізу залишаться ті самі. Тобто опір провідника прямо пропорційний його довжині:
Отже, можна скласти пропорцію. Якщо дріт довжиною
Обчислимо опір ділянки дроту довжиною
За законом Ома для ділянки кола можна визначити силу струму в дроті, якщо за умовою вольтметр показує напругу
Відповідь: 0,5.
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку знання і застосування формули для потужності електричного струму.
Потужності нагрівальних елементів однакові:
Запишемо потужності через добуток напруги
За законом Ома для ділянки кола виразимо силу струму через відношення напруги і опору і підставимо у рівність потужностей:
Визначимо опір нагрівального елемента, розрахованого на іншу напругу, але тієї ж потужності:
Відповідь: 16.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання. Закон Ома для повного кола.
Завдання скеровано на перевірку вміння застосовувати знання про співвідношення між фізичними величинами, що характеризують електричний струм, за паралельного і послідовного з’єднання.
Коли ключ не замкнений, то струм проходить через одну лампочку й амперметр. А якщо ключ замкнути, то струм проходитиме через дві лампочки, з’єднані паралельно.
За паралельного з’єднання загальний опір лампочок буде у
Сила струму
Отже, якщо опір удвічі зменшиться, то сила струму вдвічі збільшиться, тобто покази амперметра збільшаться (варіанти відповіді А і В відкидаємо).
Покази вольтметра не зміняться, тому що друга лампочка приєднана паралельно.
Відповідь: Г.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.
Завдання скеровано на перевірку розуміння послідовного і паралельного з’єднань провідників і відповідних їм фізичних величин, умінь описувати аналітично схеми (ділянки схем) електричного кола й застосовувати закон Ома для ділянки кола.
Напруга на кінцях зображеної на рисунку ділянки електричного кола складається з напруги на першому резисторі й напруги на ділянці паралельно з’єднаних резисторів 2 і 3, тому що резистор 1 і ділянка кола з резисторами 2 і 3 з’єднані послідовно. Обчислімо зазначені напруги, і тоді зможемо визначити загальну напругу на зображеній ділянці.
Почнімо з резистора 3: відомий його опір і сила струму, яку показує амперметр. За законом Ома для ділянки кола ми можемо обчислити напругу на цьому резисторі:
Напруга на кожному з паралельно з’єднаних провідників є однаковою:
За значеннями напруги на резисторі 2 та його опору можемо обчислити силу струму, що проходить крізь резистор 2:
Отже, загальний струм у ділянці кола
Визначаємо напругу на резисторі 1:
Обчислюємо загальну напругу на зображеній ділянці електричного кола:
Відповідь: 10.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі за допомогою закону Ома для повного кола.
За рисунком 1, наведеним в умові завданні, можна визначити покази амперметра в обох положеннях вимикача. Для цього визначимо ціну поділки шкали амперметра.

Рис. 1. Умова завдання
Ціна великої поділки амперметра дорівнює
Тоді в першому положенні (на рисунку 1 ліворуч) сила струму, виміряна амперметром, дорівнює
Також з рисунку можна зрозуміти, що перемикач дає змогу вибрати, який із резисторів (А чи Б) підключають у коло.
1. Дано:
1. Знайти:
Напругу на обкладинках гальванічного елемента можна визначити із закону Ома для ділянки кола:
Тоді напруга дорівнює:
2. Знайти:
Напруга на обкладинках під час зміни положення перемикача змінюється, але електрорушійна сила (ЕРС) джерела струму – ні. ЕРС для положення вимикача на резисторі А за законом Ома для повного кола:
Тоді ЕРС дорівнює:
Тоді із закону Ома для повного кола можна визначити опір провідника Б:
Відповідь: 1. 0,7. 2. 2.
ТЕМА: Перетворення енергії в коливальному контурі. Закон Джоуля – Ленца. Рівняння теплового балансу.
Завдання скеровано на оцінювання знання формул для визначення енергії коливального контуру, кількості теплоти, що виділяється під час згоряння палива, і закону Джоуля – Ленца.
Відповідь: 1В, 2А, 3Г, 4Д.
ТЕМА: Електричне коло.
Завдання скеровано на оцінювання знань умовних позначень для створення схем електричних кіл.
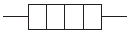 |
– нагрівальний елемент. |
 |
– резистор. |
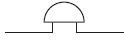 |
– електричний дзвінок. |
 |
– запобіжник. |
Відповідь: Г.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі за допомогою закону Ома для повного кола, а також вміння інтерпретувати схеми електричного кола.
1. Дано:
1. Знайти:
Реостат – це елемент кола зі змінним опором. Зазвичай реостат – це довгий провідник, повзунок якого дає змогу включити в коло його частину будь-якої довжини. Чим менша частина реостата включена в коло, тим менший його опір. Опір провідника можна визначити за його геометричними параметрами:
Фізичну будову реостата відображено в його символі для схематичного зображення електричного кола. Стрілка в позначенні показує, яку саме частину реостата включено в коло.
У цій задачі максимальний опір реостата відповідає крайньому правому положенню. За рисунком a можна визначити, що довжина провідника становить 6 клітинок. Масштаб рисунка невідомий, тому вважатимемо, що довжина реостата становить 6 умовних одиниць довжини (у. о. д.). На рисунку a в коло включена ділянка реостата, довжина якої становить 5 умовних одиниць. Ні питомий опір провідника, ні його поперечний переріз при цьому не відрізняються від цих його параметрів за максимального опору. Лише довжина ділянки вдвічі менша, тож можна обчислити опір реостата в положенні, зображеному на рисунку a:
2. Знайти:
Потужність струму в реостаті можна обчислити за формулою
За законом Ома напруга, сила струму й опір ділянки кола пов’язані між собою:
З огляду на те, що жодних відомостей про напругу в умові завдання немає, можна виразити її із закону Ома й підставити у формулу для потужності:
Аналогічно можна розрахувати опір реостата для положення, зображеного на рисунку 1:
За законом Ома для повного кола можна визначити силу струму:
Тоді для рисунків 1 і 2 можна записати такі вирази відповідно:
Відповідь: 1. 5. 2. 1,8.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля – Ленца.
Завдання скеровано на перевірку вміння використовувати закон Джоуля – Ленца.
Кількість теплоти, що виділяється під час проходження струму провідником, визначають за законом Джоуля – Ленца:
Якщо до збільшення сила струму в провіднику дорівнювала
Тоді:
Тож кількість теплоти збільшиться в 16 разів.
Відповідь: Г.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.
Завдання скеровано на оцінювання вміння визначати опір провідників за їхніми геометричними характеристиками.
Дано:
Знайти:
Електричний опір
Залежність опору провідника від його геометричних характеристик описують формулою
Після переведення міліметрів квадратних у метри квадратні можна обчислити шукану довжину дроту:
Відповідь: 40.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.
Завдання скеровано на оцінювання вміння аналізувати результати експерименту, зображені на фото, і розв’язувати розрахункові задачі з використанням законів Ома.
1. Знайти:
Схема електричного ланцюга, зображеного на фото 1 в умові завдання, така:
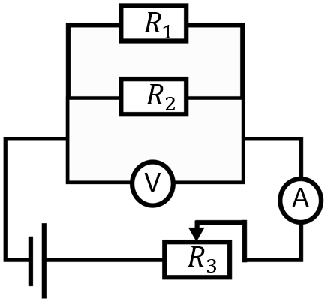
Рис. 1. Схема електричного ланцюга до розімкнення ключа
Реостат послідовно підключено до двох резисторів, підімкнутих паралельно.
Правила для послідовного підключення провідників, схематично зображеного на рисунку 2, описано формулами
де
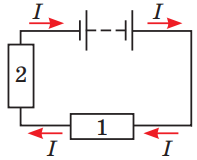
Рис. 2. Послідовне з’єднання провідників 1 і 2
Для паралельно підключених провідників (рис. 3) діють правила, описані формулами:
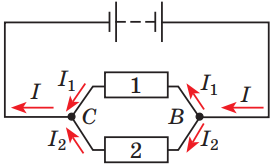
Рис. 3. Паралельне з’єднання провідників 1 і 2
Напруга, яку вимірює вольтметр, – це напруга в системі паралельно підключених провідників. А напруга
2. Знайти::
Після розімкнення ключа електричне коло змінилося – струм по гілці
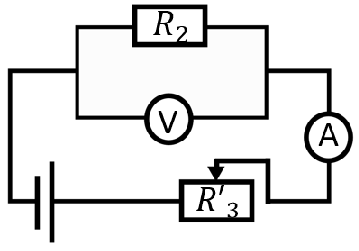
Рис. 4. Схема після розімкнення ключа
Тепер амперметр вимірює силу струму на реостаті з новим значенням опору й провіднику
Напруга, сила струму й опір на ділянці електричного кола пов’язані законом Ома, який описано формулою:
Тоді, знаючи силу струму й напругу на двох провідниках до відключення і провіднику
Після складання системи рівнянь
Із рівняння, складеного для кола після розімкнення ключа, можна визначити
опір
Відповідь: 1. 2. 2. 4.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання закону Ома для ділянки електричного кола.
За законом Ома
За умовою на цоколі лампи зазначено величини в вольтах й амперах, тобто йдеться про робочу напругу й силу струму лампи. Величини робочої напруги й сили струму ламп, а також їхнього опору в робочому стані, обчисленого за формулою
| № лампи | |||
| 1 | 0,4 | 6 | 15 |
| 2 | 0,25 | 2,5 | 10 |
| 3 | 0,3 | 6 | 20 |
| 4 | 0,25 | 3 | 12 |
Відповідь: B.
ТЕМА: Електродинаміка. Електричний струм.
Завдання скеровано на оцінювання розуміння поняття електричного струму.
Дано:
Знайти:
Сила струму – це фізична величина, яка характеризує електричний струм і чисельно дорівнює заряду, що за секунду проходить через поперечний переріз провідника:
Відповідь: 8.
ТЕМА: Електродинаміка. Закон Ома для ділянки кола. Закон Ома для повного кола.
Завдання скеровано на оцінювання вміння аналізувати результати експерименту, зображені на фото й використовувати закони Ома для розв’язування розрахункових задач.
1. Знайти:
На рисунку A зображено вимірювання вольтметром напруги на реостаті. Оскільки між великими поділками, ціна яких 1 В, на цій шкалі нанесено п’ять малих поділок, ціна малої поділки – 0,2 В. Тоді показання вольтметра – 3,4 В.
Амперметром вимірюють силу струму в колі. Ціна великої поділки на цій шкалі 0,5 А, а між двома великими поділками нанесено десять малих поділок, тож ціна малої поділки – 0,05 А. Тому показання амперметра – 0,7 А.
Опір реостата з повзунком у положенні як на рисунку A можна обчислити за законом Ома для ділянки кола:
2. Знайти:
ЕРС джерела струму
Затим потрібно визначити опір реостата (див. пункт 1 цього завдання). Покази вольтметра – 3,2 В, амперметра – 0,9 А. Тоді опір реостата становить
Тоді з першого рівняння в системі (4) можна визначити ЕРС:
Відповідь: 1. 5. 2. 4,1.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.
Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного й послідовного з’єднання провідників.
Яскравість світіння лампи залежить від її потужності, яку визначають за формулою
Позначимо напругу в колі
З рисунку зрозуміло, що лампа 1 послідовно з’єднана з лампами 2 і 3, які між собою з’єднані паралельно.
Правильне розв’язання завдання ґрунтується на розумінні законів паралельного й послідовного з’єднання провідників (див. рисунки 1–2).
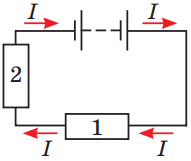
Рис. 1. Послідовне з’єднання провідників 1 і 2:
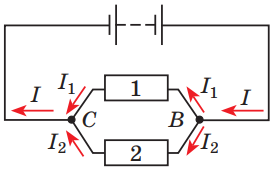
Рис. 2. Паралельне з’єднання провідників 1 і 2:
Оскільки за умовою завдання лампи 2 і 3 з’єднані паралельно, то для цієї частини кола
Для повного кола до виходу лампи 2 з ладу
З огляду на те, що опір усіх ламп однаковий, сила струму
Тож
Тобто до поломки потужність цих ламп була
Після того, як лампа 2 вийшла з ладу, її опір став дуже великим, тому крізь неї струм не потече. Електричне коло після виходу з ладу лампи 2 схематично зображено на рисунку 3.
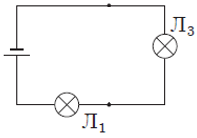
Рис. 3. Схема електричного кола після виходу з ладу лампи 2
У цьому електричному колі лампи 1 і 3 з’єднано послідовно, тому
Напруга в колі не змінилася через поломку лампи, тож, за законом Ома, у цьому колі сила струму
Отже,
Відповідь: B.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.
Завдання скеровано на оцінювання розуміння принципів роботи вольтметра й уміння розв’язувати задачі на використання закону Ома для ділянки кола.
Дано:
1. Знайти:
За законом Ома для ділянки кола можна визначити опір вольтметра:
2. Знайти:
Опір вольтметра визначає максимальну напругу, яку цим приладом можна виміряти, тому за збільшення максимальної напруги необхідно збільшувати опір вольтметра. Щоб збільшити опір вольтметра, послідовно до нього можна підключити додатковий опір.
Перш за все потрібно визначити опір вольтметра, необхідний для вимірювання напруги
Можна скористатися рівністю для додавання опору послідовно з’єднаних провідників:
Тоді додатковий опір, підключений до вольтметра такий:
Відповідь: 1. 4. 2. 8.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола.
Завдання скеровано на оцінювання розуміння схематичного зображення електричного кола й уміння використовувати закон Ома для ділянки електричного кола.
Реостат – це прилад, опір якого можна змінювати. Часто опір реостата регулюють за допомогою ковзного контакту, положення якого визначає частину провідника, уключеного в коло. На схемі електричного кола чим більша частина реостата розташована після стрілки, яка показує точку включення, тим більшим є опір цього приладу (рис. 1).
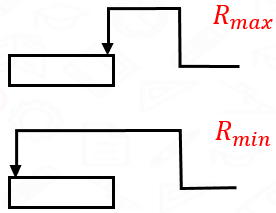
Рис. 1. Опір реостата за різних положень ковзного контакту
За умовою задачі ковзний контакт реостата перемістили в крайнє ліве положення, за рисунком це положення з мінімальним опором. Тож можна дійти висновку, що опір реостата зменшився.
Потрібно розглянути дві ситуації з відповідними показаннями амперметра, вольтметра й опором реостата – до зміни
Реостат послідовно підключено до лампи. Сила струму в послідовно з’єднаних провідниках однакова й дорівнює загальній силі струму в ділянці кола:
Загальна напруга на послідовно з’єднаних провідниках дорівнює сумі напруг на них:
Загальний опір послідовно з’єднаних провідників дорівнює сумі опорів цих провідників:
Позначивши загальну напругу в колі
Тож можна порівняти силу струму в двох випадках:
Вольтметром у схемі вимірюють напругу на лампі. Позначивши опір лампи як
Тепер можна порівняти напругу на лампі:
Відповідь: B.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.
Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного й послідовного з’єднання провідників.
Нехай
Напругу в колі можна обчислити як суму напруг на кожній із пар:
Усередині кожної пари резистори з’єднано послідовно, тому сила струму в парі дорівнюватиме сумі сил струму на кожному з резисторів:
Напруга на кожному резисторі дорівнює напрузі на всій парі:
Опір кожної пари резисторів розраховують за правилами паралельного з’єднання провідників:
Тоді можна за законом Ома розрахувати напругу на кожній парі:
Відповідь: Б, В.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на закон Ома для повного кола, а також уміння читати схеми електричного кола.
Дано:
1. Знайти:
Реостат – це елемент кола зі змінним опором. Зазвичай реостат – це довгий провідник, повзунок якого дає змогу включити в коло його частину будь-якої довжини. Чим меншу частину реостата включено в коло, тим менший його опір. Опір провідника можна визначити за його геометричними параметрами:
Фізичну будову реостата відображено й у його символі для схематичного зображення електричного кола. Стрілка в позначенні реостата показує, яку саме його частину включено в коло.
За умовою завдання максимальний опір реостата відповідає крайньому правому положенню. За рисунком 1 можна визначити, що довжина провідника в цьому разі становить 6 клітинок. Масштаб рисунка не зазначено, тому можна вважати, що довжина реостата – 6 умовних одиниць довжини (у. о. д.). На рисунку 2 в коло включено половину реостата. Ні питомий опір провідника, ні його поперечний переріз при цьому не відрізняються від ситуації, коли опір максимальний. Лише довжина провідника вдвічі менша, тож можна обчислити опір реостата в положенні на рисунку 2:
2. Знайти:
Аналогічно можна розрахувати опір реостата для положення на рис. 1:
За законом Ома для повного кола можна визначити силу струму:
Тоді для рисунків 1 і 2:
Відповідь: 1. 3. 2. 0,5.
ТЕМА: Електродинаміка. Закони постійного струму. Електрорушійна сила.
Завдання скеровано на оцінювання розуміння поняття електрорушійної сили.
Електрорушійна сила
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне й послідовне з’єднання провідників.
Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного й послідовного з’єднання провідників.
Нехай
Напругу в колі можна обчислити як суму напруг на кожній із пар:
Усередині кожної пари резистори з’єднано послідовно, тому сила струму в парі дорівнюватиме сумі сил струму на кожному з резисторів:
Напруга на кожному резисторі дорівнює напрузі на всій парі:
Опір кожної пари резисторів розраховують за правилами паралельного з’єднання провідників:
Тоді можна розрахувати напругу на кожній парі за законом Ома:
Тоді за законом Ома можна обчислити силу струму на кожному з резисторів:
Відповідь: B.
ТЕМА: Електричне коло.
Завдання скеровано на оцінювання знання умовних позначень для створення схем електричних кіл:
A – котушка індуктивності, соленоїд

Б – конденсатор

B – напівпровідниковий діод
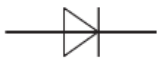
Г – батарея гальванічних елементів
 або
або
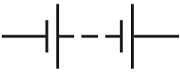
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне з'єднання провідників.
Завдання скеровано на перевірку вміння розв'язувати задачі на розрахунок електричних кіл.
Дано:
1. Знайти:
З'єднання послідовне, тому сила струму однакова на всій ділянці кола.
Із закону Ома для ділянки кола
Розрахуємо
2. Знайти:
Відповідь: 1. 3. 2. 24.
ТЕМА: Електродинаміка. Закони постійного струму. Сила струму. Опір провідників. Закон Ома для ділянки кола.
Завдання скеровано на перевірку вміння застосовувати математичні вирази законів електродинаміки i формули для визначення фізичних величин.
1. Сила струму за означенням
2. Опір за озаченням
3. Питомий опір (з попередньої формули)
4. Електрична напруга за законом Ома
Але і силу струму, і опір описано формулами за означенням, тому
Відповідь: 1A, 2Б, 3Д, 4Г.
ТЕМА: Електординаміка. Електричний струм у різних середовищах. Діод.
Завдання скеровано на перевірку вміння розв'язувати задачі на розрахунок електричних кіл і вольт-амперну характеристику діода.
За умовою діоди ідеальні, тобто коли діод має пряме підключення
На схемі діоди
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики.
Завдання скероване на оцінку розуміння принципу роботи джерела струму.
Джерела електричного струму повинні виштовхувати електрони в електричне коло. Вони мають позитивно й негативно заряджені полюси. Електрони рухаються він негативного полюса до позитивного по провідниках у колі. Проте відстань між двома полюсами джерела набагато менша за довжину будь-якого кола. Частинки, що притягуються, завжди рухаються найкоротшим шляхом. Тож чому електрони взагалі покидають джерело струму й опиняються в колі, а не просто рухаються в межах джерела?
В усіх джерелах діють сторонні сили, що змушують електрони рухатись до негативно зарядженого полюса. Сторонні сили протидіють кулонівським у джерелі, які прагнуть перемістити електрони до позитивно зарядженого полюса. Схематично дію сторонніх і кулонівських сил у джерелі струму зображено на рисунку 1. Синім кольором позначено кулонівські сили, а червоним – сторонні.
Тож джерело струму не може працювати без дії сторонніх сил усередині.
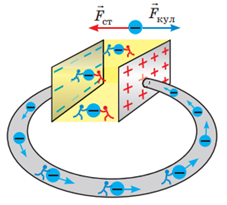
Рис. 1. Схематичне зображення дій сторонніх і кулонівських сил у джерелі струму
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне і послідовне з’єднання провідників.
Завдання скеровано на оцінювання знання закону Ома й розуміння особливостей паралельного і послідовного з’єднання провідників.
Знайти:
Спочатку потрібно позначити напругу джерела як
Правила послідовного і паралельного підключення такі:
Рис. 1. Послідовне з’єднання провідників 1 і 2
Тому сила струму, яку вимірює амперметр – це сила струму на реостаті й на системі паралельно підключених провідників. За показниками на фотографії вона дорівнює 1,5 A.
Для паралельно підключених провідників правила такі:
Рис. 2. Паралельне з’єднання провідників 1 і 2
Нехай
Оскільки резистор 1 і групу резисторів 2–5 підключено послідовно, можна записати:
Напруга на групі резисторів 2–5 дорівнює напрузі на кожній парі резисторів, а сила струму на групі резисторів – це сума сил струму на кожній із пар:
Усередині кожної пари з’єднання послідовне, тому для цих резисторів також можна записати відношення для напруги й сили струму:
Напруга, сила струму й опору пов’язані між собою законом Ома:
Можна обчислити загальний опір усіх резисторів:
Тоді можна записати співвідношення між силою струму в колі, напругою на обкладинках джерела й загальним опором резисторів у колі:
Можна також записати аналогічне співвідношення для п’ятого резистора:
Опір в обох парах резисторів дорівнює
Тож вираз для напруги п’ятого резистора теж спроститься:
Тоді
Відповідь: 4.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота і потужність електричного струму.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, що стосуються залежності опору провідника від його геометричних параметрів і впливу змін опору провідника на потужність електричного струму.
Дано:
1. Знайти:
Опір провідника залежить від його геометричних параметрів і матеріалу:
Якщо
Тоді можна обчислити зменшення опору після вкорочення:
2. Знайти:
Потужність нагрівника можна обчислити за формулою:
За законом Ома напруга, сила струму й опір ділянки кола пов’язані між собою:
Тоді, зважаючи на те, що ніяких відомостей про силу струму умові не дано, можна підставити вираз закону Ома у вираз для потужності:
Тоді, зважаючи на те, що напруга залишилась сталою, можна обчислити, на скільки відсотків збільшилася потужність після вкорочення спіралі:
Тоді
Тобто потужність збільшилася на 25 %.
Відповідь: 1. 1,25. 2. 25.
ТЕМА: Електродинаміка. Закони постійного струму.
Завдання скеровано на оцінювання розуміння поняття сторонніх сил і принципів роботи основних елементів електричного кола.
Сторонні сили – це будь-які не кулонівські сили, що діють на електрично заряджені частинки.
Джерела електричного струму повинні виштовхувати електрони в електричне коло. Вони мають позитивно й негативно заряджені полюси. Електрони рухаються від негативного полюса до позитивного по провідниках у колі. Проте відстань між двома полюсами джерела набагато менша, ніж довжина будь-якого кола. Частинки, що притягуються, завжди рухаються за найкоротшим шляхом. Тож чому електрони взагалі покидають джерело струму й опиняються в колі, а не просто рухаються в межах джерела?
В усіх джерелах діють сторонні сили, що змушують електрони рухатися до негативно зарядженого полюса. Сторонні сили протидіють кулонівським у джерелі, що прагнуть перемістити електрони до позитивно зарядженого полюса. Схематично дію сторонніх і кулонівських сил у джерелі струму зображено на рисунку 1. Стрілками синього кольору позначено кулонівські сили, а червоного – сторонні.
Тож джерело струму не може працювати без дії сторонніх сил всередині.
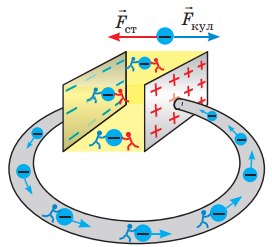
Рис. 1. Схематичне зображення дій сторонніх та кулонівських сил у джерелі струму
Відповідь: В.
ТЕМА: Електродинаміка. Закони постійного струму. Електричний струм у різних середовищах.
Завдання скеровано на оцінювання розуміння впливу струму на середовища, у яких він протікає.
Теплова дія струму полягає в тому, що будь-який провідник нагрівається під час проходження ним струму. Електрони, що рухаються під дією поля, зіштовхуються із частинками у кристалічній ґратці провідника. У результаті таких зіткнень частинки поглинають кінетичну енергію електронів, внутрішня енергія провідника росте, а отже збільшується і температура.
Електроплита працює саме завдяки цьому ефекту: металеві конфорки або спіралі нагріваються, коли по них тече струм, що й дає змогу готувати на них їжу.
У випадку Б ілюстровано йонну провідність електролітів, а у випадках В і Г – появу магнітного поля у провідниках зі струмом.
Відповідь: A.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота й потужність електричного струму.
Завдання скеровано на перевірку розуміння поняття втрати напруги.
Дано:
Знайти:
Втрата напруги – це різниця між напругою на кінцях лінії:
Втрату напруги можна розрахувати за формулою
Опір провідника залежить від його геометричних характеристик:
Тоді
Потужність джерела пов’язана з напругою і силою струму:
Тоді, виразивши силу струму через потужність і напругу джерела, можна перетворити формулу для втрати напруги:
Тоді довжина провідника
Лінія електропередач має два кабелі, тому довжина одного з них дорівнюватиме половині загальної довжини провідника: 2,5 км.
Відповідь: 2,5.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота та потужність електричного струму.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, що стосуються роботи й потужності електричного двигуна.
Дано:
1. Знайти:
Потужність пов’язана з роботою формулою
Потужність електричного двигуна можна визначити за формулою
Тож:
2. Знайти:
ККД двигуна визначають як відношення корисної роботи, виконаної ним, до повної роботи:
Корисна робота – це робота, що необхідна для підйому вантажу на висоту 2 м.
Роботу сили можна визначити за формулою
Вважатимемо, що кут між напрямком сили й переміщенням вантажу дорівнює нулю, а переміщення тіла дорівнює висоті його підйому, тож
Вантаж втримується на землі завдяки силі тяжіння, тож піднімальна сила має за модулем дорівнювати їй:
Повна робота – це робота, виконана електричним двигуном, що була розрахована в попередньому пункті. Тоді:
Відповідь: 1. 60. 2. 80.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне та послідовне з’єднання провідників.
Завдання скеровано на перевірку знання закону Ома й розуміння особливостей паралельного та послідовного з’єднання провідників.
Схему з умови завдання доцільно перемалювати в зручнішому вигляді.
Точки контакту між двома провідниками можна рухати, тож варто перемістити вертикальний контакт, що підключає
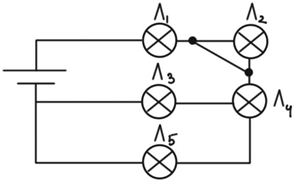
Рис. 1. Модифікована (1) схема умови задачі
Лампи
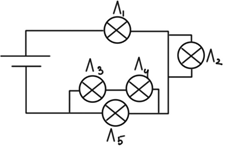
Рис. 2. Модифікована (2) схема умови задачі
Для розв’язання задачі потрібно взяти до уваги закони послідовного і паралельного з’єднання провідників.
За послідовного з’єднання (рис. 3)
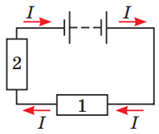
Рис. 3. Послідовне з’єднання провідників 1 і 2
За паралельного з’єднання (рис. 4)
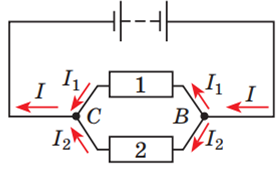
Рис. 4. Паралельне з’єднання провідників 1 і 2
Опір дротів між елементами настільки малий, що ним можна знехтувати під час розрахунків. Тож опір лампи
За законом Ома
Тож що більший опір провідника в паралельному підключенні, то менша сила струму через нього проходить. З огляду на різницю в опорі дротів і лампи струм через лампу
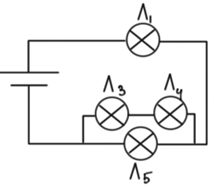
Рис. 5. Схема умови задачі
Яскравість лампи прямо пропорційна силі струму, що протікає крізь неї, тож для порівняння яскравості ламп досить порівняти силу струму, що протікає крізь них.
Нехай сила струму в колі дорівнює
За законом Ома
Тож
Усі лампи однакові, лампи
Тобто сили струму, що протікають крізь лампи, дорівнюють
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики.
Завдання скеровано на перевірку розуміння принципів підключення вимірювальних приладів в електричне коло.
Зазвичай у коло амперметр підключають послідовно, а вольтметр – паралельно (рис. 1).
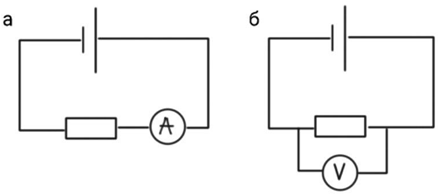
Рис. 1. Підключення в коло амперметра (а), вольтметра (б)
Нитка в лампі нагрівається за законом Джоуля:
Отже, що більша сила струму на лампочці, то більше розжарення її нитки.
Для розв’язання завдання потрібно зважити на закони послідовного (рис. 2) і паралельного (рис. 3) з’єднання провідників.
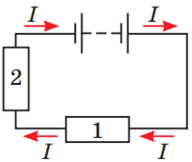
Рис. 2. Послідовне з’єднання провідників 1 і 2.
За послідовного з’єднання
Тож, щоб амперметр, уключений у коло послідовно, мало впливав на струм в колі, його опір має бути суттєво меншим за опір активних елементів (лампочки).
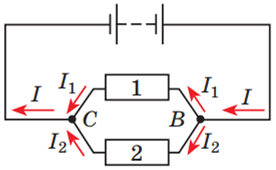
Рис. 3. Паралельне з’єднання провідників 1 і 2.
За паралельного з’єднання
За законом Ома
Тож, що більший опір провідника в паралельному підключенні, то менша сила струму через нього проходить. Для того, щоби вольтметр, підключений в коло паралельно, мало впливав на струм у колі, його опір повинен бути дуже великим.
Якщо замість вольтметра з великим опором підключити амперметр, опір якого дуже малий, то сила струму, що тече через прилад, буде більшою від очікуваної.
Сила струму в колі для паралельно підключених елементів дорівнює сумі сили струму в кожній гілці:
Тож, якщо силу струму в одній гілці збільшилася, то в іншій вона зменшиться. У результаті зменшення сили струму в лампочці зменшиться розжарення її нитки.
Відповідь: A.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку вміння розв’язувати задачі із застосування закону Ома для ділянки кола за різних з’єднань провідників.
Загальна напруга
За паралельного з’єднання провідників сила струму
Загальний опір
За законом Ома для ділянки кола
Звідси формула для обчислення
Отже, максимально можлива кількість резисторів у цьому колі може бути
Відповідь: 15.
ТЕМА: Механіка. Молекулярна фізика і термодинаміка. Електродинаміка.
Завдання скеровано на перевірку знань і розуміння принципів дії пристроїв і механізмів із різних розділів фізики.
Гальмівні механізми (дискові або барабанні) не дають обертатися колесам, унаслідок чого автомобіль зменшує швидкість. Принцип дії гальмівного механізму заснований на використанні сили тертя. Під час гальмування кінетична енергія переходить у внутрішню.
Тепловий двигун – це машина, яка працює циклічно й перетворює енергію палива на механічну роботу. Робоче тіло (газ, який виконує роботу під час свого розширення) отримує певну кількість теплоти від нагрівника. Ця теплота частково перетворюється на механічну енергію (робоче тіло виконує роботу), а частково передається холодильнику.
Індукційні генератори струму перетворюють механічну енергію на електричний струм. Складені з металевого осердя, у пази якого поміщено обмотку. Кінці обмотки з’єднані з кільцями, до кожного з яких притиснуто щітку для відведення напруги до споживача. Осердя з обмоткою (ротор) обертається в магнітному полі нерухомого постійного магніту або електромагніту.
Електричний двигун є пристроєм для перетворення електричної енергії на механічну та приведення до руху машин і механізмів. Робота електродвигуна основана на втягуванні або виштовхуванні провідника з електричним струмом у магнітному полі й дії на провідник зі струмом сили Ампера. Під час роботи двигуна рух ротора (рухомої частини двигуна) передається валу, а з нього – безпосередньо до споживача.
Відповідь: 1А, 2Б, 3В, 4Г.
ТЕМА: Електродинаміка. Закони постійного струму. Електровимірювальні прилади.
Завдання скеровано на перевірку розуміння деяких правил складання електричних кіл і підключення до них різних приладів.
Ні амперметр, ні вольтметр не мають впливати на значення вимірюваної величини, як будь-який вимірювальний прилад. До того ж в умові зазначено, що прилади та провідники є ідеальними. Це означає, що опором провідників можна знехтувати, а опір ідеального амперметра вважати рівним нулю. За цих умов послідовно підключений в електричне коло амперметр без утрат покаже значення тієї сили струму, що проходить через споживач (тут – резистор).
На відміну від амперметра опір ідеального вольтметра нескінченно великий. Такий опір не дає змоги струму проходити через вольтметр. Тому вольтметр показує точне значення напруги на ділянці кола, до якої він приєднаний паралельно. Тож підключення в електричному колі амперметра паралельно, а вольтметра послідовно зі споживачем є неправильним.
Якщо підключити вольтметр паралельно до споживача або до ділянки кола, де послідовно з’єднано амперметр і споживач, то вольтметр покаже падіння напруги на споживачі (амперметр ідеальний, тому не впливатиме на значення напруги).
Якщо підключити вольтметр паралельно лише до амперметра, за законом Ома для ділянки кола напруга на амперметрі дорівнюватиме нулю, оскільки опір амперметра вважаємо рівним нулю:
Відповідь: A.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота і потужність електричного струму.
Завдання скероване на перевірку вміння розв’язувати розрахункові задачі, що стосуються впливу змін напруги на потужність електричного струму.
Потужність струму в лампочках можна визначити за формулою:
Оскільки опір ламп не змінюється, то потужність доцільно виразити через напругу й опір. Сила струму, напруга й опір пов’язані між собою законом Ома:
Тож
Тоді
Відповідь: Г.
ТЕМА: Електродинаміка. Основи електростатики. Паралельне і послідовне з’єднання провідників.
Завдання скеровано на перевірку знання закону Ома й розуміння особливостей паралельного і послідовного з’єднання провідників.
Закони послідовного і паралельного з’єднання провідників схематично зображено на рисунках 1 і 2 відповідно.
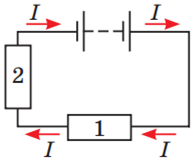
Рис. 1. Послідовне з’єднання провідників 1 і 2
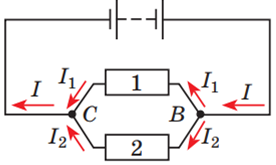
Рис. 2. Паралельне з’єднання провідників 1 і 2
З кількох резисторів номіналом
Щоб отримати необхідні додаткові
Відповідно
Для заміни резистора опором
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.
Завдання скеровано на перевірку застосування закону Ома для повного кола.
Запишімо закон Ома для повного кола для обох ситуацій:
Електрорушійна сила і внутрішній опір джерела струму є його сталими характеристиками, який би зовнішній опір не підключали. Тому виразімо електрорушійну силу з обох формул і прирівняємо ці вирази:
Виведімо формулу для обчислення внутрішнього опору джерела струму:
Відповідь: 4.
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку розуміння, що є корисною, а що – повною кількістю теплоти під час роботи електронагрівача.
Запишімо формулу для визначення коефіцієнта корисної дії
У формулі
Повну кількість теплоти можна визначити за законом Джоуля ‒ Ленца:
Або ж за формулою для визначення роботи
Підставмо вирази для корисної і повної кількості теплоти у формулу для коефіцієнта корисної дії і визначимо силу струму:
Відповідь: 6,25.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з᾽єднання провідників.
Завдання скеровано на перевірку знання і розуміння особливостей з᾽єднання провідників і їхніх характеристик.
Під час послідовного з᾽єднання електричної лампи і резистора сила струму в них буде однаковою. Зваживши на характеристики лампи, обчислімо силу струму, який можна пропускати крізь неї:
Щоб лампа працювала в нормальному режимі, треба крізь неї пропускати струм силою близько
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку вміння еквівалентно перетворювати схеми й розв’язувати розрахункові задачі, у яких ідеться про послідовне і паралельне з’єднання провідників.
Спочатку еквівалентно перебудуємо електричну схему з умови завдання, щоб було чітко видно, які з резисторів з’єднані паралельно, які ‒ послідовно, на яких саме резисторах вольтметром вимірюють напругу.
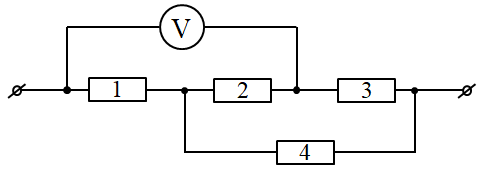
Вольтметр покаже суму напруг на послідовно з’єднаних резисторах 1 і 2. Визначмо їх.
Запишімо вирази для напруги
Резистори 2 та 3 з’єднано послідовно, тому
Визначмо загальну силу струму на ділянці кола:
Резистор 4 приєднаний паралельно до резисторів 2 та 3. Тому струм розділиться на частини
Віткою 23 пройде струм удвічі менший за струм, який пройде через резистор 4 (із закону Ома для ділянки кола
Запишімо, з огляду на це й закон Ома для ділянки кола, вирази для напруги на резисторах 2, 3 й 4:
Підставивши вирази для напруг на окремих резисторах у формулу для напруги на ділянці кола, маємо:
Розв’яжімо системи рівнянь:
Поділімо ліві і праві частини рівнянь:
Визначмо із цих відношень величини
Отже, вольтметр покаже напругу на резисторах 1 і 2:
Відповідь: 80.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля – Ленца.
Завдання скеровано на перевірку вміння застосувати закон Джоуля – Ленца.
За законом Джоуля – Ленца визначають кількість теплоти
Запишімо закон Джоуля – Ленца для зовнішнього і для повного кіл:
Обчислімо частку кількості теплоти, що виділилася на резисторі, від загальної кількості теплоти, що виділилася в електричному колі:
Відповідь: B.
ТЕМА: Електродинаміка. Закони постійного струму. Умови існування електричного струму.
Завдання скеровано на перевірку розуміння існування і протікання електричного струму в колі.
Для виникнення та існування електричного струму необхідні дві умови:
1) вільні заряджені частинки ‒ носії струму;
2) електричне поле, дія якого створює і підтримує напрямлений рух вільних заряджених частинок.
За створення електричного поля «відповідають» джерела струму ‒ пристрої, які перетворюють різні види енергії на електричну енергію. У джерелах струму виконується робота з розділення різнойменних електричних зарядів, у результаті чого один полюс джерела набуває позитивного заряду, а другий ‒ негативного; у такий спосіб створюється електричне поле.
За напрямок струму в електричному колі прийнято напрямок, у якому рухалися б цим колом позитивно заряджені частинки, тобто напрямок від позитивного полюса джерела струму до негативного. В умовному позначенні гальванічного елемента довга риска позначає позитивний, а коротка ‒ негативний полюс джерела.
На схемі ж в умові завдання гальванічні елементи або акумулятори підключені між собою однойменними полюсами, позитивними, тому струму за такого підключення в колі не буде.
Щоб амперметр показав наявність струму в колі, треба підключити додатковий опір паралельно до одного із джерел струму, щоб заряджені частинки змогли в обхід одного джерела дістатися від позитивного полюса до негативного полюса другого джерела струму.
Із запропонованих пар точок умову завдання задовольняє пара 2 та 3.
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола. Послідовне і паралельне з’єднання провідників. Закон Ома для повного кола.
Завдання скеровано на перевірку знання і розуміння послідовного з’єднання провідників, а також уміння визначати характеристики елементів електричного кола.
Для визначення опору
Крізь резистор проходитиме така сама сила струму, як і крізь світлодіоди, оскільки вони за схемою з’єднані послідовно, тобто
Для визначення спаду напруги на резисторі скористаймося законом Ома для повного кола:
Сила струму
За умовою внутрішнім опором батареї можна знехтувати, а резистор і світлодіоди з’єднані послідовно (їхні напруги додають). Тому електрорушійна сила дорівнюватиме сумі спадів напруги на резисторі
Звідси обчислімо напругу на резисторі:
Отже, тепер можна визначити опір резистора:
Відповідь: 30.
ТЕМА: Електродинаміка. Закони постійного струму. Сила струму.
Завдання скеровано на перевірку знання і розуміння поняття сили струму.
Сила струму
Відповідно до системи SI виразімо час у секундах:
Загальний заряд усіх електронів, що проходять через поперечний переріз провідника, дорівнює
Отже, визначімо шукану силу струму:
Відповідь: B.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку знання і розуміння послідовного і паралельного з’єднання провідників, а також уміння читати електричні схеми.
Перерисуймо цю ділянку кола й пронумеруймо резистори:
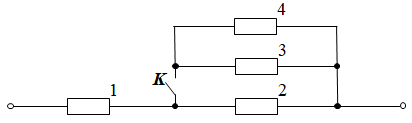
Коли вимикач
Після розмикання вимикача
Якщо резистори 1 і 2 з’єднано послідовно, загальний опір
Відповідь: B.
ТЕМА: Молярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.
Завдання скеровано на перевірку вміння визначати кількість теплоти, що віддають і поглинають тіла, а також уміння складати рівняння теплового балансу.
Кількість теплоти
Оскільки в умові дано напругу, а не силу струму, то, скориставшись законом Ома для ділянки кола
Кількість теплоти
Тоді кількість теплоти, що витрачається під час цього на теплообмін із навколишнім середовищем, є різницею енергії, яку дає кип’ятильник, й енергії, потрібної для того, щоб закип’ятити воду:
Виконаймо розрахунки:
де
Відповідь: 390.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.
Завдання скеровано на перевірку вміння читати електричні схеми й визначати за їхньою допомогою потрібні величини.
Запишімо закон Ома для повного кола:
За умовою внутрішнім опором джерела струму можна знехтувати, тож формула матиме вигляд:
Запишімо, чому дорівнюватиме сила струму до замикання ключа
Опір двох послідовно з’єднаних резисторів
Опір розгалуженої ділянки
Визначімо загальний опір
Тоді сила струму за замкненого ключа дорівнюватиме:
Визначімо, у скільки разів сила струму
Відповідь: 1,8.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у металах.
Завдання скеровано на перевірку знання і розуміння середньої швидкості поступального руху електронів.
За інтервал часу
де
При цьому переноситься заряд
За означенням сила струму
Отже, маємо:
Обчислімо шукану величину ‒ середню швидкість поступального руху електронів:
Відповідь: 0,25.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.
Завдання скеровано на перевірку знання і застосування закону Ома для повного кола.
Скористаймося законом Ома для повного кола: сила струму
Виразімо з формули шукану величину й обчислімо її:
Відповідь: B.
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне і послідовне з’єднання провідників.
Завдання скеровано на перевірку знання і розуміння послідовного і паралельного з’єднання провідників і відповідно змінювання фізичних величин, які характеризують електричний струм під час цих з’єднань.
У разі застосування шунта струм
Дізнаймося, який шунт треба приєднати паралельно амперметру, щоб збільшити верхню межу вимірювання амперметра в
Оскільки
Напруга на шунті й амперметрі однакова, тому відповідно до закону Ома маємо:
Отже, необхідний опір шунта визначаємо за формулою:
Визначмо, у скільки разів може збільшитися верхня межа вимірювання сили струму, якщо
Обчислімо опір шунта:
Відповідь: 101.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля‒Ленца.
Завдання скеровано на перевірку знання і розуміння залежності кількості теплоти від характеристик електричного струму і часу.
Закон Джоуля ‒ Ленца: кількість теплоти
До зміни сили струму кількість теплоти становила:
Після збільшення сили струму в
Визначмо, у скільки разів змінилася кількість теплоти:
Отже, після збільшення сили струму в
Відповідь: Г.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.
Завдання скеровано на перевірку вміння застосовувати закон Ома для повного кола.
Запишімо закон Ома для повного кола:
Коли вимикач розімкнутий, то вольтметр показує значення електрорушійної сили джерела струму:
Перетворімо цю формулу закону й визначмо внутрішній опір джерела струму:
За законом Ома для ділянки кола
Отже,
Відповідь: 2,5.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку вміння тлумачити електричну схему, еквівалентно її перетворювати й застосовувати відношення фізичних величин, що характеризують послідовне і паралельне з’єднання провідників.
Перебудуємо еквівалентно ділянку електричного кола, про яку йдеться в умові.
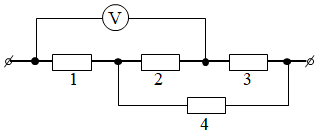
Вольтметр показує напругу на резисторах
Обчислімо напругу на першому резисторі:
Напруга на другому резисторі становитиме:
Опір усіх резисторів за умовою однаковий. Сила струму у вітці, де резистори
Силу струму
Отже,
Тоді
А сумарна напруга на резисторах
Виразімо добуток
Визначімо загальний опір ділянки кола:
Підставімо цей вираз для загального опору у формулу для напруги на ділянці кола:
Звідси
Отже, дізнаймося значення напруги, яке показує вольтметр:
Відповідь: A.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля ‒ Ленца.
Завдання скеровано на перевірку вміння застосовувати закон Джоуля ‒ Ленца й тлумачити показання приладів за певної послідовності підключення їх.
Кількість теплоти
Електричний опір резистора і час протікання струму відомі, а силу струму в резисторі можна визначити за законом Ома для повного кола:
Фотоелемент є джерелом струму. Коли до полюсів фотоелемента приєднали вольтметр (ще без навантаження ‒ резистора), вольтметр показав електрорушійну силу
Коли ж до полюсів приєднали замість вольтметра амперметр, який за умовою є ідеальним, тобто його опір
Звідси визначмо внутрішній опір фотоелемента, необхідний для визначення сили струму в резисторі:
Обчислімо силу струму в резисторі:
Визначимо кількість теплоти, яка виділиться в резисторі:
Відповідь: 125.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.
Завдання скеровано на перевірку знання і розуміння закону Ома для повного кола і послідовного з’єднання гальванічних елементів.
Запишімо закон Ома для повного кола:
Джерелом струму в колі є батарея з трьох з’єднаних послідовно гальванічних елементів опором
Електричний опір
Гальванічні елементи однакові й з’єднані послідовно, то ж електрорушійну силу
Підставимо вирази для внутрішнього опору, електрорушійної сили батареї елементів й опору лампи у формулу, що відображає закон Ома для повного кола:
Виразімо звідси силу струму:
Помножмо ліву і праву частини рівняння на
Підставимо числові значення відомих в умові величин:
Ми отримали квадратне рівняння
Обчислимо корені рівняння:
Меншим є значення сили струму
Відповідь: 0,5.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку вміння визначати загальний опір послідовного, паралельного й мішаного з’єднання провідників.
Загальний опір послідовно з’єднаних провідників
Це значення загального опору ділянки електричного кола набагато більше за
Коли всі резистори з’єднано паралельно (варіант відповіді Г), загальний опір
У разі однакового опору резисторів (як в умові завдання) формулу можна спростити:
Це значення загального опору ділянки електричного кола набагато менше за
Розгляньмо мішане з’єднання резисторів (варіанти відповіді А і Б).
У варіанті А два резистори з’єднано послідовно:
Паралельно до цих двох резисторів приєднано третій такий самий резистор опором
У варіанті Б два резистори з’єднано паралельно:
Послідовно до цих двох резисторів приєднано третій такий самий резистор опором
Отже, щоб отримати ділянку електричного кола з опором 6 Ом, потрібно з’єднати два резистори паралельно, а третій приєднати послідовно до них (за умови, що всі резистори однакові).
Відповідь: Б.
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння принципу будови коливального контуру, і вміння проаналізувати перетворення енергії в цьому контурі.
Після замикання ключа конденсатор заряджатиметься. У той момент, коли його заряд стане максимальним, струм на цій ділянці припиниться. Отже, коли ключ замкнуто, то електричний струм тече через котушку й резистор, а на конденсаторі буде тільки спад напруги (струм крізь нього не тече). На котушці не буде спаду напруги, а струм, що тече через котушку, дорівнюватиме струму, що тече через резистор. Обчислімо силу струму
Обчислімо спад напруги на конденсаторі до розмикання ключа:
Отже,
Після розмикання ключа конденсатор розряджатиметься на котушці й резисторі. Тобто виникнуть згасні (бо є резистор) електромагнітні коливання.
У початковий момент, після розмикання ключа, енергія коливань ‒ це накопичена енергія конденсатором і котушкою. Із закону збереження енергії очевидно, що вся енергія, яку має коливальний контур до розмикання ключа, перетвориться на тепло.
Визначмо кількість теплоти, яка виділяється на резисторі за час існування змінного струму в колі
Обчислімо шукану кількість теплоти:
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Електровимірювальні прилади.
Завдання скеровано на перевірку знання і розуміння, що таке вольтметр і як його правильно підключати в електричне коло.
Вольтметр ‒ це прилад для вимірювання напруги. Його приєднують до електричного кола паралельно ділянці, на якій вимірюють напругу, щоб забезпечити мінімальний вплив високого опору вольтметра на вимірювані величини.
Отже, щоб виміряти напругу на джерелі струму, треба вольтметр підключити до точок
Відповідь: Г.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.
Завдання скеровано на перевірку розуміння послідовного і паралельного з’єднань провідників і відповідних їм фізичних величин, уміння описувати аналітично схеми (ділянки схем) електричного кола й застосовувати закон Ома для ділянки кола.
Напруга на кінцях зображеної на рисунку ділянки електричного кола складається з напруги на першому резисторі й напруги на ділянці паралельно з’єднаних резисторів
Почнімо з резистора
Напруга на кожному з паралельно з’єднаних провідників є однаковою:
За значеннями напруги на резисторі
(Дійсно, опори резисторів
Отже, загальний струм у ділянці кола
Визначмо напругу на резисторі
Обчислімо загальну напругу на зображеній ділянці електричного кола:
Відповідь: B.
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Залежність опору металів від температури.
Завдання скеровано на перевірку знання і розуміння температурного коефіцієнта електричного опору й уміння застосовувати його у відповідних випадках.
Потужність електричного струму ‒ фізична величина, що характеризує швидкість виконання струмом роботи й дорівнює відношенню роботи струму до часу, за який цю роботу виконано:
Оскільки
З умови відома напруга на джерелі струму й опір вольфрамового дроту, який залежить від температури. Скориставшись законом Ома для ділянки кола, маємо формулу для визначення потужності відповідно до даних умови:
Температурний коефіцієнт електричного опору ‒ це фізична величина, яка характеризує залежність опору (питомого опору) речовини від температури:
Отже, цей вираз для опору, який визначає залежність опору від температури, підставімо у формулу для обчислення потужності:
Відповідь: 1,25.
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку знання і розуміння потужності електричного струму.
Потужність електричного струму ‒ фізична величина, що характеризує швидкість виконання струмом роботи й дорівнює відношенню роботи струму до часу, за який цю роботу виконано:
Оскільки
З умови відомі загальна напруга, на яку розрахований нагрівач, й опір кожної спіралі. Скориставшись законом Ома для ділянки кола, маємо формулу для визначення потужності відповідно до умови завдання:
Оскільки в умові завдання не вказано, як з’єднані спіралі ‒ послідовно чи паралельно, але треба виготовити нагрівач мінімальної потужності, то визначімо потужність для обох способів з’єднання і порівняємо.
Обчислімо загальний опір спіралей:
1) під час послідовного з’єднання:
2) під час паралельного з’єднання:
Тепер визначімо потужність:
1) під час послідовного з’єднання:
2) під час паралельного з’єднання:
Отже, порівнявши значення потужностей
Відповідь: 100.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.
Завдання скеровано на перевірку знання і розуміння того, від яких параметрів залежить електричний опір провідника.
Опір провідника, який має незмінний поперечний переріз, обчислюють за формулою
1. Неізольований металевий дріт склали вдвоє ‒ це означає, що довжина дроту зменшилася
Визначімо, як змінився опір дроту після змін:
Отже, опір провідника зменшився вчетверо ‒ варіант відповіді Г.
2. Неізольований металевий дріт протягли через волочильний верстат: довжина дроту збільшилася вдвічі, а маса не змінилася:
Визначимо, як змінився опір дроту після змін:
Отже, опір провідника збільшився в
3. На неізольованому металевому дроті нарізали різьбу, унаслідок чого площа його поперечного перерізу зменшилася вдвічі по всій довжині: тобто довжина залишилася тією самою
Визначимо, як змінився опір дроту після змін:
Отже, опір провідника збільшився у
4. Неізольований металевий дріт укрили ізоляцією: довжина і площа поперечного перерізу залишилися ті самі, і матеріал дроту не змінився (питомий опір той самий).
Отже, ізоляція ніяк не впливає на опір дроту, його опір не змінився ‒ А.
Відповідь: 1Г, 2Б, 3В, 4А.
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Застосування фотоефекту в техніці.
Завдання скеровано на перевірку розуміння суті фотоефекту й уміння застосовувати знання про це явище.
Супроводжувану випромінюванням (емісією) електронів взаємодію світла з речовиною називають фотоефектом.
Розрізняють зовнішній фотоефект, за якого фотоелектрони вилітають за межі тіла, і внутрішній фотоефект, за якого електрони, «вирвані» світлом із молекул й атомів, залишаються всередині тіла.
Фотоефект широко застосовують у пристроях для перетворення світлових сигналів на електричні або для безпосереднього перетворення світлової енергії на електричну.
Відповідь: A.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля ‒ Ленца.
Завдання скеровано на перевірку знання і розуміння закону, що визначає кількість теплоти, яка виділяється в провіднику зі струмом і яку він віддає довкіллю ‒ закону Джоуля ‒ Ленца.
Кількість теплоти
Цією формулою описують закон Джоуля ‒ Ленца. Запишімо його до і після змін параметрів (за умовою
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку знання і розуміння потужності струму й параметрів, від яких вона залежить.
Потужність струму
Узявши до уваги, що
Фізична величина, що характеризує саме провідник (спіраль електричного нагрівника) ‒ це електричний опір. За допомогою закону Ома для ділянки кола покажемо, як залежить потужність від опору й, відповідно, від параметрів спіралі:
Опір провідника, який має незмінний поперечний переріз:
За умовою напруга в мережі стала, залежністю електричного опору від температури можна знехтувати. Отже, потужність нагрівача буде обернено пропорційна до його довжини:
Визначімо відношення потужності нагрівача після вкорочення його вдвічі до початкової його потужності:
Отже, потужність
Відповідь: B.
ТЕМА: Електродинаміка. Закони постійного струму. Коефіцієнт корисної дії.
Завдання скеровано на перевірку знання і розуміння змісту коефіцієнта корисної дії та вміння визначати його для різних пристроїв.
Коефіцієнт корисної дії
Роботу струму визначімо як добуток потужності
Кількість теплоти під час згоряння палива визначімо як добуток питомої теплоти згоряння
Підставімо вирази для роботи і кількості теплоти у формулу для коефіцієнта корисної дії та обчислімо його:
Відповідь: 16.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність. Конденсатори.
Завдання скеровано на перевірку знання і розуміння будови конденсатора та його технічних характеристик.
Годинник зможе працювати від цього конденсатора, поки напруга на ньому буде не нижчою за
Отже, за певний час заряд конденсатора зменшиться на
Сила струму
За нижчої напруги годинник не працюватиме.
Визначімо проміжок часу, у який працюватиме годинник:
Відповідь: 25.
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку знання і розуміння того, від яких параметрів провідника залежить його електричний опір, а також застосування правил визначення характеристик електричного струму під час послідовного і паралельного з’єднання провідників.
Опір
Виразімо питомий опір:
Визначімо з умови опір
Покази вольтметра, що паралельно підключений до дротини (див. рисунок), становлять
Отже, можна визначити електричний опір дротини за законом Ома для ділянки кола:
Щоб визначити площу поперечного перерізу дротини, скористаймося методом рядів. На рисунку праворуч є ряд, утворений витками дротини. Довжина цього ряду
Ми свідомо не виразили значення діаметра дротини в метрах, оскільки вимога завдання – подати відповідь в
Тоді площу поперечного перерізу визначімо за формулою площі круга:
Підставімо цей вираз для площі у формулу для питомого опору й обчислімо його:
Відповідь: 1,25.
ТЕМА: Електродинаміка. Закони постійного струму. Джерела струму.
Завдання скеровано на перевірку знання і розуміння будови та принципу дії гальванічного елемента.
Гальванічний елемент – це хімічне джерело живлення, у якому використовують різницю електродних потенціалів двох металів (варіант В неправильний), занурених в електроліт.
Гальванічний елемент з лимона й двох дротів ‒ це простий пристрій, у якому використовують хімічну реакцію між металами та лимонною кислотою для створення електричного струму.
Хімічна реакція розпочинається не відразу, тож є змога виміряти і напругу, і силу струму. Тому цей гальванічний елемент миттєво не розрядиться.
З експериментів відомо, що такий саморобний гальванічний елемент дає дуже малу силу струму,
За умовою лампа не засвітилася, тобто сила струму була замалою для роботи лампи розжарювання.
Із запису закону Ома для повного кола
Через великий внутрішній опір джерела живлення напруга, тобто електрорушійна сила ε не могла бути настільки високою, щоб перегоріла лампа розжарювання. Треба ще долати досить великий внутрішній опір лимона, тому лампа навіть не засвітилася.
Отже, єдиною причиною того, що лампа не засвітилася, є завеликий внутрішній опір гальванічного елемента.
Відповідь: Б.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола. Послідовне та паралельне з᾽єднання провідників.
Завдання скеровано на перевірку знання і розуміння паралельного і послідовного з’єднання провідників, а також уміння застосовувати закон Ома для ділянки кола й формули, що описують ці з’єднання.
Визначмо напругу
Це і є напруга на клемах джерела струму, оскільки за паралельного з’єднання на обидві вітки електричного кола ‒ там, де резистори
Розгляньмо тепер з’єднання резисторів
Це й буде сила струму
Отже, знаючи з умови опір резистора
Відповідь:
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Явище самоіндукції.
Завдання скеровано на перевірку знання і розуміння явища самоіндукції.
Відразу після замкнення кола сила струму
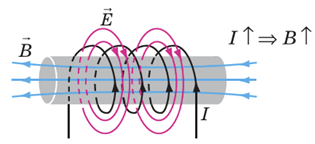
Саме тому сила струму в колі котушки (а отже, і в лампі
Явище виникнення вихрового електричного поля в провіднику, у якому тече змінний електричний струм, називають самоіндукцією.
Електрорушійну силу індукції, що створюється в провіднику внаслідок зміни його власного магнітного поля, називають електрорушійною силою самоіндукції.
Отже, під час замикання ключа
Відповідь: B.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.
Завдання скеровано на перевірку знання і розуміння, що таке діод і як він пропускає електричний струм, а також уміння читати електричні схеми.
Вакуумний діод має однобічну провідність. Буде проходити струм чи ні, залежить від того, як діод підключити в електричне коло:
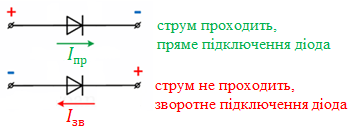
Зобразімо, як тече струм за початкових умов. Як бачимо, у цьому разі струм проходить через обидва діоди.
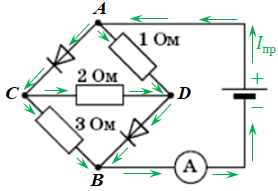
Для розуміння, того, як з’єднано резистори, зобразімо альтернативну схему. Оскільки за умовою опір діода вважаємо рівним нулю, то можна сумістити точки
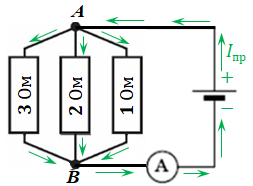
Загальний опір у разі паралельного з’єднання (внутрішнім опором джерела й амперметра нехтуємо відповідно до умови) становитиме:
Тоді напруга на джерелі струму за законом Ома дорівнюватиме:
Така ж напруга буде й коли змінимо полярність джерела. Нарисуймо, як проходитиме електричний струм за таких умов. Як бачимо, тепер резистори з’єднані послідовно, обидва діоди не пропускають струм:
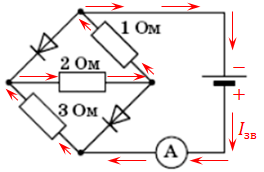
Визначмо загальний опір у разі послідовного з’єднання резисторів:
За законом Ома визначмо силу струму, що покаже амперметр за умови зміни полярності джерела:
Відповідь: А.
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму. Коефіцієнт корисної дії електронагрівача.
Завдання скеровано на перевірку знання і розуміння фізичного змісту коефіцієнта корисної дії електричного нагрівача.
Коефіцієнт корисної дії
Використаймо формули для розрахунку кількості теплоти, яку поглинає речовина під час нагрівання
Відповідь: 84.
ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.
Завдання скеровано на перевірку знання і розуміння фактичної і номінальної потужності і вміння визначати загальну потужність за будь-якого з’єднання споживачів.
Потужність, яку зазначено в паспорті електричного пристрою (або на пристрої), називають номінальною потужністю. Вимірюючи потужність струму в споживачі, ми визначаємо його фактичну потужність. Тобто значення фактичної і номінальної потужностей споживача можуть різнитися.
Якщо коло складається з кількох споживачів, то, розраховуючи їхню фактичну потужність, треба пам’ятати, що за будь-якого з’єднання споживачів загальна потужність струму в усьому колі дорівнює сумі потужностей окремих споживачів.
Потужність
Узявши до уваги, що
Але сила струму невідома, тож із паспортних даних і за допомогою закону Ома для ділянки кола
(записувати десятковим дробом не можна, оскільки доведеться округлювати нескінчений десятковий дріб, а цього робити не треба, бо це проміжні результати, а округлення їх приведе до неправильних остаточних результатів).
Лампи з’єднано послідовно. Обчислімо їхній загальний опір:
Визначімо загальну потужність двох ламп:
Відповідь: A.
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку знання і розуміння послідовного і паралельного з’єднання провідників, а також уміння читати електричні схеми.
Визначімо силу струму в електричному колі тоді, коли ключ розімкнений, і коли він замкнений.
Якщо ключ розімкнений, то струм протікатиме по трьох послідовно з’єднаних резисторах (див. рисунок в умові).
За законом Ома для повного кола сила струму
За умовою
Визначімо загальний опір трьох послідовно з’єднаних резисторів з однаковим опором:
Отже, силу струму
Якщо ключ замкнути, то за схемою до одного з трьох резисторів буде паралельно приєднаний ще один резистор (див. схему в умові). Визначімо загальний опір такого змішаного з’єднання резисторів. Спочатку запишімо загальний опір двох паралельно з’єднаних резисторів:
Отже, силу струму
Визначімо співвідношення
Відповідь: 1,2.
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання і розуміння принципу дії фотоелемента і конденсатора, а також вміння аналітично описати процеси, що в них відбуваються.
Сила струму
Зарядом конденсатора називають модуль заряду
Визначімо заряд з обох формул і прирівняймо ці вирази:
Коли фотоелемент приєднають до розрядженого конденсатора, він почне заряджатися. Напруга досягне значення
Відповідь: 60.
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля ‒ Ленца.
Завдання скеровано на перевірку знання і розуміння закону Джоуля ‒ Ленца, поняття потужності й співвідношення фізичних величин під час послідовного з’єднання провідників.
Визначити кількість теплоти, яка виділяється в провіднику зі струмом, можна за законом Джоуля ‒ Ленца: кількість теплоти
Оскільки лампи з’єднані послідовно (за умовою), то сила струму в них буде однакова:
Запишімо формули для визначення кількості теплоти в кожній лампі відповідно за однаковий проміжок часу:
Виразімо опір лампи через потужність
Використавши за умовою однаковість напруг ламп
Підставімо вирази для опорів у формули для кількості теплоти і визначимо відношення кількостей теплоти:
Відповідь: Б.
ТЕМА: Електродинаміка. Основи електростатики. З’єднання конденсаторів.
Завдання скеровано на перевірку знання і розуміння, що таке конденсатор, і вміння визначати параметри з’єднань конденсаторів.
Якщо відповідно до умови замкнути вимикач, то конденсатори будуть з’єднані послідовно. А в разі послідовного з’єднання заряди обох конденсаторів будуть однаковими та дорівнюватимуть заряду батареї:
Напруга на батареї послідовно з’єднаних конденсаторів дорівнює сумі напруг на окремих конденсаторах, що й зазначено в умові (варіант Г ‒ неправильний):
Енергія зарядженого конденсатора
Однакові конденсатори (за умовою) мають однакову електроємність:
Між пластинами конденсатора електричне поле однорідне. Для однорідного електричного поля між напруженістю
Напруга на другому конденсаторі змінилася, отже, змінилася і напруженість.
Відповідь: Б.