Розділ: Механіка
Тема: Закони збереження в механіці
Кількість завдань: 105
ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.
Завдання скеровано на перевірку знання і розуміння закону збереження механічної енергії, а також уміння застосовувати його в конкретних ситуаціях.
Суму кінетичної
У замкненій системі тіл, які взаємодіють лише консервативними силами, повна механічна енергія залишається незмінною (зберігається):
Відповідно до умови завдання запишімо вирази, які визначають кінетичну і потенціальну енергії до і після маневру.
Отже, повна механічна енергія літака на початку становить
Умова, що потенціальна енергія літака на поверхні Землі дорівнює нулю, означає, що Землю вибрано як нульовий рівень.
Після маневру швидкість
Висота ж літака над поверхнею Землі збільшилася вдвічі, тож і потенціальна енергія
Тоді повна енергія
Закон збереження повної механічної енергії передбачає перетворення кінетичної енергії на потенціальну й навпаки. Однак досвід доводить, що водночас повна механічна енергія не зберігається.
Річ у тім, що закон збереження повної механічної енергії виконується тільки тоді, коли в системі немає тертя. Однак у природі не існує рухів без тертя.
Енергія нікуди не зникає і нізвідки не з’являється: вона лише перетворюється з одного виду на інший, передається від одного тіла до іншого.
Відповідь: B.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.
Завдання скеровано на перевірку вміння застосовувати знання з різних розділів механіки ‒ руху тіла по колу, другого закону Ньютона й закону збереження механічної енергії.
У нижній точці в положенні рівноваги кульці надають мінімально необхідну швидкість (тобто кулька має кінетичну енергію
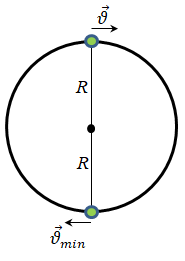
Запишімо закон збереження механічної енергії для кульки на нитці:
Оскільки кулька рухається по колу, то модуль швидкості руху кульки у верхній точці можна визначити за формулою
Отже,
За другим законом Ньютона
Визначимо мінімально необхідну швидкість руху кульки:
Відповідь: 5.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на перевірку розуміння змісту поняття механічної роботи й умов виконання її.
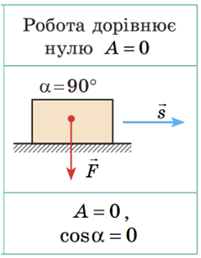
Механічна робота (робота сили)
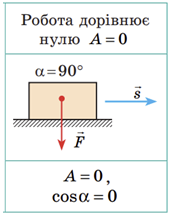
І з формули, і з рисунка випливає, що робота дорівнюватиме нулю, якщо кут між векторами сили й переміщення становить
За всіх інших значень кута
На книгу, що лежить на столі, сила тяжіння діє вертикально вниз, але книга перебуває в стані спокою відносно стола й переміщення не здійснює, тому що дія сили тяжіння скомпенсована дією сили нормальної реакції з боку стола. Тобто сила тяжіння роботу не виконує.
Крапелька води падає під час дощу, тобто здійснює переміщення саме під дією сили тяжіння, отже, сила тяжіння в цій ситуації виконує роботу.
Коли дерев’яна колода плаває на поверхні озера, дія сили тяжіння скомпенсована дією сили Архімеда, і колода у вертикальному напрямку не переміщається ‒ сила тяжіння роботу не виконує. Однак в умові зазначено, що колода плаває, тобто є горизонтальне переміщення, зумовлене не силою тяжіння. Тоді кут між векторами сили тяжіння і вектором переміщення становитиме
Єдина сила, яка діє на супутник під час руху коловою орбітою навколо Землі – це гравітаційна сила притягання Землі – сила тяжіння, що спрямована до центра Землі. Це означає, що супутник здійснює рівномірний рух по колу, його швидкість постійна, що дає змогу підтримувати незмінною відстань між супутником і центром Землі.
Згідно з теоремою про потенціальну енергію (робота всіх консервативних сил, які діють на тіло, дорівнює зміні потенціальної енергії тіла, узятій із протилежним знаком) зміни відстані між супутником і Землею не відбувається. Отже, зміна потенціальної енергії дорівнює нулю, сила тяжіння роботу не виконує.
Можна міркувати так: до вектора швидкості руху супутника в кожній точці колової орбіти, а також до вектора переміщення в кожній точці колової орбіти вектор сили тяжіння перпендикулярний, а
Отже, правильний варіант відповіді ‒ Б.
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на перевірку розуміння поняття механічної роботи.
Механічна робота (робота сили)
Випадок, коли робота дорівнюватиме нулю, зілюстровано на рисунку: на тіло, наприклад, діє сила, напрямлена вертикально вниз – сила тяжіння, а переміщення відбувається горизонтально завдяки іншій силі – силі тяги двигуна, напрямок дії якої збігається з вектором переміщення. Між вектором сили тяжіння і вектором переміщення кут дорівнює
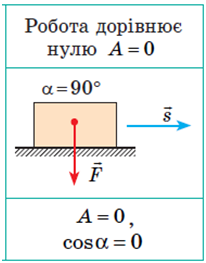
Розгляньмо випадки, наведені у варіантах відповіді завдання.
А У разі горизонтального польоту літака вектор сили тяжіння напрямлений вертикально вниз (сила тяжіння завжди напрямлена вертикально вниз), а вектор переміщення ‒ горизонтально. Отже, кут між вектором сили тяжіння і вектором переміщення дорівнює
Б і Г Коли яблуко падає вертикально з дерева, то кут між вектором сили тяжіння і вектором переміщення дорівнює
В М’яч, кинутий під кутом до горизонту, рухатиметься вздовж траєкторії, що є параболою. Якщо з’єднати початкову точку
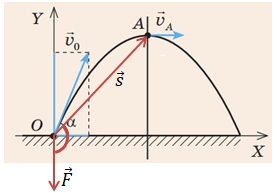
Отже, робота сили тяжіння дорівнюватиме нулю у випадку горизонтального руху літака.
Відповідь: A.
ТЕМА: Механіка. Закони збереження в механіці. Імпульс тіла. Кінетична і потенціальна енергія.
Завдання скеровано на перевірку вміння обчислювати імпульс тіла і його кінетичну енергію.
Імпульс тіла
Обчислімо значення імпульсу тіла:
Кінетична енергія
Обчислімо кінетичну енергію автомобіля:
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на перевірку розуміння поняття «механічна робота».
Механічна робота (робота сили)
Сила тяжіння діє на літак і напрямлена вертикально вниз. Але переміщення літака по вертикалі немає. За умовою літак рухається горизонтально. Отже, кут між вектором сили тяжіння та вектором переміщення дорівнює
Відповідь: Б.
ТЕМА: Рівняння теплового балансу. Потенціальна енергія.
Завдання скеровано на перевірку вміння розв’язувати комбіновані задачі на рівняння теплового балансу й потенціальну енергію тіла.
Дано:
Знайти:
Утрачену під час охолодження кульки енергію можна розрахувати за формулою
Енергію тіло втрачає, тому отримане число – від’ємне, тож знак «мінус» тут позначає лише напрямок руху енергії. У подальших розрахунках використовуватимемо значення
Коли тіло піднімається на певну висоту, то збільшується його потенціальна енергія. Її можна розрахувати за формулою:
Саме на збільшення потенціальної енергії буде витрачено
Відповідь: 0,76.
ТЕМА: Механіка. Основи динаміки. Момент сил.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі на визначення моменту сил.
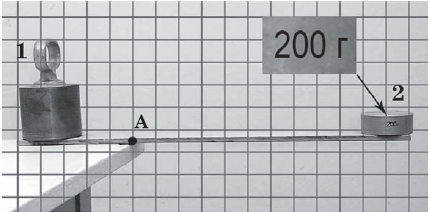
Рис. 1. Умова завдання
На рисунку 1 зображено важіль із точкою опори в точці A. Ліве плече важеля (із вантажем 1) лежить на столі, а праве плече (із вантажем 2) звисає. Важіль перебуває в рівновазі. За розміткою на рисунку можна визначити довжину правого й лівого плеча як відстань від точки прикладення сили тяжіння (центру мас тіла) до точки опори.
Довжина лівого плеча –
Довжина лівого плеча –
Дано:
Знайти:
Горизонтальна вісь, що проходить через точку A перпендикулярно до рейки – це вісь обертання важеля.
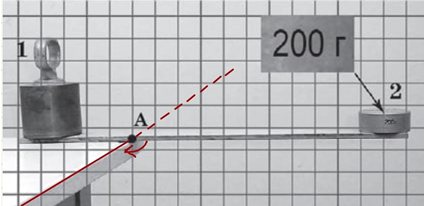
Рис. 2. Вісь обертання важеля
Момент сили відносно цієї осі дорівнюватиме:
Відповідь: 1,1.
ТЕМА: Енергія. Робота. Потужність. Сила.
Завдання скеровано на перевірку розуміння понять енергії, потужності, сили й прискорення.
Потужність
Енергія
Сила
Прискорення
Відповідь: 1В, 2Д, 3Б, 4А.
ТЕМА: ТЕМА: Механіка. Умови рівноваги. Прості механізми.
Завдання скеровано на оцінку розуміння принципів роботи простих механізмів, зокрема рухомого й нерухомого блока.
Нерухомий блок (рис. 1, а) не дає виграшу в силі – він дає змогу змінити лише напрямок прикладання сили, тобто:
Рухомий блок (рис. 1, б) дає виграш у силі у 2 рази. Тобто необхідна для піднімання вантажів за допомогою рухомого блока сила буде вдвічі менша, ніж якщо вантаж піднімати без використання механізмів:
Тож виграш у силі в системі залежить лише від кількості рухомих блоків.
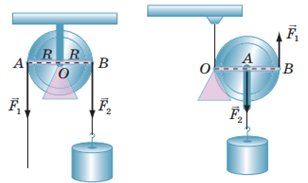
Рис. 1. Нерухомий (а) і рухомий (б) блоки
Нехай сила
Тоді після першого рухомого блока виграш у силі дорівнюватиме 2:
Другий рухомий блок знову дасть виграш у силі у 2 рази відносно попереднього блока, тобто виграш у силі – у 4 рази відносно переміщення вантажу без механізмів:
Третій рухомий блок дає виграш у силі вже у 8 разів відносно переміщення вантажу без механізмів:
Відповідь: B.
ТЕМА: Робота. Сила Архімеда.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі про силу Архімеда.
Дано:
Знайти:
Для того, щоби перевернути блок, достатньо його центр мас підняти на висоту, на якій він у вертикальному положенні. Оскільки блок циліндричний, то в обох положеннях він на половині висоти блока (рис. 1).
Рис. 1. Положення центра мас у вертикальному й горизонтальному положенні
Оскільки поперечні розміри стовпа за умовою враховувати не потрібно, то можна вважати, що під час перевертання центр мас піднімають на половину всієї висоти
Рівнодійну сил, що діють на блок, можна обчислити за формулою
Сила тяжіння діє вертикально вниз, притягуючи блок до землі, а сила Архімеда виштовхує блок вертикально вгору, інші сили на блок не діють. Якщо вважати напрямок «вертикально вниз» додатним,
Маса тіла пов’язана з його густиною формулою
Тоді
Оскільки об’єму блока невідомий, із дужок можна винести його густину:
Тоді робота, необхідна для підняття центра мас бетонного блока на половину його висоти, дорівнює
Відповідь: 6.
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Сила тяжіння. Рівномірний рух по колу. Кінетична енергія.
Завдання скеровано на перевірку вміння розв’язувати комплексні задачі про рівномірний рух по колу.
Дано:
Знайти:
Кінетичну енергію тіла можна обчислити за формулою
Під час руху супутника навколо Землі його швидкість спрямована по дотичній до кола, а прискорення – до центру.
Доцентрове прискорення можна обчислити з виразу
За другим законом Ньютона рівнодійна дорівнює добутку маси тіла на прискорення, набуте під час взаємодії:
Єдиною силою, що діє на частинки в площині напрямку руху є сила тяжіння Землі:
Тобто
Із цього рівняння можна виразити добуток маси й квадрату швидкості та підставити його у формулу для кінетичної енергії:
Відповідь: 20
ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона. Вага. Рівномірний рух по колу.
Завдання скеровано на перевірку вміння розв’язувати комплексні задачі про рівномірний рух по колу.
Дано:
Знайти:
Гойдалка рухається за траєкторією, що є частиною кола. Тож вона матиме доцентрове прискорення, напрямлене в бік кріплення підвісу гойдалки. У найнижчій точці це прискорення буде напрямлене вертикально вгору. Вага тіл, що рухаються із прискоренням, що напрямлене вертикально вгору, може бути розрахована за формулою:
Доцентрове прискорення можна обчислити з виразу
Тоді
Відповідь: 5
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку вміння використовувати закон збереження імпульсу й уміння визначати швидкість у різних системах відліку.
Дано:
1. Знайти:
За законом збереження імпульсу сума імпульсів тіл до зіткнення дорівнюватиме сумі імпульсів тіл після.
Імпульс розраховують за формулою
До зіткнення вагони рухаються незалежно й мають власні імпульси, а після зіткнення вони рухаються як одне тіло з єдиним імпульсом, спільною швидкістю і масою, яка дорівнює сумі мас двох вагонів. Тобто
2. Знайти:
Для того, щоби визначити відстань, яку вагони пройшли до зіткнення, потрібно визначити їхню швидкість один відносно одного. Вагони рухаються в одному напрямку, тому їхня швидкість один відносно одного буде меншою, ніж відносно землі. Швидкість другого вагона відносно першого можна обчислити за формулою
Початкова відстань, яку другий вагон скоротив до
Відповідь: 1. 5. 2. 52.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична й потенціальна енергія.
Завдання скеровано на перевірку вміння обчислювати потенціальну енергію тіла, що перебуває під дією сили тяжіння.
Потенціальна енергія тіла, яке рухається під дією сили тяжіння, можна визначити за формулою
Прискорення вільного падіння вважаємо постійним на Землі, маса кульки під час її руху не змінюється, тому найвищу потенціальну енергію кулька матиме в найвищій точці своєї траєкторії – точці Б.
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.
Завдання скеровано на перевірку розуміння природи кінетичної енергії.
Кінетичну енергію обчислюють за формулою
Тож кінетична енергія тіла змінюється, якщо змінюється його швидкість або маса.
У варіанті відповіді А пліт рухається ділянкою річки, що має сталі ширину й глибину. Швидкість такої течії залишається сталою. Пліт не має власної швидкості, тож якщо швидкість течії не змінюється, то й кінетична енергія плота не змінюється.
У варіанті відповіді Б м’яч закидають у баскетбольний кошик. Щоби потрапити в кошик, м’яч має рухатися по параболі (рис. 1). Модуль швидкості м’яча спочатку зменшується, у найвищій точці траєкторії він дорівнює нулю, після чого знову поступово збільшується. Якщо модуль швидкості м’яча змінюється, то і його кінетична енергія також змінюється.
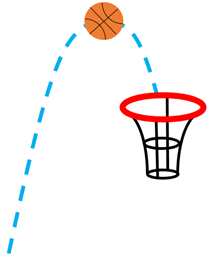
Рис. 1. Траєкторія руху м’яча
У варіанті відповіді В листочок рухається рівномірно, тож його швидкість і кінетична енергія не змінюються.
У варіанті відповіді Г равлик рухається зі сталою швидкістю – 9 см/хв, тож кінетична енергія також не змінюється.
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на оцінку вміння розв’язувати розрахункові задачі з визначення роботи сил.
Якщо тіло зісковзує по площині рівномірно, то його прискорення
Рівнодійна сил, які діють на тіло, що рухається по похилій площині (рис. 1), дорівнює векторній сумі всіх цих сил:
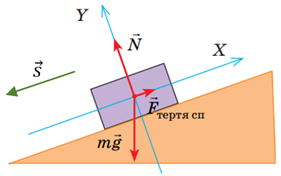
Рис. 1. Схематичне зображення сил, що діють на тіло на похилій площині
Це рівняння можна спроєктувати на осі
Тож
Силу тертя визначають за формулою
Тож
Роботу сили можна обчислити за формулою
Тоді можна записати роботу сили тяжіння і сили тертя. Кут
Кут між напрямком сили тертя і переміщенням
Оскільки модуль сили тяжіння і переміщення додатні, а
Відповідь: B.
ТЕМА: Механіка. Умови рівноваги. Прості механізми.
Завдання скеровано на оцінку розуміння принципів роботи простих механізмів, зокрема рухомого й нерухомого блоків.
Нерухомий блок (рис. 1, а) не дає виграшу в силі – він дає змогу змінити лише напрямок прикладання сили, тобто
Рухомий блок (рис. 1, б) дає виграш у силі у 2 рази. Тобто сила, необхідна для піднімання вантажів за допомогою рухомого блоку, буде вдвічі менша, ніж якщо вантаж піднімати без використання механізмів:
Тож виграш у силі в системі залежить лише від кількості рухомих блоків.
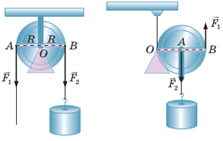
Рис. 1. а) Нерухомий блок, б) рухомий блок
Тоді нехай сила
Тоді після першого рухомого блоку виграш у силі дорівнюватиме 2:
Другий рухомий блок знову даватиме виграш у силі у 2 рази відносно попереднього блоку, а отже виграш у силі – у 4 рази відносно переміщення вантажу без механізмів:
Третій рухомий блок дає виграш у силі уже у 8 разів відносно переміщення вантажу без механізмів:
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги.
Завдання скеровано на оцінювання вміння використовувати умови рівноваги для розв’язування розрахункових задач.
Дано:
1. Знайти:
Важіль за умовою перебуває в рівновазі в обох випадках, отже сума моментів сил, що діють на нього, дорівнює нулю.
Момент сили
Щодо плеча сил для короткого й довгого плеча важеля: їхні довжини залишатимуться незмінними за заміни вантажів.
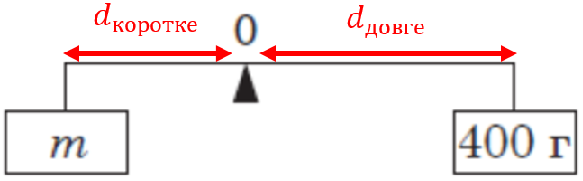
Рис. 1. Визначення плеча сили для важеля
Тоді, за умовою рівноваги важеля,
І для всіх вантажів, про які йдеться в задачі,
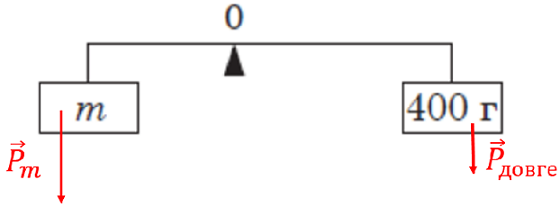
Рис. 2. Схематичне зображення дії сил на вантажі
Аналогічно тому, що зображено на рисунку 2, для ситуації, коли невідомий вантаж прикріплено до короткого плеча, можна розставити сили для ситуації, коли він прикріплений до довгого плеча.
Тож, скориставшись виразами (1), (2) і (3), можна записати систему рівнянь (4):
Потім потрібно поділити верхнє рівняння із системи (4) на нижнє:
Тоді з (5) можна виразити
2. Знайти:
З виразу (4) випливає, що
Тоді відношення
Відповідь: 1. 600. 2. 1,5.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.
Завдання скеровано на оцінювання розуміння природи кінетичної і потенціальної енергії.
Кінетична енергія
Потенціальна енергія
Для тіл, що перебувають у полі сили тяжіння (як тіла із завдання), потенціальну енергію визначають за формулою
Кінетичну енергію тіла обчислюють за формулою
Щодо ситуацій, описаних у завданні:
A Кулька, що вільно падає вниз, утрачає висоту, а отже її потенціальна енергія зменшується. До того ж тіло, що вільно падає, рухається лише під дією сили тяжіння з постійним прискоренням (прискоренням вільного падіння, що спрямоване до поверхні землі), отже швидкість тіла, яка спрямована до поверхні землі, збільшується, а разом із нею збільшується і кінетична енергія.
Б М’ячик, що рухається вгору, набирає висоту, а його потенціальна енергія збільшується. Оскільки напрямок швидкості м’ячика протилежний напрямку прискорення вільного падіння, то швидкість, а разом із нею і кінетична енергія зменшуються.
В Парашутист опускається на землю, його висота над поверхнею землі зменшується, що приводить до зменшення потенціальної енергії. Оскільки парашутист рухається рівномірно, то його швидкість не змінюється під час спуску, тож його кінетична енергія також не змінюється.
Г Літак, що летить на певній висоті з постійною швидкістю не змінює ні висоти відносно поверхні землі, ні (відповідно до умови) своєї швидкості, а отже його як кінетична, так і потенціальна енергія залишаються сталими.
Відповідь: 1А, 2В, 3Г, 4Д.
ТЕМА: Механіка. Основи динаміки. Момент сил.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з визначення моменту сил.
Момент сили
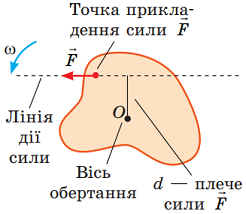
Рис. 1. Схема визначення плеча сили
Проаналізувавши рисунок 2 (його наведено в завданні), потрібно визначити плечі сил, схематично зображених на ньому.
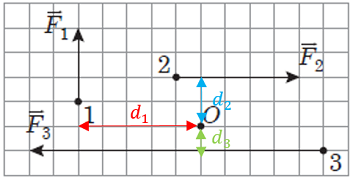
Рис. 2. Визначення плечей сил, про які йдеться в завданні
У завданні не зазначено розмір клітинок, тож можна вважати довжину сторони клітинки умовною одиницею довжини (у. о. д.).
Згідно з виразом (1):
Відповідь: A.
ТЕМА: Механіка. Умови рівноваги. Прості механізми.
Завдання скеровано на оцінювання вміння аналізувати результати експерименту, зображені на фото, і розв’язувати розрахункові задачі про рух тіла під дією однієї сили.
Знайти:
На рисунку зображено нерухомий блок. Цей простий механізм не забезпечує виграшу ні в силі, ні у відстані, а лише змінює напрямок прикладання сили.
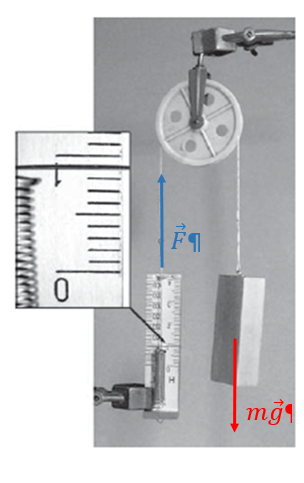
Тож сила, виміряна динамометром, – це сумарна сила, яка діє на брусок з іншого боку блоку.
На блок діє сила тяжіння
За рисунком можна визначити силу
Тоді
Відповідь: 90.
ТЕМА: Механіка. Закони збереження в механіці. Пружне зіткнення.
Завдання скеровано на оцінювання знання особливостей пружного зіткнення і вміння використовувати закони збереження.
Пружне зіткнення – це зіткнення, після якого сумарна кінетична енергія тіл зберігається.
За умовою завдання кулька, що рухалася зі швидкістю
Сумарна кінетична енергія до й після зіткнення в такому разі дорівнює:
Оскільки
Відповідь: B.
ТЕМА: Робота. Потужність. ККД.
Завдання скеровано на оцінювання вміння виконувати розрахункові задачі на поняття роботи, потужності й ККД.
Дано:
Знайти:
ККД верстата є відношенням корисної роботи, виконаної ним, до повної роботи:
Корисна робота токарного верстата полягає в сточуванні шарів речовини із заготовки за рахунок сили тертя між заготовкою і різцем. Її обчислюють за формулою
Повну роботу можна розрахувати, узявши до уваги, що енергію верстат отримує від електродвигуна. Саме енергію, передану верстату двигуном, буде використано в подальшому під час роботи. Її можна визначити з виразу
Тоді
Переміщення поверхні заготовки відносно різця можна розрахувати, якщо вважати, що за час
Тоді за формулою довжини кола
За третім законом Ньютона
Відповідь: 0,25.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.
Завдання скеровано на оцінювання розуміння понять повної механічної, кінетичної, потенціальної та внутрішньої енергії, уміння використовувати закон збереження енергії.
Механічна енергія
Кінетична енергія
Потенціальна енергія
Внутрішня енергія – це сума кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхніх взаємодій.
Для тіл у полі сили тяжіння (як парасольки у завданні) потенціальну енергію визначають за формулою
На рисунку а) зображено парасольку, що лежить на підлозі, а на рисунках б) і в) – парасольки в повітрі. Висота розташування парасольок відносно землі, а отже і їхня потенціальна енергія, у всіх цих випадках різна.
Кінетичну енергію тіла можна обчислити за формулою
У випадку в) парасолька рухається вгору з певною швидкістю і має відмінну від нуля кінетичну енергію. Натомість парасольки на рисунках а) і б) нерухомі, їхня кінетична енергія дорівнює нулю.
Механічна енергія тіла є сумою його кінетичної і потенціальної енергій. Для всіх ситуацій, описаних у завданні, потенціальні й кінетичні енергії парасольок різні, тож і їхні суми неоднакові.
Внутрішня енергія тіла найбільше залежить від його температури й деформацій. Оскільки за умовою всі ці параметри однакові для парасольок на всіх рисунках, наведених у завданні, то й внутрішня енергія однакова для них усіх.
Відповідь: A.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги.
Завдання скеровано на оцінювання вміння використовувати знання про умови рівноваги для розв’язування розрахункових задач.
Важіль – це тверде тіло, яке може обертатися навколо нерухомої осі – осі обертання.
Важіль перебуває в рівновазі, якщо сума моментів сил, що діють на нього, дорівнює нулю.
Момент сили
Проаналізувавши рисунок до завдання, можна дійти висновку, що до лівого плеча на відстані трьох поділок прикріплено три вантажі. Кожен із цих вантажів діє на плече із силою, що дорівнює його вазі.
На праве плече важеля на відстані двох поділок діє сила, яку вимірюють динамометром.
Оскільки важіль за умовою перебуває в стані рівноваги, то
Вага трьох вантажів дорівнює сумі ваги кожного з них:
На рисунку 1 позначено плечі сил
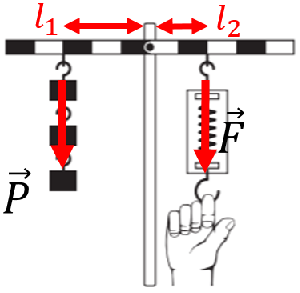
Рис. 1. Схематичний розподіл сил
Відповідь: Г.
ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі на використання формул рівноприскореного руху.
Дано:
Знайти:
Тіло набуває максимальної кінетичної енергії тоді, коли його швидкість максимальна. Оскільки тіло падає з висоти 10 м без початкової швидкості, то воно набуде максимальної швидкості просто перед стиканням із землею. Потрібно обчислити кінетичну енергію в цей момент для випадку, коли сили опору повітря немає.
Тоді, оскільки тіло кинуто без початкової швидкості й рухається лише під дією сили тяжіння з прискоренням
Далі потрібно обчислити час падіння тіла:
Аналогічно для тіла, що рухається рівноприскорено:
Оскільки швидкість тіла, що падає, повинна постійно збільшуватись аж до моменту зіткнення з поверхнею, то можна вважати, що максимальною є швидкість за момент до падіння і використати для її розрахунку час падіння тіла:
Кінетичну енергію обчислюють за формулою
Реальна кінетична енергія тіла менша, адже сила опору повітря виконує роботу проти руху тіла, тому
Відповідь: 40.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична й потенціальна енергія.
Завдання скеровано на оцінювання розуміння кінетичної і потенціальної енергії, виконання законів збереження повної механічної енергії в механіці.
Кінетична енергія
Потенціальна енергія
Внутрішня енергія – це сума кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхньої взаємодії.
Щодо ситуацій, описаних у завданні:
1 коли яблуко падає з гілки, висота, на якій воно перебуває, постійно зменшується, тобто зменшується його потенціальна енергія. Швидкість яблука постійно зростає. За законом збереження повної механічної енергії сума кінетичної і потенціальної енергії зберігається в системі, де діють лише консервативні сили. Тоді потенціальна енергія яблука переходить у кінетичну
2 коли м’яч летить у верхній кут воріт, його висота над землею і, відповідно, його потенціальна енергія збільшуються. Зважаючи на те, що прискорення, яке діє по вертикалі (прискорення вільного падіння), напрямлене до поверхні землі, швидкість, що напрямлена вгору, зменшується. Тому зменшується і кінетична енергія. Скориставшись законом збереження механічної енергії, можна дійти висновку, що кінетична енергія м’яча переходить у потенціальну
3 під час рівномірного падіння дощової краплі її висота, а отже й потенційна енергія, зменшується. Оскільки крапля рухається рівномірно, то її швидкість, а отже й кінетична енергія, не змінюється. Енергія не може зникнути, вона лише здатна перейти з одного виду в інший. Тож потенціальна енергія краплі переходить у її внутрішню енергію
4 під час кочення м’яча по футбольному полю висота м’яча над поверхнею землі і, відповідно, його потенціальна енергія не змінюються. Швидкість м’яча постійно зменшується внаслідок тертя. Тобто кінетична енергія м’яча переходить у внутрішню.
Відповідь: 1Г, 2В, 3А, 4Д.
ТЕМА: Механіка. Кінетична й потенціальна енергія.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням поняття кінетичної енергії.
Кінетичну енергію можна визначити за формулою:
Через деякий час маса ракети зменшилася в 3 рази, а швидкість збільшилася:
Тоді кінетична енергія дорівнюватиме:
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.
Завдання скеровано на оцінювання розуміння закону збереження енергії в механічних процесах і розуміння поняття консервативних сил.
Закон збереження механічної енергії виконуваний лише для тих систем, у яких тіла взаємодіють тільки консервативними силами.
Консервативні сили – це сили, робота яких не залежить від форми траєкторії, а визначена лише початковим і кінцевим механічними станами тіла.
Сила тертя не є консервативною, тому для тих систем, у яких є тертя, ніколи не діє закон збереження механічної енергії.
Відповідь: B.
ТЕМА: Механіка. Закони збереження в механіці.
Завдання скеровано на оцінювання розуміння понять імпульсу руху, кінетичної енергії й уміння використовувати закони збереження.
Дано:
1. Знайти:
За законом збереження імпульсу, коли слон починає рухатися, то платформа також має почати рухатися. Швидкість платформи буде напрямлено в протилежний від швидкості руху слона бік. Адже до початку руху імпульс як платформи, так і самого слона дорівнює нулю, бо нулю дорівнюють їхні швидкості.
Імпульс розраховують за формулою
Для розрахунку імпульсу платформи необхідно враховувати як її власну масу, так і масу слона на ній, тоді за законом збереження імпульсу
Після проєктування попереднього рівняння на напрямок руху слона можна скласти такі вирази:
2. Знайти:
Кінетичну енергію можна обчислити за виразом:
Кінетична енергія платформи залежить тільки від її власної маси і швидкості, якої вона набула після того як слон почав рухатися:
Відповідь: 1. 0,4. 2. 1,6.
ТЕМА: Механіка. Закони збереження в механіці. Пружне зіткнення
Завдання скеровано на оцінювання розуміння законів збереження енергії і меж їхньої застосовності.
Нехай
Затим потрібно розглянути три положення кулі 2. У точці A швидкість дорівнюватиме
За законом збереження кінетичної енергії сума кінетичної енергії до зіткнення двох куль дорівнюватиме її сумі після. Тому потрібно розглянути два варіанти: перший для точок A й C, де швидкість кулі 2 дорівнює нулю, і другий для точки B, де її швидкість максимальна.
Для A й C:
Для B:
Вираз
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Імпульс тіла. Закон збереження імпульсу.
Завдання скеровано на перевірку вміння розв'язувати розрахункові задачі на закон збереження імпульсу.
Дано:
Знайти:
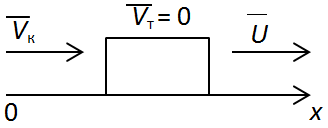
Запишемо закон збереження імпульсу:
Перейдемо до проєкцій на вісь
Відповідь: 600.
ТЕМА: Механіка. Основи динаміки. Перший закон Ньютона. Механічна робота. Потужність.
Завдання скеровано на перевірку вміння розв'язувати комбіновані розрахункові задачі на закони Ньютона й механічну роботу, потужність.
Дано:
1. Знайти:
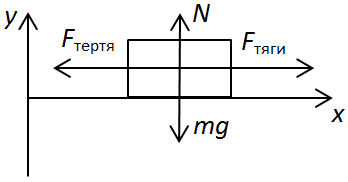
Спочатку треба записати перший закон Ньютона:
Після цього перейти до проєкцій:
за віссю
за віссю
Потужність
2. Знайти:
Робота
Відповідь: 1. 36. 2. 1,8.
ТЕМА: Механіка. Механічні коливання. Закони збереження в механиці. Коливання вантажу на пружині. Математичний маятник. Прості механізми.
Завдання скеровано на перевірку вміння застосовувати основні поняття i закони механіки, формули для визначення фізичних величин, математичні вирази законів.
1. Малі коливання на нитці можна вважати коливаннями математичного маятника. Отже, 1 – A.
2. Закручування гайки гайковим ключем – це важіль. Отже, 2 – Б.
3. Дві кульки пружно зіткнулися і їхній рух після взаємодії визначено законом збереження імпульсу. Отже, 3 – Г.
4. Період коливання тіла на пружині визначають за формулою В.
Відповідь: 1A, 2Б, 3Г, 4В.
ТЕМА: Механіка.
Завдання скеровано на перевірку знання законів збереження в механіці, знання простих механізмів.
На фото зображено використання рухомого блоку, що за умови нехтування його масою дає виграш у силі у 2 рази.
Отже,
Відповідь: Б.
ТЕМА: Механіка. Основи кінематики. Закони збереження в механіці. Вільне падіння. Кінетична і потенційна енергія.
Завдання скеровано на перевірку вміння застосовувати основні поняття і закони механіки, формули для визначення фізичних величин для розв'язування комбінованих задач із кількох розділів механіки.
За умови, що тіло кинули вертикально вгору, модуль його швидкості
Б графіком залежності кінетичної енергії тіла від часу
є парабола, вітки якої напрямлені вниз (
B графіком залежності різниці потенційної й кінетичної енергій тіла від часу
Г графіком залежності суми потенційної i кінетичної енергій тіла від часу
Отже, графіком, зображеним на рисунку, може бути тільки залежність
Відповідь: A.
ТЕМА: Динаміка рідин і газів. Потужність.
Завдання скеровано на перевірку розуміння поняття потужності та динаміки потоку рідини в трубі.
Дано:
Знайти:
Роботу сили можна визначити за формулою
На якір у воді діє сила тяжіння, сила Архімеда й зовнішня сила, що піднімає якір (рис. 1).
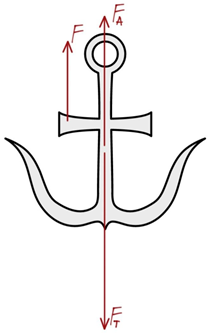
Рис. 1. Сили, що діють на якір
Формула, якою описують другий закон термодинаміки, така:
Оскільки якір піднімають повільно, можна вважати, що прискорення дорівнює нулю, тоді в проєкції на вісь OY другий закон Ньютона можна записати так:
Силу тяжіння визначають за формулою
Маса тіла, його густина й об’єм пов’язані формулою
Тож
Тоді, зважаючи на те, що напрямок сили та переміщення однакові,
Відповідь: 2.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги.
Завдання скерованo на перевірку вміння розв’язувати задачі з використанням умов рівноваги.
Дано:
Знайти:

Рис. 1. Умова задачі
На рисунку зображено важіль. Умова рівноваги для важеля – це рівність моментів сил:
Момент сил можна визначити за формулою
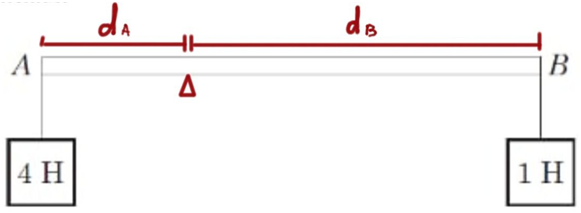
Рис. 2. Визначення плеча сили
Нехай плече сили, що прикладена в точці
Тоді умову рівності моментів можна записати так:
Відповідь: 8.
ТЕМА: Механіка. Потенціальна енергія. Сила пружності.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням формул для обчислення потенціальної енергії тіл.
Потенціальну енергію пружного тіла визначають за формулою
Саме цю енергію пружина передає кульці під час розтискання. Отримана від пружини енергія перейде в її кінетичну та потенціальну енергію. У найвищій точці свого польоту кулька має найбільшу потенціальну енергію.
Для тіл, що перебувають у полі сили тяжіння (як тіла із завдання), потенціальну енергію визначають за формулою
Тоді для першого досліду можна записати рівність
Відповідно
Для другого досліду також виконувана рівність
У цю рівність можна підставити вираз для
Усі відстані в умові необхідно виразити в метрах. Тоді
Відповідь: B.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку вміння використовувати закон збереження імпульсу.
Абсолютно непружне зіткнення – це зіткнення, після якого тіла рухаються як одне ціле.
Тож зчеплення тепловоза з вагоном можна вважати абсолютно пружним.
Для визначення швидкості поїзда після зчеплення необхідно скористатися законом збереження імпульсу:
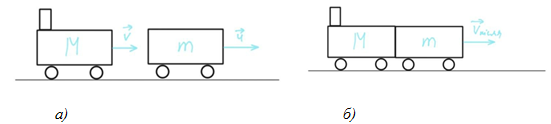
Рис. 1. Положення вагонів до зіткнення (а) та після зіткнення (б)
Оскільки вагон і тепловоз рухаються в одному напрямку , то закон збереження імпульсу можна спроєктувати на напрямок їхнього руху:
Імпульси вагонів можна обчислити за формулою
Тоді
Підставивши проєкції відповідних імпульсів у закон збереження, отримаємо:
Відповідь: Г.
ТЕМА: Механіка. Закони збереження в механіці.
Завдання скеровано на оцінювання вміння розв’язувати комплексні задачі на використання законів збереження у випадку руху тіла по колу.
Дано:
Знайти:
У такій системі діятиме закон збереження механічної енергії. Механічна енергія – це сума кінетичної і потенціальної енергії тіла:
Кінетична енергія – це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси
Потенціальна енергія – це енергія, яку має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою.
Для тіл, що перебувають у полі сили тяжіння, потенціальну енергію визначають за формулою
Якщо вважати, що в початковому положенні кулька перебуває на висоті 0 м від поверхні, то вся її механічна енергія складається лише з кінетичної енергії. Її швидкість у цей момент можна вважати саме тою мінімальною швидкістю, яку необхідно обчислити за умовою задачі:
Оскільки повна механічна енергія під час руху кульки не повинна змінюватися, то цієї кінетичної енергії має вистачити на те, щоби в найвищому положенні вона мала потенціальну енергію тіла, що перебуває на висоті
Тож за законом збереження енергії
Кулька, що рухається по колу, має доцентрове прискорення. Зважаючи на те, що радіус кола дорівнює довжині нитки, у найвищій точці його можна обчислити за формулою:
Тож за другим законом Ньютона
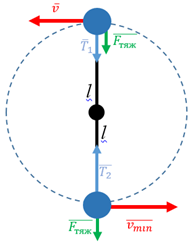
Рис. 1. Схематичне зображення дії сил на кульку під час руху
Щоби початкова швидкість була мінімальною, сила натягу нитки у верхній точці кола має дорівнювати нулю:
Тож можна підставити цей вираз для швидкості у верхній точці у вираз для закону збереження механічної енергії:
Відповідь: 5.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.
Завдання скеровано на оцінювання розуміння природи кінетичної і потенціальної енергії і вміння використовувати закони збереження повної механічної енергії.
У замкненій системі зберігається повна механічна енергія:
Кінетичну енергію визначають за формулою
Оскільки для гумової стрічки виконуваний закон Гука, то можна обчислити потенціальну енергію за формулою, що описує потенціальну енергію розтягнутої пружини:
Коли пружина стискається, то її потенціальна енергія збільшується, а отже, за законом збереження механічної енергії, кінетична енергія зменшується.
Вираз для сили пружності:
Отже, якщо пружина стискається, то й модуль сили пружності теж збільшується.
Прискорення тіла в положенні рівноваги дорівнює нулю, і чим більше тіло відхиляється він нього, тим більшим є його модуль. Тож під час стискання модуль прискорення збільшується.
Відповідь: A.
ТЕМА: Механіка. Закони збереження в механіці. Пружне зіткнення.
Завдання скеровано на оцінювання розуміння особливостей пружного зіткнення і вміння використовувати закони збереження.
Пружне зіткнення – це зіткнення, після якого сумарна кінетична енергія тіл зберігається:
Тож можна обчислити кінетичну енергію кожної з кульок до зіткнення. Нехай рухома кулька – кулька 1, а нерухома – 2:
Тоді сумарна кінетична енергія до зіткнення становить
У замкнутій системі має зберігатися сумарний імпульс тіл. Імпульс першої кульки до зіткнення становить
Імпульс другої кульки:
Тоді сумарний імпульс до зіткнення становить:
У випадку A після зіткнення швидкості першої і другої кульки дорівнюють
Імпульс першої кульки до зіткнення становить
Імпульс другої кульки
Сумарний імпульс системи після зіткнення становить
Отже імпульс не зберігається.
У випадку Б після зіткнення швидкості першої і другої кульки відповідно дорівнюють
Отже кінетична енергія після удару менша, ніж до нього. Зіткнення не пружне.
У випадку B після зіткнення швидкості першої і другої кульки відповідно дорівнюють
Отже кінетична енергія після удару менша, ніж до нього. Зіткнення не пружне.
У випадку Г після зіткнення швидкості першої і другої кульки дорівнюють
Імпульс першої кульки до зіткнення становить
Імпульс другої кульки дорівнює
Сумарний імпульс системи після зіткнення становить
Отже імпульс і кінетична енергія зберігаються – зіткнення пружне.
Відповідь: Г.
ТЕМА: Механіка. Потенціальна енергія.
Завдання скеровано на оцінювання розуміння поняття потенціальної енергії і способів її обчислення для різних тіл
Потенціальна енергія
Для тіл, що перебувають у полі сили тяжіння, потенціальну енергію визначають за формулою
Потенціальну енергію пружного тіла визначають за формулою
А Коли космічний корабель віддаляється від поверхні Землі, то він мусить виконувати роботу проти поля тяжіння Землі. У такому разі його потенціальна енергія зростає.
Б Коли контейнер піднімають на борт судна, то його висота над поверхнею землі збільшується, а отже й потенціальна енергія зростає.
В Коли тіло занурили у воду, то була виконана робота проти виштовхувальної сили. Тобто м’яч отримав додаткову енергію. Те саме відбувається із тілами, які піднімають на певну висоту (робота виконується проти поля сили тяжіння). Відразу після того, як сили перестають підтримувати тіло в положенні з більшою потенціальною енергією, воно починає рухатися до положення з найменшою потенціальною енергією. Саме тому, якщо тіло, підняте на висоту, відпустити, то воно падає. У цьому випадку тіло спливає, а його потенціальна енергія зменшується.
Г Коли спортсмен натягує тятиву, її абсолютне видовження
Відповідь: B.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги.
Завдання скеровано на оцінювання вміння використовувати умови рівноваги для розв’язування розрахункових задач.
Важіль – це тверде тіло, яке може обертатися навколо нерухомої осі – осі обертання.
Важіль перебуває в рівновазі, якщо сума моментів сил, що діють на нього, дорівнює нулю.
Момент сили
За рисунком до завдання можна визначити, що до правого плеча на відстані чотирьох поділок прикріплено три вантажі. Кожен із цих вантажів діє на плече із силою, що дорівнює їхній вазі.
На праве плече важеля на відстані трьох поділок прикріплено один вантаж, а на відстані двох поділок ми діємо силою.
Оскільки важіль за умовою перебуває в стані рівноваги, можна скористатися рівністю моментів сил:
Вага трьох вантажів дорівнює сумі ваги кожного з них:
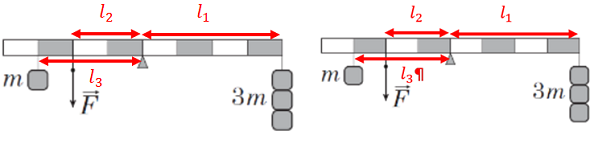
Рис. 1. Схематичний розподіл сил
Після підставлення виразу (2) у вираз (1):
Із (3) можемо виразити
Відповідь: B.
ТЕМА: Механіка. Основи кінематики. Рівноприскорений рух. Кінетична енергія.
Завдання скеровано на оцінювання вміння розраховувати кінетичну енергію для різних типів руху, зокрема рівноприскореного.
Кінетична енергія
Під час рівноприскореного руху залежність швидкості тіла від часу можна записати так:
Після підставлення виразу для швидкості рівноприскореного руху у вираз для кінетичної енергії можна дістати залежність кінетичної енергії від часу:
У виразі є
Відповідь: Б.
ТЕМА: Молекулярна фізика та термодинаміка. Рівняння теплового балансу.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з використанням рівняння теплового балансу.
Дано:
Знайти:
Потенціальну енергію води на вершині водоспаду можна розрахувати за формулою
Під час падіння потенціальна енергія води зменшується і біля підніжжя дорівнює нулю. Тож кількість теплоти, витрачена на нагрівання води під час падіння дорівнює 60 % від потенціальної енергії на вершині:
Кількість витраченої на нагрівання теплоти пов’язана зі зміною температури формулою
Тоді можна скласти рівняння:
Відповідь: 0,02.
ТЕМА: Механіка. Основи динаміки. Умова плавання тіл.
Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з використанням закону Архімеда.
Дано:
Знайти:
На камінь у воді діють дві сили – сила тяжіння, що притягує його до дна, і виштовхувальна сила Архімеда (рис. 1).
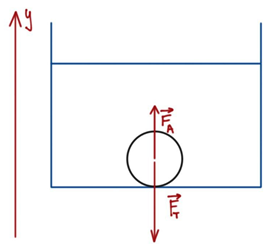
Рис. 1. Схема дії сил на камінь
Пригадаймо, що силу тяжіння можна визначити за формулою
Силу Архімеда можна визначити за формулою
Тоді можна записати другий закон Ньютона для каменя:
Спроєктуймо сили на вісь
Оскільки проєкція рівнодійної в цьому разі від’ємна, то сила тяжіння більша за виштовхувальну силу, що діє на камінь, тож камінь лежить у воді на дні.
Роботу сили можна визначити за формулою
За умови, що кут між напрямком сили й переміщенням каменя дорівнює нулю, а переміщення тіла дорівнює висоті його підйому
Робота, яку людина має виконати для піднімання тіла, – це робота проти рівнодійної сил, що діють на нього. Тому модуль піднімальної сили має дорівнювати модулю рівнодійної сил, що діють на камінь. Тоді роботу людини можна розрахувати за формулою:
Відповідь: 180
ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Робота та потужність електричного струму.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі, що стосуються роботи й потужності електричного двигуна.
Дано:
1. Знайти:
Потужність пов’язана з роботою формулою
Потужність електричного двигуна можна визначити за формулою
Тож:
2. Знайти:
ККД двигуна визначають як відношення корисної роботи, виконаної ним, до повної роботи:
Корисна робота – це робота, що необхідна для підйому вантажу на висоту 2 м.
Роботу сили можна визначити за формулою
Вважатимемо, що кут між напрямком сили й переміщенням вантажу дорівнює нулю, а переміщення тіла дорівнює висоті його підйому, тож
Вантаж втримується на землі завдяки силі тяжіння, тож піднімальна сила має за модулем дорівнювати їй:
Повна робота – це робота, виконана електричним двигуном, що була розрахована в попередньому пункті. Тоді:
Відповідь: 1. 60. 2. 80.
ТЕМА: Механіка. Основи динаміки. Закони Ньютона.
Завдання скеровано на перевірку вміння розв’язувати задачі з динаміки з аналізом світлин експерименту.
За рисунком 1 легко визначити, що на лівій нитці блоку підчеплено п’ять тягарців із масою

Рис. 1. Сили, що діють на тягарці
1. Знайти:

Рис. 2. Сили, що діють на систему
Нерухомий блок – простий механізм, він не забезпечує виграшу ні в силі, ні у відстані, а лише змінює напрямок прикладання сили.
Оскільки сили
Запис другого закону Ньютона для тягарців із масою 5m і 3m відповідно:
Спроєктуймо рівняння на вертикальну вісь, спрямовану вниз. Для цього треба пригадати, що лівий вантаж рухається вниз, а правий – угору. Їхні прискорення мають такі самі напрямки:
Тож
Силу тяжіння можна розрахувати за формулою:
2. Знайти:
Маса одного тягарця дорівнює
З рівняння для другого закону Ньютона для вантажу масою
Відповідь: 1. 2,5. 2. 3,75.
ТЕМА: Механіка. Динаміка. Рух під дією сили тяжіння.
Завдання скеровано на перевірку розуміння поняття кінетичної енергії та її зміни під час руху тіла унаслідок дії сили тяжіння.
Кінетичну енергію тіла визначають за формулою
Тіло, кинуте під кутом до горизонту, рухається внаслідок дії сили тяжіння, тобто з прискоренням, що дорівнює прискоренню вільного падіння.
Прискорення спрямоване вздовж осі
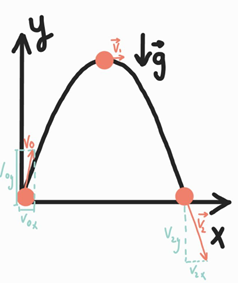
Рис. 1. Рух тіла, кинутого під кутом до горизонту
Модуль швидкості V в будь-який момент часу можна визначити за теоремою Піфагора:
Тож модуль швидкості й кінетична енергія тіла будуть найменшими тоді, коли проекція
У найвищій точці траєкторії тіло змінює напрямок свого руху: до цієї точки тіло піднімається і модуль
Відповідь: A.
ТЕМА: Механіка. Одиниці фізичних величин.
Завдання скеровано на перевірку вміння визначати одиниці фізичних величин, записані в основних одиницях СІ.
А Роботу
Силу можна визначити згідно з другим законом Ньютона за формулою
Тож для розмірностей рівність така:
Б Потужність
1 Дж записано в одиницях СІ у варіанті A, тож для розмірностей рівність така:
В Момент сили М:
Г Імпульс сили
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука.
Завдання скеровано на перевірку розуміння понять роботи й потенціальної енергії пружини.
Робота, виконана пружиною під час розтягування чи стискання, дорівнює зміні потенціальної енергії пружини, узятій із протилежним знаком:
Потенціальну енергія пружини можна обчислити за формулою
Для обчислення потенціальної енергії пружини в кожному положенні необхідно перевести в метри видовження, подане в сантиметрах:
Тоді робота, яку пружина виконує під час скорочення від 4 см до 2 см, така:
А робота, яку пружина виконує під час скорочення від 2 см до 0 см, дорівнює:
Знак «мінус» у цьому разі означає, що пружина виконувала роботу, а не зовнішнє тіло виконувало роботу над нею.
Тож
Відповідь: Г.
ТЕМА: Механіка. Молекулярна фізика і термодинаміка. Електродинаміка.
Завдання скеровано на перевірку знань і розуміння принципів дії пристроїв і механізмів із різних розділів фізики.
Гальмівні механізми (дискові або барабанні) не дають обертатися колесам, унаслідок чого автомобіль зменшує швидкість. Принцип дії гальмівного механізму заснований на використанні сили тертя. Під час гальмування кінетична енергія переходить у внутрішню.
Тепловий двигун – це машина, яка працює циклічно й перетворює енергію палива на механічну роботу. Робоче тіло (газ, який виконує роботу під час свого розширення) отримує певну кількість теплоти від нагрівника. Ця теплота частково перетворюється на механічну енергію (робоче тіло виконує роботу), а частково передається холодильнику.
Індукційні генератори струму перетворюють механічну енергію на електричний струм. Складені з металевого осердя, у пази якого поміщено обмотку. Кінці обмотки з’єднані з кільцями, до кожного з яких притиснуто щітку для відведення напруги до споживача. Осердя з обмоткою (ротор) обертається в магнітному полі нерухомого постійного магніту або електромагніту.
Електричний двигун є пристроєм для перетворення електричної енергії на механічну та приведення до руху машин і механізмів. Робота електродвигуна основана на втягуванні або виштовхуванні провідника з електричним струмом у магнітному полі й дії на провідник зі струмом сили Ампера. Під час роботи двигуна рух ротора (рухомої частини двигуна) передається валу, а з нього – безпосередньо до споживача.
Відповідь: 1А, 2Б, 3В, 4Г.
ТЕМА: Механіка. Закони збереження в механіці. Прості механізми.
Завдання скеровано на перевірку розуміння принципу дії простих механізмів – важеля і рухомого блока.
Прості механізми − це пристрої, які дають змогу виконувати роботу, докладаючи меншу силу порівняно з виконанням цієї ж роботи без них (виграємо в силі – програємо у відстані), або ж змінювати напрямок дії сили на зручніший для людини.
Важіль перебуває в рівновазі, якщо моменти сил, що обертають його за годинниковою стрілкою і проти неї, за модулем дорівнюють один одному.
Проти годинникової стрілки важіль обертатиме сила тяжіння, що діє на вантаж 1. Плече цієї сили становитиме
За годинниковою стрілкою важіль обертатиме сила, що натягує підвіс, на якому підвішено рухомий блок. Використання рухомого блока забезпечує подвійний виграш у силі. Тож для тримання вантажу 2 треба прикласти вдвічі меншу силу порівняно з його вагою. Плече цієї сили дорівнює
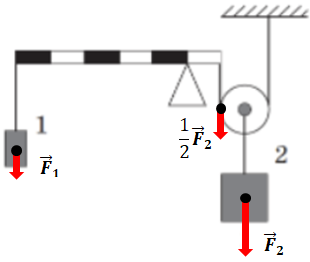
Запис правила моментів сил як умови рівноваги для тіла, що лише обертається, тобто має нерухому вісь обертання, такий:
Відповідно
Відповідь: Г.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична та потенціальна енергія.
Завдання скеровано на розуміння чинників, від яких залежить величина кінетичної енергії тіла.
Кінетична енергія – це фізична величина, якою характеризують механічний стан рухомого тіла. Кінетичну енергію
За умовою завдання маса тіл однакова, тому кінетична енергія змінюватиметься прямо пропорційно швидкості руху тіла. Із наведених у варіантах відповіді рівнянь залежності координати тіла від часу можна визначити швидкості руху кожного із чотирьох тіл. Цими рівняннями описано прямолінійний рівномірний рух тіл:
Тобто множник
Найбільша швидкість руху з-поміж наведених –
Відповідь: Б.
ТЕМА: Механічні коливання і хвилі. Коливання вантажу на пружині. Перетворення енергії під час гармонічних коливань.
Завдання скеровано на оцінку вміння розв’язувати комбіновані задачі, які передбачають обробку й аналіз результатів експерименту, зображених на рисунку, i використання законів збереження енергії в коливальному процесі.
Знайти:
З рисункa 1 можна визначити довжину гумки у двох крайніх положеннях коливання тягарця. У крайніх положеннях тягарець змінює напрямок руху на протилежний, а отже його швидкість
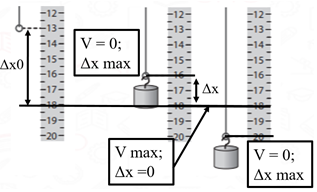
Рис. 1. Крайні положення тягарця
За цими значеннями можна обчислити амплітуду коливань:
Знаючи амплітуду коливань, можна визначити положення рівноваги – таке положення, у якому опиниться гумка під вагою тягарця, коли коливання повністю припиняться:
Під час коливань у положенні рівноваги швидкість найбільша, отже саме цю швидкість потрібно визначити.
Під час коливань зберігається повна механічна енергія системи
Кінетичну енергію можна визначити за формулою
Оскільки для гумової стрічки виконуваний закон Гука, можна обчислити потенціальну енергію за формулою, якою описують потенціальну енергію розтягнутої пружини:
Хоча повна механічна енергія системи зберігається, але значення кінетичної і потенціальної енергії постійно змінюється під час коливань.
У крайніх положеннях швидкість тягарця дорівнює нулю, а отже і його кінетична енергія теж. А от відхилення від положення рівноваги в цих положеннях найбільше, тому потенціальна енергія максимальна.
У положенні рівноваги все навпаки. Швидкість тягарця максимальна, а відхилення дорівнює нулю, отже кінетична енергія приймає найбільше значення, а потенціальна перетворюється на нуль.
Зважаючи на закон збереження енергії і спостереження, описані вище, можна записати таку рівність:
Тоді можна виразити максимальну швидкість:
Відношення
У стані спокою тягарець перебуватиме в положенні рівноваги. Тоді можна записати другий закон Ньютона:
Тоді
Після цього можна підставити отримане відношення у вираз для максимальної швидкості:
Відповідь: 28.
ТЕМА: Робота. Потужність. ККД.
Завдання скеровано на оцінювання вміння розв’язувати розрахункові задачі з обчислення роботи, потужності й коефіцієнта корисної дії (ККД).
Дано:
1. Знайти:
Корисна робота – це робота, необхідна для виконання завдання. У цьому завданні це піднімання води об’ємом
Під час піднімання води насос працює проти сили тяжіння, тож найменша сила, яку можна прикласти для підйому води, дорівнює силі тяжіння, що діє на неї. Кут між напрямком дії сили, що піднімає воду, і переміщенням води дорівнює нулю. Тож
Маса води пов’язана з її об’ємом і густиною формулою
Тоді
2. Знайти:
ККД машини можна визначити за формулою
Повну роботу можна обчислити, якщо врахувати енергію, яку споживає електричний насос. Її можна визначити за такою формулою:
Тоді
Відповідь: 1. 60. 2. 50.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку розуміння відмінності між поняттями імпульсу тіла й імпульсу сили.
Імпульс тіла
Імпульс сили й імпульс тіла можна визначити за такими формулами:
Імпульс тіла залежить від часу:
Цим рівнянням описано пряму. Загальне рівняння прямої таке:
Для залежності
Якщо кутовий коефіцієнт дорівнює нулю, то пряма є паралельною осі
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.
Завдання скеровано на перевірку розуміння графіків функціональної залежності фізичних величин, що ними описано прямолінійний рівноприскорений рух.
Кінетична енергія
Отже, кінетична енергія пропорційна квадрату швидкості
З рівняння випливає, що швидкість руху тіла прямо пропорційна часу:
Тож і кінетична енергія пропорційна квадрату часу:
Графіком залежності кінетичної енергії від часу (квадратичної функції) є парабола. З огляду на це варіанти відповіді А і Г неправильні.
Оскільки тіло піднімається, то кінетична енергія зменшуватиметься, тіло сповільнюватиметься, а потенціальна енергія зростатиме. Такому рухові відповідатиме парабола, вітки якої напрямлені вгору: із плином часу кінетична енергія зменшуватиметься до нуля у максимальній точці підняття, а коли тіло почне падати, кінетична енергія почне зростати до початкового значення, оскільки за умовою опором повітря нехтуємо, утрат механічної енергії немає.
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу. Закон збереження енергії в механічних процесах.
Завдання скеровано на перевірку вміння застосовувати закони збереження імпульсу і енергії.
1. За умовою удар куль був непружний, центральний.
Якщо швидкості руху тіл до і після зіткнення (пружного чи непружного) напрямлені вздовж прямої, що проходить через центри мас цих тіл, таке зіткнення називають центральним.
Якщо після зіткнення частина кінетичної енергії перетворюється на внутрішню енергію (витрачається на деформацію та нагрівання тіл), таке зіткнення називають непружним. Після такого удару тіла рухаються як єдине ціле.
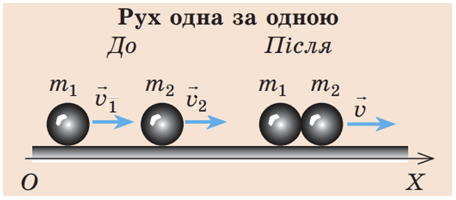
Опишімо рух куль до і після удару за допомогою закону збереження імпульсу у векторному вигляді та в проєкціях на вісь
Обчислімо швидкість руху куль після удару:
Відповідь: 4.
2. Запишімо закон збереження енергії:
Обчислімо її:
Відповідь: 0,6.
Відповідь: 1. 4. 2. 0,6.
ТЕМА: Механіка. Основи динаміки.
Завдання скеровано на перевірку розуміння різних динамічних процесів і вміння описати їх аналітично.
Ситуацію 1, коли відро з водою утримується за допомогою колодязного журавля (важеля), можна описати за допомогою правила моментів A: важіль перебуває в рівновазі, якщо сума моментів сил, які обертають важіль проти ходу годинникової стрілки, дорівнює сумі моментів сил, що обертають важіль за ходом годинникової стрілки.
Отже, умову рівноваги важеля під дією двох обертальних сил (сили тяжіння
У разі деформації тіла, як то стискання пружини (2), із боку тіла починає діяти сила, яка прагне відновити той стан тіла, у якому воно перебувало до деформації. Цю силу називають силою пружності. У разі малих пружних деформацій розтягнення або стиснення сила пружності прямо пропорційна видовженню тіла (Б):
Потужність, яку розвиває транспортний засіб, зручно визначати через силу тяги та швидкість руху. Формула справджується, і якщо в певний інтервал часу тіло рухається рівномірно, а напрямок сили тяги збігається з напрямком переміщення, і за нерівномірного руху: потужність
Отже, ситуації 3 відповідає формула B.
Силу тертя ковзання можна зменшити, змастивши дотичні поверхні, як у ситуації 4, коли деталі механізмів змащують мастилом.
Рідке мастило віддаляє дотичні поверхні одну від одної − сухе тертя замінюється значно слабшим рідким тертям.
Сила тертя ковзання
Відповідь: 1А, 2Б, 3В, 4Г.
ТЕМА: Механіка. Коливання і хвилі.
Завдання скеровано на перевірку розуміння фізичних процесів механіки і знання формул, якими описують ці процеси.
Усім тілам у Всесвіті властива гравітаційна взаємодія, виявом якої є їхнє взаємне притягання. Відповідно до закону всесвітнього тяжіння планети Венера й Марс притягуються одна до одної із силою
Якщо розтягнуту гумову нитку відпустити, то, скорочуючись, вона виконає роботу. Робота сили пружності визначена лише початковим і кінцевим станами гумової нитки, тобто сила пружності ‒ консервативна або потенціальна сила. Величину
Між дотичними поверхнями стрічки транспортера й цеглини діє сила тертя спокою, яка перешкоджає виникненню відносного руху їх. Сила тертя спокою завжди дорівнює за модулем і протилежна за напрямком рівнодійній зовнішніх сил, які намагаються зрушити тіло з місця. Після того як рівнодійна зовнішніх сил зрівняється з максимальною силою тертя спокою, тіло починає ковзання, тобто починає діяти сила тертя ковзання. Отже, максимальна сила тертя спокою дорівнює силі тертя ковзання:
Маленька сталева кулька коливається на довгій нерозтяжній нитці ‒ це модель нитяного (математичного) маятника. Період коливань
Відповідь: 1А, 2Г, 3Д, 4Б.
ТЕМА: Механіка. Закони збереження в механіці. Імпульс тіла. Кінетична енергія.
Завдання скеровано на перевірку знання формул для визначення імпульсу й кінетичної енергії тіла.
Імпульс тіла
Обчислімо значення імпульсу автомобіля:
Кінетична енергія
Обчислімо значення кінетичної енергії автомобіля:
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження механічної енергії.
Завдання скеровано на перевірку вміння застосовувати закони збереження імпульсу й енергії під час непружного удару тіл.
Якщо після зіткнення частина кінетичної енергії перетворюється на внутрішню енергію (витрачається на деформацію та нагрівання тіл), таке зіткнення називають непружним. Після такого удару тіла рухаються як єдине ціле (див. рисунок).
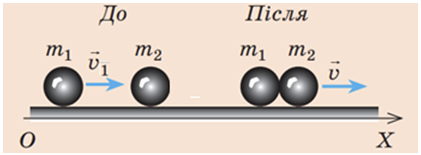
Опишімо рух куль до і після удару за допомогою закону збереження імпульсу у векторному вигляді та в проєкціях на вісь
Обчислімо швидкість руху куль після удару:
Запишімо закон збереження енергії для цієї умови:
Обчислімо її:
Відповідь: 22.
ТЕМА: Механіка. Основи динаміки (закон всесвітнього тяжіння.). Закони збереження в механіці (прості механізми, закон збереження імпульсу). Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння механічних процесів, уміння описати їх за допомогою формул і законів.
Взаємодію Землі і Місяця описуємо за допомогою закону всесвітнього тяжіння: будь-які два тіла притягуються одне до одного із силою
Відкручування гайки за допомогою гайкового ключа є прикладом застосування простого механізму ‒ важеля ‒ на практиці. Чим довшою буде ручка гайкового ключа, тим легше ми відкрутимо або сильніше закрутимо гайку, прикладаючи меншу силу. Описати цей процес можна відповідно до правила моментів:
Коливання тіла масою
Зіткнення більярдних куль, як приклад абсолютно пружного удару, опишімо за допомогою закону збереження імпульсу: у замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії. Зваживши на те, що імпульс тіла дорівнює добутку маси
Відповідь: 1Д, 2Б, 3В, 4Г.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.
Завдання скеровано на перевірку розуміння зв’язку між імпульсом тіла і його кінетичною енергією.
Кінетична енергія
На зміну кінетичної енергії м’яча після зіткнення зі стінкою вплине зміна його швидкості, маса ж залишиться незмінною.
Визначiмо зміну швидкості через зміну імпульсу
Імпульс тіла
За умовою м’яч до зіткнення зі стінкою мав імпульс
Після зіткнення зі стінкою величина імпульсу м’яча становить
Отже, швидкість зменшилася вдвічі. Порівняймо, як змінилася кінетична енергія:
Отже, кінетична енергія м’яча внаслідок зіткнення зі стінкою зменшилася вчетверо.
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку знання і вміння застосовувати закон збереження імпульсу.
Скористаймося законом збереження імпульсу для системи тіл криголам ‒крижина:
Спроєктуймо вектори імпульсів цього рівняння на горизонтальну вісь, що напрямлена вздовж напрямку руху криголама й, відповідно, руху криголама разом із крижиною після зіткнення:
Візьмімо до уваги, що після зіткнення криголам масою
Відповідь: A.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота. Потужність.
Завдання скеровано на перевірку знання і розуміння механічної роботи і потужності і вміння їх визначати за заданих умов.
1. Роботу
Це математичний запис теореми про потенціальну енергію: робота всіх консервативних сил (що не залежать від траєкторії руху тіла), які діють на тіло, дорівнює зміні потенціальної енергії
Потенціальна енергія піднятого тіла залежить від висоти, на якій перебуває тіло, тобто залежить від вибору нульового рівня, ‒ рівня, від якого буде відлічуватися висота. Нульовий рівень вибирають з міркувань зручності. А зміна потенціальної енергії, а отже, і робота сили тяжіння від вибору нульового рівня не залежать.
Отже, за нульовий рівень візьмемо підніжжя гори, де потенціальна енергія
Потенціальна енергія
Визначимо корисну роботу, яку виконує підйомник:
Відповідь: 63.
2. Потужність
Обчислимо потужність двигуна підйомника:
Відповідь: 52,5.
Відповідь: 1. 63. 2. 52,5.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах. Закон збереження імпульсу.
Завдання скеровано на перевірку знання і розуміння законів збереження в механіці й уміння їх застосовувати.
Кульку, що нерухомо висить на нитці, позначмо
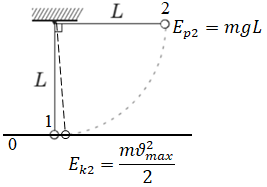
Після того як кульку
Відповідно до умови зіткнення кульок
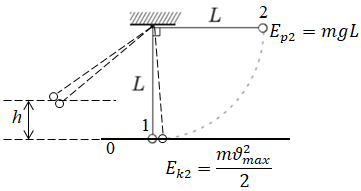
Опишімо взаємодію двох кульок законом збереження імпульсу:
Знову запишімо закон збереження енергії для кульок, які рухаються разом:
Відповідь: Б.
ТЕМА: Механіка. Основи динаміки. Умови рівноваги.
Завдання скеровано на перевірку знання і розуміння умов рівноваги тіла, а також вміння застосовувати правило моментів.
За умовою важіль
Момент сили
У цьому разі на важки і на вантаж діють сили тяжіння
Плече
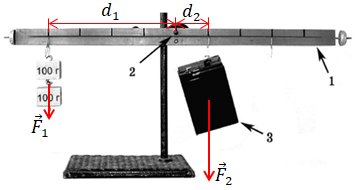
Визначимо масу вантажу
Відповідь: A.
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Перетворення енергії у гармонічних коливаннях.
Завдання скеровано на перевірку знання і розуміння закону збереження механічної енергії на прикладі математичного маятника.
Повна механічна енергія кульки, яка складається з кінетичної і потенціальної енергій, зберігатиметься: уважаємо, що опір повітря нехтовно малий, а сили, що діють у системі, є консервативними. Якщо значення одного виду енергії зменшується, то відповідно, значення іншого виду енергії збільшується.
За умовою завдання маятник рухається в бік положення рівноваги (вертикального положення). Це означає, що висота підняття кульки під час здійснення коливання зменшуватиметься, а швидкість руху кульки у напрямку положення рівноваги збільшуватиметься (див. рисунок).
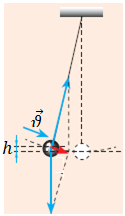
Потенціальна енергія
Отже, якщо висота зменшується, то потенціальна енергія теж зменшується.
Кінетична енергія
Отже, у разі збільшення швидкості руху кінетична енергія кульки теж збільшуватиметься.
Відповідь: Г.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.
Завдання скеровано на перевірку знання і розуміння закону збереження повної механічної енергії, а також залежності в цьому законі величин, які описують тіло або систему тіл, від часу.
Тіло, кинуте під кутом до горизонту, рухається по параболі, тож кінетична енергія тіла переходить у потенціальну, а потім, під час падіння, навпаки – потенціальна в кінетичну.
У замкненій системі тіл, які взаємодіють тільки консервативними силами, повна механічна енергія залишається незмінною (зберігається).
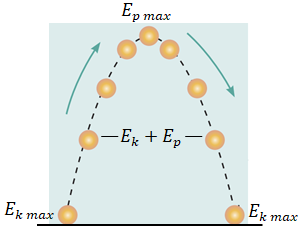
Закон збереження повної механічної енергії виконується тільки в тому разі, якщо в системі немає тертя.
За умовою на опір повітря не зважаємо, тому закон збереження повної механічної енергії справедливий.
Якщо повна механічна енергія
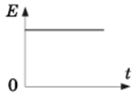
Відповідь: B.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота. Потенціальна енергія.
Завдання скеровано на перевірку розуміння закону збереження механічної енергії, уміння описати аналітично рух тіла під дією кількох сил.
Перед початком руху тіло масою
Отже,
Ковзаючи по похилій площині довжиною
Сила тертя ковзання напрямлена проти руху тіла, а переміщається воно вздовж похилої площини, то ж зазначений кут становитиме
Схематично зобразимо на похилій площині й позначимо всі сили, що діють на тіло. Сила тяжіння
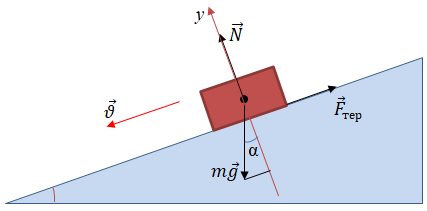
Запишімо другий закон Ньютона у векторній формі:
Сила тертя ковзання
Для того, щоб визначити
Отже,
Виразимо модуль переміщення тіла (довжину похилої площини) через дані в умові завдання:
Отже, остаточна формула для визначення роботи сили тертя ковзання набуває такого вигляду:
Відповідь: 2.
ТЕМА: Механіка. Закони збереження в механіці. Потужність.
Завдання скеровано на перевірку уміння визначати потужність.
Потужність
Робота рівнодійної всіх сил, які діють на тіло, дорівнює зміні кінетичної енергії
У результаті дії сил опору автомобіль зупиниться, тобто через час
Тобто
За умовою завдання автомобіль змінює швидкість, сповільнюється. Тому середня потужність двигуна ‒ це середнє арифметичне потужностей у певні моменти часу (так би мовити миттєвих потужностей), що дорівнюють добутку модуля сили тяги двигуна на модуль його миттєвої швидкості.
Оскільки всю енергію двигуна буде витрачено на подолання сил опору, то середня потужність двигуна дорівнюватиме середній потужності сил опору.
Отже, визначмо середню потужність сил опору:
Відповідь: Г.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку знання і розуміння закону збереження імпульсу і вміння за його допомогою описувати конкретну систему тіл.
У замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії. Запишімо закон збереження імпульсу для системи тіл, як векторну суму імпульсів
Оскільки порожній вагон штовхне навантажений і вони разом, зчепившись, продовжать рух у тому самому напрямку, що й порожній, то можемо записати закон збереження імпульсу в проєкціях:
Навантажений вагон до зіткнення з порожнім стояв нерухомо, його швидкість дорівнювала нулю. Тож і його імпульс дорівнював нулю, оскільки імпульс тіла ‒ це добуток маси тіла на швидкість його руху:
З графіка залежності імпульсу порожнього вагона від часу можна визначити, що до зіткнення імпульс порожнього вагона
Отже, можемо визначити імпульс навантаженого вагона після поштовху порожнього вагона:
Запишімо формулу для імпульсу навантаженого вагона:
А швидкість руху
Визначмо тепер масу вантажу
Відповідь: Г.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку знання і розуміння закону збереження імпульсу і руху під дією сили тяжіння.
У горизонтальному напрямку на систему осколків зовнішні сили не діють, хоча вертикально на них діє сила тяжіння (тобто система незамкнена). Отже, горизонтальна складова імпульсу не повинна змінюватися. Тому в горизонтальному напрямку виконуватиметься закон збереження імпульсу:
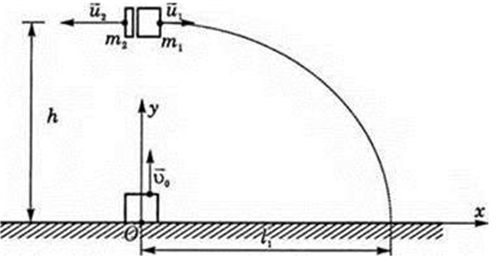
Запишемо проєкцію на вісь
Відстань
Визначмо час падіння, скориставшись тим, що з умови можна знайти час підйому. У верхній точці снаряд спочатку зупинився, а потім вже розірвався.
Запишімо рівняння для швидкості
Отже,
Підставмо вирази для швидкості і часу у формулу для відстані, яку пролетить перший (більший) осколок (
Виконаймо обчислення:
Відповідь:
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Перетворення енергії при гармонічних коливаннях.
Завдання скеровано на перевірку знання і розуміння перетворення енергії під час гармонічних коливань, а також уміння читати рівняння гармонічних коливань і брати з нього необхідні дані для розв’язання.
Потенціальна енергія
Визначмо координату маятника в момент часу
Підставмо цей вираз для координати у формулу для потенціальної енергії:
Запишімо закон збереження енергії для двох різних моментів часу ‒ для
Отже,
Робімо висновок, що
Відповідь: Б.
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.
Завдання скеровано на перевірку розуміння поняття механічної роботи.
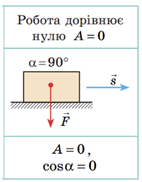
Механічна робота (робота сили)
Сила тяжіння діє на літак і напрямлена вертикально вниз. Але переміщення літака по вертикалі немає. За умовою літак рухається горизонтально. Отже, кут між вектором сили тяжіння і вектором переміщення дорівнює
Відповідь: Б.
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти.
Завдання скеровано на перевірку знання і розуміння перетворення кількості теплоти в інший вид енергії.
Унаслідок утраченої мідною кулькою внутрішньої енергії виділилася певна кількість теплоти
Під час підняття кульки на певну висоту
За умовою на підняття кульки витратиться
Виразімо звідси
Відповідь: A.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку знання і вміння застосовувати закон збереження імпульсу.
Скористаймося законом збереження імпульсу для системи двох куль:
Якщо після зіткнення частина кінетичної енергії перетворюється на внутрішню енергію (витрачається на деформацію і нагрівання тіл), таке зіткнення називають непружним. Непружне зіткнення, після якого тіла рухаються як єдине ціле, називають абсолютно непружним.
Спроєктуймо вектори імпульсів цього рівняння на горизонтальну вісь, що напрямлена вздовж напрямку руху, наприклад, першої кулі й, відповідно, руху криголама разом із крижиною після зіткнення:
Запишімо загальний імпульс системи куль до зіткнення:
Отже, зміна загального імпульсу системи куль унаслідок зіткнення дорівнюватиме нулю.
Відповідь: Г.
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу. Реактивний рух.
Завдання скеровано на перевірку знання і розуміння закону збереження імпульсу, реактивного руху.
Застосуємо закон збереження імпульсу до наведеного в завданні прикладу реактивного руху.
Реактивний рух ‒ це рух, що виникає внаслідок відділення з деякою швидкістю від тіла якоїсь його частини.
За умовою завдання відділятиметься ядро від школяра, хоча до цього і школяр, і ядро в нього в руках були в спокої.
Запишімо закон збереження імпульсу у векторній формі:
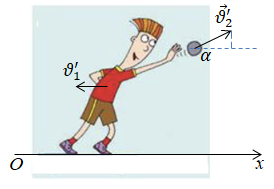
Тепер запишімо цей закон у проєкціях на горизонтальну вісь
Визначмо швидкість школяра:
Відповідь:
ТЕМА: Механіка. Закони збереження в механіці. Прості механізми. Коефіцієнт корисної дії.
Завдання скеровано на перевірку знання і розуміння простих механізмів ‒ рухомого і нерухомого блоків, а також уміння визначати коефіцієнт корисної дії механізму для підйому вантажів.
Підйомний механізм складається з двох невагомих блоків: рухомий блок (рис. 1), до якого безпосередньо прикріплено вантаж, дає виграш у силі вдвічі, але програш у відстані теж удвічі; другий блок ‒ нерухомий (рис. 2), лише змінює напрямок дії сили.
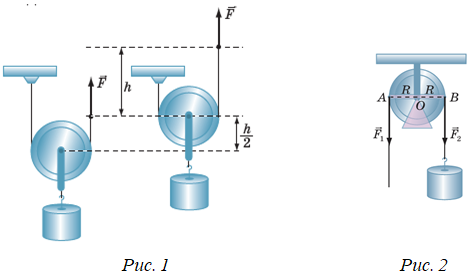
Коефіцієнт корисної дії
У цьому завданні корисною роботою
Загальне визначення механічної роботи (робота сили)
Отже, узявши до уваги, що вантаж підняли на висоту
Обчислімо коефіцієнт корисної дії
Відповідь: Г.
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рухому заряджену частинку.
На рухому заряджену частинку в магнітному полі діє сила Лоренца
За умовою частинка рухається перпендикулярно до ліній магнітної індукції.

У цьому разі
За другим законом Ньютона:
Ми виразили з рівняння швидкість, тому що кінетична енергія
За умовою після проходження частинки крізь фольгу радіус треку зменшився вдвічі, тож формула для швидкості матиме вигляд:
Тоді можемо визначити, яку частину кінетичної енергії втратила частинка під час проходження крізь фольгу:
тобто частинка втратила три чверті кінетичної енергії.
Відповідь: 0,75.
ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.
Завдання скеровано на перевірку розуміння графіків, що описують прямолінійний рівноприскорений вертикальний рух (під дією постійної сили тяжіння), і на розуміння функціональної залежності фізичних величин, що описують цей рух.
Потенціальною енергією
Потенціальна енергія піднятого тіла залежить від висоти, на якій перебуває тіло, тобто залежить від вибору нульового рівня, ‒ рівня, від якого відлічуватимуть висоту. Запишімо кінематичне рівняння, яке показує залежність висоти
За умовою завдання пластилінова кулька перебувала спочатку на певній висоті
Оскільки висота пропорційна часу в другому степені
Горизонтальна ділянка графіка, що збігається з віссю часу, коли вже потенціальна енергія дорівнює нулю, відповідає тій умові завдання, що кульку зроблено з пластиліну, тобто після непружного удару об підлогу вона не підскочить знову на певну висоту.
Відповідь: Б.
Тема: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку знання, розуміння і вміння застосувати закон збереження імпульсу.
За законом збереження імпульсу в замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії:
Оскільки за умовою тепловоз і вагон після взаємодії зчіплюються, то й швидкість їхнього спільного руху
До взаємодії і тепловоз, і вагон рухалися в одному напрямку. І після взаємодії вони продовжили рухатися в тому самому напрямку. Тож можна вектори швидкостей спроєктувати на горизонтальну вісь
Виразимо із цієї рівності їхню спільну швидкість руху після зчеплення:
Відповідь: Г.