ЗНО онлайн 2017 року з математики – основна сесія
Тестові завдання основної сесії ЗНО 2017 року з математики
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв’язувати рівняння першого степеня, застосовувати загальні методи та прийоми в процесі розв’язання рівнянь.
Розв’яжемо рівняння першого степеня відносно \(y:\)
\begin{gather*} 2y+4=x,\\[7pt] 2y=x-4,\\[6pt] y=\frac{x-4}{2}. \end{gather*}Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості. Аксіоми планіметрії.
Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур до розв’язування планіметричних задач.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.
Це завдання перевіряє знання означення степеня з раціональним показником, уміння розв’язувати показникові та лінійні рівняння.
\begin{gather*} 2^{2x}=\frac{1}{2^3},\\[6pt] 2^{2x}=2^{-3},\\[6pt] 2x=-3,\\[6pt] x=\frac{-3}{2}=-1\mathord{,}5. \end{gather*}Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики. Графічна, таблична, текстова та інші форми подання статистичної інформації.
Це завдання перевіряє вміння аналізувати інформацію, яка подана в графічній, табличній та текстовій формі.
За таблицею найбільша кількість глядачів була в четвер, а найменша – у понеділок. Ця умова виконується лише на діаграмах Г та Д. У вівторок кількість глядачів була більшою за кількість глядачів у середу, тому на діаграмі Г правильно відображено дані, наведені в таблиці.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Координати та вектори у просторі.
Це завдання перевіряє вміння знаходити відстань між двома точками в просторі, знання рівняння сфери.
Рівняння сфери $$ (x-a)^2+(y-b)^2+(z-c)^2=R^2. $$ Центр сфери \((0; 0; 0).\)
Точка \(A(0; 0; -5)\) належить сфері, тому радіус сфери \(R=5.\) Рівняння даної сфери $$ x^2+y^2+z^2=25. $$
Координати точки \(N(0; 0; 5)\) задовольняють даному рівнянню.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числа і вирази.
Це завдання перевіряє знання основних властивостей функцій, уміння розв’язувати рівняння першого степеня.
Точка перетину графіка функції \(y=2x-2\) з віссю абсцис має ординату нуль \((y=0).\) Абсцису точки знаходимо з рівняння:
\begin{gather*} 2x-2=0,\\[7pt] 2x=2,\\[7pt] x=1. \end{gather*}Точка перетину графіка з віссю абсцис \((1; 0).\)
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази та їхні перетворення.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.
Оскільки обидва дроби мають однаковий знаменник, перетворимо заданий вираз у такій послідовності:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їх властивості.
Це завдання перевіряє знання аксіом стереометрії, властивостей паралельних прямих, уміння застосовувати властивості найпростіших геометричних фігур до розв’язування планіметричних задач.
\(\angle ABC+\angle CBD+\angle DBE=180^\circ\), \(\angle CBD=\angle BDE=70^\circ\), як внутрішні різносторонні при \(m\ ||\ n\) та січною \(BD.\) Кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=180^\circ-60^\circ-70^\circ=50^\circ.\)
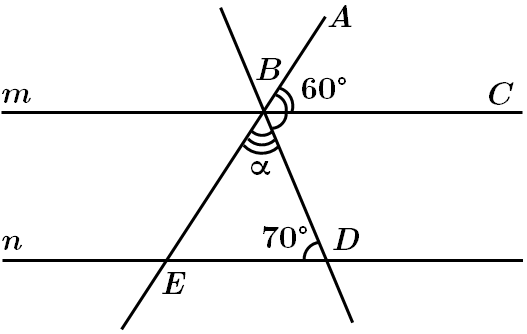
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Ірраціональні рівняння. Функції.
Це завдання перевіряє вміння розв’язувати ірраціональні рівняння, знаходити область визначення функції, знання методів розв’язування ірраціональних рівнянь.
Підносимо обидві частини рівняння до квадрата. Отримали рівняння, яке є наслідком даного:
\begin{gather*} 6-4x=16,\\[7pt] -4x=10,\\[7pt] x=-2\mathord{,}5. \end{gather*}Перевірка показує, що \(x=-2\mathord{,}5\) є коренем даного рівняння:
\begin{gather*} \sqrt{6-4\cdot (-2\mathord{,}5)}=4,\\[7pt] \sqrt{16}=4. \end{gather*}Корінь рівняння належить проміжку \([-3; -1).\)
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Паралельність і перпендикулярність прямої і площини. Паралельність площин.
Це завдання перевіряє знання можливого взаємного розташування прямих та площин у просторі.
I. Твердження є правильним, достатньо щоб пряма \(a\) була перпендикулярна до кожної з двох прямих \(c\) та \(b.\)
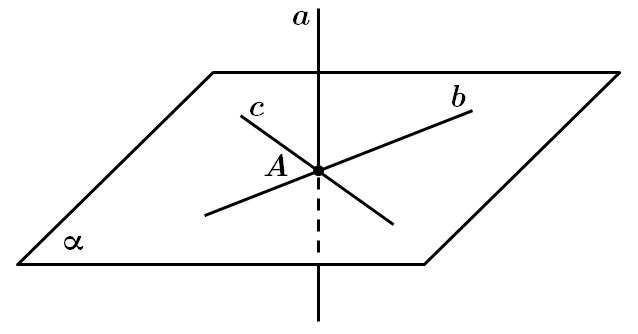
II. Твердження є правильним, через точку \(A\) можна провести безліч перпендикулярних площин до площини \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}.\) Достатньо, щоб побудована перпендикулярна площина проходила через пряму \(a\) з п. I.
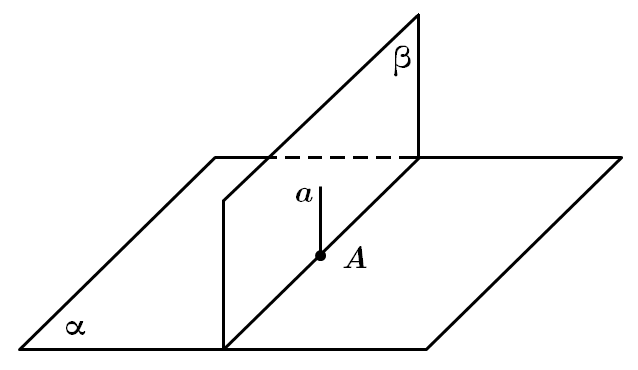
III. Твердження є неправильним. Згідно з аксіомою стереометрії: якщо дві площини мають спільну точку, то вони або збігаються, або перетинаються по прямій, яка проходить через цю точку. Тобто якщо провести через точку \(A\) паралельну площину \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) – то вона збігатиметься з площиною \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}.\)
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функціональна залежність.
Це завдання перевіряє вміння виконувати перетворення графіків функцій.
\begin{gather*} y=1-x^2,\\[7pt] y=-x^2+1. \end{gather*}1. Для побудови графіка функції \(y=-f(x)\) потрібно графік функції \(y=f(x)\) відобразити симетрично відносно осі \(Ox.\)
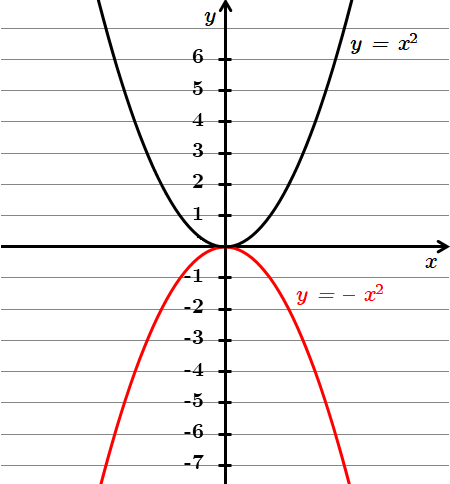
2. Для побудови графіка функції \(y=f(x)+c\) необхідно графік функції \(y=f(x)\) перенести вздовж осі \(Oy\) на \(c\) одиниць угору, якщо \(c\) – додатне число або на \(c\) одиниць вниз, якщо \(c\) – від’ємне число.
\(y=-x^2+1\) отримаємо, якщо \(y=x^2\) відобразимо симетрично відносно осі \(Ox\) та перенесенням на \(1\) одиницю вгору вздовж осі \(Oy.\)
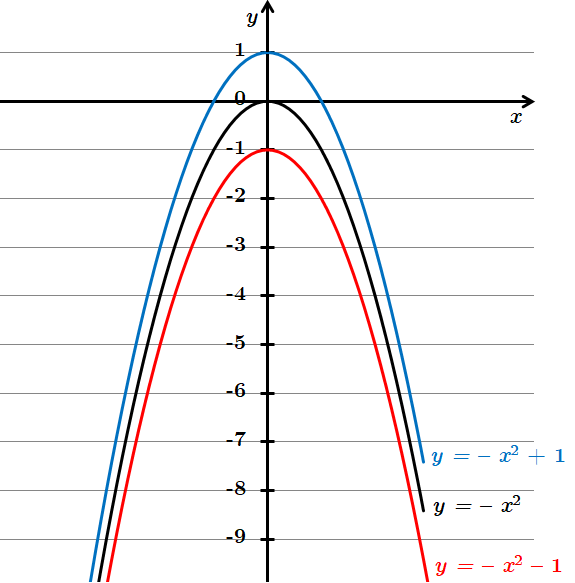
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази. Тригонометричні вирази та їхні перетворення.
Це завдання перевіряє знання основних тригонометричних тотожностей та вміння виконувати тотожні перетворення тригонометричних виразів.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Функції. Числові послідовності.
Це завдання перевіряє знання означення арифметичної прогресії, формули \(n\text{-го}\) члена та вміння розв'язувати задачі на арифметичну прогресію.
З означення арифметичної прогресії \(a_{n+1}=a_n+d.\) Так як \(a_5=a_4+3\), то \(d=3.\)
За формулою \(n\text{-го}\) члена арифметичної прогресії $$ a_n=a_1+(n-1)d, $$ знаходимо:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа та вирази. Логарифмічні вирази та їх перетворення. Функції. Основні властивості логарифмічної функції.
Це завдання перевіряє вміння виконувати перетворення логарифмічних виразів, знання властивостей логарифмічної функції.
Функція \(y=\log_2x\) зростаюча, тому
\begin{gather*} \log_28\lt\log_29\lt\log_216,\\[7pt] 3\lt \log_29\lt 4. \end{gather*}Тому \(x\in (3; 4).\)
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і почати аналізу. Функції. Логарифмічна функція. Рівняння, нерівності та їхні системи.
Це завдання перевіряє знання властивостей логарифмічної функції, уміння користуватися графічним методом розв’язування і дослідження нерівностей.
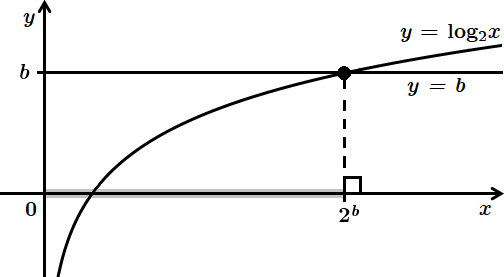
Точка перетину графіків функцій \(y=\log_2x\) та \(y=b\) буде точка з координатами \((2^b; b).\)
Розв’язуючи графічно нерівність \(\log_2x\lt b\), знаходимо частину графіка \(y=\log_2x\), яка знаходиться нижче прямої \(y=b\) та значення \(x\), яке відповідає даній частині графіка. Це \(x\in (0; 2^b).\)
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння застосовувати означення та властивості піраміди до розв’язування стереометричних задач, знаходити відстані в просторі, використовувати пряму та обернену теореми про три перпендикуляри.
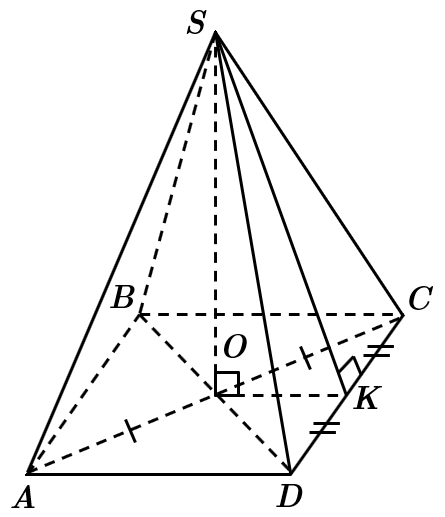
Піраміда – правильна, тому основа – квадрат, основа висоти – центр квадрата (точка перетину діагоналей).
\(P_{ABCD}=4AB=72\) см, \(AB=18\) см.
\(SK\ \perp\ CD\) – апофема, \(SK=15\) см. \(\Delta SDC\) – рівнобедрений, тому \(SK\) – висота та медіана.
\(DK=KC\), \(AD=DC\), \(AO=OC\) звідси випливає \(OK=\frac 12AD=9\) см.
\(\Delta SOK\ (\angle O=90^\circ)\) за теоремою Піфагора
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння застосовувати загальні методи та прийоми в процесі розв'язування рівнянь, нерівностей та систем.
\(x^2+64\gt 0\) при будь-яких значеннях \(x\), тому, щоб добуток \((x^2+64)(x-5)\) був більше нуля, необхідно, щоб другий множник \((x-5)\) був більшим за нуль.
\begin{gather*} x-5\gt 0,\\[7pt] x\gt 5,\\[7pt] x\in (5; +\infty). \end{gather*}Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел та дії з ними. Числові множини та співвідношення між ними.
Це завдання перевіряє знання властивостей модуля дійсного числа.
За властивістю модуля:
$$ |a|=\left\{\begin{array}{l} a,\ \text{якщо}\ a\ge 0, \\ -a,\ \text{якщо}\ a\lt 0. \end{array}\right. $$\(a-2\lt 0\) при \(a\lt 2\), тому розкривши модуль, отримаємо
\begin{gather*} 1+(-a+2)=1-a+2=3-a. \end{gather*}Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Коло та круг. Трикутники. Чотирикутники.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості геометричних фігур до розв'язування планіметричних задач та задач практичного змісту; уміння застосовувати теорему Піфагора до розв'язування прямокутного трикутника, властивості прямокутника.
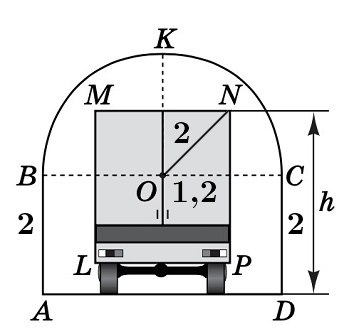
Розглянемо випадок, коли вантажівка дотикається аркового проїзду. При цьому \(ON=OC=2\) м (радіус аркового проїзду).
Оскільки \(MN=2\mathord{,}4\) м, а \(MF=FN=1\mathord{,}2\) м. \(FN=OE=1\mathord{,}2\) м. Значення \(NE\) знайдемо за теоремою Піфагора з \(\Delta NEO\ (\angle E=90^\circ).\)
Висота \(h\) вантажівки складається з суми
$$ h=CD+NE=2+1\mathord{,}6=3\mathord{,}6\ \textit{м}. $$При значенні \(3\mathord{,}6\) м вантажівка дотикається арки, тому максимально можливе значення – \(3\mathord{,}5\) м.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції
Це завдання перевіряє вміння знаходити похідні елементарних функцій, похідну суми.
За правилами диференціювання \((u\pm v)'=u'\pm v'\) та таблицею похідних знаходимо:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.
Це завдання перевіряє знання властивостей функцій, уміння встановлювати властивості числових функцій, заданих графіком.
Доберемо до кожного із запитань 1 – 4 правильну відповідь.
1. Функція є непарною, тому що графік симетричний відносно початку координат, і неперервна. Отже, 1 – A.
2. Функція має дві точки локального екстремуму: максимум та мінімум. Отже, 2 – Д.
3. Функція має три нулі – точки перетину з віссю абсцис. Отже, 3 – Г.
4. Функція є парною, тому що графік симметричний відносно осі \(Oy\), та є неперервною. Отже, 4 – В.
Відповідь: 1 – A, 2 – Д, 3 – Г, 4 – B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел та дії над ними.
Це завдання перевіряє знання означення кореня n-го степеня та його властивостей; означення степеня з натуральним, цілим та раціональним показниками, їхні властивості.
Доберемо до кожного із запитань 1 – 4 правильну відповідь.
1. \((a^m)^n=a^4\), то \(a^{mn}=a^4\), \(mn=4.\) Отже, 1 – B.
2. \(a^m\cdot a^n=a^4\), то \(a^{m+n}=a^4\), \(m+n=4.\) Отже, 2 – A.
3. \(\sqrt[8]{a^m}=\sqrt{a^n}\), то \(a^{\frac m8}=a^{\frac n2}\), \(\frac m8=\frac n2\), \(2m=8n\), \(m=4n.\) Отже, 3 – Г.
4. \(\frac{a^n}{a^m}=\frac{1}{a^4}\), то \(a^{n-m}=a^{-4}\), \(n-m=-4\), \(m-n=4.\) Отже, 4 – Б.
Відповідь: 1 – B, 2 – А, 3 – Г, 4 – Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє знання теореми косинусів, уміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач, співвідношення між сторонами та кутами прямокутного трикутника.
Доберемо до кожного із запитань 1 – 4 правильну відповідь.
1. Якщо \(a=b=c\), то \(\Delta ABC\) – рівносторонній.
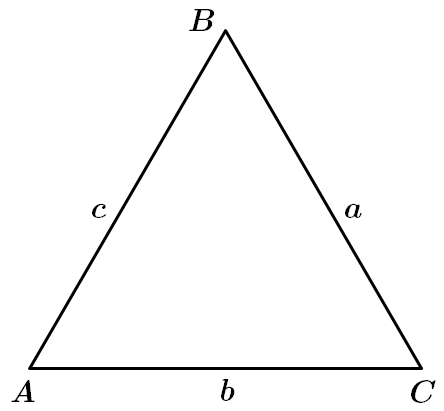
Усі кути рівностороннього трикутника дорівнюють \(60^\circ\), \(\angle C=60^\circ.\)
Отже, правильна відповідь – B.
2. Якщо \(c^2=a^2+b^2\), то \(\Delta ABC\) – прямокутний за наслідком з теореми косинусів.
Отже, правильна відповідь – Г.
3. Якщо \(a=c=\frac{b}{\sqrt{2}}\), то \(\Delta ABC\) – рівнобедрений з бічними сторонами \(a=c\) та основою \(b.\)
\(BH\ \perp\ AC.\) Так як \(CB=BA\), то \(CH=HA=\frac b2\) (висота є медіаною).
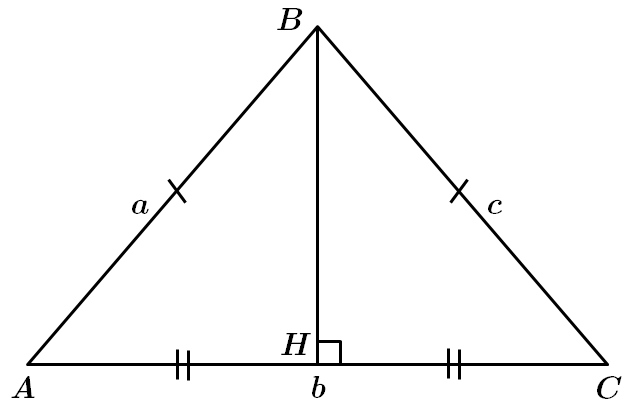
У \(\Delta BHC\ (\angle H=90^\circ)\), \(\cos C=\frac{CH}{CB}\), \(\cos C=\frac b2:a=\frac b2:\frac{b}{\sqrt{2}}=\frac{\sqrt{2}}{2}\), \(\angle C=45^\circ.\)
Отже, правильна відповідь – Б.
4. Якщо \(c^2=a^2+b^2-2ab\cdot \left(-\frac 12\right)\) за теоремою косинусів \(\cos C=-\frac 12\), \(\angle C=120^\circ.\)
Отже, правильна відповідь – Д.
Відповідь: 1 – B, 2 – Г, 3 – Б, 4 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання. Планіметрія. Трикутники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь, знання формул для обчислення площ поверхонь тіл обертання, знання теореми Піфагора, співвідношення між сторонами та кутами прямокутного трикутника.
Доберемо до кожного із запитань 1 – 4 правильну відповідь.
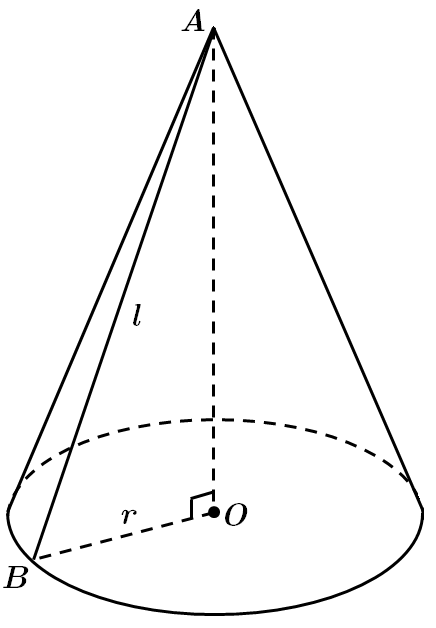
1. Якщо \(S_\text{б.п.}=3S_\text{осн}\), то \(S_\text{б.п.}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}rl\), \(S_\text{осн}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r^2\), \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}rl=3\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r^2\), \(l=3r.\) Отже, 1 – B.
2. Якщо висота конуса дорівнює радіусу основи, то \(AO=OB=r\), \(\Delta AOB\) – прямокутний рівнобедрений, за теоремою Піфагора \(AB^2=OB^2+AO^2\), \(l^2=r^2+r^2\), \(l=r\sqrt{2}.\) Отже, 2 – Б.
3. Якщо проекція твірної на площину основи конуса удвічі менша за твірну, то \(l=2r.\) \(OB\) – проекція твірної \(AB\) на площину основи. Отже, 3 – А.
4. Якщо площа повної поверхні конуса дорівнює \(5\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}r^2\)
Отже, 4 – Г.
Відповідь: 1 – В, 2 – Б, 3 – А, 4 – Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Відношення та пропорції. Відсотки. Основні задачі на відсотки. Текстові задачі.
Це завдання перевіряє вміння знаходити число за значенням його відсотка, розв'язувати задачі на відсоткові розрахунки.
1. Оскільки \(2\) грн \(40\) коп це \(3\text{%}\), то Андрій вніс $$ 2\mathord{,}4 : 0\mathord{,}03 = 240 : 3 = 80\ \textit{грн}. $$
2. Оскільки Андрій вніс до терміналу \(80\) грн, то на телефон була внесена сума $$ 80 - 2\mathord{,}4 = 77\mathord{,}6\ \textit{грн} $$ з урахуванням комісії. $$ 77\mathord{,}6 : 5 = 15\mathord{,}52. $$ Таким чином, бонусів нарахують $$ 15\cdot 8=120. $$
Відповідь: 1. \(80.\)
2. \(120.\)
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники. Чотирикутники.
Це завдання перевіряє знання теореми Фалеса, властивостей середньої лінії трикутника, трапеції, теореми Піфагора, уміння застосовувати властивості геометричних фігур до розв'язання планіметричних задач.
1. Оскільки площа квадрата \(KBCM\ 18\) см\(^2\), то
\(KM\) з'єднує середини діагоналей \(AC\) та \(BD\), належить середній лінії \(LN.\)
\(\Delta ACE\ (\angle E=90^\circ)\ CE\ \perp\ AD\), \(KM\) – середня лінія \(KM=\frac 12AE\), \(AE=2KM=2\cdot 3\sqrt{2}=6\sqrt{2}\) см.
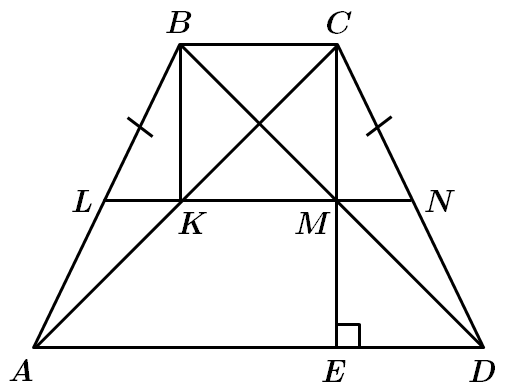
За теоремою Фалеса \(MK\ ||\ AD\), оскільки середина \(AC\), тому точка \(M\) – середина \(CE.\) \(CE=2CM=6\sqrt{2}\) см.
За теоремою Піфагора
2. Оскільки \(LK\) – середня лінія \(\Delta BAC\), \(MN\) – середня лінія \(\Delta BCD\), то
Відповідь: 1. \(12.\)
2. \(72.\)
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння знаходити область визначення функції, розв'язувати нерівності першого степеня.
Область визначення знаходимо з розв'язку нерівності \begin{gather*} 56-4x \gt 0\\[7pt] -4x\gt -56\ |:(-4)\\[7pt] x\lt 14. \end{gather*}
Найбільше ціле двоцифрове число – \(13.\)
Відповідь: \(13.\)
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв'язувати текстові задачі, застосовувати рівняння до розв'язування текстових задач, знання методів розв'язування раціональних рівнянь.
Нехай швидкість автобуса \(x\) км/год, тоді швидкість автомобіля
$$ 1\frac 15x=1\mathord{,}2x\ \text{км}/\text{год}. $$\(150\) км автобус проїжджає за \(\frac{150}{x}\) год, а автомобіль за \(\frac{150}{1\mathord{,}2x}\) год. Це на \(30\) хв \(\left(\frac 12\ \textit{год}\right)\) менше. Розв'яжемо рівняння
\begin{gather*} \frac{150}{x}-\frac{150}{1\mathord{,}2x}=\frac 12,\\[6pt] \frac{150\cdot(1\mathord{,}2-1)}{1\mathord{,}2x}=\frac 12,\\[6pt] \frac{150\cdot 0\mathord{,}2}{1\mathord{,}2x}=\frac 12,\\[6pt] x=\frac{150\cdot 0\mathord{,}2\cdot 2}{1\mathord{,}2}=50\ \text{км}/\text{год}. \end{gather*}Час, за який автомобіль долає відстань між \(A\) та \(B\) $$ \frac{150}{1\mathord{,}2\cdot 50}=2\mathord{,}5\ \textit{год}. $$
Відповідь: \(2\mathord{,}5.\)
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірносі та елементи статистики. Ймовірність випадкової події.
Це завдання перевіряє знання означення ймовірності події, уміння обчислювати ймовірності випадкових подій, розв'язувати нерівності першого степеня, раціональні.
Цукерок з молочного шоколаду – \(3\), з чорного шоколаду – \(m.\)
Ймовірність навмання витягнути цукерку з молочного шоколаду $$ P=\frac{3}{3+m}. $$
Якщо ймовірність менше \(0\mathord{,}25\), то
\begin{gather*} \frac{3}{3+m}\lt 0\mathord{,}25,\\[6pt] \frac{3}{3+m}\lt \frac 14,\\[6pt] \frac{3}{3+m}-\frac 14\lt 0,\\[6pt] \frac{12-(3+m)}{4\cdot (3+m)}\lt 0,\\[6pt] \frac{9-m}{4\cdot (3+m)}\lt 0. \end{gather*}Оскільки знаменник дробу набуває тільки додатні значення, то
\begin{gather*} 9-m\lt 0,\\[7pt] -m\lt -9,\\[7pt] m\gt 9. \end{gather*}\(m\) – кількість цукерок, тому набуває цілі, додатні значення. \(m=10.\)
Відповідь: \(10.\)
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.
Це завдання перевіряє вміння знаходити координати вектора, знаходити скалярний добуток векторів, застосовувати координати й вектори до розв'язування планіметричних задач.
\(\overrightarrow{AB}\ \perp \overrightarrow{a}\), \(\ \overrightarrow{a}(4;3).\) Точка \(A(-2; 0)\), а точка \(B\) лежить на прямій \(y=2x\), тому \(B(x; 2x).\)
Координати вектора \(\overrightarrow{AB}(x+2; 2x).\) Координати \(\overrightarrow{a}\) та \(\overrightarrow{AB}\) взаємно перпендикулярні, тому скалярний добуток їх дорівнює нулю.
\begin{gather*} \overrightarrow{a}\cdot \overrightarrow{AB}=0,\\[7pt] 4(x+2)+3\cdot 2x=0,\\[7pt] 4x+8+6x=0,\\[7pt] 10x+8=0,\\[7pt] 10x=-8,\\[7pt] x=-0\mathord{,}8. \end{gather*}Відповідь: \(-0\mathord{,}8.\)
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ.
Це завдання перевіряє вміння використовувати перетворення графіків функцій для побудови графіків, знаходити первісну, обчислювати площу плоских фігур за допомогою інтеграла.
1. Знайдемо координати точок перетину графіка \(f\) з осями координат
2. Побудова графіка. \(f(x)=x^2-6x+9\) – квадратична функція, графік – парабола. \(f(x)=(x-3)^2.\)
Побудуємо перетворенням графіка функції \(y=x^2\) на \(3\) одиниці вправо вздовж осі \(Ox.\)
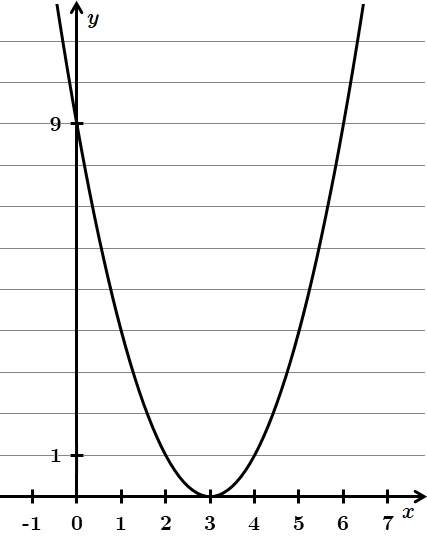
3.
4. Площa фігури.
Відповідь: 1. \((0; 9)\), \((3; 0).\)
3. \(\frac{x^3}{3}-3x^2+9x+C.\)
4. \(9\) кв. од.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості перпендикулярних прямих і площин до розв'язування стереометричних задач; знання формул для обчислення об'ємів многогранників, уміння використовувати пряму та обернену теорему про три перпендикуляри для знаходження кута між площинами.
Нехай \(ABCA_1B_1C_1\) – дана правильна призма. \(\Delta ABC\) – рівносторонній, висота призми – бічне ребро.
Площина \((AB_1K)\) перетинає \((B_1BC)\) по прямій \(B_1K\), \((AB_1K)\cap (ABC)=AK\), \((A_1B_1K)\cap (AB_1B)=AB_1.\)
\(BB_1\ \perp\ (ABC)\), \(B_1K\) – похила, \(BK\) – проекція похилої \(B_1K\) на площину \(ABC.\)
\(AK\) – медіана та висота \(\Delta ABC\), тому \(AK\ \perp\ BK.\) За теоремою оберненою до теореми про три перпендикуляри \(B_1K\ \perp\ AK.\)
За ознакою перпендикулярності прямої та площини \((BCB_1)\ \perp\ AK.\)
\((B_1KA)\cap (ABC)=AK\Rightarrow \angle B_1KB=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) – лінійний кут відповідного двогранного при ребрі \(AK.\)
\(AK=d.\) У \(\Delta ABK\ (\angle K=90^\circ)\), \(\angle B=60^\circ\),
Відповідь: \(\frac{d^3}{3}\mathrm{tg}\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}.\)
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв'язувати рівняння, що містять змінну під знаком модуля; розв'язувати рівняння з параметрами, рівняння, що містять логарифмічні вирази, вміння знаходити область визначення функцій.
Знайдемо ОДЗ: $$ \left\{\begin{array}{l} y-a\gt 0,\\ 4a^2+x-x^2\gt 0. \end{array}\right. $$
Розкриємо модулі:
Розв'яжемо методом підстановки:
Розглянемо 2 випадки:
1) \(D=0.\)
Перевірка:
вирази під знаком логарифма від'ємні, тому не належать ОДЗ.
Висновок: пара чисел \(\left(-\frac 12; -\frac 34\right)\) не є розв'язком.
2) \(D\gt 0\), тобто \(a\ne -\frac 14\)
\begin{gather*} \left[\begin{array}{l} x_1=\frac{-1+4a+1}{2}=2a,\\ x_2=\frac{-1-4a-1}{2}=-2a-1. \end{array}\right. \end{gather*}Відповідні значення \(y\)
\begin{gather*} \left[\begin{array}{l} y_1=3a,\\ y_2=-5a-2. \end{array}\right. \end{gather*}Зробимо перевірку:
1) \((2a; 3a)\)
При \(a\gt 0\) розв'язок \((2a; 3a).\)
2) \((-2a-1; -5a-2)\)
При \(a\lt -\frac 13\) розв'язок \((-2a-1; -5a-2).\)
При інших значеннях \(a\) система немає розв'язків.
Відповідь: при \(a\in (0; +\infty)\ (2a; 3a)\);
при \(a\in \left(-\infty; -\frac 13\right)\ (-2a-1; -5a-2)\);
при \(a\in \left[-\frac 13; 0\right]\) немає розв'язків.
Знайшли помилку? Пишіть на