ЗНО онлайн 2017 року з математики – додаткова сесія

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння розв'язувати рівняння другого степеня.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.

Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.

Функція \(y=f(x)\) визначена й зростає на проміжку \([-3; 2]\), тому більшому значенню аргумента відповідає більше значення функції.

З наведених точок може належати тільки точка \(L(1; 4).\)

Точка \((0; 2)\) належить графіку. Отже, точка з абсцисою \(x=1\) може мати ординату \(y\gt 2.\)

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.

Це завдання перевіряє знання аксіом планіметрії, уміння застосовувати властивості найростіших геометричних фігур до розв'язування планіметричних задач.

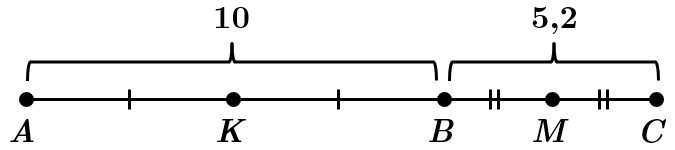
Нехай точка \(K\) – середина \(AB\), а точка \(M\) – середина \(BC.\)

\begin{gather*} KM=KB+BM=\frac 12AB+\frac 12BC=\\[6pt] =\frac 12(AB+BC)=(10+5\mathord{,}2):2=7\mathord{,6}\ \textit{см}. \end{gather*}

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики. Початки теорії ймовірностей та елементи статистики.

Це завдання перевіряє вміння аналізувати графічну, табличну, текстову та інші форми подання статистичної інформації.

У таблиці наведено шкали температури повітря. З неї зрозуміло, що найнижча температура була о \(6\text{-й}\) год, а найвища – о \(15\text{-й}\) год. Цій умові відповідають лише графіки A та Д.

Порівнюючи ці графіки, знаходимо, що даним таблиці задовольняє графік Д.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел.

Це завдання перевіряє вміння порівнювати дійсні числа.

З двох дробів з однаковими чисельниками більший той, у якого менший знаменник.

Отже, \(\frac{5}{18}\lt \frac{5}{17}.\)

З двох дробів з однаковими знаменниками більший той, у якого більший чисельник.

Отже, \(\frac{5}{17}\lt \frac{6}{17}.\)

Маємо \(\frac{5}{18}\lt \frac{5}{17}\lt \frac{6}{17}.\)

Відповідь: Б.

ТЕМА: Геометрія. Стереометрія. Координати та вектори у просторі.

Це завдання перевіряє знання формули для обчислення відстані між двома точками та формули середини відрізка.

Точка \(M\) – середина відрізка \(AB.\) Знаходимо координати точки \(M\) за формулою середини відрізка:

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел. Числові множини та співвідношення між ними.

Це завдання перевіряє вміння порівнювати дійсні числа.

Подвійна нерівність \(5\le 3^x\le 15\) буде вірною при \(x=2:\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Функції. Тригонометричні функції, їхні основні властивості.

Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком, використовувати перетворення графіків функцій.

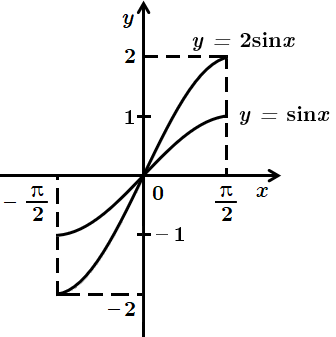
На рисунку зображено перетворення графіка функції \(y=\sin x\rightarrow y=2\sin x.\)

Перетворення графіка \(y=kf(x)\) розтягує графік вздовж осі \(Oy\) в \(k\) раз.

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази та їхні перетворення.

Це завдання перевіряє знання формул скороченого множення, уміння виконувати тотожні перетворення раціональних виразів.

Розкриємо дужки та спростимо отриманий вираз:

A \((x+2)(x-2)=x^2-4.\)

Б \(x(x+4)=x^2+4x.\)

B \((x+2)^2+4x=x^2+4x+4+4x=x^2+8x+4.\)

Г \((x+2)^2=x^2+4x+4.\)

Д \((x-2)^2+4x=x^2-4x+4+4x=x^2+4.\)

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.

Це завдання перевіряє знання теореми косинусів, властивостей ромба, уміння розв'язувати планіметричні задачі.

Дано: ромб \(ABCD\), \(AB=12\) см, \(\angle A=120^\circ.\)

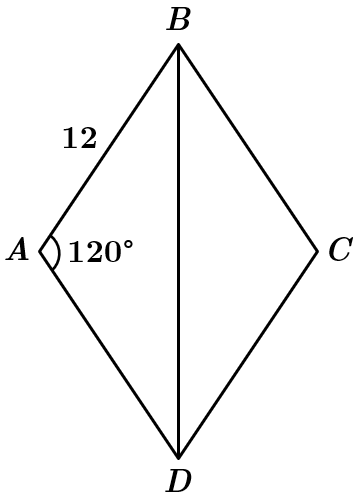
Більша діагональ лежить напроти більшого кута ромба \(\angle A=\angle C=120^\circ.\) Тому \(BD\) – більша діагональ.

У трикутнику \(DAB\ \angle A=120^\circ\), \(AB=AD=12\) см. За теоремою косинусів:

\begin{gather*} BD^2=AB^2+AD^2-2\cdot AB\cdot AD\cdot \cos A=\\[6pt] =12^2+12^2-2\cdot 12\cdot 12\cdot \left(-\frac 12\right)=\\[6pt] =2\cdot 12^2+12^2=3\cdot 12^2. \end{gather*}

Отже, $$BD=\sqrt{3\cdot 12^2}=12\sqrt{3}\ \textit{см}.$$

Відповідь: Г.

ТЕМА: Геометрія. Стереометрія. Прямі і площини у просторі.

Це завдання перевіряє вміння застосовувати означення, ознаки та властивості паралельних і перпендикулярних прямих і площин.

I. Твердження хибне, тому що, якщо пряма лежить і в площині \(\mathbf{\alpha}\), і в площині \(\mathbf{\beta}\), то ці площини мають спільні точки, а це суперечить умові \(\mathbf{\alpha}\ ||\ \mathbf{\beta}.\)

II. Твердження є правильним. Пряма, перпендикулярна до площини \(\mathbf{\alpha}\), перпендикулярна й площині \(\mathbf{\beta}.\)

III. Твердження хибне, тому що пряма, що лежить в одній з паралельних площин, може бути паралельною або мимобіжною з прямими, які лежать в іншій паралельній площині.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Це завдання перевіряє знання методів розв'язування раціональних нерівностей, уміння застосовувати методи та прийоми в процесі розв'язування нерівностей.

\begin{gather*} \frac{2x-4}{x+1}\lt 0,\\[6pt] \frac{2(x-2)}{x+1}\lt 0,\\[6pt] \frac{x-2}{x+1}\lt 0. \end{gather*}

Розв'яжемо методом інтервалів: $$(x-2)(x+1)\lt 0.$$

 $$x\in (-1; 2).$$

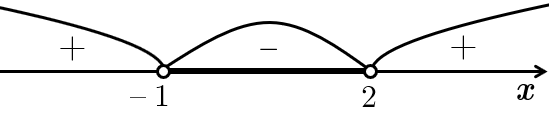
Відповідь: B.

ТЕМА: Планіметрія. Чотирикутники.

Це завдання перевіряє знання властивостей квадрата, уміння застосовувати властивості квадрата до розв'язування планіметричних задач практичного змісту.

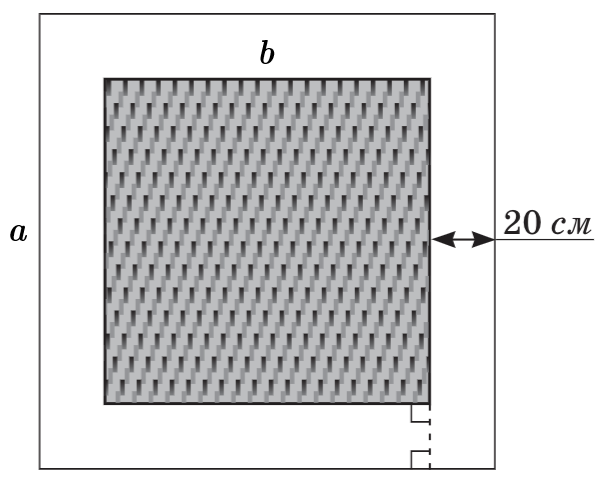
Нехай сторона квадрата (підлоги)

\(a=P:4=18:4=4\mathord{,}5\) м.

Сторона квадрата (килима)

\(b=a-0\mathord{,}4=4\mathord{,}5-0\mathord{,}4=4\mathord{,}1\) м.

\(P=4b=4\cdot 4\mathord{,}1=16\mathord{,}4\) м – периметр килима.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів та знаходити їхнє числове значення при заданих значеннях змінних.

\(2\sin \mathbf{\alpha}=\cos \mathbf{\alpha}.\) Поділимо обидві частини рівності на вираз \(\cos \mathbf{\alpha}\ne 0.\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.

Це завдання перевіряє знання формули \(n\text{-го}\) члена арифметичної прогресії, уміння розв'язувати задачі на арифметичні прогресії.

За формулою \(n\text{-го}\) члена \(a_n=a_1+d(n-1)\) знаходимо кількість від'ємних членів прогресії:

Найбільше ціле, яке є розв'язком нерівності \(n=14\), є розв'язком задачі.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Це завдання перевіряє знання модуля дійсного числа та його властивостей.

За властивістю модуля дійсного числа

Спрощуємо вираз:

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл.

Це завдання перевіряє вміння застосовувати формулу Ньютона-Лейбніцa для обчислення визначеного інтеграла.

$$ \mathop{\int}\limits_{0}^2 f(x)dx=8. $$

За формулою Ньютона-Лейбніца:

Звідси,

Відповідь: A.

ТЕМА: Геометрія. Стереометрія. Многогранники.

Це завдання перевіряє вміння застосовувати означення та властивості основних видів многогранників, знання формули для обчислення площі поверхні.

Дано: правильна трикутна піраміда, тому основа – правильний трикутник, основа висоти – центр трикутника.

\(AB=BC=AC=10\) см, \(DA=DB=DC=13\) см. \(DK\ \perp\ BC\) – апофема, \(CK=KB=5\) см.

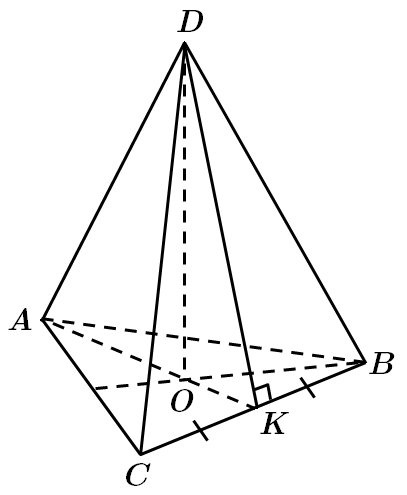
У \(\Delta DKB\ (\angle K=90^\circ)\) за теоремою Піфагора:

$$ S_\text{біч}=p_\text{осн}\cdot l, $$ де \(p_\text{осн}\) – півпериметр основи, \(DK=l\) – апофема.

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Логарифмічні рівняння.

Це завдання перевіряє вміння розв'язувати логарифмічні рівняння.

Використаємо властивість логарифма: $$ \log_a b^n=n\cdot \log_a b, $$

Звідси, \(x=9\) корінь рівняння. Проміжок, якому належить корінь рівняння \((8; 10].\)

Відповідь: Д.

ТЕМА: Алгебра та початки аналізу. Функції.

Це завдання перевіряє знання основних властивостей і графіків функцій, уміння будувати графіки елементарних функцій, встановлювати властивості числових функцій, заданих формулою або графіком.

1. Правильна відповідь – А.

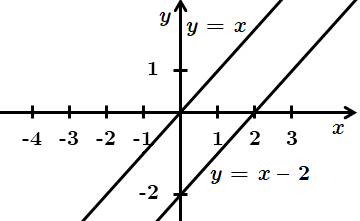
2. Правильна відповідь – В.

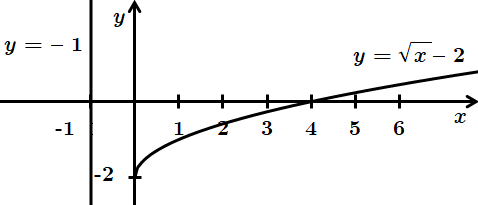
3. Правильна відповідь – Г.

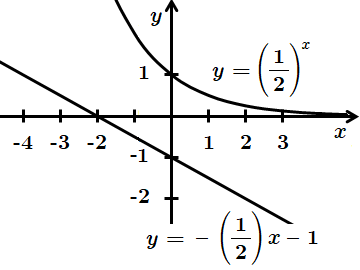
4. Правильна відповідь – Б.

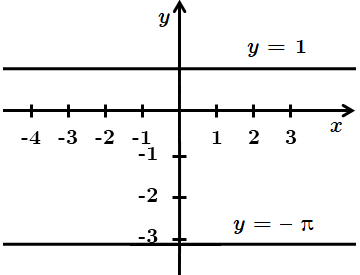
Відповідь: 1 – A, 2 – B, 3 – Г, 4 – Б.

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Раціональні вирази та їх перетворення.

Це завдання перевіряє вміння виконувати дії з раціональними числами, виконувати тотожні перетворення раціональних виразів і знаходити їхнє числове значення при заданих значеннях змінної.

1. \(\frac 73a=\frac 73\cdot 15=\frac{7\cdot 15}{3}=35\)

ділиться націло на \(5.\) Отже, 1 – Д.

2. \(2a-1=2\cdot 15-1=29\)

є простим числом. Отже, 2 – Б.

3. \(a^2+12a+36=(a+6)^2=(15+6)^2=21^2\)

ділиться націло на \(3.\) Отже, 3 – Г.

4. \(a^2+13^2=15^2+13^2=225+169=394\)

є парним числом. Отже, 4 – В.

Відповідь: 1 – Д, 2 – Б, 3 – Г, 4 – В.

ТЕМА: Геометрія. Планіметрія. Трикутники.

Це завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.

1. \(\angle ABC=60^\circ\) (кут рівностороннього трикутника). Отже, 1 – В.

2. \(\Delta ACD\) – рівнобедренний, тому

$$\angle A=\angle D=(180^\circ-\angle ACD): 2=(180^\circ-40^\circ):2=70^\circ.$$

Отже, 2 – Д.

3. \(\angle BAD=\angle BAC+\angle CAD=60^\circ+70^\circ=130^\circ.\)

Кутом між прямими, що перетинаються, називають менший із кутів, що утворився при перетині цих прямих. Кут між прямими \(AB\) та \(AD\) – це гострий кут, тому він дорівнює \(180^\circ-130^\circ=50^\circ\) (суміжний з \(\angle BAD\)). Отже, 3 – Б.

4. \(\angle BAD=130^\circ.\) \(AK\) – бісектриса \(\angle BAC\), \(AP\) – бісектриса \(\angle CAD.\)

\begin{gather*} \angle KAP=\angle KAC+\angle CAP=\frac 12 \angle BAC+\frac 12 \angle CAD=30^\circ+35^\circ=65^\circ. \end{gather*}

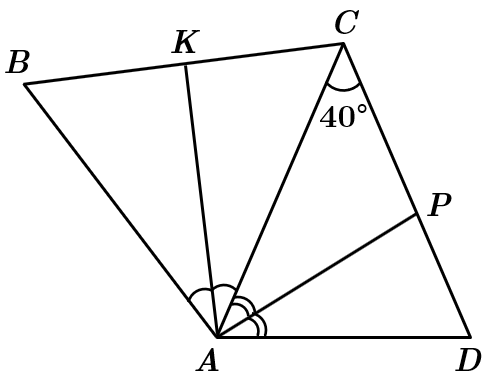
Отже, 4 – Г.

Відповідь: 1 – В, 2 – Д, 3 – Б, 4 – Г.

ТЕМА: Геометрія. Стереометрія. Тіла обертання.

Це завдання перевіряє вміння встановлювати за розгорткою поверхні вид геометричного тіла.

1. Квадрат обертається навколо сторони – отримаємо циліндр. Отже, 1 – А.

2. Квадрат обертається навколо діагоналі – отримаємо два конуси зі спільною основою. Отже, 2 – Г.

3. Прямокутна трапеція обертається навколо бічної сторони – отримаємо зрізаний конус. Отже, 3 – В.

4. Прямокутна трапеція обертається навколо більшої основи трапеції – отримаємо циліндр і конус зі спільною основою. Отже, 4 – Б.

Відповідь: 1 – А, 2 – Г, 3 – В, 4 – Б.

ТЕМА: Алгебра та початки аналізу. Відношення та пропорції. Відсотки. Основні задачі на відсотки.

Це завдання перевіряє вміння знаходити відношення чисел у вигляді відсотка, відсоток від числа, число за значенням його відсотка.

1. Індійський чай \(180\) г – це складає \(\frac{10}{23}\) від маси суміші.

Отже,

маса суміші.

2. Якщо індійський чай складає \(100\text{%}\), то цейлонський – \(130\text{%}\), тому що маса чаїв складається у відношенні \(10 : 13.\) Отже, цейлонського чаю на \(30\text{%}\) більше.

Відповідь: 1. \(414.\)
                   2. \(30.\)

26

ТЕМА: Геометрія. Планіметрія. Коло та круг. Чотирикутники. Геометричні величини та їхні вимірювання. Трикутники.

Це завдання перевіряє знання про коло, круг та їхні елементи, формул для обчислення площі кругового сектора, прямокутника.

1. Площу кругового сектора знаходимо за формулою $$ S_\text{сек}=\frac{\mathbf{\pi}R^2}{360^\circ}\cdot \mathbf{\alpha}, $$ де \(\mathbf{\alpha}\) – центральний кут.

2. Нехай \(a\) – спільна дотична до секторів. За властивістю дотичної до кола \(AO\ \perp\ a\), \(CO\ \perp\ a\), тому точка \(O\) лежить на прямій \(AC.\)

У \(\Delta ABC\ (\angle B=90^\circ)\) – єгипетський, тому \(AB=8\) см.

Відповідь: 1. \(6.\)
                   2. \(48.\)

ТЕМА: Алгебра та початки аналізу. Функції. Нерівності. Функціональна залежність.

Це завдання перевіряє вміння знаходити область визначення функції, розв'язувати лінійні нерівності.

Область визначення знаходимо з розв'язку нерівності: \begin{gather*} 50-3x\ge 0,\\[7pt] -3x\ge -50,\\[7pt] 3x\le 50,\\[7pt] x\le 50:3,\\[7pt] x\le 16\frac 23. \end{gather*}

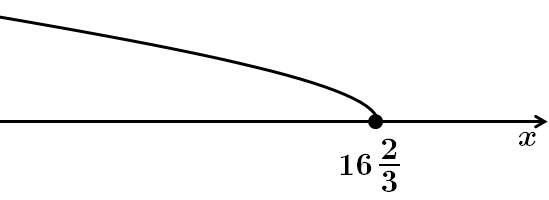
Найбільше ціле двоцифрове число, що належить області визначення – це число \(16.\)

Відповідь: \(16.\)

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Текстові задачі.

Це завдання перевіряє вміння розв'язувати текстові задачі, застосовувати рівняння до розв'язування текстових задач, знання методів розв'язування раціональних рівнянь.

Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом.

Човен проходить за течією \(24\) км за \(5\) годин, тому швидкість човна була:

\(24:5=4\mathord{,}8\) км/год.

Проти течії човен проходить \(12\) км за \(3\) години, тому швидкість човна проти течії:

\(12:3=4\) км/год.

Швидкість течії знаходимо таким чином:

\((4\mathord{,}8-4):2=0\mathord{,}8:2=0\mathord{,}4\) км/год.

Відповідь: \(0\mathord{,}4.\)

ТЕМА: Алгебра та початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики.

Це завдання перевіряє вміння обчислювати ймовірність випадкових подій.

Нехай \(P_1\) – ймовірність того, що спортсмен влучить у мішень, а \(P_2\) – ймовірність того, що не влучить.

За умовою \(P_1=7P_2\) та \(P_1+P_2=1.\)

Розв'яжемо систему рівнянь:

Розв'яжемо рівняння

Відповідь: \(0\mathord{,}875.\)

ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.

Це завдання перевіряє вміння виконувати дії з векторами, знаходити скалярний добуток векторів, знання правил додавання векторів, множення вектора на число.

Умова перпендикулярності векторів – їх скалярний добуток дорівнює нулю.

Відповідь: \(-0\mathord{,}6.\)

ТЕМА: Алгебра та початки аналізу. Функції. Похідна функції, її геометричний зміст. Похідні елементарних функцій. Правила диференціювання. Квадратична функція.

Це завдання перевіряє вміння будувати графік квадратичної функції, встановлювати властивості числових функцій, заданих формулою або графіком, знаходити похідні елементарних функцій, кутовий коефіцієнт дотичної.

1. Координати точок перетину графіка функції з осями:

\((2; 0)\), \((-5; 0)\) – точки перетину з віссю \(Ox.\)

\((0; -10)\) – точкa перетину з віссю \(Oy.\)

2. \(f(x)=x^2+3x-10\)

1) \(a=1\) – гілки направлені вгору.

2) вершина параболи:

\((-1\mathord{,}5; -12\mathord{,}25)\) – вершина.

3) точки перетину з осями:

\((0; -10); (2; 0); (-5; 0).\)

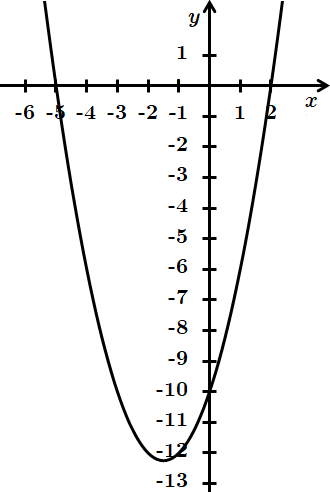
3. \(f'(x)=2x+3.\)

4. Кутовий коефіцієнт дотичної до графіка функції в точці \(x_0=-1\) – це значення похідної функції в даній точці.

\(k=f'(x_0)=f'(-1)=2\cdot (-1)+3=1.\)

Відповідь: 1. \((2; 0)\), \((-5; 0)\), \((0; -10).\)
                   3. \(f'(x)=2x+3.\)
                   4. \(1.\)

ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.

Це завдання перевіряє вміння знаходити кут між площинами, застосовувати властивості геометричних фігур до розв'язування задач, уміння розв'язувати задачі на обчислення об'ємів геометричних тіл.

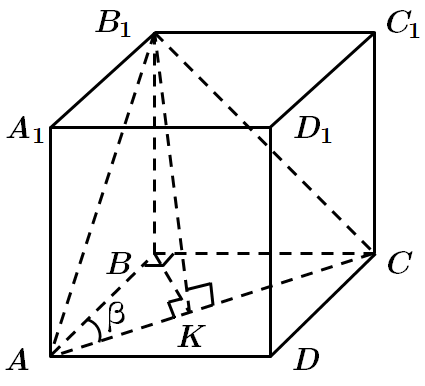
1. Площина, що проходить через діагональ \(AC\) та вершину \(B_1\) – це \((AB_1C).\) \((AB_1C)\) та \((ABB_1)\) має спільну пряму \(AB_1\), тому вони перетинаються по прямій \(AB_1\), \((ACB_1)\cap (BB_1C_1)=B_1C.\) Отже, переріз призми січною площиною – \(\Delta AB_1C.\)

2. Проведемо \(BK\ \perp\ AC\) у \((ABC).\)

За теоремою про три перпендикуляри \(B_1K\ \perp\ AC\), звідси \(AC\ \perp\ (BB_1K)\Rightarrow \angle B_1KB\) – лінійний кут відповідного двогранного. Кут між площинами \((AB_1C)\) та \((ABC)=\angle B_1KB=\mathbf{\alpha}.\)

3. У \(\Delta ABC\ (\angle B=90^\circ)\), \(AC=a\), \(\angle A=\mathbf{\beta}\), \(AB=a\cos \mathbf{\beta}\), \(BC=a\sin \mathbf{\beta}.\)

4. \(S_\text{осн}=S_{ABCD}=AB\cdot BC=a^2\sin \mathbf{\beta}\cdot \cos \mathbf{\beta}.\)

5. У \(\Delta BKA\ (\angle K=90^\circ)\), \(BK=AB\cdot \sin \mathbf{\beta}=a\cos \mathbf{\beta}\sin \mathbf{\beta}.\)

6. У \(\Delta BB_1K\ (\angle B=90^\circ)\), \(\angle B_1KB=\mathbf{\alpha}\), \(BB_1=BK\cdot \operatorname{tg}\ \mathbf{\alpha}=a\cos \mathbf{\beta}\cdot \sin \mathbf{\beta}\cdot \operatorname{tg}\ \mathbf{\alpha}.\)

7.\(V_\text{пр}=S_\text{осн}\cdot H\), де \(S_\text{осн}=S_{ABCD}\), \(H=BB_1.\)

Використавши формулу синуса подвійного кута, відповідь можнa записати у вигляді:

Відповідь: \(\frac 14a^3\sin^2 2\mathbf{\beta}\ \operatorname{tg}\ \mathbf{\alpha}.\)

ТЕМА: Алгебра та початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.

Це завдання перевіряє вміння використовувати властивості модуля, розв'язувати ірраціональні та квадратні рівняння, розв'язувати системи рівнянь з параметром.

Знайдемо область допустимих значень: $$ \text{ОДЗ:}\ \left\{\begin{array}{l} 3ax-8x-6y\ge 0,\\ x\ge 0. \end{array}\right. $$

Якщо квадрати двох виразів рівні, то вирази або рівні, або протилежні.

1) Розв'яжемо першу систему:

Розв'яжемо способом підстановки:

Отже,

Знайдемо, при яких значеннях параметра \(a\) ці пари чисел є розв'язками

\(a\) – будь-яке. \((0; 0)\) – розв'язок системи при будь-якому значенні \(a.\)

2) Розв'яжемо другу систему:

підстановкою знаходимо:

при будь-якому значенні \(a.\)

Знаходимо, при яких значеннях \(a\)

При \(a\ge 0\) розв'язок \((3a; -4a).\)

Відповідь: при \(a\in (-\infty; 0]\ (0; 0)\);
                   при \(a\in \left(0; 4\frac 23\right]\ (0; 0)\), \((3a; -4a)\);
                   при \(a\in \left(4\frac 23; +\infty\right)\ (0; 0)\), \((3a; -4a)\), \((3a-14; 3a-14).\)