ЗНО онлайн 2018 року з математики – пробний тест
Тестові завдання пробного тесту ЗНО 2018 року з математики
ТЕМА: Числа та вирази. Дійсні числа.
Це завдання перевіряє знання властивостей дій з дійсними числами, уміння округлювати десяткові дроби.
Для того, щоб округлити дріб до десятих, необхідно знати цифру, яка стоїть у розряді сотих.
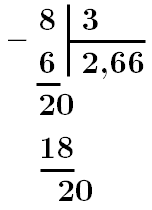
Якщо ця цифра
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Функції. Функціональна залежність. Лінійна функція, її властивості.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
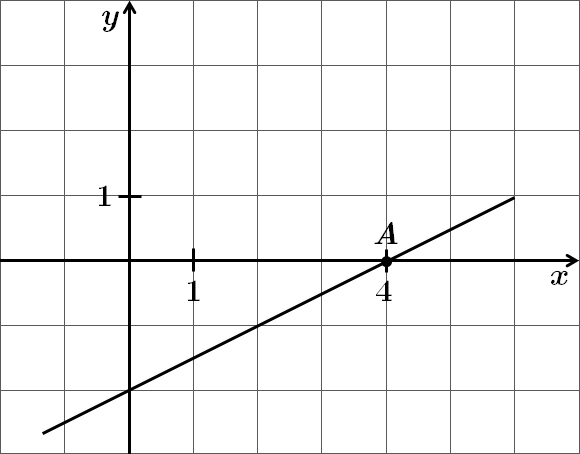
Графік функції перетинає вісь абсцис у точці
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Рівняння, нерівності та їхні системи. Показникові рівняння.
Це завдання перевіряє вміння розв'язувати показникові рівняння.
Отже, корінь рівняння
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники.
Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур, різних видів трикутників до розв'язування планіметричних задач.
Отже,
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.
Це завдання перевіряє знання означення степеня з натуральним показником, їхні властивості, властивості та означення кореня
При
Використали властивість степеня з натуральним показником:
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння застосовувати означення та властивості основних видів многогранників до розв'язування стереометричних задач; знання формул для обчислення площ поверхонь.
Данo куб, тому грань – квадрат, площею
Діагональ куба знаходимо за формулою
Отже,
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.
Це завдання перевіряє знання модуля дійсного числа та його властивості; вміння розв'язувати рівняння першого ступеня.
За властивістю модуля дійсного числа, рівняння
Сума коренів рівняння дорівнює
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази та їхні перетворення.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.
Використали формулу "різниця квадратів":
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і почаки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики.
Це завдання перевіряє вміння аналізувати вибіркові характеристики рядів даних, зокрема медіану.
Дані таблиці розставимо за зростанням. Медіаною ряда чисел називається число, яке стоїть посередині впорядкованого за зростанням ряду чисел.
У ряду
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком, використовувати перетворення графіків функцій.
Є два види перетворення:
1. Паралельне перенесення вздовж осі ординат:
Для побудови графіка функції
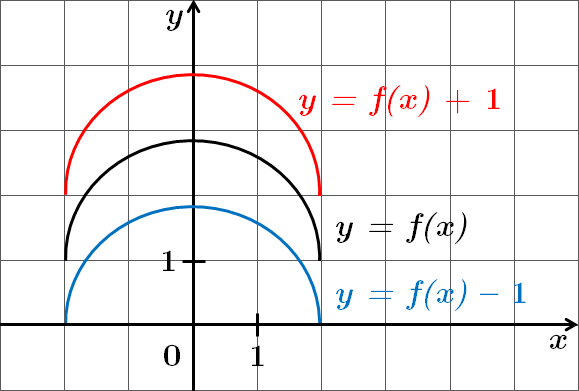
2. Паралельне перенесення вздовж осі абсцис:
Для побудови графіка функції
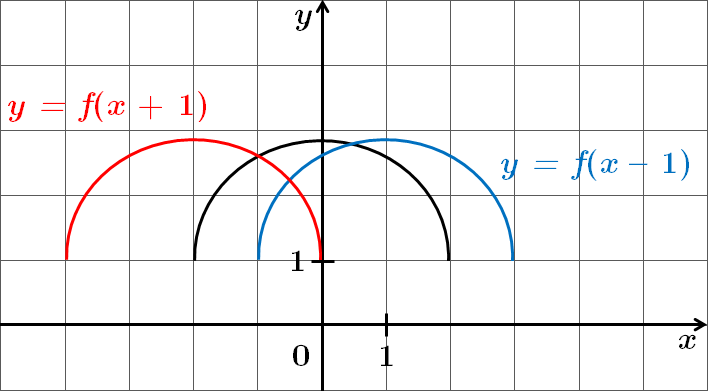
Застосувавши властивості паралельного перенесення до функції
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання аксіом стереометрії, ознаки паралельності прямої та площини, ознаку мимобіжності прямих.
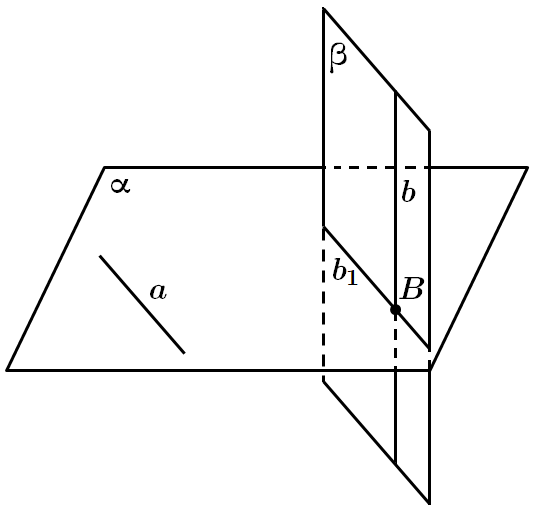
Задано дві мимобіжні прямі
Проведемо в площині
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази.
Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів та знаходити числове значення при заданих значеннях змінних.
Якщо
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.
Це завдання перевіряє вміння виконувати дії з векторами.
На рисунку зображено квадрат
Отже,
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв'язувати системи рівнянь другого степеня.
Розв'яжемо способом додавання
Підставимо
Розв'язок системи рівнянь
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.
Це завдання перевіряє знання властивостей парних та непарних функцій.
Функція
Функція
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їхні перетворення.
Це завдання перевіряє вміння знаходити числове значення тригонометричних виразів, порівнювати числові вирази.
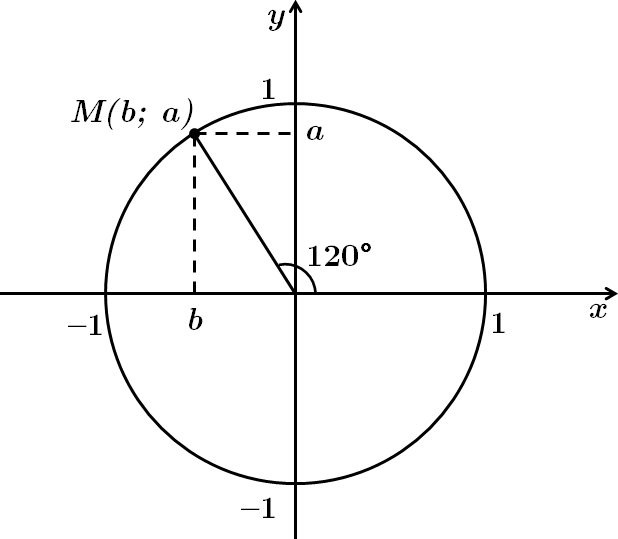
Враховуючи знаки тригонометричних функцій
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Раціональні нерівності.
Це завдання перевіряє знання методів розв'язування раціональних нерівностей.
Зведемо до спільного знаменника
Розв'яжемо методом інтервалів:
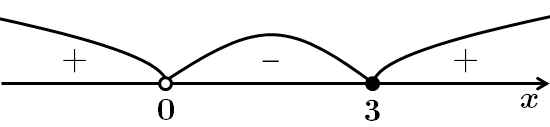
Отже,
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Геометричні величини та їх вимірювання.
Це завдання перевіряє вміння обчислювати довжину кола та його дуг, використовувати формули знаходження довжини кола до розв'язування планіметричних задач і задач практичного змісту.
Знаходимо довжини
Емблема також складається ще з одного кола, радіусом
Довжина матеріалу складає
Вартість матеріалу
З-поміж наведених сум грошей найменша, якої достатньо, щоб придбати матеріал це
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл.
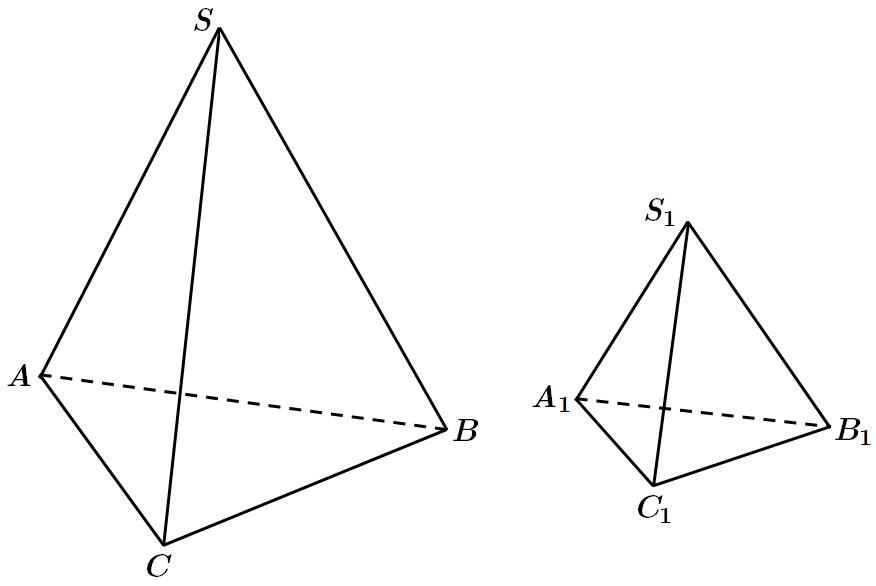
Дано
Відношення площ подібних трикутників дорівнює квадрату відношення відповідних сторін:
Площа бічної поверхні піраміди
Відповідь: Д.
Знайшли помилку? Пишіть на
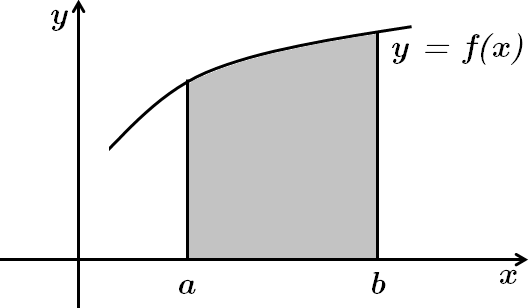
ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур.
Це завдання перевіряє вміння застосовувати формулу Ньютона-Лейбнiца для обчислення визначеного інтеграла.
Використали формулу Ньютона-Лейбніца:
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність. Квадратична, показникова, логарифмічна та степенева функції, їхні основні властивості.
Це завдання перевіряє вміння знаходити область значень функцій.
Область значень функції — це множина всіх можливих значень, які приймає функція при всіх допустимих значеннях аргументу.
Зобразимо схематично графіки функцій та визначимо область значень кожної з них.
1.
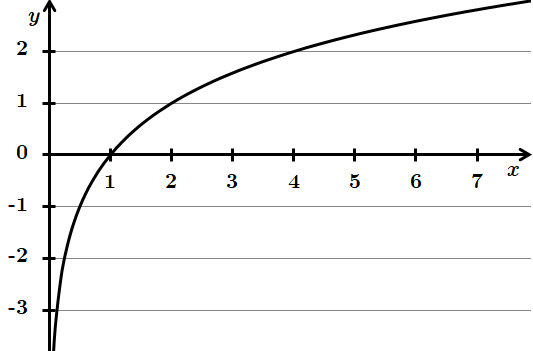
Отже, 1 – Д.
2.
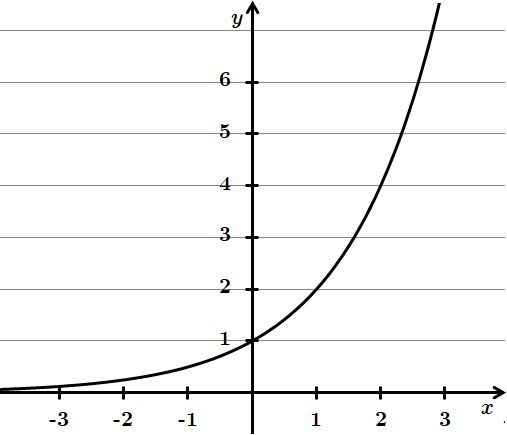
Отже, 2 – Г.
3.
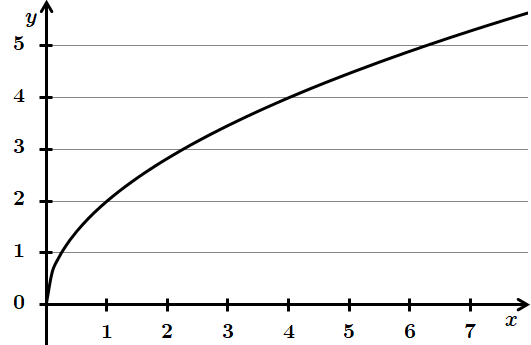
Отже, 3 – B.
4.
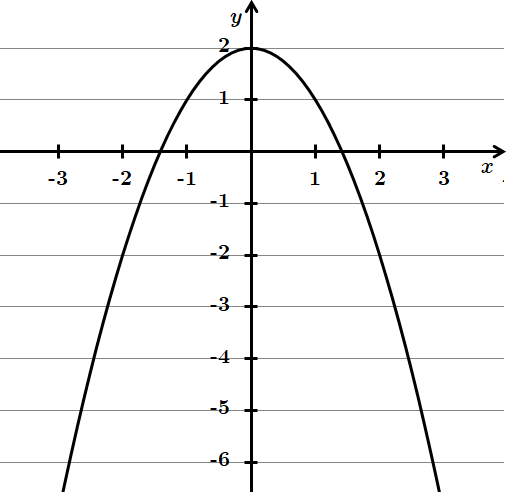
Отже, 4 – A.
Відповідь: 1 – Д, 2 – Г, 3 – В, 4 – А.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа (натуральні, цілі, раціональні та ірраціональні).
Це завдання перевіряє вміння виконувати дії з дійсними числами, використовувати ознаки подільності, знаходити найменше спільне кратне кількох чисел, розрізняти види чисел.
1.
Отже, правильна відповідь – Б.
2.
Отже, правильна відповідь – A.
3.
Отже, правильна відповідь – Г.
4.
Отже, правильна відповідь – Д.
Відповідь: 1 – Б, 2 – А, 3 – Г, 4 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг. Трикутники.
Це завдання перевіряє знання властивостей дотичної до кола, центральних та вписаних кутів, видів трикутників та їхніх основних властивостей.
1. За властивістю дотичної до кола
Отже, 1 – В.
2.
Отже, 2 – A.
3. Градусна міра дуги
У
Градусна міра дуги
Отже, 3 – Г.
4. За властивістю вписаного кута:
Отже, 4 – Б.
Відповідь: 1 – В, 2 – A, 3 – Г, 4 – Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє знання формул для обчислення об'ємів многогранників і тіл обертання.
1. Об'єм циліндра знаходимо за формулою
Отже, 1 – B.
2. Об'єм конуса знаходимо за формулою
Отже, 2 – Б.
3. Об'єм кулі знаходимо за формулою
Отже, 3 – A.
4. Об'єм призми знаходимо за формулою
Отже, 4 – Г.
Відповідь: 1 – B, 2 – Б, 3 – А, 4 – Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Відношення та пропорції. Відсотки. Основні задачі на відсотки. Текстові задачі.
Це завдання перевіряє вміння знаходити відношення чисел у вигляді відсотка, розв'язувати задачі на відсоткові розрахунки.
1. Нехай на виставці представлено
Кількість картин від загальної кількості робіт становить
2. Якщо вважати, що кількість скульптур складає
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Геометричні перетворення.
Це завдання перевіряє знання співвідношення між сторонами і кутами прямокутного трикутника, ознаки та властивості подібних фігур; уміння застосовувати властивості трикутників та чотирикутників до розв'язування планіметричних задач.
1.
За властивостю катета, який лежить напроти кута
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Це завдання перевіряє знання означення геометричної прогресії, формули
За умовою
Розв'яжемо методом підстановки:
Отже,
При
При
За умовою прогресія зростаюча, тому
Знаменник зростаючої геометричної прогресії завжди додатній
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі. Рівняння, нерівності та їхні системи. Раціональні рівняння.
Це завдання перевіряє вміння розв'язувати рівняння, що зводиться до квадратного, розв'язувати текстові задачі.
Нехай порожній басейн заповнюється з другої труби за
За
Корені рівняння
Отже, друга труба наповнює басейн за
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики. Перестановки, комбінації, розміщення.
Це завдання перевіряє вміння розв'язувати нескладні задачі комбінаторного характеру.
Кількість способів розташування
Так як супровідні автомобілі можуть помінятися місцями, то способів складання колони
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині. Геометричні величини та їх вимірювання.
Це завдання перевіряє знання прямокутної системи координат на площині, координати точки, формули площі трапеції.
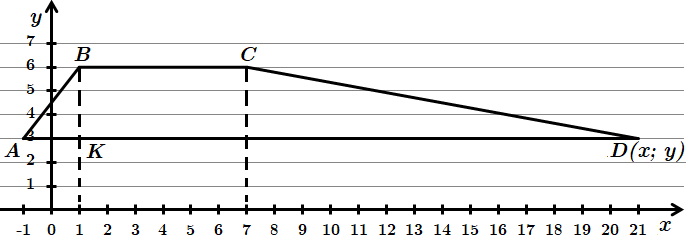
Позначимо задані точки на координатній площині.
Задано трапеція
звідси
Так як точка
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Квадратична функція. Похідна функції, її геометричний зміст. Похідні елементарних функцій. Правила диференціювання.
Це завдання перевіряє вміння будувати графік квадратичної функції, встановлювати властивості числових функцій, заданих формулою, знаходити похідні елементарних функцій, знаходити числове значення похідної функції в точці для заданого значення аргументу; знання рівняння дотичної до графіка функції в точці.
1. Знаходимо точки перетину графіка
За теоремою Вієта
2. Вершина параболи
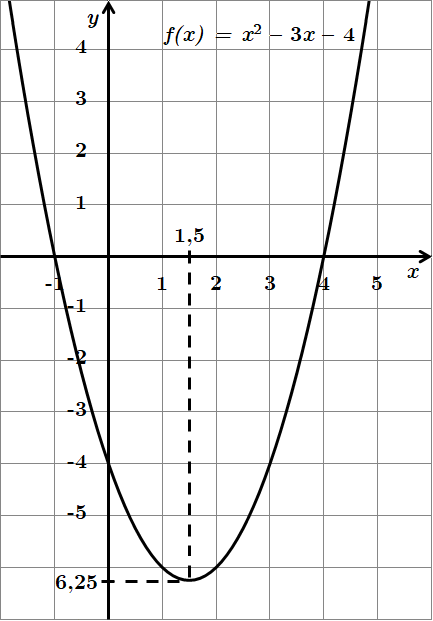
3. Знаходимо похідну функції:
4. Рівняння дотичної до графіка функції має вигляд:
Відповідь: 1.
3.
4.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та пощини у просторі.
Це завдання перевіряє знання кута між площинами, перерізів многогранників; уміння застосовувати властивості основних видів многогранників до розв'язування стереометричних задач.
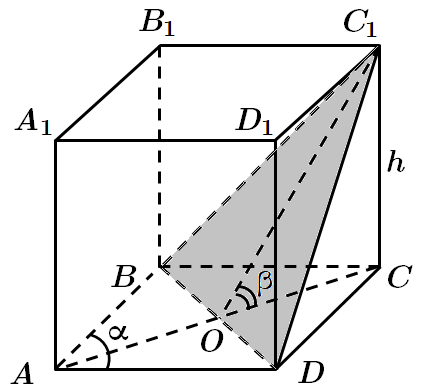
1. Якщо
2. Побудуємо переріз призми площиною
Точки
Отже,
3.
Отже,
4. У
5. За властивістю ромба
У
6.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Ірраціональні нерівності.
Це завдання перевіряє знання методів розв'язування ірраціональних нерівностей, уміння розв'язувати нерівності з параметрами.
Розв'язок нерівності
Таким чином,
Розв'яжемо (1) систему методом інтервалів:
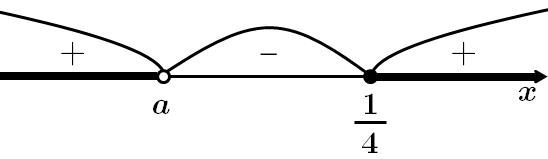
Отже, при
Розв'яжемо (2) систему:
Розглянемо 2 випадки:
1)
Для розв'язку методом інтервалів необхідно з'ясувати при яких значеннях
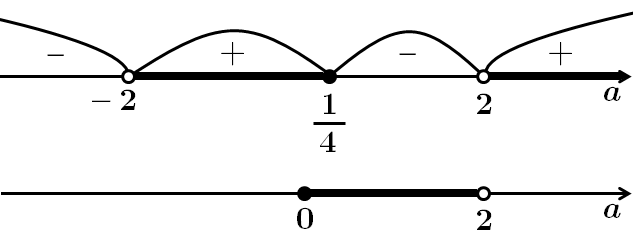
При
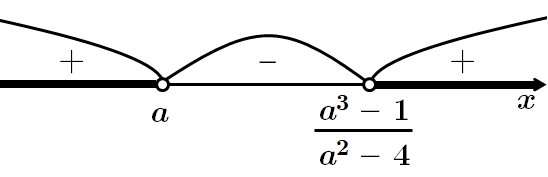
При
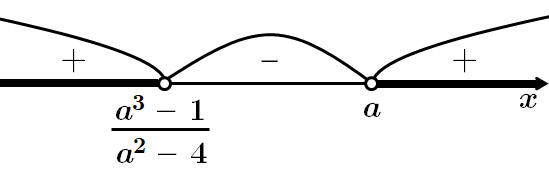
При
2)

Відповідь: при
при
при
при
при
Знайшли помилку? Пишіть на




