ЗНО онлайн 2018 року з математики – основна сесія

ТЕМА: Найпростіші геометричні фігури на площині та їхні властивості.

Це завдання перевіряє вміння застосовувати властивості найпростіших геометричних фігур до розв'язування планіметричних задач, знання властивості вертикальних кутів.

\(\angle \style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}=60^\circ\) як вертикальний з даним кутом \(60^\circ.\)

\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}+40^\circ=180^\circ\) оскільки складають розгорнутий кут.

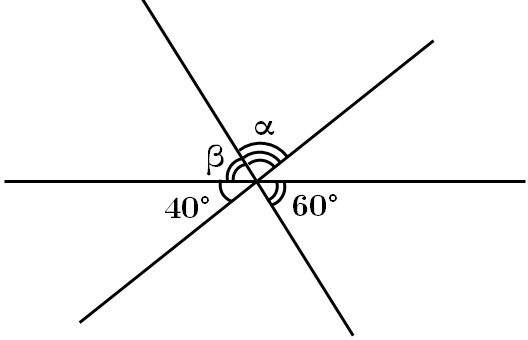
Відповідь: A.

ТЕМА: Числа і вирази. Дійсні числа (натуральні, цілі, раціональні та ірраціональні). Ознаки подільності чисел на \(5\), \(10.\)

Це завдання перевіряє вміння використовувати ознаки подільності.

Друзі купили кілька однакових тістечок вартістю \(10\) грн кожне, тому вартість покупки виражається цілим числом, кратним \(10.\) Крім того друзі купили \(5\) однакових булочок вартістю \(x\) грн кожна, вартість цієї покупки виражається числом, кратним \(5.\) Числа \(10\) і \(5\) кратні \(5\), тому загальна вартість всієї покупки виражається числом, кратним \(5.\)

Відповідь: Д.

ТЕМА: Функціональна залежність. Лінійні, квадратичні, степеневі, показникові, логарифмічні та тригонометричні функції, їхні основні властивості.

Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком.

Найбільше значення функції \(f(x)\) на проміжку \([-4; 6]\) досягається при \(x=-4.\)

Отже, \(f(-4)=5.\)

Відповідь: Г.

ТЕМА: Рівняння, нерівності та їхні системи. Логарифмічні рівняння. Функціональна залежність. Логарифмічна функція.

Це завдання перевіряє вміння розв'язувати логарифмічні рівняння.

\(\log_4(x-1)=3.\) За означенням логарифма можна записати \(x-1=4^3.\)

Звідси \(x-1=64\), \(x=65.\)

Відповідь: Г.

ТЕМА: Стереометрія. Многогранники, тіла й поверхні обертання.

Це завдання перевіряє вміння розв'язувати задачі на обчислення об'єму геометричних тіл.

Об'єм кулі знаходиться за формулою $$ V=\frac 43\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^3. $$ У завданні необхідо знайти об'єм півкулі, тому

$$ V=\left(\frac 43\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^3\right):2=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^3}{3}. $$

Відповідь: Б.

ТЕМА: Рівняння, нерівності та їхні системи. Ірраціональні рівняння.

Це завдання перевіряє знання методів розв'язування ірраціональних рівнянь, уміння розв'язувати ірраціональні рівняння.

Підносимо обидві частини рівняння до квадрата й знаходимо \(x.\)

Відповідь: Д.

ТЕМА: Функції. Функціональна залежність.

Це завдання перевіряє вміння знаходити область визначення функції.

$$ y=\frac{x+1}{x-2}. $$

Область визначення функції – усі дійсні числа, крім \(x=2\) (при даному значенні вираз \(\frac{x+1}{x-2}\) не має змісту).

\(x\in (-\infty; 2)\cup (2; +\infty).\)

Відповідь: A.

ТЕМА: Стереометрія. Прямі та площини у просторі. Взаємне розміщення прямих у просторі.

Це завдання перевіряє знання означення паралельних прямих.

У просторі задано паралельні прямі \(m\) i \(n.\) За означенням паралельних прямих вони лежать в одній площині та не перетинаються. Тому правильне твердження I, але неправильне ІІІ.

Через дві прямі в площині можна провести пряму, що перетинає обидві прямі \(m\) i \(n.\) Правильне твердження ІІ.

Отже, правильні твердження І та ІІ.

Відповідь: Д.

ТЕМА: Числа і вирази. Раціональні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів.

Розкриваємо дужки, зводимо подібні доданки.

Відповідь: B.

ТЕМА: Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості. Трикутники. Суміжні та вертикальні кути, паралельні та перпендикулярні прямі. Геометричні перетворення.

Це завдання перевіряє вміння застосовувати властивості паралельних прямих, ознаки подібності трикутників до розв'язування планіметричних задач.

Зробимо додаткову побудову і терез точку \(K\) проведемо пряму \(AB\), перпендикулярну до прямих \(a\) i \(b.\)

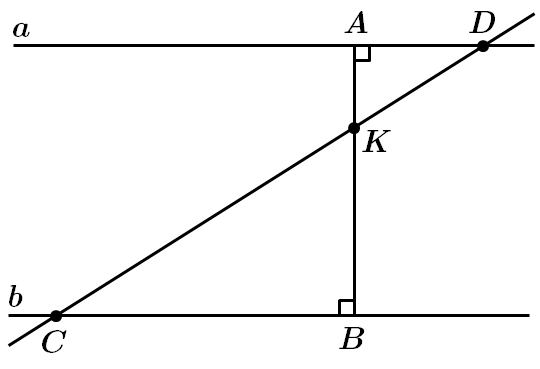
Розглянемо трикутники \(ADK\) та \(BCK.\) Вони подібні за двома кутами: \(\angle ADK=\angle BCK\) як внутрішні різносторонні при \(a\ ||\ b\) та січною \(CD.\)

\(\angle DAK=\angle KBC=90^\circ\) за побудовою.

У подібних трикутниках відповідні сторони пропорційні, отже $$ \frac{AK}{KB}=\frac{KD}{CK}. $$

Відстань від точки \(K\) до прямої \(a\) – це довжина перпенидкуляра \(KA=1\) см \begin{gather*} \frac{1}{KB}=\frac 25,\\[6pt] KB=2\mathord{,}5\ \textit{см}. \end{gather*}

Відстань між прямими \(a\) i \(b\) – це довжина спільного перпендикуляра

\(AB=AK+KB=1+2\mathord{,}5=3\mathord{,}5\) см.

Відповідь: B.

ТЕМА: Елементи комбінаторики, початки теорії імоверностей та елементи статистики. Вибіркові характеристики.

Це завдання перевіряє вміння обчислювати та аналізувати вибіркові характеристики рядів даних (середнє значення).

Знайдемо, який середній час витратив учень на дорогу до школи:

Середній час, який учень витратив на дорогу до дому:

На дорогу до дому учень витратив на \(5\) хв. більше.

Відповідь: Г.

ТЕМА: Числа і вирази. Тригонометричні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

Відповідь: Д.

ТЕМА: Рівняння, нерівності та їхні системи. Лінійні, квадратні рівняння та їхні системи.

Це завдання перевіряє вміння розв'язувати системи рівнянь першого та другого степеня, застосовувати загальні методи та прийоми в процесі розв'язування систем рівнянь.

З першого рівняння добуток \(xy=-12.\)

Отримаємо:

Якщо \((x_0; y_0)\) – розв'язок системи, то \(x_0=-6.\)

Відповідь: A.

ТЕМА: Стереометрія. Многогранники.

Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь, встановлювати за розгорткою поверхні вид геометричного тіла.

На рисунку зображена розгортка правильної призми, тому основа – правильний трикутник. \(P_\text{осн}=12\) см, тому сторона основи \(4\) см.

Бічне ребро позначимо через \(H.\) Периметр розгортки складається з

За формулою $$ S_\text{біч.пов.}=P_\text{осн}\cdot H $$ знаходимо $$ S_\text{біч.пов.}=12\cdot 6 =72\ \textit{см}^2. $$

Відповідь: Г.

ТЕМА: Числа і вирази. Логарифмічні вирази та їхні перетворення.

Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів, знання властивостей логарифма.

Використаємо властивості логарифму

Відповідь: Б.

ТЕМА: Функції. Функціональна залежність. Тригонометричні функції, їхні основні властивості.

Це завдання перевіряє вміння встановлювати властивості тригонометричних функцій, заданих графіком.

Задана функція з періодом \(T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\), тому \(f(x+T)=f(x).\)

Область значень функції \(E|y|=[-1; 1]\), тому точки з ординатами \(2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\), \(5\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\) не належать графіку.

Нулі функції \(-\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2}+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}k\), \(k\in Z\), тому \((3\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}; 0)\) та \((5\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}; 0)\) не належать графіку.

Значення \(y=-1\) функція набуває при \(x=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}+2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}k\), \(k\in Z.\)

Отже, відповідь \((5\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}; -1).\)

Відповідь: Д.

ТЕМА: Рівняння, нерівності та їхні системи. Показникові нерівності.

Це завдання перевіряє вміння розв'язувати нерівності, що містять показникові вирази, застосовувати загальні методи та прийоми (застосування властивостей функцій) у процесі розв'язування нерівності.

Винесемо спільний множник \(2^x\) за дужки:

Функція \(y=2^x\) зростаюча, тому \(x\ge 4\), \(x\in [4; +\infty).\)

Відповідь: Б.

ТЕМА: Функції. Похідна функції. Похідні елементарних функцій. Правила диференціювання.

Це завдання перевіряє вміння знаходити похідну елементарних функцій, знаходити суми двох функцій.

Знайдемо похідну за правилом знаходження похідної суми двох функцій та похідної степеневої функції: $$ f'(x)=4x^3+1. $$

Відповідь: A.

ТЕМА: Планіметрія. Коло та круг. Трикутники. Чотирикутники.

Це завдання перевіряє вміння застосовувати властивості різних видів трикутників та чотирикутників до розв'язування планіметричних задач та задач практичного змісту.

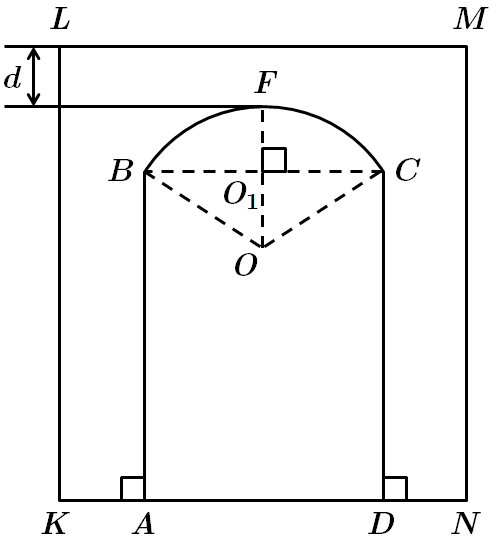
Нехай точка \(O\) – центр кола, дуга якого \(BFC.\)

Радіус кола – \(OB=OF=OC=1\) м.

\(BC\ ||\ AD\), \(AB\ ||\ CD.\) \((AB\ \perp\ BC\), \(CD\ \perp\ AD\) за властивістю паралельних прямих \(AB\ ||\ CD)\). Отже, \(ABCD\) – прямокутник, \(BC=AD=1\mathord{,}6\) м.

\(BC\cup OF=O_1\), \(BC\ \perp\ OF.\)

\(\Delta BOC\) – рівнобедрений, \(OO_1\) – висота та медіана, $$ BO_1=\frac 12BC=\frac 12AD=0\mathord{,}8\ \textit{м}. $$

\(\Delta BOO_1\ (\angle O_1=90^\circ)\) за теоремою Піфагора:

Відповідь: Г.

ТЕМА: Функції. Функціональна залежність. Лінійні, квадратичні, показникові функції, їхні основні властивості.

Це завдання перевіряє вміння знаходити область значень функції, встановлювати властивості числових функцій, заданих формулою.

1. Пряма \(y=4\mathord{,}5\) перетинає графік \(y=3^x\) у точці з абсцисою \(x_0=2.\)

\(3^2=4\mathord{,}5\cdot 2=9.\)

Отже, правильна відповідь – В.

2. Пряма \(y=-4\) не має спільних точок з графіком \(y=x^2-1.\)

\(y=x^2-1\) – графік – парабола з гілками вгору та вершиною \((0; -1)\), a \(y=-4\) – пряма, паралельна осі абсцис.

Отже, правильна відповідь – Б.

3. Пряма \(y=2x+4\) є паралельною прямій \(y=2x\), бо вони мають однаковий кутовий коефіцієнт \(k=2.\)

Отже, правильна відповідь – A.

4. Пряма \(y=x\) є бісектрисою І та ІІІ координатних чвертей, бо кутовий коефіцієнт \(k=1\), тому \(\mathrm{tg}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=1\), \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}=45^\circ\) – кут нахилу прямої до додатнього напряму осі \(Ox.\)

Отже, правильна відповідь – Д.

Відповідь: 1 – В, 2 – Б, 3 – А, 4 – Д.

ТЕМА: Числа і вирази. Дійсні числа.

Це завдання перевіряє знання властивостей степеня з цілим показником, уміння використовувати властивості модуля числа.

1. \(a^0=1\), отже, правильна відповідь – Б.

2. \(a^2=(-3)^2=9\gt 1\), отже, правильна відповідь – A.

3. \(\frac{|a|}{a}\) при \(a\lt 0\ |a|=-a\).

\(\frac{-a}{a}=-1\), отже, правильна відповідь – Г.

4. \(\sqrt[3]{a}=\sqrt[3]{-3}\lt \sqrt[3]{-1}\), отже, правильна відповідь – Д.

Відповідь: 1 – Б, 2 – А, 3 – Г, 4 – Д.

ТЕМА: Стереометрія. Многогранники, тіла й поверхні обертання.

Це завдання перевіряє знання властивостей тіл і поверхонь обертання та їхніх елементів, уміння розв'язувати задачі на обчислення об'ємів геометричних тіл.

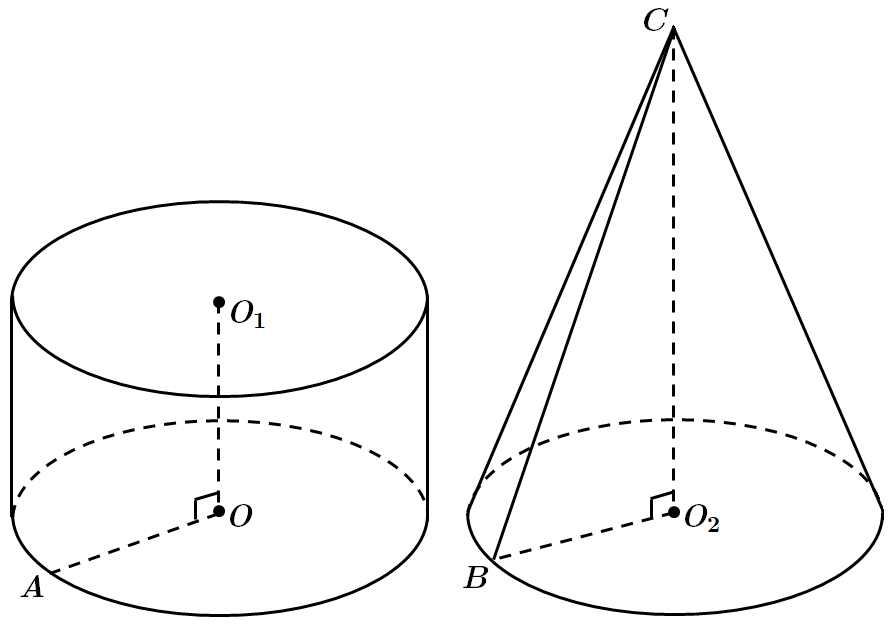
1. \(V_\text{ц}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2H=100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\) см\(^3\), отже \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\cdot 25\cdot H=100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\), \(H=4\) см. Висота циліндра \(4\) см

Отже, правильна відповідь – A.

2. \(V_\text{к}=\frac 13\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2\cdot h=100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\) см\(^3\), \(\frac 13\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\cdot 25\cdot h=100\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\), \(h=12\) см.

Отже, правильна відповідь – Г.

3. \(S_\text{осн.цил.}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2=25\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\) см\(^2\), \(R^2=25\), \(R=5\) см.

\(R_\text{ц}=R_\text{к}=5\) см.

Отже, правильна відповідь – Б.

4. \(\Delta BO_2C\ (\angle O_2=90^\circ)\) за теоремою Піфагора

Отже, правильна відповідь – Д.

Відповідь: 1 – A, 2 – Г, 3 – Б, 4 – Д.

ТЕМА: Планіметрія. Чотирикутники. Геометричні величини та їх вимірювання.

Це завдання перевіряє знання властивостей паралелограмів, уміння застосовувати властивості різних видів чотирикутників до розв'язування планіметричних задач, використовувати формули площ паралелограмів.

1.

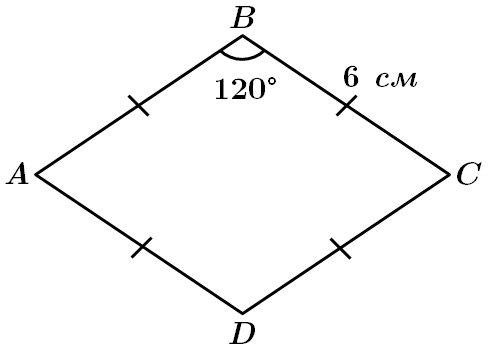
Отже, 1 – Д.

2.

\begin{gather*} r=\frac a2,\\[6pt] a=2r=2\cdot 2=4\ \textit{см},\\[7pt] S=a^2=4^2=16. \end{gather*} Отже, 2 – Б.

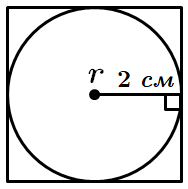
3.

\(\Delta ABE\ (\angle E=90^\circ)\) – єгипетський \(BE=3\) см.

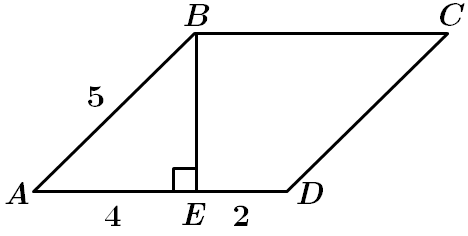
Отже, 3 – B.

4.

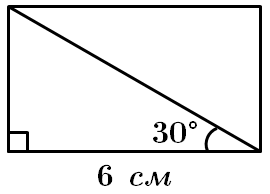
Отже, 4 – Г.

Відповідь: 1 – Д, 2 – Б, 3 – В, 4 – Г.

ТЕМА: Числа і вирази. Відношення та пропорції. Відсотки. Основні задачі на відсотки. Текстові задачі.

Це завдання перевіряє знання правил виконання відсоткових розрахунків, уміння розв'язувати задачі на відсоткові розрахунки.

1. Для визначення ширини автомагістралі використовують формулу

$$ h_\text{маг}=8b+r+2\Delta. $$

Якщо \(h_\text{маг}=40\mathord{,}2\) м, \(r=10\) м, \(\Delta =1\mathord{,}5\) м, то

2. Заплановано збільшити ширину кожної смуги руху транспорту на \(10\text{%}\) за рахунок лише зменшення ширини \(r\) розділювальної смуги. Кількість смуг руху – \(8\), тому потрібно зменшити ширину \(r\) на $$ 3\mathord{,}4\cdot 8\cdot 0\mathord{,}1=2\mathord{,}72\ \textit{м}. $$

Відповідь: 1. \(3\mathord{,}4.\)
                   2. \(2\mathord{,}72.\)

ТЕМА: Трикутники.

Це завдання перевіряє знання властивостей медіани, середньої лінії трикутника, уміння застосовувати властивості різних видів трикутників до розв'язання планіметричних задач.

\(BM\) – медіана, точка \(K\) – середина медіани.

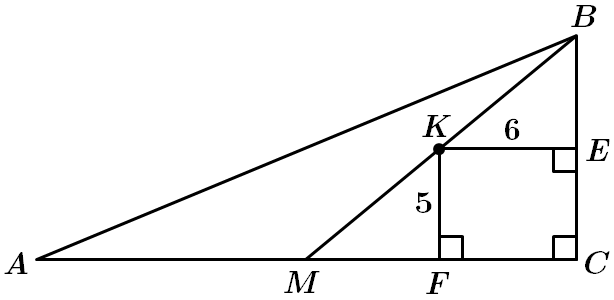
1. Відстань від точки \(K\) до \(AC\) – це \(KF=5\) см, \(KF\ \perp\ AC.\)

Відповідно, \(KE\ \perp\ BC,\) \(KE=6\) см.

\(KE\ \perp \ BC\), \(AC\ \perp\ BC\rightarrow\ KE\ ||\ AC.\)

За теоремою Фалеса, точка \(E\) – середина \(BC\), тому \(KE\) – середня лінія \(\Delta MBC.\)

За властивістю середньої лінії, \begin{gather*} KE=\frac 12MC,\\[6pt] MC=2KE=2\cdot 6=12\ \textit{см}. \end{gather*} Оскільки \(BM\) – медіана, то \(AC=2MC=24\) см.

Отже, довжина катета \(AC=24\) см.

2. Аналогічно, \(KF\) – середня лінія \(\Delta CMB\), тому \(BC=2KF=10\) см.

За теоремою Піфагора, у \(\Delta ABC\ (\angle C=90^\circ)\)

За властивістю прямокутного трикутника, радіус описаного кола дорівнює половині гіпотенузи. Отже, радіус кола $$ 26 : 2 = 13\ \textit{см}. $$

Відповідь: 1. \(24\) см.
                   2. \(13\) см.

ТЕМА: Функції. Числові послідовності. Геометрична прогресія.

Це завдання перевіряє знання формули суми n перших членів геометричної прогресії, уміння розв'язувати задачі на геометричну прогресію..

За умовою \begin{gather*} q=\frac 23,\\[6pt] S_4=65. \end{gather*}

Знаходимо перший член цієї прогресії за формулою

Відповідь: \(27.\)

ТЕМА: Алгебра. Рівняння, нерівності та їхні системи. Раціональні рівняння. Застосування рівнянь до розв'язування текстових задач.

Це завдання перевіряє вміння розв'язувати раціональні рівняння, застосовувати рівняння до розв'язування текстових задач.

Нехай щодня планували виробляти \(\frac{240}{n}\) стільців. Оскільки завдання виконали на \(2\) дні раніше запланованого терміну, то щодня виробляли \(\frac{240}{n-2}\) стільців. Денна норма збільшилась на \(4\) стільця, тому складемо рівняння

За теоремою Вієта знаходимо корені рівняння: \(n=-10\) або \(n=12.\)

Оскільки \(n\) – кількість днів, то визначається натуральним числом, то правильна відповідь: \(12\) днів.

Відповідь: \(12.\)

ТЕМА: Елементи комбінаторики, початки теорії імовірностей та елементи статистики. Комбінації. Комбінаторні правила суми та добутку.

Це завдання перевіряє знання означення комбінацій, комбінаторні правила суми й добутку, уміння розв'язувати нескладні задачі комбінаторного характеру.

Кількість усіх можливих комбінацій з \(n\) елементів по \(k\) елементів знаходимо за формулою $$ C_n^k=\frac{n!}{(n-k)!k!}. $$

Кількість способів вибрати \(3\) фотографії з \(8\) зі своїм зображенням знаходимо за формулою $$ C_8^3=\frac{8!}{(8-3)!3!}=\frac{8!}{5!3!}. $$

Кількість способів вибрати \(2\) фотографії з \(6\) для сайту $$ C_6^2=\frac{6!}{(6-2)!2!}=\frac{6!}{4!2!}. $$

Кількість способів вибрати означені в умові фотографії знаходимо за комбінаторним правилом добутку:

Відповідь: \(840.\)

ТЕМА: Планіметрія. Координати та вектори на площині.

Це завдання перевіряє знання поняття колінеарних векторів, координат вектора, уміння застосовувати вектори до розв'язування планіметричних задач.

За умовою задачі, \(\overrightarrow{AB}\ ||\ \overrightarrow{a}.\)

Нехай абсциса точки \(B\) буде \(x\), тоді точка \(B(x; 3).\) Ордината дорівнює \(3\) тому, що точка \(B\) лежить на прямій \(y=3.\)

У колінеарних векторів відповідні координати пропорційні, тому

Відповідь: \(-5\mathord{,}2.\)

ТЕМА: Алгебра. Функції. Степенева та лінійна функції, їхні основні властивості. Визначений інтеграл.

Це завдання перевіряє знання основних властивостей та графіків функцій, уміння будувати графіки елементарних функцій, застосовувати формулу Ньютона-Лейбниця для обчислення визначеного інтеграла, обчислювати площу плоских фігур за допомогою інтеграла.

1. Побудуємо графік функції \(f(x)=x^3.\)

2. Побудуємо графік функції \(g(x)=4|x|.\)
при \(x\ge 0\) будуємо \(g(x)=4x.\)

при \(x\lt 0\) будуємо \(g(x)=-4x.\)

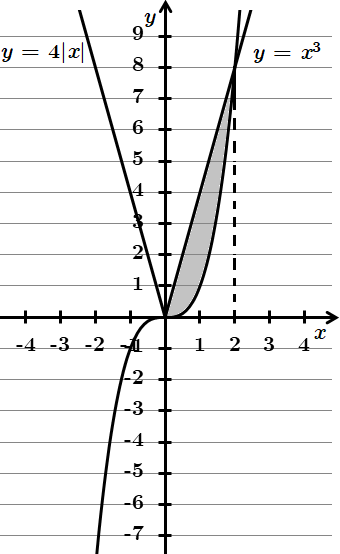
3. Абсциси точок перетину графіків \(f\) i \(g\) знаходимо графічно \(x=0\) та \(x=2\), або як розв'язки рівняння \(x^3=4|x|.\) При \(x\ge 0\)

Проміжку \(x\in [0; +\infty)\) належать корені \(x=0\) та \(x=2.\)

При \(x\lt 0\)

Отже, абсциси точок перетину графіків \(f\) i \(g\) \(x_1=0\), \(x_2=2.\)

4. Площу фігури, обмеженої графіками функцій f i g знаходимо за допомогою визначеного інтеграла:

Відповідь: 3. \(x_1=0\), \(x_2=2.\)
                   4. \(4\) кв. од.

ТЕМА: Стереометрія. Многогранники. Піраміда. Прямі та площини у просторі.

Це завдання перевіряє знання ознак паралельності прямої та площини, властивостей паралельних площин, кута між прямою та площиною, уміння будувати перерізи многогранників, властивостей правильної піраміди.

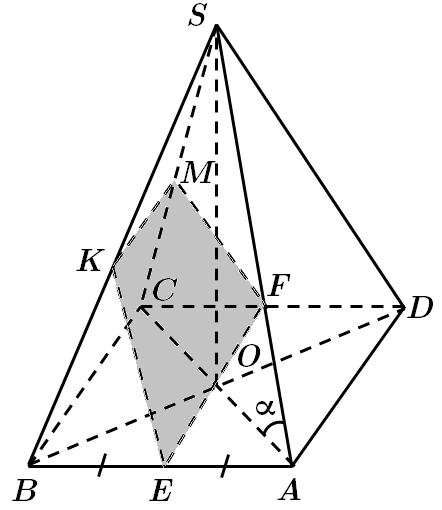
1. \(SABCD\) – правильна піраміда, тому в основі лежить квадрат \(ABCD\) і основа висоти є центром квадрата, тобто точкою перетину діагоналей.

Бічне ребро \(SA\) утворює з площиною основи кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}.\) \(SO\ \perp\ (ABC)\), \(SA\) – похила, \(OA\) – проекція \(SA\) на площину основи, тому

\(\angle (SA, (ABC))=\angle SAO=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}.\)

Побудуємо переріз піраміди площиною \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\ || (SAD).\) За властивістю паралельних площин паралельні площини \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) та \(SAD\) перетинаються третьою, площиною \(ABC\) по паралельних прямих, тому будуємо \(EF\ ||\ AD\) через точку \(O.\)

\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\ ||\ (ASD)\) та перетинаються площиною \((ASB)\) по паралельним прямим, тому будуємо \(KE\ || SA\) (слід січної площини на \((ASB).\)

\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\ ||\ (ASD)\) перетинаються \((SCD)\) по \(MF\ || SD.\) З'єднаємо точку \(K\) та точку \(M\), що належать \((BSC).\) \(KMFE\) – шуканий переріз.

2. Точка \(E\) – середина \(AB\), \(KE\ || SA\) за побудовою, тому \(KE\) – середня лінія \(\Delta SBA\rightarrow BK=KS.\)

Точка \(F\) середина \(DC\), \(MF\ || SD\) за побудовою, тому \(MF\) – середня лінія \(\Delta SDC\rightarrow CM=MS.\)

У \(\Delta BCS\ KM\) середня лінія, тому \(KM\ ||\ BC\), \(EF\ ||\ BC\) (за побудовою), \(KM\ ||\ BC\) – тому \(KM\ ||\ EF\) за ознакою паралельних прямих. Отже, \(KMFE\) – трапеція.

\(SABCD\) правильна піраміда, тому \(\Delta SBA=\Delta SCD\), \(KE=MT\) як відповідні середні лінії. Отже, \(KMFE\) – рівнобічна трапеція.

3. \(AB=c\), то діагональ квадрата \(ABCD\ AC=c\sqrt{2}\), \(AO=\frac 12AC=\frac{c\sqrt{2}}{2}.\)

У \(\Delta SOA\ (\angle O=90^\circ).\)

Знаходимо периметр трапеції:

Відповідь: 3. \(\frac{3\cos \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}+\sqrt{2}}{2\cos \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}}\cdot c.\)

ТЕМА: Алгебра. Рівняння, нерівності та їхні системи. Лінійні, квадратні, раціональні, логарифмічні рівняння, нерівності.

Це завдання перевіряє вміння розв'язувати логарифмічні нерівності, розв'язувати рівняння, нерівності з параметрами.

Знаходимо ОДЗ: $$ \left\{\begin{array}{l} x\gt 0,\\ x^2+(a-4)x+4-2a\ne 0, \end{array}\right. $$ крім того, для параметра a є також обмеження: a > 0 та a ≠ 1 (a є основою логарифма).

Розв'яжемо квадратне рівняння

За умови \(a\gt 0\), \(D\gt 0\) при будь-якому значенні \(a.\)

Отримали ОДЗ:

Знайдемо нулі функції, яка знаходиться в лівій частині нерівності.

Розглянемо для кожного проміжку з області допустимих значень розв'язок нерівності.

I.

При \(a\lt 0\) нерівність не має змісту, тому розв'язків немає.

II. \begin{gather*} 2-a=2,\\[7pt] a=0 \end{gather*} не має розв'язків.

III.

\(x\in [1; 2-a)\cup (2; +\infty).\)

IV.

V.

\(x\in (0; 2-a)\cup [1; 2).\)

VI.

\(x\in [1; 2).\)

VII.

\(x\in [1; 2).\)

Відповідь: при \(a\in (0; 1)\ x\in [1; 2-a)\cup (2; +\infty)\);
                   при \(a\in (1; 2)\ x\in (0; 2-a)\cup [1; 2)\);
                   при \(a\in [2; +\infty)\ x\in [1; 2).\)