ЗНО онлайн 2018 року з математики – додаткова сесія
Тестові завдання додаткової сесії ЗНО 2018 року з математики
ТЕМА: Алгебра. Числа і вирази. Дійсні числа та дії з ними.
Це завдання перевіряє вміння виконувати дії з дійсними числами.
Якщо
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Найпростіші геометричні фігури на площині та їхні властивості.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості найпростіших геометричних фігур до розв'язування задач практичного змісту.
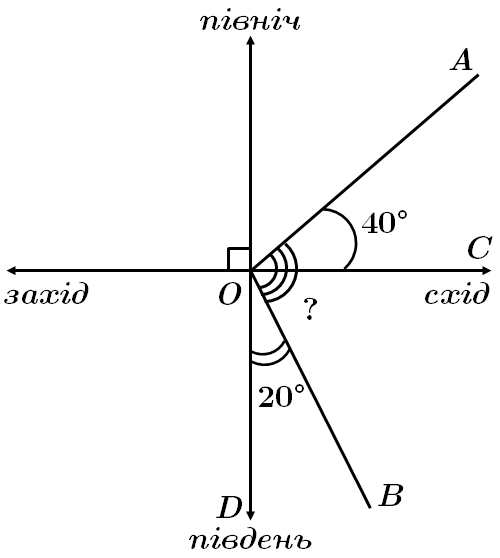
Кут
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра. Числа і вирази. Дійсні числа.
Це завдання перевіряє вміння використовувати ознаки подільності до розв'язування задач.
Якщо цукерки можна поділити між двома або трьома дітьми, то їх кількість визначається числом, кратним
Якщо цукерки не можна поділити порівну між чотирма дітьми, то їх кількість не є кратною
З наведених чисел кратні
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра. Функції. Функціональна залежність.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
Точка
На графіку є тільки одна точка з ординатою
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Рівняння, нерівності та їхні системи. Лінійні рівняння.
Це завдання перевіряє вміння розв'язувати лінійні рівняння.
Значення
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Стереометрія. Поверхні обертання.
Це завдання перевіряє знання властивостей кулі та сфери та вміння розв'язувати стереометричні задачі.
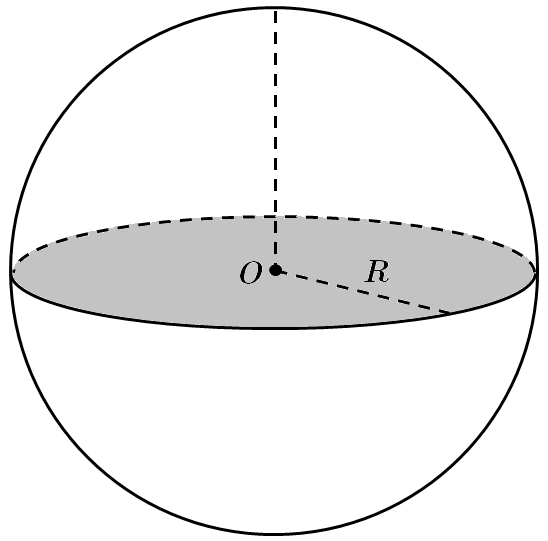
Площа великого круга дорівнює
Площа сфери визначається за формулою:
Отримаємо:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Рівняння, нерівності та їхні системи. Логарифмічні рівняння.
Це завдання перевіряє вміння розв'язувати рівняння, що містять логарифмічні вирази, знання властивостей логарифма.
Застосуємо означення логарифма
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання взаємного розміщення прямої та площини у просторі.
За наслідками з аксіом стереометрії: через пряму і точку, яка їй належить, проходить площина, і до того ж тільки одна.
Через точку
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Функції. Степенева функція.
Це завдання перевіряє знання графіка степеневої функції, вміння будувати графіки елементарних функцій, використовувати перетворення графіків функцій.
Графік функції
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Числа і вирази. Тригонометричні вирази та їхні перетворення.
Це завдання перевіряє знання формул зведення, означення котангенса числового аргументу.
За формулою зведення
Отримаємо,
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Елементи статистики. Вибіркові характеристики.
Це завдання перевіряє вміння обчислювати та аналізувати вибіркові характеристики рядів даних (середнє значення).
Для того, щоб знайти скільки часу на день у середньому учень користується Інтернетом, необхідно знайти середнє арифметичне значень
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра. Числа і вирази. Раціональні вирази та їхні перетворення.
Це завдання перевіряє знання формул скороченого множення, уміння виконувати тотожні перетворення раціональних виразів та знаходити їхнє числове значення при заданих значеннях змінних.
Підставимо у перше рівняння замість суми
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Геометричні перетворення.
Це завдання перевіряє вміння застосовувати означення паралелограма, ознак подібності трикутників до розв'язування планіметричних задач.
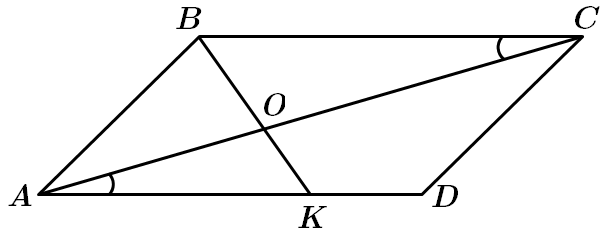
Розглянемо
Отже,
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра. Числа і вирази. Степеневі вирази та їхні перетворення.
Це завдання перевіряє вміння виконувати тотожні перетворення степеневих виразів та знаходити їхнє числове значення при заданих значеннях змінних.
Якщо
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра. Функції. Функціональа залежність. Лінійні, квадратичні, степеневі, показникові, логарифмічні та тригонометричні функції, їхні основні властивості.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком, досліджувати на парність (непарність).
Для наведених функцій область визначення не є симетричною у функції
Серед інших умова
Така властивість є у функції
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Стереометрія. Многограники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення об'ємів геометричних тіл, знання формул для обчислення площ трикутників.
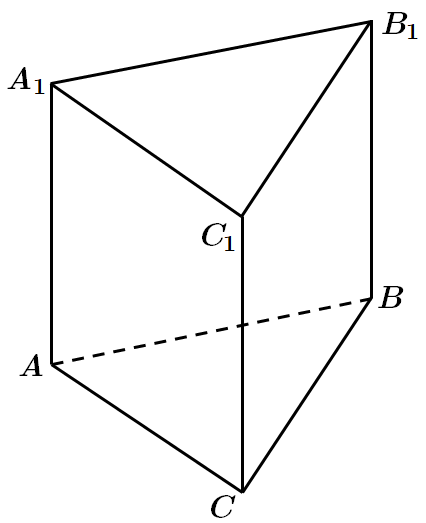
Дана трикутна призма
Усі бічні грані – квадрати, тому основа призми – рівносторонній трикутник. Площу рівностороннього трикутника можна знайти за формулою
За умовою
Об'єм призми
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа, порівняння чисел та дії над ними.
Це завдання перевіряє вміння розрізняти види чисел та числових проміжків, виконувати дії з дійсними числами.
Це число належить проміжку
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Фунції. Похідна функції. Похідні елементарних функцій. Правила диференціювання.
Це завдання перевіряє вміння знаходити похідні елементарних функцій; похідну суми; знання таблиці похідних елементарних функцій.
Використали формулу
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Коло та круг.
Це завдання перевіряє знання властивості дотичної до кола, вміння застосовувати набуті знання до розв'язування планіметричних задач та задач практичного змісту.
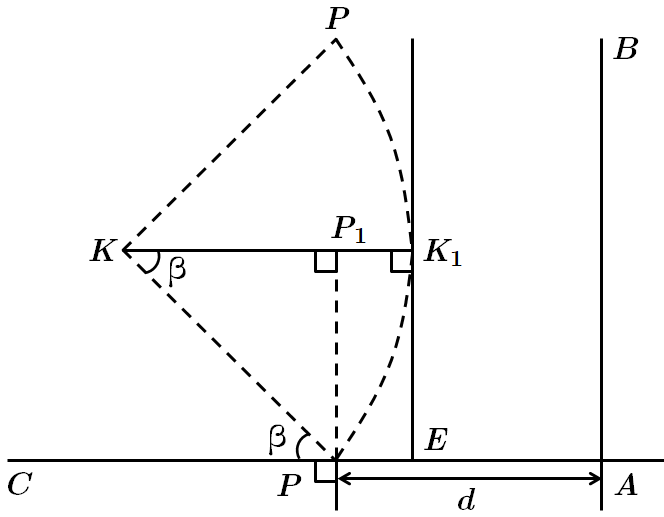
Проведемо
За властивістю дотичної до кола
У
Серед наведених відстаней найменша
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра, початки аналізу. Рівняння, нерівності та їхні системи. Лінійні нерівності та їхні системи.
Це завдання перевіряє вміння розв'язувати нерівності першого степеня, нерівності, що містять змінну під знаком модуля.
Цю нерівність можна розв'язати двома способами:
І спосіб.
Вираз
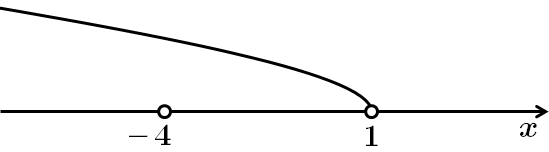
ІІ спосіб.
Розв'язуємо методом інтервалів:
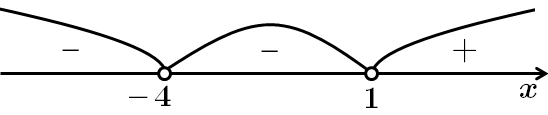
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.
Це завдання перевіряє вміння знаходити область визначення, область значень функції, встановлювати властивості числових функцій, заданих графіком.
1. Функція спадає на проміжку
2. Графік функції є фрагментом графіка функції
3. Множиною значень функції є проміжок
4. Функція зростає на проміжку
Відповідь: 1 – Г, 2 – Б, 3 – В, 4 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа. Логарифмічні вирази.
Це завдання перевіряє знання означення та властивості кореня n-го степеня, степеня з натуральним показником, основної логарифмічної тотожності.
1.
2.
3.
4.
Відповідь: 1 – А, 2 – Д, 3 – Г, 4 – Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання співвідношення між сторонами і кутами прямокутного трикутника, теореми косинусів; уміння застосовувати властивості різних видів чотирикутників до розв'язування планіметричних задач.
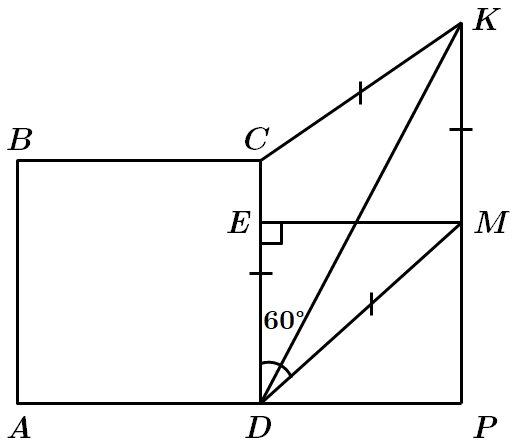
1. Периметр ромба
Отже, 1 – В.
2. Більша діагональ ромба лежить напроти більшого кута ромба.
У
Отже, 2 – Г.
3.Відстань від точки
У
Отже, 3 – Б.
4.
Отже, 4 – Д.
Відповідь: 1 – В, 2 – Г, 3 – Б, 4 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл, знання формул для обчислення площ поверхонь конуса та циліндра.
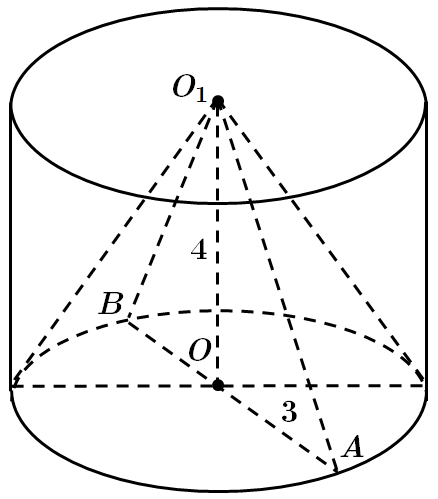
Нехай
1.
Отже, 1 – Г.
2.
Отже, 2 – Д.
3. Площа основи конуса дорівнює площі основи циліндра.
Отже,
Отже, 3 – A.
4. Площа бічної поверхні конуса
У
Отже, 4 – B.
Відповідь: 1 – Г, 2 – Д, 3 – А, 4 – В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Відсотки. Основні задачі на відсоки. Текстові задачі. Квадратні рівняння.
Це завдання перевіряє вміння застосовувати рівняння до розв'язування текстових задач, розв'язувати задачі на відсотки.
1. Нехай у кожному ряду висадили
Отже, в кожному ряду
2. Усього кущів у першому рядку
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг. Чотирикутники. Геометричні величини та їх вимірювання.
Це завдання перевіряє знання дотичної до кола та її властивості, формули довжини кола; уміння застосовувати ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач.
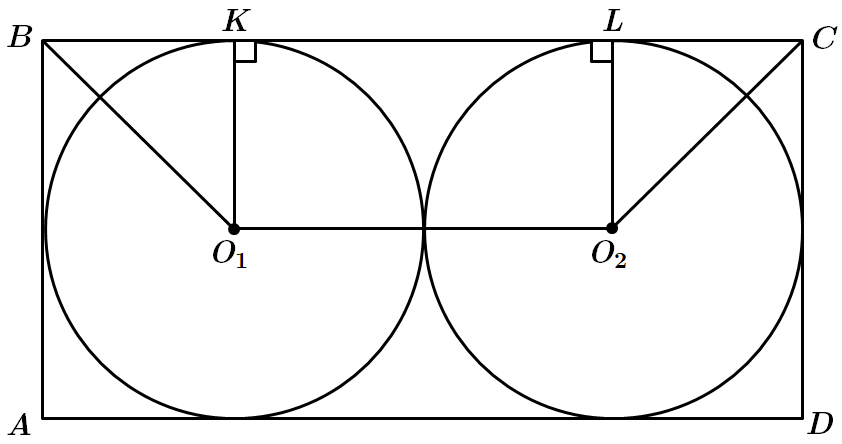
1.Довжина кола знаходиться за формулою
Отже,
2. У прямокутник
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Це завдання перевіряє знання формули суми
Нехай
Різниця арифметичної прогресії
За формулою суми
За умовою,
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Відношення та пропорції. Текстові задачі.
Це завдання перевіряє знання відношень, пропорцій, основної властивості пропорції; уміння розв'язувати текстові задачі арифметичним способом.
Лідія редагує
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики. Перестановки, комбінації, розміщення. Комбінаторні правила суми та добутку.
Це завдання перевіряє знання означення комбінації комбінаторного правила добутку; уміння розв'язувати нескладні задачі комбінаторного характеру.
Клієнт вибирає
З
Отже, якщо необхідно вибрати і м'ясну, і овочеву добавку, то за комбінаторним правилом добутку знаходимо:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Коло. Круг. Координати та вектори на площині.
Це завдання перевіряє знання кола, круга та їхніх елементів; теореми синусів, рівняння кола.
Запишемо рівняння кола в канонічному вигляді
Центр кола
За наслідком з теореми синусів
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність. Лінійні, квадратичні, степеневі, показникові, логарифмічні та тригонометричні функції, їхні властивості. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур.
Це завдання перевіряє вміння будувати графіки елементарних функцій, встановлювати властивості числових функцій, заданих формулою або графіком, обчислювати площу плоских фігур за допопомогою інтеграла.
1.
2.
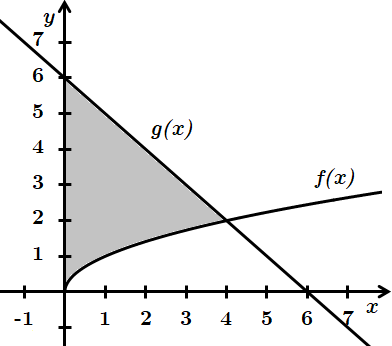
3. Знайдемо точку перетину графіків
Абсциса точки перетину
4. Обчислимо площу фігури, обмеженої графіками функцій
Отже, правильна відповідь –
Відповідь: 3.
4.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє знання многогранників та їхніх елементів, перерізів многогранників; уміння застосовувати властивості многогранників до розв'язування стереометричних задач.
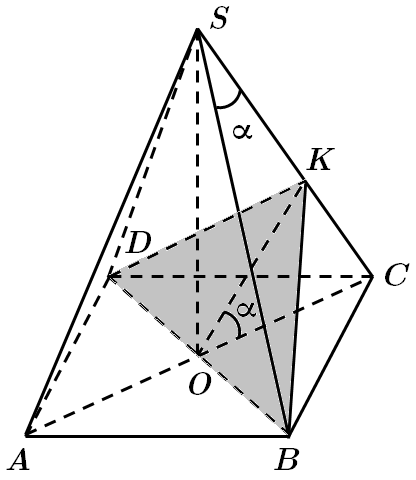
1. Проведемо
Отже,
Так як
2.
3.
У
У
Відповідно до умови завдання необхідно побудувати переріз піраміди
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Показникові, квадратичні, раціональні нерівності.
Це завдання перевіряє вміння розв'язувати нерівності, що містять показникові вирази, квадратні нерівності, нерівності з параметрами.
При
нерівність
При
має тільки розв'язок
При
При
При
Відповідь: при
при
при
при
Знайшли помилку? Пишіть на




