ЗНО онлайн 2019 року з математики – пробний тест
Тестові завдання пробного тесту ЗНО 2019 року з математики
ТЕМА: Алгебра та початки аналізу. Числа та вирази. Дійсні числа.
Це завдання перевіряє вміння виконувати дії з дійсними числами.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом.
Нехай
Тоді
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Функції. Лінійна функція.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком, використовувати перетворення графіків функцій.
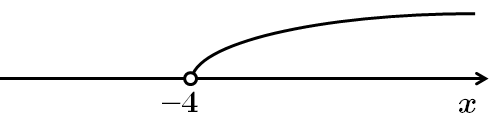
Графік функції
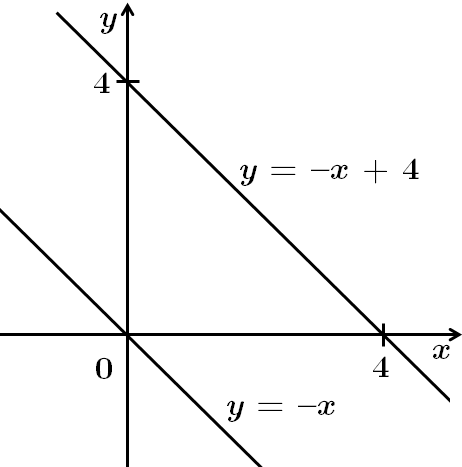
Отже, правильна відповідь Д.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні рівняння.
Це завдання перевіряє вміння розв'язувати рівняння, що містять змінну під знаком модуля.
Отже, за наведених чисел коренем рівняння є
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики. Вибіркові характеристики.
Це завдання перевіряє вміння аналізувати графічну, табличну, текстову та інші форми подання статистичної інформації.
На круговій діаграмі показано розподіл кількості столів, які продано. Загальна кількість проданих столів становила
Журнальні столи становлять
Журнальних столів менше на
Отже, їх менше на
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла й поверхні обертання.
Це завдання перевіряє вміння застосовувати властивості конуса до розв'язування стереометричних задач.
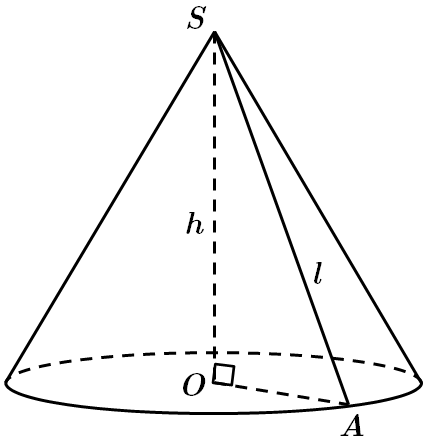
У
Отже, правильна відповідь А.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Показникові рівняння.
Це завдання перевіряє вміння розв'язувати показникові рівняння.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг.
Це завдання перевіряє знання про коло та його елементи, центральні кути, дуги.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа і вирази. Дійсні числа.
Це завдання перевіряє знання означення степеня з натуральним показником, їхні властивості.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє знання про піраміду, формулу об'єму піраміди.
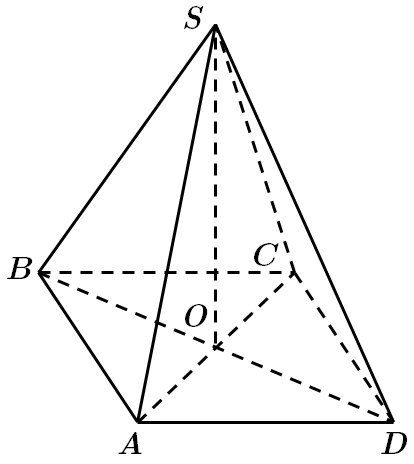
Піраміда
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Функції. Похідна функції. Функціональна залежність.
Це завдання перевіряє вміння використовувати перетворення графіків функцій, знання екстремумів функції.
На рисунку зображено графік функції
Графік функції
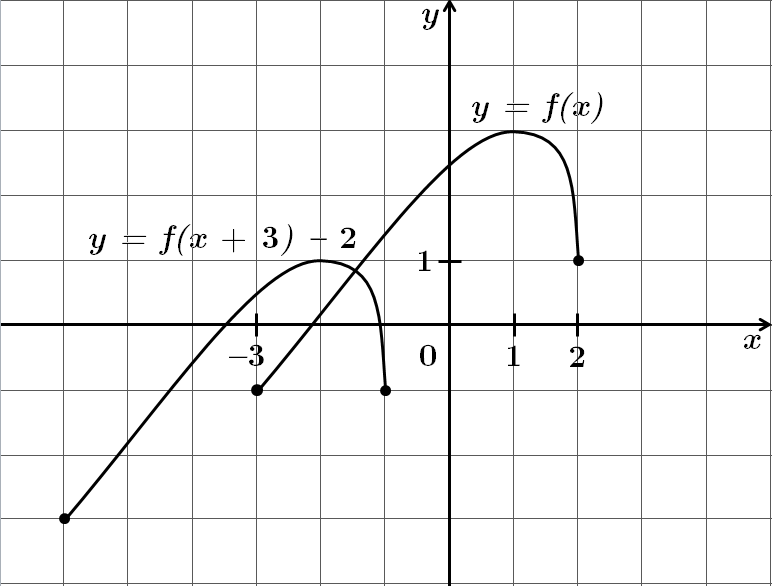
Отже, правильна відповідь – A.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє вміння класифікувати трикутники за сторонами та кутами, знання теореми про суму кутів трикутника, кола, описаного навколо трикутника.
Якщо
За нерівністю трикутника
Центр кола, описаного навколо тупокутного трикутника
Отже, правильна відповідь – Д.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Функції. Квадратична функція.
Це завдання перевіряє вміння знаходити нулі функції.
Нулі функції знаходимо з рівняння
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа і вирази. Тригонометричні вирази та їхні перетворення.
Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів та знаходити їхнє числове значення при заданих значеннях змінних, знання формул зведення.
Отже, значення виразу належить проміжку
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Раціональні рівняння.
Це завдання перевіряє вміння розв'язувати раціональні рівняння.
зводимо до спільного знаменника:
Корінь рівняння
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа і вирази. Дійсні числа.
Це завдання перевіряє знання означення кореня
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Лінійні нерівності.
Це завдання перевіряє вміння розв'язувати лінійні нерівності, використовувати формули скороченого множення для тотожного перетворення виразів.
Використаємо формулу
Отже,
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння застосовувати означення та властивості прямокутного паралелепіпеда до розв'язування стереометричних задач і задач практичного змісту.
Площа плівки, якою обгорнута коробка – це площа поверхні прямокутного паралелепіпеда.
Основа паралелепіпеда – прямокутник зі сторонами
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Функції. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур.
Це завдання перевіряє знання означення первісної функції, вміння обчислювати площу плоских фігур за допомогою інтеграла.
На рисунку зображено графік непарної функції
Функція інтегрована на симетричному проміжку
Так як площі фігур розташованих вище та нижче осі
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Функції. Степенева, показникова, тригонометрична функції.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком.
1.
Отже, 1 – B.
2.
Отже, 2 – Б.
3.
Отже, 3 – A.
4.
Отже, 4 – Д.
Відповідь: 1 – В, 2 – Б, 3 – А, 4 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа і вирази. Раціональні, логарифмічні, степеневі вирази та їхні перетворення.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних, степеневих, логарифмічних виразів.
1.
Отже, 1 – Д.
2.
Отже, 2 – Б.
3.
Отже, 3 – В.
4.
Отже, 4 – Г.
Відповідь: 1 – Д, 2 – Б, 3 – В, 4 – Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє вміння застосовувати означення, ознаки та властивості різних видів чотирикутників до розв'язування планіметричних задач.
1.
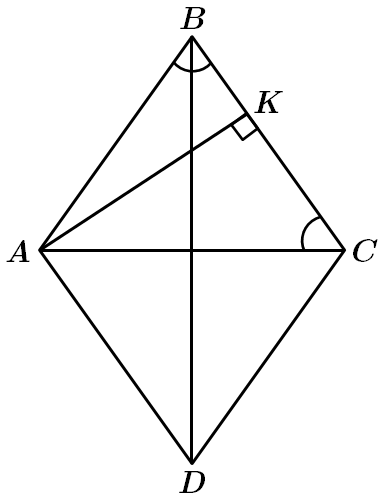
Отже, 1 – Г.
2.
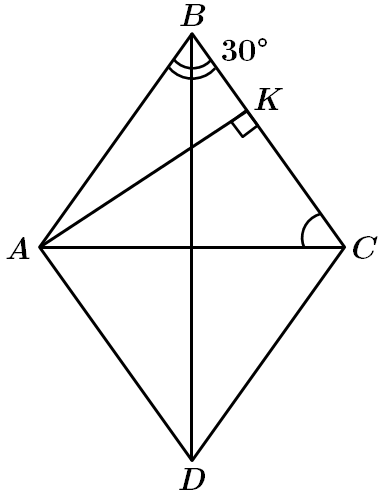
Отже, 2 – В.
3.
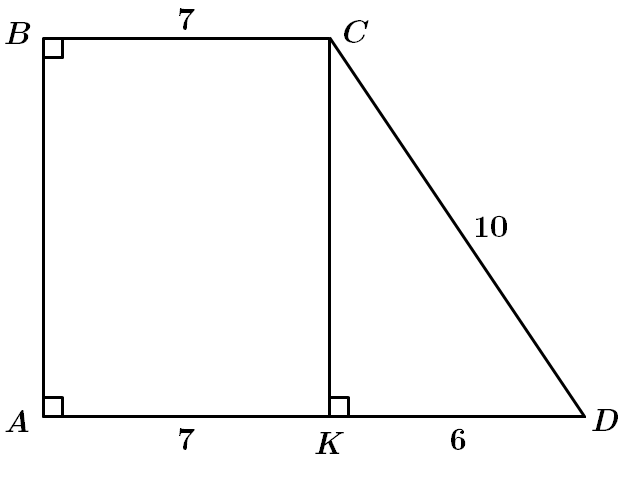
Додаткова побудова
Отже, 3 – Б.
4.
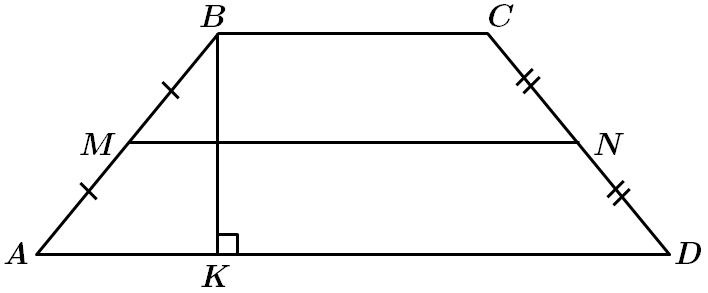
Отже, 4 – Д.
Відповідь: 1 – Г, 2 – В, 3 – Б, 4 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.
Це завдання перевіряє вміння застосовувати ознаки та властивості паралельних прямих і площин, знання перерізів многогранників.
1.
2.
3.
4.
Відповідь: 1 – А, 2 – В, 3 – Д, 4 – Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа і вирази. Відсотки. Основні задачі на відсотки. Текстові задачі.
Це завдання перевіряє вміння розв'язувати задачі на відсоткові розрахунки, розв'язувати задачі арифметичним способом.
За
1. Якщо покупець купить
2. Найбільш економний варіант покупки –
Покупець заплатить на
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Коло та круг.
Це завдання перевіряє знання про центральні та вписані кути, прямокутник, формули для обчислення площі трикутників.
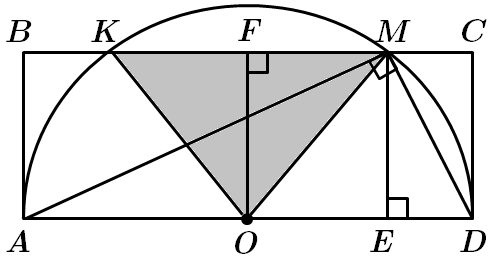
1.
За властивістю висоти до гіпотенузи:
Нехай
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Функції. Числові послідовності.
Це завдання перевіряє знання формули n-го члена геометричної прогресії, означення геометричної прогресії.
Використаємо формулу
За умовою всі члени прогресії додатні числа, тому
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом.
За течією річки човен проходить
Проти течії річки човен проходить
Власна швидкість човна:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики. Перестановки, комбінації, розміщення.
Це завдання перевіряє вміння розв'язувати задачі комбінаторного характеру, знання комбінаторного правила добутку.
Для оформлення салону замовили
Оскільки всі квіти різного кольору, то кількість способів формування замовлення знаходимо за формулою комбінацій та комбінаторним правилом добутку:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Планіметрія. Координати і вектори на площині.
Це завдання перевіряє вміння виконувати дії з векторами, знаходити скалярний добуток, координати вектора.
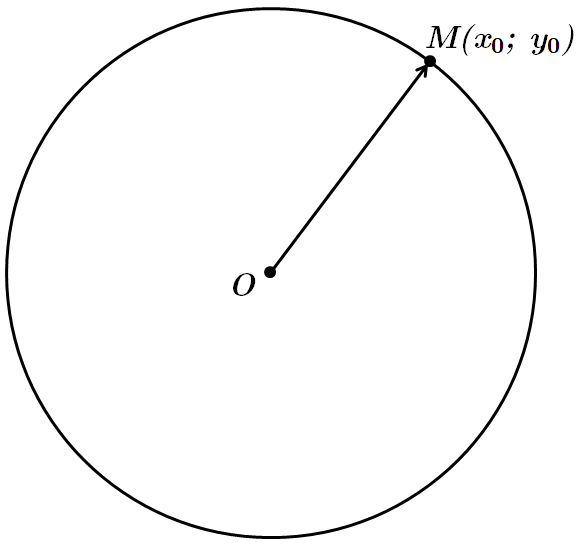
Коло із центром в точці
За умовою
Складемо систему рівнянь:
За умовою
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Функції. Степеневі функції. Похідна функції, її геометричний зміст.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком, знаходити похідні елементарних функцій, знаходити числове значення похідної функції в точці, складати рівняння дотичної до графіка функції в точці.
1. Графік функції
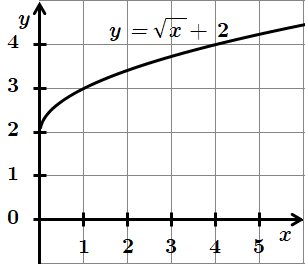
2. Координати точки
Одержуємо
3.
4. Рівняння дотичної, проведеної до графіка функції
Відповідь: 3.
4.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Тіла та поверхні обертання.
Це завдання перевіряє вміння знаходити зазначені відстані та величини кутів у просторі, перерізи тіл обертання площиною, затосовувати властивості тіл та поверхонь обертання до розв'язування стереометричних задач.
1. Перерізом кулі площиною
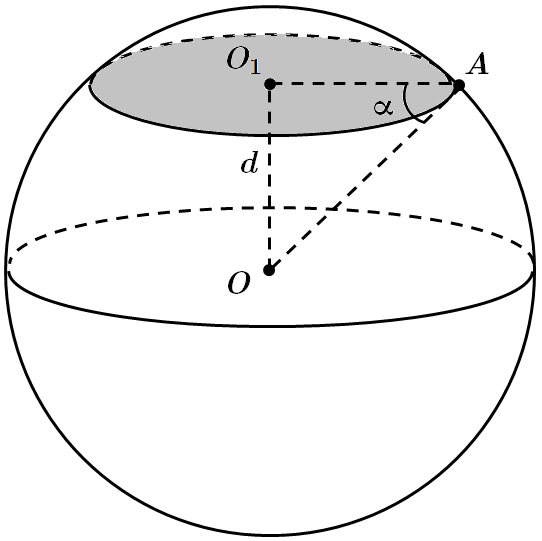
2.
3.
Відповідь: 3.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра та початки аналізу. Рівняння, нерівності та їхні системи. Логарифмічні, тригонометричні нерівності та їхні системи.
Це завдання перевіряє вміння розв'язувати системи нерівностей, що містять логарифмічні та тригонометричні вирази, розв'язувати нерівності та системи з параметрами.
1.
2.
Розглянемо випадки:
I.
II.
III.
Розв'язуємо нерівність
Перша система розв'язків не має, друга система еквівалентна нерівності
3. Множиною розв'язків заданої системи для кожного значення
Відповідь:
Знайшли помилку? Пишіть на




