ЗНО онлайн 2019 року з математики – основна сесія
Тестові завдання основної сесії ЗНО 2019 року з математики
Алгебра і початки аналізу. Числа і вирази.
Це завдання перевіряє вмінняя виконувати тотожні перетворення раціональних виразів, знання означення степеня з цілим показником та її властивостей.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг.
Це завдання перевіряє знання кола та його елементів.
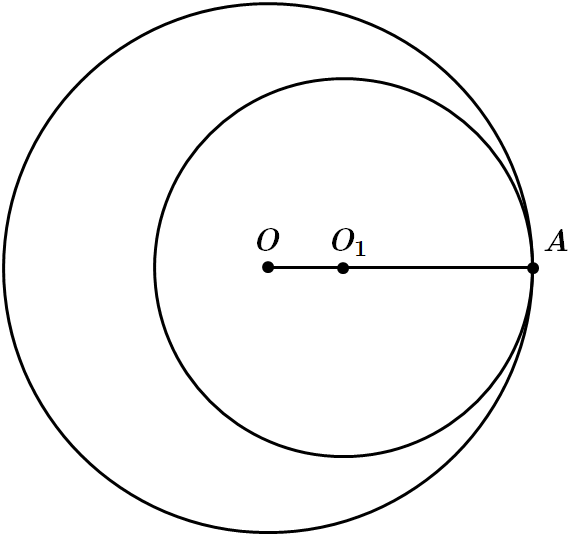
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Це завдання перевіряє вміння розв'язувати рівняння з однією змінною, використовувати методи розв'язування раціональних рівнянь.
Якщо рівняння має вигляд добутку множників, що дорівнює нулю, то принаймні один з множників повинен дорівнювати нулю.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом, виконувати тотожні перетворення раціональних виразів.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння встановлювати за разгорткою поверхні вид геометричного тіла.
Бічні грані – прямокутники, тому на рисунку зображено призму.
Основа призми – трикутник.
Отже, на рисунку розгортка трикутної призми.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Це завдання перевіряє знання формули об'єму конуса.
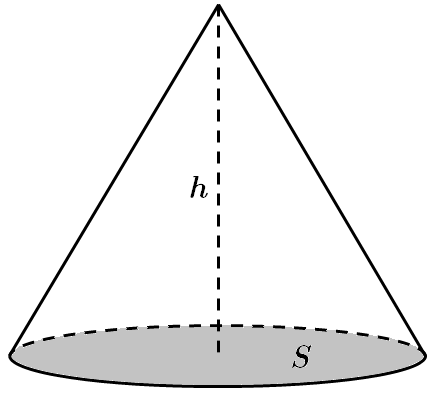
Об'єм конуса дорівнює третині добутку площі основи на висоту:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.
Це завдання перевіряє вміння встановлювати властивості числових функцій заданих графіком.
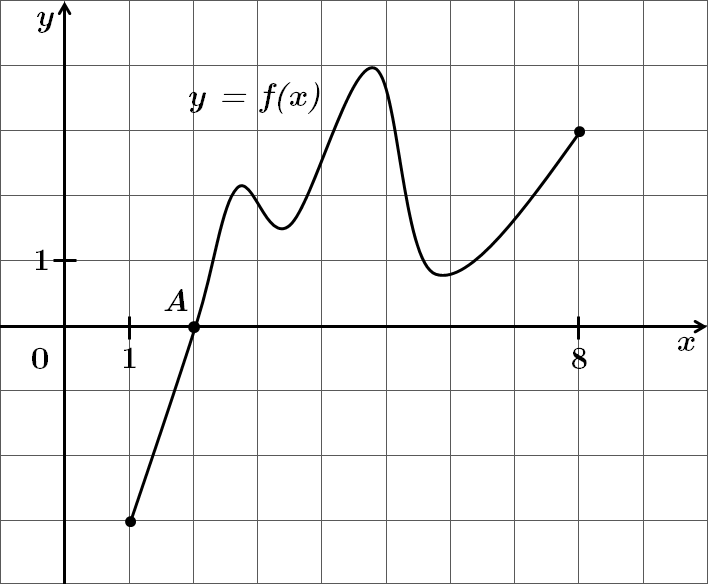
Нулі функції – точки перетину графіка функції з віссю
На рисунку бачимо лише одну точку перетину графіка функції з віссю
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв'язувати нерівності, що містять змінну під знаком модуля.
Використовуючи геометричну інтерпритацію модуля отримаємо розв'зок нерівності

Отже, з наведених чисел
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Степенева функція.
Це завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком.
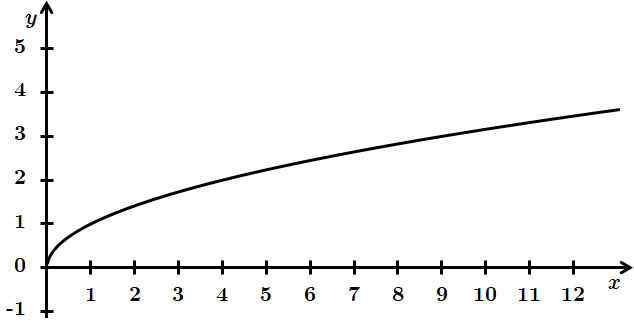
Ця функція зростає на всій області визначення, не є парною, періодичною, не має точок екстремуму.
Функція набуває лише невід'ємних значень.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази.
Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи статистики.
Це завдання перевіряє вміння аналізувати графічну, табличну, текстову та інші форми подання статистичної інформації.
Кількість працівників знаходимо з діаграми:
Отже, відповідь – B.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази та їхні перетворення.
Це завдання перевіряє знання формул скороченого множення, розкладу многочлена на множники, уміння виконувати тотожні перетворення раціональних виразів.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє знання властивостей паралелограма.
I. Сума кутів, прилеглих до будь-якої сторони паралелограма, дорівнює
II. Протилежні сторони паралелограма рівні. Отже, твердження ІІ правильне.
III.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Функції. Дійсні числа. Логарифмічні вирази. Логарифмічна функція.
Це завдання перевіряє вміння порівнювати дійсні числа, виконувати тотожні перетворення логарифмічних виразів.
Функція
З наведених проміжків число належить
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.
Це завдання перевіряє вміння будувати графіки елементарних функцій, використовувати перетворення графіків функцій.
Функції
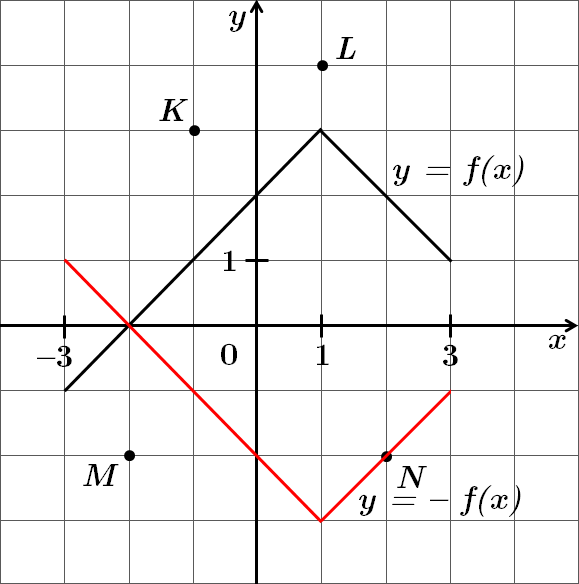
Точка
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння та їхні системи.
Це завдання перевіряє вміння розв'язувати системи рівнянь першого степеня.
Розв'язок
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння розв'язувати задачі на обчислення площ поверхонь геометричних тіл, знання многогранників та їхніх елементів.
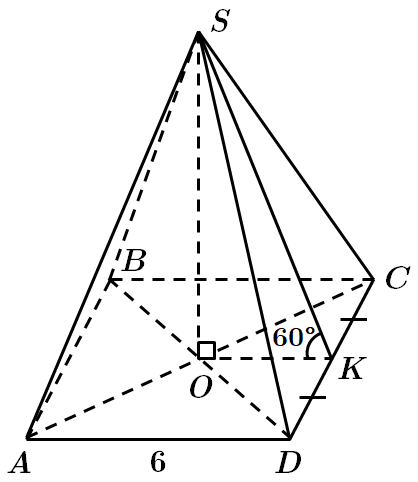
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл.
Це завдання перевіряє вміння обчислювати площу плоских фігур за допомогою інтеграла.
Якщо фігура обмежена графіками двох функцій, то границі інтегрування – точки їх перетину.
Функції
Отже, правильна відповідь Г.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє вміння застосовувати властивості різних видів трикутників до розв'язування планіметричних задач та задач практичного змісту.
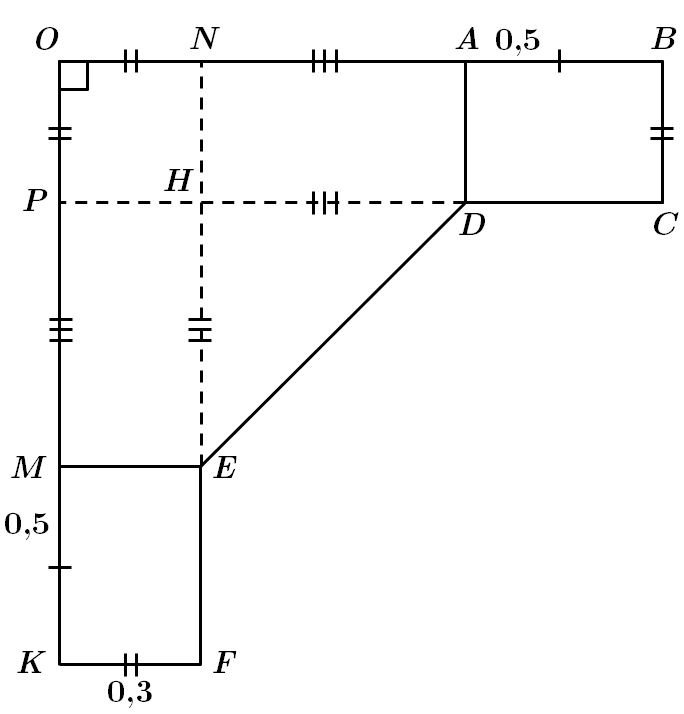
За теоремою Піфагора
Число
Серед відповідей цю нерівність задовольняє число
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Це завдання перевіряє вміння розв'язувати показникові рівняння.
Корінь рівняння належить проміжку
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Лінійні, квадратичні, тригонометричні, логарифмічні функції.
Це завдання перевіряє вміння будувати графіки елементарних функцій, встановлювати властивості числових функцій, заданих формулою або графіком.
1.
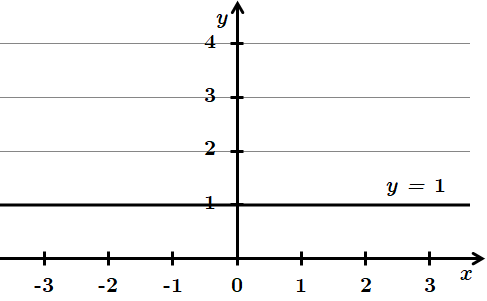
Не має спільних точок з віссю
2.
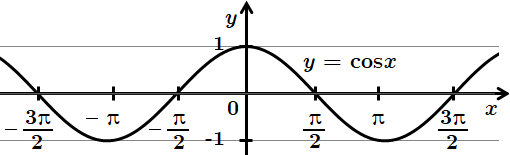
Має безліч спільних точок з віссю
3.
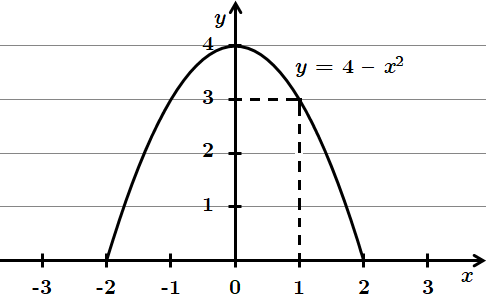
Проходить через точку
4.
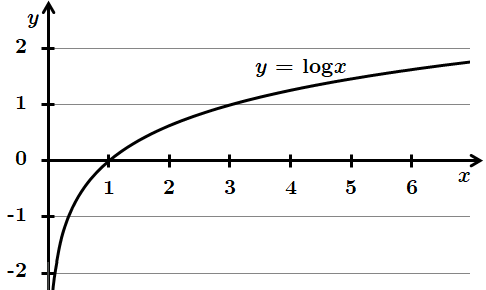
Не перетинає вісь
Відповідь: 1 – Г, 2 – B, 3 – Д, 4 – A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.
Це завдання перевіряє вміння розрізняти види чисел.
1.
2.
Отже, 2 – Д.
3.
Отже, 3 – Г.
4.
Отже, 4 – A.
Відповідь: 1 – Б, 2 – Д, 3 – Г, 4 – A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє знання про трапецію та її властивості; середню лінію трапеції, вписані в коло та описані навколо кола чотирикутники, теореми Піфагора.
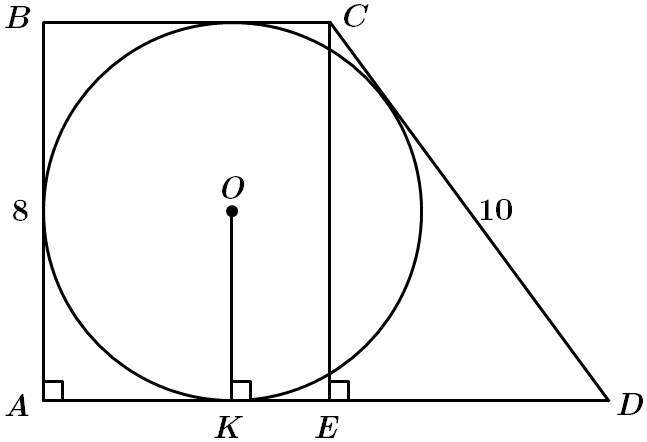
1. Висота трапеції – діаметр кола
Отже, 1 – Б.
2.
3. За властивістю чотирикутника, описаного навколо кола
4. Середня лінія трапеції дорівнює
Відповідь: 1 – Б, 2 – A, 3 – Г, 4 – B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.
Це завдання перевіряє знання про взаємне розміщення прямих у просторі, площин у просторі, многогранників та їхніх елементів.
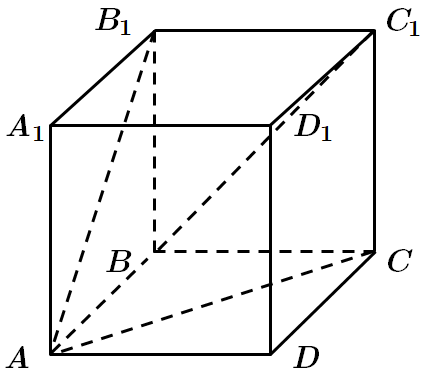
1.
Отже, 1 – B.
2. Прямі
Отже, 2 – Б.
3.
Отже, 3 – Д.
4.
Отже, 4 – A.
Відповідь: 1 – B, 2 – Б, 3 – Д, 4 – A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Відсотки. Основні задачі на відсотки. Текстові задачі.
Це завдання перевіряє вміння розв'язувати текстові задачі на відсоткові розрахунки.
1. Розглянемо можливі варіанти доставки багажу:
– усі вантажі доставлять окремо:
– усі вантажі доставлять разом:
вантаж важить:
– один вантаж доставлять окремо від двох інших:
Отже, найменша сума грошей –
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє вміння застосовувати властивості ромба до розв'язування планіметричних задач; знання теореми Піфагора, формули площі трикутника.
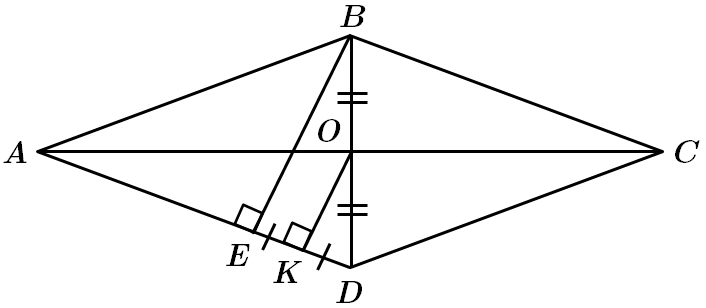
1.
2.
У
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності. Рівняння.
Це завдання перевіряє знання основної властивості арифметичної прогресії; уміння розв'язувати квадратні рівняння.
Задана арифметична прогресія:
За властивістю арифметичної прогресії:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі. Рівняння.
Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом, розв'язувати рівняння першого степеня.
Нехай
| Від |
|||
| Від |
Оскільки відстань від
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики. Перестановки. Комбінаторні правила добутку.
Це завдання перевіряє вміння розв'язувати нескладні задачі комбінаторного характеру; знання комбінаторного правила добутку.
Солісті –
Варіантів скласти послідовності виступів солістів
Варіантів скласти послідовність гуртів
За комбінаторним правилом добутку знаходимо кількість варіантів виступів:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг. Координати та вектори на площині.
Це завдання перевіряє знання про коло, круг та їхні елементи, прямокутну систему координат; уміння застосовувати координати до розв'язування планіметричних задач.
Рівняння кола зведемо до стандартного вигляду:
Коло з центром у точці
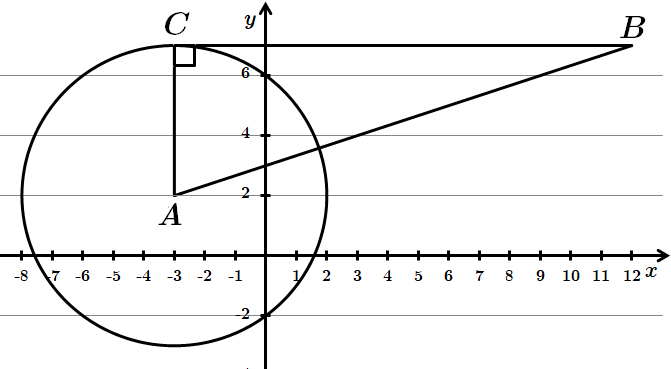
Отже,
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Степеневі функції. Похідна функції, її геометричний зміст.
Це завдання перевіряє вміння будувати графіки елементарних функцій, знаходити похідні елементарних функцій, кутовий коефіцієнт дотичної до графіка функції.
1-2.
Обчислимо кілька значень функції та побудуємо графік.
Якщо
Перша точка:
Якщо
Друга точка:
Позначимо ці точки на координатній площині та проведемо через них пряму.
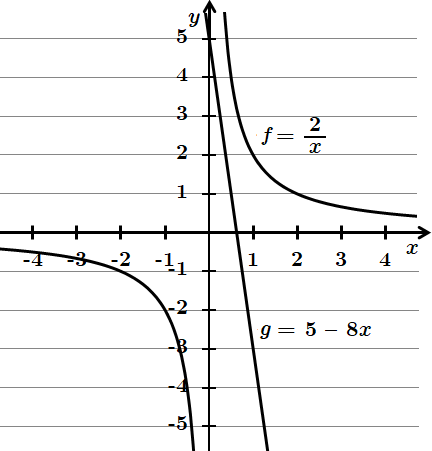
3.
4. Оскільки дотична паралельна прямій
Тоді,
Відповідь: 3.
4.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла й поверхні обертання. Прямі й площини у просторі.
Це завдання перевіряє вміння будувати перерізи тіл обертання, застосовувати властивості циліндра до розв'язування стереометричних задач; ознаки паралельності прямої та площини.
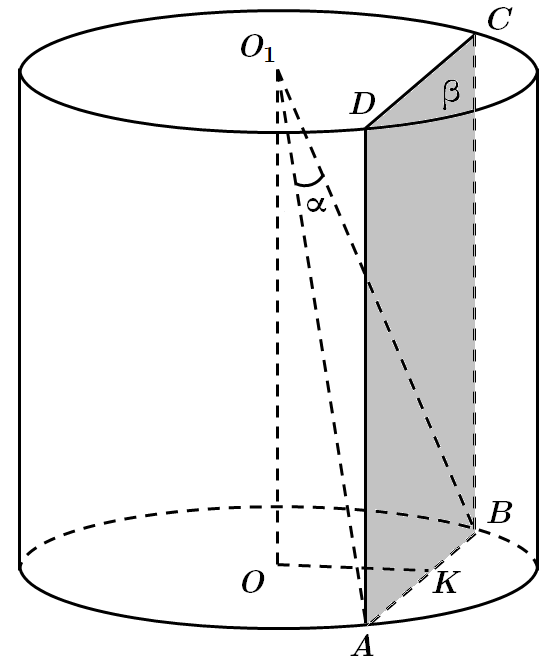
1. Побудуємо твірні
Твірні
(за ознакою паралельності прямої та площини).
2. Проведемо
Отримали, що
Отже,
3.
У
У
Площа переріза
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Рівняння, нерівності та їхні системи. Показникові рівняння та нерівності. Показникова функція.
Це завдання перевіряє вміння розв'язувати дробно-раціональні нерівності, показникові нерівності, а також їхні системи; розв'язувати нерівності та системи з параметрами; користуватися графічним методом розв'язування і дослідження рівнянь, нерівнстей та їхні системи.
1. Розв'яжемо першу нерівність методом інтервалів:
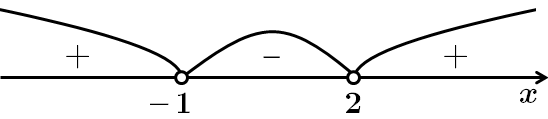
2. Розв'яжемо другу нерівність графічно. Спростимо вираз:
Побудуємо графік функції
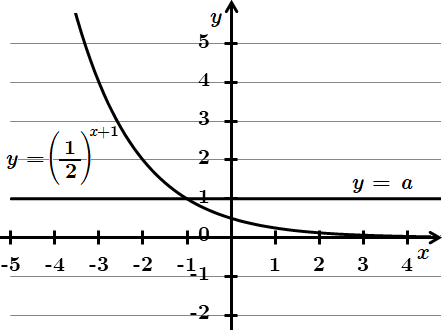
1) При
2) При
Відповідь: при
при
3. Розв'яжемо систему нерівностей:
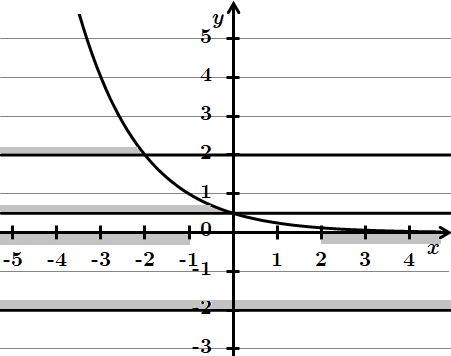
При
При
При
При
Відповідь: 1.
2.
3.
Знайшли помилку? Пишіть на




