ЗНО онлайн 2019 року з математики – додаткова сесія
Тестові завдання додаткової сесії ЗНО 2019 року з математики
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Лiнiйнi, квадратичні, степеневі, показникові, логарифмiчнi та триroнометричнi функції, їх основні властивості та графіки.
Це завдання перевіряє вміння встановлювати властивості функції, заданої графіком.
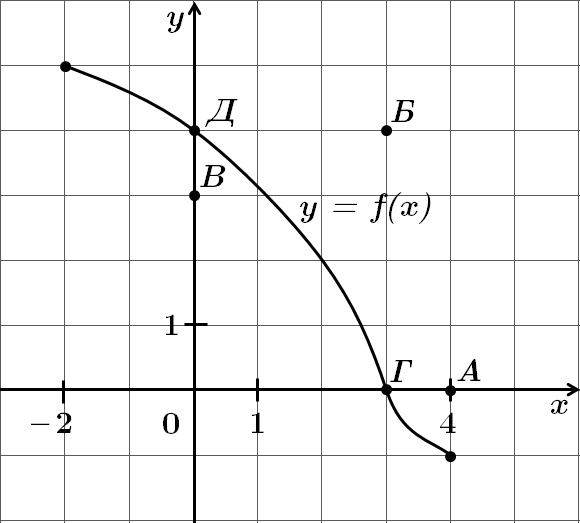
Графік функції перетинає вісь
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.
Це завдання перевіряє вміння розв'язувати квадратні нерівності.
Розв'яжемо методом інтервалів:
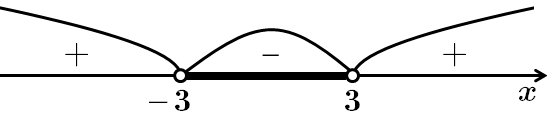
З наведених чисел лише число
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання теореми про суму кутів трикутника, властивостей суміжних та вертикальних кутів, властивості прямокутника.
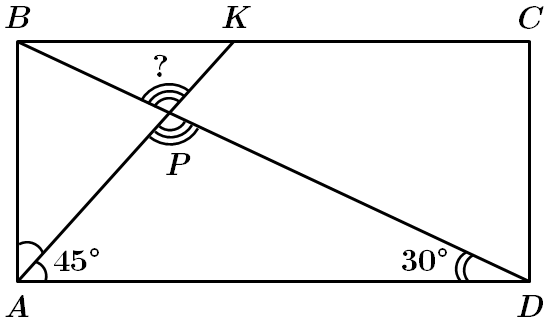
У трикутнику
Звідси
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв'язувати текстові задачі арифметичним способом.
За
Отже,
За кожні
Отже,
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла і поверхні обертання.
Це завдання перевіряє вміння встановлювати за розгорткою поверхні вид геометричного тіла.
Бічні грані – трикутники, основа – квадрат.
Отже, на рисунку розгортка чотирикутної піраміди.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.
Це завдання перевіряє вміння розв'язувати показникові нерівності.
Розв'яжемо показникову нерівність:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Лiнiйнi, квадратичні, степеневі, показникові, логарифмiчнi та триroнометричнi функції, їх основні властивості та графіки.
Це завдання перевіряє вміння встановлювати властивості функції, заданої графіком.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики.
Це завдання перевіряє вміння аналізувати графічну, табличну, текстову та інші форми подання статистичної інформації.
Кількість відвідувачів менше ніж
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла і поверхні обертання. Тіла і поверхні обертання та їх елементи, основні види тіл і поверхонь обертання: циліндр, конус, зрізаний конус, куля, сфера.
Це завдання перевіряє знання формули об'єму циліндра.
Об'єм циліндра обчислюємо за формулою
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рацiональнi, iррацiональнi, степеневі, показникові, логарифмiчнi, тригонометричні вирази та їхні перетворення.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.
Спростимо вираз за допомогою формул скороченого множення:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Функціональна залежність.
Це завдання перевіряє вміння виконувати елементарні перетворення графіків функцій.
За допомогою елементарних перетворень
Отже, отримаємо графік функції
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рацiональнi, iррацiональнi, степеневі, показникові, логарифмiчнi, тригонометричні вирази та їхні перетворення.
Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.
Спростимо вираз:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Многокутники.
Це завдання перевіряє знання про вписані в коло та описані навколо кола многокутники.
У будь-який трикутник можна вписати коло. Отже, I твердження правильне.
У чотирикутник можно вписати коло, якщо суми протилежних сторін рівні. Отже, в прямокутник не можна вписати коло, але у ромб – так.
Отже, ІІ твердження – неправильне, ІІІ – правильне.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа. Числові множини та співвідношення між ними.
Це завдання перевіряє вміння виконувати дії з дійсними числами та порівнювати їх.
Оцінимо вираз.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла і поверхні обертання. Тіла і поверхні обертання та їх елементи, основні види тіл і поверхонь обертання: циліндр, конус, зрізаний конус, куля, сфера.
Це завдання перевіряє вміння застосовувати означення та властивості призми, знання формули площі бічної поверхні призми.
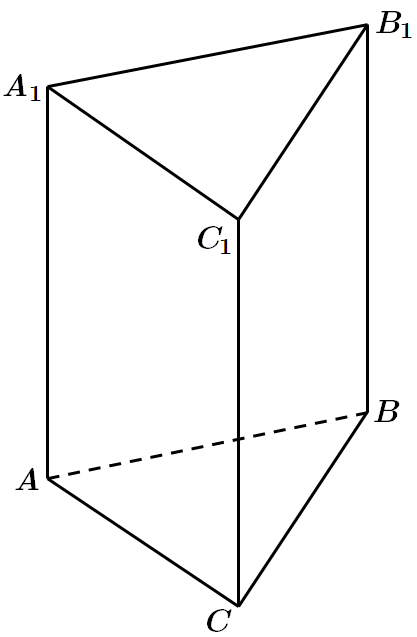
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.
Це завдання перевіряє вміння розв'язувати системи лінійних рівнянь.
Почленно додамо рівняння:
Розв'язок системи
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл. Застосування визначеного інтеграла до обчислення площ плоских фігур.
Це завдання перевіряє вміння обчислювати площу плоских фігур за допомогою інтеграла.
Площу зафарбованої фігури знаходимо за допомогою визначеного інтеграла. Границі інтегрування – абсциси точок перетину графіків:
За правилом: від "верхньої" лінії віднімаємо "нижню", знаходимо площу зафарбованої фігури.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники.
Це завдання перевіряє вміння застосувати означення та властивості різних видів трикутників до розв'язання задач практичного змісту.
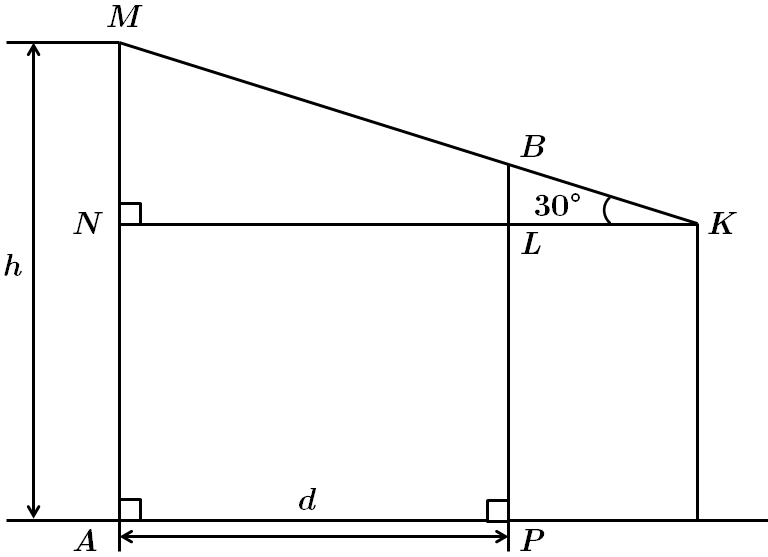
З-поміж наведених відстаней найменша
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.
Це завдання перевіряє знання методів розв'язування тригонометричних рівнянь.
Рівняння
Відповідь: A.
Знайшли помилку? Пишіть на
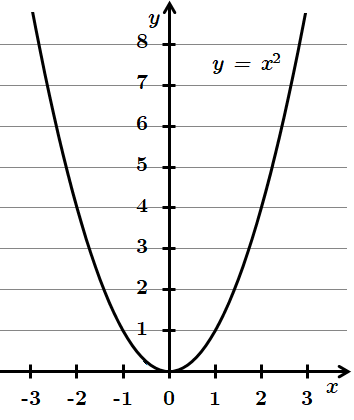
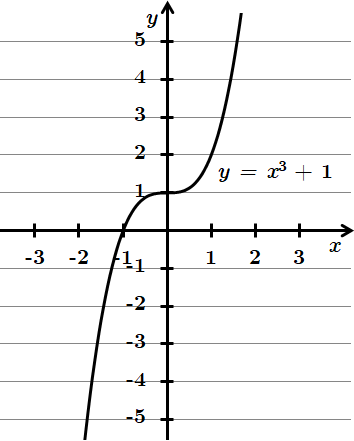
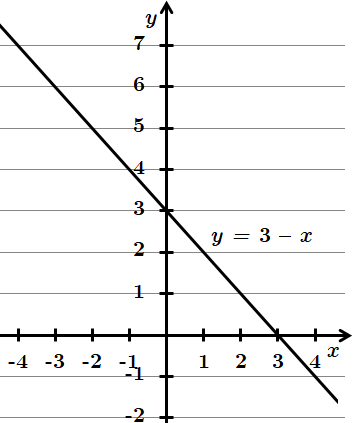
ТЕМА: Алгебра і початки аналізу. Функції. Лiнiйнi, квадратичні, степеневі, показникові, логарифмiчнi та триroнометричнi функції, їх основні властивості та графіки.
Це завдання перевіряє вміння встановлювати властивості функції, заданої графіком.
1.
2.
3.
4.
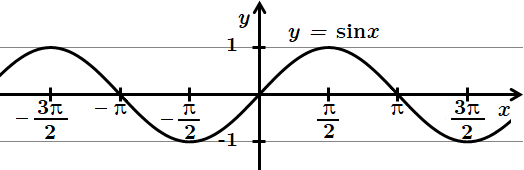
Відповідь: 1 – Г, 2 – Б, 3 – А, 4 – B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рацiональнi, iррацiональнi, степеневі, показникові, логарифмiчнi, тригонометричні вирази та їхні перетворення.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних та ірраціональних виразів, знання властивостей кореня
1.
2.
3.
4.
Відповідь: 1 – Б, 2 – B, 3 – Д, 4 – Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Геометричні величини та їх вимірювання.
Це завдання перевіряє знання про середню лінію трапеції, вміння застосовувати властивості трапеції до розв'язування планіметричних задач.
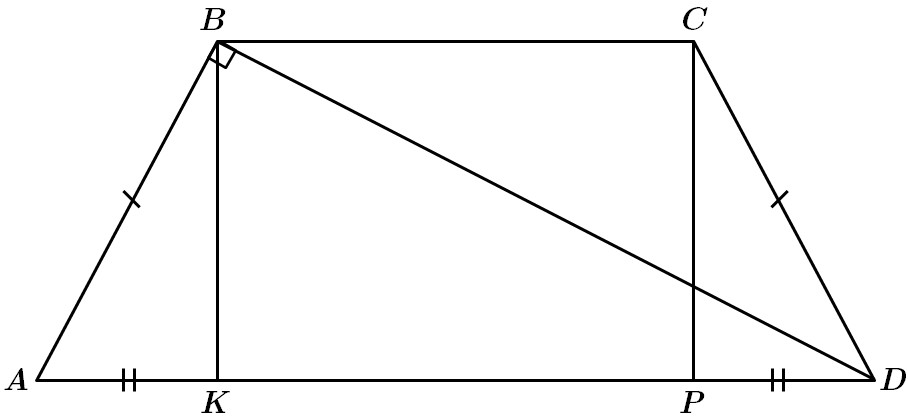
1. Довжина середньої лінії трапеції дорівнює:
Отже, 1 – Г.
2.
Отже, 2 – А.
3.
За властивістю висоти прямокутного трикутника, проведеної до гіпотенузи:
Отже, 3 – Б.
4. У
Отже, 4 – В.
Відповідь: 1 – Г, 2 – А, 3 – Б, 4 – В.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Аксіоми і теореми стереометрії. Взаємне розміщення прямих у просторі, прямої та площини у просторі, площин у просторі.
Це завдання перевіряє знання взаємного розміщення прямих та площин у просторі.
1.
2.
Отже, 2 – A.
3.
4.
Відповідь: 1 – Б, 2 – A, 3 – Д, 4 – B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Відношення та пропорції. Відсотки. Основні задачі на відсотки. Текстові задачі.
Це завдання перевіряє вміння знаходити відношення чисел у вигляді відсотка, відсоток від числа, число за значенням його відсотка.
1.
2. Для того, щоб при незмінності кількості дітей старшої групи (
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання теореми Піфагора, співвідношення між сторонами і кутами прямокутного трикутника, формули площі прямокутного трикутника.
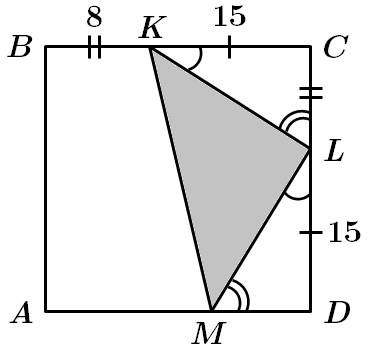
1.
У
2. Нехай
Отже,
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності. Означення геометричної прогресії.
Це завдання перевіряє знання властивостей геометричної прогресії, уміння розв'язувати квадратні рівняння.
Якщо
За властивістю геометричної прогресії:
Ненульове значення
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.
Це завдання перевіряє вміння застосовувати рівняння до розв'язування текстових задач.
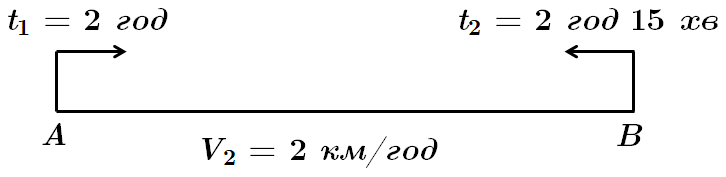
Нехай власна швидкість телохода
Отже, власна швидкість теплохода
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики.
Це завдання перевіряє вміння розв'язувати нескладні комбінаторні задачі.
Кількість способів вибрати тарілку –
Якщо влаштовує варіант вибрати або тарілку, або чашку та блюдце, то, використовуючи комбінаторне правило додавання, отримаємо
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.
Це завдання перевіряє вміння знаходити координати середини відрізка, виконувати дії з векторами, знаходити скалярний добуток векторів.
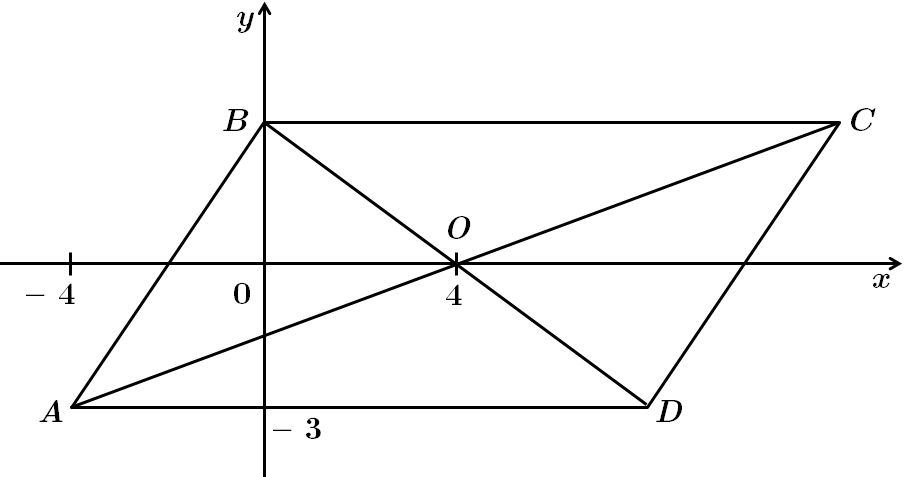
Запишемо рівняння кола у вигляді:
За формулою знаходження координат середини відрізка знаходимо координати точки
Знайдемо координати векторів
Знайдемо довжини векторів:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Похідна функції, її геометричний зміст.
Це завдання перевіряє вміння будувати графіки елементарних функцій, розв'язувати задачі з використанням геометричного змісту похідної.
Задано функції
1.
2.
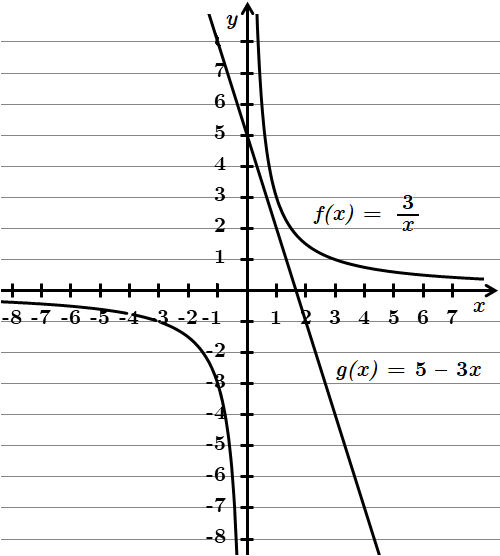
3.
4. Дотичні до графіка функції
Отже,
Підставимо значення похідної в точці в похідну:
Відповідь: 3.
4.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Тіла обертання.
Це завдання перевіряє вміння застосовувати означення та властивості конуса до розв'язування стереометричних задач.
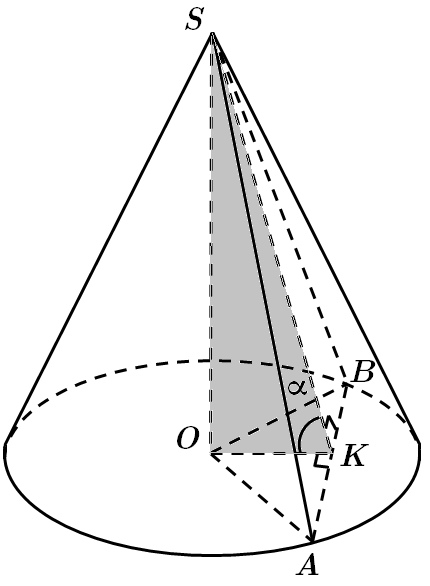
1.
2. Проведемо
За ознакою перпендикулрності прямої та площини
3. У
У
У
У
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та системи. Лiнiйнi, квaдpaтні, рацiональнi, iррацiональнi, показникові, логарифмiчнi, тригонометричні рівняння, неpiвності та їx системи.
Це завдання перевіряє вміння розв'язувати раціональні нерівності, логарифмічні нерівності з параметрами та їхні системи.
1. Розв'яжемо методом інтервалів першу нерівність:
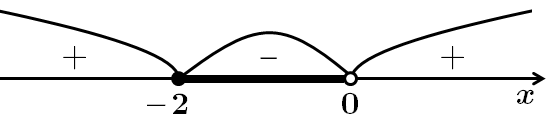
Отже,
2. Розв'яжемо другу нерівність:
1) При
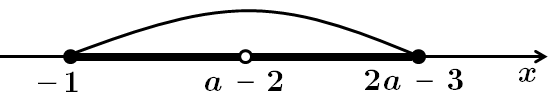
2) При
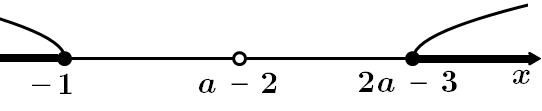
Відповідь: при
при
при
3. Розв'яжемо систему нерівностей:
при
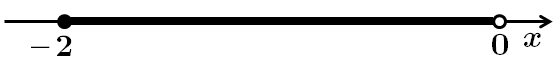
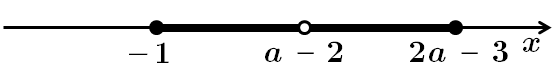
при
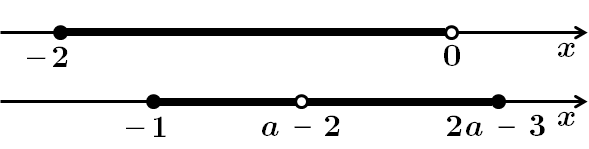
при

при
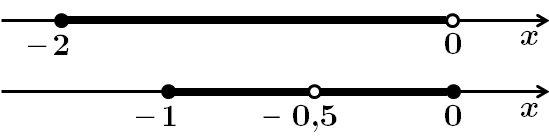
Відповідь: 1.
2. при
при
при
3. при
при
при
при
при
Знайшли помилку? Пишіть на




