ЗНО онлайн 2021 року з математики – демоваріант
Тестові завдання демоваріанта національного мультитесту (ЗНО) 2021 року з математики
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики. Графічна, таблична, текстова та інші форми подання статистичної інформації.
Це завдання перевіряє вміння аналізувати статистичну інформацію, подану у вигляді діаграми.
На діаграмі відображено інформацію про кількість проданих телевізорів.
У січні –
лютому –
березні –
квітні –
травні –
червні –
Правильна відповідь – B (у березні продано телевізорів більше, ніж у лютому).
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Це завдання перевіряє вміння розв’язувати текстові задачі.
Упаковка містить
Отже, найменша кількість упаковок, яких вистачить для всіх учасників семінару -
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє вміння застосовувати властивості многогранників.
Прямою трикутною призмою є призма, основою якої є трикутник, а бічні ребра перпендикулярні до площини основи. Це означає, що всі бічні грані - прямокутники.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв’язувати квадратні рівняння.
Розв'яжемо квадратне рівняння:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Це завдання перевіряє знання властивостей паралелограмів, суміжних кутів.
За властивістю суміжних кутів
За властивістю паралелограма
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Це завдання перевіряє знання властивостей та графіків функцій.
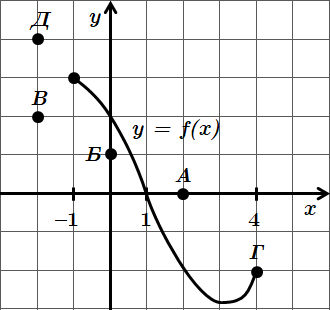
Правильна відповідь – Г
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.
Спростимо вираз за формулою "різниці квадратів":
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Це завдання перевіряє вміння знаходити числове значення буквеного виразу.
За формулою
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання властивостей степенів.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Це завдання перевіряє знання властивостей паралелограмів, нерівності трикутника.
I. Протилежні сторони будь-якого паралелограма рівні (властивість параллелограма).
II. Довжина сторони будь-якого трикутника менша за суму довжин двох інших сторін (нерівність трикутника).
III. Твердження неправильне.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв’язувати системи лінійних рівнянь.
Розв'яжемо систему лінійних рівнянь методом додавання:
Підставимо значення
Розв'язок системи
Обчислимо добуток
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Похідні елементарних функцій.
Це завдання перевіряє вміння знаходити похідні елементарних функцій, правил знаходження похідних.
За таблицею похідних:
Отже,
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв’язувати показникові нерівності.
Функція
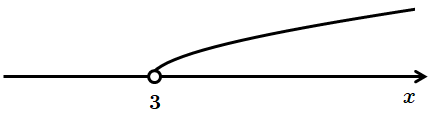
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Це завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Це завдання перевіряє знання властивостей, формули площі поверхні циліндра.
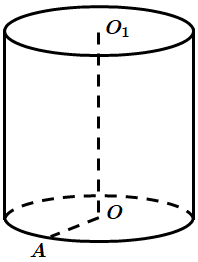
Площа бічної поверхні
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання властивостей ромба, прямокутного трикутника, вміння розв’язувати прямокутні трикутники.
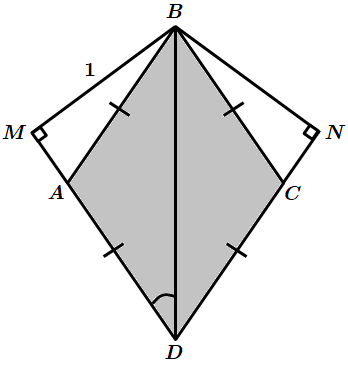
кута
За властивістю катета, протилеглого до кута
Відповідь, найближча до точної
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Лiнiйнi, квадратичні, степеневі, показникові, логарифмiчнi та тригoнометричнi функції, їх основні властивості та графіки.
Це завдання перевіряє знання властивостей функцій та їх графіків.
1. Графік функції є фрагментом графіка функції
2. Графік функції двічі перетинає графік функції
3. Функція зростає на проміжку
Відповідь: 1 – Б, 2 – А, 3 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Це завдання перевіряє вміння виконувати дії з раціональними числами, логарифмічними виразами, порівнювати числа, знання властивостей модуля числа.
1.
2.
3.
Відповідь: 1 – B, 2 – A, 3 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Це завдання перевіряє знання властивостей прямокутника, прямокутного та рівнобедреного трикутників, теореми Піфагора.
1. За умовою завдання у прямокутник
2. Центр кола, описаного навколо прямокутника, лежить на перетині діагоналей. Радіус кола – половина діагоналі
Отже, 2 – A.
3.
Відповідь: 1 – Б, 2 – A, 3 – В.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Це завдання перевіряє знання ознак паралельності прямої та площини, аксіом стереометрії.
1. Точки
2.
3.
Відповідь: 1 – Б, 2 – A, 3 – Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв’язувати задачі на пропорційну залежність, відсоткові розрахунки.
1.
Складемо пропорцію:
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг.
Це завдання перевіряє знання властивостей вписаного та центрального кутів, уміння знаходити довжину дуги кола.
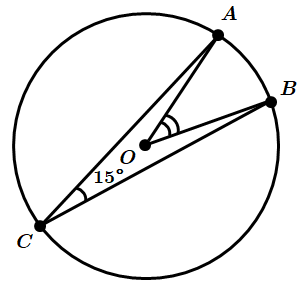
1. За властивістю вписаного кута
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Вектори і координати у просторі.
Це завдання перевіряє вміння знаходити координати вектора, його довжину, координати середини відрізка.
1. Точка
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Це завдання перевіряє знання формули суми
1. За формулою
2. За формулою суми
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики.
Це завдання перевіряє знання класичного означення ймовiрностi події, уміння обчислювати ймовірність випадкових подій.
У шухляді олівці та ручки.
Нехай ручок було
Відомо, що ймовірність вибрати навмання одну ручку
Олівців лежить у шухляді
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.
Це завдання перевіряє вміння розв'язувати задачі на рух.
Нехай швидкість велосипедиста
На дорогу з міста
Мотоцикліст виїхав на
Відстань між містами
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази.
Це завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння розв’язувати лінійні рівняння з модулем.
За властивістю модуля
У відповідь запишемо суму розв'язків:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики.
Це завдання перевіряє вміння розв’язувати нескладні комбінаторні задачі.
Кількість варіантів вибору в місті з
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Визначений інтеграл.
Це завдання перевіряє вміння будувати графіки функцій, використовуючи елементарні перетворення графіків, знаходити площу фігури, обмеженої лініями, застосовувати формулу Ньютона-Лейбнiца для обчислення визначеного інтеграла.
1.
2. Побудуємо графік функції, використовуючи елементарне перетворення графіка функції
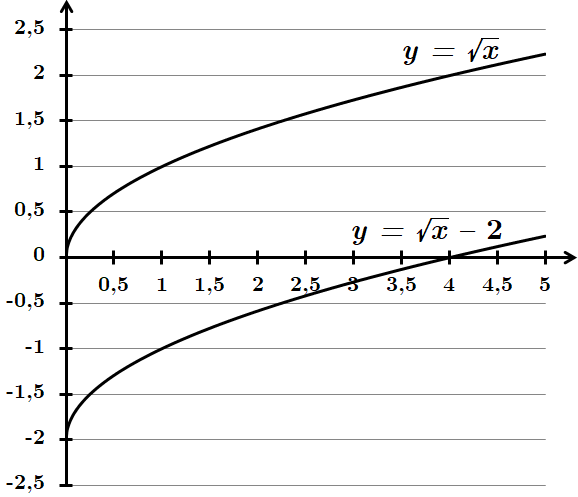
3. Точка перетину графіка з віссю
4.
Наприклад, при
5.
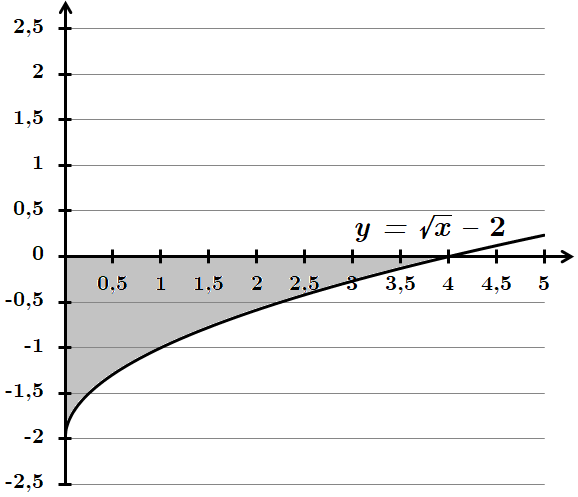
Оскільки графік функції лежить нижче від осі
6. Обчислимо площу фігури:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє знання властивостей правильної піраміди, кута між прямою та площиною, вміння знаходити об’єм піраміди.
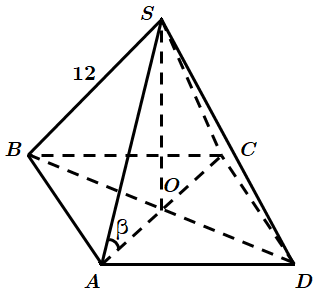
1.
2.
3.
Відповідь: 2.
3.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Це завдання перевіряє знання властивостей правильної піраміди, кута між площинами, вміння розв’язувати прямокутні трикутники.
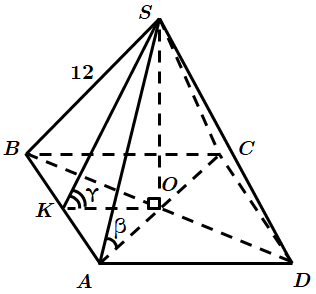
1.
За теоремою про три перпендикуляри похила
2.
За теоремою Піфагора
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Це завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, доводити нерівності.
Виділили квадрат двочлена з виразу
Отже, вираз
Якщо
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння та нерівності.
Це завдання перевіряє вміння розв’язувати ірраціональні рівняння, показникові рівняння з параметром, раціональні нерівності.
1. Розв'яжемо рівняння:
2. Розв'яжемо в залежності від параметра
Нерівність
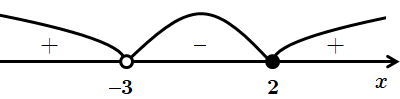
Рівняння
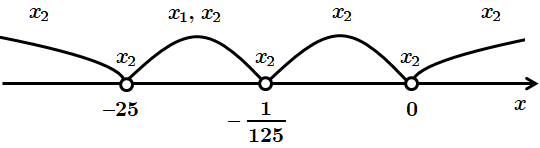
При
При
Відповідь:
1.
2. при
при
Знайшли помилку? Пишіть на




