ЗНО онлайн 2020 року з математики – пробний тест
Тестові завдання пробного тесту ЗНО 2020 року з математики
Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє знання правил округлення цілих чисел.
В числі
Округлення до сотень означає, що ми дивимося на число, яке позначає десятки, щоб вирішити – збільшувати сотні чи залишити як є. Оскільки
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей прямокутника, вміння знаходити периметр.
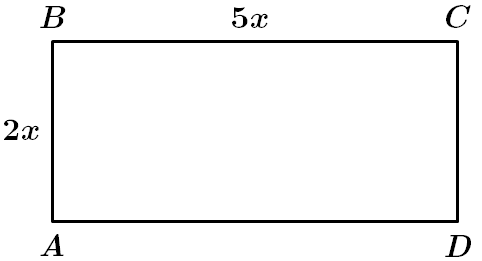
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи. Лінійні рівняння.
Завдання перевіряє вміння розв'язувати лінійні рівняння.
Помножимо обидві частини рівняння на
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання властивостей призми.
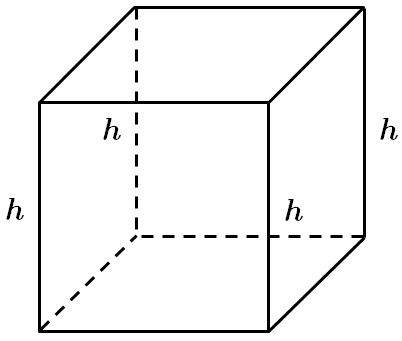
У прямокутному паралелепіпеді бічні ребра є висотами. Отже,
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє знання властивостей степенів.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
За умовою, абсциса точки від'ємна, а ордината – додатна. З наведених варіантів відповідей задовольняє Б і Г. Після перевірки за графіком встановлюємо, що
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності.
Завдання перевіряє вміння розв'язувати степеневі рівняння.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання перевіряє вміння розв'язувати задачі на обчислення площі поверхні циліндра.
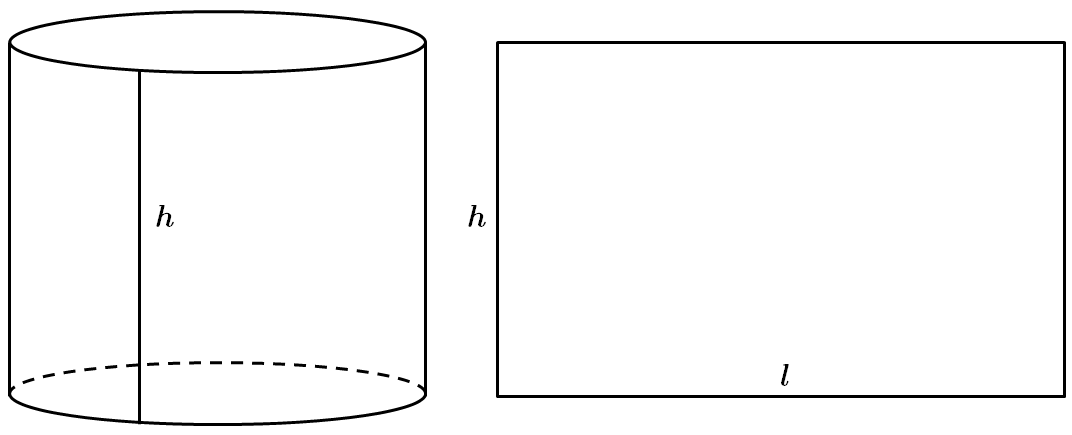
Розгорткою бічної поверхні циліндра є прямокутник.
Площа бічної поверхні
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей.
Завдання перевіряє вміння обчислювати ймовірність випадкової події.
Ймовірність випадкової події знаходимо за формулою:
Отже,
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів.
Використаємо основну властивість пропорції:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей трапеції.
I – неправильне твердження. Трапеція – це чотирикутник, у якого дві сторони паралельні (основи), а дві інші – ні (бічні).
IІ – правильне твердження. Основи трапеції – паралельні відрізки, бічна сторона – січна. Кути, прилеглі до бічної сторони – внутрішні односторонні кути, і за властивістю паралельних прямих їх сума дорівнює
III – неправильне твердження. Наведемо контрприклад. У прямокутній трапеції сума протилежних кутів не дорівнює
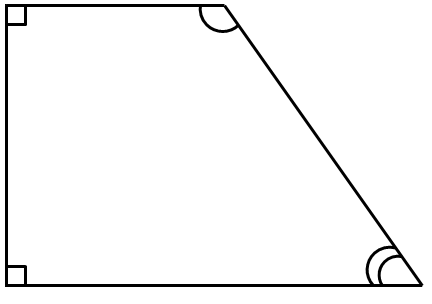
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє знання властивостей показникової функції.
Графік проходить через точку
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності.
Завдання перевіряє вміння розв'язувати логарифмічн рівняння.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.
За властивістю пропорції
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння і нерівності.
Завдання перевіряє вміння розв'язувати систему лінійних нерівностей.
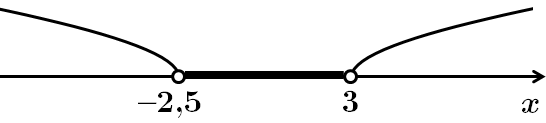
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання властивостей піраміди, означення кута між прямою та площиною.
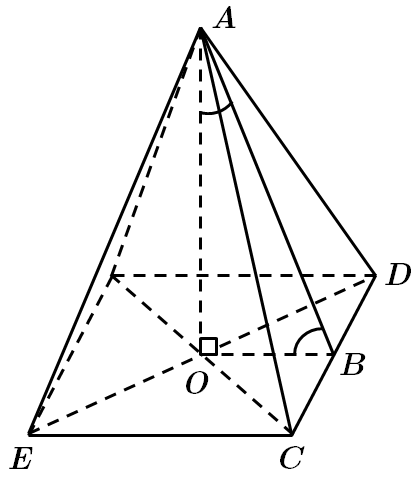
Висота піраміди
Отже,
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє знання властивостей тригонометричної функції.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Похідна функції. Первісна.
Завдання перевіряє вміння знаходити похідну функції, знання означення первісної.
За означенням первісної
Отже,
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Геометричні величини та їх вимірювання.
Завдання перевіряє вміння знаходити довжини відрізків, розв'язувати задачі практичного змісту.
У
Ширина смуги
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою або графіком.
1.
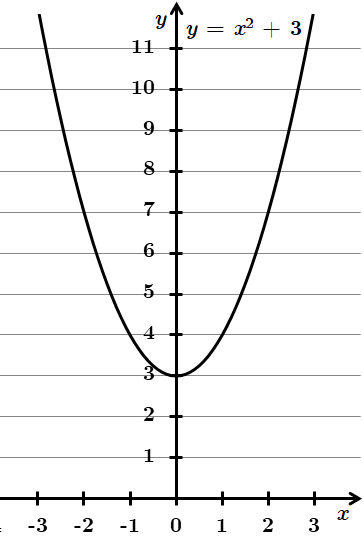
Симетричний відносно осі y. Отже, 1 – A.
2.
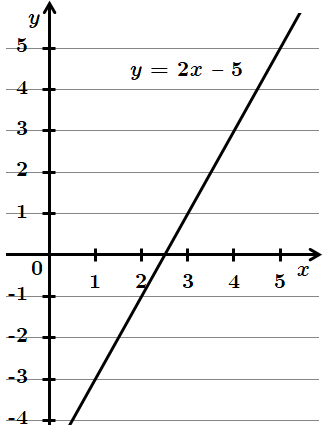
Набуває від'ємного значення в точці
3.
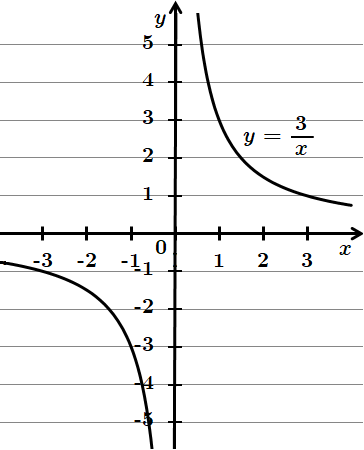
Симетричний відносно початку координат. Отже, 3 – Д.
Відповідь: 1 – A, 2 – B, 3 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння порівнювати дійсні числа, використовувати властивості модуля до розв’язування задач.
З рисунку визначаємо, що
1.
Значенню
Отже, 1 – Г.
2.
Отже, нас цікавить точка яка належить проміжку
На рисунку даному проміжку належить точка
Отже, 2 – B.
3.
Значенню
Отже, 3 – A.
Відповідь: 1 – Г, 2 – B, 3 – A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання властивостей ромба.
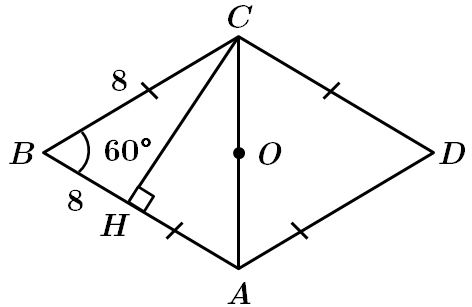
1.
2.
3. Центр кола, вписаного в ромб – точка перетину діагоналей точка
За властивістю ромба
Відповідь: 1 – B, 2 – Б, 3 – A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.
Завдання перевіряє вміння застосовувати означення та властивості паралельних прямих і площин.
1. Точка
2.
3.
Відповідь: 1 – Д, 2 – B, 3 – Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Текстові задачі.
Завдання перевіряє вміння розв'язувати текстові задачі.
1. Нехай вартість оренди одного велосипеда для дитини
2. Вартість оренди одного шолома та однієї пари рукавичок
Тобто,
Вартість оренди трьох шоломів та трьох пар рукавичок дорівнює
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє вміння застосовувати властивості паралелограма до розв'язування планіметричних задач.
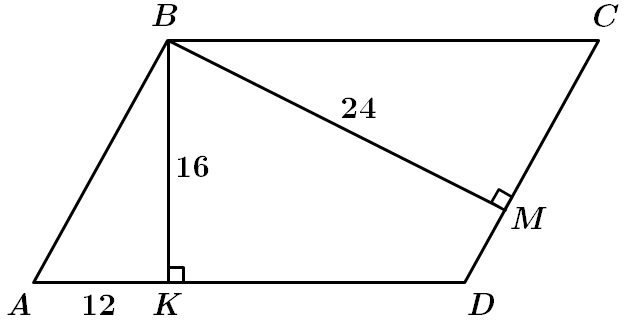
1. У
2. За формулою
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Завдання перевіряє вміння розв'язувати задачі на геометричну прогресію.
1. Використовуємо формули
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи математичної статистики. Вибіркові характеристики.
Завдання перевіряє вміння обчислювати та аналізувати вибіркові характеристики рядів даних (середнє значення).
Знаходимо середнє арифметичне за формулою:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Завдання перевіряє вміння розв’язувати текстові задачі, застосовувати системи рівнянь до розв’язування текстових задач.
Нехай тривалість одного рекламного ролика
Трейлер триває
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів і площ поверхонь конуса.
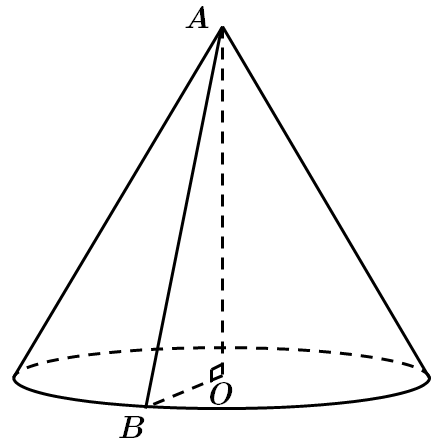
Площа основи конуса –
Об'єм конуса знаходимо за формулою:
У
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики.
Завдання перевіряє вміння розв'язувати задачі, використовуючи перестановки, комбінаторне правило добутку.
Оскільки спочатку інформацію промовляють українською, то таких варіантів – один.
Далі
За правилом добутку знаходимо загальнку кількість можливих варіантів:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг. Трикутники. Координати та вектори на площині.
Завдання перевіряє вміння знаходити координати середини відрізка, складати рівняння кола, застосовувати властивості прямокутного трикутника, використовувати формули площі трикутника.
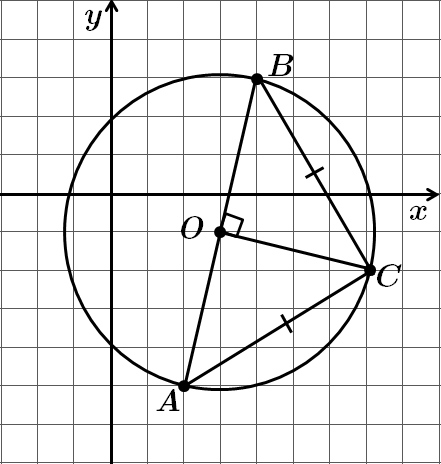
Коло задане рівнянням
Запишемо у стандартному вигляді
Точка
Отже,
Висота, проведена до гіпотенузи, – медіана та радіус описаного кола.
Отже,
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння будувати графіки лінійної та логарифмічної функцій, встановлювати властивості числових функцій, заданих формулою або графіком.
1.
2.
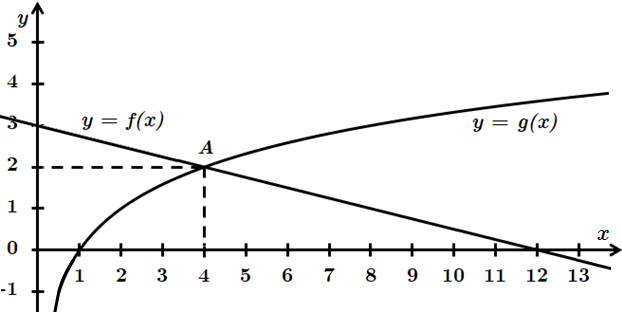
3. Точка перетину графіків
4. Розв'язок нерівності
Тобто знаходимо такі значення
Відповідь: 3.
4.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.
Завдання перевіряє вміння будувати перерізи призми, знання теореми про три перпендикуляри, кута між прямою та площиною, вміння розв’язувати стереометричні задачі.
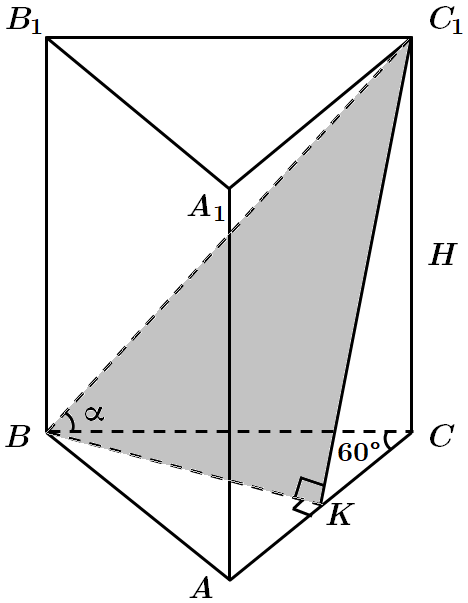
1.
Кутом між
2. За умовою
3.
Оскільки
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати раціональні, ірраціональні та показникові рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.
1. Розв'яжемо заміною:
ОДЗ:
За теоремою, оберненою до теореми Вієта
2. Розв'яжемо рівняння залежно від значень параметра:
Дріб дорівнює нулю, коли його чисельник дорівнює нулю.
(1)
Підставимо в ОДЗ:
якщо
(2)
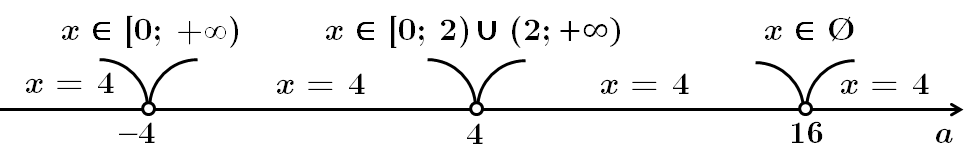
Відповідь: 1.
2. якщо
якщо
якщо
якщо
Знайшли помилку? Пишіть на




