ЗНО онлайн 2020 року з математики – основна сесія
Тестові завдання основної сесії ЗНО 2020 року з математики
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє знання означення степеня з цілим показником та його властивості.
Використаємо властивість
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.
Завдання перевіряє знання властивостей суміжних та вертикальних кутів, теореми про суму кутів трикутника.
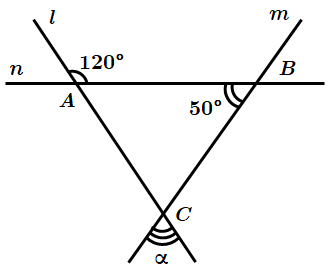
Сума кутів
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє вміння розв’язувати текстові задачі арифметичним способом.
За
Отже,
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Завдання перевіряє вміння розв’язувати лінійні рівняння.
Помножимо обидві частини рівняння на
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання перевіряє знання про многогранники та їхні елементи.
Довжина всіх ребер куба
Усього в куба
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
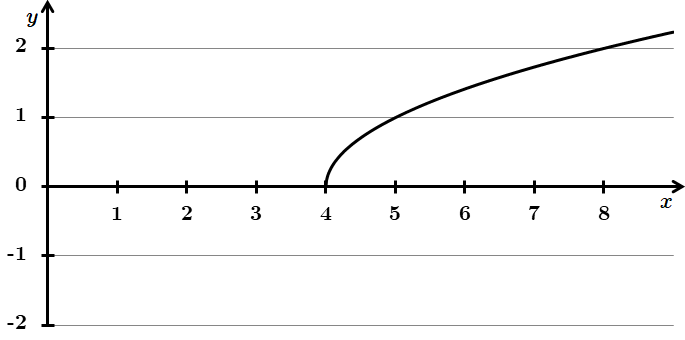
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
Нуль функції – значення
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Завдання перевіряє вміння розв’язувати квадратні рівняння.
Розв'яжемо квадратне рівняння:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики.
Завдання перевіряє вміння розв’язувати комбінаторні задачі.
Піднятись на гору можна
Усього варіантів вибору маршруту
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання перевіряє знання паралелограма, ромба, квадрата та їх властивостей.
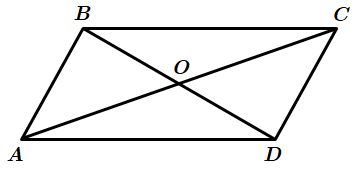
I правильне. Діагоналі ромба є бісектрисами його кутів.
II неправильне. Діагоналі точкою перетину діляться навпіл – властивість паралелограма.
III правильне. Діагоналі перпендикулярні – властивість будь-якого квадрата.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
На рисунку Б зображено ескіз графіка показникової функції
Функція спадна, проходить через точку
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Стереометрія. Трикутники. Тіла обертання.
Завдання перевіряє знання про конус та його елементи, співвідношення між сторонами і кутами прямокутного трикутника.
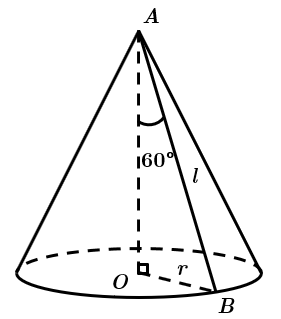
У
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє знання формул скороченого множення, вміння виконувати тотожні перетворення раціональних виразів.
Розкладемо вираз
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння виконувати перетворення графіків функцій.
Якщо графік функції
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів, знання основних співвідношень між тригонометричними функціями одного аргументу.
Спростимо вираз
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати системи лінійних нерівностей.
Розв'яжемо систему нерівностей
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати логарифмічні рівняння, порівнювати дійсні числа.
За означенням логарифма
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння порівнювати дійсні числа.
Запишемо подвійною нерівністю:
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Стереометрія. Трикутники. Многогранники.
Завдання перевіряє знання про призму та її елементи, вміння знаходити площу трикутника.
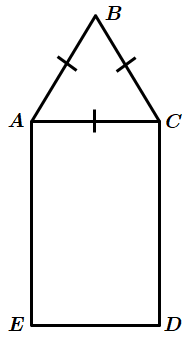
Площа основи призми – площа
За формулою
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг.
Завдання перевіряє вміння знаходити довжину кола та його дуги.
Довжина кола
Оскільки до каркаса прикрілено
Найближча до точної відповідь Б.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Первісна.
Завдання перевіряє знання означення первісної функції.
Функція
Формула, яка задає всі первісні функції
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою.
1.
Отже, 1 – Б.
2.
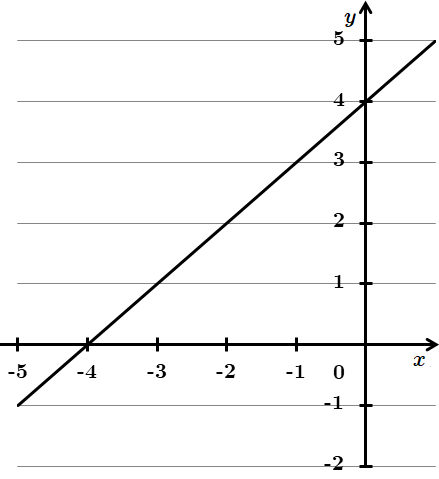
Отже, 2 – Г.
3.
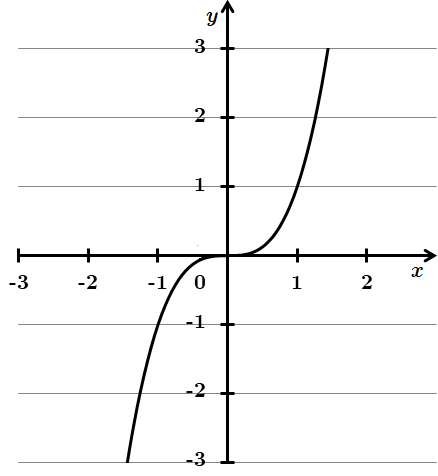
Отже, 3 – Д.
Відповідь: 1 – Б, 2 – Г, 3 – Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння використовувати властивості модуля до розв’язування задач, виконувати тотожні перетворення раціональних, логарифмічних виразів.
1.
Отже, 1 – Г.
2.
За означенням модуля
3.
Отже, 3 – B.
Відповідь: 1 – Г, 2 – A, 3 – B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання перевіряє вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції, знання теореми Піфагора.
1.
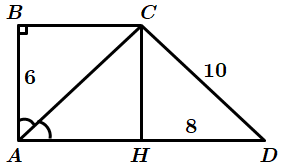
Отже, 1 – A.
2.
У
Отже, 2 – Б.
3.
Cередня лінія трапеції
Відповідь: 1 – A, 2 – Б, 3 – Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Завдання перевіряє знання формул для обчислення площі поверхні та об’єму циліндра, циліндра та його елементів.
1. Твірна дорівнює
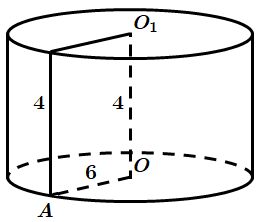
Отже, 1 – В.
2.
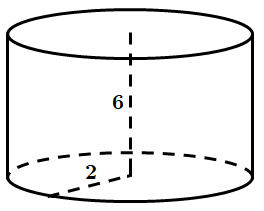
Отже, 2 – Г.
3.
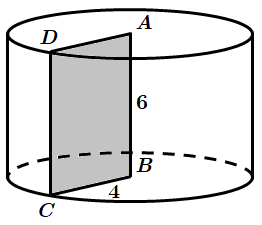
Отже, 3 – A.
Відповідь: 1 – В, 2 – Г, 3 – А.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання перевіряє вміння розв’язувати тестові задачі арифметичним способом, розв’язувати задачі на відсоткові розрахунки.
1. За
2. За
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло і круг. Чотирикутники. Трикутники.
Завдання перевіряє знання про коло та його елементи, теореми Піфагора, знання формули для обчислення площі трикутника.
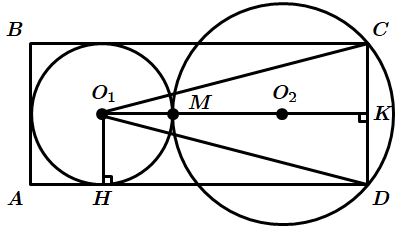
1.
За теоремою Піфагора
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Завдання перевіряє знання формули n-го члена арифметичної прогресії, вміння розв’язувати задачі на арифметичну прогресію.
1.
2.
Відповідь: 1.
2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Завдання перевіряє вміння застосовувати рівняння до розв’язування текстових задач.
Нехай власна швидкість човна
| За течією | |||
| Проти течії |
Відстань проти течії човен подолав за час, вдвічі менший, ніж за течією.
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи математичної статистики. Вибіркові характеристики.
Завдання перевіряє вміння обчислювати та аналізувати вибіркові характеристики рядів даних (середнє значення).
Середню температуру знаходимо як середнє арифметичне значень
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.
Завдання перевіряє вміння розв’язувати задачі на обчислення об’єму піраміди, знання теореми Піфагора та властивості квадрата.
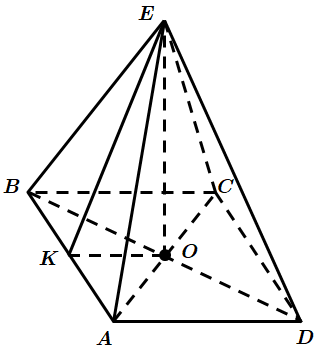
У
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи теорії ймовірностей.
Завдання перевіряє вміння обчислювати ймовірність випадкової події, знання правила добутку для знаходження ймовірності.
Серед
Отже, ймовірність того, що студент проживає у гуртожитку
Серед
Отже,
За правилом добутку ймовірність того, що обидва студенти проживають у гуртожитку
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Координати та вектори на площині.
Завдання перевіряє знання властивості рівних векторів, координат вектора; уміння складати рівняння кола, знаходити координати середини відрізка.
Коло задано рівнянням
Запишемо в стандартному вигляді:
Точка
Нехай точка
Отже,
Точка
За формулами
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання перевіряє вміння будувати графіки лінійної та тригонометричної функцій, встановлювати властивості числових функцій, заданих формулою або графіком, вміння розв’язувати тригонометричні рівняння.
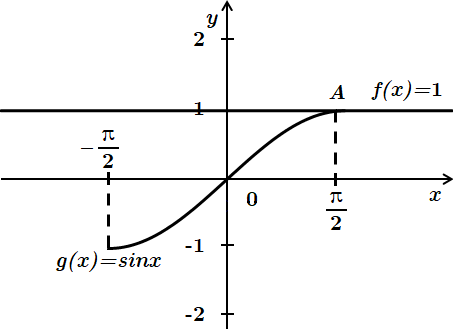
3. Точка
4.
Відповідь: 3.
4.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія Стереометрія. Прямі та площини у просторі. Многогранники.
Завдання перевіряє вміння будувати перерізи призми, знання теореми про три перпендикуляри, кута між прямою та площиною, вміння розв’язувати стереометричні задачі.
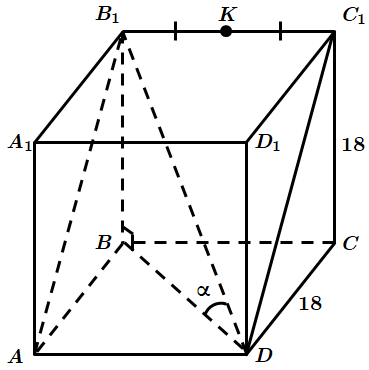
1. Нехай
Через пряму
За властивістю паралельних площин
2.
Отже,
3.
У
У
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання перевіряє вміння розв’язувати ірраціональні та показникові рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.
1. Розв'яжемо рівняння
2. Розв'яжемо рівняння
Перевіримо, при яких значеннях
якщо
якщо
Перевіримо, при яких значеннях
Розв'яжемо методом інтервалів:

Запишемо загальну відповідь:
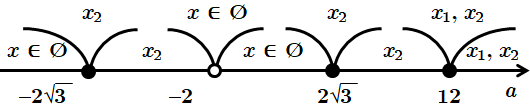
Відповідь: якщо
якщо
якщо
Знайшли помилку? Пишіть на




