ЗНО онлайн 2020 року з математики – додаткова сесія

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури та їхні властивості.

Завдання перевіряє знання властивостей вертикальних i суміжних кутів, паралельних прямих.

\(\angle\mathbf{\beta}=\angle\mathbf{\gamma}\) як вертикальний. \(\mathbf{\alpha}+\mathbf{\gamma}=180^\circ.\) За властивістю паралельних прямих. \(\mathbf{\alpha}\), \(\mathbf{\gamma}\) – внутрішні односторонні. $$ \mathbf{\alpha}=180^\circ-\mathbf{\gamma}=180^\circ-125^\circ=55^\circ. $$

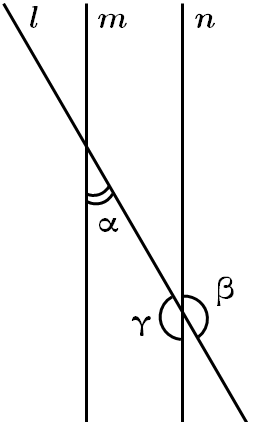
Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння знаходити неповну частку, остачу від ділення одного натурального числа на інше.

\(194\) учні можна розсадити в їдальні
\(194 : 6 = 32\) (остача \(2\)).

Таким чином, учні розсядуться по \(6\) учнів за \(32\) столи та \(2\) учні сядуть за \(33\text{-й}\) стіл.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє відношення та пропорції. Перевіряє знання основної властивості пропорції.

Розв'яжемо рівняння, використавши основну властивість пропорції: \begin{gather*} \frac 8x=\frac 25,\\[6pt] 2\cdot x=8\cdot 5,\\[6pt] x=20. \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.

Функція \(y=f(x)\) зростає при \(x\in [-3; 1].\)

Відповідь: Д.

ТЕМА: Геометрія Стереометрія. Тіла обертання.

Завдання перевіряє знання формул для обчислення площ поверхонь циліндра.

\(S_\text{бічної}=56\mathbf{\pi}\), \(S_\text{поверхні}=S_\text{бічної}+2S_\text{основи}=92\mathbf{\pi}.\)

Отже, \(92\mathbf{\pi}=56\mathbf{\pi}+2S_\text{основи}.\)

\(2S_\text{основи}=36\mathbf{\pi}\), \(S_\text{основи}=18\mathbf{\pi}.\)

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв'язувати квадратні рівняння.

Розв'яжемо рівняння:

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки аналізу.

Завдання перевіряє вміння обчислювати ймовірності випадкових подій, користуючись її означенням.

Монет номіналом менше \(50\) копійок – \(17\) (\(5\) монет номіналом \(10\) копійок, \(12\) монет – по
\(25\) копійок). Усього монет – \(20.\)

Отже, ймовірність того, що номінал навмання взятої монети менше \(50\) копійок становить: $$ P=\frac{17}{20}. $$

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.

Спростимо вираз, використавши формулу скороченого множення

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання перевіряє знання властивостей ромба, трапеції, прямокутника, властивостей чотирикутників, вписаних в коло.

Навколо чотирикутника можна описати коло, якщо сума протилежних кутів дорівнює \(180^\circ.\) Отже, навколо ромба та довільної трапеції не можна описати коло, але навколо довільного прямокутника – так.

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою.

Ескіз графіка функції \(y=\sqrt{x}\) зображений на рисунку Д.

Відповідь: Д.

ТЕМА: Геометрія Стереометрія. Тіла обертання.

Завдання перевіряє знання формул для обчислення площі поверхні кулі.

Площа сфери знаходиться за формулою: \(S=4\mathbf{\pi}R^2.\) Виразимо з формули \(R:\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

За формулою $$ \operatorname{tg}\ \mathbf{\alpha}=\frac{\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}} $$ спростимо: $$ \frac{\cos\mathbf{\alpha}\cdot\operatorname{tg}\ \mathbf{\alpha}}{\sin^2\mathbf{\alpha}}=\frac{\frac{\cos\mathbf{\alpha}\cdot\sin\mathbf{\alpha}}{\cos\mathbf{\alpha}}}{\sin^2\mathbf{\alpha}}=\frac{\sin\mathbf{\alpha}}{\sin^2\mathbf{\alpha}}=\frac{1}{\sin\mathbf{\alpha}}. $$

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння використовувати перетворення графіків функцій.

Елементарними перетвореннями графік функції \(y=x^2\) перемістили на \(2\) одиниці вліво вздовж осі \(Ox\) та отримали графік фукнції \(y=(x+2)^2.\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння використовувати властивості модуля до розв'язування задач.

Властивість модуля \begin{gather*} |a|=\left[\begin{array}{l} a,\ \text{якщо}\ \ a\ge 0;\\ -a,\ \text{якщо}\ \ a\lt 0. \end{array}\right.\\[7pt] 1-\sqrt{3}\lt 0. \end{gather*} Отже, $$ |1-\sqrt{3}|=-(1-\sqrt{3})=-1+\sqrt{3}=\sqrt{3}-1. $$

Відповідь: Б.

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання формул для обчислення площ поверхонь призми, площі трикутника.

\(\Delta ABC\) – рівнобедрений. \(AB=AC=13\) см, \(BC=10\) см.

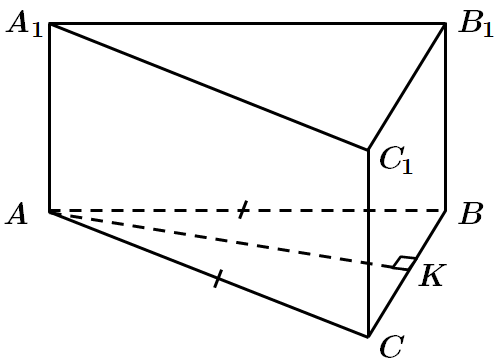
Бічні грані – прямокутники. Найбільша за площею бічна грань \(AA_1C_1C\) або \(A_1B_1BA.\)

У \(\Delta ABC\ AK\perp BC\) – висота та медіана. \(KC=5\) см.

У \(\Delta AKC\ (\angle K=90^\circ)\) за теоремою Піфагора

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв'язувати логарифмічні рівняння, знання числових проміжків.

За означенням логарифма \begin{gather*} \log_ab=c,\ \ b=a^c,\\[6pt] \log_{\frac 13}(x+1)=-2,\ \ x+1=\left(\frac 13\right)^{-2},\\[6pt] x+1=3^2,\ \ x+1=9,\ \ x=8.\\[7pt] 7\lt 8\le 9. \end{gather*} Отже, \(x\in (7; 9].\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Завдання перевіряє знання означення первісної.

Загальний вигляд первісної функції \(f(x)\)

\(F(x)=10x^5+C\), де \(C\) – довільне число.

Тоді, \(G(x)=10x^5+7.\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв'язувати систему лінійних нерівностей.

Розв'яжемо системи лінійних нерівностей:

\begin{gather*} \left\{\begin{array}{l} 4x-7\ge 2x+1,\\ x\ge -3, \end{array}\right.\ \ \left\{\begin{array}{l} 4x-2x\ge 1+7,\\ x\ge -3, \end{array}\right.\\[7pt] \left\{\begin{array}{l} 2x\ge 8,\\ x\ge -3, \end{array}\right.\ \ \left\{\begin{array}{l} x\ge 4,\\ x\ge -3. \end{array}\right. \end{gather*}

Отже, розв'язок нерівності \(x\in [4; +\infty).\)

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія.

Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач практичного змісту.

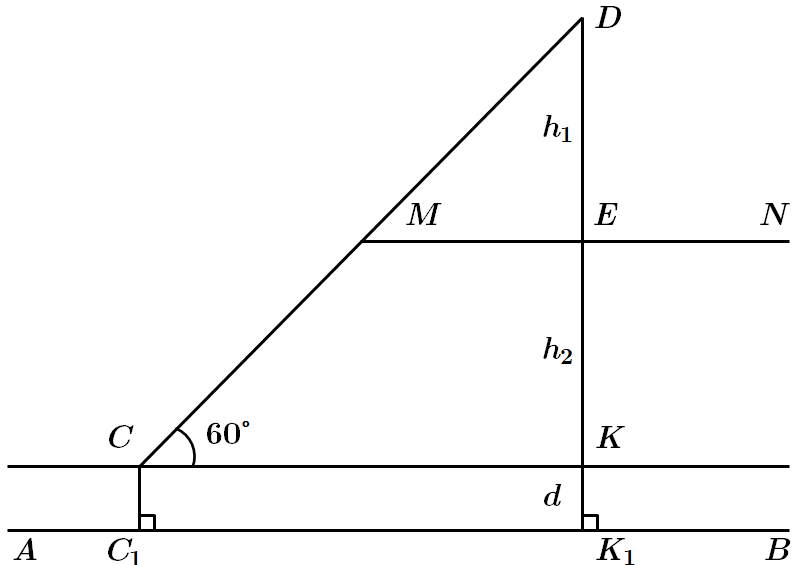
Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком.

1. Графік проходить через точку \((3; -2).\) Отже, 1 – Д.

2. Функція набуває лише додатних значень. Отже, 2 – Г.

3. Функція має лише один нуль (одна точка перетину з віссю \(Ox\)).
Отже, 3 – А.

Відповідь: 1 – Д, 2 – Г, 3 – А.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє знання властивостей степенів, вміння виконувати тотожні перетворення раціональних, степеневих виразів.

1. \(a^4:a^3=a^{4-3}=a^1=a.\) Отже, 1 – Г.

2. \(\frac{a^2-a}{1-a}=\frac{a(a-1)}{-(a-1)}=-a.\) Отже, 2 – Д.

3. \(7^{-\log_7a}=7^{\log_7a^{-1}}=a^{-1}=\frac 1a.\) Отже, 3 – B.

Відповідь: 1 – Г, 2 – Д, 3 – B.

ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.

Завдання перевіряє знання про подібні трикутники, властивість середньої лінії трапеції, властивості паралелограма.

\(BO:OK=2:3\), \(P_{ABCM}=84\), \(BC=12.\)

1. \(AB\ ||\ CM\) за умовою \(BC\ ||\ AM\) за властивістю трапеції. \(ABCM\) – паралелограм.

\(P_{ABCM}=2(AB+BC)=2(AB+12)=84\), \(AB=30.\)
Отже, 1 – Б.

2. \(\Delta BOC\) подібний \(\Delta KOM\) (за \(2\) кутами). \(\angle BOC=\angle MOK\) – вертикальні. \(\angle OBC=\angle OKM\) – внутрішні різносторонні.

Отже, 2 – B.

3. \(AD=2AM+MK=2\cdot 12+18=24+18=42.\)

Середня лінія трапеції дорівнює $$ \frac{BC+AD}{2}=\frac{12+42}{2}=\frac{54}{2}=27. $$ Отже, 3 – Г.

Відповідь: 1 – Б, 2 – B, 3 – Г.

ТЕМА: Геометрія. Стереометрія. Тіла обертання.

Завдання перевіряє знання формул для обчислення площ поверхонь та об'єму конуса.

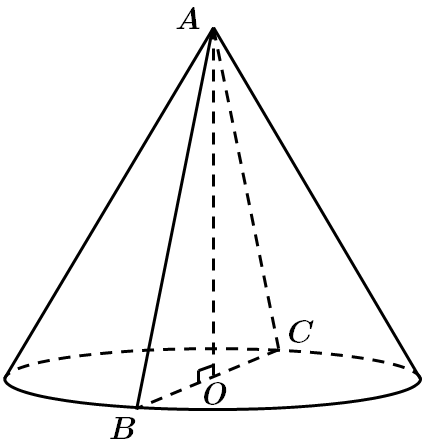
1. \(R=OB=6\), \(d=BC=12.\) Отже, 1 – Б.

2. \(R=OB=3\), \(AO=H=3\sqrt{3}.\)

\(\Delta AOB (\angle O=90^\circ)\) за теореою Піфагора \begin{gather*} AB^2=BO^2+AO^2=9+27=36,\\[7pt] AB=AC=BC=6. \end{gather*} Отже, 2 – A.

3. \(R=OB=4\), \(AO=H=3\), $$ S_\text{бічна}=\mathbf{\pi}Rl, $$ де \(l=AB=\sqrt{3^2+4^2}=5\), $$ S_\text{бічна}=\mathbf{\pi}\cdot 4\cdot 5=20\mathbf{\pi}. $$ Отже, 3 – Г.

Відповідь: 1 – Б, 2 – A, 3 – Г.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння розв'язувати задачі на відсоткові розрахунки та пропорції.

1. П'ята частина від вартості чохла – знижка. Отже, чохол буде коштувати \(\frac 45\)
від \(200\) грн. \(\frac{200\cdot 4}{5}=160\) грн.

Карта пам'яті – в подарунок. Сума грошей \(P\), які заплатить Михайло: $$ P=4500+160=4660\ \textit{грн}. $$

2. Якщо Михайло купував би не за акційними умовами, то заплатив би $$ 4500+200+300=5000\ \textit{грн}. $$ \(P\) від \(5000\) становить: $$ \frac{4660}{5000}\cdot 100\text{%}=\frac{466}{5}\text{%}=93\mathord{,}2\text{%}. $$

Відповідь: 1. \(4660.\)
                   2. \(93\mathord{,}2.\)

ТЕМА: Геометрія. Планіметрія. Чотирикутники. Коло та круг.

Завдання перевіряє вміння застосовувати властивості різних видів трикутників до розв'язування планіметричних задач.

\(BK=8\) см, \(KM=10\) см – діаметр.

1. \(BK=MD=8\) см, \(KM=10\) см.

За властивістю прямокутника, діагоналі рівні. \begin{gather*} AC=BD=BK+KM+MD=8+10+8=26\ \textit{см}. \end{gather*}

2. \(P_{ABCD}=2(AB+BC)\), \(AB=KM=10\) см.

\(\Delta ABD (\angle A=90^\circ)\) за теоремою Піфагора

Відповідь: 1. \(26.\)
                   2. \(68.\)

ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.

Завдання перевіряє знання формули \(n\text{-го}\) члена арифметичної прогресії.

1. За формулою \(n\text{-го}\) члена \(a_n=a_1+d(n-1).\)

\(a_2=a_1+d\), \(a_6=a_1+5d.\)

Отже, \(a_2-a_6=a_1+d-(a_1+5d)=a_1+d-a_1-5d=-4d=7\mathord{,}2.\)

\(d=7\mathord{,}2:(-4)=-1\mathord{,}8.\)

2. \(a_4=0\mathord{,}7\), \(a_4=a_1+3d\),

\(a_1=a_4-3d=0\mathord{,}7-3\cdot (-1\mathord{,}8)=0\mathord{,}7+5\mathord{,}4=6\mathord{,}1.\)

Відповідь: 1. \(-1\mathord{,}8.\)
                   2. \(6\mathord{,}1.\)

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати текстові задачі, застосовувати системи рівнянь до розв’язування текстових задач.

Нехай \(x\) грн – вартість квитка на ранковий сеанс, тоді \((x+15)\) грн – на вечірній.

\(4\) квитки на ранковий сеанс коштують \(4x\) грн, а \(6\) квитків на вечірній – \(6(x+15)\) грн.

За умовою, \begin{gather*} 6(x+15)-4x=220,\\[7pt] 6x+90-4x=220,\\[7pt] 2x=220-90,\\[7pt] 2x=130,\\[7pt] x=65. \end{gather*} \(65\) грн коштує квиток на ранковий сеанс.

Відповідь: \(65.\)

ТЕМА: Алгебра і початки аналізу. Елементи математичної статистики. Вибіркові характеристики.

Завдання перевіряє вміння обчислювати та аналізувати вибіркові характеристики рядів даних (середнє значення).

Знайдемо середнє значення за формулою:

Відповідь: \(9\mathord{,}8.\)

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє вміння розв’язувати задачі на обчислення об’ємів піраміди.

\(KABCD\) – правильна піраміда. \(ABCD\) – квадрат, \(AB=9\sqrt{2}\) см, \(BK=15\) см.

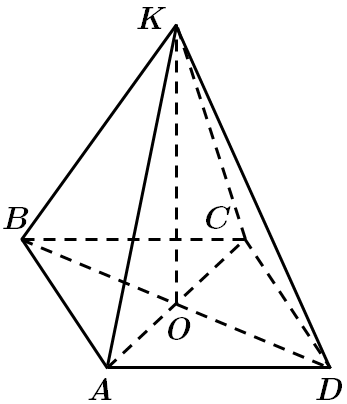
У квадраті \(BD=AB\cdot\sqrt{2}=9\sqrt{2}\cdot \sqrt{2}=18\) см.

У \(\Delta KOB\ (\angle O=90^\circ)\) за теоремою Піфагора \(BK^2=BO^2+KO^2\),

\(KO=\sqrt{15^2-9^2}=\sqrt{6\cdot 24}=\sqrt{6\cdot 6\cdot 4}=6\cdot 2=12\) см – висота піраміди.

\(S_{ABCD}=AB^2=(9\sqrt{2})^2=81\cdot 2=162\) см\(^2.\)

Об'єм піраміди знаходимо за формулою:

Відповідь: \(648.\)

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики.

Завдання перевіряє вміння розв‘язувати задачі, використовуючи перестановки, комбінаторне правило добутку.

На місце водія є \(2\) можливості посадити водія. Решта копанії розсядуться довільно. Кількість варіантів розсадити на пасажирські місця знаходимо за формулою: \begin{gather*} P(n)=n!,\\[7pt] P(5)=5!=120. \end{gather*}

Усього способів зайняти місця $$ 120\cdot 2=240. $$

Відповідь: \(240.\)

ТЕМА: Геометрія. Планіметрія. Трикутники. Координати та вектори на площині.

Завдання перевіряє вміння застосовувати властивості рівнобедреного трикутника, знаходити площу трикутника.

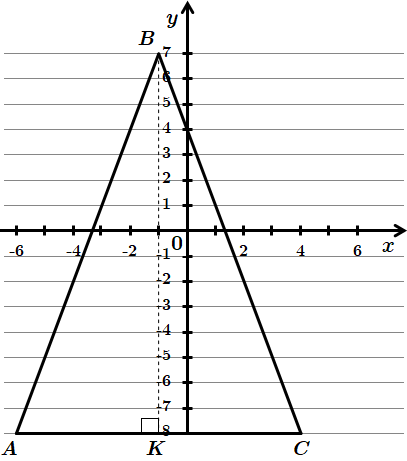
Накреслимо трикутник \(ABC. AB=BC.\) Отже, точка \(B\) має абсцису \(-1.\) \((AC=10).\) Нехай координати точки \(B(-1; y).\)

Точка \(B\) лежить на прямій \(y=2x+9,\) тому \(y=2(-1)+9=7,\) \(B(-1; 7).\) \(BK\perp AC.\) \(BK=15\) висота та медіана.

Відповідь: \(75.\)

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння будувати графіки лінійної та тригонометричної функцій, розв’язувати тригонометричні рівняння, встановлювати властивості числових функцій, заданих формулою або графіком.

Побудуємо графіки функцій

\(f(x)=\frac 12\) – пряма

\(g(x)=\sin x\) – синусоїда, \(x\in\left[-\frac{\mathbf{\pi}}{2}; \frac{\mathbf{\pi}}{2}\right].\)

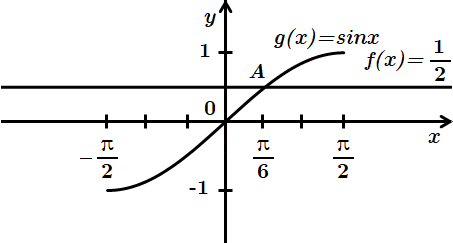
3. Спільна точка графіків функцій \(f\) та \(g\) є точка \(A\left(\frac{\mathbf{\pi}}{6}; \frac 12\right).\)

4. Множина всіх коренів \(f(x)=g(x)\) на інтервалі \((-\infty; +\infty)\) \begin{gather*} \sin x=\frac 12;\\[6pt] x=(-1)^n$1\ \frac 12+\mathbf{\pi}n,\ n\in Z;\\[6pt] x=(-1)^n\frac{\mathbf{\pi}}{6}+\mathbf{\pi}n, n\in Z. \end{gather*}

Відповідь: 3. \(\left(\frac{\mathbf{\pi}}{6};\frac 12\right).\)
                   4. \((-1)^n\frac{\mathbf{\pi}}{6}+\mathbf{\pi}n, n\in Z.\)

ТЕМА: Геометрія Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння будувати перерізи призми, знання теореми про три перпендикуляри, кута між прямою та площиною, вміння розв’язувати стереометричні задачі.

\(ABCDA_1B_1C_1D_1\) – прямокутний паралелепіпед, \(ABCD\) – прямокутник, бічні ребра – висоти паралелепіпеда, \(CC_1D_1D\) – квадрат, \(B_1C=8\) – діагональ бічної грані.

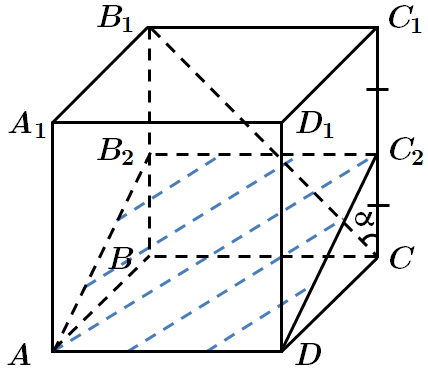
1. Точка \(C_2\) – середина ребра \(CC_1.\)

Побудуємо переріз площиною \(\mathbf{\gamma}\) через \(AD\) та точку \(C_2.\) \((AA_1D_1D)\ ||\ (BB_1C_1C)\) як протилежні грані паралелепіпеда. За властивістю паралельних площин, \(\mathbf{\gamma}\) перетинає паралельні площини по паралельних прямих.

Побудуємо \(B_2C_2\ ||\ BC(BB_1C).\) $$ \left.\begin{array}{l} \mathbf{\gamma}\cap (DD_1C_1)=DC_2\\ \mathbf{\gamma}\cap (AA_1B_1)=AB_2 \end{array}\right| \rightarrow AB_2C_2D - \text{шуканий переріз}. $$

2. Перший спосіб.
\(AB_2C_2D\) – паралелограм. \(AD=B_2C_2\), \(AD\ ||\ B_2C_2\) – ознака паралелограма.
\(C_2C\perp (ABC)\), \(C_2D\) – похила, \(CD\) – проекція похилої.
\(AD\perp DC\) (сторони прямокутника), тому \(C_2D\perp AD\) за теоремою про три перпенидкуляри.
Отже, в паралелограмі \(AB_2C_2D\ \angle D=90^\circ\), тому \(AB_2C_2D\) – прямокутник.

Другий спосіб.
У прямокутнику \(ABCD\) діагоналі \(AC=BD\) (за властивістю прямокутника). $$ \left.\begin{array}{l} B_2B\perp (ABC)\\ C_2C\perp (ABC) \end{array}\right| \rightarrow \left.\begin{array}{l} B_2D,\ \ C_2A - \text{похилі}.\\ BD,\ \ CA - \text{проекції похилих}. \end{array}\right. $$ За властивістю: рівним проекціям відповідають рівні похилі, \(B_2D=C_2A.\)
Отже, у прямокутнику \(AB_2C_2D\) рівні діагоналі. За ознакою прямокутника доводимо, що \(AB_2C_2D\) – прямокутник.

3. \(B_1C_1\perp (DCC_1)\)
\(B_1C\) – похила до площини \((DCC_1)\)
\(CC_1\) – проекція похилої.
За означенням кута між прямою та площиною

У \(\Delta C_2CD\ (\angle C=90^\circ)\) за теоремою Піфагора

Відповідь: \(16\sqrt{5}\sin2\mathbf{\alpha}.\)

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати ірраціональні та показникові рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

1. Розв'яжемо показникове рівняння:

2. \((3^{x+1}+3^{x+3}-10)\cdot (\sqrt{x^2+a}-\sqrt{3a-6-x^2})=0.\) \begin{gather*} \left[\begin{array}{l} 3^{x+1}+3^{x+3}-10=0,\\ \sqrt{x^2+a}-\sqrt{3a-6-x^2}=0, \end{array}\right. \\[7pt] \ \ \left[\begin{array}{l} x_1=-1,\\ \sqrt{x^2+a}=\sqrt{3a-6-x^2}. \end{array}\right. \end{gather*}

ОДЗ: \(3a-6-x^2\ge 0.\)

\(x_1=-1\) буде коренем рівняння, якщо буде належати ОДЗ.

Розв'яжемо друге рівняння:

Рівняння має корені, якщо \(a-3\ge 0\), \(a\ge 3.\)

Розглянемо параметричну пряму

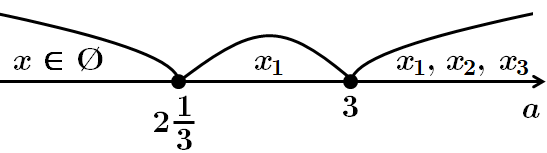
при \(a=3\ \ x_2=x_3=0.\)

Відповідь: 1. \(x=-1\)

                   2. якщо \(a\in \left(-\infty; 2\frac 12\right)\), то \(x\in\varnothing\)
                       якщо \(a\in \left[2\frac 13; 3\right)\), то \(x=-1\)
                       якщо \(a\in [3; +\infty)\), то \(x\in\{-1; \sqrt{a-3}; -\sqrt{a-3}\}.\)