ЗНО онлайн 2021 року з математики – пробний тест

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння аналізувати дані, подані графіком або таблицею.

А неправильно, бо зупинка тривала 1 годину, а не 4.

Б неправильно, бо туристи не пройшли 20 км.

В неправильно, бо туристи пройшли до зупинки більшу відстань, ніж після зупинки.

Г правильна відповідь. Туристи зробили зупинку через 4 години.

Відповідь: Г.

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку знання про многогранники та їх основні елементи.

\begin{gather*} AA_1=BB_1=CC_1=DD_1\\[7pt] AB=CD=C_1D_1=A_1B_1\\[7pt] AD=BC=B_1C_1=A_1D_1. \end{gather*} Сума усіх ребер дорівнює $$ 4(AA_1+AB+AD)=4\cdot 60=240\ (\text{см}) $$

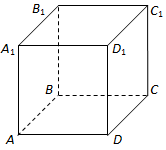
Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеня.

\begin{gather*} \frac{x}{10}=2,5;\\[6pt] x=2,5\cdot 10=25. \end{gather*}

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку вміння застосовувати означення та властивості трапеції.

І спосіб:
\(\angle ADB=\angle CBD=35^\circ\) як внутрішні різносторонні при \(BC\ ||\ AD\) та січної \(BD\). $$ \triangle BCD\ \angle B+\angle C+\angle D=180^\circ, $$ отже $$ \angle C=180^\circ - (20^\circ+35^\circ)=125^\circ. $$

ІІ спосіб:

За властивістю трапеції

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку розуміння змісту поняття екстремуму функції, знання геометричного змісту похідної.

На рисунку функція зростає при \(x \in [-2;-1]\), а спадає – при \(x\in [-1;4]\). Отже, \(x_0=-1\) – точка максимуму цієї функції (точка екстремуму).

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази та їх перетворення.

Завдання скеровано на перевірку знання формул скороченого множення, вміння виконувати тотожні перетворення виразів.

Спростимо вираз:

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення виразів.

З формули \(T=2\mathbf{\pi}\sqrt{LC}\) визначимо \(L\). \begin{gather*} T^2=(2\mathbf{\pi}\sqrt{LC})^2,\\[7pt] T^2=4\mathbf{\pi}^2LC,\\[6pt] L=\frac{T^2}{4\mathbf{\pi}^2C}. \end{gather*}

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази Дійсні числа та дії над ними.

Завдання скеровано на перевірку знання означення степеня з натуральним показником.

Спростимо вираз:

Використали властивості степенів: $$ (a\cdot b)^n=a^n\cdot b^n\ \text{та}\ a^m:a^n=a^{m-n} $$

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку знання властивостей та ознак паралелограма.

З наведених тверджень привильними є твердження II i III.

Протилежні кути паралелограма рівні (властивість).

Відстані від точки перетину діагоналей до протилежних сторін рівні. $$ \triangle BEO=\triangle DKO $$ за гіпотенузою та гострим кутом.

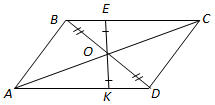
Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних рівнянь.

Розв'яжемо систему рівнянь методом додавання: \begin{gather*} \left\{ \begin{array}{l l} 6(x+5)+10y=3 & \\ 2x=y+4& \end{array}\right. \left\{ \begin{array}{l l} 6x+30+10y=3 & \\ 2x-y=4& \end{array}\right. \\[7pt] \left\{ \begin{array}{l l} 6x+10y=-27 & \\ 2x-y=4\ \ |\cdot (-3)& \end{array}\right. \left\{ \begin{array}{l l} 6x+10y=-27 & \\ -6x+3y=-12& \end{array}\right. \\[7pt] 13y=-39,\ \ y=-3. \end{gather*}

Підставимо значення \(y=-3\) у друге рівняння: \begin{gather*} 2x-(-3)=4;\ \ 2x+3=4; \\[6pt] 2x=1;\ \ x=\frac 12\\[6pt] x_0=\frac 12;\ \ y_0=-3. \end{gather*}

У відповідь запишемо суму $$ x_0+y_0=\frac 12+(-3)=-2,5. $$

Відповідь: А.

ТЕМА: Алгебра і початки аналізу. Функції. Похідна функції. Таблиця похідних та правила диференціювання.

Завдання скеровано на перевірку вміння знаходження похідної частки двох функцій.

Знайдемо похідну функції за правилом диференціювання частки:

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати показникові нерівності.

Розв'яжемо нерівність: \begin{gather*} 4\cdot 3^x\lt 3^x + 6,\\[7pt] 4\cdot 3^x-3^x\lt 6,\\[7pt] 3\cdot 3^3 \lt 6,\\[7pt] 3^x \lt 2,\\[7pt] x\lt \log_3 2,\\[7pt] x\in (-\infty;\ \log_3 2). \end{gather*}

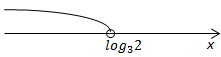
Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Функції. Тригонометричні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів, знання властивостей періодичних функцій.

Спростимо вираз: \(2\cos (450^\circ+\mathbf{\alpha})-\sin\mathbf{\alpha}\).

Функція \(y=\cos x\) періодична з періодом \(T=2\mathbf{\pi}\), отже \(\cos(x+T)=\cos x\).

оскільки $$ \cos(90^\circ+\mathbf{\alpha})=-\sin\mathbf{\alpha}. $$

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку знання властивостей прямокутника, трапеції, вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.

\(BK=KC=8\ \text{см},\ AK -\) бісектриса \(\angle A\).

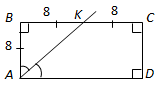
1. \(\angle A=90^\circ,\ \angle BAK=\angle KAD=45^\circ\).

2. \(\triangle ABK\ (\angle B=90^\circ)\ \angle K= 45^\circ\), отже \(AB=BK=8\ \text{см}\).

3. \(ABCD\) – прямокутник. За властивістю прямокутника

Відповідь: B.

ТЕМА: Геометрія. Стереометрія. Многогранники. Тіла обертання.

Завдання скеровано на перевірку вміння розв’язувати задачі, зокрема практичного змісту на обчислення площ поверхонь геометричних тіл.

\(AB=10\ \text{см},\ OK=1\ \text{см}\).

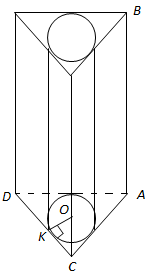
Бічні грані правильної трикутної призми виготовлені з паперу.

Площу паперу, витраченого на виготовлення коробки, визначимо за формулою площі бічної поверхні призми.

Радіус основи вписаного циліндра - це радіус кола, вписаного в правильний трикутник, \(OK=r=1\ \text{см}\).

Сторону трикутника знайдемо за формулою:

Відповідь, найближча до точної, – \(105\ \text{см}^2\).

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком, досліджувати на парність (непарність) функції.

1.

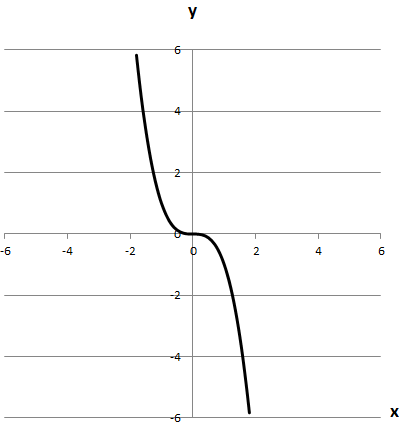
Симетричний відносно початку координат. Отже, 1 - Г.

2.

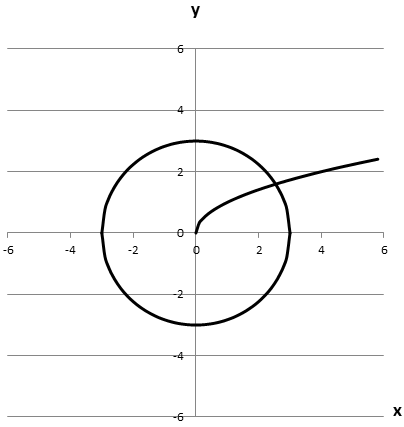
Має з графіком рівняння \(x^2+y^2=9\) лише одну спільну точку. Отже, 2 - Б.

3.

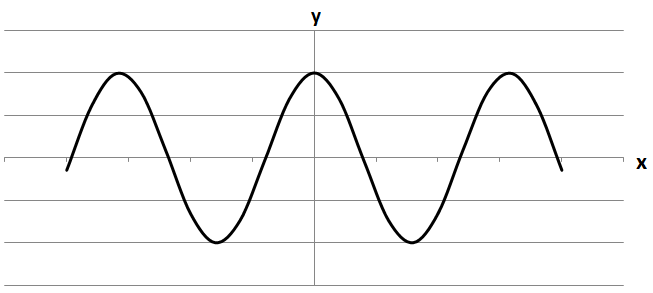
Симетричний відносно осі \(y\). Отже, 3 - В.

Відповідь: 1Г, 2Б, 3В.

ТЕМА: Геометрія. Планіметрія. Трикутники.

Завдання скеровано на перевірку знання видів трикутників та їх основних властивостей, кола, описаного навколо трикутника, теореми синусів.

1. Рис. 1 – рівносторонній трикутник, отже, центри вписаного та описаного кіл збігаються, 1 - А.

2. Рис. 3 – оскільки катет прямокутного трикутника в 2 рази менше гіпотенузи, то він лежить напроти кута 30°. Отже, 2 - В.

3. Рис. 5 – за теоремою синусів: \begin{gather*} \frac{6}{\sin 150^\circ}=2R,\ \frac{6}{\sin 30^\circ}=2R,\\[6pt] R=\frac{6}{2\cdot 1/2}=6\ (\text{см}), \end{gather*} радіус більший за 5 см, отже, 3 - Д.

Відповідь: 1A, 2В, 3Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.

Завдання скеровано на перевірку вміння виконувати дії з дійсними числами, порівнювати числа, розуміння поняття числового проміжку.

1. \((a-2,7)=4,5-2,7=1,8\in\ (1;\ 2)\), отже 1 - В.

2. \(\sqrt[3]{3,5-4,5}=\sqrt[3]{-1}=-1\in\ (-2;\ 0)\), отже 2 - A.

3. \begin{gather*} \log_5 a=\log_5 4,5;\\[7pt] \log_5 1\lt\log_5 4,5\lt \log_5 5.\\[7pt] y=\log_5 x\ \text{зростаюча функція}\\[7pt] 0\lt\log_5 4,5\lt 1, \end{gather*} отже, 3 - Б

Відповідь: 1В, 2А, 3Б.

ТЕМА: Геометрія. Стереометрія. Тіла обертання.

Завдання скеровано на перевірку вміння розрізняти на розгортках елементи тіл обертання, знаходити їх основні елементи.

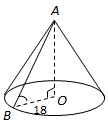
1. \(C=2\mathbf{\pi}R=36\mathbf{\pi}\ =>\ R=18\), отже 1 - Б.

2.

отже 2 - А.

3. Радіусом сектора, що є розготкою бічної поверхні конуса, є твірна \(AB\).

отже 3 - В.

Відповідь: 1Б, 2А, 3В.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними. Відсотки. Основні задачі на відсотки.

Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом, знаходити відсоток від числа.

1. Ціна пального під час першого заправлення становила 20 грн за 1 л. Для другого заправлення ціна зросла на 2,5% та стала $$ 20\cdot 102,5:100=20,5\ (\text{грн}). $$

2. За два заправлення автомобіля пальним всього витрачено грошей

Відповідь: 1. 20,5. 2. 1620.

ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.

Завдання скеровано на перевірку знання властивостей ромба, подібних трикутників, теореми Піфагора.

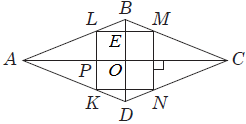
1. За теоремою Піфагора, \(PL^2=AL^2-AP^2=100-64=36.\) \(PL=6\ \text{см}\).

2. \(\triangle APL\sim \triangle LEB\) (за гострим кутом). \(\angle LAP=\angle BLE\) - відповідні при \(AP\ ||\ LE\) та січної \(AB\). \begin{gather*} \frac{AP}{LE}=\frac{LP}{BE};\ \frac 86=\frac{6}{BE},\\[6pt] BE=\frac{6\cdot 6}{8}=4,5\ \text{см},\\[6pt] BO=BE+EO=4,5+6=10,5\ \text{см},\\[7pt] BD=2\cdot BO=21\ \text{см}. \end{gather*}

Відповідь: 1. 12. 2. 21.

ТЕМА: Геометрія. Стереометрія. Координати і вектори у просторі.

Завдання скеровано на перевірку вміння виконувати дії з векторами, знаходити координати та модуль вектора.

1. Нехай \(\text{т.}\ B(x;\ y;\ z).\ \overline{AB}(x-3;\ y+7;\ z-11)\). Отже, \begin{gather*} x-3=9,\ x=12,\\[7pt] y+7=12,\ y=5,\\[7pt] z-11=-8,\ z=3. \end{gather*} ордината \(\text{т.}\ B\ y_B=5\).

2.

Відповідь: 1. 5. 2. 51.

ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.

Завдання скеровано на перевірку розуміння змісту поняття «сума n-перших членів арифметичної прогресії», знання формули суми n-перших членів арифметичної прогресії, формули n-го члена арифметичної прогресії.

Сума \(n\)-перших членів арифметичної прогресії: $$ S_n=\frac{5,2-0,8n}{2}\cdot n $$

1.

2.

Оскільки \(a_1=2,2,\ a_1+a_2=3,6\). Отже, \(a_2=1,4\) $$ d=a_2-a_1=1,4-2,2=-0,8. $$ За формулою \(n\)-го члена арифметичної прогресії,

Відповідь: 1. 1,2. 2. –0,2.

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.

Завдання скеровано на перевірку знання класичного означення ймовірності події, вміння аналізувати графічну форму подання статистичних даних.

Робіт з оцінкою Д - 4, всього робіт - 32.

Отже, ймовірність того, що першою буде відібрано роботу з оцінкою Д $$ P=\frac{4}{32}=\frac 18=0,125 $$ Відповідь, яку округлили до сотих, становить $$ 0,125\approx 0,13 $$

Відповідь: 0,13.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їх системи. Відношення та пропорції.

Завдання скеровано на перевірку вміння розв’язувати текстові задачі за допомогою рівнянь на пропорційні величини та пропорційний поділ.

Нехай \(x\ \text{с}\) – тривалість жовтого сигналу, систематизуємо дані:
Зелений - \(12x\ \text{с}\)
Червоний - \((12x-15)\ \text{с}\)
Жовтий - \(x\ \text{с}\).

Тривалість зеленого сигналу відноситься до сумарної тривалості червоного та жовтого сигналів як 3 до 2.

Отже, \begin{gather*} \frac{12x}{12x-15+x}=\frac 32,\ \ \frac{12x}{13x-15}=\frac 32,\\[6pt] 3(13x-15)=2\cdot 12x,\ \ 39x-45=24x,\\[7pt] 15x=45,\ \ x=3. \end{gather*} Тривалість червоного сигналу: $$ 12x-15=12\cdot 3-15=36-15=21\ \text{с}. $$

Відповідь: 21.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення ірраціональних виразів та знаходити їх числове значення.

Відповідь: 7.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння, використовуючи означення та властивості модуля.

Якщо \(x\geq 0\), то \(|x|=x\). Отже, \(x+4x=3,\ 5x=3,\ x=0,6\).

Якщо \(x\lt 0\), то \(|x|=-x\). Отже, \(x-4x=3,\ -3x=3,\ x=-1\).

У відповідь запишемо їхню суму \(0,6+(-1)=-0,4\).

Відповідь: –0,4.

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.

Завдання скеровано на перевірку вміння розв’язувати задачі, використовуючи розміщення (без повторень), комбінаторні правила суми та добутку.

Кількість способів вибрати 2 теми з 10 запропонованих знаходимо за формулою розміщень:

Відповідь: 90.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння знаходити область значень функції, будувати графіки квадратичних функцій, установлювати властивості числових функцій, заданих формулою, використання перетворення графіків функцій, знаходити первісну функції.

1. \begin{gather*} y(0)=2\cdot 0+8=8\\[7pt] y=0,\ \ 2x+8=0,\ \ x=-4\\[7pt] y(9)=2\cdot 9+8=26. \end{gather*}

2. \(M(-4;\ 0)\) – точка перетину графіка функції з віссю \(x\).

3.

4. Первісна функції \(f\), яка проходить через точку \(M(-4;\ 0)\) \begin{gather*} 0=(-4)^2+8\cdot (-4)+C,\\[7pt] 0=16-32+C,\ \ C=16\\[7pt] F(x)=x^2+8x+16. \end{gather*}

5. Побудуємо графік функції \(F(x)=x^2+8x+16\), \(F(x)=(x+4)^2\).

Використаємо елементарні перетворення графіків:

\(F(x)=x^2 \rightarrow F(x)=(x+4)^2\) переносимо вліво на 4 одиниці вздовж осі \(Ox\).

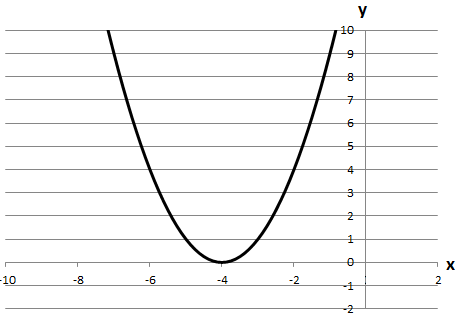
6. Область визначення функції \(F(x)\ E(y)=[0;\ +\infty)\).

Функцію \(G(x)=3F(x)+1\) отримаємо з функції \(F(x)\) стисканням в 3 рази до осі \(Oy\) та паралельним перенесенням на 1 одиницю вгору вздовж осі \(Oy\).

Отже, \(E(G)=[1;\ \infty)\).

Відповідь:

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку вміння розв’язувати задачі на обчислення об’ємів геометричних тіл, знання основних властивостей піраміди.

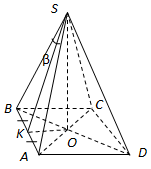
1. \(SABCD\) - правильна піраміда. \(ABCD\) - квадрат, \(SO\) - висота, \(AC\cap BD=0\).

\(SK\perp AB,\ SK=6\) - апофема.

\(\angle BSA=\mathbf{\beta}\) - плоский кут при вершині \(S\).

2. \(\triangle BSA\) - рівнобедрений \(\rightarrow SK\) - висота, бісектриса та медіана. \begin{gather*} \angle KSA=\frac{\mathbf{\beta}}{2},\ \ SK=6.\\[6pt] AK=SK\operatorname{tg} S=6\operatorname{tg}\frac{\mathbf{\beta}}{2}.\\[6pt] AB=2AK=12\operatorname{tg}\frac{\mathbf{\beta}}{2}. \end{gather*}

3. \(OK=AK=6\operatorname{tg}\frac{\mathbf{\beta}}{2}\) (\(\triangle AOB\) - рівнобедрений прямокутний). $$ S_{ABCD}=AB^2=\left(12\operatorname{tg}\frac{\mathbf{\beta}}{2}\right)^2=144\operatorname{tg}^2\frac{\mathbf{\beta}}{2}. $$ У \(\triangle SOK\ (\angle O=90^\circ)\) за теоремою Піфагора:

Відповідь: 2. \(12\operatorname{tg}\frac{\mathbf{\beta}}{2}\)
3. \(\frac{288\operatorname{tg}^2\frac{\mathbf{\beta}}{2}\sqrt{\cos\mathbf{\beta}}}{\cos\frac{\mathbf{\beta}}{2}}\)

ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.

Завдання скеровано на перевірку вміння знаходити кути у просторі, знання про двогранний кут, лінійний кут двогранного кута.

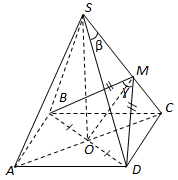
1. \(\triangle DSC=\triangle BSC\) (\(SABCD\) - правильна піраміда), \(DM\perp SC\), \(BM\perp SC\) - відповідні висоти в рівних трикутниках. \((DSC)\cap(BSC)=SC\). \begin{gather*} \left. \begin{array}{ c c c} SC\perp MD & \\ SC\perp MB & \\ BM\cap DM& \end{array}\right| \rightarrow (BMD)\perp SC\rightarrow \end{gather*} \(\angle BMD\) - лінійний кут відповідного двогранного між \((BSC)\) та \((DSC)\).
\(\angle BMD=\mathbf{\gamma}\).

2. 1) \(\triangle SOD\ (\angle O=90^\circ)\)

2) \(\triangle BMD\) - рівнобедрений (\(BM=MD)\) \(MO\) - бісектриса, висота та медіана. $$ \angle BMD=\angle OMD=\frac{\mathbf{\gamma}}{2}. $$

3) \begin{gather*} \triangle SMD\ (\angle M=90^\circ)\\[6pt] MD=SD\cdot\sin\mathbf{\beta}=\frac{6\sin\mathbf{\beta}}{\cos\frac{\mathbf{\beta}}{2}}=\\[6pt] =\frac{6\cdot 2\sin\frac{\mathbf{\beta}}{2}\cos\frac{\mathbf{\beta}}{2}}{\cos\frac{\mathbf{\beta}}{2}}=12\sin\frac{\mathbf{\beta}}{2}. \end{gather*}

4)

Відповідь: \(2\arcsin\left(\frac{1}{\sqrt{2}\cos\frac{\mathbf{\beta}}{2}}\right)\).

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних та раціональних виразів.

Доведемо тотожність

що й вимогалось довести.

При доведенні використали формули: \begin{gather*} \sin2x=2\sin x\cos x\\[6pt] \sin^2x+\cos^2x=1\\[6pt] x^3-y^3=(x-y)(x^2+xy+y^2). \end{gather*}

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні, квадратні рівняння та рівняння з параметрами.

1. Знайдемо множину допустимих значень змінної \(x\):

2. Розв'яжемо рівняння залежно від значень \(a\): \begin{gather*} \left\{ \begin{array}{ l l} \left[ \begin{array}{l l} x-2=0 & \\ x^2-3(a-1)x+2a^2-3a=0& \end{array}\right. &\\ x\in (-\infty;\ -0,5)\cup (-0,5;\ 1,5) & \end{array}\right. \end{gather*}

1) \(x-2=0,\ \ x=2\ \notin\) ОДЗ.

2) \(x^2-3(a-1)x+2a^2-3a=0\).

Розв'яжемо квадратне рівняння: \begin{gather*} D=\left(-3(a-1)\right)^2-4(2a^2-3a)=\\[7pt] =9(a^2-2a+1)-8a^2+12a=(a-3)^2\\[6pt] x_1=\frac{3(a-1)+(a-3)}{2}=2a-3;\\[6pt] x_2=\frac{3(a-1)-(a-3)}{2}=a. \end{gather*}

Знайдемо значення переметра \(a\), при яких \(x_1=2a-3\) належить ОДЗ: \begin{gather*} \left[ \begin{array}{l l} 2a-3\lt -0,5 & \\ -0,5\lt 2a-3\lt 1,5& \end{array}\right. \left[ \begin{array}{l l} a\lt 1,25 & \\ 1,25\lt a\lt 2,25& \end{array}\right. \\[7pt] a\in (-\infty;\ 1,25)\cup (1,25;\ 2,25). \end{gather*} Для кореня \(x_2=a\) \begin{gather*} \left[ \begin{array}{l l} a\lt -0,5 & \\ a\in (-0,5;\ 1,5)& \end{array}\right. \\[7pt] a\in (-\infty;\ -0,5)\cup (-0,5;\ 1,5). \end{gather*}

Відповідь:
якщо