ЗНО онлайн 2021 року з математики – основна сесія

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння аналізувати дані, подані графіком або таблицею.

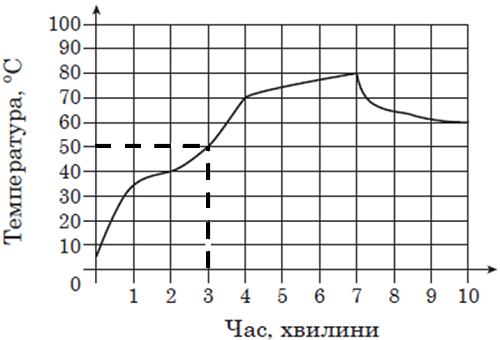
Температура двигуна була не більшою за 50 °C протягом 3 хвилин.

Відповідь: В.

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку знання про многогранники та їх основні елементи, вміння розв’язування задач, зокрема практичного змісту.

Якщо радіус кульки 6 см, то діаметр – 12 см.

Для того, щоб кульки помістилися у шухлядці, її висота може бути 13 см.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеню.

Розв'яжемо лінійне рівняння:

\begin{gather*} 1-5x=0\\[7pt] -5x=-1\\[6pt] x=\frac{-1}{-5}\\[6pt] x=\frac 15 \end{gather*}

Відповідь: B.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку знання формули суми кутів чотирикутника.

Сума кутів будь-якого чотирикутника 360°. Сума трьох кутів – 280°, тому четвертий кут: $$ 360^\circ-280^\circ=80^\circ $$

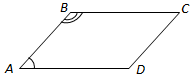
Якщо гострі кути паралелограма \(\angle A=\angle C=80^\circ\), то \(\angle B=\angle D=180^\circ - 80^\circ = 100^\circ\).

Сума кутів, прилеглих до будь-якої сторони паралелограма, дорівнює 180° (як внутрішні односторонні при паралельних прямих і січної).

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів.

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих графіком.

Дано: лінійна функція \(y=-2x+3\).

\(k=-2\), отже, функція спадна
\(b=3\), отже, точка перетину графіка з віссю \(Oy\) (0; 3).

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.

Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом.

Атмосферний тиск \(p= 760-\frac{10h}{100}\).

На висоті \(h\) метрів атмосферний тиск знижується на 10 мм рт. ст. кожні 100 м.

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку знання властивостей та ознак ромба.

І. Навколо чотирикутника можна описати коло, якщо сума протилежних кутів дорівнює 180°. Ця властивість у будь-якому ромбі не виконується. Отже, твердження неправильне.

ІІ. Діагоналі ромба взаємно перпендикулярні (властивість ромба). Правильне твердження.

ІІІ. У будь-якому ромбі всі сторони рівні (означення ромба). Правильне твердження.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати ірраціональні рівняння.

Розв'яжемо ірраціональне рівняння: $$ \sqrt{x+12}=3 $$ піднесемо обидві частини рівняння до квадрату.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Функції. Первісна функції.

Завдання скеровано на перевірку вміння знаходження первісної степеневої функції.

Знаходимо первісну степеневої функції:

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.

Завдання скеровано на перевірку знання властивостей степенів з цілим показником.

Використовуємо властивості степенів: $$ a^n\cdot b^n=(a\cdot b)^n;\ \ a^n:b^n=a^{n-m}. $$

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні нерівності.

Функція \(y=\log_{0,9}(3x)\) – спадна, отже, знак нерівності змінюємо на протилежний. Враховуючи ОДЗ, отримаємо: \begin{gather*} \left\{ \begin{array}{l l} 3x\gt 0 & \\ 3x\lt 0,9^2& \end{array}\right. \left\{ \begin{array}{l l} x\gt 0 & \\ 3x\lt 0,81& \end{array}\right. \left\{ \begin{array}{l l} x\gt 0 & \\ x\lt 0,27& \end{array}\right. \end{gather*}

\(x\in\ (0;\ 0,27)\)

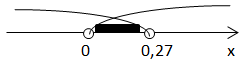
Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Тригонометричні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів.

Формула синуса подвійного кута \(\sin 2x=2\sin x\cos x\) є в довідкових матеріалах.

Відповідь: В.

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку вміння розв’язувати задачі на обчислення площ поверхонь геометричних тіл.

\(EABCD\) – правильна піраміда, \(ABCD\) – квадрат зі стороною 6 см.

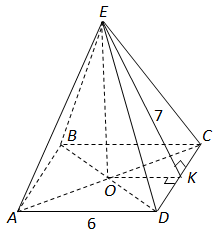
Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Трикутники.

Завдання скеровано на перевірку знання властивостей трикутника, вміння розв’язувати задачі практичного змісту.

Побудуємо математичну модель задачі:

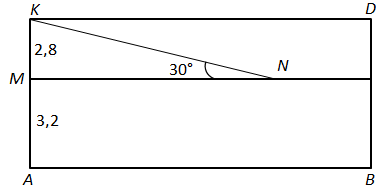
Катет \(KM\) протилеглий куту \(30^\circ\) дорівнює половині гіпотенузи \(KN\). $$ 5,5 \leq 5,6\lt 6 $$

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком, досліджувати на парність (непарність) функції.

1. \((x-3)^2+(y-4)^2=4,\ \ (3;\ 4)\) – центр кола, \(R=2\).

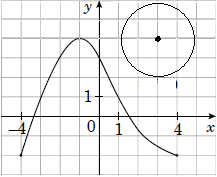
Графік функції не має спільних точок з колом. Отже, 1 - Г.

2.

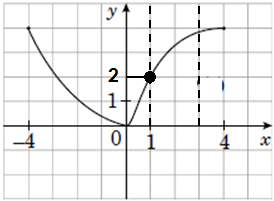
Найменше значення функції на проміжку \([1;\ 3]\) дорівнює \(2\). Отже, 2 - Б.

3. Графік функції тричі перетинає пряму \(y=1\). Отже, 3 - Д.

Відповідь: 1Г, 2Б, 3Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні, логарифмічні вирази та їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення виразів, порівнювати числа, розуміння поняття числового проміжку.

1. $$ a^2=\left(-2\frac 13\right)^2=\left(-\frac 73\right)^2=\frac{49}{9}=5\frac 49 $$ число більше від 5, отже, 1 - А.

2. \begin{gather*} a+|a|=a+(-a)=0,\ \text{оскільки}\ a\lt 0.\\[6pt] |a|= \left\{ \begin{array}{l l} a,\ \text{якщо}\ a\geq 0, & \\ -a,\ \text{якщо}\ a\lt 0,& \end{array}\right. \end{gather*} Отже, 2 - Д.

3. \begin{gather*} \log_5 5^a=a\log_5 5=a\cdot 1=a=-2\frac 13, \end{gather*} є від'ємним числом, отже, 3 - В.

Відповідь: 1A, 2Д, 3В.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку знання властивостей квадрата, трапеції; вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.

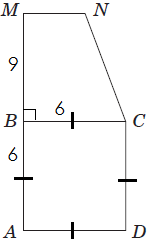
\(S_{ABCD}=S_{BMNC}=36\ \text{см}^2,\ \ AM=15\ \text{см}\).

1. \(S_{ABCD}=AB^2=36\ \text{см}^2,\ AB=6\ \text{см}\) – сторона квадрата, отже, 1 - Г.

2. У прямокутній трапеції \(BM\) – висота.
\(BM=AM-AB=15-6 = 9\ \text{см}\), отже, 2 - Д.

3. \begin{gather*} S_{BMNC}=\frac{MN+BC}{2}\cdot BM,\\[6pt] 36=\frac{MN+6}{2}\cdot 9,\\[6pt] 72 = (MN+6)\cdot 9\\[7pt] MN =2\ \text{см}. \end{gather*} отже, 3 - A

Відповідь: 1Г, 2Д, 3A.

ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.

Завдання скеровано на перевірку знання поняття відстані від точки до площини, між паралельними площинами.

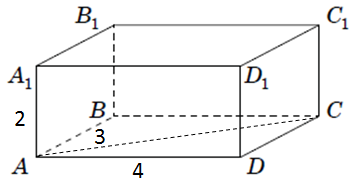
Усі грані цього прямокутного паралепіпеда – прямокутники.

1. \(CB\perp (AA_1B_1)\) – відстань від т.\(C\) до \((AA_1B_1),\ CB=4\), отже, 1 - B.

2. \(CC_1\perp (ABC),\ AC\subset\ (ABC)\rightarrow\) відстань від т.\(A\) до \(CC_1\) – це відрізок \(AC.\)
\(AC^2=AD^2+DC^2,\ AC=\sqrt{3^2+4^2}=5\). Oтже, 2 - Г.

3. \((ABC)||(A_1B_1C_1)\). Отже, відстань між ними – це довжина бічного ребра. \(AA_1=2\). Отже, 3 – A.

Відповідь: 1B, 2Г, 3A.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними. Відсотки. Основні задачі на відсотки.

Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом, знаходити відсоток від числа.

1. Повернуті гроші – це вартість квитка й половина вартості плацкарти. Крім того, стягнуть збір 18 грн.

2. Сума грошей \(P\) від вартості документа становить: $$ \frac{90}{240}\cdot 100\ \text{%}=37,5\ \text{%} $$

Відповідь: 1. 90. 2. 37,5.

ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.

Завдання скеровано на перевірку знання властивостей трикутників та їх основних властивостей.

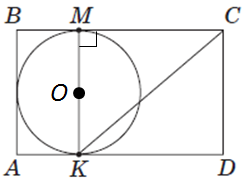
\(P_{ABMK}=24\ \text{см}\ \ KC=17\ \text{см}.\)

1.

2. \(2OM=MK=8\ \text{см}, \triangle MKC\ (\angle M=90^\circ)\) - за теоремою Піфагора

Відповідь: 1. 4. 2. 152.

ТЕМА: Геометрія. Стереометрія. Координати і вектори у просторі.

Завдання скеровано на перевірку вміння виконувати дії з векторами, знаходити координати та скалярний добуток векторів.

1. \begin{gather*} A(x;\ y;\ z)\ \ \overline{AB}(7-x;\ -2-y;\ 0-z)\\[7pt] \overline{AB}(7-x;\ -2-y;\ -z)\\[7pt] \overline{AB}(-3;\ 8;\ 1)\\[7pt] 7-x=-3,\ x=10,\\[7pt] -2-y=8,\ y=-10,\\[7pt] -z=1,\ z=-1. \end{gather*} ордината \(\text{т.}\ A\ =\ -10\).

2.

За формулою скалярного добутку:

Відповідь: 1. –10. 2. –111.

ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.

Завдання скеровано на перевірку знання властивостей арифметичної прогресії, знання формули n-го члена арифметичної прогресії.

Арифметичну прогресію задано \(a_n=2,6n-7\)

1. \(a_7=2,6\cdot 7-7=18,2-7=11,2\)

2.

Отже,

Відповідь: 1. 11,2. 2. 7,8.

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.

Завдання скеровано на перевірку знання класичного означення ймовірності події, правила добутку ймовірностей.

У класі 26 дітей. Учительна навмання формує пари дітей. Імовірність того, що Дарина сидітеме за однією партою з дівчинкою: $$ P(A)=\frac{14}{25}=0,56 $$

Дівчат у класі, крім Дарини, чотирнадцять. Усього дітей у класі (без Дарини) – 25.

Відповідь: 0,56.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їх системи. Відношення та пропорції.

Завдання скеровано на перевірку вміння розв’язувати текстові задачі за допомогою рівнянь, на пропорційні величини та пропорційний поділ.

Нехай \(x\) – коефіцієнт пропорційності. Дезінфікувальний розчин містить:
\(2x\ \text{г}\) – концентрату
\(7x\ \text{г}\) – води
\(\frac{7x}{10}\ \text{г}\) – ароматичної рідини. Разом \(485\ \text{г}\)

\begin{gather*} 2x+7x+0,7x=485\\[7pt] 9,7x=485\\[7pt] x=50. \end{gather*} Концентрату потрібно $$ 2x=2\cdot 50=100\ \text{г}. $$

Відповідь: 100.

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення ірраціональних виразів та знаходити їх числове значення.

Вираз \(3a-4=3\cdot 0,7-4=2,1-4=-1,9\).

Отже, \(|3a-4|=-3a+4\).

Значення виразу $$ -6a+4=-6\cdot 0,7+4=-4,2+4=-0,2. $$

Відповідь: –0,2.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати рівняння, що зводяться до квадратних.

Рівняння \(x^4-x^2-20=0\) – біквадратне. Розв'яжемо заміною:

Повернемось до заміни:

Добуток його дійсних коренів: $$ x_1\cdot x_2=\sqrt{5}\cdot (-\sqrt{5})=-5. $$

Відповідь: –5.

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.

Завдання скеровано на перевірку знання означення перестановок, комбінаторних правил суми та добутку.

Послідовність розміщення 6 новин у стрічці:

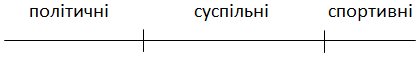
Кількість розміщень політичних новин в стрічці \(2!\), а суспільних новин – \(3!\). Спортивна новина 1 та йде останньою.

За правилом добутку кількість розміщення цих 6 новин: $$ 2!\cdot 3!=1\cdot 2\cdot 1\cdot 2\cdot 3=12 $$

Відповідь: 12.

ТЕМА: Алгебра і початки аналізу. Функції. Дослідження функції за допомогою похідної. Побудова графіків функції.

Завдання скеровано на перевірку вміння знаходити похідну функції, нулів функції, екстремумів функції, будувати графіки функцій; знання достатньої умови зростання (спадання) функції.

Задано функцію \(y=x^3-3x\)

1.

2. Точки перетину графіка \(y=x^3-3x\) із віссю \(x\) знаходимо за умови \(y=0\): \begin{gather*} x^3-3x=0,\ \ x(x^2-3)=0,\\[7pt] x(x-\sqrt{3})(x+\sqrt{3})=0\\[7pt] \left [ \begin{array}{l l} x=0 & \\ x=\sqrt{3}& \\ x=-\sqrt{3}& \end{array}\right. \end{gather*} \((0;\ 0),\ (\sqrt{3};\ 0),\ (-\sqrt{3};\ 0)\) – точки перетину з віссю \(x\).

3.

4. \begin{gather*} f'(x)=0,\ \ 3x^2-3=0,\\[7pt] 3(x^2-1)=0,\ \ 3(x-1)(x+1)=0\\[7pt] \left [ \begin{array}{l l} x-1=0 & \\ x+1=0& \end{array}\right. \ \ \left [ \begin{array}{l l} x=1 & \\ x=-1& \end{array}\right. \end{gather*}

5. Визначимо проміжки зростання і спадання функції

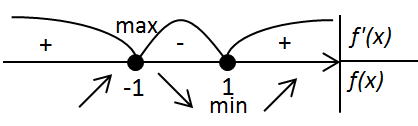
При \(f'(x)\gt 0\) функція зростає, при \(f'(x)\lt 0\) – спадає. Отже,
\(f(x)\) зростає при \(x \in (-\infty;\ -1]\) i \([1;\ +\infty)\);
\(f(x)\) спадає при \(x\in [-1;\ 1]\).

Точки екстремуму: \(x_{max}=-1;\ \ x_{min}=1\),
екстремуми функції: \(f_{max}=f(-1)=2;\ \ f_{min}=f(1)=-2\).

6.

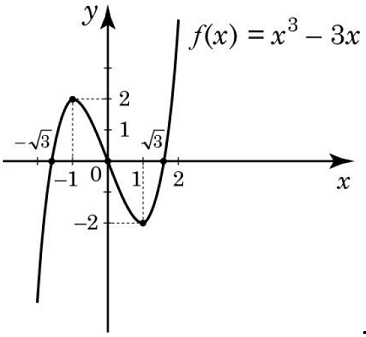
Відповідь:

1. \(x=0,\ \ y=0,\)
\(x=-1,\ \ y=2,\)
\(x=2,\ \ y=2\).
2. \((0;\ 0),\ (\sqrt{3};\ 0),\ (-\sqrt{3};\ 0)\).
3. \(f'(x)=3x^2-3\).
4. \(x=1;\ \ x=-1\).
5. Проміжки зростання: \((-\infty;\ -1],\ [1;\ +\infty)\)
проміжок спадання: \([-1;\ -1]\)
\(x_{max}=-1;\ \ x_{min}=1\).
\(f_{max}=2;\ \ f_{min}=-2\).

ТЕМА: Геометрія. Стереометрія. Тіла обертання.

Завдання скеровано на перевірку вміння знаходити кути у просторі, побудову осьового перерізу циліндру.

1. Осьовий переріз циліндра (прямокутник \(ABCD\)) зображено на рисунку:

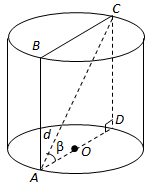
2. Твірна \(CD\) перпендикулярна основі, \(CA\) – діагональ, \(AD\) – проекція діагоналі на нижню основу циліндра. Отже, \(\angle CAD=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\).

3. Об'єм циліндра знаходимо за формулою: $$ V=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2H, $$ де \(R=OA=OD\) – радіус основи циліндра, \(H=CD\) – висота.

Отже,

Відповідь: \(\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}d^3\cos^2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\cdot \sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}}{4}\)

ТЕМА: Геометрія. Стереометрія. Тіла обертання. Прямі та площини у просторі.

Завдання скеровано на перевірку вміння знаходити кути у просторі, знання про двогранний кут, лінійний кут двогранного кута.

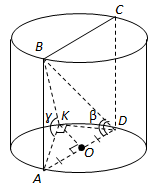
1. Прямокутник \(ABCD\) - осьовий переріз циліндра.

\(AC=BD=d\). Точка \(K\) лежить на колі нижньої основи циліндра \(\smile AK=90^\circ\), тому \(\angle AOK=90^\circ\).

Пряма \(KD\) – пряма перетину площини \((KBD)\) з площиною нижньої основи.

\(\angle AKD=90^\circ\) (як вписаний кут, що спирається на діаметр), то \(AK\perp KD\).

Таким чином, \(\angle AKB=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\) – лінійний кут двогранного кута між площинами (\(BKD)\) і площиною основи циліндра.

2. \(\triangle AKD\) – рівнобедрений (\(KO\) – медіана та висота) \(AD=d\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\), тому за теоремою Піфагора:

Отже, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}=\mathrm{arctg}\left(\sqrt{2}\mathrm{tg}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\right)\).

Відповідь: 2. \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}=\mathrm{arctg}\left(\sqrt{2}\mathrm{tg}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\right)\).

ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних та раціональних виразів.

Доведемо тотожність.
I спосіб:

Отже, вирази рівні.

ІІ спосіб:

Розкладемо вираз \(2a^2+5a-3\) на множники:

Розклали за формулою: \(ax^2+bx+c=a(x-x_1)(x-x_2)\), де \(x_1,\ x_2\) – корені квадратного тричлена.

Отримаємо, \begin{gather*} \frac{(2a-1)(a+3)}{a+3}=\frac{1-2a}{-1}\\[6pt] 2a-1=2a-1, \end{gather*} вирази рівні.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.

Завдання скеровано на перевірку вміння розв’язувати показникові, квадратні рівняння та рівняння з параметрами.

1. Розв'яжемо систему, якщо \(a=0\).

Підставимо у друге рівняння замість \(4^{\sqrt{y}}\) число 2.

Отже, за \(a=0\) розв'язком системи є \((-3;\ 0,25)\).

2. Нехай \(a\ne 0\).

Почленно додамо рівняння \begin{gather*} ax^2+3ax+4\cdot 4^{\sqrt{y}}-2x-4\cdot 4^{\sqrt{y}}+2=8\\[7pt] ax^2+3ax-2x-6=0,\\[7pt] ax^2+(3a-2)x-6=0. \end{gather*}

Отримаємо квадратне рівняння.

Система рівносильна сукупності систем:

Оскільки \(4^{\sqrt{y}}\geq 1\ \left(y\geq 0,\ \sqrt{y}\geq 0,\ 4^{\sqrt{y}}\geq 4^0\right)\), отримуємо

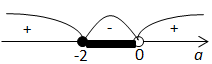
Тоді \begin{gather*} \left\{ \begin{array}{l l} x=\frac 2a, & \\ \sqrt{y}=\log_4\frac{a-2}{2a}, & \end{array}\right. \left\{ \begin{array}{l l} x=\frac 2a, & \\ y=\log^2_4\frac{a-2}{2a}. & \end{array}\right. \end{gather*}

Відповідь:
1. \((-3;\ 0,25)\)
2. якщо \(a\in (-\infty;\ -2)\cup [0;\ +\infty)\), то розв'язком є \((-3;\ 0,25)\)
якщо \(a\in [-2;\ 0)\), то розв'язками є \((-3;\ 0,25)\) та \(\left(\frac 2a;\ \log^2_4\frac{a-2}{2a}\right)\).