ЗНО онлайн 2021 року з математики – додаткова сесія
Тестові завдання додаткової сесії ЗНО 2021 року з математики
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.
Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом.
| Поверхи | Номери квартир |
| 1 | 1–6 |
| 2 | 7–14 |
| 3 | 15–22 |
| 4 | 23–30 |
| 5 | 31–38 |
Отже, квартира №31 знаходиться на 5 поверсі.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи математичної статистики.
Завдання скеровано на перевірку вміння аналізувати інформацію, подану у графічній формі.
Кількість відвідувачів у червні становила
На діаграмі Г правильно зображено розподіл відвідувачів.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання скеровано на перевірку знання про сферу та її основні елементи, вміння розв’язувати стереометричні задачі.
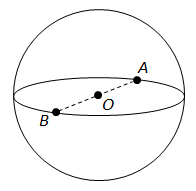
Відстань між точками на сфері – це хорда.
Найбільша відстань між двома точками на сфері – найбільша за довжиною хорда – діаметр
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати рівняння другого степеня, знання теореми Вієта.
І спосіб: заходимо корні рівняння
ІІ спосіб: за теоремою Вієта:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання теореми про суму кутів трикутника.
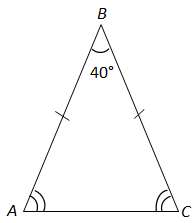
Сума кутів трикутника
За властивістю рівнобедреного трикутника
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих графіком.
Функція, графік якої проходить через початок координат, проходить через точку
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.
Завдання скеровано на перевірку знання аксіом планіметрії, нерівності трикутника, рівності трикутників.
Точки
I.

точка
II.
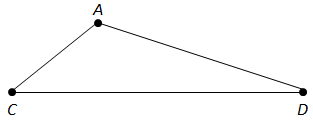
точка
III.
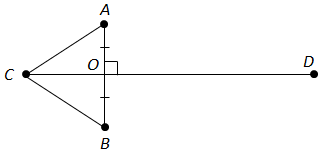
Правильними є твердження І та ІІІ.
Відповідь: В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.
Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом.
Температуру породи на глибині, що на
Температура підвищується, отже, в формулі знак "
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних виразів.
Використаємо основну тригонометричну тотожність
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння.
Розв'яжемо рівняння
Використаємо властивість пропорції
належить проміжку
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.
Завдання скеровано на перевірку знання властивостей степенів з цілим показником, логарифмічних виразів.
Запишемо числа
Правильна подвійна нерівність
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Первісна функції.
Завдання скеровано на перевірку знання геометричного змісту визначеного інтеграла.
Використаємо геометричний зміст визначеного інтеграла та формулу Ньютона-Лейбніца, знаходимо площу фігури:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання скеровано на перевірку вміння розв’язувати задачі на обчислення площ поверхонь геометричних тіл.
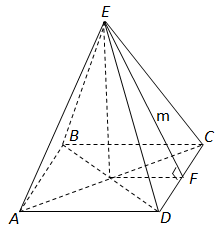
За формулою
запишемо площу бічної поверхні (де
Отже,
Відповідь: В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати показникові нерівності.
Розв'яжемо показникову нерівність:
Функція
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники.
Завдання скеровано на перевірку знання властивостей трикутника, трапеції; вміння розв’язувати задачі практичного змісту.
Побудуємо математичну модель задачі:

Відстань між паралельними сторонами
У
Уздовж сторін
Всього стовпчиків має бути
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком.
Побудуємо задані графіки функцій
1.
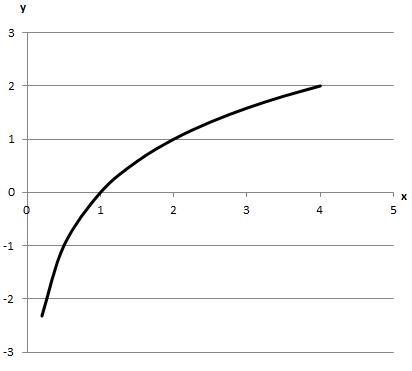
Не перетинає вісь
2.
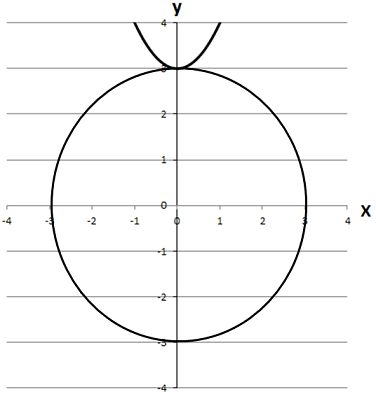
Має лише одну спільну точку з графіком рівняння
3.
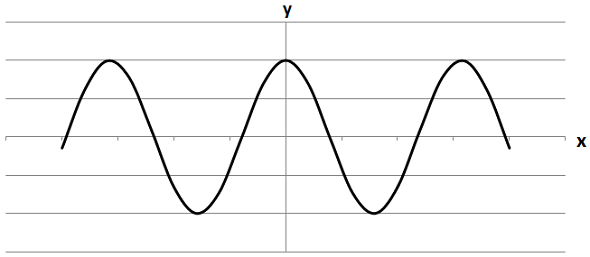
Розташований у всіх координатних чвертях. Отже, 3 - В.
Відповідь: 1А, 2Г, 3В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Раціональні вирази, вирази з модулем та їх перетворення.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення виразів, порівнювати числа, розуміння поняття числового проміжку.
1.
2.
3.
Відповідь: 1Б, 2В, 3Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники. Прямі та площини у просторі.
Завдання скеровано на перевірку знання поняття відстані від точки до площини, між паралельними площинами.
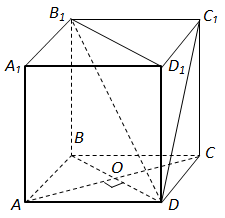
1. Довжина діагоналі куба дорівнює
2. Бічне ребро
3. Осьовий переріз куба
Відповідь: 1В, 2А, 3Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей паралелограма, ромба; вміння використовувати формули площ геометричних фігур для розв’язування планіметричних задач.
1. На рис. 1 зображено ромб. За властивістю ромба діагоналі перетинаються під прямим кутом. Отже, 1 – A.
2.
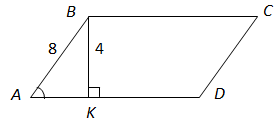
У
3.
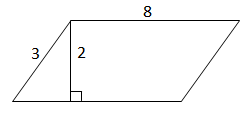
За формулою
Відповідь: 1А, 2Б, 3Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними. Відсотки. Основні задачі на відсотки.
Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом, знаходити відсоток від числа.
1. У 100 г морозива міститься:
| маса, г | енергетична цінність 1 г, ккал | енергетична цінність в 100 г | |
| Білки | 3,5 | 4 | 4 · 3,5=14 |
| Жири | 12 | 9 | 12 · 9=108 |
| Вуглеводи | 21 | 4 | 21 · 4=84 |
| Разом | 14+108+84=206 |
2. Морозиво, з'їдене Ладою, становило
У
У
Відповідь: 1. 206. 2. 309.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники. Чотирикутники. Круг.
Завдання скеровано на перевірку знання основних властивостей геометричних фігур.
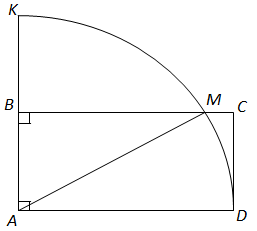
1. Площа сектора
Площа круга
2.
У
Відповідь: 1. 20. 2. 240.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Координати і вектори у просторі.
Завдання скеровано на перевірку вміння виконувати дії з векторами, знаходити координати та скалярний добуток векторів.
1.
2.
Відповідь: 1. 8. 2. –188.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Завдання скеровано на перевірку знання властивостей арифметичної прогресії, знання формули n-го члена арифметичної прогресії.
Арифметичну прогресію
1.
2.
Відповідь: 1. -16,6. 2. -7,2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.
Завдання скеровано на перевірку знання класичного означення ймовірності події.
Нехай імовірність того, що переможе Антон буде
Оскільки сума ймовірностей дорівнює 1, то
Відповідь: 0,25.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Рівняння, нерівності та їх системи. Відношення та пропорції.
Завдання скеровано на перевірку вміння розв’язувати текстові задачі за допомогою рівнянь.
Нехай доповідь триває
Доповіді й презентації тривали
Відповідь: 4.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Логарифмічні вирази та їх перетворення.
Завдання скеровано на перевірку знання вміння виконувати тотожні перетворення логарифмічних виразів.
Використаємо властивості степені та логарифмів
Відповідь: 25.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати нерівності з модулем.
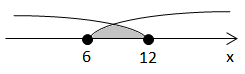
Сума всіх цілих розв'язків:
Відповідь: 63.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.
Завдання скеровано на перевірку вміння розв’язувати задачі, використовуючи розміщення.
Кількість способів вибрати 3 смайлики з 15 знаходимо за формулою розміщень:
Відповідь: 2730.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Дослідження функції за допомогою похідної. Побудова графіків функції.
Завдання скеровано на перевірку вміння знаходити похідну функції, нулів функції, екстремумів функції, будувати графіки функцій; знання достатньої умови зростання (спадання) функції.
Задано функцію
1.
| x | y |
| –1 | 11 |
| 0 | 0 |
| 2 | –16 |
2. Точки перетину графіка
3.
Використали правило знаходження похідної степеневої функції
4. Нулі функції
5. Знайдемо знаки похідної функції.
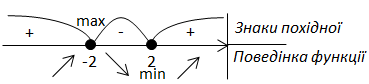
Точки екстремуму:
Знайдемо екстремуми функції:
6.
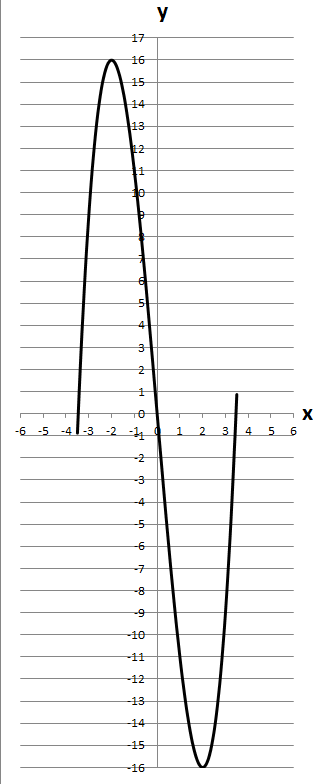
Відповідь:
1.
2.
3.
4.
5. Проміжки зростання:
проміжок спадання:
точки екстремуму:
екстремуми:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання.
Завдання скеровано на перевірку вміння знаходити кути у просторі, побудову осьового перерізу циліндру, знаходження об’єму.
1.
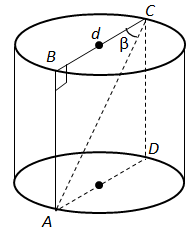
2. Твірна
3. Об'єм циліндра знаходимо за формулою:
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання. Прямі та площини у просторі.
Завдання скеровано на перевірку вміння знаходити кути у просторі, знання про двогранний кут, лінійний кут двогранного кута.
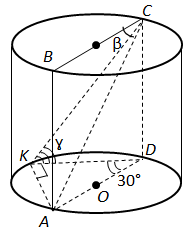
1. Вписаний кут
2. У
Відповідь: 2.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних та раціональних виразів.
Розкладемо квадратний тричлен на множники:
що й треба було довести.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати показникові, квадратні рівняння та рівняння з параметрами.
1. Розв'яжемо систему, якщо
2. Визначимо всі розв'язки системи:
Розв'яжемо квадратне рівняння:
Знайдемо значення
Отже,
якщо
Якщо
Отже, розв'язки
розв'яжемо методом інтервалів:
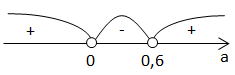
Відповідь:
1.
2. якщо
якщо
Знайшли помилку? Пишіть на




