НМТ онлайн 2022 року з математики – демоваріант

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння розв’язувати текстові задачі арифметичним способом, використовувати ознаки подільності чисел.

Нехай кількість бізе була \(x\) одиниць, тоді бісквітів – \(5x\) одиниць.

Отже, всього тістечок було $$ x+5x=6x. $$

Кількість тистечок може бути числом, кратним \(6\). З наведених чисел це може бути \(72.\)

Відповідь: Д.

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.

Завдання перевіряє знання властивостей суміжних кутів та паралелограма.

\(\angle ABM+\angle ABC=180^\circ\) за властивістю суміжних кутів.

За властивістю паралелограма $$ \angle B=\angle D=155^\circ. $$

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

Розв'яжемо лінійне рівняння:

\begin{gather*} 2x-3=4\\[7pt] 2x=4+3\\[7pt] 2x=7\\[7pt] x=3,5 \end{gather*}

Відповідь: Б.

ТЕМА: Геометрія Стереометрія. Тіла обертання.

Завдання перевіряє вміння обчислення об’єму циліндра.

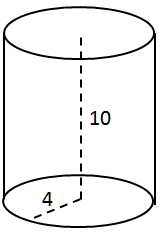
Об'єм циліндра знаходимо за формулою: $$ V=\mathbf{\pi}R^2H, $$ де \(H=10\ \text{см},\ R=4\ \text{см}\). $$ V=\mathbf{\pi}\cdot 4^2\cdot 10=160\mathbf{\pi}\ (\text{см}^3). $$

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє знання властивостей квадратичної функції.

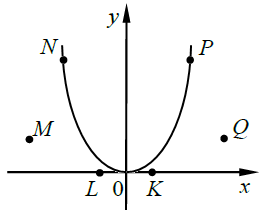
Графіком квадратичної функції \(y=x^2\) є парабола, яка симетрична осі \(Oy.\) Отже, якщо точка \(P\) належить графіку, то симетрична їй точка \(N\) може належати цьому графіку.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння розв’язувати задачі арифметичним способом, розв’язувати задачі на відсоткові розрахунки.

Число, \(25\text{%}\) якого дорівнює \(50,\) знаходимо \(50:25\cdot 100=200.\)

Або \begin{gather*} 25\text{%} - 50,\\[7pt] 100\text{%} - x. \end{gather*}

Отже, \begin{gather*} \frac{25}{100}=\frac{50}{x},\\[6pt] x=\frac{50\cdot 100}{25}=200. \end{gather*}

Або \(25\text{%}\) – це \(\frac 14\) від числа. Отже, число дорівнює \(50\cdot 4=200.\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння виконувати перетворення графіків функцій.

Графік функції \(y=\sqrt{x}\) паралельно перенесли на \(2\) одиниці ліворуч уздовж осі \(x.\) Отримали функцію \(y=\sqrt{x+2}.\)

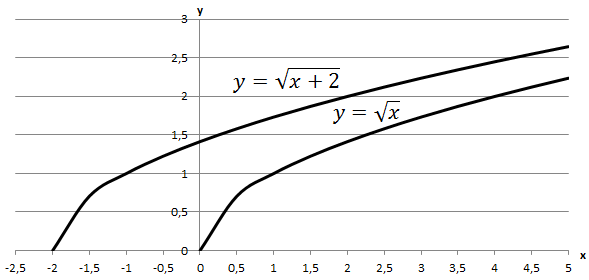
Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє знання формул скороченого множення, вміння виконувати тотожні перетворення раціональних виразів.

Спростимо вираз:

$$ 3(1-x)(1+x)=3(1-x^2)=3-3x^2. $$

Використали формулу різниці квадратів: $$ (a-b)(a+b)=a^2-b^2. $$

Відповідь: A.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання перевіряє вміння застосовувати властивості трапеції, властивостей паралельних прямих.

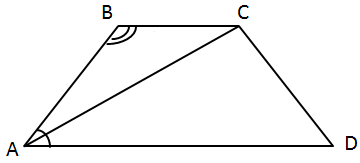
I. \(\angle BAD+\angle ABC=180^\circ\) правильне твердження. За властивістю трапеції сума кутів, прилеглих до бічної сторони, дорівнює \(180^\circ.\)

II. \(\angle BCA=\angle CAD\) правильне твердження. \(BC || AD,\ CA\) – січна. \(\angle BCA\) та \(\angle CAD\) – внутрішні різносторонні.

III. \(AC=BD\) неправильне твердження. Діагоналі довільної трапеції не рівні.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати показникові рівняння.

Розв'яжемо показникове рівняння: \begin{gather*} \left(\frac 13\right)^{2x-1}=9. \end{gather*}

Зведемо до однакової основи: \begin{gather*} \left(\frac 13\right)^{2x-1}=\left(\frac 13\right)^{-2}\\[6pt] 2x-1=-2,\ \ 2x=-2+1,\\[6pt] 2x=-1,\ \ x=-\frac 12. \end{gather*}

Корінь рівняння \(x=-0,5\) належить проміжку \((-1;\ 0].\)

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Функції. Похідна.

Завдання перевіряє вміння знаходити похідну функції, похідну суми.

Знаходимо похідну функції $$ y=2x+\cos x. $$

За правилом \((u+v)'=u'+v'\) \begin{gather*} y'=2-\sin x \end{gather*}

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати системи лінійних нерівностей.

Розв'яжемо систему лінійний нерівностей: \begin{gather*} \left\{ \begin{array}{ l l} 3x-5\lt 2x, & \\ 12-9x\le 3x, & \end{array}\right. \ \ \left\{ \begin{array}{ l l} 3x-2x\lt 5, & \\ -9x-3x\le -12, & \end{array}\right. \\[7pt] \left\{ \begin{array}{ l l} x\lt 5, & \\ -12x\le -12 & \end{array}\right. \ \ \left\{ \begin{array}{ l l} x\lt 5, & \\ x\ge 1. & \end{array}\right. \end{gather*}

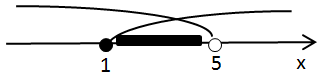
Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.

За властивістю логарифма числа

\begin{gather*} \log_a{b^n}=n\cdot \log_a{b},\\[7pt] \log_{a^k}{b}=\frac 1k\log_a{b},\\[7pt] \log_2{64}=\log_2{2^6}=6\cdot \log_2{2}=6,\\[7pt] \log_{64}{2}=\log_{2^6}{2}=\frac 16\log_2{2}=\frac 16. \end{gather*}

Отже, у порядку зростання числа $$ \log_{64}{2},\ \ \log_{2}{64},\ \ 11 $$

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою.

1. \(f(x)=2^x\)

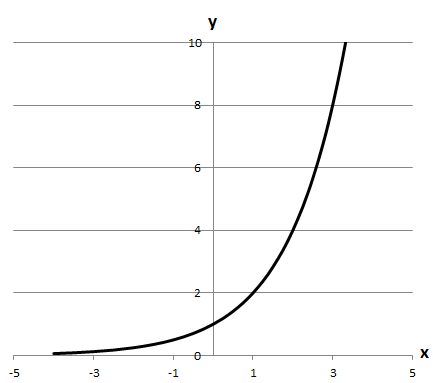
Б область значень \((0;\ +\infty).\)

2. \(f(x)=\mathrm{tg}\ x\)

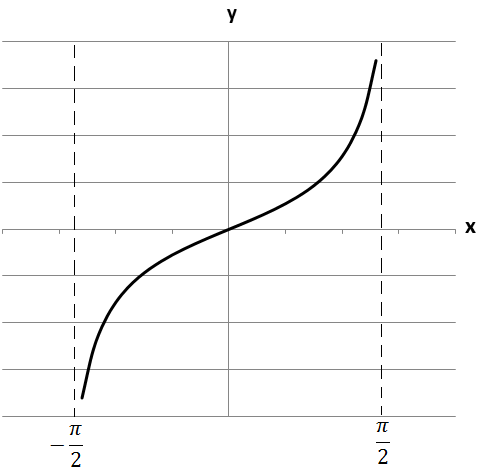
A функція непарна (графік симетричний осі \(y\)).

3. \(f(x)=2x+1\)

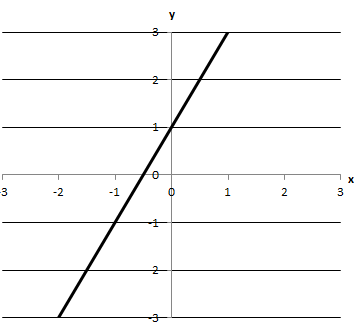
Д графік має лише дві точки перетину з осями координат.

Відповідь: 1Б, 2А, 3Д.

ТЕМА: Алгебра і початки аналізу. Числа і вирази.

Завдання перевіряє вміння використовувати властивості модуля, виконувати тотожні перетворення ірраціональних, тригонометричних виразів, розрізняти види чисел та числових проміжків.

Знайдемо значення виразу

1. \(|-1,6|+2=1,6+2=3,6\in [3;\ +\infty)\) Д.

2. \begin{gather*} \frac{\sqrt{24}}{\sqrt{3}}=\sqrt{\frac{24}{3}}=\sqrt{8}\\[7pt] \sqrt{4}\lt \sqrt{8}\lt\sqrt{9}\\[7pt] 2\lt\sqrt{8}\lt 3. \end{gather*} Отже, \(\sqrt{8}\in [2;\ 3)\) – Г.

3. \(2\cos\frac{\mathbf{\pi}}{3}=2\cdot \frac 12=1\in [1;\ 2)\) – B.

Відповідь: 1Д 2Г 3В.

ТЕМА: Геометрія. Планіметрія. Трикутники.

Завдання перевіряє вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.

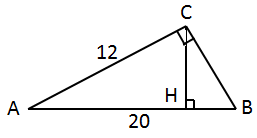
1. За теоремою Піфагора: \begin{gather*} AB^2=AC^2+BC^2\\[7pt] BC^2=20^2-12^2=400-144=256.\\[7pt] BC=16\ \text{см}. \end{gather*} Отже, правильна відповідь – Д.

2. Радіус кола, описаного навколо прямокутного трикутника, дорівнює половині гіпотенузи. Отже, \(R=\frac 12 AB=10\ \text{см}.\) Отже, правильна відповідь – B.

3. \(CH\perp AB\)

Висоту \(CH\) можна знайти, прирівнявши площу трикутника

\begin{gather*} S=\frac 12 a\cdot b\ \text{та}\ S=\frac 12 ch_c, \end{gather*} де \(a,\ b\) – катети, \(c\) – гіпотенуза.

Або знайти висоту за допомогою метричних співвідношень у прямокутному трикутнику:

\(\Delta ACH\ (\angle H=90^\circ)\) за теоремою Піфагора:

Отже, правильна відповідь – Б.

Відповідь: 1Д, 2В, 3Б.

ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, знання теореми Піфагора та властивості квадрата.

\(SABCD\) – правильна піраміда. \(ABCD\) – квадрат, \(\text{точка}\ O\) – центр квадрата.

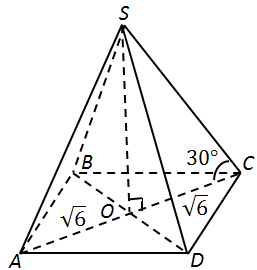
1. \(AC=2AO=2\sqrt{6}\) діагоналі квадрата в точці перетину діляться навпіл. Отже, 1 – Г.

2. \(\Delta SOC\ (\angle O=90^\circ)\)

Oтже, 2 – A.

3. У правильній піраміді бічні ребра рівні \(AS=CS.\) \(\Delta SOC\ (\angle O=90^\circ)\) за теоремою Піфагора

Oтже, 3 – Б.

Відповідь: 1Г, 2А, 3Б.

ТЕМА: Алгебра і початки аналізу. Функції Числові послідовності.

Завдання перевіряє вміння розв’язувати задачі на арифметичну прогресію, знання формули суми n-перших членів та n-го члена арифметичної прогресії.

За формулою $$ S_n=\frac{2a_1+d(n-1)}{2}\cdot n $$ знаходимо суму перших шести членів.

За формулою \(n\)-го члена $$ a_n=a_1+d(n-1) $$ знаходимо \(a_1:\) \begin{gather*} a_3=a_1+2d,\ \ 20=a_1+2\cdot(-3,2),\\[7pt] 20=a_1-6,4,\ \ a_1=26,4,\\[6pt] S_6=\frac{2\cdot 26,4-3,2(6-1)}{2}\cdot 6=\\[6pt] =\frac{52,8-16}{2}\cdot 6=110,4. \end{gather*}

Відповідь: 110,4.

ТЕМА: Геометрія Стереометрія. Прямі та площини у просторі. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, задачі на обчислення площі поверхні призми.

\(BD=6\ \ AC=8\).

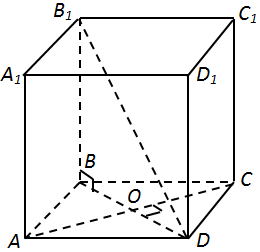
1. Діагональ призми – це похила на площину основи. Отже, меншій похилій відповідає менша проекція. \(BD\) – менша проекція, отже, \(B_1D\) – менша похила. \(B_1D=10.\)

2. \(\Delta BB_1D\ \ (\angle B=90^\circ)\ BB_1^2+BD^2=B_1D^2\) за теоремою Піфагора $$ BB_1=\sqrt{100-36}=8 $$

3. Діагоналі ромба перетинаються під кутом \(90^\circ.\) \begin{gather*} AC\cap BD=0\\[7pt] \Delta COD\ (\angle O=90^\circ)\\[6pt] OC=\frac 12 AC=4,\ \ OD=\frac 12 BD=3 \end{gather*} за теоремою Піфагора \begin{gather*} CD=\sqrt{CO^2+OD^2}=\sqrt{3^2+4^2}=5. . \end{gather*}

4. За формулою \(S_\text{бічної}=P_\text{основи}\cdot H\) \begin{gather*} P_\text{основи}=4\cdot CD=20,\ \ H=BB_1=8\\[7pt] S_\text{бічної}=20\cdot 8=160. \end{gather*}

Відповідь: 160.