НМТ онлайн 2022 року з математики – основна сесія
Тестові завдання основної сесії національного мультитесту (ЗНО) 2022 року з математики
ТЕМА: Алгебра і початки аналізу. Елементи математичної статистики. Вибіркові характеристики.
Перевіряє вміння аналізувати графічну, табличну, текстову та інші форми подання статистичних даних.
На рисунку видно, що найбільша відстань між точками, тобто найбільша різниця між найвищою та найнижчою температурою була у четвер. Отже, привальна відповідь – Г.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Перевіряє вміння розв'язувати текстові задачі арифметичним способом.
На першому поверсі –
Отже,
Відповідь: В.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Перевіряє знання про многогранники та їхні елементи, основні види многогранників: призму, паралелепіпед, піраміду.
На рисунку зображена розгортка чотирикутної піраміди. Отже, правильна відповідь – Б.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Перевіряє вміння розв'язувати квадратні рівняння, знання теореми Вієта.
Добуток коренів рівняння за теоремою Вієта для зведеного квадратного рівняння:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури та їхні властивості.
Перевіряє знання властивостей, паралельних прямих, суми кутів трикутника.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
Графік функції проходить через точку
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Перевіряє вміння виконувати тотожні перетворення раціональних виразів, властивості степенів.
Скоротили дріб використовуючи властивість степенів:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Перевіряє вміння встановлювати властивості числових функцій, заданих графіком. використовувати перетворення графіків функцій.
Якщо графік функції
Застосували елементарне перетворення графіка функції.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.
При розв'язанні застосували властивості логарифмів:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія Стереометрія. Тіла обертання.
Перевіряє знання формул для обчислення об'єму циліндра.
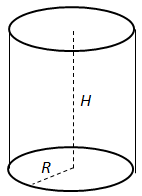
Об'єм циліндра
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Перевіряє вміння розв'язувати системи лінійних та ірраціональних рівнянь.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Похідна функції.
Перевіряє вміння знаходити похідні функцій, знаходити числове значення похідної функції в точці для заданого значення аргументу.
Похідна функції:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Перевіряє вміння розв’язувати показникові нерівності.
Зведемо до однакової основи:
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.
За основною тригонометричною тотожністю:
Відповідь: Г
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Перевіряє вміння встановлювати властивості числових функцій, заданих графіком.
1. Графік є фрагментом графіка функції
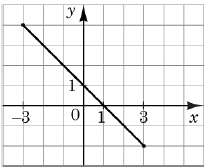
2. Графік функції двічі перетинає графік функції
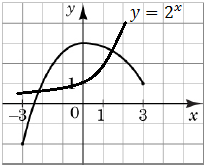
3. Функція зростає на проміжку
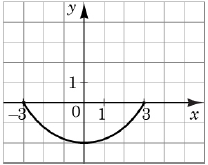
Відповідь: 1Б, 2А, 3Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Перевіряє вміння виконувати тотожні перетворення числових виразів.
1.
2.
3.
Відповідь: 1Г 2Б 3В.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Перевіряє знання властивостей прямокутника, вміння знаходити довжини відрізків, градусні міри кутів, площі геометричних фігур.
1.
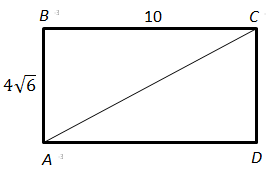
За теоремою Піфагора:
2.
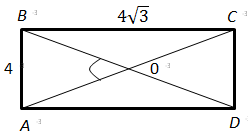
Отже, 2 – Б.
3.
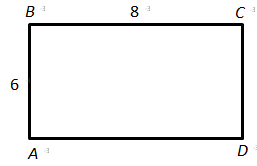
Відповідь: 1Г, 2Б, 3B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія Стереометрія. Координати у просторі.
Перевіряє знання прямокутної системи координат у просторі, координати точки.
1. Точка на осі
2. Точки, що належить відрізку
3. Точка
Відповідь: 1Г, 2Д, 3А.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Перевіряє знання формули n-го члена та властивостей геометричної прогресії.
За властивістю геометричної прогресії знаменник
Відповідь: 3,75.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Перевіряє знання властивостей трапеції та її середньої лінії, вміння застосовувати означення та властивості різних видів трикутників до розв'язування планіметричних задач.
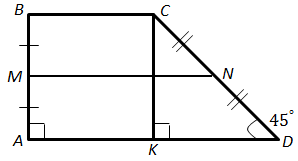
1.
2. Отже,
3. Проведемо
4.
5.
Відповідь: 8.
Знайшли помилку? Пишіть на




