НМТ онлайн 2023 року з математики – демоваріант

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння розв’язувати текстові задачі арифметичним способом.

За \(220\ \text{грн}\) можна купити \(6\) шоколадок \((220 : 35 = 6\ \text{і}\ 10\ \text{грн остача}),\) а за кожні три шоколадки отримати по одній безкоштовно, це ще дві шоколадки \((6 : 3 = 2).\)

Отже, за \(220\ \text{грн}\) можна купити \(6\) шоколадок і ще дві шоколадки отримати безкоштовно, тобто разом \(8\) шоколадок.

Отже, правильна відповідь – Г.

Відповідь: Г.

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє знання про многогранники та їхні елементи.

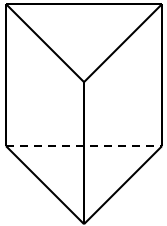
У трикутної призми \(3\) бічні грані та \(2\) грані основ.

Отже, кількість граней призми – \(5.\)

Відповідь: B.

ТЕМА: Геометрія. Планіметрія.

Завдання перевіряє знання властивості трикутника про суму кутів.

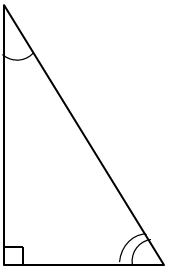
Сума кутів трикутника – \(180^\circ .\) Сума гострих кутів – \(90^\circ .\)

Отже, \(115^\circ\) – це сума прямого та гострого кута. Тоді гострий кут \(115^\circ -90^\circ =25^\circ .\) Другий гострий кут трикутника.

Гострі кути \(65^\circ\) та \(25^\circ .\)

Найменший кут цього трикутника \(25^\circ .\)

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння виконувати тотожні перетворення ірраціональних виразів.

$$ \frac{\sqrt[3]{128}}{\sqrt[3]{2}}=\sqrt[3]{\frac{128}{2}}=\sqrt[3]{64}=4. $$ Застосували властивість: $$ \sqrt[n]{\frac ab}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}},\ \ a,\ b \gt 0. $$

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

$$ \frac x2 +\frac x3= 2, $$ зведемо до спільного знаменника: \begin{gather*} \frac{3x+2x}{6}=2,\\[6pt] \frac{5x}{6}=2,\\[6pt] 5x=12,\\[6pt] x=2,4. \end{gather*}

Відповідь: B.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.

Графіком лінійної функції є пряма. Всі точки прямої, паралельної осі абсцис, мають однакові ординати.

Якщо пряма проходить через \(\text{т.}\ A(-2;\ 3),\) то функція задається формулою: \(y=3.\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння виконувати тотожні перетворення логарифмічних виразів.

$$ \log_2(8a)=\log_28+\log_2a=3+4=7. $$

Застосували властивість логарифма $$ \log_a(b\cdot c)=\log_ab+\log_ac. $$

Відповідь: Б.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання перевіряє знання паралелограма, ромба, квадрата та їх властивостей.

I. Діагоналі будь-якого ромба ділять його кути навпіл (властивість ромба).

IІ. Неправильне твердження.

IІІ. Діагоналі будь-якого квадрата взаємно перпендикулярні (це властивість ромба, а квадрат є ромбом із прямими кутами).

Отже, правильна відповідь – Д.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє знання формул скороченого множення, вміння виконувати тотожні перетворення раціональних виразів.

\begin{gather*} \frac{a^2+16}{a-4}-\frac{8a}{a-4}=\frac{a^2+16-8a}{a-4}=\\[6pt] =\frac{(a-4)^2}{a-4}=a-4. \end{gather*}

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати показникові нерівності, нерівності з модулем.

\begin{gather*} \left\{ \begin{array}{l} \left(\frac 13\right)^x\lt 81,\\ |x|\le 5; \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} \left(\frac 13\right)^x\lt \left(\frac 13\right)^{-4},\\ -5\le x\le 5; \end{array} \right. \end{gather*} функція \(y=\left(\frac 13\right)^x\) складна, оскільки основа степені \(\frac 13\lt 1.\)

Отже, \begin{gather*} \left\{ \begin{array}{l} x\gt -4,\\ -5\le x\le 5. \end{array} \right. \end{gather*}

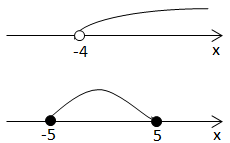
Розв'язок системи – спільний розв'язок двох нерівностей. Отже, \(x\in (-4;\ 5].\)

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.

Завдання перевіряє вміння застосовувати властивості трикутників, прямокутника до розв’язування планіметричних задач.

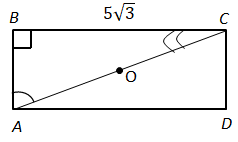
За умовою завдання більша сторона прямокутника дорівнює \(5\sqrt{3}.\)

У прямокутному трикутнику \(\Delta ABC\ (\angle B = 90^\circ)\) гострі кути \(60^\circ\) (із умови завдання) і \(30^\circ\ (180^\circ – 90^\circ – 60^\circ = 30^\circ).\) Напроти більшої сторони \(BC\) лежить більший кут, тому \(\angle A = 60^\circ,\) тоді \(\angle C = 30^\circ.\)

У \(\Delta ABC\) \begin{gather*} \frac{BC}{AC}=\sin A,\\[6pt] AC=\frac{BC}{\sin A}=\frac{5\sqrt{3}}{\frac{\sqrt{3}}{2}}=10. \end{gather*}

Центр кола, описаного навколо прямокутника, є точка перетину діагоналей – середина діагоналі \(AC.\ \ R=\frac 12 AC=5.\)

Довжина кола \(L=2\mathbf{\pi}R=10\mathbf{\pi}.\)

Відповідь: A.

ТЕМА: Алгебра і початки аналізу. Функції Числові послідовності.

Завдання перевіряє знання формули n-го члена арифметичної прогресії, вміння розв’язувати задачі на арифметичну прогресію.

\(a_n=a_1+d(n-1)\) – формула n-го члена арифметичної прогресії. \begin{gather*} a_1=4,\ \ a_2=-1.\\[7pt] d=a_2-a_1=-1-4=-5. \end{gather*}

Підставимо \(a_1\) та \(d\) у формулу

Відповідь: А.

ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.

Завдання перевіряє вміння розв’язувати стереометричні задачі на обчислення невідомих елементів піраміди, знання теореми Піфагора та властивості квадрата.

\(PABCD\) – правильна чотирикутна піраміда, тому \(ABCD\) – квадрат, \(O\) – точка перетину діагоналей, \(PO\) – висота.

\(P_{ABCD}=4AB=72\ \text{см},\ \ AB=18\ \text{см}.\)

\(PK\) – апофема (висота бічної грані). \(OK\perp AB\) (за теоремою про три перпендикуляри).

\begin{gather*} OK=\frac 12 AB=9\ \text{см}.\\[7pt] \Delta POK\ (\angle O=90^\circ) \end{gather*} за теоремою Піфагора:

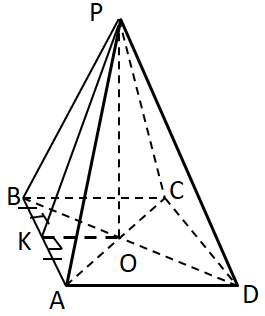
Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати найпростіші тригонометричні рівняння.

\(\sin x=\frac{\sqrt{3}}{2}\) найпростіше тригонометричне рівняння. Корені знаходимо за формулою:

На відрізку \(x\in [0;\ 3\mathbf{\pi}]\) знаходимо корені:

Отже, правильна відповідь – Д.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою чи графіком.

1. \(y=\operatorname{tg}x\) – Г.

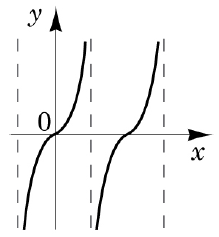
2. \(y=\left(\frac 12\right)^x\) показникова функція – Д.

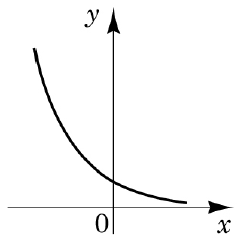
3. \(y=\frac 1x\) обернена пропорційність – А.

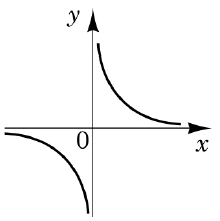
Відповідь: 1Г 2Д 3А.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє знання властивостей дійсних чисел.

1. Дільником числа \(8\) є числа, на які \(8\) ділиться без остачі. Серед наведених чисел – це \(8.\) Отже, правильна відповіль – A.

2. Просте число – це число, яке має тільки два дільники – \(1\) та саме число. Серед наведених – це \(17.\) Отже, правильна відповідь – B.

3. Квадратом натурального числа є число \(16=4^2.\) Отже, правильна відповідь – Б.

Відповідь: 1А, 2В, 3Б.

ТЕМА: Геометрія. Планіметрія. Геометричні перетворення.

Завдання перевіряє знання геометричних перетворень на площині: симетрії відносно прямої та точки.

1 – Б. симетрія відносно осі \(x.\)

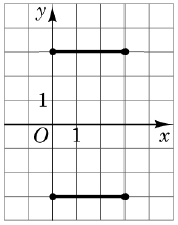
2 – Г. симетрія відносно осі \(y.\)

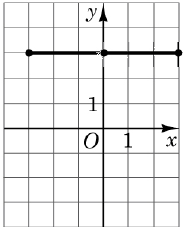
3 – Д. симетрія відносно точки \(O.\)

Відповідь: 1Б, 2Г, 3Д.

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Завдання перевіряє знання означення геометричного змісту визначеного інтеграла, вміння обчислювати площу плоских фігур.

\(\int_0^{7}f(x)dx.\) Геометричний зміст визначеного інтеграла – площа фігури, обмеженої лініями: графіком \(f(x),\) \(x=0,\) \(x=7\) та віссю \(x.\)

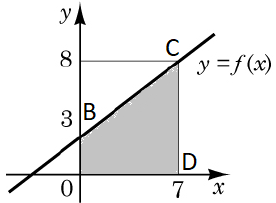
Відповідь: 38,5.

ТЕМА: Алгебра і початки аналізу. Елементи математичної статистики. Вибіркові характеристики.

Завдання перевіряє вміння обчислювати та аналізувати вибіркові характеристики рядів даних (середнє значення).

Нехай Михайлу треба отримати \(x\) оцінок \(\text{"}10\text{"}.\)

Середнє арифметичне значень:

Отже, Михайлу треба отримати \(12\) оцінок \(\text{"}10\text{"}.\)

Відповідь: 12.

ТЕМА: Геометрія. Стереометрія. Тіла обертання.

Завдання перевіряє знання про конус та його елементи, властивості подібних фігур.

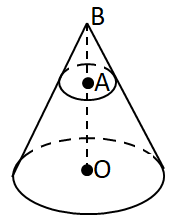
Площина, паралельна основі, відтинає подібний конус.

Коефіцієнт подібності $$ k=\frac{AB}{AO}=\frac 12. $$ Об'єми подібних тіл відносяться як $$ k^3=\left(\frac 12\right)^3=\frac 18. $$

Отже, об'єм меншого конуса \(64:8=8\ (\text{см}).\)

Відповідь: 8.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати логарифмічні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

\(\log_2^2x-(a-1)\log_2x-a=0.\)

ОДЗ: \(x\gt 0.\)

Зробимо заміну: \(\log_2x=t.\)

Корені квадратного рівняння:

\begin{gather*} t_1=\frac{(a-1)+(a+1)}{2}=a\\[6pt] t_2=\frac{a-1-(a+1)}{2}=-1. \end{gather*}

Повертаємось до заміни:

\begin{gather*} \left[ \begin{array}{l} \log_2x=-1,\\ \log_2x=a; \end{array} \right. \ \ \ \left[ \begin{array}{l} x_1=\frac 12,\\ x_2=2^a. \end{array} \right. \end{gather*}

\(x_1\notin (30;\ 100),\) тому даному проміжку повинен належати \(x_2.\)

\begin{gather*} 30\lt x_2\lt 100,\ \ 30\lt 2^a\lt 100.\\[7pt] \text{при}\ a=5\ (a\in \mathbb{Z}). \end{gather*}

Наймеше значення \(a=5.\)

Відповідь: 5.