НМТ онлайн 2023 року з математики – 2 сесія

Тестові завдання другої сесії національного мультитесту (ЗНО) 2023 року з математики

12345678910111213141516171819202122

Зачекайте, йде розрахунок...

Завдання 1 з 22

На рисунку відображено інформацію про результати опитування пасажирів транспортної мережі деякого міста щодо визначення якості пасажирських перевезень (у балах за шкалою $1–10$). Визначте кількість опитуваних, які поставили оцінку, вищу за $8$ балів.

А19

Б100

В200

Г275

Д475

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Елементи математичної статистики. Вибіркові характеристики.

Завдання перевіряє вміння аналізувати графічну, табличну, текстову та інші форми подання статистичних даних.

На рисунку відображено інформацію про результати опитування пасажирів.

Оцінку, вищу за $8$ балів, поставили $75$ та $25$ опитуваних, які визначили якість на $9$ та $10$ балів.

Отже, правильна відповідь Б – $75+25=100\ \text{опитуваних}.$

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26821

Завдання 2 з 22

Із точки $O,$ яка лежить на прямій $AB,$ проведено промені $OM$ і $OK$ (див. рисунок). Відомо, що $\angle BOM = 30^\circ,$ $\angle MOK = 80^\circ.$ Визначте градусну міру кута $AOK.$ Уважайте, що промені $OK,\ OM$ і пряма $AB$ лежать в одній площині.

А$60^\circ$

Б$70^\circ$

В$80^\circ$

Г$150^\circ$

Д$170^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їх властивості.

Завдання перевіряє знання аксіом планіметрії.

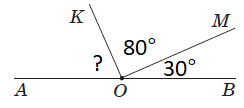
$\angle AOK+\angle KOM+\angle MOB=180^\circ.$

$\angle AOK=180^\circ-(30^\circ+80^\circ)=70^\circ.$

Отже, правильна відповідь – Б.

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26824

Завдання 3 з 22

У магазині канцтоварів ручка коштує $6$ грн, а набір із двох ручок – $10\ \text{грн.}$ Яку найбільшу кількість таких ручок можна купити в цьому магазині на суму до $58\ \text{грн?}$

А8

Б9

В10

Г11

Д12

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння розв’язувати текстові задачі арифметичним способом.

Набір із двох ручок коштує $10$ гривень. На $58$ гривень можна купити $5$ наборів. На це буде витрачень $50$ гривень. На $8$ гривень, що залишаться, можна купити ще одну ручку за $6$ гривень. Отже, найбільша кількість ручок, які можна купити, $11.$

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26823

Завдання 4 з 22

Розв’яжіть рівняння $0,01x=-1.$

А-1000

Б-100

В-10

Г-1

Д100

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати лінійні рівняння.

Розв'яжемо лінійне рівняння $0,01x=-1,$ \begin{gather*} x=-1:0,01;\\[7pt] x=-100. \end{gather*}

Отже, правильна відповідь – Б.

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26825

Завдання 5 з 22

Визначте координати вектора $\overrightarrow{c}=\overrightarrow{b}-\overrightarrow{a},$ якщо $\overrightarrow{a}(2; 1; -5)$ i $\overrightarrow{b}(-7; 0; 3).$

А$\overrightarrow{c}\ (-9; -1; 8)$

Б$\overrightarrow{c}\ (9; 1; -8)$

В$\overrightarrow{c}\ (-5; 1; -2)$

Г$\overrightarrow{c}\ (-5; -1; 2)$

Д$\overrightarrow{c}\ (-14; 0; -15)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Стереометрія. Координати та вектори у просторі.

Завдання перевіряє вміння виконувати дії з векторами.

\begin{gather*} \overline{a}(2;\ 1;\ -5),\ \overline{b}(-7;\ 0;\ 3),\ \overline{c}=\overline{b}-\overline{a}\\[7pt] \overline{c}\left(-7-2;\ 0-1;\ 3-(-5)\right),\ \overline{c}(-9;\ -1;\ 8). \end{gather*}

Відповідь: A.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26826

Завдання 6 з 22

На рисунку зображено графік функції $y = f(x),$ визначеної на проміжку $[–2; 4].$ Цей графік перетинає вісь $x$ в одній із зазначених точок. Укажіть цю точку.

А(4; 0)

Б(3; 4)

В(0; 3)

Г(3; 0)

Д(0; 4)

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою чи графіком.

Точка перетину графіка функції з віссю $x$ має координати $(3;\ 0).$

Отже, правильна відповідь – Г.

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26827

Завдання 7 з 22

Укажіть проміжок, якому належить корінь рівняння $$ \frac{x}{18-2x}=\frac 14. $$

А$(-\infty; -3)$

Б$[-3; 0)$

В$[0; 4)$

Г$[4; 8)$

Д$[8; +\infty)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання перевіряє вміння розв’язувати раціональні рівняння.

Розв'яжемо рівняння застосувавши основну властивість пропорції:

\begin{gather*} \frac{x}{18-2x}=\frac 14,\ \ x\cdot 4=18-2x,\ \ 4x+2x=18,\\[6pt] 6x=18,\ \ x=18:6,\ \ x=3. \end{gather*}

Корінь рівняння належить проміжку $[0;\ 4).$

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26828

Завдання 8 з 22

Укажіть формулу для обчислення об’єму $V$ правильної чотирикутної піраміди, сторона основи й висота якої дорівнюють $a.$

А$V=a^3$

Б$V=\frac{4a^2}{3}$

В$V=4a^2$

Г$V=\frac{a^3}{3}$

Д$V=\frac{a^3}{4}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання перевіряє вміння розв’язувати стереометричні задачі, знання властивостей піраміди.

Об'єм піраміди знаходимо за формулою $$ V=\frac 13 S_\text{осн}\cdot H. $$

Піраміда правильна, тому в основі лежить квадрат. Сторона квадрата – $a.$ $S_\text{кв}=S_\text{осн}=a^2.$ Висота піраміди дорівнює $a$ за умовою $H=a.$

Отже, $V=\frac 13\cdot a^2\cdot a=\frac{a^3}{3}.$

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26829

Завдання 9 з 22

Укажіть проміжок, якому належить значення виразу $\left(\frac 14\right)^{-2}.$

А$(-\infty; -10]$

Б$(-10; 0]$

В$(0; 1]$

Г$(1; 10]$

Д$(10; +\infty)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє знання властивостей степенів, вміння виконувати тотожні перетворення виразів.

$\left(\frac 14\right)^{-2}=\left(\frac 41\right)^2=16.$ Значення виразу належить проміжку $(10;\ +\infty).$

Використали властивість степенів:

$$ a^{-n}=\frac{1}{a^n}\ \ \text{для}\ \ a\ne 0,\ \ n\in \mathbb{N}. $$

Відповідь: Д.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26830

Завдання 10 з 22

Які з наведених тверджень є правильними?

I. Пряма, що проходить через центр кола і лежить із цим колом в одній площині, має з ним дві спільні точки.

II. Діаметр кола, перпендикулярний до його хорди, проходить через середину цієї хорди.

III. Можна провести два діаметри кола, що не мають жодної спільної точки.

Алише II

Блише I та IIІ

Влише II та III

Глише I та IІ

ДІ, ІІ та ІІІ

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Коло та круг.

Завдання перевіряє знання властивостей кола та його елементів, хорд.

I. Пряма, що проходить через центр кола, містить діаметр кола. Отже, має з ним дві спільні точки.

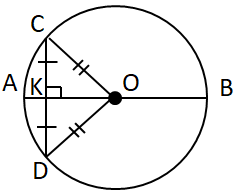
II. $AB\perp CD.$ $\Delta COD$ – рівнобедрений, $OC=OD.$ Отже, висота $OK,$ проведена до основи, є медіаною. $K$ – середина хорди $CD.$

III. Діаметри кола проходять через центр кола, а отже, мають завжди спільну точку – центр кола.

Правильні твердження лише І та ІІ, тому відповідь Г.

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26833

Завдання 11 з 22

Якщо функція $F(x) = x^3 + 4$ є однією з первісних функції $f(x),$ тоді $f(x) =$

А$3x^2+4$

Б$3x^2$

В$3x$

Г$2x^2$

Д$\frac{x^4}{4}+C$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції. Первісна та визначений інтеграл.

Завдання перевіряє знання означення первісної функції.

За означенням первісної функції $F'(x)=f(x).$

Отже,

$$ f(x)=(x^3+4)'=(x^3)'+4'=3x^2. $$

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26834

Завдання 12 з 22

$\left(-2x^4\right)^3=$

А$-6x^7$

Б$-8x^{12}$

В$-8x^7$

Г$8x^{12}$

Д$6x^{12}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє знання властивостей степенів.

За властивістю степенів:

\begin{gather*} (a\cdot b)^n=a^n\cdot b^n,\ \ (a^n)^m=a^{nm},\\[7pt] (-2x^4)^3=(-2)^3\cdot (x^4)^3=-8x^{12}. \end{gather*}

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26835

Завдання 13 з 22

Менша сторона прямокутника дорівнює $4\ \text{см,}$ а кут між його діагоналями – $60^\circ$ (див. рисунок). Визначте площу $(\text{см}^2)$ прямокутника.

А$8\sqrt{3}$

Б$16$

В$16\sqrt{3}$

Г$32$

Д$32\sqrt{3}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.

Завдання перевіряє знання прямокутника та трикутника, їхніх властивостей.

$AB=4\ \text{см},\ \angle AOB=60^\circ.$

$\Delta AOB$ – рівносторонній. $AB=BO=OA=4\ \text{см}.$ За властивістю прямокутника $AC=BD=2BO=8\ \text{см}.$

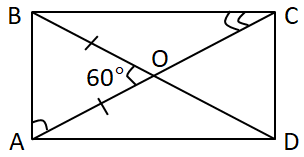
Площа прямокутника $$ S=\frac 12\cdot d^2\cdot \sin 60^\circ=\frac 12\cdot 8^2\cdot \sin 60^\circ=\frac 12\cdot 64\cdot \frac{\sqrt{3}}{2}=16\sqrt{3}\ (\text{см}^2). $$

Або іншим способом:

\begin{gather*} \Delta ABC\ (\angle B=90^\circ),\ \angle A=60^\circ,\ AB=4\ \text{см}\\[7pt] BC=AB\cdot \operatorname{tg}60^\circ=4\sqrt{3}\ \text{см}\\[7pt] S=AB\cdot BC=4\cdot 4\sqrt{3}=16\sqrt{3}\ (\text{см}^2). \end{gather*}

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26836

Завдання 14 з 22

Укажіть вираз, тотожно рівний виразу $(\cos x-\sin x)^2.$

А$\cos 2x$

Б$\cos 2x-\sin 2x$

В$\cos 2x-1$

Г$1-\sin 2x$

Д$1$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання перевіряє вміння виконувати тотожні перетворення тригонометричних виразів.

\begin{gather*} (\cos x-\sin x)^2=\cos^2x-2\cos x\cdot \sin x+\sin^2 x=\\[7pt] =1-2\sin x\cos x=1-\sin 2x. \end{gather*}

Застосували формули скороченого множення $$ (a-b)^2=a^2-2ab+b^2 $$ та тригонометрії

\begin{gather*} \sin^2\mathbf{\alpha}+\cos^2\mathbf{\alpha}=1\\[7pt] \sin 2\mathbf{\alpha}=2\sin\mathbf{\alpha}\cos\mathbf{\alpha}. \end{gather*}

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26837

Завдання 15 з 22

Розв’яжіть нерівність $\log_{0,3}(x+3)\gt \log_{0,3}4.$

А$(1; +\infty)$

Б$(7; +\infty)$

В$(-\infty; 1)$

Г$(0; 1)$

Д$(-3; 1)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати логарифмічні нерівності.

Розв'яжемо тригонометричну нерівність $\log_{0,3}(x+3)\gt \log_{0,3}4.$

Функція є спадною, бо основа логарифма $0,3\lt 1.$ Отже, $x+3\lt 4$ та за ОДЗ $x+3\gt 0.$

Розв'язком нерівності буде розв'язок системи лінійних нерівностей:

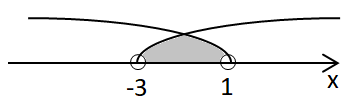
\begin{gather*} \left\{ \begin{array}{l} x+3\lt 4,\\ x+3\gt 0, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x\lt 4-3,\\ x\gt -3, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} x\lt 1,\\ x\gt -3. \end{array} \right. \end{gather*}

$x\in (-3;\ 1).$

Відповідь: Д.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26838

Завдання 16 з 22

Доберіть до кожного початку речення (1–3) його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення

1Функція $y=\sqrt{x+1}$

2Функція $y=4-x^2$

3Функція $y=3^{-x}$

Закінчення речення

Амає точку локального максимуму.

Бмає точку локального мінімуму.

Вє непарною.

Гзростає на всій області визначення.

Днабуває лише додатних значень.

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих графіком та формулою.

Графіки функцій схематично виглядають таким чином:

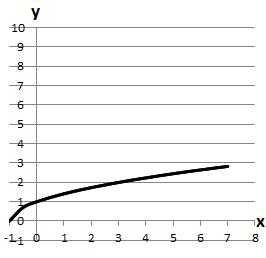
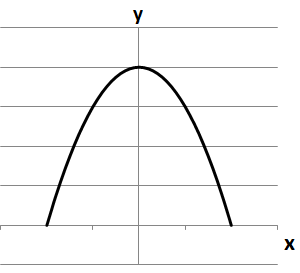
1. $y=\sqrt{x+1}$ зростає на всій області визначення – Г.

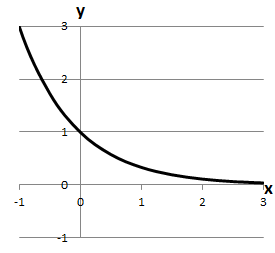
2. $y=4-x^2$ має точку локального максимуму при $x=0,\ f_{max}(0)=4$ – A.

3. $y=3^{-x}$ функція набуває лише додатних значень – Д.

Відповідь: 1Г 2А 3Д.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26839

Завдання 17 з 22

Доберіть до числового виразу (1–3) рівний йому за значенням вираз (А – Д).

Вираз

1$\frac{1}{\sqrt{10}-3}$

2$|3-\sqrt{10}|$

3$\log_5{125}$

Вираз

А$\sqrt{10}-3$

Б$3-\sqrt{10}$

В$\sqrt{10}+3$

Г$3$

Д$25$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання перевіряє вміння встановлювати властивості числових функцій, заданих формулою чи графіком.

Спростимо вирази:

1. – В. $\frac{1}{\sqrt{10}-3}=\frac{\sqrt{10}+3}{(\sqrt{10}-3)(\sqrt{10}+3)}=\frac{\sqrt{10}+3}{10-9}=\sqrt{10}+3.$

2. – A. $|3-\sqrt{10}|=\sqrt{10}-3.$ Вираз $3-\sqrt{10}\lt 0,$ тому $|3-\sqrt{10}|=-(3-\sqrt{10})=-3+\sqrt{10}.$

3. – Г. $\log_5125=\log_55^3=3\log_55=3.$

Відповідь: 1В, 2А, 3Г.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26840

Завдання 18 з 22

Периметр рівнобедреного трикутника $ABC$ (див. рисунок) дорівнює $32\ \text{см.}$ $AB = BC = 10\ \text{см.}$ Узгодьте відрізок (1–3) з його довжиною (А – Д).

Відрізок

1$AC$

2висота, проведена з вершини $B$

3радіус кола, описаного навколо трикутника $ABC$

Довжина відрізка, см

А6,25

Б7,5

В8

Г12

Д12,5

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Трикутники.

Завдання перевіряє вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знання теореми Піфагора, наслідків з теореми синусів.

$P=32\ \text{см},\ AB=BC=10\ \text{см}.$

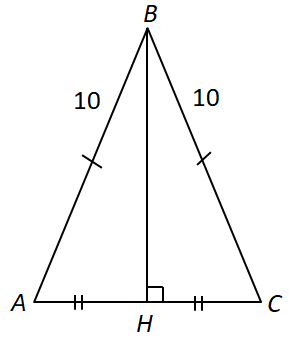
1 – Г. $P=AB+BC+AC=10+10+AC=32,\ \ AC=12\ \text{см}.$

2 – B. Висота $BH\perp AC,\ \ BH$ – медіана, $AH=HC=\frac 12AC=6\ \text{см}.$ $\Delta ABH\ (\angle H=90^\circ)$ за теоремою Піфагора $BH=\sqrt{100-36}=\sqrt{64}=8\ \text{см}.$

3 – A. $\Delta ABH\ (\angle H=90^\circ)$ $\sin A=\frac{BH}{AB}=\frac{8}{10}=0,8.$ За наслідком із теореми синусів:

\begin{gather*} \frac{BC}{\sin\mathbf{\alpha}}=2R,\ \ \frac{10}{0,8}=2R,\\[6pt] R=\frac{10}{1,6}=\frac{100}{16}=\frac{25}{4}=6,25. \end{gather*}

Відповідь: 1Г, 2В, 3А.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26841

Завдання 19 з 22

Студент вивчав японську мову за такою методикою: у перший день він запам’ятав $6$ ієрогліфів, а кожного наступного дня – на $2$ ієрогліфи більше, ніж попереднього. Скільки всього ієрогліфів запам’ятав цей студент за $25$ днів від першого дня вивчення японської мови?

Впишіть відповідь:

750

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функції Числові послідовності.

Завдання перевіряє знання формули n-го члена арифметичної прогресії, вміння розв’язувати задачі на арифметичну прогресію.

Математичною моделлю задачі є задача на арифметичну прогресію: $$ a_1=6,\ \ d=2,\ \ S_{25}\ -\ ? $$

\begin{gather*} S_n=\frac{a_1+a_n}{2}\cdot n,\ \ S_{25}=\frac{a_1+a_{25}}{2}\cdot 25\\[6pt] a_{25}=a_1+24d=6+24\cdot 2=6+48=54\\[6pt] S_{25}=\frac{6+54}{2}\cdot 25=30\cdot 25=750. \end{gather*}

Отже, за $25$ днів студент запам'ятав $750$ ієрогліфів.

Відповідь: 750.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26842

Завдання 20 з 22

З трьох хлопців та трьох дівчат добирають чотирьох учасників до музичного квартету. Скільки всього є варіантів такого вибору?

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики.

Завдання перевіряє здатність застосування формул комбінаторики, зокрема сполук, до розв’язування комбінаторних задач.

Склад музичного квартету – $4$ будь-які учасники (хлопці чи дівчата). Отже, вибирають з $6$ учасників, порядок вибору неважливий, тому застосуємо формулу сполук: $$ \mathrm{C_n^m=\frac{n!}{m!(n-m)!}}. $$

\begin{gather*} \mathrm{C_6^4}=\frac{6!}{4!2!}=\frac{5\cdot 6}{2}=15. \end{gather*}

Відповідь: 15.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26843

Завдання 21 з 22

Осьовим перерізом циліндра є квадрат зі стороною $8\ \text{см.}$ Визначте площу $S\ (\text{см}^2)$ бічної поверхні цього циліндра. У відповіді запишіть значення виразу $\frac{S}{\mathbf{\pi}}$

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Стереометрія. Тіла обертання.

Завдання перевіряє знання про циліндр та його елементи.

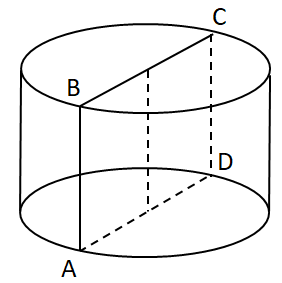
Осьовим перерізом циліндра $ABCD$ є квадрат. $AB=BC=CD=AD=8\ \text{см}.$

\begin{gather*} S_\text{б}=2\mathbf{\pi}RH,\ \ \text{де} R=\frac 12AD=4\ \text{см},\\[6pt] H=AB=8\ \text{см},\\[6pt] S_\text{б}=2\mathbf{\pi}\cdot 4\cdot 8=64\mathbf{\pi}\ \text{см}^2,\\[6pt] \frac{S}{\mathbf{\pi}}=\frac{64\mathbf{\pi}}{\mathbf{\pi}}=64. \end{gather*}

Відповідь: 64.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26844

Завдання 22 з 22

Визначте додатне значення $m,$ за якого один із коренів рівняння $x^2 – (2m – 4)x + 16 = 0$ на $6$ більший від іншого.

Впишіть відповідь:

Показати відповідь Читати пояснення

Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання перевіряє вміння розв’язувати квадратні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

$x^2-(2m-4)x+16=0,\ \ x_1\gt x_2\ \text{на}\ 6.$

Знайдемо дискримінант рівняння:

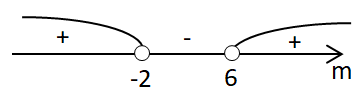
\begin{gather*} D=b^2-4ac=(2m-4)^2-4\cdot 1\cdot 16=\\[7pt] =4m^2-16m+16-64=4m^2-16m-48\gt 0\\[7pt] 4(m^2-4m-12)\gt 0,\ \ 4(m-6)(m+2)\gt 0, \end{gather*}

Додатнє значення $m,$ при якому рівняння має два різних кореня $m\gt 6.$

За теоремою Вієта і враховуючи умову завдання:

\begin{gather*} \left\{ \begin{array}{l} x_1+x_2=2m-4,\\ x_1\cdot x_2=16,\\ x_1-x_2=6, \end{array} \right. \ \ \ \left\{ \begin{array}{l} x_2+6+x_2=2m-4,\\ (x_2+6)x_2=16,\\ x_1=x_2+6, \end{array} \right. \\[7pt] 2x_2=2m-10,\ \ x_2=m-5. \end{gather*}

Підставимо значення $x_2$ у друге рівняння:

\begin{gather*} (m-5+6)(m-5)=16,\ \ (m+1)(m-5)=16,\\[7pt] m^2-5m+m-5-16=0,\ \ m^2-4m-21=0. \end{gather*}

Корені рівняння:

\begin{gather*} \left\{ \begin{array}{l} m_1=7,\\ m_2=-3\ \ne\ m\gt 6. \end{array} \right. \end{gather*}

Отже, додатнє значення $m=7.$

Відповідь: 7.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 547. Запитання: 26845

Новини

Навчання на нульовому курсі може розпочатись на кілька тижнів пізніше
Спеціальності, що мають особливу підтримку держави
У МОН заявили, що у 2029 році майже не буде вступників до вишів

Інформація

Усі завдання ЗНО з математики за темами
Усі тести ЗНО з математики онлайн
Завдання й відповіді ЗНО з математики минулих років
Усе про тест ЗНО з математики
Програма ЗНО з математики
Тести ЗНО онлайн з інших предметів
Дорожня карта учасника ЗНО
Дорожня карта вступника на бакалавра

Facebook

Twitter