НМТ онлайн 2024 року з математики – демоваріант
Демоваріант національного мультитесту (ЗНО) 2024 року з математики
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.
Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом.
Отже, правильна відповідь А.
Відповідь: А.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.
Завдання скеровано на перевірку вміння знаходити середнє арифметичне декількох значень.
Знайдемо середнє арифметичне десяти значень:
\begin{gather*} \frac{2\cdot 1+3\cdot 3+4\cdot 4+x\cdot 1}{10}=3,5\\[6pt] 2+9+16+x=35\\[7pt] x=35-27\\[7pt] x=8 \end{gather*}Отже, правильна відповідь – Г.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання скеровано на перевірку знань про многогранники та їхні елементи.
Бічною гранню прямої призми є прямокутник.
Отже, правильна відповідь – Б.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів.
Якщо $$ m=n-1, $$ то
Отже, правильна відповідь – B.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Коло та круг.
Завдання скеровано на перевірку знання властивостей кола та його елементів.
\(OA=12\ \text{см},\ O_1A=8\ \text{см}.\) $$ OO_1=OA-O_1A=12-8=4\ (\text{см}). $$
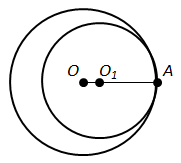
Отже, правильна відповідь – Г.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеня.
Розв'яжемо нерівність \(0,2x-54\lt 0\): \begin{gather*} 0,2x\lt 54\\[6pt] x\lt \frac{54}{0,2}\\[6pt] x\lt 270\\[7pt] x\in(-\infty; 270). \end{gather*}
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
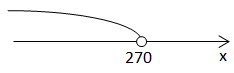
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
Нулі функції – значення \(x,\) при якому функція дорівнює \(0.\)
Отже, нулі функції – точки перетину з віссю \(x.\)
На риcунку така точка одна, отже, правильна відповідь – Б.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа та дії над ними.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів.
Розкриємо дужки і спростимо вираз:
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Трикутники.
Завдання скеровано на перевірку знання властивостей трикутника.
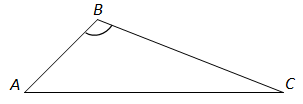
I. \(\angle B\) – тупий, тому \(\angle B\gt 90^\circ.\) Сума кутів трикутника дорівнює \(180^\circ,\) тому \(\angle A+\angle C \lt 90^\circ.\) Твердження правильне.
IІ. За нерівністю трикутника \(AB+BC\gt AC.\) Отже, твердження неправильне.
IІІ. У тупокутному трикутнику центр описаного кола лежить поза межами трикутника. Твердження правильне.
Отже, привильні твердження І та ІІІ.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання скеровано на перевірку вміння перетворення раціональних виразів, знання модуля дійсного числа та його властивостей.
Якщо \(a\gt 1,\) то \(|a-1|=-a+1.\)
За означенням модуля числа $$ |a|=-a\ \text{при}\ a\lt 0. $$ Отже, $$ |a-1|+|-7|=-a+1+7=-a+8. $$
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати системи рівнянь першого степеня та показникових.
Розв'яжемо систему рівнянь: \begin{gather*} \left\{ \begin{array}{l} x+y=5,\\ 4^x=16^{-1}; \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} x+y=5,\\ 4^x=4^{-2}; \end{array} \right. \\[7pt] \left\{ \begin{array}{l} -2+y=5,\\ x=-2; \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} y=7,\\ x=-2. \end{array} \right. \end{gather*} \(x_0=-2;\ y_0=7.\) Отже $$ x_0\cdot y_0=-2\cdot 7=-14. $$
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники. Піраміда.
Завдання скеровано на перевірку знань властивостей піраміди та її елементів, розв’язування задач на трикутники.
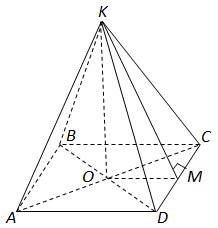
1. Піраміда правильна – в основі лежить квадрат \(ABCD.\)
2. \(KM\) – висота бічної грані $$ (KM\perp DC),\ KM=15\ \text{см}. $$
За теоремою про три перпендикуляри \begin{gather*} KO\perp\ (ABC),\\[7pt] KM\perp DC\ (\text{похила}),\\[7pt] OM - \text{проекція похилої},\\[6pt] OM=\frac 12 AD=\frac 12\cdot 18=9\ (\text{см}).\\[6pt] \text{Звідси},\ OM\perp CD. \end{gather*}
4. \(\Delta KOM\ (\angle O=90^\circ)\) за теоремою Піфагора:
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння.
\(\log_{\frac 13}(x+1)=-2.\) За означенням логарифма \begin{gather*} x+1=\left(\frac 13\right)^{-2},\ \ x+1=3^2,\\[6pt] x+1=9,\ \ x=8 \in (7; 9]. \end{gather*}
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання теореми синусів, властивостей паралельних прямих.
\(AB || CD,\ BD\) січна. \(\angle CBD=\angle BDA=45^\circ\) як внутрішні різності.
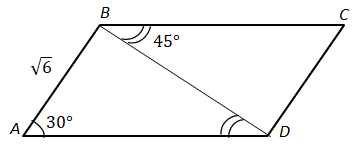
За теоремою синусів у \(\Delta ABD\):
\begin{gather*} \frac{BD}{\sin A}=\frac{AB}{\sin D};\\[6pt] BD=\frac{AB\cdot \sin A}{\sin D}=\frac{\sqrt{6}\cdot \sin 30^\circ}{\sin 45^\circ}=\\[6pt] =\frac{\sqrt{6}\cdot 1\cdot 2}{2\cdot \sqrt{2}}=\sqrt{3}\ (\text{см}). \end{gather*}Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння знаходити похідну функції.
$$ f(x)=x(x^3+1),\ \ f(x)=x^4+x. $$За формулою \((x^n)'=nx^{n-1}\) знайдемо похідну функції $$ f'(x)=4x^3+1. $$
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння установлювати властивості числових функцій, заданих формулою або графіком.
1. \(y=\sqrt{x-4}\) не визначена в точці \(x=1,\) бо \(x-4\ge 0,\ x\ge 4.\) Отже, правильна відповідь – Б.
2. \(y=2\) при будь-якому значенні \(x.\) Отже, набуває додатного значення в точці \(x=-3,\) правильна відповідь – Г.
3. \(y=x^3\) є непарною \begin{gather*} y(-x)=(-x)^3=-x^3=-y(x)\\[7pt] D(y)=R. \end{gather*} Отже, правильна відповідь – Д.
Відповідь: 1Б 2Г 3Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази. Дійсні числа.
Завдання скеровано на перевірку знання властивостей степенів з цілим показником, тотожних перетворень раціональних та логарифмічних виразів.
1. \(a^4:a^3=a^{4-3}=a^1=a.\) Отже, правильна відповіль – Д.
2. $$ \frac{a^2-a}{1-a}=\frac{a(a-1)}{-(a-1)}=\frac{a}{-1}=-a. $$ Отже, правильна відповідь – Г.
3. $$ 7^{-\log_7 a}=7^{\log_7 a^{-1}}=a^{-1}=\frac 1a. $$ Застосували правила \begin{gather*} a^{-n}=\frac{1}{a^n},\\[6pt] \log_a b^n=n\cdot \log_a b,\\[7pt] a^{\log_a b}=b. \end{gather*} Отже, правильна відповідь – B.
Відповідь: 1Д, 2Г, 3B.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку знання властивостей квадрата та трапеції, площ чотирикутників.
\(S_{ABCD}=S_{BMNC}=36\ \text{см}^2,\ AM=15\ \text{см}.\)
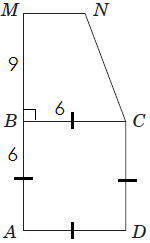
1 – Г. \begin{gather*} S_{ABCD}=a^2=AB^2=36\ \text{см}^2,\\[7pt] AB=6\ \text{см} - \text{сторона квадрата.} \end{gather*}
2 – Д. \begin{gather*} AM=AB+BM,\\[7pt] BM=15-6=9\ \text{см}. \end{gather*}
\(BMNC\) – прямокутна трапеція. Отже, висота трапеції – бічна сторона \(MB=9\ \text{см}.\)
3 – A. \begin{gather*} S_{BMNC}=\frac{MN+BC}{2}\cdot MB,\\[6pt] \frac{MN+6}{2}\cdot 9=36,\ \ (MN+6)\cdot 9=72,\\[6pt] MN+6=8, MN=2\ \text{см}. \end{gather*}
Відповідь: 1Г, 2Д, 3A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Числові послідовності.
Завдання скеровано на перевірку знання властивостей арифметичної прогресії, знання формули n-го члена арифметичної прогресії, вміння розв’язування текстових задач, зокрема з практичним змістом.
Дерев'яні колоди складені таким чином: \(13;\ 12;\ ...\ 2;\ 1.\) Для того, щоб визначити кількість колод, створимо математичну модель задачі.
В арифметичної прогресії \(a_1=13,\ a_{13}=1.\) Знайдемо суму \(n\text{-перших}\) членів прогресії.
Отже, колод у стосі \(91\).
Відповідь: 91.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.
Завдання скеровано на перевірку вміння розв’язувати задачі, використовуючи перестановки, комбінаторні правила добутку.
Кількість можливостей розмістити політичні новини - \(2,\) суспільних - \(3!=6,\) спортивну - \(1.\)
Отже, за правилом добутку кількість різних полідовностей розміщення новин $$ 2\cdot 6\cdot 1=12. $$
Відповідь: 12.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Координати і вектори у просторі.
Завдання скеровано на перевірку вміння виконувати дії з векторами, знаходити координати та скалярний добуток векторів.
\(\overrightarrow{AB}(-3; 8; 1),\ B(7; -2; 0), O(0; 0; 0).\)
Нехай \(A(x; y; z).\ \overline{AB}(7-x; -2-y; 0-z).\)
Отже,
Відповідь: -111.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їх системи.
Завдання скеровано на перевірку вміння розв’язувати тригонометричні рівняння, нерівності другого степеня та їх системи з параметрами.
Тригонометричне рівняння \(\sin\left(x+\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{3}\right)=2a^2+5a-6\) має корені при \(|2a^2+5a-6|\le 1.\)
1)
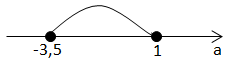
2)
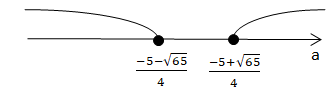
Розв'язок системи:
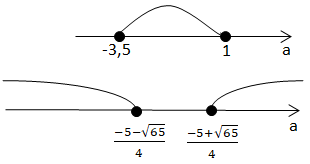
Найменше значення \(a=-3,5.\)
Відповідь: -3,5.
Знайшли помилку? Пишіть на