НМТ онлайн 2024 року з математики – 1 сесія

ТЕМА: Геометрія. Планіметрія.

Завдання скеровано на перевірку знання властивості зовнішнього кута трикутника.

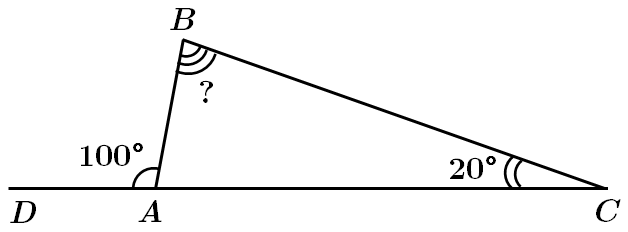
За властивістю зовнішнього кута трикутника:

\begin{gather*} \angle DAB=\angle B+\angle C. \end{gather*}

Отже, \(\angle B=100^\circ-20^\circ=80^\circ.\)

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку знання формул скороченого множення, вміння виконувати тотожні перетворення раціональних виразів.

За формулою скороченого множення \(a^2-b^2=(a-b)(a+b)\) розкладемо на множники:

Отже, правильна відповідь – A.

Відповідь: A.

ТЕМА: Геометрія Стереометрія. Тіла обертання.

Завдання скеровано на перевірку знання основних елементів циліндра.

Твірна циліндра – відрізок, який сполучає відповідні точки кіл кругів, які є основами циліндра.

З-поміж наведених – це \(AB.\)

Отже, правильна відповідь – Д.

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання скеровано на перевірку вміння розв’язувати рівняння першого степеня, використовуючи означення та властивості модуля.

\begin{gather*} |3x+2|=2\\[7pt] 3x+2=2\\[7pt] 3x=0\\[7pt] x=0\\[7pt] \text{або}\\[7pt] 3x+2=-2\\[7pt] 3x=-4\\[6pt] x=-\frac 43. \end{gather*}

З наведених чисел \(-\frac 43\) є коренем рівняння.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку вміння розв’язувати текстові задачі арифметичним способом.

Порція салату містить банани, апельсини та яблука у відношенні \(1:2:3.\) Отже, апельсини складають \(\frac 26=\frac 13\) від усіх фруктів.

Микола використав \(24\) фрукти, а це \(\frac 13\cdot 24=8\) апельсинів.

Відповідь: В.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння виконувати перетворення графіків функцій.

Для побудови графіка функції \(f(x-a)\) необхідно графік функції \(f(x)\) перенести вздовж осі \(Ox\) на \(a\) одиниць вправо, якщо \(a\) – додатне число і на \(a\) одиниць вліво, якщо \(a\) – від’ємне число.

Отже, для побудови графіка \(f(x-4)\) треба перемістити \(f(x)\) на \(4\) одиничних відрізки вправо вздовж осі \(Ox.\)

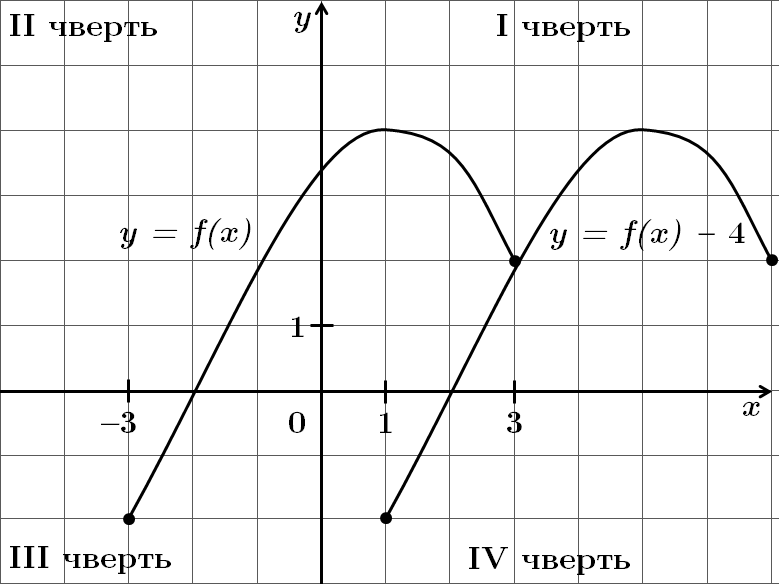
Отже, правильна відповідь – Г.

Відповідь: Г.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення ірраціональних виразів.

Використали властивість арифметичного корення \(n\text{-го}\) степеня:

Відповідь: A.

ТЕМА: Геометрія. Стереометрія. Многогранники.

Завдання скеровано на перевірку знання формул для обчислення площ поверхонь піраміди.

Сторона основи піраміди \(8\ \text{см},\) а апофема на \(2\ \text{см}\) більше, тому її довжина \(10\ \text{см}.\)

За формулою $$ S_\text{б}=\frac 12P_\text{осн}\cdot m, $$ де \(P_\text{осн}\) – периметр основи \(m\) – апофема, знаходимо площу бічної поверхні:

Відповідь: Г.

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку знання про паралелограм, ромб, квадрат та їх властивості.

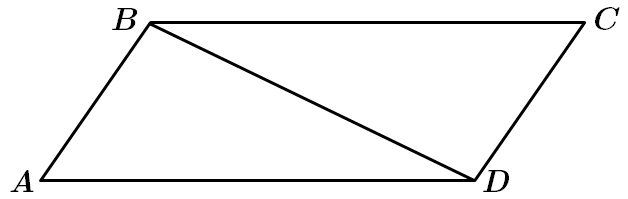
I. Твердження неправильне. Сума двох сусідніх сторін паралелограма не може дорівнювати його діагоналі, тому що за нерівністю трикутника \(AB+AD\gt BD.\)

II. Твердження правильне. Існує паралелограм, в якому один з кутів вдвічі більше за інший. Наприклад, з кутами \(60^\circ\) i \(120^\circ.\)

III. Твердження правильне. Існує паралелограм – ромб, у якого діагоналі перпендикулярні.

Відповідь: В.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних та показникових нерівностей.

Розв'яжемо систему нерівностей: \begin{gather*} \left\{ \begin{array}{l} 5^x\lt 25,\\ 2-x\lt 8, \end{array} \right. \ \ \ \ \left\{ \begin{array}{l} 5^x\lt 5^2,\\ x\gt -6, \end{array} \right. \\[7pt] \left\{ \begin{array}{l} x\lt 2,\\ x\gt -6. \end{array} \right. \end{gather*}

\(x\in (-6; 2).\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Функції Числові послідовності.

Завдання скеровано на перевірку знання формули \(n\text{-го}\) члена арифметичної прогресії, вміння розв’язувати задачі на арифметичну прогресію.

За формулою \(n\text{-го}\) члена

Обчислимо значення виразу \begin{gather*} a_6-a_4=a_1+5d-(a_1+3d)=\\[7pt] =a_1+5d-a_1-3d=2d. \end{gather*}

При \(d=-6,\ \ 2d=2\cdot(-6)=-12.\)

Відповідь: Д.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення логарифмічних виразів.

Застосували властивості логарифмів: $$ \log_a b^n=n\log_a b,\ \ \log_{a^k}b=\frac 1k\log_ab. $$

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Рівняння.

Завдання скеровано на перевірку вміння розв’язувати тригонометричні рівняння.

При \(n=0\ \ x=-\frac{\mathbf{\pi}}{12}.\)

Відповідь: А.

ТЕМА: Геометрія. Планіметрія. Трикутники.

Завдання скеровано на перевірку знання властивостей прямокутного трикутника, співвідношення між сторонами та кутами прямокутного трикутника.

Відповідь: Б.

ТЕМА: Алгебра і початки аналізу. Функції.

Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.

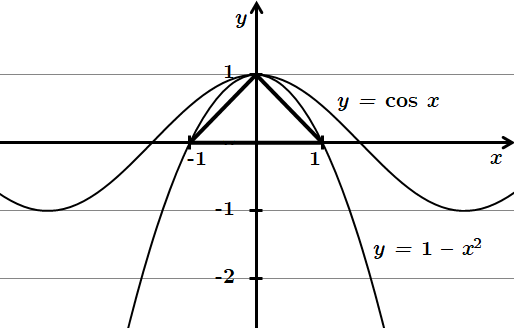
1. \(y=0\) це вісь \(Ox.\) Отже, спільних точок прямої та ламаної \(ABCA\) – безліч, правильна відповідь – Д.

2. Спільних точок параболи \((y=1-x^2)\) та ламаної \(ABCA\) – три: \((0; 1),\ (1; 0),\ (-1; 0),\) правильна відповідь – Г.

3. Спільних точок функції \(y=\cos x\) та ламаної \(ABCA\) – лише одна \((0, 1).\) Отже, правильна відповідь – Б.

Відповідь: 1Д 2Г 3Б.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку знання означення степеня з цілим показником та її властивості, означення синуса.

1. \(a^{-1}=\frac 1a=\frac 13\) є раціональним числом, що не є цілим. Отже, правильна відповіль – А.

2. \(a^0=1\) є натуральним числом. Отже, правильна відповіль – Б.

\(y=\sin x\) – періодична функція з найменшим додатним періодом \(2\mathbf{\pi}.\) Отже, правильна відповіль – Д.

Відповідь: 1А, 2Б, 3Д.

ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.

Завдання скеровано на перевірку вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції, знання теореми Піфагора, описані навколо кола чотирикутники.

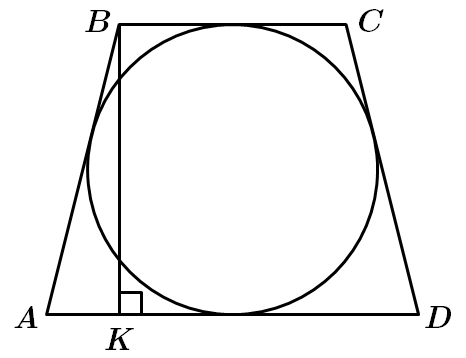
Якщо у чотирикутник можна вписати коло, то сума довжин протилежних сторін рівна.

1 – В. Середня лінія трапеції дорівнює \begin{gather*} \frac{BC+AD}{2}=\frac{50}{2}=25\ \text{см}. \end{gather*}

2 – Г. За умовою \begin{gather*} AB-BC=14\ \text{см}, BC=AD-14,\\[7pt] BC+AD=50,\ \ AD-14+AD=50,\\[7pt] 2AD=64,\ \ AD=32\ \text{см}. \end{gather*}

3 – Б. \(BC=50-32=18\ \text{см}.\) \(ABCD\) – рівнобічна трапеція, \(AB=CD.\)

за теоремою Піфагора: \begin{gather*} AB^2=AK^2+BK^2,\\[7pt] BK^2=25^2-7^2=625-49=576,\\[7pt] BK=24\ \text{см}. \end{gather*}

Відповідь: 1В, 2Г, 3Б.

ТЕМА: Алгебра і початки аналізу. Функції. Первісна.

Завдання скеровано на перевірку знання правил знаходження первісної, визначеного інтеграла.

Відповідь: 10.

ТЕМА: Алгебра і початки аналізу. Числа та вирази.

Завдання скеровано на перевірку вміння знаходити середнє арифметичне, розв’язувати лінійну нерівність.

\(4\) чорних ручки по \(27\ \text{грн},\) \(6\) червоних ручки по \(15\ \text{грн},\) \(n\) синіх ручок по \(10\ \text{грн}.\) Середня ціна однієї ручки \begin{gather*} \frac{4\cdot 27+6\cdot 15+n\cdot 10}{4+6+n}\lt 13,\\[6pt] \frac{108+90+10n}{10+n}\lt 13, \end{gather*} \(n\) – число додатне, тому можна помножити нерівність на \((10+n).\) \begin{gather*} 198+10n\lt 13(10+n),\\[7pt] 198+10n\lt 130+13n,\\[7pt] 3n\gt 68,\ \ n\gt\frac{68}{3},\ \ n\gt 22\frac 23. \end{gather*} Найменше можливе \(n=23.\)

Відповідь: 23.

ТЕМА: Геометрія. Стереометрія. Планіметрія. Многогранники. Трикутники. Чотирикутники.

Завдання скеровано на перевірку вміння розв’язувати задачі на обчислення

\(A(4; \sqrt{10}; 3),\ M(-2; 0; 1).\) Призма правильна, тому \(ABCD\) – квадрат.

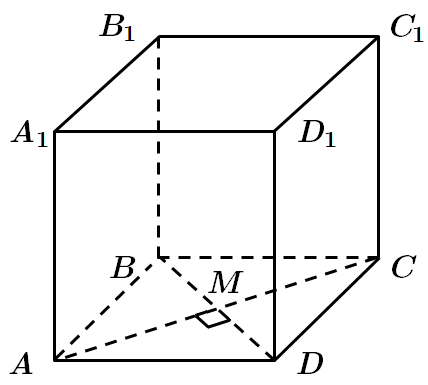
Діагоналі квадрата перпендикулярні. У \(\Delta AMD (\angle M=90^\circ)\) \(AM=MD=\sqrt{50}.\) За теоремою Піфагора

Висота \(AA_1=3AB=30.\) $$V=S_\text{осн}H,$$ де \(S_\text{осн}\) – площа квадрата, \(H\) – висота.

\begin{gather*} S_\text{осн}=AD^2=100.\\[7pt] V=100\cdot 30=3000. \end{gather*}

Відповідь: 3000.

ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.

Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.

$$\frac{x^2-ax+4}{x-5}=0.$$ ОДЗ:

Рівняння буде мати один корінь за умов:
1) \(D=0\) та \(x\ne 5;\)
2) \(D\gt 0,\) але один з коренів дорівнює \(5.\)

Розглянемо обидва випадки: \begin{gather*} \text{1)}\ \ D=0,\ \ a^2-16=0,\ \ a^2=16,\\[7pt] a=4\ \text{або}\ a=-4\\[6pt] x=\frac a2=\frac 42=2\ \text{або}\ x=-2. \end{gather*} Отже, корінь один. \begin{gather*} \text{2)}\ \ D\gt 0,\ \ a^2-16=0,\\[7pt] a\in (-\infty; -4)\cup (4; +\infty) \end{gather*}

\begin{gather*} x_1=\frac{a+\sqrt{a^2-16}}{2},\\[6pt] x_2=\frac{a-\sqrt{a^2-16}}{2}. \end{gather*}

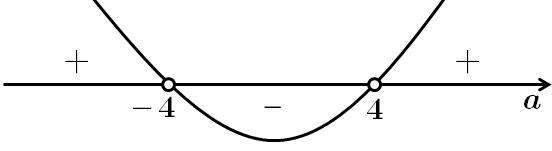
Нехай \(x_1=5,\) тоді

Нехай \(x_2=5,\) отже

Отже, рівняння має один корінь при \(a=4,\ a=-4, a=5\mathord{,}8.\) Добуток усіх значень \(a\) дорівнює: $$4\cdot (-4)\cdot 5\mathord{,}8=-92\mathord{,}8.$$

Відповідь: -92,8.