НМТ онлайн 2024 року з математики – 2 сесія
Тестові завдання другої сесії національного мультитесту (ЗНО) 2024 року з математики
ТЕМА: Алгебра і початки аналізу. Елементи теорії ймовірностей.
Завдання скеровано на перевірку вміння обчислювати ймовірність випадкової події.
Усього в літаку
Імовірність того, що пасажиру дістанеться місце біля проходу, знаходиться за формулою
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання скеровано на перевірку знання формул скороченого множення.
За формулою скороченого множення
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання скеровано на перевірку вміння порівнювати дійсні числа, знання властивостей модуля.
Розв'язком нерівності
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Елементарні геометричні фігури на площині та їхні властивості.
Завдання скеровано на перевірку знання властивостей кутів, аксіом планіметрії.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники.
Завдання скеровано на перевірку знання про многогранники та їхні елементи, ознаки паралельності прямої та площини.
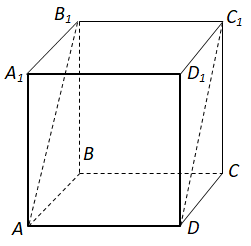
Протилежні грані куба – паралельні площини.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
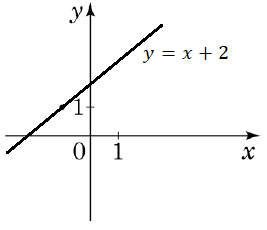
Графік лінійної функції
Відповідь: В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа і вирази.
Завдання скеровано на перевірку знання властивостей степенів, уміння виконувати дії з дійсними числами.
Маса одного протона
Маса
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Стереометрія. Чотирикутники. Многогранники.
Завдання скеровано на перевірку знання про піраміду та її елементи, вміння знаходити площу ромба та об’єм піраміди.
Об'єм піраміди обчислуємо за формулою:
За умовою завдання основою піраміди є ромб, діагоналі якого
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення ірраціональних виразів.
Обчислимо
При
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія.
Завдання скеровано на перевірку знання властивості медіани трикутника, центра описаного кола трикутника.
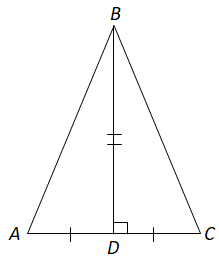
I. Серединний перпендикуляр до сторони рівностороннього трикутника ділить його на два рівних трикутники.
II. Точка перетину серединних перпендикулярів трикутника є центром описаного кола. У прямокутному трикутнику центр описаного кола – середина гіпотенузи. Отже, твердження є правильним.
III. У тупокутному трикутнику центр описаного кола знаходиться поза трикутником. Отже, твердження є неправильним.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання скеровано на перевірку вміння розв’язувати системи лінійних рівнянь.
Розв'яжемо систему:
Почленно додамо рівняння:
Отже,
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції Числові послідовності.
Завдання скеровано на перевірку знання формули суми геометричної прогресії, її властивостей.
Визначаємо
Отже,
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення логарифмічних виразів.
Застосували властивості логарифмів:
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння.
Завдання скеровано на перевірку вміння розв’язувати показникові рівняння.
Зведемо до однакової основи:
Рівняння має два корені. Найменший з них
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку знання властивості трапеції, прямокутного трикутника.
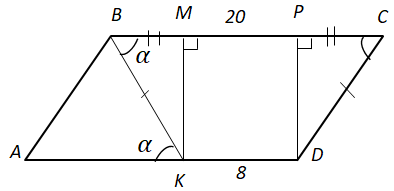
У
Площу паралелограма знаходимо за формулою:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції.
Завдання скеровано на перевірку вміння встановлювати властивості числових функцій, заданих графіком.
1. Найбільше значення функції
2. Найменше значення функції на відрізку
3.
Відповідь: 1Г 2Д 3В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Числа та вирази.
Завдання скеровано на перевірку знання властивостей степенів, уміння виконувати дії дійсними числами.
1 – А.
2 – В.
3 – Б.
Відповідь: 1А, 2В, 3Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку вміння застосовувати властивості трикутників до розв’язування планіметричних задач, знаходити довжину середньої лінії трапеції.
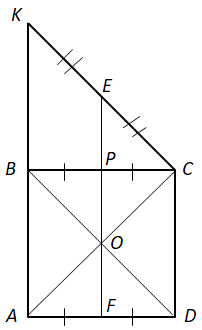
1 – A.
2 – Г.
3 – Б. Центр кола, описаного навколо квадрата, – це точка перетину діагоналей – точка
Центр кола, описаного навколо прямокутного трикутника, – середина гіпотенузи – точка
Відповідь: 1A, 2Г, 3Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функції. Первісна.
Завдання скеровано на перевірку вміння находити первісну, обчислювати площу плоских фігур за допомогою інтеграла.
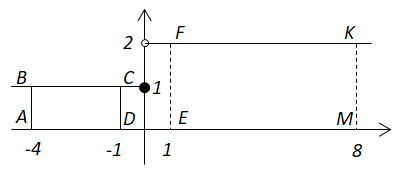
Обчислити значення виразу
1) застосувати геометричний зміст визначеного інтеграла;
2) алгебраїчним.
1 спосіб:
2 спосіб:
Відповідь: 31.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики.
Завдання скеровано на перевірку знання означення перестановки, вміння розв’язувати комбінаторні задачі.
Якщо першим уроком буде фізкультура, а інші п'ять можна переставляти, то різних варіантів скласти розклад знаходимо за комбінаторною формулою перестановок
Всього існує
Відповідь: 240.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання. Координати на площині.
Завдання скеровано на перевірку знання про конус та його елементи, формули площ поверхонь конуса, формул для обчислення відстані між двома точками.
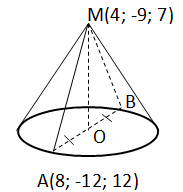
Знайдемо довжину
Відповідь:
Відповідь: 37,5.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Рівняння, нерівності та їхні системи.
Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння, аналізувати та досліджувати рівняння, розв’язувати рівняння з параметром.
Лінійне рівняння не має коренів при
При
Логарифмічне рівняння не буде мати розв'язок, якщо
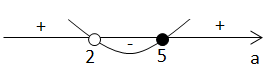
Відповідь: 14.
Знайшли помилку? Пишіть на




