НМТ онлайн 2025 року з математики – 1 сесія

12345678910111213141516171819202122

Зачекайте, йде розрахунок...

Завдання 1 з 22

На графіку функції відображено зміну температури повітря в травні протягом доби. Визначте за графіком кількість годин, протягом яких температура не перевищувала $10^\circ\ \mathrm{C}.$

А$7$

Б$9$

В$14$

Г$2$

Д$22$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.

Завдання скеровано на перевірку розуміння графічної форми подання статистичної інформації.

Температура не перевищувала потрібного значення $10^\circ\mathrm{C}$ з $00\mathord{:}00$ до $7\mathord{:}00$ години та ще з $22\mathord{:}00$ до $24\mathord{:}00.$ Разом це становить $9$ годин.

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34371

Завдання 2 з 22

Емблема компанії має вигляд круга, від центра $O$ якого проведено радіуси $OA$, $OB$ і $OC$ (див. рисунок). Визначте градусну міру кута $AOB$, якщо радіуси поділяють круг на три рівні частини.

А$100^\circ$

Б$90^\circ$

В$180^\circ$

Г$120^\circ$

Д$60^\circ$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Геометричні величини та вимірювання їх.

Завдання скеровано на перевірку вміння знаходити величини кутів, розв’язувати планіметричні задачі.

Повний кут має градусну міру $360^\circ.$ Радіуси $OA$, $OB$, $OC$ поділяють кут на $3$ рівних частини.

Отже, $\angle AOB=360^\circ :3=120^\circ.$

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34373

Завдання 3 з 22

Позначте число, що є розв'язком системи нерівностей $$ \left\{ \begin{array}{l} x\gt -3, \\ x\le 7. \end{array} \right. $$

А$-10$

Б$-7$

В$-3$

Г$5$

Д$10$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Лінійні нерівності.

Завдання скеровано на перевірку вміння розв’язувати системи лінійних нерівностей.

$$ \left\{ \begin{array}{l} x\gt -3,\\ x\le 7. \end{array} \right. $$

Зобразимо множину розв'язків кожної нерівності на одній координатній прямій:

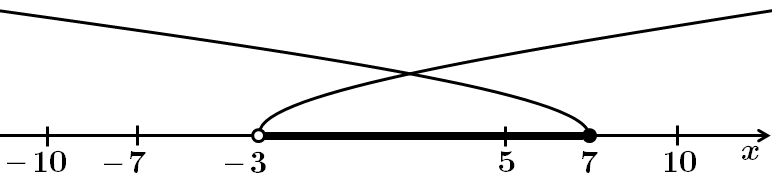
Розв'язком системи є проміжок $x\in (-3; 7].$ З наведених чисел, лише число $5$ належить даному проміжку.

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34374

Завдання 4 з 22

$0\mathord{,}6x^3\cdot 5x^4=$

А$30x^7$

Б$3x^7$

В$30x^{12}$

Г$3x^{12}$

Д$0\mathord{,}3x^{12}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Дійсні числа.

Завдання скеровано на перевірку знання означення степеня з натуральним показником, його властивостей.

$$ 0\mathord{,}6x^3\cdot 5x^4=0\mathord{,}6\cdot 5\cdot x^{3+4}=3x^7. $$

Використали властивість степеня з натуральним показником. При множенні степенів з однаковими основами показники додаються, а основа залишається без змін: $$ a^n\cdot a^m=a^{n+m}, $$ (де $a$ – будь-яке число, $n$ i $m$ – натуральні числа).

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34375

Завдання 5 з 22

На рисунку зображено трикутну піраміду $SABC$ з основою $ABC.$ Скільки всього площин, паралельних площині основи піраміди, можна провести через її вершину $S$?

Ажодної

Блише одну

Влише дві

Глише три

Дбільше як три

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі.

Завдання скероване на перевірку розуміння властивостей паралельних площин.

У піраміді $SABC$ точка $S$ не лежить у площині $(ABC).$

Через точку, яка не лежить у площині, можна провести тільки одну площину, паралельну даній.

Отже, через точку $S$ можна провести лише одну площину паралельну площині $ABC.$

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34376

Завдання 6 з 22

Укажіть функцію, графік якої зображено на рисунку 2, якщо він отриманий внаслідок паралельного перенесення графіка функції $y=f(x)$ (див. рис. 1).

А$y=2f(x)$

Б$y=f(x+2)$

В$y=f(x-2)$

Г$y=f(x)+2$

Д$y=f(x)-2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функціональна залежність.

Завдання скеровано на перевірку вміння виконувати перетворення графіків функцій.

Є два види перетворення:

1. Паралельне перенесення вздовж осі ординат: $$ y=f(x)\rightarrow y=f(x)+c. $$

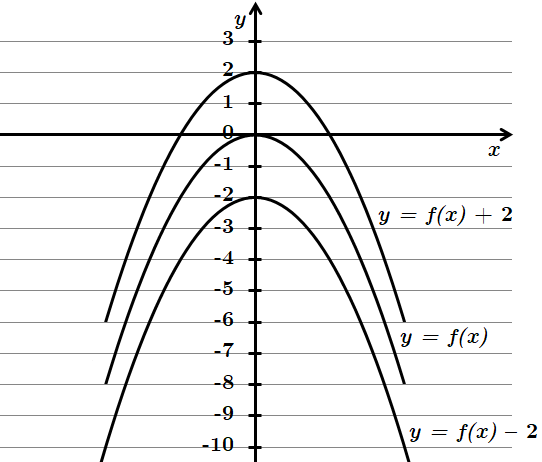
Для побудови графіка функції $y=f(x)+c$ необхідно графік функції $y=f(x)$ перенести вздовж осі $Oy$ на $c$ одиниць угору, якщо $c$ – додатне число або на $c$ одиниць вниз, якщо $c$ – від’ємне число.

2. Паралельне перенесення вздовж осі абсцис: $$ y=f(x)\rightarrow y=f(x-a). $$

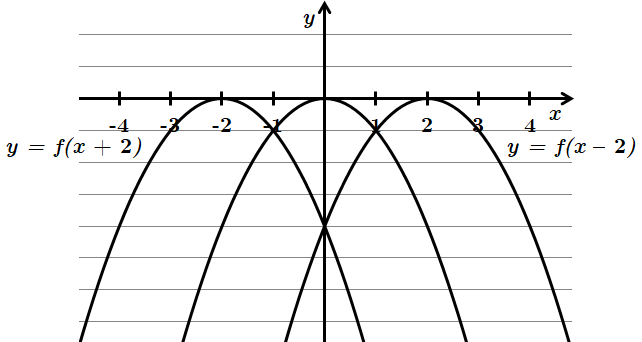
Для побудови графіка функції $y=f(x-a)$ необхідно графік функції $y=f(x)$ перенести вздовж осі $Ox$ на $a$ одиниць вправо, якщо $a$ – додатне число і на $a$ одиниць вліво, якщо $a$ – від’ємне число.

Застосувавши властивості паралельного перенесення до функції $y=f(x)$, при перенесенні вліво на $2$ одиниці отримаємо графік функції $y=f(x+2).$

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34378

Завдання 7 з 22

Під час миття рук милом із крана витікає $25$ л води, з них $60\ \text{%}$ марнують під час намилювання. Скільки літрів води можна зберегти, якщо закривати кран перед намилюванням рук?

А$19$

Б$15$

В$12$

Г$10$

Д$6$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Текстові задачі.

Завдання скеровано на перевірку вміння розв’язувати основні задачі на відсотки.

Знаходимо $60\ \text{%}$ від $25$ л: $$ 25\cdot \frac{60}{100}=15. $$

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34379

Завдання 8 з 22

У прямокутній системі координат у просторі задано точки $A(5; -4; 0)$ і $B(7; 2; - 2).$ Визначте точку $C$, симетричну точці $A$ відносно точки $B.$

А$C(1; 3; -1)$

Б$C(2; 6; -2)$

В$C(6; -1; -1)$

Г$C(3; -10; 2)$

Д$C(9; 8; -4)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Стереометрія.

Завдання скеровано на перевірку знання формули для обчислення координат середини відрізка.

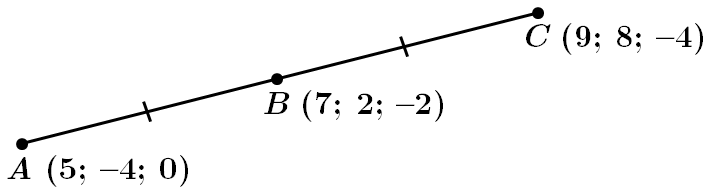
Точка $C$ симетрична точці $A$ відносно точки $B.$ Точка $B$ – середина відрізка $AC.$

$A(5; -4; 0)$, $B(7; 2; -2).$ Нехай точка $C(x_C; y_C; z_C).$

За формулою координати середини відрізка:

\begin{gather*} x_B=\frac{x_A+x_C}{2},\ \ 7=\frac{5+x_C}{2},\ \ x_C=9,\\[6pt] y_B=\frac{y_A+y_C}{2},\ \ 2=\frac{-4+y_C}{2},\ \ y_C=8,\\[6pt] z_B=\frac{z_A+z_C}{2},\ \ -2=\frac{0+z_C}{2},\ \ z_C=-4,\\[6pt] C(9; 8; -4). \end{gather*}

Відповідь: Д.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34380

Завдання 9 з 22

$\log_55^{10}=$

А$5$

Б$10$

В$50$

Г$5^{10}$

Д$10^{5}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Логарифмічні вирази.

Завдання скеровано на перевірку знання означення та властивостей логарифмів.

$$ \log_55^{10}=10\cdot \log_55=10\cdot 1=10. $$

Застосували властивості логарифмів:

\begin{gather*} \log_ab^n=n\log_ab,\\[7pt] \log_aa=1. \end{gather*}

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34381

Завдання 10 з 22

Які з наведених тверджень є правильними для будь-якого трикутника?

I. Сума будь-яких двох сторін трикутника менша за третю його сторону.

II. Сума будь-яких двох кутів трикутника більша за $90^\circ.$

III. Навпроти найбільшої сторони трикутника лежить найбільший його кут.

Алише І

Блише ІІ

Влише III

Глише І та ІІІ

ДІ, ІІ та ІІІ

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Трикутники.

Завдання скеровано на перевірку знань основних властивостей трикутника, нерівності трикутника.

I. Твердження неправильне. За нерівністю трикутника, сума довжин двох сторін трикутника більша за довжину третьої.

II. Твердження неправильне. Сума двох кутів трикутника не завжди більша за $90^\circ.$ До прикладу, у трикутнику кути можуть бути $20^\circ$, $20^\circ$, $140^\circ.$ Тоді сума двох гострих кутів: \begin{gather*} 20^\circ+20^\circ=40^\circ,\\[7pt] 40^\circ\lt 90^\circ. \end{gather*}

III. Твердження правильне. За властивістю трикутника, навпроти більшої строни лежить більший кут, навпроти меншої сторони – менший кут, навпроти рівних сторін – рівні кути.

Відповідь: В.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34382

Завдання 11 з 22

Розв'яжіть рівняння $$ \frac{2x-7}{3}=\frac{5x+4}{2}. $$

А$-\frac 29$

Б$-1\frac{7}{19}$

В$-2\frac{4}{11}$

Г$-3\frac 23$

Д$-\frac{2}{19}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра. Лінійні рівняння.

Завдання скеровано на перевірку вміння розв’язувати лінійні рівняння, знання основної властивості пропорції.

$$ \frac{2x-7}{3}=\frac{5x+4}{2}. $$

Застосуємо основну властивість пропорції: \begin{gather*} \frac ab=\frac cd,\\[6pt] a\cdot d=b\cdot c,\\[7pt] 2(2x-7)=3(5x+4),\\[7pt] 4x-14=15x+12,\\[7pt] 4x-15x=12+14,\\[7pt] -11x=26,\\[6pt] x=-\frac{26}{11},\\[6pt] x=-2\frac{4}{11}. \end{gather*}

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34383

Завдання 12 з 22

В арифметичній прогресії $(a_n)$ відомо, що $a_6-a_1=-30.$ Обчисліть значення виразу $a_1-a_3.$

А$12$

Б$10$

В$-15$

Г$-10$

Д$-12$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Числові послідовності.

Завдання скеровано на перевірку знання формули $n\text{-го}$ члена арифметичної прогресії.

Арифметрична прогресія $(a_n)$, $a_6-a_1=-30.$

За формулою $n\text{-го}$ члена

\begin{gather*} a_n=a_1+d(n-1),\\[7pt] a_6=a_1+5d,\\[7pt] a_1+5d-a_1=-30,\\[7pt] 5d=-30,\\[7pt] d=-6. \end{gather*}

Обчислимо значення виразу

\begin{gather*} a_1-a_3=a_1-(a_1+2d)=\\[7pt] =a_1-a_1-2d=-2d=-2\cdot (-6)=12. \end{gather*}

Відповідь: A.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34384

Завдання 13 з 22

$x(x-2y)-(x-y)^2=$

А$-y^2$

Б$y^2$

В$-4xy+y^2$

Г$-2xy+y^2$

Д$-4xy-y^2$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Раціональні вирази і їх перетворення.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів, знання формул скороченого множення.

Розкриємо дужки:

\begin{gather*} x(x-2y)-(x-y)^2=\\[7pt] =x^2-2xy-(x^2-2xy+y^2)=\\[7pt] =x^2-2xy-x^2+2xy-y^2=-y^2. \end{gather*}

Відповідь: A.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34385

Завдання 14 з 22

Позначте проміжок, якому належить корінь рівняння $1-\log_{0\mathord{,}5}x=3.$

А$(-\infty; -3)$

Б$[-3; 0)$

В$[0; 3)$

Г$[3; 10)$

Д$[10; +\infty)$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Логарифмічні рівняння.

Завдання скеровано на перевірку вміння розв’язувати логарифмічні рівняння.

\begin{gather*} 1-\log_{0\mathord{,}5}x=3,\\[7pt] \log_{0\mathord{,}5}x=-2,\\[7pt] x=0\mathord{,}5^{-2},\\[6pt] x=\left(\frac 12\right)^{-2}=2^2=4,\\[6pt] 4\in [3; 10). \end{gather*}

Використали означення логарифма: $\log_ab=c$, $a^c=b$ та застосували формулу: $$ a^{-n}=\frac{1}{a^n}. $$

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34386

Завдання 15 з 22

У рівнобічній трапеції $ABCD$ точка $O$ є серединою основи $AD$, $\angle AOB=45^\circ$, $AD:BC=5:2$ (див. рисунок). Визначте площу трапеції $ABCD$, якщо $AD=b.$

А$\frac{7}{50}b^2$

Б$\frac{7}{25}b^2$

В$\frac{7\sqrt{2}}{50}b^2$

Г$\frac{b^2}{14}$

Д$\frac{4b^2}{25}$

Позначте відповіді:

А	Б	В	Г	Д

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія.

Завдання скеровано на перевірку властивостей трапеції та трикутника, їх властивостей.

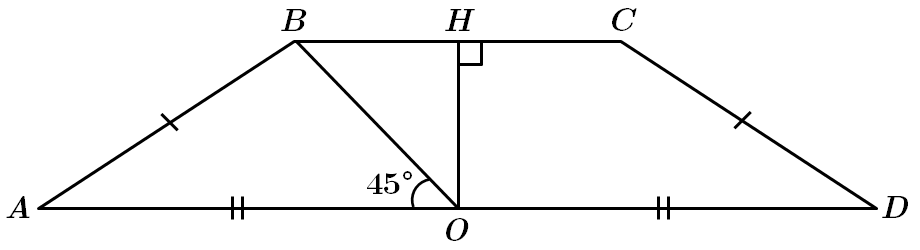
1. $AD=b$, точка $O$ – середина $AD$, тому $AO=OD.$ Проведемо перпендикуляр $OH\ \perp BC.$

2. Трапеція $ABCD$ – рівнобічна, тому $BH=HC.$

\begin{gather*} AD:BC=5:2,\\[6pt] BC=\frac{2AD}{5}=\frac{2b}{5},\\[6pt] BH=\frac 12BC=\frac b5. \end{gather*}

3. $\angle AOB=45^\circ$, $\angle AOH=90^\circ.$ Отже, $\angle BOH=45^\circ$ а $\Delta BHO$ – прямокутний рівнобедрений. $BH=HO=\frac b5.$

4. Площу трапеції знаходимо за формулою: $$ S=\frac{a+b}{2}\cdot h, $$ де $a$, $b$ – основи, $h$ – висота.

$$ S=\frac{BC+AD}{2}\cdot OH=\left(\frac{2b}{5}+b\right):2\cdot \frac b5=\frac{7b\cdot b}{5\cdot 2\cdot 5}=\frac{7b^2}{50}. $$

Відповідь: A.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34387

Завдання 16 з 22

Доберіть до функції (1-3) її властивість (А - Д).

Функція

1$y=-x^3$

2$y=\sqrt{x}$

3$y=\cos x$

Властивість функції

Аграфік функції розміщено лише у другій координатній чверті

Бграфік функції має з графіком рівняння $x^2+y^2=9$ лише одну спільну точку

Вє парною

Гнабуває всіх значень з проміжку $(-\infty; +\infty)$

Дграфік функції не має спільних точок із прямою $x=0$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Функціональна залежність.

Завдання скеровано на перевірку вміння будувати графіки функцій, встановлювати властивості числових функцій.

1. Набуває всіх значень з проміжку $(-\infty; +\infty).$

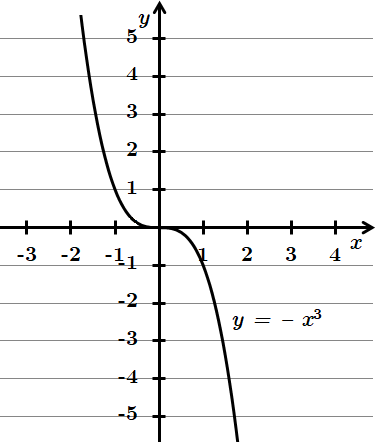
Отже, 1 – Г.

2. Графік функції має з графіком рівняння $x^2+y^2=9$ лише одну спільну точку.

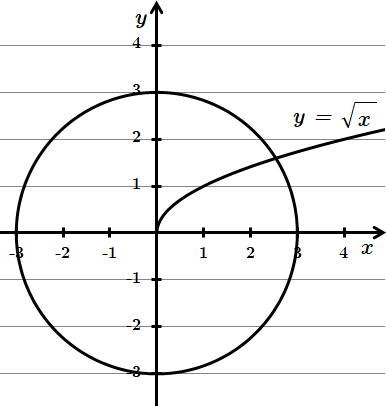
Отже, 2 – Б.

3. $y=\cos x$ – є парною.

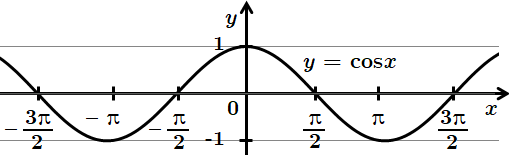
Відповідь: 1Г, 2Б, 3В.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34388

Завдання 17 з 22

Доберіть до числового виразу (1-3) його значення (А – Д).

Числовий вираз

1$\sin\left(-\frac{\mathbf{\pi}}{6}\right)$

2$\mathbf{\pi}-|\mathbf{\pi}+2|$

3$\left(-\frac{1}{\sqrt{2}}\right)^2$

Значення виразу

А$\frac 12$

Б$-2$

В$2$

Г$-\frac 12$

Д$\sqrt{2}$

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.

Завдання скеровано на перевірку вміння виконувати тотожні перетворення тригонометричних, ірраціональних виразів, знання модуля числа та його властивостей.

1. $\sin \left(-\frac{\mathbf{\pi}}{6}\right)=-\sin\frac{\mathbf{\pi}}{6}=-\frac 12.$

$y=\sin x$ – непарна, тому $\sin(x)=-\sin x.$

Отже, правильна відповідь – Г.

2. $\mathbf{\pi}-|\mathbf{\pi}+2|=\mathbf{\pi}-(\mathbf{\pi}+2)=\mathbf{\pi}-\mathbf{\pi}-2=-2.$

Отже, правильна відповідь – Б.

3. $\left(-\frac{1}{\sqrt{2}}\right)^2=\left(\frac{1}{\sqrt{2}}\right)^2=\frac 12.$

Отже, правильна відповідь – A.

Відповідь: 1Г, 2Б, 3A.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34389

Завдання 18 з 22

Прямокутник $ABKM$ складається з квадрата $ABCD$ та прямокутника $CKMD$ (див. рисунок). Периметр квадрата $ABCD$ дорівнює $40$ см, а довжина відрізка $CM$ – $26$ см. До кожного початку речення (1-3) доберіть його закінчення (А – Д) так, щоб утворилося правильне твердження.

Початок речення

1Сторона квадрата $ABCD$ дорівнює

2Довжина відрізка $CK$ дорівнює

3Відстань між центром квадрата $ABCD$ та точкою перетину діагоналей прямокутника $ABKM$ дорівнює

Закінчення речення

А$16$ см.

Б$12$ см.

В$10$ см.

Г$24$ см.

Д$17$ см.

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Планіметрія. Чотирикутники.

Завдання скеровано на перевірку вміння застосовувати властивості прямокутника та квадрата, розв’язування трикутників.

1. $P_{ABCD}=40$ см, $AB=BC=CD=DA=40: 4=10$ см.

Отже, правильна відповідь – В.

$AB=CD=KM=10$ см. $\Delta CKM\ (\angle K=90^\circ)$ за теоремою Піфагора:

\begin{gather*} CM^2=CK^2+KM^2,\\[7pt] CK^2=CM^2-KM^2=26^2-10^2=576,\\[7pt] CK=24\ \text{см}. \end{gather*}

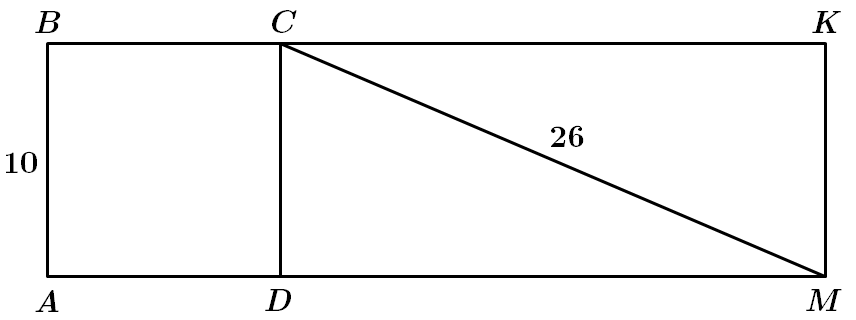
Отже, правильна відповідь – Г.

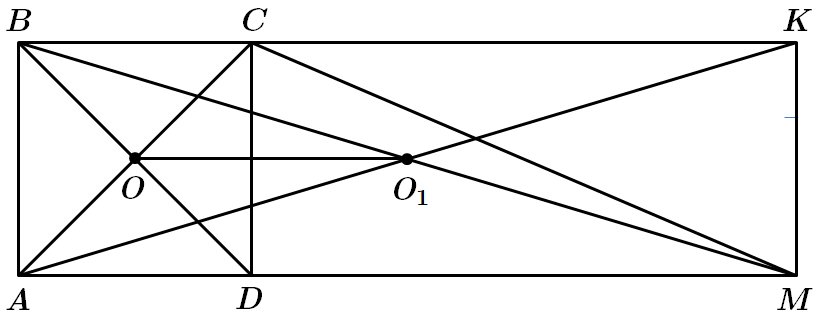
3. Відстань між точкою $O$ – центр квадрата, $O_1$ – точка перетину діагоналей прямокутника $ABKM$ – відрізок $OO_1.$ $BO_1=O_1M.$

У $\Delta DBM\ OO_1$ – середня лінія. За властивістю середньої лінії $$ OO_1=\frac 12DM=\frac 12\cdot 24=12\ \text{см}. $$

Отже, правильна відповідь – Б.

Відповідь: 1В, 2Г, 3Б.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34390

Завдання 19 з 22

Дотична, проведена до графіка функції $y=f(x)$ у точці з абсцисою $x_0=3$, паралельна прямій $y=1\mathord{,}5x+5.$ Обчисліть значення похідної функції $g(x)=\frac{18}{x}-f(x)$ в точці $x_0=3.$

Впишіть відповідь:

-3.5

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Похідна функції.

Завдання скеровано на перевірку вміння знаходити похідну суми, знаходити числове значення похідної функції в точці для заданого значення аргументу, кутового коефіцієнта дотичної.

\begin{gather*} g(x)=\frac{18}{x}-f(x),\\[6pt] g'(x)=-\frac{18}{x^2}-f'(x). \end{gather*}

Дотична, проведена до графіка функції $y=f(x)$ у точці з абсцисою $x_0=3$ паралельна прямій $y=1\mathord{,}5x+5.$

\begin{gather*} f'(x_0)=k=1\mathord{,}5,\\[6pt] g'(x_0)=g'(3)=-\frac{18}{3^2}-1\mathord{,}5=-2-1\mathord{,}5=-3\mathord{,}5. \end{gather*}

Відповідь: $-3\mathord{,}5.$

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34391

Завдання 20 з 22

На рисунку зображено схему салону пасажирського літака. У салоні налічується $n$ рядів, у кожному з яких розташовано по $6$ крісел (обабіч проходу по $3$). Реєструючи пасажира, електронна система навмання вибирає для нього посадкове місце. Імовірність того, що першому зареєстрованому пасажиру дістанеться місце біля проходу в першому або останньому ряду, дорівнює $\frac{1}{45}.$ Визначте $n.$

Впишіть відповідь:

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Ймовірність випадкової події.

Завдання скеровано на перевірку вміння обчислювати ймовірність випадкових подій, знання класичного означення ймовірної події.

Всього у салоні літака $n$ рядів по $6$ місць в кожному. Отже, всього у літаку $6n$ місць.

Місць біля проходу в першому або останньому ряду $4.$ Імовірність того, що пасажиру дістанеться таке місце – $\frac{1}{45}.$

За означенням імовірність це відношення кількості результатів, що сприяють цій події ($4$ місця біля проходу), до загальної кількості всіх можливих рівноймовірних результатів ($6n$ – загальна кількість місць). Тому

\begin{gather*} \frac{1}{45}=\frac{4}{6n},\\[6pt] 6n=4\cdot 45,\\[7pt] n=30. \end{gather*}

Відповідь: $30.$

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34392

Завдання 21 з 22

Циліндр і пряма чотирикутна призма мають рівні висоти. Основою призми є ромб, діагоналі якого дорівнюють $12$ см i $16$ см. Радіус основи циліндра дорівнює стороні ромба. Обчисліть об'єм (см$^3$) заданої призми, якщо площа бічної поверхні циліндра дорівнює $400\mathbf{\pi}$ см$^2.$

Впишіть відповідь:

1920

Пропустити Відповісти Наступне Показати відповідь Читати пояснення

Наступне Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Геометрія. Стереометрія. Многогранники, тіла обертання.

Завдання скеровано на перевірку знань властивостей призми та циліндра, вміння розв’язувати задачі на обчислення об’ємів і площ поверхонь геометричних тіл.

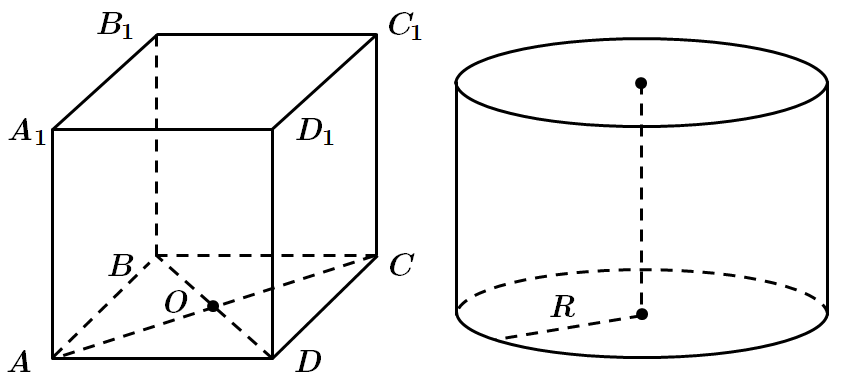
1. В основі призми – ромб з діагоналями $12$ см і $16$ см.

$AO=OC=8$ см, $BO=OD=6$ см. $AC\ \perp\ BD.$ $\Delta AOD$ – прямокутний. За теоремою Піфагора

\begin{gather*} AD^2=AO^2+OD^2=8^2+6^2=100\ \textit{см}^2\\[7pt] AD=10\ \textit{см}. \end{gather*}

2. Радіус основи циліндра $R=AD=10$ см.

3. Площа поверхні циліндра

\begin{gather*} S_\text{б}=2\mathbf{\pi}RH,\\[7pt] 2\mathbf{\pi}\cdot 10\cdot H=400\mathbf{\pi},\\[7pt] H=20\ \textit{см}. \end{gather*}

4. Висота призми дорівнює висоті циліндра $H=20$ см.

5. Об'єм призми

\begin{gather*} V=S_\text{осн}\cdot H. \end{gather*}

Площу ромбу можна знайти за формулою:

\begin{gather*} S_\text{осн}=\frac 12d_1d_2,\\[6pt] S_\text{осн}=\frac 12\cdot 12\cdot 16=96\ \textit{см}^2,\\[6pt] V=96\cdot 20=1920\ \textit{см}^3. \end{gather*}

Відповідь: 1920.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34393

Завдання 22 з 22

Визначте найбільше значення $a$, за якого рівняння $$ \frac{3^{2a-5x+2}-\sqrt{27}}{\sqrt{x}+\sqrt{3-x}}=0 $$ має корінь.

Впишіть відповідь:

7.25

Показати відповідь Читати пояснення

Завершити тест

Пояснення доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Пояснення

ТЕМА: Алгебра і початки аналізу. Розв’язування показникових, раціональних рівнянь.

Завдання скеровано на перевірку вміння розв’язувати показникові, раціональні і ірраціональні рівняння й нерівності та їх системи з параметрами.

1. Область допустимих значень

\begin{gather*} \left\{ \begin{array}{l} x\ge 0,\\ 3-x\ge 0,\\ \sqrt{x}+\sqrt{3-x}\ne 0, \end{array} \right.\\[7pt] \left\{ \begin{array}{l} x\ge 0,\\ x\le 3. \end{array} \right.\\[7pt] x\in [0; 3]. \end{gather*}

2. Розв'яжемо рівняння:

\begin{gather*} 3^{2a-5x+2}-\sqrt{27}=0,\\[7pt] 3^{2a-5x+2}=3\sqrt{3},\\[7pt] 3^{2a-5x+2}=3^{1\mathord{,}5},\\[7pt] 2a-5x+2=1\mathord{,}5,\\[7pt] 5x=2a+0\mathord{,}5,\\[7pt] x=0\mathord{,}4a+0\mathord{,}1. \end{gather*}

Для того, щоб рівняння мало корінь

\begin{gather*} 0\le 0\mathord{,}4a+0\mathord{,}1\le 3,\\[7pt] -0\mathord{,}1\le 0\mathord{,}4a\le 2\mathord{,}9,\\[6pt] -\frac 14\le a\le \frac{29}{4},\\[6pt] -\frac 14\le a\le 7\frac 14. \end{gather*}

Найбільше значення $a=7\frac 14=7\mathord{,}25.$

Відповідь: $7\mathord{,}25.$

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 671. Запитання: 34394

Новини

Зимовий вступ на нульовий курс: роз’яснення Міносвіти
Що таке «небюджетна» конкурсна пропозиція
Як вступити до українських вишів абітурієнтам, що перебувають за кордоном

Інформація

Усі завдання ЗНО з математики за темами
Усі тести ЗНО з математики онлайн
Завдання й відповіді ЗНО з математики минулих років
Усе про тест ЗНО з математики
Програма ЗНО з математики
Тести ЗНО онлайн з інших предметів
Дорожня карта учасника ЗНО
Дорожня карта вступника на бакалавра

Facebook

Twitter