НМТ онлайн 2025 року з математики – 2 сесія
ТЕМА: Алгебра і початки аналізу. Елементи комбінаторики, початки теорії ймовірностей та елементи математичної статистики.
Завдання скеровано на перевірку розуміння графічної форми подання статистичної інформації.
Якщо учні готувались до контрольної роботи не менш як
Кількість учнів:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Геометричні величини та вимірювання їх.
Завдання скеровано на перевірку знань властивостей паралельних прямих та паралелограмів, умінь розв’язувати планіметричні задачі.
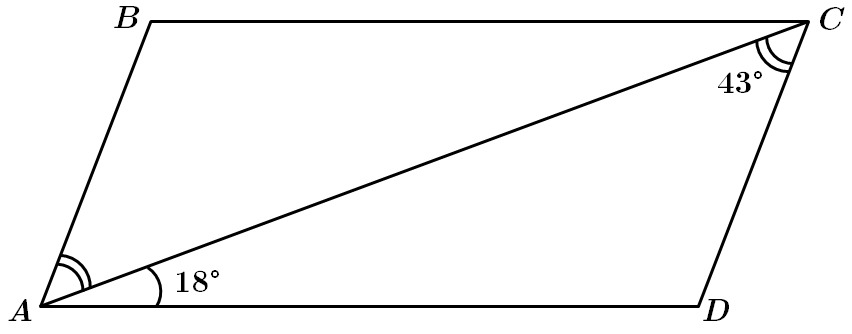
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.
Завдання скеровано на перевірку знання означення модуля числа та його властивостей.
З наведених чисел – це
Відповідь: В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними. Раціональні вирази.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів, зводити подібні доданки.
В даному виразі зведені подібні доданки.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Прямі та площини у просторі. Многогранники.
Завдання скеровано на перевірку знань ознаки паралельності прямої та площини, властивостей призми.
За ознакою паралельності прямої і площини, якщо пряма
Аналогічно,
Отже, таких площин лише дві.
Відповідь: В.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функціональна залежність.
Завдання скеровано на перевірку вміння використовувати перетворення графіків функцій.
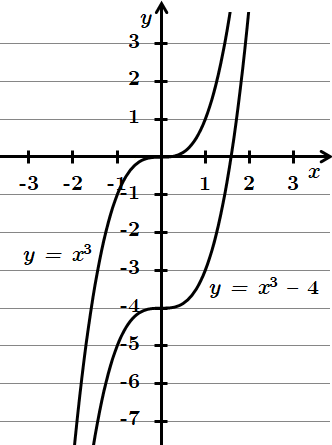
За властивістю паралельного перенесення графіка функції вздовж осі
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Текстові задачі.
Завдання скеровано на перевірку вміння розв’язувати основні задачі на відсотки.
Покупець придбав гаманець зі знижкою
Складімо пропорцію:
За властивістю пропорції:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Тіла обертання. Координати у просторі.
Завдання скеровано на перевірку знань формули відстані між точками у просторі, властивостей кулі.

Знаходимо відстань між точками
Якщо б кулі були однакового радіусу, то дорівнювали б
З наведених значень – це
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення раціональних виразів.
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія.
Завдання скеровано на перевірку знання властивостей трапеції та трикутника.
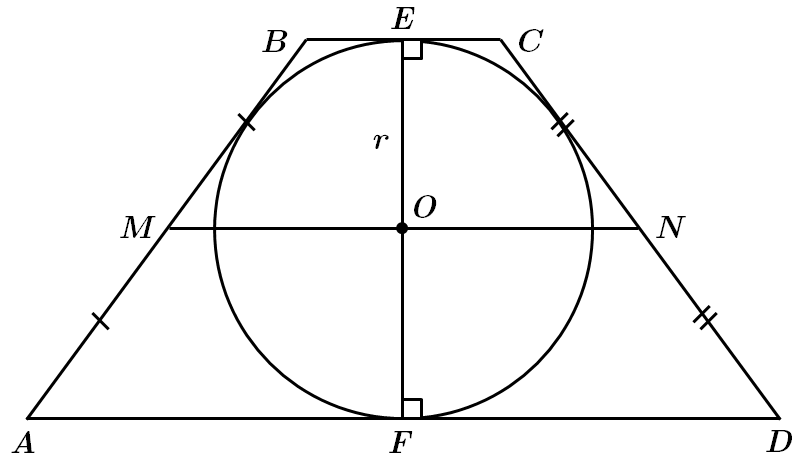
I. Якщо в трапецію можна вписати коло, то воно буде дотикатись до всіх її сторін, а отже, до основ.
II, III твердження не є правильними, бо точка перетину діагоналей не належить середній лінії, та центр описаного кола не обов'язково лежить на більшій основі.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Показникові рівняння.
Завдання скеровано на перевірку вміння розв’язувати показникові рівняння, виконувати тотожні перетворення степеневих виразів.
Зведемо до однакової основи ліву та праву частину показникового рівняння:
Відповідь: Д.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Похідна функції.
Завдання скеровано на перевірку вміння знаходити похідну суми, знаходити числове значення похідної функції в точці для заданого значення аргументу.
Похідна функції
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Дійсні числа.
Завдання скеровано на перевірку знання означення степеня з натуральним показником, його властивостей.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу Логарифмічні нерівності.
Завдання скеровано на перевірку вміння розв’язувати логарифмічні нерівності, знання властивостей логарифмічної функції.
Функція
Отже, розв'язком нерівності буде розв'язок системи:
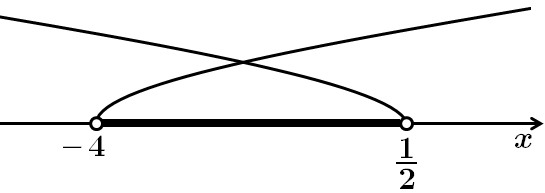
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники. Трикутники.
Завдання скеровано на перевірку вміння застосовувати властивості прямокутника та прямокутного трикутника.
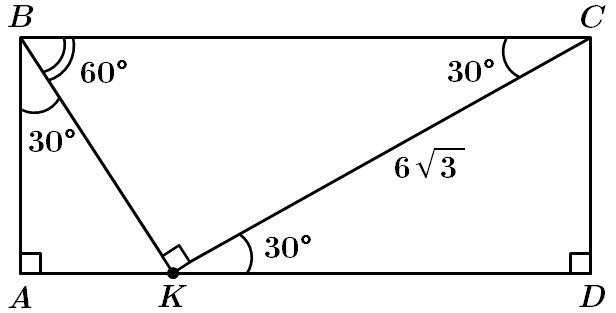
У
У прямокутнику
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функціональна залежність.
Завдання скеровано на перевірку вміння будувати графіки функцій, знання властивостей лінійної функцій.
1.
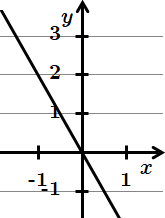
Отже, 1 – Г.
2.
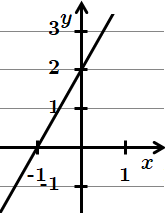
Отже, 2 – А.
3.
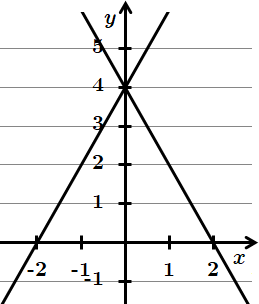
Отже, 3 – Б.
Відповідь: 1Г, 2А, 3Б.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Дійсні числа та дії з ними.
Завдання скеровано на перевірку вміння виконувати тотожні перетворення ірраціональних, логарифмічних та степеневих виразів.
1.
Отже, правильна відповідь – B.
2.
Отже, правильна відповідь – Г.
3.
Отже, правильна відповідь – Б.
При спрощенні виразу застосовували формули:
Відповідь: 1В, 2Г, 3Б.
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Планіметрія. Чотирикутники.
Завдання скеровано на перевірку вміння застосовувати властивості трапеції та квадрата, розв’язування трикутників.
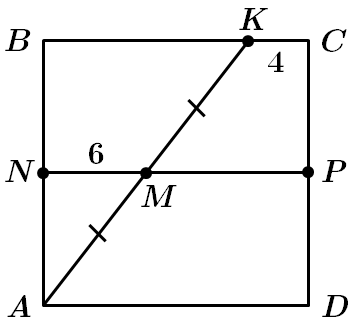
1 – В. Точка
У
2 – A.
У трапеції
За властивістю середньої лінії:
3 – Г.
За теоремою Піфагора:
Відповідь: 1В, 2А, 3Г.
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Функціональна залежність.
Завдання скеровано на перевірку вміння застосовувати властивості числових функцій.
Функція
Функція
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Ймовірність випадкової події.
Завдання скеровано на перевірку вміння обчислювати ймовірність випадкових подій, знання класичного означення ймовірної події.
У салоні
У перших трьох рядах розташовано
Імовірність того, що пасажиру дістанеться таке місце,
За умовою ця імовірність дорівнює
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Геометрія. Стереометрія. Многогранники, тіла обертання.
Завдання скеровано на перевірку знань властивостей піраміди та конуса, вміння розв’язувати задачі на обчислення площ поверхонь геометричних тіл.
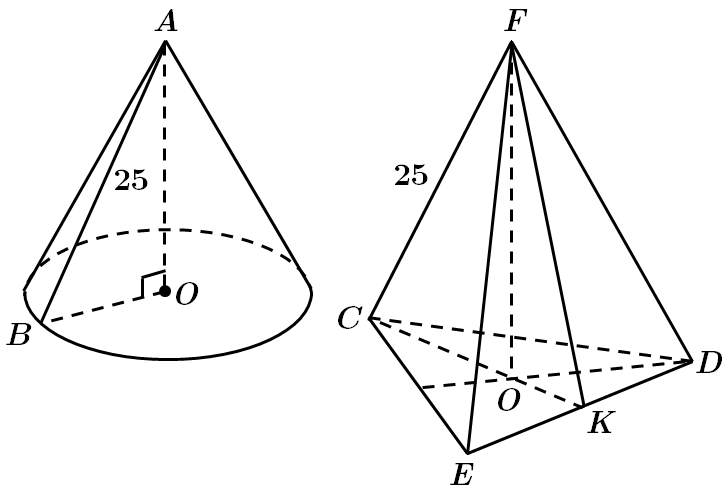
Твірна консуса
Площа бічної поверхні конуса
У піраміді
Площа бічної поверхні піраміди
Відповідь:
Знайшли помилку? Пишіть на
ТЕМА: Алгебра і початки аналізу. Розв’язування раціональних рівнянь.
Завдання скеровано на перевірку вміння розв’язувати раціональні рівняння, та їх системи з параметрами.
Розв'яжемо систему графічним способом.
Для того, щоб система мала єдиний розв'язок, треба, щоб графіки мали одну спільну точку.
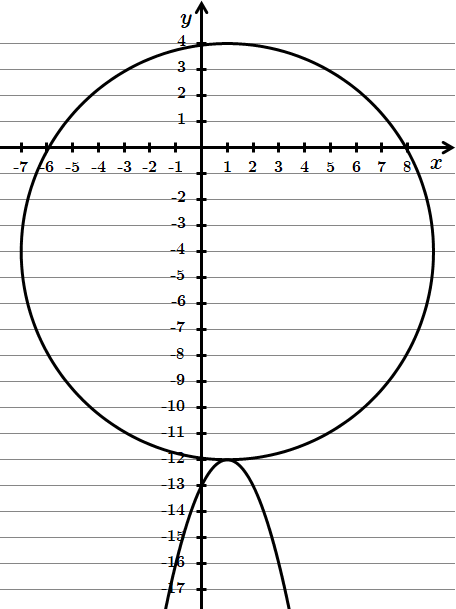
Отже,
Відповідь:
Знайшли помилку? Пишіть на




