ЗНО онлайн 2013 року з фізики – основна сесія

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на перевірку знання і розуміння фізичних величин, що характеризують рівномірний рух тіла по колу, і їхнього графічного зображення.

Рух по колу ‒ це криволінійний рух. Під час прямолінійного руху напрямок вектора швидкості \(\overrightarrow{v}\) збігається з напрямком переміщення \(\overrightarrow{s}.\) Розділивши траєкторію руху тіла на малі прямолінійні ділянки \(\Delta l,\) бачимо, що вектор швидкості все більше наближається до дотичної (рис. а, б). У кожній точці миттєва швидкість напрямлена вздовж дотичної до траєкторії руху тіла, тобто перпендикулярно до радіуса кола (рис. в).

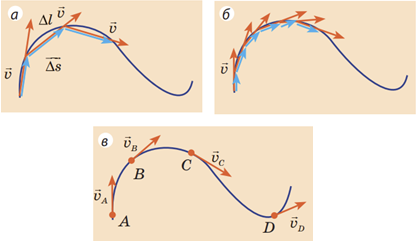
Вектор прискорення \(\overrightarrow{a}\) під час рівномірного руху тіла по колу напрямлений до центра кола (уздовж радіуса) ‒ саме тому прискорення рівномірного руху тіла по колу називають доцентровим прискоренням. Оскільки миттєва швидкість \(\overrightarrow{v}\) руху тіла напрямлена по дотичній, а дотична перпендикулярна до радіуса, то $$ \overrightarrow{a}\perp\overrightarrow{v}. $$

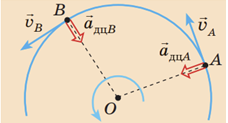
(Докладне доведення напрямку доцентрового прискорення наведено в підручнику: Фізика (рівень стандарту, за навчальною програмою авторського колективу під керівництвом Локтєва В. М.) : підруч. для 10 кл. закл. загал. серед. освіти / [В. Г. Бар’яхтар, С. О. Довгий, Ф. Я. Божинова, О. О. Кірюхіна] ; за ред. В. Г. Бар’яхтара, С. О. Довгого. ‒ Харків: Вид-во «Ранок», 2018. ‒ c. 49‒50.)

Отже, правильне розташування векторів миттєвої швидкості і прискорення для рівномірного руху по колу зображено на рисунку В.

На рисунку А напрямки швидкості і прискорення збігаються ‒ це випадок прямолінійного рівноприскореного руху (тіло розганяється). На рисунку Б напрямки швидкості і прискорення протилежні ‒ це випадок прямолінійного рівноприскореного руху (тіло гальмує). На рисунку Г зображено випадок, ідентичний випадку А, але тіло рухається не горизонтально праворуч (рисунок А), а в тому напрямку, що на рисунку Г.

Відповідь: B.

Тема: Механіка. Основи динаміки. Вага тіла.

Завдання скеровано на перевірку знання і розуміння ваги в різних випадках.

Перевантаження ‒ це збільшення ваги. А вага \(\overrightarrow{P}\) ‒ це сила, з якою всі тіла внаслідок гравітаційного притягання (\(\overrightarrow{F}_\text{тяж}\)) стискають або прогинають опору або розтягують підвіс.

Єдиний випадок, коли вага тіла за модулем дорівнює силі тяжіння, це якщо тіло перебуває в стані спокою або прямолінійного рівномірного руху: \begin{gather*} P=F_\text{тяж}=mg. \end{gather*}

В усіх інших випадках тіло відчуватиме або збільшення ваги (перевантаження): $$ P=m(g+a), $$ або зменшення ваги: $$ P=m(g-a), $$ де \(m\) ‒ маса тіла, \(g\) ‒ прискорення вільного падіння, \(a\) ‒ прискорення руху тіла.

Отже, автогонщик не зазнаватиме перевантаження, рухаючись зі сталою швидкістю прямою трасою (рух без прискорення \(a=0\)).

В усіх інших названих в умові випадках рух автогонщика буде прискореним, і він відчуватиме збільшення ваги (перевантаження).

Відповідь: Б.

ТЕМА: Механіка. Основи динаміки. Закон Гука.

Завдання скеровано на перевірку знання і розуміння закону Гука і його застосування до відповідної ситуації.

З’єднаймо послідовно дві однакові за довжиною \((x_1=x_2)\) частини розрізаної пружини. Якщо ми прикладемо силу \(\overrightarrow{F}\) (див. рисунок), то така сама сила діятиме окремо і на одну половинку, і на другу: $$ \overrightarrow{F}=\overrightarrow{F}_1=\overrightarrow{F}_2. $$

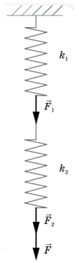
За третім законом Ньютона в пружині виникатиме сила пружності, рівна за модулем прикладеній силі і напрямлена протилежно:

За законом Гука модуль сили пружності прямо пропорційний видовженню тіла \(x\) (\(k\) ‒ жорсткість пружини): $$ F_\text{пруж}=k|x|. $$

Запишімо тепер рівність сил: $$ kx=k_1x_1=k_2x_2. $$

За умовою $$ x_1=x_2=\frac x2, $$ тож $$ kx=k_1\cdot \frac x2=k_2\cdot \frac x2. $$

Виходячи із цього запису, якщо ми зменшили довжину пружини у 2 рази, то жорсткість пружини повинна збільшитися вдвічі. Лише за цієї умови рівність буде правильною. Отже, $$ k_1=k_2=2k. $$

Відповідь: B.

Тема: Механіка. Закони збереження в механіці. Закон збереження імпульсу.

Завдання скеровано на перевірку знання, розуміння і вміння застосувати закон збереження імпульсу.

За законом збереження імпульсу в замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії: $$ M\overrightarrow{v}+m\overrightarrow{u}=M\overrightarrow{v'}+m\overrightarrow{u'}. $$

Оскільки за умовою тепловоз і вагон після взаємодії зчіплюються, то й швидкість їхнього спільного руху \(\overrightarrow{w}\) буде однакова: $$ \overrightarrow{w}=\overrightarrow{v'}=\overrightarrow{u'}. $$

До взаємодії і тепловоз, і вагон рухалися в одному напрямку. І після взаємодії вони продовжили рухатися в тому самому напрямку. Тож можна вектори швидкостей спроєктувати на горизонтальну вісь \(Ox\) і записати закон збереження імпульсів в проєкціях: $$ Mv+\mu=(M+m)w. $$

Виразимо із цієї рівності їхню спільну швидкість руху після зчеплення: $$ w=\frac{Mv+\mu}{M+m}. $$

Відповідь: Г.

Тема: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Стала Авогадро.

Завдання скеровано на перевірку знання і розуміння сталої Авогадро й кількості речовини.

У будь-якій речовині кількістю \(1\ \text{моль}\) міститься однакова кількість атомів або молекул, ‒ стільки, скільки атомів Карбону міститься у вуглеці масою \(12\ \text{г}.\) Це стала Авоґадро \(N_А,\) її одиниця – \(\text{моль}^{-1}.\)

Фізичну величину, яка дорівнює частці від ділення кількості структурних частинок речовини \(N\) на число Авогадро, називають кількістю речовини \(\mathbf{\nu}:\) $$ \mathbf{\nu}=\frac{N}{N_A}, $$ де \(N(X)\) ‒ кількість структурних частинок речовини \(X.\)

Отже, щоб визначити кількість молекул \(N\) газу \(X\) у балоні, треба помножити одну порцію молекул \((N_А)\) на кількість цих порцій \((\mathbf{\nu}):\)

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку знання і розуміння поняття роботи в термодинаміці та його геометричного змісту.

Робота газу чисельно дорівнює площі фігури під графіком залежності \(p(V).\)

Під час ізобарного процесу роботу газу можна визначити за формулою $$ A=p\Delta V. $$

Геометричний зміст роботи під час ізобарного процесу відображено на графіках:

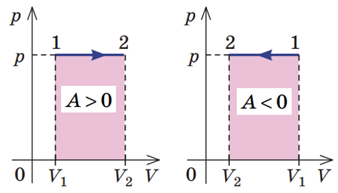
Геометричний зміст роботи під час довільного процесу: робота газу чисельно дорівнює площі криволінійної трапеції під графіком залежності \(p(V):\)

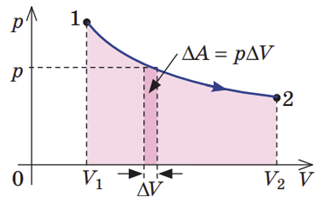
Проаналізувавши циклічні процеси, робимо висновок, що найбільшу роботу газ виконав під час циклу В.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря та вимірювання її.

Завдання скеровано на перевірку знання і розуміння відносної вологості повітря і розуміння будови приладу для її вимірювання ‒ психрометра.

Психрометр складається з двох термометрів ‒ сухого, який вимірює температуру довкілля, і вологого ‒ його колба обгорнута тканиною, кінчик якої опущений у посудину з водою (див. рисунок).

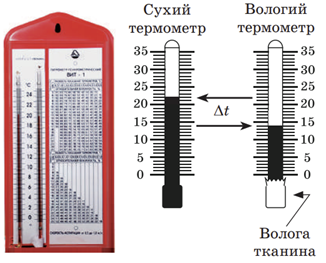
Вода з тканини випаровується, і вологий термометр показує нижчу температуру, ніж сухий. Що нижча відносна вологість повітря, то швидше випаровується рідина й то більша різниця показів сухого і вологого термометрів.

Якщо ж обидва термометри психрометра показують однакову температуру (як в умові), тобто різниця показів сухого і вологого термометрів дорівнюватиме нулю, це означає, що вміст вологи в повітрі наблизився до максимального значення, тобто відносна вологість повітря дорівнює \(100\ \text{%}.\)

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Змочування.

Завдання скеровано на перевірку знання і розуміння явищ змочування і незмочування.

Змочувальна рідина у капілярі піднімається по стінці, утворюється увігнута поверхня рідини – увігнутий меніск (рис. а). Незмочувальна рідина опускається в капілярі, утворюючи опуклий меніск (рис. б).

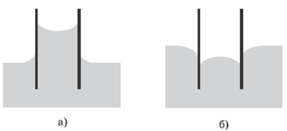
Відповідно до умови рідина в капілярі піднялася вище, ніж у посудині. Із цього робимо висновок, що ця рідина змочувальна. А отже, рідина на скляній поверхні не збереже свою сферичну форму, а прагнутиме розтектися по ній.

Форма вільної поверхні рідини залежить від сил взаємодії молекул рідини з молекулами твердого тіла. Якщо сили взаємодії між молекулами рідини менші від сил взаємодії між молекулами рідини і твердого тіла, рідина змочує поверхню твердого тіла. Найбільше рідина розтіклася на поверхні, зображеній на рисунку Г, ‒ це правильна відповідь.

Можна також скористатися важливою характеристикою змочування (незмочування). Це крайовий кут \(\mathbf{\theta}\) (див. рисунок).

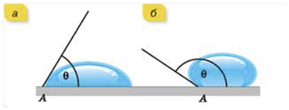
Цей кут відраховують між межею рідина ‒ газ і поверхнею твердого тіла (зверніть увагу, що крайовий кут усередині рідини).

Випадок $$ 0\le \mathbf{\theta} \lt 90^\circ $$ відповідає змочуванню, а випадок $$ 90^\circ\lt \mathbf{\theta} \le 180^\circ $$ ‒ незмочуванню.

Випадки відповідно повного змочування та повного незмочування (рисунок А):

Отже, інформація про крайовий кут підтверджує, що правильним за даної умови є рисунок Г.

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.

Завдання скеровано на перевірку знання видів електричних зарядів і розуміння, як може змінюватися заряд тіла.

За умовою крапля є електрично нейтральною, отже, кількість позитивно заряджених частинок дорівнює кількості негативно заряджених частинок. Носієм найменшого негативного заряду є електрон. Цей заряд зазвичай позначають символом e; його значення: $$ e=-1,6\cdot 10^{-19}\ \text{Кл}. $$

Носій найменшого позитивного заряду ‒ протон \(p.\) Заряд протона за модулем дорівнює заряду електрона: \begin{gather*} p=+1,6\cdot 10^{-19}\ \text{Кл}. \end{gather*}

Відповідно до умови спочатку з поверхні краплі вилетів електрон. Це означає, що негативно заряджених частинок стало на одну менше, тобто позитивно заряджених частинок залишилося на одну більше ‒ заряд краплі став позитивним і дорівнюватиме заряду одного протона: $$ Q=+1,6\cdot 10^{-19}\ \text{Кл}. $$

Потім крапля поглинула протон, тож заряд краплі збільшився на заряд ще одного протона:

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики. З’єднання конденсаторів.

Завдання скеровано на перевірку знання і розуміння, що таке конденсатор, і вміння визначати параметри з’єднань конденсаторів.

Якщо відповідно до умови замкнути вимикач, то конденсатори будуть з’єднані послідовно. А в разі послідовного з’єднання заряди обох конденсаторів будуть однаковими та дорівнюватимуть заряду батареї: $$ q=q_1=q_2. $$

Напруга на батареї послідовно з’єднаних конденсаторів дорівнює сумі напруг на окремих конденсаторах, що й зазначено в умові (варіант Г ‒ неправильний): $$ U=U_1+U_2. $$

Енергія зарядженого конденсатора \(W\) залежить від того, чи заряджений він, чи ні, і на скільки. До замикання вимикача енергія електричного поля залежала лише від фізичних характеристик першого конденсатора. Другий конденсатор був розряджений, тобто його енергія дорівнювала нулю. А після замикання вимикача енергія електричного поля батареї з двох конденсаторів визначатиметься не лише загальною напругою й однаковим зарядом, а й загальною електроємністю \(C,\) яка буде відмінною від електроємності кожного окремого конденсатора: $$ W=\frac{C_\text{заг}U^2}{2}. $$

Однакові конденсатори (за умовою) мають однакову електроємність:

Між пластинами конденсатора електричне поле однорідне. Для однорідного електричного поля між напруженістю \(E\) і напругою \(U\) є зв’язок: $$ E=\frac Ud, $$ де \(d\) ‒ відстань між пластинами; \(U\) ‒ напруга на конденсаторі.

Напруга на другому конденсаторі змінилася, отже, змінилася і напруженість.

Відповідь: Б.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля ‒ Ленца.

Завдання скеровано на перевірку знання і розуміння закону Джоуля ‒ Ленца, поняття потужності й співвідношення фізичних величин під час послідовного з’єднання провідників.

Визначити кількість теплоти, яка виділяється в провіднику зі струмом, можна за законом Джоуля ‒ Ленца: кількість теплоти \(Q\) прямо пропорційна квадрату сили струму \(I,\) опору \(R\) провідника та часу \(t\) проходження струму: $$ Q=I^2Rt. $$

Оскільки лампи з’єднані послідовно (за умовою), то сила струму в них буде однакова: $$ I_1=I_2=I. $$

Запишімо формули для визначення кількості теплоти в кожній лампі відповідно за однаковий проміжок часу:

Виразімо опір лампи через потужність \(P\) й напругу \(U,\) скориставшись законом Ома для ділянки кола:

Використавши за умовою однаковість напруг ламп \((U_1=U_2=U),\) запишімо формули для визначення опору ламп:

Підставімо вирази для опорів у формули для кількості теплоти і визначимо відношення кількостей теплоти:

Відповідь: Б.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у газах. Несамостійний і самостійний розряди.

Завдання скеровано на перевірку знання і розуміння видів самостійних газових розрядів.

Залежно від тиску й температури газу, конфігурації електродів і напруги між ними розрізняють чотири види самостійних газових розрядів: іскровий, тліючий (жеврійний), дуговий, коронний.

У завданні на фотографії зображено коронний газовий розряд. Візуально коронний розряд проявляється у вигляді світіння (корони) навколо гострих кутів електрода. Він виникає за тиску порядку атмосферного в сильному (напруженість поля \(E\gt 500\ \text{кВ/м}),\) різко неоднорідному електричному полі. Такі поля формуються поблизу електродів із великою кривизною поверхні (вістря, тонкий дріт тощо). Коронний розряд являє собою слабке фіолетове світіння у вигляді корони (пучків, пензликів). Його використовують для очищення газів (електрофільтри), у лічильниках елементарних частинок (лічильники Гейгера ‒ Мюллера); на виникненні цього розряду ґрунтується дія блискавковідводу. У природі зазвичай спостерігають перед грозою або під час грози на гострих кінцях високих предметів (веж, щогл, вершин скал тощо). Коронний розряд має ще одну назву ‒ вогні святого Ельма.

Відповідь: Б.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Досліди Фарадея. Явище електромагнітної індукції.

Завдання скеровано на перевірку знання і розуміння дослідів Фарадея, причин виникнення індукційного струму й уміння застосувати ці знання до конкретної практичної ситуації.

Судячи з рисунка, струм пропускають по котушці, що міститься ліворуч на феромагнітному осерді. На кінцях котушки є клеми, за допомогою яких котушку можна приєднати до джерела струму, реостата, вимикача тощо. Котушка зі струмом є штучним електромагнітом, навколо якого існує магнітне поле.

Котушка праворуч, яка замкнена на амперметр, є нерухомим провідним контуром, розташованим у магнітному полі електромагніту (котушки ліворуч).

За означенням явища електромагнітної індукції індукційний (наведений) електричний струм буде виникати в котушці праворуч у разі зміни сили струму в котушці ліворуч. Змінити силу струму в котушці можна, наприклад, замикаючи і розмикаючи електричне коло котушки ліворуч, або, наприклад, рухаючи повзунок реостата, якщо приєднати його послідовно з котушкою (відповідно до осучаснених дослідів Фарадея). Що швидше змінюватиметься значення сили струму, то сильніше мінятиметься магнітне поле котушки ліворуч.

Але в цьому разі сили, що діють з боку змінного магнітного поля, не можуть зробити хаотичний рух заряджених частинок всередині котушки праворуч напрямленим. Чому ж у цій котушці виникає індукційний струм? Річ у тім, що змінне магнітне поле завжди супроводжує поява в навколишньому просторі вихрового електричного поля (силові лінії такого поля є замкненими). Саме електричне поле, а не магнітне, діє на вільні заряджені частинки в котушці праворуч та надає їм напрямленого руху, створюючи в такий спосіб індукційний струм.

Тепер проаналізуймо графік з умови. Є ділянки графіка, де струм має стале значення. Це інтервали часу від \(1\) до \(2\) секунди, і від \(4\) до \(5\) секунди. У цих випадках магнітне поле, що існує навколо котушки ліворуч не є змінним, а отже, не виникатиме вихрове електричне поле й індукційний струм в котушці праворуч. Тож амперметр нічого не покаже.

За проміжок часу від \(0\) до \(1\) секунди сила струму змінилася в котушці ліворуч на три позиції, а за проміжок часу від \(2\) до \(4\) секунд ‒ на одну позицію. Це означає, що зміна магнітного поля в першому випадку більша, ніж у другому. А значить, і індукційний струм від \(0\) до \(1\) секунди, який зафіксує амперметр, буде більшим за індукційний струм від \(2\) до \(4\) секунди.

Відповідь: A.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку знання і розуміння сили Лоренца, уміння застосувати правило визначення напрямку її дії в конкретній ситуації.

Електронний пучок ‒ це потік електронів, що рухаються за близькими траєкторіями в одному напрямку, має розміри, значно більші в напрямку руху, ніж у поперечній площині.

Коли над центром екрана осцилографа розмістили магніт, то на електрони подіяло магнітне поле. А магнітне поле діє на рухомі заряджені частинки із силою Лоренца, напрямок дії якої визначається за правилом лівої руки: лінії магнітної індукції \(\overrightarrow{B}\) «ловимо» в долоню, чотири витягнуті пальці спрямовуємо за напрямком руху \(\overrightarrow{v}\) позитивно зарядженої частинки (або протилежно до руху негативно зарядженої), і тоді відігнутий на \(90^\circ\) великий палець укаже напрямок сили Лоренца \(\overrightarrow{F}_\text{Л}\) (див. рисунок для негативно зарядженої частинки ‒ електрона).

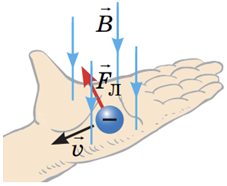
Якщо ми дивимося на екран осцилографа, то пучок електронів напрямлений до нас, тобто чотири витягнуті пальці направляємо протилежно до напрямку руху електронів ‒ перпендикулярно до екрану від нас).

За умовою завдання магніт піднесли зверху екрана північним полюсом донизу, отже, лінії магнітної індукції магнітного поля будуть напрямлені вертикально вниз, входити в долоню.

Тоді відігнутий на \(90^\circ\) великий палець буде напрямлений ліворуч ‒ укаже напрямок сили Лоренца \(\overrightarrow{F}_\text{Л}.\)

Відповідь: A.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Перетворення енергії під час гармонічних коливаннях.

Завдання скеровано на перевірку знання і розуміння суті повного коливання нитяного маятника й перетворень його енергії під час коливань.

Нитяний маятник є фізичною моделлю маятника настінного годинника.

Виберімо положення рівноваги маятника за нульовий рівень, де потенціальна енергія дорівнюватиме нулю. Здійснюючи коливання, маятник відхиляється на певний кут, піднімаючись на певну максимальну висоту.

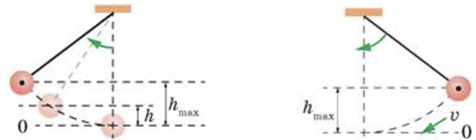
За одне повне коливання (маятник повинен повернутися в початкове положення), маятник два рази піднімається на максимальну висоту. Отже, за одне коливання потенціальна енергія маятника двічі набуває максимального значення.

Тепер обчислімо, скільки ж повних коливань здійснив маятник за хвилину, коливаючись із частотою \(2\ \text{Гц}.\)

Визначімо час одного коливання ‒ період. Частота \(\mathbf{\nu}\) і період \(T\) коливань пов’язані так: \begin{gather*} T=\frac{1}{\mathbf{\nu}}\\[6pt] T=\frac{1}{2\ \text{Гц}}=0,5\ \text{с}. \end{gather*}

За час \(t\) (хвилину) маятник виконає кількість \(N\) повних коливань:

І, зваживши на те (як ми вже раніше довели), що за кожне коливання потенціальна енергія маятника двічі набуватиме максимального значення, то за хвилину потенціальна енергія буде максимальною \(240\) разів.

Відповідь: Г.

ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.

Завдання скеровано на перевірку знання і розуміння законів поширення променя в збиральній лінзі, уміння схематично зобразити його хід.

Спочатку добудуймо фокальну площину, яка проходить через фокус лінзи точку \(F,\) перпендикулярно до головної оптичної осі, що перпендикулярна до лінзи.

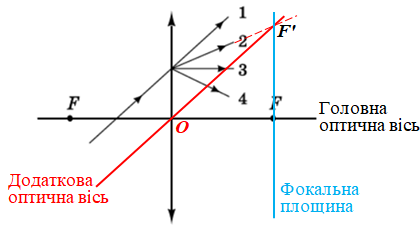
Далі побудуймо додаткову оптичну вісь, що проходить так само, як і головна, крізь оптичний центр лінзи точку \(O,\) але паралельно променю, що падає на лінзу. Пам’ятаймо, що промінь, який проходить крізь оптичний центр лінзи, не заломлюється.

Отримуємо точку перетину додаткової оптичної осі і фокальної площини (див. схематичний рисунок). Це є додатковий фокус \(F'.\)

Будь-який пучок паралельних променів (у цій умові це промінь, що падає на лінзу і промінь, що поширюється вздовж додаткової оптичної осі), навіть якщо ці промені не паралельні головній оптичній осі, після заломлення в збиральній лінзі завжди перетинаються в одній точці ‒ у головному фокусі \(F\) або додатковому \(F'\) (лежить на фокальній площині).

Тож після проходження крізь збиральну лінзу промінь поширюватиметься вздовж напрямку \(2,\) тому що саме продовження променя \(2\) пройде через додатковий фокус \(F'\) (див. рисунок).

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Інтерференція світла та її практичне застосування.

Завдання скеровано на перевірку знання і розуміння явища інтерференції світла за умови інтерференції світла на тонких плівках.

Світлова хвиля частково відбивається від зовнішньої поверхні плівки (хвиля 1), частково проходить через плівку і, відбившись від її внутрішньої поверхні, повертається в повітря (хвиля 2). Оскільки хвиля 2 проходить більшу відстань, ніж хвиля 1, між ними існує різниця ходу. Обидві хвилі когерентні, адже створені одним джерелом, тому внаслідок накладання їх спостерігають стійку інтерференційну картину. Якщо хвиля 2 відстає від хвилі 1 на парне число півхвиль, то спостерігають посилення світла (інтерференційний максимум), якщо на непарне ‒ послаблення світла (інтерференційний мінімум). Саме інтерференцією світла зумовлений колір, наприклад, багатьох комах (див. рисунок).

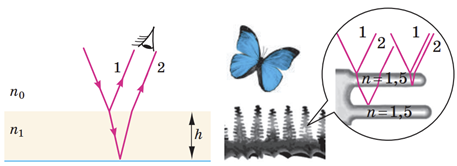
Біле світло поліхроматичне (складається з хвиль різної довжини), тому для посилення світлового випромінювання різного кольору потрібна різна товщина плівки: якщо плівка різної товщини освітлюється білим світлом, то вона має райдужне забарвлення (райдужні мильні бульбашки, райдужна оліїста плівка нафтопродуктів на поверхні води). Крім того, різниця ходу хвиль залежить від кута падіння світла на плівку (зі збільшенням кута падіння різниця ходу збільшується), тому тонкі плівки грають веселкою ‒ змінюють колір, коли змінюється кут, під яким ми дивимося на плівку. Зверніть увагу: якщо товщина плівки в кілька разів більша за довжину світлової хвилі, то інтерференційні смуги розташовані надто близько й око не здатне їх розділити ‒ смуги збігаються, і ми бачимо біле світло.

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Рівняння Ейнштейна для фотоефекту.

Завдання скеровано на перевірку знання і розуміння законів фотоефекту й рівняння Ейнштейна для зовнішнього фотоефекту.

Запишімо рівняння Ейнштейна для зовнішнього фотоефекту: $$ E_\text{ф}=A_\text{вих}+E_\text{k max} - $$ унаслідок поглинання фотона металом катода фотоелемента енергія фотона \((E_\text{ф}=h\mathbf{\nu})\) може бути повністю передана електрону й витратитися на здійснення роботи виходу \((A_\text{вих}=h\mathbf{\nu}_\text{min})\) і надання електрону кінетичної енергії \((E_\text{k max}=\frac{mv_\text{max}^2}{2}=eU_\text{з}).\)

За одним із законів фотоефекту для кожної речовини існує максимальна довжина світлової хвилі \(\mathbf{\lambda}_\text{max}=\mathbf{\lambda}_\text{черв}\) (червона межа фотоефекту), за якої починається фотоефект. Опромінення речовини світловими хвилями, які мають більшу довжину, фотоефекту не викликає. Максимальна довжина світлової хвилі (мінімальна частота) відповідає мінімальній енергії фотона:
якщо $$ h\mathbf{\nu}\lt A_\text{вих}, $$ то електрони не вилітатимуть із речовини. Умова $$ h\mathbf{\nu}_\text{min}=\frac{hc}{\mathbf{\lambda}_\text{max}}=A_\text{вих} $$ визначає червону межу фотоефекту.

Запишімо рівняння для фотоефекту, ураховуючи вирази для величин: $$ h\mathbf{\nu}=h\mathbf{\nu}_\text{min}+eU_\text{з} - $$ з досягненням певної затримувальної (запірної) напруги \(U_\text{з}\) навіть найшвидші електрони не дістануться анода, а отже, фотострум припиниться: $$ \frac{hc}{\mathbf{\lambda}}=\frac{hc}{\mathbf{\lambda}_\text{черв}}+eU_\text{з}. $$

Виразімо із цього рівняння шукану величину ‒ запірну напругу: $$ U_\text{з}=\frac{hc}{e}\left(\frac{1}{\mathbf{\lambda}}-\frac{1}{\mathbf{\lambda}_\text{черв}}\right). $$

Відповідь: A.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Кванти світла (фотони).

Завдання скеровано на перевірку знання і розуміння гіпотези Планка й формули для визначення енергії фотона.

За гіпотезою Планка випромінювання електромагнітних хвиль атомами й молекулами речовини відбувається не безперервно, а дискретно, тобто окремими порціями, енергія \(E\) кожної з яких прямо пропорційна частоті \(\mathbf{\nu}\) випромінювання: $$ E=h\mathbf{\nu}=\frac{hc}{\mathbf{\lambda}}, $$ де \(h\) ‒ стала Планка, \(\mathbf{\lambda}\) ‒ довжина хвилі фотона, \(c\) ‒ швидкість руху фотона, що дорівнює швидкості поширення світла у вакуумі. Згодом порції енергії стали називати квантами енергії, а потім фотонами.

Визначімо співвідношення енергій \(E_1\) і \(E_2\) фотонів з різними довжинами хвиль

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи. Рух по колу.

Завдання скеровано на перевірку вміння визначати напрямок швидкості руху тіла й напрямок прискорення тіл під час різних видів руху.

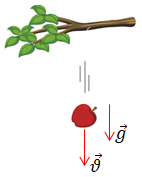
1. Яблуко в безвітряну погоду падатиме вертикально, тож і напрямок швидкості \(\overrightarrow{v}\) його руху теж буде напрямлений вертикально вниз (див. рисунок).

Падіння тіл у безповітряному просторі, тобто падіння лише під дією сили тяжіння, називають вільним падінням. У разі вільного падіння всі тіла падають на Землю з однаковим прискоренням ‒ прискоренням вільного падіння \(\overrightarrow{g}.\) Вектор прискорення вільного падіння завжди напрямлений вертикально вниз.

Отже, кут між напрямком швидкості руху яблука й напрямком прискорення становитиме нуль, тобто прискорення напрямлене в напрямку швидкості руху ‒ варіант відповіді В.

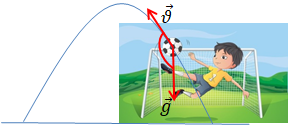
2. Коли футбольний м’яч піднімається, спрямований під кутом до горизонту (див. рисунок), то швидкість \(\overrightarrow{v}\) руху м’яча буде напрямлена по дотичній до траєкторії руху вгору ‒ до параболи. А прискорення \(\overrightarrow{g}\) вільного падіння під час руху м’яча по параболі буде напрямлене завжди вертикально вниз.

Отже, кут між векторами \(\overrightarrow{v}\) і \(\overrightarrow{g}\) буде тупий ‒ варіант відповіді Б.

3. Коли автомобіль гальмує, рухаючись прямолінійно, то напрямок прискорення \(\overrightarrow{a}\) буде протилежним до напрямку руху, тобто до напрямку швидкості \(\overrightarrow{v}\) руху автомобіля (див. рисунок) ‒ варіант відповіді А.

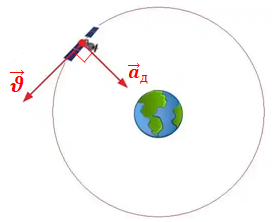
4. Штучний супутник рухається навколо Землі по коловій орбіті. Швидкість \(\overrightarrow{v}\) його руху в кожній точці кола напрямлена по дотичній до кола. А доцентрове прискорення \(\overrightarrow{a}_\text{д}\) спрямоване до центра кола (див. рисунок).

Отже, у цьому разі доцентрове прискорення буде напрямлене під прямим кутом до напрямку швидкості руху ‒ варіант відповіді Д.

Відповідь: 1В, 2Б, 3А, 4Д.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси.

Завдання скеровано на перевірку розуміння ізопроцесів і їхньої графічної інтерпретації.

1. Розгляньмо, які з графіків відповідають ізотермічному процесу ‒ \(T=\mathrm{const}.\) Це графіки на рисунках А і Б ‒ тиск змінюється, температура залишається сталою. Процес розширення означає, що об’єм \(V\) збільшується, а тиск \(p\) падає (див. рисунок). Відповідно до рівняння Клапейрона для ізотермічного процесу: $$ pV=\mathrm{const}\Rightarrow p\downarrow V\uparrow=\mathrm{const} $$ (стрілочка, напрямлена вгору, означає зростання значення величини; стрілочка, напрямлена вниз, означає зменшення значення величини).

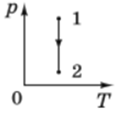
Отже, процесу ізотермічного розширення відповідає графік на рисунку А.

2. Відповідно розглянемо одразу ізотермічне стискання ‒ графік на рисунку Б.

Процес стискання означає, що об’єм \(V\) зменшується, а тиск \(p\) зростає (див. рисунок). Відповідно до рівняння Клапейрона для ізотермічного процесу: $$ pV=\mathrm{const}\Rightarrow p\uparrow V\downarrow=\mathrm{const}. $$

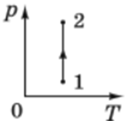
Отже, процесу ізотермічного стискання відповідає графік на рисунку Б.

3. Розгляньмо ізобарний процес ‒ \(p=\mathrm{const}.\) Можна було б припустити, що правильним буде графік, який відповідає сталому тиску, зображений на рисунку Д.

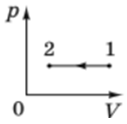
Під час цього об’єм \(V\) зменшується (див. рисунок). Але ж тоді, відповідно до рівняння Клапейрона для ізобарного процесу температура \(T\) теж буде зменшуватися: $$ \frac VT=\mathrm{const}\Rightarrow \frac{V\downarrow}{T\downarrow}=\mathrm{const}. $$

Тобто на рисунку Д зображений графік ізобарного охолодження.

На рисунку Г тиск змінюється, це не відповідає ізобарному процесу. Тоді розгляньмо рисунок В, на якому зображено графік залежності об’єму від абсолютної температури:

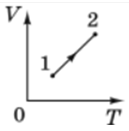
Якщо зафіксувати тиск і нагрівати газ, то об’єм повинен збільшуватися. Отже, відповідно до рівняння Клапейрона для ізобарного процесу якщо температура \(T\) підвищуватиметься, то й об’єм \(V\) теж збільшуватиметься: $$ \frac VT=\mathrm{const}\Rightarrow \frac{V\uparrow}{T\uparrow}=\mathrm{const}. $$

Отже, на рисунку В зображено графік ізобарного нагрівання.

4. І нарешті розгляньмо рисунок Г, що залишився. Як бачимо, графік на ньому відповідає сталому об’єму ‒ ізохорний процес \(V=\mathrm{const}.\)

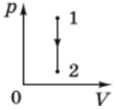
З’ясуймо, чи буде це процес охолодження. З графіка видно, що тиск \(p\) зменшується (див. рисунок). Отже, відповідно до рівняння Клапейрона для ізохорного процесу температура \(T\) теж знижуватиметься: $$ \frac pT=\mathrm{const}\Rightarrow \frac{p\downarrow}{T\downarrow}=\mathrm{const}. $$

Отже, графік на рисунку Г відповідає ізохорному охолодженню.

Відповідь: 1А, 2В, 3Г, 4Б.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Властивості електромагнітного випромінювання різних діапазонів.

Завдання скеровано на перевірку знання і розуміння властивостей електромагнітного випромінювання різних діапазонів.

1. Інфрачервоне (теплове) випромінювання (довжина хвилі від \(760\ \text{нм}\) до \(1–2\) мм) ‒ застосовують у приладах нічного бачення (Б).

Інфрачервоні промені випромінюють будь-які тіла, що мають температуру, вищу за абсолютний нуль. Саме на цьому ґрунтується їхнє застосування в тепловізорах ‒ приладах нічного бачення. Людське око не здатне бачити інфрачервоне випромінювання, адже енергії квантів недостатньо, щоб збудити нервові клітинки в оці. Але багато представників фауни мають пристосування ‒ своєрідні прилади нічного бачення, які здатні сприймати ці промені. Інфрачервоне випромінювання зазвичай є корисним для людини, але у великих дозах може спричинити запаморочення, знепритомніння ‒ тепловий і сонячний удари.

2. Ультрафіолетове випромінювання (довжина хвилі від \(10\) до \(400\) нм) ‒ спричиняє засмагу (А).

Ультрафіолет випромінюють Сонце й інші зорі, електричні дуги, спеціальні кварцові лампи. Людське око не реагує на ультрафіолетове випромінювання. Найімовірніше, це пов’язано з еволюцією, адже ці промені добре поглинає вода в рогівці ока. Ультрафіолет має високу хімічну активність, тому у великих дозах негативно впливає на людину. Саме тому не варто перебувати на сонці, коли сонячне випромінювання найінтенсивніше. Проте в невеликих дозах ультрафіолет є корисним: він сприяє виробленню вітаміну D, зміцнює імунну систему, стимулює низку важливих життєвих функцій в організмі.

3. Рентгенівське випромінювання (\(X\)-випромінювання) ‒ електромагнітні хвилі довжиною від \(0,001\ \text{нм}\) до \(100\ \text{нм}\) ‒ виникає в результаті гальмування швидких електронів на аноді (Г).

Рентгенівське випромінювання виникає внаслідок взаємодії швидких електронів з атомами катода в рентгенівській трубці – вакуумній скляній колбі з двома електродами. Між електродами створюється висока напруга \((10–500\ \text{кВ}),\) а катодом пропускають електричний струм; коли катод нагрівається, то з його поверхні починають вилітати (емітувати) електрони. Електрони, які випромінює катод, розганяє до величезних швидкостей електричне поле. Рентгенівське випромінювання найширше застосовують у медицині, адже воно має властивість проходити крізь непрозорі предмети (наприклад, тіло людини). Кісткові тканини менш прозорі для рентгенівського випромінювання, ніж інші тканини організму людини, тому кістки чітко видно на рентгенограмі. Рентгенівське випромінювання чинить руйнівну дію на клітини організму, тому застосовувати його потрібно надзвичайно обережно. Рентгенівську зйомку використовують також у промисловості (для виявлення дефектів), хімії (для аналізу сполук), фізиці (для дослідження структури кристалів).

4. Гамма \((\mathbf{\gamma})\)-випромінювання ‒ електромагнітні хвилі довжиною менш ніж \(0,05\ \text{нм}\) ‒ виникає в результаті самочинного розпаду атомних ядер (Д).

Гамма-випромінювання випускають збуджені атомні ядра під час ядерних реакцій, радіоактивних перетворень атомних ядер і перетворень елементарних частинок. Гамма-випромінювання використовують у дефектоскопії (виявлення дефектів усередині деталей); радіаційній хімії (наприклад, у процесі полімеризації); сільському господарстві й харчовій промисловості (стерилізація харчів); медицині (стерилізація приміщень, променева терапія). На організми гамма-випромінювання чинить мутагенний (стійкі спадкові зміни) і канцерогенний (здатність викликати злоякісні пухлини) вплив. Разом із тим чітко спрямоване й дозоване гамма-випромінювання застосовують для знищення ракових клітин (променева терапія).

Відповідь: 1Б, 2А, 3Г, 4Д.

ТЕМА: Квантова фізика. Елементи теорії відносності.

Завдання скеровано на перевірку знання досягнень фізичної науки й авторів цих відкриттів.

1. Вимірювання тиску світла ‒ Лебедєв П. (А).

Тиском світла називається тиск, який чинять електромагнітні світлові хвилі, які падають на поверхню будь-якого тіла. Гіпотезу про існування тиску висунув Дж. Максвел у своїй електромагнітній теорії світла.

Експериментально існування світлового тиску вперше встановив 1900 р. фізик П.М. Лебедєв. Для вимірювання світлового тиску він спрямував інтенсивний світловий потік на легкі металеві пластинки, підвішені на тонкій нитці в балоні, з якого було викачано повітря. Пластинки лівого ряду підвісу були чорними, а пластинки правого ‒ блискучими. Тому тиск світла на пластинки лівого ряду був меншим, ніж на пластинки правого ряду. Унаслідок цього під впливом світла підвіс повертався на певний кут, за значенням якого можна було визначити силу закручування і, отже, світловий тиск.

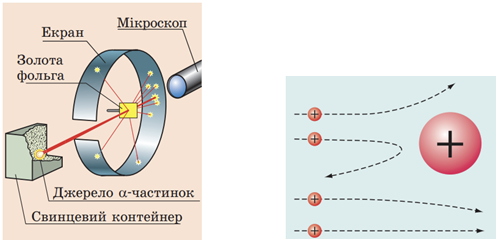
2. Створення планетарної моделі атома ‒ Резерфорд Е. (Б).

У 1908–1911 рр. під керівництвом Ернеста Резерфорда науковці досліджували будову атома. Вони спрямовували на тонку золоту фольгу вузький пучок \(\mathbf{\alpha}\text{-частинок}\) зі свинцевого контейнера. Виявили, що переважна більшість \(\mathbf{\alpha}\text{-частинок}\) проходить крізь фольгу, не змінюючи напрямку руху, лише деякі відхиляються від початкової траєкторії. Приблизно одна з \(20 000\) частинок відскакувала від фольги, начебто натикаючись на якусь перешкоду. І Резерфорд висунув гіпотезу про існування ядра в атомі. За результатами дослідів Резерфорд запропонував ядерну (планетарну) модель будови атома:

• в атомі позитивно заряджене ядро оточене негативно зарядженими частинками ‒ електронами, які обертаються навколо ядра, як планети навколо Сонця;
• саме в ядрі зосереджена мало не вся маса атома.

3. Створення теорії фотоефекту ‒ Ейнштейн А. (В).

Зовнішній фотоефект відкрив 1887 року німецький фізик Генріх Герц. Детальніше це явище дослідив Олександр Столєтов. У досліді він використав вакуумну камеру з двома електродами (катод і анод) усередині, на які подається напруга від джерела постійного струму. Під дією світла, яке потрапляє в камеру через спеціальне віконце, катод випромінює електрони. Рухаючись від катода до анода в електричному полі, електрони створюють фотострум. Якщо збільшувати напругу на електродах, сила фотоструму теж зросте. Змінюючи почергово інтенсивність і частоту світла, що падає на катод, а також матеріал катода, О. Столєтов сформулював три закони зовнішнього фотоефекту. Але лише більш як через \(20\) років завдяки своєму рівнянню для зовнішнього фотоефекту А. Ейнштейн зміг пояснити всі закони фотоефекту. Саме ідею М. Планка про кванти використав Ейнштейн для пояснення законів фотоефекту. За пояснення явища фотоефекту А. Ейнштейн одержав найвищу наукову нагороду ‒ Нобелівську премію (1921 р.).

4. Створення першого ядерного реактора ‒ Фермі Е. (Г).

Фермі 1938 року одержав Нобелівську премію за «демонстрацію існування нових радіоактивних елементів, утворених під час опромінення нейтронами, і за пов’язані відкриття ядерних реакцій, викликані повільними нейтронами». До весни 1941 року розробляв теорію ланцюгової реакції в урано-графітовій системі, а вже влітку розпочав серію експериментів, головним завданням яких було вимірювання нейтронного потоку. Разом з Г. Андерсоном провів близько тридцяти дослідів. У червні 1942 року було досягнуто значення коефіцієнта розмноження нейтронів, більшого за одиницю. Це означало можливість отримання ланцюгової реакції у достатньо великій ґратці з урану й графіту й послужило початком розроблення конструкції водно-графітового реактора. Фермі також спроєктував гігантський намет із тканини для оболонок аеростатів навколо конструкції реактора. Так з’явилася можливість підтримувати відповідний склад середовища, що оточувало реактор. Будівництво реактора розпочалося в Металургійній лабораторії Чиказького університету в жовтні, а завершилося 2 грудня 1942 року. У лабораторії під стадіоном англ. Stagg Field Stadium на цьому реакторі під назвою англ. Chicago Pile-1 (CP-1) було проведено експеримент, що продемонстрував першу самопідтримну ланцюгову ядерну реакцію.

Відповідь: 1А, 2Б, 3В, 4Г.

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.

Завдання скеровано на перевірку знання і розуміння додавання швидкостей і вміння застосовувати цей закон до будь-яких ситуацій.

Скористаймося законом додавання швидкостей:
швидкість \(\overrightarrow{v}_{12}\) руху першого човна в нерухомій системі відліку (відносно другого човна) дорівнює геометричній сумі швидкості \(\overrightarrow{v}_{1 \text{бер}}\) руху першого човна в рухомій системі відліку (відносно берега) й швидкості \(\overrightarrow{v}_{\text{бер} 2}\) руху рухомої системи відліку відносно нерухомої (ніби берега відносно другого човна): $$ \overrightarrow{v}_{12}=\overrightarrow{v}_{1 \text{бер}}+\overrightarrow{v}_{\text{бер} 2} $$ (рух і спокій є відносними, тож в наведеному в умові прикладі як нерухому систему відліку ми обрали систему відліку, пов’язану з другим човном. У такому разі система відліку, пов’язана з берегом, буде рухомою, а напрямок її руху буде протилежним напрямку руху першого човна).

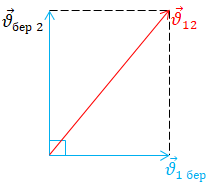
Модуль швидкості \(\overrightarrow{v}_{12}\) руху першого човна відносно другого човна знайдемо за теоремою Піфагора:

Відповідь: 5.

ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умова плавання тіл.

Завдання скеровано на перевірку знання і розуміння повітроплавання тіл, уміння описувати його за допомогою формул.

Позначмо всі сили, що діють на систему тіл у повітрі: повітряна куля з газом ‒ вантаж. Це сила тяжіння \(m_\text{в1}\overrightarrow{g},\) що діє на вантаж, сила тяжіння \(m_\text{r1}\overrightarrow{g},\) що діє на повітряну кулю (лише на газ, за умовою вагою оболонки можна знехтувати), виштовхувальна сила (сила Архімеда) \(\overrightarrow{F}_\text{A},\) що діє з боку повітря на цю систему тіл (див. рисунок).

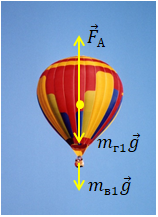
За другим законом Ньютона векторна сума всіх сил дорівнюватиме нулю, оскільки в умові не зазначено, що повітряна куля разом з вантажем піднімається вгору, отже, зупинимося на крайньому випадку, коли система не рухається ‒ куля просто утримує вантаж на певній висоті: $$ m_\text{в1}\overrightarrow{g}+m_\text{r1}\overrightarrow{g}+\overrightarrow{F}_\text{A}=0. $$

Запишімо це рівняння в проєкціях: $$ (m_\text{в1}+m_\text{r1})g=F_\text{A}. $$

Розпишімо силу Архімеда: $$ F_\text{A}=\mathbf{\rho}_\text{пов}gV, $$ де \(\mathbf{\rho}_\text{пов}\) ‒ густина повітря, \(g\) ‒ прискорення вільного падіння, \(V\) ‒ вважатимемо, що це об’єм повітря в кулі (за умовою вагою оболонки кулі можна знехтувати). Об’єм вантажу об’єктивно малий у порівнянні з розмірами повітряної кулі, тож ним можна знехтувати.

Підставімо вираз для виштовхувальної сили в рівняння другого закону Ньютона:
‒ до нагрівання газу в кулі: $$ (m_\text{в1}+m_\text{r1})g=\mathbf{\rho}_\text{пов}gV, $$ ‒ після нагрівання газу в кулі: $$ (m_\text{в2}+m_\text{r2})g=\mathbf{\rho}_\text{пов}gV, $$

Урахуємо співвідношення густин повітря і газу:
‒ до нагрівання: $$ \mathbf{\rho}_\text{r1}=\frac 16\mathbf{\rho}_\text{пов}, $$ відповідно $$ m_\text{r1}=\mathbf{\rho}_\text{r1}\cdot V=\frac 16\mathbf{\rho}_\text{пов}\cdot V, $$ ‒ після нагрівання: $$ \mathbf{\rho}_\text{r2}=\frac{1}{12}\mathbf{\rho}_\text{пов}, $$ відповідно $$ m_\text{r2}=\mathbf{\rho}_\text{r2}\cdot V=\frac{1}{12}\mathbf{\rho}_\text{пов}\cdot V. $$ \begin{gather*} m_\text{в1}+\frac 16\mathbf{\rho}_\text{пов}\cdot V=\mathbf{\rho}_\text{пов}V,\\[6pt] m_\text{в2}+\frac{1}{12}\mathbf{\rho}_\text{пов}\cdot V=\mathbf{\rho}_\text{пов}V. \end{gather*}

Визначимо відношення мас вантажу після і до нагрівання:

Отже, після нагрівання газу, яким заповнена повітряна куля, допустима маса вантажу, який зможе підняти куля, збільшиться в \(1,1\ \text{раза}.\)

Відповідь: 1,1.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння визначати тип ізопроцесу й роботу газу відповідно до першого закону термодинаміки.

Роботу \(A\) газу в термодинаміці визначають за формулою \begin{gather*} A=p\Delta V, \end{gather*} де \(p\) ‒ тиск газу, \(\Delta V\) ‒ зміна об’єму газу.

Для того, щоб знати, що відбувається з тиском й об’ємом, необхідно розібратися, який процес відбувається з газом під час кожного етапу циклу.

Розгляньмо ділянку \(1‒2.\) Це ізобарний процес ‒ \(p=\mathrm{const}.\) Під час цього процесу, як видно з графіка, абсолютна температура \(T\) газу підвищується. Відповідно до рівняння Клапейрона для ізобарного процесу об’єм \(V\) газу теж буде збільшуватися:

Отже, процес \(1‒2\) ‒ це процес ізобарного нагрівання.

Оскільки температура підвищилася на дві позиції, то й об’єм збільшився на \(2\ \text{позиції},\) а тиск залишився тим самим: $$ A_{1-2}=p\cdot 2V. $$

Розгляньмо ділянку \(3‒4.\) Це теж ізобарний процес ‒ \(p=\mathrm{const}.\) Під час цього процесу, як видно з графіка, абсолютна температура \(T\) газу знижується. Відповідно до рівняння Клапейрона для ізобарного процесу об’єм \(V\) газу теж зменшуватиметься: \begin{gather*} \frac VT=\mathrm{const}\Rightarrow \frac{V\downarrow}{T\downarrow}=\mathrm{const}. \end{gather*}

Отже, процес \(3-4\) ‒ це процес ізобарного охолодження.

Оскільки температура знизилася на дві позиції, то і об’єм теж зменшився на \(2\ \text{позиції},\) а тиск залишився тим самим: $$ A_{3-4}=p\cdot 2V. $$

Визначімо відношення абсолютних (за модулем) значень робіт газу на ділянках \(1‒2\) і \(3‒4:\) $$ \frac{A_{1-2}}{A_{3-4}}=\frac{p\cdot 2V}{p\cdot 2V}=1. $$

Отже, газ виконав однакові роботи, тільки під час процесу \(1‒2\) газ розширювався, а під час процесу \(3‒4\) стискався.

Відповідь: 1.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Кількість теплоти. Пароутворення (випаровування і кипіння).

Завдання скеровано на перевірку знання і розуміння фазових переходів речовини.

Спочатку вода нагріється до температури кипіння \(100\ ^\circ\mathrm{C}.\) Для цього потрібна буде кількість теплоти \(Q_1:\) $$ Q_1=cm_\text{в}\Delta t, $$ де \(c\) ‒ питома теплоємність води, \(m_\text{в}\) ‒ маса води, \(\Delta t\) ‒ зміна температури води.

Потім для перетворення усієї води на пару необхідна буде кількість теплоти \(Q_2:\) $$ Q_2=Lm_\text{в}, $$ де \(L\) ‒ питома теплота пароутворення води.

Під час процесу пароутворення температура води і пари не змінюватиметься, залишатиметься рівною \(100\ ^\circ\mathrm{C},\) уся кількість теплоти піде на подолання сил притягання між молекулами води.

Оскільки електроплитка буде та сама, коли вода нагріватиметься до кипіння, а потім випаровуватиметься, зможемо записати формули для потужності електроплитки під час обох процесів:

Прирівняймо праві частини цих рівностей, де \(\mathbf{\tau}_1\) і \(\mathbf{\tau}_2\) ‒ проміжки часу для доведення води до кипіння і для її випаровування відповідно: $$ \frac{cm_\text{в}\Delta t}{\mathbf{\tau}_1}=\frac{Lm_\text{в}}{\mathbf{\tau}_2}. $$

Скоротімо масу води, яка невідома, і визначімо час випаровування води:

Значення часу ми не переводили в систему SI, оскільки в умові є вимога подати відповідь у хвилинах. А значення температури не подали в системі SI, оскільки зміна температури за шкалою Кельвіна дорівнює зміні температури за шкалою Цельсія: \(\Delta T=\Delta t,\) тобто ціна поділки шкали Кельвіна дорівнює ціні поділки шкали Цельсія: \(1\ ^\circ\mathrm{C}=1\ \text{К}.\)

Відповідь: 50.

ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.

Завдання скеровано на перевірку знання і розуміння принципу дії фотоелемента і конденсатора, а також вміння аналітично описати процеси, що в них відбуваються.

Сила струму \(I\) ‒ це фізична величина, яка чисельно дорівнює заряду \(q\) фотоелектронів, що вириваються з поверхні фотоелемента за певний час \(t:\) $$ I=\frac qt. $$

Зарядом конденсатора називають модуль заряду \(q\) однієї з його обкладок. Електроємність \(C\) конденсатора визначають за формулою: $$ C=\frac qU $$ де \(U\) ‒ напруга між обкладками.

Визначімо заряд з обох формул і прирівняймо ці вирази: \begin{gather*} q=It,\\[7pt] q=UC,\\[7pt] It=UC,\\[6pt] t=\frac{UC}{I},\\[6pt] t=\frac{6\ \text{В}\cdot 100\cdot 10^{-6}\ \text{Ф}}{10\cdot 10^{-6}\ \text{А}}=60\ \text{с}. \end{gather*}

Коли фотоелемент приєднають до розрядженого конденсатора, він почне заряджатися. Напруга досягне значення \(6\ \text{В}\) за \(60\ \text{с}.\)

Відповідь: 60.

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.

Завдання скеровано на перевірку знання і розуміння послідовного і паралельного з’єднання провідників, а також уміння читати електричні схеми.

Визначімо силу струму в електричному колі тоді, коли ключ розімкнений, і коли він замкнений.

Якщо ключ розімкнений, то струм протікатиме по трьох послідовно з’єднаних резисторах (див. рисунок в умові).

За законом Ома для повного кола сила струму \(I\) дорівнюватиме: $$ I=\frac{\mathbf{\varepsilon}}{R+r}, $$ де \(\mathbf{\varepsilon}\) ‒ електрорушійна сила джерела струму, \(R\) ‒ загальний опір навантаження (усіх провідників, які підключені до джерела), \(r\) ‒ внутрішній опір джерела струму.

За умовою \begin{gather*} r=0,\ \text{тоді}\\[6pt] I=\frac{\mathbf{\varepsilon}}{R+r}=\frac{\mathbf{\varepsilon}}{R},\\[6pt] \mathbf{\varepsilon}=IR=U, \end{gather*} де \(U\) ‒ напруга в колі (залишиться сталою, якщо ключ замкнути, бо джерело струму те саме).

Визначімо загальний опір трьох послідовно з’єднаних резисторів з однаковим опором: $$ R_\text{заг1}=R_1+R_2+R_3=3R. $$

Отже, силу струму \(I_1\) в разі розімкнутого ключа визначатимуть за формулою $$ I_1=\frac{U}{R_\text{заг1}}=\frac{U}{3R}. $$

Якщо ключ замкнути, то за схемою до одного з трьох резисторів буде паралельно приєднаний ще один резистор (див. схему в умові). Визначімо загальний опір такого змішаного з’єднання резисторів. Спочатку запишімо загальний опір двох паралельно з’єднаних резисторів:

Отже, силу струму \(I_2\) в разі замкненого ключа визначімо за формулою \begin{gather*} I_2=\frac{U}{R_\text{заг2}}=\frac{U\cdot 2}{5R}. \end{gather*}

Визначімо співвідношення \(I_2\) і \(I_1\):

Відповідь: 1,2.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Явище самоіндукції. Індуктивність.

Завдання скеровано на перевірку знання і розуміння закону самоіндукції.

Відразу після розімкнення кола сила струму \(I\) в колі зменшується. Магнітна індукція поля, створеного струмом, теж зменшується. Змінне магнітне поле створює вихрове електричне поле, яке в цьому разі підтримуватиме струм у котушці.

Явище виникнення вихрового електричного поля в провіднику, у якому тече змінний електричний струм, називають явищем самоіндукції.

Скористаймося законом самоіндукції: електрорушійна сила самоіндукції \(\mathbf{\varepsilon}_{is}\) прямо пропорційна швидкості зміни сили струму в провіднику: $$ \mathbf{\varepsilon}_{is}=L\frac{\Delta I}{\Delta t}, $$ де \(L\) ‒ індуктивність котушки.

Визначімо час існування струму в котушці після розмикання кола:

Відповідь: 0,01.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона. Електромагнітні хвилі та швидкість поширення їх. Електродинаміка. Основи електростатики. З’єднання конденсаторів.

Завдання скеровано на перевірку розуміння принципу роботи коливального контуру.

Радіохвилі ‒ це електромагнітні хвилі, які поширюються зі швидкістю світла \(c.\)

Довжину хвилі \(\mathbf{\lambda}\) визначімо за формулою $$ \mathbf{\lambda}=cT, $$ де \(T\) ‒ період власних електромагнітних коливань у коливальному контурі. Його можна визначити за формулою Томсона: $$ T=2\mathbf{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки контуру, \(C\) ‒ електроємність конденсатора контуру.

Отже, довжину хвилі, на яку налаштовано радіоприймач, обчислімо за формулою $$ \mathbf{\lambda}_1=c\cdot 2\mathbf{\pi}\sqrt{LC_1}. $$

Після приєднання паралельно до конденсатора ще одного, утричі більшої ємності, загальна електроємність $$ C_2=C_1+3C_1=4C_1, $$ бо за паралельного з’єднання конденсаторів їхні електроємності додають одну до одної.

Тепер радіоприймач буде налаштований на довжину хвилі \(\mathbf{\lambda}_2:\) \begin{gather*} \mathbf{\lambda}_2=c\cdot 2\mathbf{\pi}\sqrt{L4C_1}. \end{gather*}

Поділімо ліві і праві частини формул для довжин хвиль:

Відповідь: 8.

ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Побудова зображень, які дає плоске дзеркало.

Завдання скеровано на перевірку знання і розуміння законів відбивання, правил побудови зображень, які дає плоске дзеркало.

Продовжмо спочатку відбитий промінь з точки \(K\) до точки торкання з горизонтом ‒ точка \(F.\) Утворився \(\Delta KOF.\) Нам треба визначити \(\angle KFO.\)

Визначімо кут, під яким промінь \(DK\) падає на дзеркало. Проведімо промінь \(BK\) паралельно до горизонту \(AF.\) Тоді \(\angle BKC=50^\circ,\) як пара до \(\angle AOC\) ‒ зовнішні односторонні кути двох паралельних прямих \(AO\) i \(BK\) і січної \(CO.\)

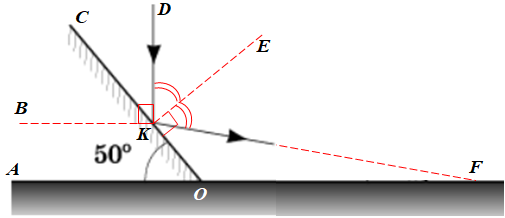
Оскільки за умовою промінь \(KD\) падає вертикально, тобто перпендикулярно до горизонту, то \(\angle BKD=90^\circ,\) отже \(\angle CKD=90^\circ-50^\circ=40^\circ.\)

Тепер можемо визначити кут падіння променя на дзеркало ‒ \(\angle DKE\) ‒ це кут між променем \(KD\) і добудованим перпендикуляром \(KE\) до дзеркала.

За законами відбивання кут відбивання променя дорівнюватиме куту падіння: $$ \angle EKF=\angle DKE=90^\circ-40^\circ=50^\circ. $$

Тепер розгляньмо \(\Delta KOF.\)

\(\angle FKO=90^\circ-50^\circ=40^\circ\) ‒ між відбитим променем \(KF\) і площиною дзеркала.

\(\angle KOF=180^\circ-50^\circ=130^\circ\) оскільки \(\angle AOF=180^\circ\) ‒ розгорнутий.

А оскільки сума кутів трикутника дорівнює \(180^\circ,\) то шуканий кут $$ \angle KFO=180^\circ-40^\circ-130^\circ=10^\circ. $$

Відповідь: 10.

ТЕМА: Коливання і хвилі. Оптика. Оптична сила лінзи. Формула тонкої лінзи.

Завдання скеровано на перевірку знання і розуміння будови ока й уміння застосовувати формулу тонкої лінзи.

Відстанню найкращого зору називають найменшу відстань, на якій око бачить предмет практично не напружуючись. Для людини з нормальним зором відстань найкращого зору становить приблизно \(25\ \text{см}\ (d_0=25\ \text{см}).\) У такої людини фокус оптичної системи ока в ненапруженому стані розташований на сітківці, тобто паралельні промені, що потрапляють в око, після заломлення збираються на сітківці (див. рисунок).

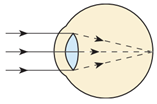
В умові завдання йдеться про далекозору людину. У разі далекозорості фокус оптичної системи ока в ненапруженому стані розташований за сітківкою (див. рисунок) і зображення предметів на сітківці також є нечітким, розмитим. Відстань найкращого зору в цьому разі більша за \(25\ \text{см}\ (d=40\ \text{см}),\) тому, розглядаючи предмет, людина віддаляє його від очей. Далекозорість коригують носінням окулярів зі збиральними лінзами або збиральних контактних лінз.

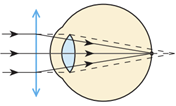
Запишімо формулу тонкої лінзи для випадку, коли людина читає без окулярів: $$ D_\text{ока}=\frac 1d+\frac 1f, $$ де \(D_\text{ока}\) ‒ оптична сила лінзи ока (кришталика), \(d\) ‒ відстань від кришталика до предмета (до книжки), \(f\) ‒ відстань від кришталика до сітківки ока (до «екрана»).

Якщо окуляри дібрано правильно, людині буде зручно читати, тримаючи книжку на відстані \(d_0\) від очей ‒ на відстані найкращого зору. Окуляри ж дадуть уявне зображення тексту на відстані \(d\) від очей, і це зображення буде предметом для ока. Отже, запишімо формулу тонкої лінзи для системи лінз ‒ лінза ока й лінза окулярів: $$ D_\text{ока}+D_\text{окулярів}=\frac{1}{d_0}+\frac 1f, $$ де \(D_\text{окулярів}\) ‒ оптична сила лінзи окулярів, \(d_0\) ‒ відстань від кришталика до предмета (до книжки), \(f\) ‒ відстань від кришталика до сітківки ока (до «екрана») ‒ вона залишається тією самою, що й для випадку, коли людина читає без окулярів, оскільки ця відстань залежить від внутрішньої будови ока кожної людини.

Визначімо оптичну силу окулярів, розв’язавши систему рівнянь (від другого рівняння віднімемо перше):

Відповідь: 1,5.