ЗНО онлайн 2012 року з фізики – основна сесія

Пояснення

ТЕМА: Механіка. Основи динаміки. Інерціальні системи відліку.

Завдання скеровано на перевірку знання і розуміння поняття інерціальних систем відліку, а також фізичних величин у цих системах.

Інерціальною системою відліку називають систему відліку, відносно якої спостерігають явище інерції.

Інерцією називають явище збереження тілом стану спокою або рівномірного прямолінійного руху за умови, що на нього не діють інші тіла й поля або їхні дії скомпенсовані.

Систему відліку утворюють тіло відліку, пов’язана з ним система координат і прилад для відліку часу.

Швидкість руху досліджуваного тіла, його переміщення і напрямок руху залежатимуть від того, що буде вибрано за тіло відліку, з якою сталою швидкістю воно рухатиметься, як будуть зорієнтовані осі координат. Наприклад, якщо розглядати рух автомобіля в потоці відносно інших машин, то його швидкість може дорівнювати нулю, а відносно дерева на тротуарі автомобіль рухатиметься з певною швидкістю. Або якщо змінимо напрямок осі на протилежний, то напрямок руху автомобіля відносно до напрямку осі теж зміниться на зворотний.

Натомість прискорення залишиться незмінною величиною в будь-якій інерціальній системі відліку. Зміна швидкості руху тіла буде однаковою відносно систем відліку, що зберігають стан спокою або рухаються з певною сталою швидкістю.

Відповідь: Б.

Пояснення

ТЕМА: Механіка. Основи кінематики. Рух тіла під дією сили тяжіння.

Завдання скеровано на перевірку знання і розуміння поняття відносності руху, додавання швидкостей і знання властивостей зображення, що дає плоске дзеркало.

Намалюємо пояснювальний рисунок: початок координат пов’яжемо з точкою \(O\) на поверхні Землі, з якої камінець кинули під кутом до горизонту; вісь \(Oy\) спрямуємо вертикально вгору; вісь \(Ox\) ‒ горизонтально.

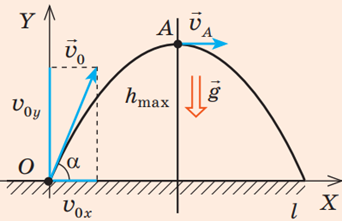
У вибраній системі відліку рух уздовж осі \(Ox\) ‒ рівномірний: $$ v_{0x}=v_0\cos\mathbf{\alpha}, $$ рух уздовж осі \(Oy\) ‒ рівноприскорений: $$ v_{0y}=v_0\sin\mathbf{\alpha}. $$

У найвищій точці своєї траєкторії ‒ точці \(A\) швидкість руху камінця відносно поверхні озера становитиме \(v_{0x}=v_0\cos\mathbf{\alpha},\) оскільки вертикальний складник швидкості \(v_{0y}\) дорівнюватиме нулю ‒ камінець на мить перестане підійматися і після цього почне падати, одночасно рухаючись горизонтально.

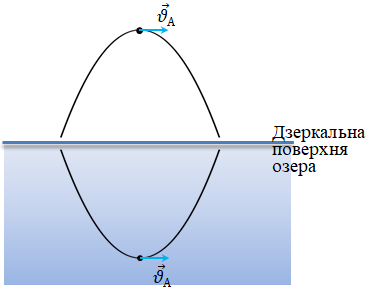
Зображення камінця в дзеркальній поверхні озера рухатиметься з тією ж швидкістю \(v_{0x}=v_0\cos\mathbf{\alpha}\) і в той самий бік, що й сам камінець (за властивостями зображення, яке дає плоске дзеркало).

Один відносно одного камінець і зображення в ту мить, коли камінець перебуває на максимальній висоті підйому і ще не почав падати, але перестав підійматися, не рухатимуться. Тобто вони й не наближаються і не віддаляються, а швидкість руху камінця відносно його зображення в цю мить дорівнюватиме нулю.

Відповідь: Г.

Пояснення

ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.

Завдання скеровано на перевірку розуміння графіків, що описують прямолінійний рівноприскорений вертикальний рух (під дією постійної сили тяжіння), і на розуміння функціональної залежності фізичних величин, що описують цей рух.

Потенціальною енергією \(E_\text{п}\) піднятого на висоту \(h\) тіла масою \(m\) називають величину $$ E_\text{п}=mgh, $$ де \(g\) ‒ прискорення вільного падіння.

Потенціальна енергія піднятого тіла залежить від висоти, на якій перебуває тіло, тобто залежить від вибору нульового рівня, ‒ рівня, від якого відлічуватимуть висоту. Запишімо кінематичне рівняння, яке показує залежність висоти \(h\) тіла, що за умовою вільно падає (початкова швидкість \(v_0=0\)), від часу \(t:\)

За умовою завдання пластилінова кулька перебувала спочатку на певній висоті \(h_0.\) Із часом висота кульки над підлогою зменшувалася. Тож графіки А і В не відповідають цій умові, бо вони показують збільшення потенціальної енергії із часом.

Оскільки висота пропорційна часу в другому степені $$ h\sim t^2, $$ то залежність буде квадратичною (графік Г ‒ це лінійна залежність), а схематичним графіком буде вітка параболи. Тобто цим умовам відповідає графік Б.

Горизонтальна ділянка графіка, що збігається з віссю часу, коли вже потенціальна енергія дорівнює нулю, відповідає тій умові завдання, що кульку зроблено з пластиліну, тобто після непружного удару об підлогу вона не підскочить знову на певну висоту.

Відповідь: Б.

Пояснення

ТЕМА: Механіка. Основи динаміки. Рух тіл під дією однієї або кількох сил.

Завдання скеровано на перевірку знання і розуміння руху тіла під дією кількох сил, уміння застосовувати другий закон Ньютона.

За умовою брусок із тягарцями тягнуть прямолінійно рівномірно. Назвімо сили, що діють на цю систему тіл: сила тяжіння \(\overrightarrow{F}_\text{тяжіння}\) (напрямлена вертикально вниз), сила нормальної реакції опори \(\overrightarrow{N}\) (напрямлена вертикально вгору, за модулем дорівнює силі тяжіння), сила тяги \(\overrightarrow{F}_\text{тяги}\) (визначаємо за показами динамометра на фотографії 1 в умові; за модулем дорівнює силі пружності, що виникає в пружині динамометра), сила тертя ковзання \(\overrightarrow{F}_\text{тертя}\) (напрямлена протилежно до сили, з якою тягнуть брусок, за модулем дорівнює цій силі тяги).

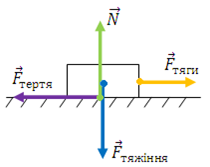
Запишімо другий закон Ньютона: $$ m\overrightarrow{a}=\overrightarrow{F}_\text{тяжіння}+\overrightarrow{N}+\overrightarrow{F}_\text{тяги}+\overrightarrow{F}_\text{тертя}. $$

Вертикально напрямлені сили \(\overrightarrow{F}_\text{тяжіння}\) і \(\overrightarrow{N}\) скомпенсовані, оскільки рух за умовою горизонтальний: $$ F_\text{тяжіння}=N. $$

Рух рівномірний, а отже, прискорення \(\overrightarrow{a}\) дорівнює нулю: $$ 0=F_\text{тяги}-F_\text{тертя}. $$

Знак мінус, тому що сили напрямлені протилежно.

Визначімо коефіцієнт тертя між бруском і рейкою: $$ \mathbf{\mu}=\frac{F_\text{тяги}}{F_\text{тяжіння}}. $$

Силу тяги визначімо за показами динамометра на рисунку 1: $$ F_\text{тяги}=0,9\ \text{Н}. $$

Силу тяжіння визначімо за показами динамометра на рисунку 2: \begin{gather*} F_\text{тяжіння}=3,6\ \text{Н},\\[7pt] \mathbf{\mu}=\frac{F_\text{тяги}}{F_\text{тяжіння}}=\frac{0,9\ \text{Н}}{3,6\ \text{Н}}=0,25. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу. Механіка. Елементи механіки рідин і газів. Тиск нерухомої рідини на дно й стінки посудини.

Завдання скеровано на перевірку знання і розуміння зв’язку між макроскопічними параметрами газу, а також на розуміння атмосферного й гідростатичного тиску.

Виразімо зв’язок між макроскопічними параметрами повітря (тиском \(p,\) об’ємом \(V\) і температурою \(T\)) в бульбашці, коли вона перебуває на глибині (положення 1), а потім спливає до поверхні озера (положення 2) за допомогою рівняння Клапейрона (маса і молярна маса повітря в бульбашці не змінюються): \begin{gather*} \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}. \end{gather*}

За умовою температура стала, отже, \begin{gather*} T_1=T_2,\\[7pt] p_1V_1=p_2V_2. \end{gather*}

Тиск \(p_1\) на глибині дорівнюватиме сумі атмосферного \(p_\text{атм}\) і гідростатичного \(p_\text{гідр}\) тиску: \begin{gather*} p_1=p_\text{атм}+p_\text{гідр},\\[7pt] p_1=p_\text{атм}+\mathbf{\rho}gh, \end{gather*} де \(\mathbf{\rho}\) ‒ густина рідини, \(g\) ‒ прискорення вільного падіння, \(h\) ‒ глибина.

А тиск біля поверхні дорівнює атмосферному тиску: \begin{gather*} p_2=p_\text{атм}. \end{gather*}

Запишімо відношення об’ємів, підставивши вирази для тисків:

Отже, об’єм бульбашки збільшиться у 2,5 раза.

Відповідь: B.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основне рівняння молекулярно-кінетичної теорії.

Завдання скеровано на перевірку знання і розуміння формули-наслідку з основного рівняння молекулярно-кінетичної теорії і формули, що виражає зв’язок середньої кінетичної енергії поступального руху молекул і температури.

Тиск \(p\) газу повністю визначає його абсолютна температура \(T\) й концентрація \(n\) молекул газу: $$ p=nkT, $$ де \(k=1,38\cdot 10^{-23}\ \text{Дж/К}\) ‒ стала Больцмана.

Запишімо це рівняння до підвищення температури й після: \begin{gather*} p_1=n_1kT_1,\\[7pt] p_2=n_2kT_2. \end{gather*}

За умовою абсолютна температура підвищилася втричі: $$ T_2=3T_1. $$

Також за умовою змінилася концентрація ‒ фізична величина, яка дорівнює кількості структурних одиниць речовини \(N\) в одиниці об’єму газу \(V\) (об’єм, який займає газ у балоні, залишився незмінним, тому що балон закритий): \begin{gather*} n_1=\frac{N_1}{V},\\[6pt] n_2=\frac{N_2}{V},\\[6pt] N_2=\frac 12N_1+\frac 12N_1\cdot 2. \end{gather*}

Відповідно до умови кожна друга молекула розпалася на два атоми. Отже, $$ N_2=\frac 12N_1(1+2)=1,5N_1. $$

Тепер визначімо, у скільки разів збільшився тиск газу:

Отже, тиск газу в балоні збільшиться в 4,5 раза.

Відповідь: B.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку розуміння ізопроцесів і їхньої графічної інтерпретації.

Розгляньмо кожну ділянку графіка на рисунку з умови.

Ділянка 1‒2: тиск сталий \(p=\mathrm{const}\) (ізобарний процес), абсолютна температура \(T\) підвищується. Якщо зафіксувати тиск і нагрівати газ, то об’єм повинен збільшуватися. Отже, відповідно до рівняння Клапейрона для ізобарного процесу об’єм \(V\) теж збільшуватиметься: \begin{gather*} \frac VT=\mathrm{const}\Rightarrow \frac{V\uparrow}{T\uparrow}=\mathrm{const} \end{gather*} (стрілочка, напрямлена вгору, означає зростання значення величини; стрілочка, напрямлена вниз, означає зменшення значення величини).

Отже, ділянка 1‒2 графіка відповідає ізобарному нагріванню.

Ділянки 2‒3 й 4‒1 відповідають ізотермічному процесу, коли \(T=\mathrm{const},\) а тиск \(p\) зростає (див. рисунок). Це означає, що відповідно до рівняння Клапейрона для ізотермічного процесу об’єм зменшуватиметься: $$ pV=\mathrm{const}\Rightarrow p\uparrow V\downarrow =\mathrm{const}. $$

Отже, ділянки 2‒3 й 4‒1 графіка відповідають ізотермічному стисканню.

Ділянка 3‒4: якщо зафіксувати об’єм й охолоджувати газ, то тиск повинен зменшуватися. Отже, відповідно до рівняння Клапейрона для ізохорного процесу якщо температура \(T\) знижуватиметься, то й тиск теж зменшуватиметься: $$ \frac pT=\mathrm{const}\Rightarrow \frac{p\downarrow}{T\downarrow}=\mathrm{const}. $$

Отже, ділянка 3‒4 графіка відповідає ізохорному охолодженню.

Тепер за визначеними процесами знайдімо відповідний графік у системі координат \(V,\ T.\)

За першим процесом ‒ ізобарне нагрівання ‒ можемо виключити рисунок Г: на його ділянці 1‒2 температура знижується.

Процес 2‒3 ‒ це ізотермічне стискання. Виключаємо рисунок Б: на ньому ділянка графіка 2‒3 відповідає ізотермічному розширенню.

Процес 3‒4 (ізохорне охолодження) на рисунках А і В збігається.

А от за процесом 4‒1 ‒ ізотермічне стискання ‒ правильним буде лише рисунок А. На рисунку Б ділянка графіка 4‒1 відповідає ізотермічному розширенню.

Відповідь: A.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку розуміння суті адіабатного процесу і закономірностей змін макроскопічних фізичних параметрів газу під час цього процесу.

Адіабатний процес ‒ це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти, передана системі, дорівнює нулю. Отже, варіанти відповіді, у яких зазначено, що газ отримує тепло, можна відкинути.

Перший закон термодинаміки для адіабатного процесу має вигляд: $$ \Delta U+A=0,\ \text{або}\ A=-\Delta U. $$

Це означає, що в ході адіабатного розширення газ виконує додатну роботу \(A\) за рахунок зменшення внутрішньої енергії \(\Delta U,\) температура газу знижується, тиск також знижується, а об’єм збільшується.

Отже, правильною буде відповідь, що газ не отримує тепла, а його внутрішня енергія зменшується.

Відповідь: Б.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку розуміння роботи в термодинаміці.

Роботу газ виконуватиме, якщо змінюватиметься його об’єм. Якщо об’єм газу збільшується, то газ виконує додатну роботу. Якщо об’єм газу зменшується, то робота газу від’ємна.

Під час ізобарного процесу роботу \(A\) газу можна визначити за формулою \begin{gather*} A=p\Delta V, \end{gather*} де \(p\) ‒ тиск, \(\Delta V\) ‒ зміна об’єму.

Скористаймося рівнянням стану ідеального газу (рівнянням Менделєєва ‒ Клапейрона): $$ p\Delta V=\frac mMR\Delta T, $$ де \(m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(R\) ‒ універсальна газова стала, \(\Delta T\) ‒ зміна абсолютної температури.

Отже, роботу, яку виконує розріджений азот, можна визначити за формулою

Відповідь: B.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Плавлення і тверднення тіл.

Завдання скеровано на перевірку знання і розуміння зміни внутрішньої енергії речовини під час переходу з одного агрегатного стану в інший.

Після досягнення температури \(0\ ^\circ\mathrm{C}\) лід починає плавитися (танути), а його температура не змінюється попри те, що нагрівач продовжує працювати й передавати льоду певну кількість теплоти. Уся енергія, що надходить від нагрівача, витрачається на руйнування кристалічної ґратки льоду. У цей інтервал часу внутрішня енергія \(\Delta U\) льоду продовжує збільшуватися. І збільшиться вона на ту кількість теплоти \(Q,\) яка необхідна для плавлення льоду масою \(m=3\ \text{кг}:\) $$ \Delta U=Q=qm, $$ де \(q\) ‒ питома теплота плавлення;

Отже, внутрішня енергія льоду, що розтанув, збільшилася на \(9,9\cdot 10^5\ \text{Дж}.\)

Відповідь: B.

Пояснення

ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.

Завдання скеровано на перевірку знання і розуміння зв’язку між напруженістю електричного поля і напругою на пластинах конденсатора, а також залежності напруженості від відстані між його пластинами.

Поле між пластинами плоского конденсатора є однорідним, тому зв’язок між напруженістю \(E\) поля між пластинами й напругою \(U\) на пластинах конденсатора такий: $$ U=Ed, $$ де \(d\) ‒ відстань між пластинами конденсатора.

За умовою напруженість електричного поля зменшиться вдвічі: $$ E_2=0,5E_1. $$

Визначімо відношення відстаней між пластинами конденсатора:

Отже, відстань між пластинами конденсатора треба збільшити вдвічі.

Відповідь: B.

Пояснення

ТЕМА: Електродинаміка. Основи електростатики. Потенціал і різниця потенціалів.

Завдання скеровано на перевірку розуміння енергетичної характеристики електростатичного поля.

Силовою характеристикою електричного поля є напруженість. Електричне поле, вектори напруженості якого однакові в усіх точках простору, називають однорідним. Напруженість поля більшає в міру наближення до заряду (на наближення вказують стрілочки на рисунку). Отже, напруженість у точці \(C\) буде більшою за напруженість у точці \(A:\) $$ E_A\lt E_C. $$

Якщо відстань між лініями напруженості в деякій області простору є однаковою (див. рисунок), то так само однаковою є напруженість поля в цій області: $$ E_B=E_D. $$

Потенціал – це енергетична характеристика електростатичного поля. Силові лінії поля напрямлені в бік зменшення потенціалу. Що більша напруженість, то швидше зменшується потенціал під час переміщення вздовж силової лінії (напруженість характеризує швидкість зміни потенціалу). Отже, потенціал у точці \(A\) буде більший за потенціал у точці \(C:\) $$ \mathbf{\varphi}_A\gt \mathbf{\varphi}_C. $$

І відповідно в точках \(B\) і \(D\) потенціал буде однаковий: $$ \mathbf{\varphi}_B=\mathbf{\varphi}_D. $$

Відповідь: B.

Пояснення

ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.

Завдання скеровано на перевірку знання і розуміння фактичної і номінальної потужності і вміння визначати загальну потужність за будь-якого з’єднання споживачів.

Потужність, яку зазначено в паспорті електричного пристрою (або на пристрої), називають номінальною потужністю. Вимірюючи потужність струму в споживачі, ми визначаємо його фактичну потужність. Тобто значення фактичної і номінальної потужностей споживача можуть різнитися.

Якщо коло складається з кількох споживачів, то, розраховуючи їхню фактичну потужність, треба пам’ятати, що за будь-якого з’єднання споживачів загальна потужність струму в усьому колі дорівнює сумі потужностей окремих споживачів.

Потужність \(P\) струму чисельно дорівнює роботі \(A\) струму за одиницю часу \(t:\) $$ P=\frac At. $$

Узявши до уваги, що \(A=UIt,\) маємо: $$ P=UI, $$ де \(U\) ‒ напруга на ділянці кола, на якій визначають потужність струму; \(I\) ‒ сила струму в ділянці.

Але сила струму невідома, тож із паспортних даних і за допомогою закону Ома для ділянки кола \(\left(I=\frac UR\right)\) зможемо визначити незмінну характеристику кожної лампи ‒ електричний опір \(R:\)

(записувати десятковим дробом не можна, оскільки доведеться округлювати нескінчений десятковий дріб, а цього робити не треба, бо це проміжні результати, а округлення їх приведе до неправильних остаточних результатів).

Лампи з’єднано послідовно. Обчислімо їхній загальний опір:

Визначімо загальну потужність двох ламп: $$ P=\frac{U^2}{R}=\frac{220^2\cdot 40}{220^2}\ \text{Вт}=40\ \text{Вт}. $$

Відповідь: A.

Пояснення

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у вакуумі.

Завдання скеровано на перевірку знання і розуміння термоелектронної емісії.

Випромінювання електронів із поверхні металів називають електронною емісією. З огляду на те, як була передана електронам необхідна енергія, розрізняють кілька видів емісій. Щоб створити електричний струм у вакуумі, найчастіше використовують термоелектронну емісію.

Термоелектронна емісія ‒ випромінювання електронів нагрітими тілами.

Отже, правильним є варіант відповіді випромінювання електронів катодом під час його нагрівання.

Відповідь: B.

Пояснення

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у розчинах і розплавах електролітів. Закони електролізу.

Завдання скеровано на перевірку знання, розуміння і вміння застосовувати закони Фарадея для електролізу.

Відповідно до першого закону Фарадея для електролізу маса \(m\) речовини, яка виділяється на електроді під час електролізу, прямо пропорційна силі струму \(I\) та часу \(t\) його проходження крізь електроліт: $$ m=kIt, $$ де \(k\) ‒ коефіцієнт пропорційності, який називають електрохімічним еквівалентом.

Запишімо формули для визначення маси речовини до змін і після: \begin{gather*} m_1=kI_1t_1,\\[7pt] m_2=kI_2t_2. \end{gather*}

За умовою силу струму збільшили втричі: $$ I_2=3I_1, $$ а час електролізу зменшили вшестеро: $$ t_2=\frac 16t_1. $$

Отже,

Тобто маса речовини, що виділиться після змін на електроді, зменшиться вдвічі.

Відповідь: Г.

Пояснення

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Явище електромагнітної індукції (генератор змінного струму).

Завдання скеровано на перевірку знання і розуміння будови й принципу дії генератора змінного струму.

Генератор змінного струму ‒ це пристрій, який перетворює механічну енергію в електричну на основі явища електромагнітної індукції.

Електромагнітна індукція ‒ явище створення в просторі вихрового електричного поля змінним магнітним потоком (за допомогою руху (обертання) котушки (ротора) в магнітному полі нерухомого електромагніту (статора)). Одним із наслідків електромагнітної індукції є виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється. Саме вихрове електричне поле діє на вільні заряджені частинки в провіднику та надає їм напрямленого руху, створюючи індукційний струм. Тому є ще одне означення генератора змінного струму ‒ це джерело електричної енергії, яке створює електрорушійну силу (ЕРС), що періодично змінюється.

Відповідь: A.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний (математичний) маятник.

Завдання скеровано на перевірку знання і розуміння фізичних величин, що характеризують коливання математичного маятника.

Математичний маятник ‒ це фізична модель коливальної системи, яка складається з матеріальної точки, підвішеної на невагомій і нерозтяжній нитці, і гравітаційного поля. Положення рівноваги маятника ‒ це положення, у якому маятник висить непорушно строго вертикально, сила тяжіння \(m\overrightarrow{g}\) врівноважується силою натягу \(\overrightarrow{T}\) нитки (див. рисунок).

Одразу можна сказати, що вага маятника за означенням буде максимальною у вертикальному положенні (положенні рівноваги). Отже, варіант відповіді Г ‒ неправильний.

Частота коливань маятника теж залишиться незмінною, оскільки в умові сказано, що коливання незгасні.

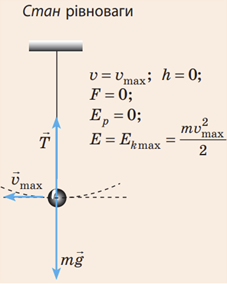
У ході коливань маятника його потенціальна та кінетична енергії безперервно змінюються. Потенціальна енергія є максимальною в точках повороту й дорівнює нулю в момент проходження маятником положення рівноваги. Кінетична енергія в точках повороту дорівнює нулю й сягає максимального значення в момент проходження маятником положення рівноваги. Отже, мінімальною в момент проходження маятником положення рівноваги буде потенціальна енергія.

Відповідь: A.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Звукові хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення та періодом (частотою).

Завдання скеровано на перевірку знання і розуміння поширення механічних хвиль і зміни під час цього їхніх характеристик.

Швидкість поширення хвилі в основному визначають пружні властивості середовища, у якому хвиля поширюється, тому, якщо хвиля переходить з одного середовища в інше, то швидкість \(v\) її поширення змінюється, а частота \(\mathbf{\nu}\) хвилі залишається незмінною, оскільки її визначає частота коливань джерела хвилі. Тому, власне, усі три варіанти відповіді Б, В, Г, де частота змінюється, можна відкинути, як неправильні.

Але ще впевнимося в правильності варіанта А, довівши, що довжина \(\mathbf{\lambda}\) хвилі збільшиться під час переходу звукової хвилі з повітря у воду. Відповідно до формули хвилі в разі переходу хвилі з одного середовища в інше довжина хвилі змінюється, оскільки змінюється швидкість поширення хвилі: $$ v=\mathbf{\lambda}\mathbf{\nu}\Rightarrow \mathbf{\lambda}=\frac{v}{\mathbf{\nu}} $$

За умовою швидкість поширення звуку в повітрi дорівнює \(340\ \text{м/с},\) а у воді ‒ \(1500\ \text{м/с}.\) Отже, чисельник збільшується, а знаменник залишається сталим ‒ довжина хвилі збільшується.

Відповідь: A.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Довжина хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).

Завдання скеровано на перевірку знання і розуміння поняття періоду коливань, довжини хвилі й уміння визначати її за графіком.

Поширення коливань у пружному середовищі називають механічною хвилею.

За час, що дорівнює періоду \(T,\) хвиля зі швидкістю \(v\) поширюється на відстань, яку називають довжиною хвилі \(\mathbf{\lambda}:\) $$ \mathbf{\lambda}=vT. $$

Отже, період вертикальних коливань поплавка (чергове підняття поплавка на гребені хвилі) дорівнюватиме: $$ T=\frac{\mathbf{\lambda}}{v}. $$

Визначімо за графіком з умови довжину хвилі. Довжина хвилі \(\mathbf{\lambda}\) ‒ це відстань між двома найближчими точками, які коливаються однаково (синхронно). Якщо зафіксувати певний момент часу, то через відстань, яка дорівнює довжині \(\mathbf{\lambda}\) хвилі, форма хвилі повториться.

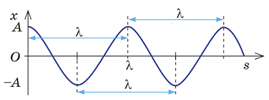
Розгляньмо рисунок в умові завдання. Виберімо точки, що рухаються синхронно.

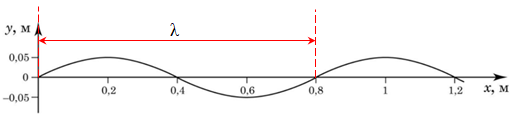
Отже, довжина хвилі, як видно з графіка, дорівнює \(0,8\ \text{м}.\)

Обчислімо тепер значення періоду коливань поплавка: $$ T=\frac{0,8\ \text{м}}{1\ \text{м/с}}=0,8\ \text{с}. $$

Відповідь: B.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.

Завдання скеровано на перевірку знання і розуміння принципу будови й дії трансформатора.

Основною причиною шуму трансформаторів є фізичне явище – магнітострикція. Коротко це означає: якщо на лист електротехнічної сталі діяти магнітним полем, цей лист згинатиметься сам собою.

Найпростіший трансформатор складається із замкненого осердя (магнітопроводу) і двох обмоток (див. рисунок). Осердя (сердечник) виготовлено з тонких пластин трансформаторної сталі.

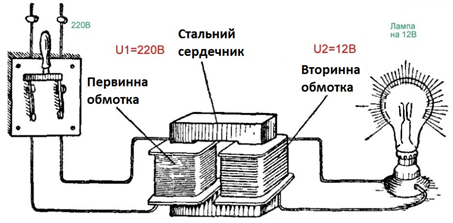
Явища зміни форми й розмірів феромагнітних тіл досліджували ще у ХІХ столітті. Англійський дослідник Джеймс Джоуль 1842 року помітив, що під дією магнітного поля тонкий залізний об’єкт подовжується в одному напрямку й скорочується в іншому, зберігаючи колишній об’єм. Таку деформацію супроводжують звуки: уявімо собі, що ми почуємо, якщо спробуємо зігнути лист металу або навіть звичайної фольги.

В умовах дії електромагнітного поля подібний процес набуває стабільної частоти. Частота гулу досить низька, що й дає змогу людському вуху його вловлювати. Оскільки йдеться про змінний струм, магнітне поле встигає двічі за фазу змінити свій напрямок, розгойдуючи усі мікрообласті металу сердечника. В Україні побутова електрична мережа з напругою \(220\ \text{В}\) працює за частоти \(50\ \text{Гц}.\) Це означає, що трансформаторні обмотки коливаються вдвічі частіше – із частотою \(100\ \text{Гц}.\) Для порівняння в США, де загальні мережі видають \(110\ \text{В}\) за \(60\ \text{Гц},\) трансформатори звучать вище – із частотою \(120\ \text{Гц}.\)

Відповідь: Б.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.

Завдання скеровано на перевірку знання і розуміння електромагнітного коливання і його частоти.

За умовою частота вільних електромагнітних коливань $$ 1\ \text{кГц}=1000\ \text{Гц}. $$

Це означає, що за секунду відбувається \(1000\) коливань. Тобто за кожне з \(1000\) коливань конденсатор коливального контуру встигає двічі перезарядитися, тож струм у котушці двічі набуває максимального значення і двічі він дорівнює нулю. У той момент, коли конденсатор повністю розряджений (рисунок в і ж), сила струму сягне максимального значення. А коли конденсатор повністю заряджений, то сила струму в котушці дорівнює нулю (рисунок а і д).

Отже, щосекунди сила струму в котушці індуктивності дорівнюватиме нулю \(2000\) разів. Щодо рисунка и, де пластини конденсатора вже знову повністю заряджені так само, як і на початку коливання (рисунок а), а струм в котушці дорівнює нулю: це вже початок наступного повного коливання, як на рисунку а. Коли відбулося пів коливання ‒ пройшло пів періоду (рисунок д) ‒ конденсатор повністю заряджений, він перезарядився, тобто заряд на його обкладках змінився на протилежний.

Схематичне зображення повного електромагнітного коливання:

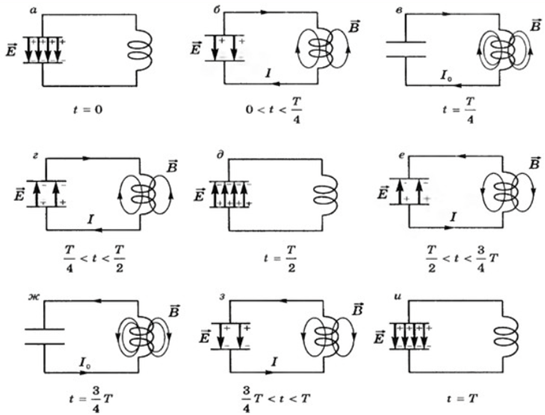
Відповідь: B.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона.

Завдання скеровано на перевірку знання і розуміння формули Томсона, уміння визначати довжину електромагнітної хвилі.

За час, що дорівнює періоду \(T,\) хвиля зі швидкістю \(v\) поширюється на відстань, яку називають довжиною \(\mathbf{\lambda}\) хвилі: $$ \mathbf{\lambda}=vT. $$

За умовою цієї задачі хвиля поширюється зі швидкістю світла: $$ v=c=3\cdot 10^8\ \text{м/с}. $$

Період \(T\) коливань коливального контуру радіоприймача визначімо за формулою Томсона: $$ T=2\mathbf{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора.

Дістанемо загальну формулу для визначення довжини хвилі, на яку настроєний радіоприймач:

Відповідь: B.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Закони заломлення світла.

Завдання скеровано на перевірку знання, розуміння і застосування законів відбивання і заломлення світла.

Як зображено на рисунках А і Б, частина пучка зазнає дзеркального відбивання на верхній або нижній поверхні пластинки. У точках, де світло відбивається, уявно будуємо перпендикуляр до межі середовищ, і тоді за законами відбивання кут падіння дорівнює куту відбивання.

Також на рисунках Б і В заломлення показано правильно. Оскільки оптична густина скла більша за оптичну густину повітря, кут заломлення світла в склі має бути меншим від кута падіння світла з повітря.

На рисунку В на поверхнях плоскопаралельної пластинки світло двічі зазнає заломлення (після цього пучок поширюється в тому самому напрямку, але зміщується). Це правильно.

На рисунку Г не показано заломлення внаслідок перетинання світлом нижньої грані пластинки. Це неправильно.

Відповідь: Г.

Пояснення

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Квантові постулати Бора.

Завдання скеровано на перевірку знання і розуміння моделі атома Бора і його постулатів.

Ернест Резерфорд 1911 р. після дослідів із розсіяння α-частинок запропонував планетарну (ядерну) модель будови атома: атом складається з позитивно зарядженого ядра, у якому зосереджена мало не вся маса атома; біля ядра по певних орбітах обертаються електрони.

Модифікацію планетарної моделі запропонував 1913 р. данський фізик Нільс Бор (1885–1962), який був упевнений, що розглядати будову атома треба під кутом квантових уявлень. Бор припустив існування особливих станів атомів і сформулював два постулати.

Перший постулат Н. Бора (про стаціонарні стани): атомна система може перебувати лише в особливих стаціонарних (квантових) енергетичних станах, кожному з яких відповідає певне значення енергії; перебуваючи в стаціонарному стані атом не випромінює енергію.

Другий постулат Н. Бора (про квантові стрибки): під час переходу з одного стаціонарного енергетичного стану в інший атом випромінює або поглинає квант електромагнітної енергії.

Повертаючись в основний стан, атоми, відповідно до постулатів Бора, випромінюють електромагнітні хвилі чітко визначених частот, а отже, і довжин. Якщо газ розріджений і перебуває в атомарному (не молекулярному) стані, то на екрані спектрографа спостерігають різнокольорові лінії, розділені широкими темними смугами. Сукупність цих ліній називають лінійчастим спектром випромінювання.

Існує і зворотне явище: якщо біле світло пропускати через речовину в газуватому стані, то спостерігають темні лінії на фоні неперервного спектра. Сукупність цих ліній називають лінійчастим спектром поглинання.

Лінійчастий спектр будь-якого хімічного елемента не збігається з лінійчастими спектрами інших хімічних елементів, а отже, є своєрідною візитівкою елемента.

Відповідь: Б.

Пояснення

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.

Завдання скеровано на перевірку знання і розуміння радіоактивних перетворень.

Атомне ядро утворюють нуклони: позитивно заряджені протони й електронейтральні нейтрони. Сумарну кількість протонів і нейтронів в атомі називають нуклонним або масовим числом і позначають буквою \(A.\)

Кількість протонів у ядрі називають зарядовим або протонним числом і позначають буквою \(Z.\) Порядковий номер хімічного елемента в періодичній системі дорівнює кількості протонів у ядрі (зарядовому числу).

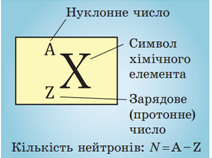
Пригадаймо правила зміщення для \(\mathbf{\alpha}\text{-розпаду}.\)

Під час \(\mathbf{\alpha}\text{-розпаду}\) (випромінення ядра атома Гелію \(^4_2\mathrm{He}\)) кількість нуклонів у ядрі зменшується на \(4,\) протонів ‒ на \(2,\) тому утворюється ядро елемента \(\mathrm{Y},\) порядковий номер якого на \(2\) одиниці менший від порядкового номера елемента \(\mathrm{X}:\) $$ ^A_Z\mathrm{X\ \rightarrow\ ^4_2He}\ +\ ^{A-4}_{Z-2}\mathrm{Y}. $$

Отже, електричний заряд ядра внаслідок \(\mathbf{\alpha}\text{-розпаду}\) зменшиться на \(2e.\)

Відповідь: B.

Пояснення

ТЕМА: Механіка. Основи динаміки. Елементи механіки рідин і газів. Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Капілярні явища.

Завдання скеровано на перевірку знання і розуміння явищ або виникнення сил і вміння пояснити їхній фізичний зміст.

1. Капіляр (від лат. capillaris ‒ волосяний) ‒ трубка з вузьким внутрішнім каналом. З капілярами пов’язані так звані капілярні явища. Капілярний ефект ‒ явище підвищення або зниження рівня рідини в капілярах, як порівняти з тим значенням, яке відповідає закону сполучених посудин.

Під викривленою поверхнею рідини виникає надлишковий (від’ємний або додатний) тиск, який прямо пропорційний поверхневому натягу рідини (тобто силам, що намагаються стягнути цю поверхню, прагнуть зменшити площу поверхні рідини) й обернено пропорційний радіусу кривизни меніска. Завдяки цьому тиску рідина піднімається в капілярах, які змочує (рисунок а), й опускається в капілярах, які не змочує (рисунок б).

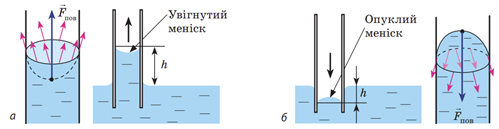
Правильний варіант відповіді ‒ Г.

2. Архімедова (виштовхувальна) сила зумовлена тим, що тиск рідини збільшується з глибиною. На нижню поверхню зануреного в рідину тіла рідина тисне з більшою силою, ніж на верхню. Унаслідок цього рівнодійна сил тиску рідини на всі ділянки поверхні тіла напрямлена вгору ‒ ця рівнодійна і є архімедовою силою.

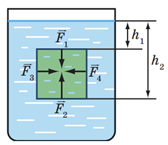
Сили гідростатичного тиску \(\overrightarrow{F}_3\) і \(\overrightarrow{F}_4,\) що діють на бічні грані кубика, є протилежними за напрямком і рівними за значенням, оскільки площі бічних граней однакові й ці грані розташовані на однаковій глибині. Такі сили зрівноважують одна одну.

А от сили гідростатичного тиску \(\overrightarrow{F}_1\) і \(\overrightarrow{F}_2,\) що відповідно діють на верхню і нижню грані кубика, одна одну не зрівноважують. Нижня грань перебуває на більшій глибині, ніж верхня, тому сила тиску \(\overrightarrow{F}_2,\) яка діє на нижню грань кубика, більша за силу тиску \(\overrightarrow{F}_1,\) що діє на верхню грань. Рівнодійна цих сил дорівнює різниці значень сил \(\overrightarrow{F}_2\) і \(\overrightarrow{F}_1\) і напрямлена в бік дії більшої сили, тобто вертикально вгору.

Правильний варіант відповіді ‒ Б.

3. Сила пружності ‒ це сила, яка виникає під час деформації тіла й напрямлена протилежно напрямку зміщення частин цього тіла в процесі деформації. Сила пружності є проявом дії міжмолекулярних сил.

У твердих тілах частинки коливаються біля положень рівноваги й взаємодіють міжмолекулярними силами притягання і відштовхування. У положеннях рівноваги ці сили зрівноважені. У разі деформації тіла у взаємному розташуванні його частинок виникають певні зміни.

Якщо відстань між частинками зростає, то міжмолекулярні сили притягання стають сильнішими за сили відштовхування.

Якщо ж частинки зближуються, то сильнішими стають міжмолекулярні сили відштовхування.

Іншими словами: у разі деформації частинки прагнуть відновити положення рівноваги. Сили, що виникають у разі зміни положення однієї частинки, дуже малі. Однак коли ми деформуємо тіло, то змінюється взаємне розташування величезної кількості частинок. Додавання сил дає помітну рівнодійну, яка протидіє деформації тіла. Це і є сила пружності.

Правильний варіант відповіді ‒ А.

4. Невагомість ‒ це відсутність ваги. Приберіть у тіла опору або підвіс ‒ і воно опиниться в стані невагомості. Опір повітря теж є своєрідною опорою. Невагомість ‒ це такий стан тіла, за якого тіло не діє на опору чи підвіс. Тіло поблизу поверхні Землі перебуває в стані невагомості, якщо на нього діє тільки одна сила ‒ сила тяжіння. На короткий час невагомість легко створити вдома, на вулиці, в класі тощо. Ви можете, наприклад, підстрибнути і на мить опинитися в стані невагомості: у такому разі, поки ви падаєте, опір повітря є нехтовно малим, тож можна вважати, що на вас діє лише сила тяжіння.

Постійно в стані невагомості перебувають космічні орбітальні станції і все, що в них є. Це пов’язано з тим, що космічні кораблі «постійно падають» на Землю через її притягання і водночас залишаються на орбіті завдяки своїй величезній швидкості.

Падіння тіл у безповітряному просторі лише під дією сили тяжіння називають вільним падінням.

Експериментально було доведено, що швидкість будь-якого тіла, яке вільно падає, щосекунди збільшується приблизно на \(9,8\ \text{м/с}.\) Тобто всі тіла, що рухаються вертикально вгору або вниз, рухатимуться прямолінійно рівноприскорено з прискоренням вільного падіння \(9,8\ \text{м/с}^2.\)

Правильний варіант відповіді ‒ В.

Відповідь: 1Г, 2Б, 3А, 4В.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.

Завдання скеровано на перевірку знання і розуміння станів речовини та їхніх властивостей.

Рідина ‒ один із фазових (агрегатних) станів речовини. Молекули рідини в цілому розташовані хаотично, однак у розташуванні найближчих молекул зберігається певний (ближній) порядок. Під дією зовнішніх сил вона набуває форми тієї посудини, у якій міститься, а об’єм рідини залишається незмінним (1Д).

Розрідженим називають газ, тиск якого нижчий від атмосферного. Розріджений газ можна вважати ідеальним газом.

Ідеальний газ ‒ це фізична модель газу, молекули якого приймають за матеріальні точки, що не взаємодіють одна з одною на відстані й пружно взаємодіють у моменти зіткнення. Стан ідеального газу описують рівнянням Менделєєва – Клапейрона: \begin{gather*} pV=\frac mMRT, \end{gather*} де \(p\) ‒ тиск газу, \(V\) ‒ об’єм газу, \(m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(R\) ‒ універсальна газова стала, \(T\) ‒ температура газу. За умовою \(T=\mathrm{const},\) отже, в правій частині рівняння всі величини сталі. Залишімо в лівій частині рівняння лише тиск \(p:\) $$ p=\frac{mRT}{M\cdot V}\Rightarrow p\sim \frac 1V. $$

Дійсно, після перетворення рівняння видно, що тиск обернено пропорційний об’єму (2Г).

Монокристал ‒ тверде тіло, частинки якого утворюють єдину кристалічну ґратку. Упорядковане розташування частинок у монокристалі є причиною того, що монокристали мають плоскі грані й незмінні кути між гранями; фізичні властивості монокристалів залежать від вибраного в них напрямку. Залежність фізичних властивостей кристала від вибраного в ньому напрямку називають анізотропією (від грец. anisos ‒ нерівний і tropos ‒ напрямок, властивість). Отже, монокристали є анізотропними (3В).

Насиченою парою називають пару, яка перебуває в стані динамічної рівноваги зі своєю рідиною, тобто кількість молекул, які повертаються в рідину, дорівнюватиме кількості молекул, які за той самий час залишають рідину. Концентрація молекул насиченої пари ‒ найбільша можлива концентрація молекул пари за певної температури.

Тиск, створюваний насиченою парою, є найбільшим тиском, який може створити пара рідини за певної температури. Якщо зменшити об’єм, який займає насичена пара, то на короткий проміжок часу концентрація молекул пари збільшиться, динамічна рівновага порушиться і кількість молекул, що надходять у рідину, перевищить кількість молекул, які залишають її поверхню. Конденсація переважатиме над випаровуванням доти, доки концентрація молекул пари не зменшиться до концентрації молекул насиченої пари, а тиск не дорівнюватиме тиску насиченої пари. Зі збільшенням об’єму, який займає насичена пара, навпаки, переважатиме процес випаровування, і внаслідок цього знову встановиться початковий тиск. Отже, на відміну від ідеального газу, тиск насиченої пари не залежить від її об’єму (4Б).

Відповідь: 1Д, 2Г, 3В, 4Б.

Пояснення

ТЕМА: Електродинаміка. Основи електростатики. Закони постійного струму.

Завдання скеровано на перевірку знання і розуміння одиниць електродинамічних величин і їхнього фізичного змісту.

Одиниця електричного заряду \(q\) в SI ‒ кулон: $$ [q]=1\ \text{Кл}. $$

\(1\ \text{Кл}\) ‒ це заряд, який проходить через поперечний переріз провідника за \(1\ \text{с}\) за сили струму в провіднику \(1\ \text{А}\) (1Д).

Одиниця напруженості \(\overrightarrow{E}\) електричного поля в SI: $$ [E]=1\ \frac{\text{Н}}{\text{Кл}}. $$

Напруженість електричного поля \(\overrightarrow{E}\) в певній точці ‒ векторна фізична величина, якою характеризують електричне поле. Напруженість дорівнює відношенню сили \(\overrightarrow{F},\) з якою електричне поле діє на пробний заряд, поміщений у цю точку поля, до значення \(q\) цього заряду (2Б).

Одиниця потенціалу \(\mathbf{\varphi}\) в SI ‒ вольт: $$ [\mathbf{\varphi}]=1\ \text{В}=1\ \frac{\text{Дж}}{\text{Кл}}. $$

Потенціал \(\mathbf{\varphi}\) електростатичного поля в певній точці ‒ це скалярна фізична величина, якою характеризують енергетичні властивості поля. Потенціал дорівнює відношенню потенціальної енергії \(W_p\) електричного заряду, поміщеного в певну точку поля, до значення \(q\) цього заряду (3А).

Одиниця електричного опору \(R\) в SI ‒ ом: $$ [R]=1\ \text{Ом}=1\ \frac{\text{В}}{\text{А}}. $$

\(1\ \text{Ом}\) ‒ це опір такого провідника, у якому за напруги на кінцях \(1\ \text{В}\) сила струму дорівнює \(1\ \text{А}\) (4В).

Відповідь: 1Д, 2Б, 3А, 4В.

Пояснення

ТЕМА: Квантова фізика. Елементи теорії відносності. Фотоефект. Радіоактивність. Методи реєстрації йонізувального випромінювання.

Завдання скеровано на перевірку знання і розуміння відкриттів (винаходів).

Відкриття явища радіоактивності ‒ А. Беккерель (Д)

Історія відкриття радіоактивності почалася з відкриття рентгенівського випромінювання. Поштовхом до досліджень стало припущення, що рентгенівське випромінювання може виникати внаслідок флуоресценції деяких речовин, опромінених сонячним світлом. Такою речовиною і скористався французький фізик Анрі Антуан Беккерель (1852–1908) у лютому 1896 р. Для досліджень він випадково вибрав здатну до флуоресценції маловідому сіль Урану. Було з’ясовано, що уранова сіль дійсно висилає випромінювання, яке має велику проникну здатність. Сіль Урану сама, без впливу зовнішніх чинників, висилає невидиме випромінювання. Пізніше таке випромінювання назвуть радіоактивним випромінюванням; здатність речовин до радіоактивного випромінювання ‒ радіоактивністю; а нукліди, ядра яких мають таку здатність, ‒ радіонуклідами.

Відкриття трьох видів радіоактивного випромінювання ‒ Е. Резерфорд (В)

Ернест Резерфорд експериментально встановив (1899), що солі Урану випромінюють три типи променів, які по-різному відхиляються в магнітному полі:
– промені першого типу відхиляються так само, як потік додатно заряджених частинок; їх назвали альфа-променями;
– промені другого типу відхиляються в магнітному полі так само, як потік негативно заряджених частинок (у протилежну сторону); їх назвали бета-променями;
– промені третього типу, які не відхиляються магнітним полем, назвали гамма-променями.

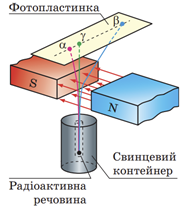
Створення приладу, за допомогою якого можна спостерігати траєкторію руху зарядженої частинки ‒ Ч. Вільсон (Г)

Загальний принцип реєстрації йонізувального випромінювання полягає в реєстрації дії, яку чинить це випромінювання.

Камера Вільсона ‒ це трековий детектор. Вона являє собою ємність, заповнену парою спирту або ефіру. Коли поршень різко опускають, то внаслідок адіабатного розширення пара охолоджується і стає перенасиченою. Коли в перенасичену пару потрапляє заряджена частинка, на своєму шляху вона йонізує молекули пари ‒ отримані йони стають центрами конденсації. Ланцюжок крапель cконденсованої пари, який утворюється вздовж траєкторії руху частинки (трек частинки), знімають на камеру або фотографують.

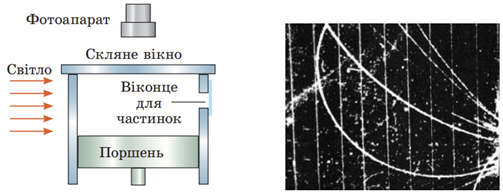
Створення теорії фотоефекту ‒ А. Ейнштейн (Б)

Зовнішній фотоефект відкрив 1887 року німецький фізик Генріх Герц. Детальніше це явище дослідив Олександр Столєтов. У досліді він використав вакуумну камеру з двома електродами (катод і анод) усередині, на які подають напругу від джерела постійного струму. Під дією світла, яке потрапляє в камеру через спеціальне віконце, катод випромінює електрони. Рухаючись від катода до анода в електричному полі, електрони створюють фотострум. Якщо збільшувати напругу на електродах, сила фотоструму теж зросте. Змінюючи почергово інтенсивність і частоту світла, що падає на катод, а також матеріал катода, О. Столєтов сформулював три закони зовнішнього фотоефекту. Але лише більш як через 20 років завдяки своєму рівнянню для зовнішнього фотоефекту А. Ейнштейн зміг пояснити всі закони фотоефекту. Саме ідею М. Планка про кванти використав Ейнштейн для пояснення законів фотоефекту. За пояснення явища фотоефекту А. Ейнштейн одержав найвищу наукову нагороду ‒ Нобелівську премію (1921 р.).

Відповідь: 1Д, 2В, 3Г, 4Б.

Пояснення

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей. Рівномірний рух.

Завдання скеровано на перевірку знання і розуміння прямолінійного рівномірного руху, а також вміння додавати швидкості.

Для того щоб визначити час \(t,\) протягом якого пасажир бачитиме зустрічний поїзд, треба знати довжину \(l\) (дана в умові) і швидкість \(v\) руху цього поїзда відносно пасажира. Визначмо її.

Скористаймося законом додавання швидкостей: швидкість \(\overrightarrow{v}\) руху тіла в нерухомій системі відліку дорівнює геометричній сумі швидкості \(\overrightarrow{v}_\text{рух}\) руху тіла в рухомій системі відліку й швидкості \(\overrightarrow{v}_\text{нерух}\) руху рухомої системи відліку відносно нерухомої: \begin{gather*} \overrightarrow{v}=\overrightarrow{v}_\text{рух}+\overrightarrow{v}_\text{нерух}. \end{gather*}

Оскільки рух і спокій є відносними, то відповідно до умови завдання як нерухому систему відліку можна вибрати й систему відліку, пов’язану з пасажиром, що сидить біля вікна у вагоні поїзда 1. У такому разі земля буде рухомою системою відліку, напрямок її руху буде протилежним до напрямку руху поїзда 1, а швидкість руху землі відносно поїзда 1 (із пасажиром) за модулем дорівнюватиме швидкості руху цього поїзда.

Введемо позначення: швидкість руху \(\overrightarrow{v}_{21}\) ‒ це буде швидкість руху поїзда 2 відносно поїзда 1 (пасажира) ‒ нерухомої системи відліку; швидкість руху \(\overrightarrow{v}_2\) ‒ це швидкість руху поїзда 2 в рухомій системі відліку, тобто відносно землі (та, яку дано в умові, \(45\ \text{км/год}\)); швидкість руху \(\overrightarrow{v}_1\) ‒ це швидкість рухомої системи відліку (землі) відносно нерухомої \((63\ \text{км/год}),\) тобто відносно поїзда 1:

Рух поїздів прямолінійний рівномірний, тож скористаймося відповідною формулою:

Відповідь: 10.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг рідин. Сила поверхневого натягу.

Завдання скеровано на перевірку знання і розуміння дії сили поверхневого натягу і вміння застосовувати другий закон Ньютона у відповідній ситуації.

Зобразимо на рисунку всі сили, що діють на дротинку: вертикально вниз ‒ сила тяжіння \(\overrightarrow{F}_\text{тяж}\) і сили поверхневого натягу \(\overrightarrow{F}_\text{пов}\) з обох боків дротинки як на рисунку; вертикально вгору ‒ прикладена зовнішня сила \(\overrightarrow{F}_\text{зовн}.\)

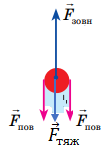
Щоб можна було відірвати дротинку від поверхні рідини, зовнішня сила, напрямлена вгору, повинна дорівнювати сумі сил, що напрямлені вертикально вниз: $$ F_\text{зовн}=F_\text{тяж}+2F_\text{пов}. $$

Запишімо вирази для зазначених сил і визначімо шукану величину ‒ поверхневий натяг рідини \(\mathbf{\sigma}:\)

де \(m\) ‒ маса дротинки, \(g\) ‒ прискорення вільного падіння, \(l\) ‒ довжина дротинки.

Відповідь: 45.

Пояснення

ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму. Коефіцієнт корисної дії електронагрівача.

Завдання скеровано на перевірку знання і розуміння фізичного змісту коефіцієнта корисної дії електричного нагрівача.

Коефіцієнт корисної дії \(\mathbf{\eta}\) показує, яка частина енергії \(Q_\text{ел. струму}\) електричного струму, що тече в електронагрівачі, становить корисно спожита кількість теплоти \(Q_\text{кор}\) (тут – кількість теплоти, яка пішла на нагрівання води): $$ \mathbf{\eta}=\frac{Q_\text{кор}}{Q_\text{ел. струму}}\cdot 100\ \text{%}. $$

Використаймо формули для розрахунку кількості теплоти, яку поглинає речовина під час нагрівання \(Q_\text{кор},\) і кількість теплоти \(Q_\text{ел. струму},\) яка виділяється в провіднику зі струмом: \begin{gather*} Q_\text{кор}=cm(t_2-t_1), \end{gather*} де \(c\) ‒ питома теплоємність води, \(m\) ‒ маса води, \(t_1\) і \(t_2\) ‒ початкова і кінцева температура води відповідно; $$ Q_\text{ел. струму}=I^2Rt=\frac{U^2t}{R}, $$ де \(I\) ‒ сила струму, \(U\) ‒ напруга, \(R\) ‒ опір, \(t\) ‒ час.

Відповідь: 84.

Пояснення

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рухому заряджену частинку.

На рухому заряджену частинку в магнітному полі діє сила Лоренца \(F_\text{Л}:\) $$ F_\text{Л}=|q|Bv\sin\mathbf{\alpha} $$ де \(|q|\) ‒ модуль заряду частинки, \(B\) ‒ магнітна індукція, \(v\) ‒ швидкість руху частинки, \(\mathbf{\alpha}\) ‒ кут між напрямком руху частинки й напрямком магнітної індукції магнітного поля.

За умовою частинка рухається перпендикулярно до ліній магнітної індукції.

У цьому разі \(\mathbf{\alpha}=90^\circ\)  \((\overrightarrow{v}\perp \overrightarrow{B}),\) тому \(F_\text{Л}=|q|Bv,\) адже \(\sin\mathbf{\alpha}=1.\) Частинка масою \(m\) рухається рівномірно по колу радіуса \(R\) перпендикулярно до ліній магнітної індукції, а сила Лоренца надає частинці доцентрового прискорення \(\overrightarrow{a}_\text{дц}.\)

За другим законом Ньютона: \begin{gather*} F_\text{Л}=ma_\text{дц},\\[6pt] |q|Bv=m\frac{v^2}{R},\\[6pt] v=\frac{|q|BR}{m}. \end{gather*}

Ми виразили з рівняння швидкість, тому що кінетична енергія \(E_k\) залежить від неї: $$ E_k=\frac{mv^2}{2}=\frac m2\cdot \left(\frac{|q|BR}{m}\right)^2. $$

За умовою після проходження частинки крізь фольгу радіус треку зменшився вдвічі, тож формула для швидкості матиме вигляд: $$ v_1=\frac{|q|BR}{2m}, $$ а кінетична енергія \(E_{k1}\) після зміни радіуса дорівнюватиме:

Тоді можемо визначити, яку частину кінетичної енергії втратила частинка під час проходження крізь фольгу:

тобто частинка втратила три чверті кінетичної енергії.

Відповідь: 0,75.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла.

Завдання скеровано на перевірку знання і розуміння прямолінійного поширення світла, законів відбивання світлових променів від плоского дзеркала й уміння розв’язувати задачі, використовуючи комбінації кутів.

Промінь, що падає під кутом \(\mathbf{\varphi}=50^\circ\) до горизонту ‒ \(AO.\) Зробімо додаткову побудову перпендикуляра \(CO\) до поверхні дзеркала. За законами відбивання $$ \angle AOC=\angle COD. $$

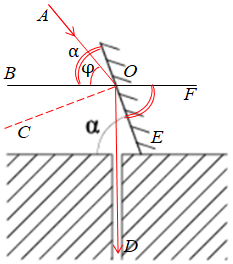
Складімо рівняння для визначення кута нахилу дзеркала до горизонту ‒ кута \(\mathbf{\alpha},\) комбінуючи кути на рисунку:

\(\angle EOF=\mathbf{\alpha}\) ‒ як вертикальні. Оскільки \(\angle AOC=\angle COD,\) то \begin{gather*} \mathbf{\alpha}=140^\circ-\mathbf{\alpha},\\[7pt] 2\mathbf{\alpha}=140^\circ,\\[7pt] \mathbf{\alpha}=70^\circ. \end{gather*}

Відповідь: 70.

Пояснення

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Лазер.

Завдання скеровано на перевірку знання і розуміння енергії фотона й уміння визначати потужність випромінювання лазера.

Потужність \(P\) випромінювання лазера визначають за формулою: $$ P=\frac{E_\text{ф}}{t}, $$ де \(E_\text{ф}\) ‒ енергія світлового потоку, що випромінює лазер, \(t\) ‒ час випромінювання.

Енергія \(E_1\) одного фотона становить: $$ E_1=h\mathbf{\nu}=\frac{hc}{\mathbf{\lambda}}, $$ де \(h\) ‒ стала Планка, \(\mathbf{\nu}\) ‒ частота випромінювання, \(c\) ‒ швидкість поширення світла у вакуумі, \(\mathbf{\lambda}\) ‒ довжина хвилі.

Тоді енергія всіх \(N\) фотонів, що випускає лазер щосекунди, дорівнюватиме: $$ E_\text{ф}=E_1\cdot N=\frac{hc\cdot N}{\mathbf{\lambda}}. $$

Обчислімо потужність випромінювання лазера:

Відповідь: 2,2.