ЗНО онлайн 2011 року з фізики – основна сесія

ТЕМА: Механіка. Основи кінематики. Додавання швидкостей. Рівномірний рух.

Завдання скеровано на перевірку знання і розуміння прямолінійного рівномірного руху, а також вміння додавати швидкості.

Щоб визначити швидкість руху товарного потяга, треба зрозуміти, як було визначено час \(t,\) протягом якого пасажирський потяг проходив повз зустрічний товарний потяг. Рух потягів прямолінійний рівномірний, тож скористаймося відповідною формулою: $$ t=\frac lv. $$

Уявімо, як голови потягів порівнялися, й із цього моменту пішов відлік часу.

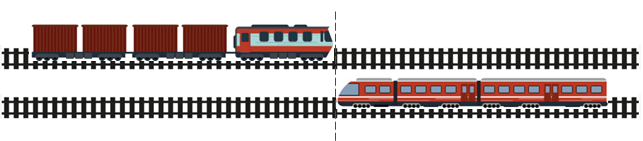
Щоб потяги повністю розминулися, голова пасажирського потяга повинна пройти вздовж усього товарного, а потім ще весь пасажирський потяг повинен пройти повз хвіст товарного потяга.

Тож загальний шлях \(l,\) який пройде голова пасажирського потяга з моменту, коли голови потягів порівнялися і до моменту, коли порівняються їхні хвости, становитиме суму довжин обох потягів ‒ пасажирського \(l_\text{п}\) і товарного \(l_\text{т}:\) $$ l= l_\text{п}+l_\text{т}. $$

Якщо потяги рухалися один відносно одного, то й швидкість їхнього руху треба розглядати не відносно землі, а відносно один одного.

Скористаймося законом додавання швидкостей: швидкість \(\overrightarrow{v}\) руху тіла в нерухомій системі відліку (пасажирського потяга відносно товарного) дорівнює геометричній сумі швидкості \(\overrightarrow{v}_\text{п}\) руху тіла в рухомій системі відліку (пасажирського потяга відносно землі) і швидкості \(\overrightarrow{v}_\text{т}\) руху рухомої системи відліку відносно нерухомої (наче землі відносно товарного потяга, що те саме ‒ товарного потяга відносно землі): $$ v=v_\text{п}+v_\text{т}. $$

Запишімо ще раз формулу для часу й визначмо швидкість товарного потяга:

Відповідь: А.

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу в рівномірному й рівноприскореному рухах.

Завдання скеровано на перевірку знання і розуміння графічної інтерпретації шляху, пройденого тілом.

Шлях чисельно дорівнює площі фігури під графіком швидкості руху:

для прямолінійного рівномірного руху	для прямолінійного рівноприскореного руху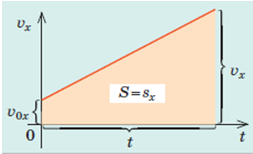
для будь-якого руху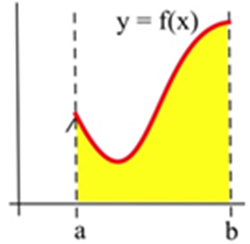

Отже, розгляньмо й порівняймо площі фігур під графіками швидкості руху тіл А, Б, В й Г. Відповідно до умови обмежмо праворуч ці фігури вертикальною прямою, що пройде через позначку \(6\ \text{с}\) на осі часу. А знизу й ліворуч фігури обмежено осями. Тоді розмір площі залежатиме тільки від графіка залежності проєкції швидкості руху тіла від часу. Зробімо висновок:

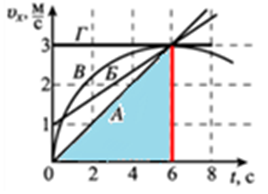найменший шлях пройде тіло А	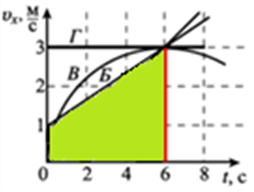шлях, який пройшло тіло Б
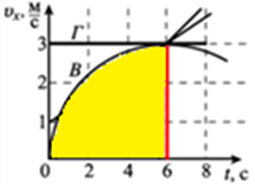шлях, який пройшло тіло В	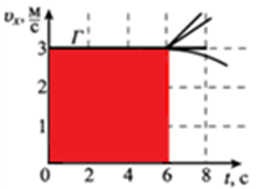найбільший шлях пройде тіло Г

Відповідь: Г.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.

Завдання скеровано на перевірку знання і розуміння поняття рівнодійної сил, а також вміння графічно пов’язати динаміку й кінематику процесу.

Сформулюймо другий закон Ньютона: прискорення \(\overrightarrow{a},\) якого набуває тіло внаслідок дії сили \(\overrightarrow{F},\) прямо пропорційне цій силі й обернено пропорційне масі \(m\) тіла: $$ \overrightarrow{a}=\frac{\overrightarrow{F}}{m}. $$

Здебільшого на тіло діють кілька сил. Якщо тіло можна вважати матеріальною точкою, то всі ці сили можна замінити однією – рівнодійною. Рівнодійна дорівнює геометричній сумі сил, які діють на тіло: $$ \overrightarrow{F}=\overrightarrow{F}_1+\overrightarrow{F}_2+\text{...}+\overrightarrow{F}_n, $$ тому другий закон Ньютона зазвичай записують так: \begin{gather*} \overrightarrow{a}=\frac{\overrightarrow{F}_1+\overrightarrow{F}_2+\text{...}+\overrightarrow{F}_n}{m},\\[6pt] \text{aбо}\\[7pt] \overrightarrow{F}_1+\overrightarrow{F}_2+\text{...}+\overrightarrow{F}_n=m\overrightarrow{a}. \end{gather*}

Якщо сили, що діють на тіло, скомпенсовано, тобто рівнодійна дорівнює нулю $$ \overrightarrow{F}_1+\overrightarrow{F}_2+\text{...}+\overrightarrow{F}_n=0, $$ тіло не змінюватиме швидкості свого руху ані за значенням, ані за напрямком: $$ \overrightarrow{a}=0, $$ отже, рухатиметься рівномірно прямолінійно або перебуватиме в спокої.

Графіком проєкції швидкості \(v_x\) у разі прямолінійного рівномірного руху є відрізок прямої, паралельної осі часу \(t,\) адже швидкість руху не змінюється із часом. Отже, у завданні цій умові відповідає ділянка графіка \(BC.\)

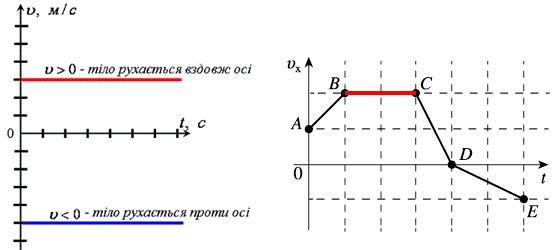
Відповідь: Б.

ТЕМА: Механіка. Закони збереження в механіці. Прості механізми. Коефіцієнт корисної дії.

Завдання скеровано на перевірку знання і розуміння простих механізмів ‒ рухомого і нерухомого блоків, а також уміння визначати коефіцієнт корисної дії механізму для підйому вантажів.

Підйомний механізм складається з двох невагомих блоків: рухомий блок (рис. 1), до якого безпосередньо прикріплено вантаж, дає виграш у силі вдвічі, але програш у відстані теж удвічі; другий блок ‒ нерухомий (рис. 2), лише змінює напрямок дії сили.

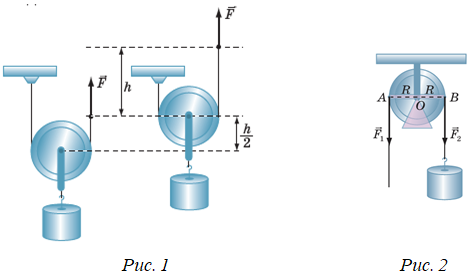
Коефіцієнт корисної дії \(\mathbf{\eta}\) (ККД) простого механізму – це відношення корисної роботи \(A_\text{кор},\) яку виконує механізм, до повної роботи \(A_\text{пов},\) яка витрачається на його роботу. Тобто це міра ефективності механізму, що показує, яка частина витраченої енергії перетворюється на корисну роботу: $$ \mathbf{\eta}=\frac{A_\text{кор}}{A_\text{пов}}\cdot 100\ \text{%}. $$

У цьому завданні корисною роботою \(A_\text{кор}\) є підняття вантажу на висоту \(h\) за рахунок зміни потенціальної енергії \((E_{p0}-E_p)\) тіла: $$ A_\text{кор}=E_{p0}-E_p=mgh, $$ де \(m\) – маса вантажу, \(g\) ‒ прискорення вільного падіння, \(h\) – висота, на яку підіймають вантаж.

Загальне визначення механічної роботи (робота сили) \(A\) – це фізична величина, яка характеризує зміну механічного стану тіла й дорівнює добутку модуля сили \(F,\) модуля переміщення \(s\) і косинуса кута \(\mathbf{\alpha}\) між вектором сили й вектором переміщення: $$ A=Fs\cos\mathbf{\alpha}. $$

Отже, узявши до уваги, що вантаж підняли на висоту \(h\) від початкового положення, а мотузку підтягнули під дією прикладеної сили на \(2h,\) запишімо формулу для визначення повної роботи: $$ A=Fs\cos\mathbf{\alpha}=F2h, $$ \(\cos\mathbf{\alpha}=\cos 0^\circ=1,\) тому що вектор сили, що долає вагу вантажу, і вектор переміщення лежать на співнапрямлених прямих.

Обчислімо коефіцієнт корисної дії \(\mathbf{\eta}\) (ККД) цього підйомного механізму:

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Основи молекулярно-кінетичної теорії. Маса і розмір молекул. Концентрація.

Завдання скеровано на перевірку знання і розуміння графічної інтерпретації залежності фізичних величин, а саме, концентрації молекул газу від об’єму.

Концентрація \(n\) молекул газу ‒ фізична величина, яка дорівнює числу \(N\) молекул в одиниці об’єму \(V\) газу: $$ n=\frac NV. $$

Як бачимо з формули, концентрація обернено залежить від об’єму: $$ n\sim \frac 1V. $$

За умовою газ стискають в посудині, отже, об’єм зменшується (знаменник зменшується), значить, концентрація збільшується. При цьому кількість молекул газу не змінюється ‒ газ міститься в посудині, його стискають рухомим поршнем, про витік газу мова не йде, отже, зміна концентрації залежатиме тільки від зміни об’єму.

Така обернена залежність величин відповідає математичній функції $$ y=\frac 1x, $$ графіком якої є вітки гіперболи.

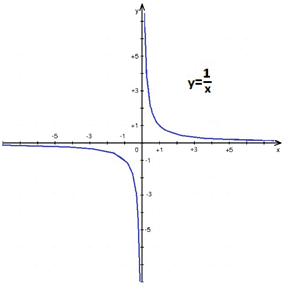
Відповідно, графіком залежності концентрації молекул газу від об’єму буде вітка гіперболи з додатними значеннями (об’єм і концентрація не можуть бути від’ємними).

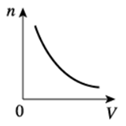
Графіки Б й В, які відображають лінійну залежність величин, не відповідають шуканій оберненій залежності. А за графіком Г зі збільшенням об’єму концентрація збільшується, що є неправильним у визначеній математичній залежності концентрації від об’єму.

Відповідь: A.

ТЕМА: Молекулярна фізика й термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку знання і розуміння зміни стану ідеального газу, а також вміння скласти рівність тисків.

Гелій до нагрівання мав певну температуру \(T_1\) і займав певний об’єм \(V_1.\) Цей газ створював тиск \(p\) на стінки посудини й на поршень. Зверху ж на рухомий поршень діє атмосферний тиск \(p_\text{атм},\) а також сам поршень теж діє з певним тиском \(p_\text{п}\) на гелій в посудині (див. рисунок).

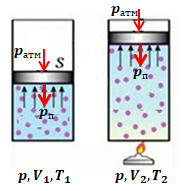
Отже, можемо прирівняти тиск, який створює гелій, і суму тисків атмосферного і поршня, оскільки поршень не рухається: $$ p=p_\text{атм}+p_\text{п}. $$

Розпишімо, чому дорівнює тиск гелію і тиск поршня. Відповідно до рівняння стану ідеального газу (рівняння Менделєєва ‒ Клапейрона) $$ pV_1=\frac mMRT_1, $$ де \(m\) ‒ маса газу, \(M\) ‒ молярна маса, \(R\) ‒ універсальна газова стала.

Тиск, який створює поршень, визначатимемо за формулою $$ p_\text{п}=\frac FS, $$ де \(S\) ‒ площа поверхні, на яку поршень створює тиск; а \(F=P=m_\text{п}g\) ‒ сила тиску, якою у цьому прикладі є вага \(P,\) що дорівнює добутку маси \(m_\text{п}\) поршня і прискорення \(g\) вільного падіння.

Потім за умовою гелій нагріли до температури \(T_2,\) відповідно збільшився об’єм до \(V_2.\) Тиск при цьому залишився сталим, оскільки маса газу не змінилася, а поршень легко рухається в посудині, тобто відбувся ізопроцес, а саме, ізобарне нагрівання: $$ pV_2=\frac mMRT_2. $$

Запишімо загальне рівняння зміни стану газу після зміни абсолютної температури на \(\Delta T\) і відповідно зміни об’єму на \(\Delta V:\) $$ p\Delta V=\frac mMR\Delta T, $$ звідки тиск дорівнюватиме $$ p=\frac{mR\Delta T}{M\Delta V}. $$

Підставімо всі вирази для відповідних величин у рівність тисків: $$ \frac{mR\Delta T}{M\Delta V}=p_\text{атм}+\frac{m_\text{п}g}{S}. $$

Обчислімо значення правої частини рівності, щоб математично легше було визначити зміну об’єму \(\Delta V:\)

Отже, визначмо, на скільки збільшиться об’єм гелію:

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку знання і розуміння ізопроцесів у газах і їхніх графіків.

Процес змінювання стану газу незмінної маси, що відбувається за сталого тиску \(p,\) називають ізобарним. Згідно з рівнянням Клапейрона $$ \frac{pV_1}{T_1}=\frac{pV_2}{T_2}, $$ де \(V_1\) і \(T_1\) ‒ об’єм й абсолютна температура газу в стані \(1;\) а \(V_2\) і \(T_2\) ‒ параметри газу в стані \(2.\) Після скорочення на \(p\) дістанемо: $$ \frac{V_1}{T_1}=\frac{V_2}{T_2}. $$

Графіки ізобарних процесів називають ізобарами. У координатах \(p, V\) ізобари перпендикулярні до осі тиску (див. рисунок).

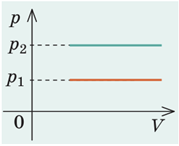
Отже, процесу за сталого тиску \((p=\mathrm{const})\) газу відповідає графік Г.

Графік А відповідає процесу за сталого об’єму \((V=\mathrm{const}):\)

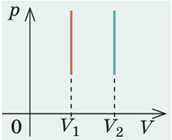
Графік Б ‒ це ізотерма, графік ізотермічного процесу \((T=\mathrm{const}):\)

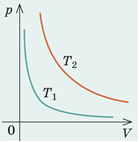
Проаналізувавши графік В, бачимо, що зростає й об’єм, і тиск, тож відповідно до рівняння Клапейрона підвищуватиметься температура: $$ \frac{pV}{T}=\mathrm{const}. $$

Відповідь: Г.

ТЕМА: Молекулярна фізика й термодинаміка. Основи термодинаміки. Питома теплоємність речовини.

Завдання скеровано на перевірку знання і розуміння питомої теплоємності речовини, а також зміни стану речовини.

Питома теплоємність речовини – це фізична величина, що характеризує речовину й чисельно дорівнює кількості теплоти, яку треба передати речовині масою \(1\ \text{кг},\) щоб нагріти її на \(1\ ^\circ\mathrm{С}.\) Питому теплоємність позначають символом \(c\) й визначають за формулою: $$ c=\frac{Q}{m\Delta T}, $$ де \(Q\) – кількість теплоти; \(m\) – маса речовини; \(\Delta T\) – зміна температури.

За умовою постійна потужність теплопередачі \(P,\) тож кількість теплоти, яку отримувала вода, визначмо за формулою $$ Q=A=P\Delta t, $$ де \(A\) – робота, виконана за проміжок часу \(\Delta t.\)

З’ясуймо, яка ділянка графіка відповідає рідкому стану води, тому що за умовою саме в цьому стані треба визначити питому теплоємність. Проаналізуймо графік. В умові зазначено, що в момент часу \(t=0\) с вода була у твердому стані (лід). Протягом проміжку часу \(\Delta t_1\) температура підвищувалася – лід нагрівався.

Потім протягом \(\Delta t_2\) температура залишалася незмінною. Це означає, що змінився агрегатний стан – після досягнення температури \(0\ ^\circ\mathrm{C}\) лід починає плавитися, а його температура не змінюється (горизонтальна ділянка графіка протягом \(\Delta t_2\)) незважаючи на те, що нагрівач продовжує працювати й передавати льоду певну кількість теплоти. Уся енергія, що надходить від нагрівника, іде на руйнування кристалічної ґратки льоду. У цей інтервал часу внутрішня енергія льоду продовжує збільшуватися.

Після перетворення всього льоду на воду (права крайня точка горизонтальної ділянки графіка протягом \(\Delta t_2\)), температура води починає зростати (ділянка графіка протягом \(\Delta t_3\)) і підвищується на \(\Delta T_2,\) тобто починає зростати кінетична енергія руху молекул. Саме для цієї ділянки обчислюватимемо питому теплоємність (наступна горизонтальна ділянка графіка протягом \(\Delta t_4\) відповідає фазовому переходу з рідкого стану в газуватий, а далі протягом \(\Delta t_5\) гріється утворена пара).

Отже, дістанемо вираз для визначення питомої теплоємності води в рідкому стані: $$ c=\frac{Q}{m\Delta T}=\frac{P\Delta t_3}{m\Delta T_2}. $$

Відповідь: B.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Поверхневий натяг рідин. Сила поверхневого натягу.

Завдання скеровано на перевірку знання і розуміння сили поверхневого натягу.

Крапля утримується біля невеликого отвору піпетки доти, доки сила поверхневого натягу більша за силу тяжіння, що діє на цю краплю. Маса краплі більшає, шийка краплі тоншає, і сила поверхневого натягу вже не може компенсувати дію сили тяжіння.

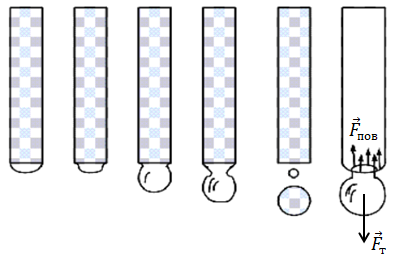
Відрив же станеться тоді, коли ці дві сили стануть рівними. Уважатимемо, що маса однієї краплі з умови завдання саме така, за якої крапля відривається від піпетки, а діаметр шийки краплі дорівнює діаметру отвору піпетки (за умовою): \begin{gather*} F_\text{пов}=F_\text{т},\\[7pt] \mathbf{\sigma}l=m_1g, \end{gather*} де \(\mathbf{\sigma}\) ‒ поверхневий натяг, \(l=2\mathbf{\pi}R\) ‒ лінія, що обмежує поверхню рідини; \(m_1=\frac MN\) ‒ маса однієї краплі, коли загальна маса \(N\) крапель становить \(M;\) \(g\) ‒ прискорення вільного падіння.

Визначмо поверхневий натяг рідини:

Відповідь: Б.

ТЕМА: Молекулярна фізика й термодинаміка. Властивості газів, рідин і твердих тіл. Кристалічні та аморфні тіла.

Завдання скеровано на перевірку знання і розуміння поділу твердих тіл за властивостями на кристалічні та аморфні.

У твердому кристалічному стані в речовині молекули розташовані в певному порядку (утворюють кристалічні ґратки) на відстанях, що приблизно дорівнюють розмірам самих молекул, тому сили міжмолекулярної взаємодії втримують їх біля положення рівноваги.

Зазначмо, що молекули деяких твердих тіл у цілому розташовані безладно. Такий стан речовини називають аморфним. Речовини в аморфному стані нагадують дуже в’язкі рідини. Якщо покласти в посудину кристалики солі, вони ніколи не зберуться в один великий кристал. А от якщо покласти в посудину шматочки смоли, яка є аморфною речовиною, то через кілька днів смола зілляється і набуде форми посудини.

На відміну від кристалічних, аморфні речовини не мають певної температури плавлення, а переходять у рідкий стан поступово розм’якшуючись. Аморфний стан речовин нестабільний ‒ поступово відбувається кристалізація.

Отже, перехід у рідкий стан відбувається різко тільки тілом, що складається з кристалічної речовини, після досягнення певної температури – температури плавлення.

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона.

Завдання скеровано на перевірку знання і розуміння того, від яких фізичних величин і як залежить сила Кулона.

Закон Кулона: сила \(F\) взаємодії двох нерухомих точкових зарядів \(q_1\) і \(q_2\) прямо пропорційна добутку модулів цих зарядів й обернено пропорційна квадрату відстані \(r\) між ними: $$ F=k\frac{|q_1|\cdot |q_2|}{r^2}, $$ де \(k\) ‒ коефіцієнт пропорційності.

Отже, якщо відстань між точковими зарядженими тілами зменшити в \(n\) разів, то сила \(F'\) кулонівської взаємодії між ними збільшиться в \(n^2\) разів:

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики. Робота електричного поля з переміщення заряду. Потенціал і різниця потенціалу.

Завдання скеровано на перевірку знання і розуміння закону збереження енергії під час переміщення заряду електричним полем.

Позитивно заряджена порошинка за умовою розганяється, тобто її кінетична енергія \(W_k\) збільшується. Відповідно до закону збереження енергії потенціальна енергія \(W_p\) порошинки в електростатичному полі зменшується, тож і потенціал \(\mathbf{\varphi}\) зменшується \((\mathbf{\varphi} \sim W_p).\) А серед варіантів відповіді є тільки одне значення потенціалу, яке менше за \(200\ \text{В}\), ‒ \(100\ \text{В}.\)

Скористаймося законом збереження енергії, щоб довести це розрахунками: \begin{gather*} W_{p1}+W_{k1}=W_{p2}+W_{k2},\\[6pt] q\mathbf{\varphi}_1+\frac{mv^2_1}{2}=q\mathbf{\varphi}_2+\frac{mv^2_2}{2}, \end{gather*} де \(\mathbf{\varphi}_1\) і \(\mathbf{\varphi}_2\) ‒ потенціали у відповідних до умови завдання точках поля, \(v_1\) і \(v_2\) ‒ швидкості порошинки у відповідних точках, \(q\) ‒ заряд порошинки, \(m\) ‒ маса порошинки.

Візьмімо до уваги, що за умовою \(v_1=0,\) а заряд порошинки позитивний \(q=+5\cdot 10^{-6}\ \text{Кл}.\) Отримаємо

Відповідь: A.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Залежність опору металів від температури. Залежність опору напівпровідників від температури.

Завдання скеровано на перевірку розуміння фізичної природи електричного струму в різних середовищах, а також залежності сили струму від температури.

Згідно з класичною електронною теорією модель внутрішньої будови металу – це утворені позитивно зарядженими йонами кристалічні ґратки, які перебувають у «газі» вільних електронів. Якщо в металевому провіднику створити електричне поле, то на хаотичний рух електронів накладеться дрейф електронів у напрямку сили, що діє на електрони з боку електричного поля. Цей дрейф електронів і є електричним струмом у металах. Якщо підвищувати температуру металевого провідника, то йони у вузлах кристалічної ґратки коливатимуться з більшою амплітудою, хаотичність руху електронів збільшиться, тож вони частіше зіштовхуватимуться з йонами. Відповідно опір (питомий опір) збільшуватиметься (див. графік), а сила струму зменшуватиметься за законом Ома для ділянки кола: $$ I=\frac UR, $$ де \(I\sim \frac 1R\) ‒ сила струму \(I,\) що обернено пропорційна до електричного опору \(R.\)

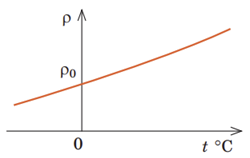
Якщо ж стержень з металу охолодити, то навпаки, його опір (питомий опір) зменшиться. Цю пряму залежність також можна бачити з формули залежності опору \(R\) металів від температури \(t:\) \begin{gather*} R=R_0(1+\mathbf{\alpha}t),\\[7pt] R\sim t, \end{gather*} де \(R_0\) ‒ опір провідника за температури \(0\ ^\circ\mathrm{C};\) \(\mathbf{\alpha}\) ‒ температурний коефіцієнт електричного опору.

Напівпровідники, як це випливає з їхньої назви, за своєю провідністю посідають проміжне місце між провідниками й діелектриками. Серед валентних електронів обов’язково є електрони, кінетична енергія яких достатня, щоб покинути зв’язки й стати вільними. Якщо напівпровідниковий кристал помістити в електричне поле, то вільні електрони рухатимуться до позитивного полюса джерела струму, тому в напівпровіднику виникне електричний струм. Якщо напівпровідник нагріти або опромінити світлом, кількість вільних електронів і дірок збільшиться, відповідно збільшиться і провідність напівпровідника. На відміну від металевих провідників питомий опір напівпровідників зазвичай зменшується з підвищенням температури (див. графік), відповідно, сила струму збільшується.

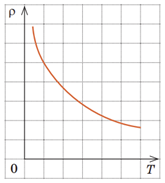
Якщо ж стержень із напівпровідника охолодити, то навпаки, його опір (питомий опір) збільшиться.

Відповідь: B.

ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.

Завдання скеровано на перевірку знання і розуміння електроємності конденсатора, того, від яких фізичних величин вона залежить.

Відношення заряду \(q\) конденсатора до різниці потенціалів \((\mathbf{\varphi}_1-\mathbf{\varphi}_2)\) між його обкладками не залежить ані від \(q,\) ані від \((\mathbf{\varphi}_1-\mathbf{\varphi}_2),\) а отже, може слугувати характеристикою конденсатора. Таку характеристику називають електроємністю конденсатора.

Електроємність конденсатора визначають за формулами: $$ C=\frac{q}{\mathbf{\varphi}_1-\mathbf{\varphi}_2},\ \text{або}\ C=\frac qU, $$ де \(U\) ‒ напруга між обкладками конденсатора, яка в цьому разі дорівнює різниці потенціалів між ними.

Значення заряду й напруги візьмімо з графіка в умові завдання: $$ q=4\cdot 10^{-4}\ \text{Кл},\ \ U=200\ \text{В}. $$

Обчислімо шукану величину ‒ електроємність конденсатора: $$ C=\frac{4\cdot 10^{-4}\ \text{Кл}}{200\ \text{В}}=2\cdot 10^{-6}\ \text{Ф}. $$

Відповідь: Г.

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.

Завдання скеровано на перевірку знання і розуміння, що таке діод і як він пропускає електричний струм, а також уміння читати електричні схеми.

Вакуумний діод має однобічну провідність. Буде проходити струм чи ні, залежить від того, як діод підключити в електричне коло:

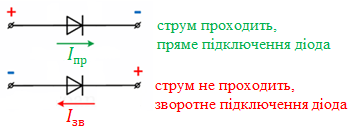
Зобразімо, як тече струм за початкових умов. Як бачимо, у цьому разі струм проходить через обидва діоди.

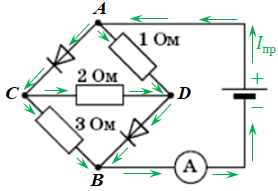
Для розуміння, того, як з’єднано резистори, зобразімо альтернативну схему. Оскільки за умовою опір діода вважаємо рівним нулю, то можна сумістити точки \(A\) й \(C\) та точки \(B\) й \(D.\) Матимемо паралельне з’єднання резисторів.

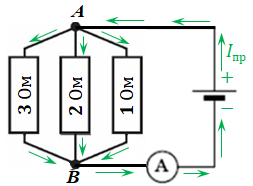
Загальний опір у разі паралельного з’єднання (внутрішнім опором джерела й амперметра нехтуємо відповідно до умови) становитиме:

Тоді напруга на джерелі струму за законом Ома дорівнюватиме:

Така ж напруга буде й коли змінимо полярність джерела. Нарисуймо, як проходитиме електричний струм за таких умов. Як бачимо, тепер резистори з’єднані послідовно, обидва діоди не пропускають струм:

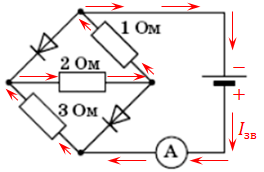
Визначмо загальний опір у разі послідовного з’єднання резисторів:

За законом Ома визначмо силу струму, що покаже амперметр за умови зміни полярності джерела:

Відповідь: А.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рухому заряджену частинку.

Силу, з якою магнітне поле діє на рухому заряджену частинку, називають силою Лоренца.

Сила Лоренца завжди перпендикулярна до швидкості руху частинки, тому вона не виконує роботу і не змінює кінетичну енергію частинки, ‒ під дією сили Лоренца заряджена частинка рухається рівномірно. Проте траєкторія руху частинки буде різною ‒ залежно від того, під яким кутом частинка влетіла в магнітне поле і чи є магнітне поле однорідним.

За умовою протон влітає в магнітне поле перпендикулярно до ліній магнітної індукції. У цьому разі $$ \mathbf{\alpha}=90^\circ(\overrightarrow{v}\ \perp\ \overrightarrow{B}). $$

Протон рухатиметься рівномірно по колу перпендикулярно до ліній магнітної індукції \(\overrightarrow{B},\) а сила Лоренца \(\overrightarrow{F}_\text{Л}\) надає йому доцентрового прискорення \(\overrightarrow{a}_\text{дц}.\)

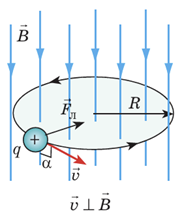
Відповідь: Б.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера. Електродвигун.

Завдання скеровано на перевірку знання і розуміння принципу дії електроприладів.

Силу, з якою магнітне поле діє на провідник зі струмом називають силою Ампера.

На плоский замкнений контур зі струмом, розташований в однорідному магнітному полі, сили Ампера створюють обертальний момент. Обертання рамки зі струмом у магнітному полі використовують в електричних двигунах ‒ пристроях, у яких електрична енергія перетворюється на механічну.

На рисунку зображено модель електричного двигуна.

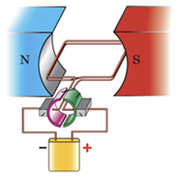
Реостат ‒ це пристрій зі змінним опором, призначений для регулювання сили струму в електричному колі. Змінюючи довжину провідника в реостаті, можна змінити його опір.

Лампа розжарювання ‒ це тип лампи, у якій світло випромінюється внаслідок нагрівання нитки розжарювання електричним струмом до високої температури.

Електрочайник ‒ це побутовий електричний прилад, призначений для швидкого нагрівання і кип’ятіння води за допомогою електричного нагрівального елемента (спіралі або диска), який розміщено всередині корпусу (теплова дія струму).

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Вимушені механічні коливання. Явище резонансу.

Завдання скеровано на перевірку знання і розуміння видів механічних коливань і їхніх характеристик.

Коливання ‒ це зміни стану системи біля певної точки рівноваги, які точно або приблизно повторюються із часом. За характером взаємодії з навколишніми тілами й полями розрізняють вільні коливання, вимушені коливання, автоколивання.

Вільні коливання ‒ це коливання, які відбуваються під дією внутрішніх сил системи й виникають після того, як систему виведено зі стану рівноваги. Амплітуда цих коливань із часом зменшується, і через певний інтервал часу, якщо немає надходжень енергії від зовнішнього джерела, коливання припиняються. Такі коливання називають згасними (затухаючими).

Вимушені коливання ‒ це коливання, які відбуваються в системі тільки під дією зовнішнього періодичного впливу. Під час вимушених коливань може виникнути явище резонансу ‒ різке збільшення амплітуди коливань у разі, якщо частота зовнішнього періодичного впливу збігається з власною частотою коливань системи. Амплітуда вимушених коливань визначається інтенсивністю зовнішнього періодичного впливу і з часом не змінюється. Такі коливання називають незгасними (незатухаючими).

Відповідь: B.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Явище самоіндукції.

Завдання скеровано на перевірку знання і розуміння явища самоіндукції.

Відразу після замкнення кола сила струму \(I\) в колі збільшується. Усередині котушки виникає змінне магнітне поле, магнітна індукція \(\overrightarrow{B}\) якого теж збільшується. Змінне магнітне поле створює вихрове електричне поле \(\overrightarrow{E},\) яке в цьому разі протидіятиме струму в котушці (правило Ленца).

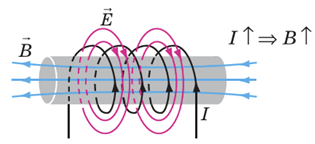
Саме тому сила струму в колі котушки (а отже, і в лампі \(2\)) зростатиме не відразу, а поступово. Зрозуміло, що в провідниках, які підводять струм до лампи \(1,\) також виникає вихрове електричне поле, але створена ним ЕРС є незначною.

Явище виникнення вихрового електричного поля в провіднику, у якому тече змінний електричний струм, називають самоіндукцією.

Електрорушійну силу індукції, що створюється в провіднику внаслідок зміни його власного магнітного поля, називають електрорушійною силою самоіндукції.

Отже, під час замикання ключа \(K\) лампа \(2\) загоряється пізніше, ніж лампа \(1,\) тому що в котушці виникає електрорушійна сила самоіндукції, що перешкоджає зростанню струму в ній.

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.

Завдання скеровано на перевірку знання і розуміння побудови зображень предмета в тонкій збиральній лінзі, а також вміння визначати потрібні величини за допомогою формули тонкої лінзи.

Для визначення відстані між лінзою та зображенням предмета скористаймося формулою тонкої лінзи: $$ \frac 1F=\frac 1d+\frac 1f, $$ де \(F\) ‒ фокусна відстань, \(d\) ‒ відстань від предмета до лінзи, \(f\) ‒ відстань від лінзи до зображення предмета.

Фізичну величину, яка характеризує лінзу та є оберненою до фокусної відстані \(F\) лінзи, називають оптичною силою лінзи \(D\) (для збиральної лінзи оптична сила додатна): $$ \frac 1F=D. $$

Запишімо формулу тонкої лінзи в такому вигляді: $$ D=\frac 1d+\frac 1f. $$

За умовою предмет розташовано в подвійному фокусі лінзи, оскільки \begin{gather*} F=\frac 1D=\frac{1}{2\ \text{дптр}}=0\mathord{,}5\ \text{м},\\[6pt] \text{а}\ d=1\ \text{м}=2F, \end{gather*} то зображення предмета буде дійсним, за розмірами дорівнюватиме предмету, перевернуте.

Оскільки зображення предмета дійсне, то відстань \(f\) (від лінзи до зображення) треба брати зі знаком \(+.\)

Визначмо відстань \(f\) між лінзою і зображенням предмета: \begin{gather*} D=\frac 1d+\frac 1f,\\[6pt] 2\ \text{дптр}=\frac{1}{1\ \text{м}}+\frac 1f,\\[6pt] \frac 1f=(2-1)\frac{1}{\text{м}},\\[6pt] f=1\ \text{м}. \end{gather*}

Отже, зображення отримаємо теж в подвійному фокусі лінзи, то $$ f=1\ \text{м}=2F. $$

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на перевірку знання і розуміння рівнянь гармонічних коливань.

Коливання, під час яких координата \(\mathbf{\chi}\) тіла, що коливається, змінюється із часом \(t\) за законом косинуса (або синуса), називають гармонічними коливаннями:

де \(A\) ‒ амплітуда коливань, \(\mathbf{\omega}\) ‒ циклічна частота коливань, \(\mathbf{\varphi}_0\) ‒ початкова фаза коливань.

Коли координата тіла змінюється за гармонічним законом (за законом косинуса або синуса), швидкість і прискорення руху тіла теж змінюються гармонічно: перша похідна координати тіла за часом \(\mathbf{\chi}'(t)\) ‒ це рівняння швидкості руху тіла, а друга похідна координати тіла по часу \(\mathbf{\chi}''(t)\) ‒ це рівняння прискорення руху тіла.

В умові завдання маємо гармонічне рівняння прискорення руху тіла. Підставивши в це рівняння значення часу \(t=\frac 56\ \text{с},\) зможемо визначити прискорення руху тіла в цей момент часу:

Проєкцію сили на вісь \(Ox,\) що діє на тіло масою \(m,\) можна тепер визначити за другим законом Ньютона:

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.

Завдання скеровано на перевірку знання і розуміння коли і як треба застосовувати формули релятивістської і класичної механіки.

Рух тіл зі швидкостями, порівнюваними зі швидкістю світла, розглядають у розділі фізики «Релятивістська механіка» й описують спеціальними формулами.

В умові завдання треба визначити вираз, за яким можна обчислити відстань між електронами через певний час. Тут достатньо скористатися формулою класичної механіки для обчислення відстані під час прямолінійного рівномірного руху: $$ l=vt. $$

Електрони рухаються в протилежних напрямках. Один із них відносно ядра за час \(t\) пролетить відстань: $$ l_1=v_1t=0\mathord{,}8c\cdot t. $$

Другий електрон за час \(t\) пролетить відносно ядра ту саму відстань, однак у протилежному напрямку: $$ l_2=v_2t=0\mathord{,}8c\cdot t. $$

Загальна відстань між ними через час \(t\) становитиме: $$ l=l_1+l_2=0\mathord{,}8ct+0\mathord{,}8ct=1\mathord{,}6ct. $$

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.

Завдання скеровано на перевірку знання і застосування правил альфа- і бета-розпадів.

Запишімо реакцію розпаду ядра атома Торію \(^{230}_{\ \ 90}\mathrm{Th},\) зваживши, що відбулося чотири \(\mathbf{\alpha}\text{-розпади}\) й один \(\mathbf{\beta}\text{-розпад}\): $$ ^{230}_{\ \ 90}\mathrm{Th}\rightarrow\ ^A_Z\mathrm{X}+4\cdot\ ^4_2\mathrm{He}+1\cdot ^{\ \ \ 0}_{-1}e, $$ де \(^A_Z\mathrm{X}\) ‒ ізотоп шуканого елемента, \(^4_2\mathrm{He}\) ‒ \(\mathbf{\alpha}\text{-частинка},\) \(^{\ \ \ 0}_{-1}e\) ‒ \(\mathbf{\beta}\text{-частинка}.\)

Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.

Пригадаймо також правила зміщення для \(\mathbf{\alpha}-\) і \(\mathbf{\beta}\text{-розпадів}.\)

Під час \(\mathbf{\alpha}\text{-розпаду}\) (випромінення ядра атома Гелію \(^4_2\mathrm{He}\)) кількість нуклонів у ядрі зменшується на \(4,\) протонів ‒ на \(2,\) тому утворюється ядро елемента \(\mathrm{X}_2,\) порядковий номер якого на \(2\) одиниці менший від порядкового номера ядра елемента \(\mathrm{X}_1,\) що розпадається: $$ ^A_Z\mathrm{X}_1\rightarrow\ ^4_2\mathrm{He}+\ ^{A-4}_{Z-2}\mathrm{X}_2. $$

Під час \(\mathbf{\beta}\text{-розпаду}\) (випромінення електрона \(_{-1}^{\ \ \ 0}e\)) кількість нуклонів у ядрі не змінюється, водночас кількість протонів збільшується на \(1,\) тому утворюється ядро елемента \(\mathrm{X}_2,\) порядковий номер якого на одиницю більший за порядковий номер вихідного елемента \(\mathrm{X}_1:\) $$ ^A_Z\mathrm{X}_1\rightarrow\ ^{\ \ \ 0}_{-1}e+\ ^{\ \ \ \ \ A}_{Z+1}\mathrm{X}_2. $$

Тепер відповідно до закону збереження електричного заряду й закону збереження енергії-маси, а також правил зміщення визначімо \(\mathrm{A}\) ‒ нуклонне (масове) й \(\mathrm{Z}\) ‒ протонне (зарядове) числа ізотопа елемента \(\mathrm{X}:\)

Отже, унаслідок такого розпаду ізотопа Торію утворився ізотоп Бісмуту \(^{214}_{\ \ 83}\mathrm{Bi}.\)

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на перевірку знання і розуміння фізичних величин, що описують фотоефект.

Фотоефектом називають явище взаємодії світла з речовиною, яке супроводжується випромінюванням (емісією) електронів.

Для кожної речовини існує максимальна довжина світлової хвилі $$ \mathbf{\lambda}_\text{max}=\mathbf{\lambda}_\text{черв} $$ (червона межа фотоефекту), за якої починається фотоефект. Опромінення речовини світловими хвилями, які мають більшу довжину, фотоефекту не викликає.

Максимальна довжина світлової хвилі (мінімальна частота) відповідає мінімальній енергії фотона: якщо $$ h\mathbf{\nu}\lt A_\text{вих}, $$ то електрони не вилітатимуть із речовини. Умова $$ h\mathbf{\nu}_\text{min}=\frac{hc}{\mathbf{\lambda}_\text{max}}=A_\text{вих} $$ визначає червону межу фотоефекту. Це значення найчастіше лежить у червоній частині видимого спектру.

Термін «червона межа» увів А. Столєтов, який усебічно дослідив фотоефект наприкінці XIX ст. Третій закон Столєтова стверджує, що для кожної речовини є деяка мінімальна частота фотонів, нижче якої фотоефект зникає.

Саме червоною межею фотоефекту визначено використання червоного освітлення під час друкування фотографій у першій половині XX ст. і раніше. Червона межа фотоефекту матеріалів того часу лежала в жовтій області видимого світла.

Тому фотопластинки проявляли за червоного освітлення. Згодом почали використовувати матеріали з меншою роботою виходу, червона межа фотоефекту для них перемістилася в інфрачервону область, і проявляли їх у повній темряві.

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на перевірку знання і розуміння поступального й обертального руху; а також уміння визначати суму векторів за правилом паралелограма й формулою діагоналі.

Розгляньмо рух кожної точки колеса машини одночасно як рівномірний поступальний рух і рівномірний обертальний рух відносно центра колеса з лінійною швидкістю \(\overrightarrow{v}_\text{об}.\)

Напрямок вектора швидкості \(\overrightarrow{v}_\text{пост}\) поступального руху збігається з напрямком руху машини \(\overrightarrow{v},\) тому для всіх точок колеса цей напрямок однаковий (на рисунку його позначено векторами зеленого кольору). Для кожної точки колеса поступальна швидкість дорівнює швидкості руху самої машини: $$ \overrightarrow{v}_\text{пост}=\overrightarrow{v}. $$

Поступальна швидкість завжди напрямлена горизонтально вправо, як зображено на рисунку.

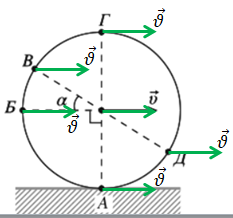
А вектор лінійної швидкості обертального руху \(\overrightarrow{v}_\text{об}\) напрямлений по дотичній, побудованій у кожній точці колеса (на рисунку його позначено векторами червоного кольору).

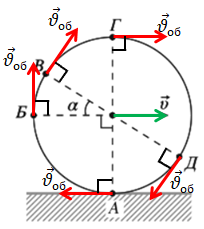
Скористаймося законом додавання швидкостей для визначення швидкості будь-якої точки колеса відносно Землі: $$ \overrightarrow{v}_\text{точки}=\overrightarrow{v}_\text{пост}+\overrightarrow{v}_\text{об} $$

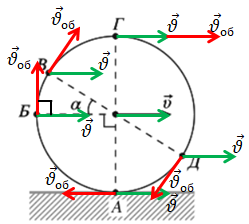
За умовою колесо машини рухається без проковзування, тож швидкість точки \(A,\) що стикається з дорогою, дорівнюватиме нулю: $$ v_A=0\ (\text{відповідь 1}) $$

Отже, швидкість поступального руху дорівнює лінійній швидкості обертального руху за модулем. Дійсно, для точки A швидкості руху \(\overrightarrow{v}_\text{пост}\) і \(\overrightarrow{v}_\text{об}\) лежать на одній прямій, напрямлені в протилежні боки й рівні за модулем, тож сума цих векторів дорівнює нулю. Тобто можемо записати, що $$ v_\text{пост}=v_\text{об}=v, $$ як ми довели на початку розв’язання. Тоді $$ \overrightarrow{v}_\text{точки}=\overrightarrow{v}+\overrightarrow{v}. $$

Точка Б: як видно з рисунка, вектори швидкостей розміщені під прямим кутом. На цих векторах можна добудувати квадрат, тобто скористатися правилом паралелограма. І тоді діагональ квадрата це сума векторів за цим правилом. Скористаймося теоремою Піфагора:

Точка Г: вектори лежать на одній прямій і напрямлені в один бік:

Для точок В й Д скористаймося і правилом паралелограма, і формулою визначення довжини діагоналі \(d\) паралелограма:

$$ d=\sqrt{a^2+b^2+2ab\cos\mathbf{\alpha}} $$ (\(a\) та \(b\) ‒ сторони паралелограма; \(\mathbf{\alpha}\) ‒ кут між сторонами \(a\) та \(b\) паралелограма).

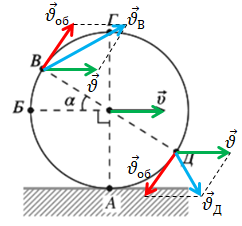
(кут між векторами визначмо з рисунка за побудовою; \(\cos⁡(90^\circ-\mathbf{\alpha})=\sin\mathbf{\alpha}\) ‒ за формулами зведення).

Підставімо відповідно до умови значення кута й визначмо швидкість точки В:

Точка Д:

Відповідь: 1А, 2Д, 3Б, 4В.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Магнітне поле, електромагнітна індукція.

Завдання скеровано на перевірку вміння застосовувати теоретичні знання з електродинаміки для пояснення принципу дії відповідних технічних пристроїв.

1. Лампа розжарювання є прикладом прояву теплової дії струму (Д): унаслідок проходження електричного струму спіраль лампи дуже сильно нагрівається. Узагалі робота всіх електричних нагрівачів ґрунтується на тепловій дії струму: у таких пристроях енергія електричного струму перетворюється на внутрішню енергію нагрівача.

2. В основі принципу дії генератора змінного струму лежить явище електромагнітної індукції (В). Це явище полягає в тому, що внаслідок зміни магнітного потоку, який пронизує провідник, у провіднику виникає електричний струм. У генераторі змінного струму обертається котушка (ротор) у магнітному полі. Завдяки цьому відбувається зміна магнітного потоку, що пронизує котушку, і, як наслідок, виникає змінна електрорушійна сила (ЕРС) і змінний струм. Виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється, ‒ це наслідок електромагнітної індукції, практично важливий для генерації електричного струму.

3. Посудину з високою стійкістю до впливів кислот, лугів і розчинників, у якій відбувається електроліз, називають електролітичною ванною (електролізером). Проходження електричного струму крізь розчин або розплав електроліту зумовлює хімічні реакції на поверхні поділу електрод ‒ розчин (розплав електроліту). Отже, хімічна дія струму (Г) проявляється під час його проходження крізь розчин електроліту, який міститься в електролітичній ванні.

4. Принцип дії компаса заснований на взаємодії магнітного поля постійних магнітів (А) компаса з горизонтальною складовою магнітного поля Землі. Обертова магнітна стрілка вільно повертається навколо осі, розташовуючись уздовж силових ліній магнітного поля. Тож стрілка завжди вказує одним кінцем у напрямку ліній магнітної індукції, що йдуть до Південного магнітного полюса (Північного географічного полюса).

Відповідь: 1Д, 2В, 3Г, 4А.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на перевірку знання і розуміння рівнянь гармонічних коливань.

Коливання, під час яких координата \(\mathbf{\chi}\) тіла, що коливається, змінюється із часом \(t\) за законом косинуса (або синуса), називають гармонічними коливаннями:

де \(A\) ‒ амплітуда коливань, \(\mathbf{\omega}\) ‒ циклічна частота коливань, \(\mathbf{\varphi}_0\) ‒ початкова фаза коливань.

З умови відоме рівняння гармонічних коливань: $$ \mathbf{\chi}=0\mathord{,}4\cos\left(4\mathbf{\pi}t+\frac{\mathbf{\pi}}{3}\right). $$

1. Амплітуда. Множник перед функцією косинуса ‒ це і є амплітудне (максимальне) значення координати \(\mathbf{\chi}\) тіла ‒ \(0\mathord{,}4\ \text{м}\) (Г).

2. Початкова фаза. Це фаза коливань у момент початку відліку часу ‒ це доданок під знаком функції косинуса, який не помножено на час ‒ \(\frac{\mathbf{\pi}}{3}\) (Б).

3. Період. Знаючи з рівняння циклічну частоту \(\mathbf{\omega}\) коливань, що множиться на час у доданку під знаком функції косинуса, можна визначити період коливань \(T:\) \begin{gather*} \mathbf{\omega}=\frac{2\mathbf{\pi}}{T},\\[6pt] T=\frac{2\mathbf{\pi}}{\mathbf{\omega}}=\frac{2\mathbf{\pi}}{4\mathbf{\pi}}=\frac 12=0\mathord{,}5\ \text{c}\ \text{(А)}. \end{gather*}

4. Циклічна частота. Ми вже взяли з рівняння в умові значення циклічної частоти в попередньому пункті 3 ‒ це множник біля \(t\) ‒ \(4\mathbf{\pi}\frac{1}{c}\) (Д).

Відповідь: 1Г, 2Б, 3А, 4Д.

ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.

Завдання скеровано на перевірку знання і розуміння абсолютного показника заломлення середовища.

Фізичну величину, яка характеризує оптичну густину середовища й показує, у скільки разів швидкість поширення світла в середовищі \((v)\) менша, ніж його швидкість \((c)\) у вакуумі, називають абсолютним показником \(n\) заломлення середовища: $$ n=\frac cv. $$

Звідси можемо визначити швидкість поширення світла в середовищі \(v,\) а потім узявши до уваги зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою), зможемо обчислити потрібні характеристики світлових хвиль, що поширюються в зазначених в умові завдання середовищах:

Формулу, що зв’язує довжину хвилі \(\mathbf{\lambda},\) швидкість \(v\) її поширення і частоту \(\mathbf{\nu},\) називають формулою хвилі: $$ v=\mathbf{\lambda}\mathbf{\nu}. $$

Обчислімо добутки довжини хвилі \(\mathbf{\lambda}\) й частоти \(\mathbf{\nu},\) щоб установити відповідність із середовищем:

Відповідь: 1В, 2Б, 3А, 4Г.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Період і частота.

Завдання скеровано на перевірку знання і розуміння періоду обертання і його залежності від певних характеристик руху, а також застосування другого закону Ньютона для визначення його.

На супутник, що рухається коловою орбітою навколо планети, діє лише сила тяжіння \(\overrightarrow{F}_\text{т}\) ‒ сила, з якою Земля (або інше астрономічне тіло) притягує до себе тіла, що перебувають на її поверхні або поблизу неї.

Запишімо рівняння другого закону Ньютона (\(\overrightarrow{F}\) ‒ рівнодійна сил, що діють на супутник):

де \(m\) ‒ маса тіла (супутника), \(a_\text{дц}\) ‒ доцентрове прискорення, оскільки рух супутника є рівномірним рухом по колу; \(g\) ‒ прискорення вільного падіння.

Масу в рівнянні можна скоротити, а для доцентрового прискорення і прискорення вільного падіння запишімо відповідні формули: $$ a_\text{дц}=\frac{v^2}{R}, $$ (де \(v\) ‒ лінійна швидкість руху тіла по колу, \(R\) ‒ радіус кола). $$ g=G\frac{M}{R^2}, $$ (де \(G\) ‒ гравітаційна стала, \(M\) ‒ маса Землі або іншої планети, \(R\) ‒ радіус Землі або іншої планети).

Як отримуємо формулу для прискорення вільного падіння:

‒ за законом всесвітнього тяжіння $$ F_\text{т}=G\frac{mM}{(R+h)^2}=G\frac{mM}{R^2}, $$ (де \(h\) ‒ висота, на якій перебуває тіло над поверхнею Землі або іншої планети; якщо \(h\lt\lt R,\) то радіус планети і радіус колової орбіти можна прирівняти);

‒ за формулою для сили тяжіння \(F_\text{т}= mg.\)

Прирівняймо праві частини цих формул й отримаємо формулу для прискорення вільного падіння: \begin{gather*} G\frac{mM}{R^2}=mg,\\[6pt] g=G\frac{M}{R^2}. \end{gather*}

Повернімося до другого закону Ньютона:

Лінійну швидкість \(v\) рівномірного руху тіла по колу визначаємо за періодом обертання і радіусом колової траєкторії. Для рівномірного руху швидкість визначмо як відношення шляху \(l\) до часу \(t:\) $$ v=\frac <. $$

Дійсно, за час \(t\) одного оберту, тобто період \(T,\) тіло долає відстань \(l,\) що дорівнює довжині кола: $$ l=2\mathbf{\pi}R, $$ тоді $$ v=\frac <=\frac{2\mathbf{\pi}R}{T}. $$

Отже,

Звідси період обертання $$ T=\sqrt{\frac{4\mathbf{\pi}^2R^3}{GM}}. $$

Визначмо співвідношення періодів обертання штучних супутників планет \(Z\) і Земля, зваживши на те, що за умовою $$ M_Z=2M_3 $$ (відношення мас планет), $$ d_Z=\frac 12 d_3 $$ (відношення діаметрів планет), отже, $$ R_Z=\frac 12R_3. $$

Отже, період обертання супутника навколо планети \(Z\) учетверо менший за період обертання супутника навколо Землі.

Відповідь: \(0\mathord{,}25.\)

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу. Реактивний рух.

Завдання скеровано на перевірку знання і розуміння закону збереження імпульсу, реактивного руху.

Застосуємо закон збереження імпульсу до наведеного в завданні прикладу реактивного руху.

Реактивний рух ‒ це рух, що виникає внаслідок відділення з деякою швидкістю від тіла якоїсь його частини.

За умовою завдання відділятиметься ядро від школяра, хоча до цього і школяр, і ядро в нього в руках були в спокої.

Запишімо закон збереження імпульсу у векторній формі: $$ m_1\overrightarrow{v}_1+m_2\overrightarrow{v}_2=m_1\overrightarrow{v'}_1+m_2\overrightarrow{v'}_2, $$ де \(m_1\) і \(m_2\) ‒ маси школяра та ядра відповідно, \(\overrightarrow{v}_1\) і \(\overrightarrow{v}_2\) ‒ швидкості руху школяра та ядра відповідно до поштовху ядра, \(\overrightarrow{v'}_1\) і \(\overrightarrow{v'}_2\) ‒ швидкості руху школяра і ядра відповідно після поштовху ядра.

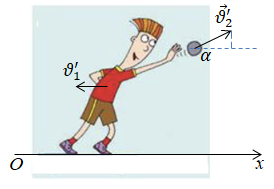
Тепер запишімо цей закон у проєкціях на горизонтальну вісь \(Ox:\) $$ 0=-m_1v'_1+m_2v'_2\cos\mathbf{\alpha}. $$

Визначмо швидкість школяра:

Відповідь: \(0\mathord{,}4.\)

ТЕМА: Молекулярна фізика й термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу. Ізопроцеси в газах. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку знання і розуміння ізопроцесів і вміння визначати роботу газу.

Проаналізуймо кожен процес циклу.

Процес \(1\rightarrow 2\) ‒ це процес ізобарного нагрівання (тиск \(p=\mathrm{const},\) абсолютна температура ідеального газу підвищується \(T_2\gt T_1,\) відповідно об᾽єм збільшується \(V_2\gt V_1\)). Запишімо рівняння Менделєєва ‒ Клапейрона: $$ (p\Delta V)_{1-2}=\mathbf{\nu}R(T_2-T_1), $$ де \(\mathbf{\nu}\) ‒ кількість речовини, \(R\) ‒ універсальна газова стала.

Робота \(A_{1-2}\) газу внаслідок цього ізобарного розширення дорівнюватиме добутку тиску \(p\) й зміни об’єму \(\Delta V:\)

Оскільки \(T_1=T,\) а \(T_2=3T\) (де \(T\) ‒ одиничний відрізок ‒ дивись рисунок), то:

Процес \(2\rightarrow 3\) ‒ це ізотермічний процес \((T=\mathrm{const}).\) Відповідно до рівняння Клапейрона \begin{gather*} p_2V_2=p_3V_3,\\[7pt] p_3\lt p_2\Rightarrow V_3\gt V_2. \end{gather*} Це процес ізотермічного розширення.

Процес \(3\rightarrow 4\) ‒ це процес ізобарного охолодження (тиск \(p=\mathrm{const},\) абсолютна температура ідеального газу спадає \(T_4\lt T_3,\) відповідно об’єм теж зменшується \(V_4\lt V_3\)). Запишімо рівняння Менделєєва ‒ Клапейрона: $$ (p\Delta V)_{3-4}=\mathbf{\nu}R(T_4-T_3). $$

Робота \(A_{3-4}\) газу внаслідок цього ізобарного стиснення також дорівнюватиме добутку тиску \(p\) і зміни об’єму \(\Delta V:\)

Оскільки \(T_3=3T,\) а \(T_4=T\) (де \(T\) ‒ одиничний відрізок ‒ див. рисунок), то:

Робота \(A_{3-4}\) є від’ємною, оскільки

Процес \(4\rightarrow 1\) ‒ це ізотермічний процес \((T=\mathrm{const}).\) Відповідно до рівняння Клапейрона

Це процес ізотермічного стиснення.

Обчислімо співвідношення абсолютних значень робіт \(A_{1-2}\) й \(A_{3-4}:\)

Відповідь: \(1\).

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола. Послідовне та паралельне з᾽єднання провідників.

Завдання скеровано на перевірку знання і розуміння паралельного і послідовного з’єднання провідників, а також уміння застосовувати закон Ома для ділянки кола й формули, що описують ці з’єднання.

Визначмо напругу \(U_3\) на резисторі \(3\) за законом Ома для ділянки кола: \begin{gather*} U_3=I_3R_3,\\[7pt] U_3=20\cdot 10^{-3}\ \text{А}\cdot 30\ \text{Ом}=0\mathord{,}6\ \text{В}. \end{gather*}

Це і є напруга на клемах джерела струму, оскільки за паралельного з’єднання на обидві вітки електричного кола ‒ там, де резистори \(1, 2, 4,\) і на вітку, де резистор \(3,\) ‒ буде подано однакову напругу від джерела струму: \begin{gather*} U=U_3=U_{124}. \end{gather*}

Розгляньмо тепер з’єднання резисторів \(1, 2\) й \(4.\) Резистори \(1\) і \(2\) з’єднано між собою паралельно, а резистор \(4\) приєднано до них послідовно. Визначивши загальний опір цієї ділянки кола, зможемо обчислити силу струму, який проходить через цю вітку кола:

Це й буде сила струму \(I_4=I_{124},\) що проходитиме крізь резистор \(4,\) оскільки його послідовно з’єднано з резисторами \(1\) і \(2\) (сила струму \(I_{124}=0\mathord{,}01\ \text{А}\) між якими пропорційно поділиться).

Отже, знаючи з умови опір резистора \(4,\) і визначивши силу струму в ньому, можемо обчислити напругу на цьому резисторі:

Відповідь: \(0\mathord{,}4.\)

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Закон електромагнітної індукції.

Завдання скеровано на перевірку знання і розуміння закону електромагнітної індукції.

Скористаймося законом електромагнітної індукції: електрорушійна сила індукції \(\mathbf{\varepsilon}_i\) дорівнює швидкості зміни магнітного потоку \(\frac{\Delta Ф}{\Delta t},\) який пронизує поверхню, обмежену контуром: $$ \mathbf{\varepsilon}_i=\frac{\Delta Ф}{\Delta t}. $$

Знак мінус відображає правило Ленца: індукційний струм, який виникає в замкненому провідному контурі, має такий напрямок, що створений цим струмом магнітний потік перешкоджає зміні магнітного потоку, який спричинив появу індукційного струму.

Відповідно до рисунка, за \(30\ \text{мс}\) магнітний потік змінився від \(60\ \text{мВб}\) до \(180\ \text{мВб}.\) Обчислімо модуль електрорушійної сили, що індукується в контурі: $$ \mathbf{\varepsilon}_i= \frac{(180-60)\cdot 10^{-3}\ \text{Вб}}{30\cdot 10^{-3}\ \text{с}}=4\ \text{В}. $$

Відповідь: \(4.\)

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на перевірку знання і розуміння гармонічних коливань і їхніх характеристик, а також вміння визначати їх.

Коливання, під час яких координата \(y\) тіла, що коливається, змінюється із часом \(t\) за законом косинуса (або синуса), називають гармонічними коливаннями:

де \(A\) ‒ амплітуда коливань, \(\mathbf{\omega}\) ‒ циклічна частота коливань, \(\mathbf{\varphi}_0\) ‒ початкова фаза коливань.

Тоді рівняння гармонічних коливань маятника автомобіля матиме загальний вигляд: $$ y=y_\text{max}\sin\mathbf{\omega} t. $$

Робимо висновок, що іграшковий автомобіль рухається прямолінійно рівномірно вздовж осі \(Ox\) (див.  рисунок). Тоді для визначення проєкції швидкості \(v_x\) руху цього автомобіля скористаймося формулою $$ v_x=\frac{\Delta x}{\Delta t}, $$ де \(\Delta x\) ‒ відстань, яку пройде автомобіль за час \(\Delta t.\)

Період коливань \(T\) ‒ це час \(\Delta t,\) за який хвиля поширюється на відстань \(\Delta x,\) що називають довжиною цієї хвилі; або довжина хвилі \(\mathbf{\lambda}\) ‒ це відстань між двома найближчими точками, які коливаються синхронно.

З графіка візьмемо дві синхронні точки по осі \(Ox\) ‒ \(0\ \text{см}\) і \(20\ \text{см},\) тоді

Для математичного (нитяного) маятника період коливань \(T\) можна визначити за формулою $$ T=2\mathbf{\pi}\sqrt{\frac lg}, $$ де \(l\) ‒ довжина маятника, \(g\) ‒ прискорення вільного падіння.

Обчислімо швидкість руху автомобіля: $$ v_x=\frac{\Delta x}{\Delta t}=\frac{0\mathord{,}2\ \text{м}}{0\mathord{,}628\ \text{с}}\approx 0\mathord{,}32\ \text{м/с}. $$

Відповідь: \(0\mathord{,}32.\)

ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає плоске дзеркало.

Завдання скеровано на перевірку знання і розуміння побудови зображення в плоскому дзеркалі.

Загальні характеристики зображень у плоских дзеркалах:

1. Плоске дзеркало дає уявне зображення предмета.

2. Зображення предмета в плоскому дзеркалі й сам предмет є симетричними відносно поверхні дзеркала, і це означає:

1) зображення предмета дорівнює за розміром самому предмету;

2) зображення предмета розташоване на тій самій відстані від поверхні дзеркала, що й предмет;

3) відрізок, який сполучає точку на предметі з відповідною їй точкою на зображенні, є перпендикулярним до поверхні дзеркала.

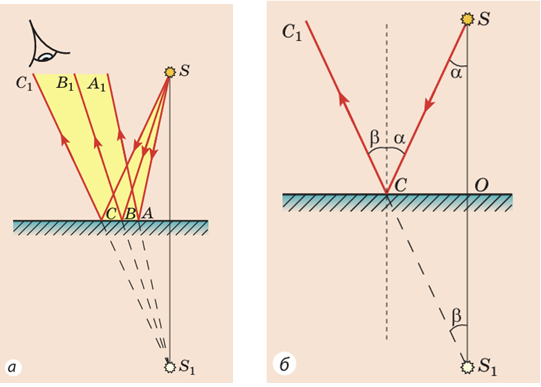
Отримання зображення точкового джерела світла
в плоскому дзеркалі: \(S\) ‒ джерело світла; \(S_1\) ‒ уявне зображення джерела світла.

Якщо між дзеркалами \(1\) і \(2\) помістити лампу \(A,\) то промені від неї потраплятимуть на дзеркала, багато разів відбившись від них, розходитимуться, даючи щоразу на своєму продовженні уявні зображення (рис. 1).

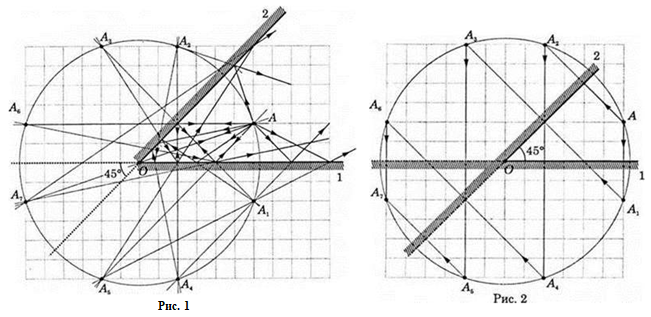
Для побудови зображення в системі з двох дзеркал достатньо уявно продовжити їхні площини після перетину й будувати зображення відносно кожної площини дзеркал окремо, уважаючи, що утворене одним дзеркалом зображення можна вважати предметом для другого ‒ принцип Гюйгенса. Усього в дзеркалах, установлених під кутом \(45^\circ\) один до одного, утворюється сім зображень (рис. 2). Точка \(A\) й усі її зображення розташовані по колу з радіусом \(OA\) із центром у точці перетину
дзеркал \(O.\)

Відповідь: \(7.\)