ЗНО онлайн 2014 року з фізики – пробний тест

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Доцентрове прискорення.

Завдання скеровано на перевірку знання і розуміння рівномірного руху матеріальної точки по колу і доцентрового прискорення.

Рівномірний рух тіла по колу ‒ це такий криволінійний рух, за якого траєкторією руху тіла є коло, а лінійна швидкість руху не змінюється із часом.

У разі рівномірного руху тіла по колу вектор прискорення напрямлений до центра кола ‒ саме тому прискорення рівномірного руху тіла по колу називають доцентровим прискоренням \(\overrightarrow{a}_\text{дц};\) модуль доцентрового прискорення обчислюють за формулою \begin{gather*} a_\text{дц}=\frac{v^2}{R}, \end{gather*} де \(v\) ‒ лінійна швидкість; \(R\) ‒ радіус кола.

Переведімо значення швидкості в систему SI: $$ 18\frac{\text{км}}{\text{год}}=18\cdot\frac{1000\ \text{м}}{3600\ \text{с}}=5\frac{\text{м}}{\text{с}}. $$

Обчислимо шукану величину ‒ доцентрове прискорення: $$ a_\text{дц}=\frac{(5\ \text{м/с})^2}{10\ \text{м}}=2,5\ \text{м/с}^2. $$

Відповідь: В.

ТЕМА: Механіка. Основи динаміки. Додавання сил. Другий закон Ньютона.

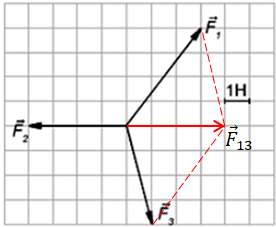
Завдання скеровано на перевірку знання і розуміння рівнодійної сил, прикладених до тіла, і вміння її знаходити за допомогою геометричної побудови.

Здебільшого (як в умові) на тіло діють кілька сил. Якщо тіло можна вважати матеріальною точкою, то всі ці сили можна замінити однією ‒ рівнодійною. Рівнодійна дорівнює геометричній сумі сил, які діють на тіло: $$ \overrightarrow{F}=\overrightarrow{F}_1+\overrightarrow{F}_2+\overrightarrow{F}_3. $$

Суму двох векторів визначають за правилом паралелограма або за правилом трикутника.

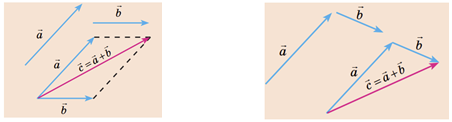
Візьмімо, наприклад, пару векторів \(\overrightarrow{F}_1\) і \(\overrightarrow{F}_3\) й добудуємо на них паралелограм, як на рисунку:

Діагональ, яка виходить із точки, у якій збігаються початки вибраних векторів, буде їхньою рівнодійною \(\overrightarrow{F}_{13}.\)

З рисунка зрозуміло, що вектор сили \(\overrightarrow{F}_2\) і вектор \(\overrightarrow{F}_{13}\) лежать на одній прямій і напрямлені в різні боки. До того ж вони однакової довжини, тобто рівні за модулем. Отже, ці сили компенсують одна одну. Тобто їхня рівнодійна дорівнює нулю: $$ F=F_2-F_{13}=0\ \text{Н}. $$

Відповідь: A.

ТЕМА: Механіка. Основи динаміки. Рух тіл під дією кількох сил.

Завдання скеровано на перевірку розуміння того, які сили діють на тіло, уміння описати стан тіла за допомогою другого закону Ньютона.

Зображена система зв’язаних брусків не рухатиметься, якщо сили натягу нитки на обох її кінцях, створені кожним бруском, однакові.

Зобразімо на рисунку сили, що діють уздовж поверхонь похилих площин і які впливатимуть на стан системи брусків. Це проєкції сил тяжіння \((m_1\overrightarrow{g}\ \text{i}\ m_2\overrightarrow{g})\) і сил натягу нитки (\(\overrightarrow{T}_1=\overrightarrow{T}_2=\overrightarrow{T},\) оскільки бруски з’єднано спільною ниткою). Проєкції сил, перпендикулярних до поверхонь похилих площин (сили нормальної реакції опори \(\overrightarrow{N}_1\ \text{i}\ \overrightarrow{N}_2\) і вага \(\overrightarrow{P}_1\ \text{i}\ \overrightarrow{P}_2\)), скомпенсовані й на рух системи тіл не впливають.

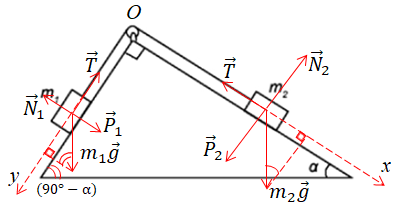
Запишімо другий закон Ньютона для обох брусків у проєкціях на осі вздовж поверхонь похилих площин:

Прирівняймо вирази для сили натягу нитки й визначімо співвідношення мас:

Відповідь: B.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.

Завдання скеровано на перевірку знання і вміння застосовувати закон збереження імпульсу.

Скористаймося законом збереження імпульсу для системи двох куль: $$ \overrightarrow{p}_1+\overrightarrow{p}_2=\overrightarrow{p}^{\ \ '}_1+\overrightarrow{p}^{\ \ '}_2, $$ де \(\overrightarrow{p}_1\) і \(\overrightarrow{p}_2\) ‒ імпульси куль до зіткнення, \(\overrightarrow{p}^{\ \ '}_1\) і \(\overrightarrow{p}^{\ \ '}_2\) ‒ імпульси куль після зіткнення відповідно.

Якщо після зіткнення частина кінетичної енергії перетворюється на внутрішню енергію (витрачається на деформацію і нагрівання тіл), таке зіткнення називають непружним. Непружне зіткнення, після якого тіла рухаються як єдине ціле, називають абсолютно непружним.

Спроєктуймо вектори імпульсів цього рівняння на горизонтальну вісь, що напрямлена вздовж напрямку руху, наприклад, першої кулі й, відповідно, руху криголама разом із крижиною після зіткнення: $$ p_1-p_2=0, $$ \(p'_1+p'_2=(m_1+m_2)\cdot v'=0,\) оскільки після зіткнення обидві кулі зупинилися за умовою (швидкість після зіткнення \(v'=0\)).

Запишімо загальний імпульс системи куль до зіткнення:

Отже, зміна загального імпульсу системи куль унаслідок зіткнення дорівнюватиме нулю.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти.

Завдання скеровано на перевірку знання і розуміння перетворення кількості теплоти в інший вид енергії.

Унаслідок утраченої мідною кулькою внутрішньої енергії виділилася певна кількість теплоти \(Q:\) \begin{gather*} Q=cm\Delta t, \end{gather*} де \(c\) ‒ питома теплоємність міді, з якої зроблена кулька, \(m\) ‒ маса кульки, \(\Delta t\) ‒ зміна температури.

Під час підняття кульки на певну висоту \(h\) збільшиться її потенціальна енергія \(E_p\) від нуля до якогось значення: $$ E_p=mgh, $$ де \(g\) ‒ прискорення вільного падіння.

За умовою на підняття кульки витратиться \(1\ \text{%}\) від кількості теплоти, що виділиться: \begin{gather*} 0,01\cdot Q=E_p,\\[7pt] 0,01\cdot cm\Delta t=mgh,\\[7pt] 0,01\cdot c\Delta t=gh. \end{gather*}

Виразімо звідси \(h\) й обчислімо її:

Відповідь: A.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку знання і розуміння ізопроцесів в газах і вміння будувати й читати графіки відповідних ізопроцесів.

В умові завдання є графік ізобарного процесу ‒ для газу деякої маси відношення об’єму газу до температури є незмінним, якщо тиск газу не змінюється \((p=\mathrm{const}):\) \begin{gather*} \frac{V_1}{T_1}=\frac{V_2}{T_2},\\[6pt] \text{або}\ \frac VT=\mathrm{const}=\frac mM\cdot \frac Rp. \end{gather*}

Збільшуючи чисельник (об’єм), треба в стільки ж разів збільшувати знаменник (абсолютну температуру), щоб значення дробу було незмінним.

Графік ізобарного процесу називають ізобарою. Як випливає із закону Ґей-Люссака, за незмінного тиску об’єм газу даної маси прямо пропорційний його температурі: \begin{gather*} V=\mathrm{const}\cdot T,\\[6pt] \text{або}\ T=\mathrm{const}\cdot V. \end{gather*}

Графіком цієї залежності в координатах \(T,\ V\) є пряма, що проходить через початок координат (див. рисунок в умові). Аналізуючи графік, доходимо висновку, що з наближенням до абсолютного нуля об’єм ідеального газу має зменшитися до нуля. Зрозуміло, що це неможливо, оскільки реальні гази за низьких температур перетворюються на рідини.

У координатах \(p,\ V\) і \(p,\ T\) ізобари перпендикулярні до осі тиску. Єдиний рисунок із варіантів відповіді, на якому зображено графік \(p=\mathrm{const}\) ‒ варіант В:

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Змочування.

Завдання скеровано на розуміння того, як поводиться змочувальна або незмочувальна рідина в капілярах.

Унаслідок зіткнення з твердим тілом сферична форма краплі здебільшого не зберігається. Форма вільної поверхні рідини залежить від сил взаємодії молекул чи інших структурних частинок рідини зі структурними частинками твердого тіла.

Якщо сили взаємодії між структурними частинками рідини більші, ніж сили взаємодії між структурними частинками рідини та твердого тіла, рідина не змочує поверхню твердого тіла. Наприклад, ртуть не змочує скло, а вода не змочує вкриту сажею поверхню.

Крапелька ртуті розтечеться по поверхні цинкової пластинки, а крапелька води – на скляній поверхні. Отже, якщо сили взаємодії між структурними частинками рідини менші від сил взаємодії між молекулами рідини і твердого тіла, то рідина змочує поверхню твердого тіла.

За умовою крапля рідини розпливається тонким шаром по скляній поверхні, отже, змочує цю поверхню. Тому змочуватиме й вертикальний скляний капіляр.

Що тонший капіляр, то вище підніматиметься в ньому рідина. Рівень рідини в капілярі не може бути нижчим від загального рівня рідини в посудині, у яку капіляр уставлено.

Оскільки рідина змочує стінки капіляра, то біля його стінок вона набуватиме ввігнутої форми і ззовні, і зсередини.

Отже, єдиний правильний із-поміж наведених – рисунок А: рідина в капілярі піднялася вище від загального рівня, а вода і ззовні, і зсередини змочує скло.

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду.

Завдання скеровано на перевірку вміння застосовувати закон збереження електричного заряду.

Закон збереження електричного заряду: повний заряд електрично замкненої системи тіл залишається незмінним під час усіх взаємодій, які відбуваються в цій системі: $$ q_1+q_2+\dots +q_n=\mathrm{const}, $$ де \(q_1,\ q_2,\ \dots ,\ q_n\) ‒ заряди тіл, які утворюють систему; \(n\) ‒ кількість тіл.

За умовою

Отже, після з’єднання кульок тонким провідником заряд перерозподілиться порівну між кульками, і заряд кульки \(1\) дорівнюватиме заряду кульки \(2:\)

Відповідь: B.

ТЕМА: Електродинаміка. Основи електростатики. З’єднання конденсаторів.

Завдання скеровано на перевірку знання і розуміння з’єднання конденсаторів, уміння визначати їхні характеристики.

Енергію \(W\) зарядженого до напруги \(U\) конденсатора (батареї конденсатора), який має електроємність \(C_\text{заг}\) і заряд \(Q,\) обчислюють так: $$ W=\frac{Q^2}{2C_\text{заг}}. $$

Визначімо загальний заряд \(Q\) і загальну електроємність \(C_\text{заг}\) батареї двох конденсаторів (саме ці величини зазначено в умові).

У разі паралельного з’єднання конденсаторів позитивно заряджені обкладки всіх конденсаторів з’єднують в один вузол, а негативно заряджені ‒ в інший вузол (див. рисунок).

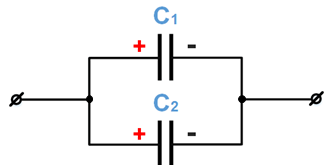
У такому разі загальний заряд \(Q\) батареї конденсаторів дорівнює алгебричній сумі зарядів окремих конденсаторів: $$ Q=q_1+q_2, $$ де \(q_1\) і \(q_2\) ‒ заряд першого і другого конденсаторів відповідно.

За умовою заряд першого конденсатора дорівнює \(q_1=q,\) а другий конденсатор незаряджений, тобто \(q_2=0.\) Тоді загальний заряд батареї $$ Q=q. $$

З’єднані в один вузол обкладки є одним провідником, тому потенціали обкладок і різниця потенціалів (напруга \(U\)) між обкладками всіх конденсаторів однакові: $$ U=U_1=U_2. $$

Отже, за паралельного з’єднання конденсаторів допустима робоча напруга батареї визначена робочою напругою одного конденсатора. Візьмемо до уваги, що \begin{gather*} Q=C_\text{заг}U,\\[7pt] q_1=C_1U,\\[7pt] q_2=C_2U. \end{gather*}

Тому $$ C_\text{заг}U=C_1U+C_2U. $$

А загальна електроємність \(C_\text{заг}\) батареї з двох паралельно з’єднаних конденсаторів $$ C_\text{заг}=C_1+C_2. $$

Зважаючи, що електроємності конденсаторів рівні $$ C_1=C_2=C, $$ загальна електроємність $$ C_\text{заг}=2C. $$

Визначімо енергію електричного поля утвореної системи конденсаторів: $$ W=\frac{Q^2}{2C_\text{заг}}=\frac{q^2}{2\cdot 2C}=\frac{q^2}{4C}. $$

Відповідь: Б.

ТЕМА: Електродинаміка. Закони постійного струму. Джерела струму.

Завдання скеровано на перевірку знання і розуміння будови та принципу дії гальванічного елемента.

Гальванічний елемент – це хімічне джерело живлення, у якому використовують різницю електродних потенціалів двох металів (варіант В неправильний), занурених в електроліт.

Гальванічний елемент з лимона й двох дротів ‒ це простий пристрій, у якому використовують хімічну реакцію між металами та лимонною кислотою для створення електричного струму.

Хімічна реакція розпочинається не відразу, тож є змога виміряти і напругу, і силу струму. Тому цей гальванічний елемент миттєво не розрядиться.

З експериментів відомо, що такий саморобний гальванічний елемент дає дуже малу силу струму, \(\sim 10^{-3}\ \text{А}.\)

За умовою лампа не засвітилася, тобто сила струму була замалою для роботи лампи розжарювання.

Із запису закону Ома для повного кола $$ I=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}}{R+r} $$ випливає, що сила струму \(I\) в такому джерелі невелика, бо дуже великий внутрішній опір \(r\) лимона.

Через великий внутрішній опір джерела живлення напруга, тобто електрорушійна сила ε не могла бути настільки високою, щоб перегоріла лампа розжарювання. Треба ще долати досить великий внутрішній опір лимона, тому лампа навіть не засвітилася.

Отже, єдиною причиною того, що лампа не засвітилася, є завеликий внутрішній опір гальванічного елемента.

Відповідь: Б.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на перевірку розуміння фізичної природи електричного струму в різних середовищах, а також залежності сили струму від температури.

Електроліти ‒ тверді або рідкі речовини, які мають йонну провідність. Якщо в розчин або розплав помістити електроди, приєднані до різнойменних полюсів джерела струму, то, подібно до вільних електронів у металах, йони дрейфуватимуть у певному напрямку: позитивні йони (катіони) ‒ до негативного електрода (катода); негативні йони (аніони) ‒ до позитивного електрода (анода). Тобто в розчині виникне електричний струм. З підвищенням температури кількість йонів в електроліті значно збільшується, тому попри збільшення кількості ефективних зіткнень опір електроліту зменшується (див. графік), відповідно сила струму збільшується.

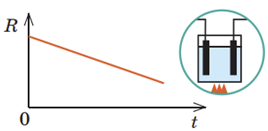
Напівпровідники, як це випливає з їхньої назви, за своєю провідністю посідають проміжне місце між провідниками й діелектриками. Серед валентних електронів обов’язково є електрони, кінетична енергія яких достатня, щоб покинути зв’язки й стати вільними. Якщо напівпровідниковий кристал помістити в електричне поле, то вільні електрони рухатимуться до позитивного полюса джерела струму, тому в напівпровіднику виникне електричний струм. Якщо напівпровідник нагріти або опромінити світлом, кількість вільних електронів і дірок збільшиться, відповідно збільшиться і провідність напівпровідника. На відміну від металевих провідників питомий опір напівпровідників зазвичай зменшується з підвищенням температури (див. графік), а отже, сила струму збільшується.

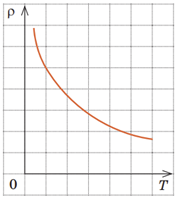
Згідно з класичною електронною теорією модель внутрішньої будови металу – це утворена позитивно зарядженими йонами кристалічна ґратка, яка перебуває в «газі» вільних електронів. Якщо в металевому провіднику створити електричне поле, то на хаотичний рух електронів накладеться дрейф електронів у напрямку сили, що діє на електрони з боку електричного поля. Цей дрейф електронів і є електричним струмом у металах. Якщо підвищувати температуру металевого провідника, то йони у вузлах кристалічної ґратки коливатимуться з більшою амплітудою, хаотичність руху електронів збільшиться, тож вони частіше зіштовхуватимуться з йонами. Відповідно опір (питомий опір) збільшуватиметься (див. графік), а сила струму зменшуватиметься за законом Ома для ділянки кола: $$ I=\frac UR, $$ де \(I\sim \frac 1R\) ‒ сила струму \(I,\) що обернено пропорційна до електричного опору \(R.\)

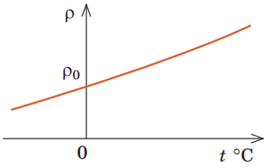
У природних умовах гази складаються з нейтральних атомів і молекул, тому вони є діелектриками. Для створення вільних електричних зарядів гази піддають зовнішнім впливам (впливу зовнішнього йонізатора). Під впливом йонізатора (нагрівання або опромінення) нейтральні молекули діляться на позитивний йон і вільний електрон (див. рисунок). Далі електрон може об’єднатися з нейтральною молекулою, утворюючи тим самим негативний йон.

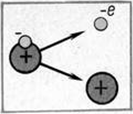
Описані вище процеси називають йонізацією газу.

За наявності електричного поля йони й електрони рухаються впорядковано, утворюючи електричний струм.

Отже, у газах електричний струм зумовлений спрямованим рухом позитивних і негативних йонів і вільних електронів.

Під час збільшення температури концентрація носіїв струму в газах зростає, що приводить до зменшення опору (див. рисунок). Відповідно сила струму зростатиме.

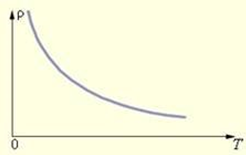
Єдине з наведених середовище, у якому підвищення температури спричиняє зменшення сили струму, ‒ метал.

Відповідь: B.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітне поле. Магнітна індукція.

Завдання скеровано на перевірку знання і розуміння магнітної індукції, уміння визначати полюси котушки за правилом правої руки.

Алюмінієвий дріт, намотаний на каркас, називають котушкою. Якщо цим дротом пропустити електричний струм, котушка стане штучним магнітом. Треба визначити полюси такого магніту, тоді зможемо визначити, як поводитимуться магніти, підвішені з ним поруч на нитках.

За напрямок струму в замкненому електричному колі прийнято напрямок, у якому частинки, що мають позитивний заряд, рухаються по колу, тобто напрямок від позитивного полюса джерела струму до негативного (див. рисунок).

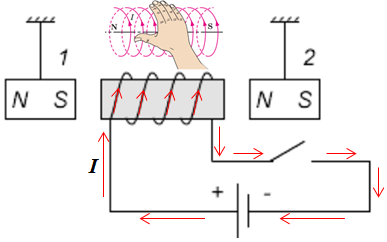
Котушка зі струмом має два полюси ‒ південний \(S\) і північний \(N.\) Полюси котушки розташовані на її торцях, і їх легко визначити за допомогою правила правої руки:
якщо чотири зігнуті пальці правої руки спрямувати за напрямком струму \(I\) в котушці, то відігнутий на \(90^\circ\) великий палець укаже напрямок на північний полюс котушки, тобто напрямок вектора магнітної індукції всередині котушки (див. рисунок).

Отже, ліворуч у котушки північний полюс, а праворуч ‒ південний. Підвішені магніти зорієнтовані різнойменними полюсами до полюсів котушки, тому притягуватимуться і зліва, і справа до котушки.

Відповідь: A.

Коливання і хвилі. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.

Завдання скеровано на перевірку знання і розуміння параметрів, від яких залежить період коливань нитяного маятника.

Період коливань \(T\) нитяного (математичного) маятника визначають за формулою $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac lg}, $$ де \(l\) ‒ довжина маятника; \(g\) ‒ прискорення вільного падіння.

За умовою довжини обох ниток однакові: $$ l_1=l_2. $$

У формулу також входить прискорення вільного падіння, але в умові не зазначено, що кульки в різних місцях, тому вважаємо, що прискорення вільного падіння однакове для обох кульок.

З формули зрозуміло, що період коливань нитяного маятника не залежить від маси тіла. Тож ні від густини (у металу й дерева значення густини різні), ні від об’єму (за умовою радіуси кульок однакові) період коливань також не залежить.

Період коливань математичного маятника не залежить від маси маятника, а визначається лише довжиною нитки та прискоренням вільного падіння в тому місці, де розташований цей маятник.

Отже, періоди малих коливань кульок із різних матеріалів на нитках однакової довжини будуть однакові: $$ T_1=T_2. $$

Відповідь: Б.

ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.

Завдання скеровано на перевірку знання суті і розуміння закономірностей коливань тіла на пружині, сил, що діють на тіло в певній ситуації.

Позначмо на рисунку сили, які діють на кульку, що підвішена до пружини й поки не коливається на ній (див. рисунок ліворуч). На кульку діє сила тяжіння \(\overrightarrow{F}_\text{тяж}\) і сила пружності \(\overrightarrow{F}_\text{пруж с}.\) Кулька перебуває в положенні рівноваги: у середній точці, сили врівноважені, рівнодійна сил дорівнює нулю.

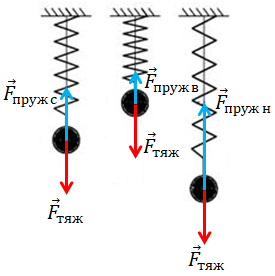
Коли кулька переміститься у верхню точку (див. рисунок посередині), сила пружності \(\overrightarrow{F}_\text{пруж в}\) зменшиться (може зменшитися навіть до нуля), натомість сила тяжіння \(\overrightarrow{F}_\text{тяж}\) змін не зазнає. У цьому разі рівнодійна обох сил буде відмінна від нуля і напрямлена вертикально вниз.

У нижній точці навпаки: сила пружності \(\overrightarrow{F}_\text{пруж н}\) збільшиться (можливо, що й до максимального значення), а сила тяжіння \(\overrightarrow{F}_\text{тяж}\) не зміниться. Рівнодійна сил, відмінна від нуля, буде напрямлена вгору.

Отже, сили, що діють на кульку, будуть урівноважені лише в положенні рівноваги, тобто в середній точці.

Відповідь: Б.

ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.

Завдання скеровано на перевірку знання суті і розуміння закономірностей коливального процесу в коливальному контурі, а також уміння описувати цей процес відповідним рівнянням.

Коливання в коливальному контурі (у котушці зокрема) відбуваються за гармонічним законом (законом косинуса або синуса): \begin{gather*} i=I_{max}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t,\\[7pt] \text{або}\\[7pt] i=I_{max}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t, \end{gather*} де \(i\) – миттєве значення сили струму, \(I_{max}\) – амплітудне значення сили струму, \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\) – циклічна частота змінного струму, \(t\) – час.

У будь-якій реальній коливальній системі завжди є втрати енергії. Під час електромагнітних коливань – на нагрівання провідників, випромінювання електромагнітних хвиль. Частина енергії електромагнітного поля під час кожного коливання перетворюється на внутрішню (теплову) енергію тощо. Унаслідок цього амплітуда коливань із часом зменшується. А через певний інтервал часу, якщо немає надходжень енергії від зовнішнього джерела, коливання припиняються (згасають). Тому вільні коливання завжди є згасними. Але в умові зазначено, що амплітуда коливань не змінюється, отже, вважатимемо коливання незгасними.

В умові не задано амплітудне значення сили струму, тож зосередимося на визначенні циклічної частоти \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}:\) $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}, $$ де \(T\) – період коливань.

Період власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де \(L\) – індуктивність котушки, \(C\) – електроємність конденсатора.

Отже, за цих умов єдиним рівнянням, що описує залежність сили струму \(i\) в котушці від часу \(t,\) може бути рівняння $$ i=0,15\sin250t. $$

Відповідь: A.

ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.

Завдання скеровано на перевірку знання і розуміння законів поширення променя в збиральній лінзі, уміння схематично зобразити його хід.

Спочатку добудуймо фокальну площину, яка проходить через фокус лінзи точку \(F,\) перпендикулярно до головної оптичної осі, що перпендикулярна до лінзи.

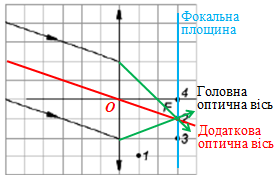
Далі побудуймо додаткову оптичну вісь, що проходить так само, як і головна, крізь оптичний центр лінзи точку \(O,\) але паралельно променям, що падають на лінзу. Пам’ятаймо, що промінь, який проходить крізь оптичний центр лінзи, не заломлюється.

Отримуємо точку перетину додаткової оптичної осі і фокальної площини (див. схематичний рисунок). Ця точка збіглася з точкою \(2\) з умови. Це є додатковий фокус.

Будь-який пучок паралельних променів, навіть якщо ці промені не паралельні головній оптичній осі, після заломлення в збиральній лінзі завжди перетинаються в одній точці ‒ у головному фокусі \(F\) або додатковому (лежить на фокальній площині).

Тож після проходження крізь збиральну лінзу промені перетнуться в точці \(2.\)

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Прямолінійність поширення світла в однорідному середовищі.

Завдання скеровано на перевірку знання і розуміння закону прямолінійного поширення світла, а також понять повної тіні й півтіні.

Джерело світла, яке випромінює світло однаково в усіх напрямках і розмірами якого, зважаючи на відстань до місця спостереження, можна знехтувати, називають точковим джерелом світла.

Найкращим прикладом точкових джерел світла є зорі, адже ми спостерігаємо їх із Землі, тобто з відстані, що в мільйони разів перевищує розміри самих зір.

Джерела світла, що не є точковими, називають протяжними джерелами світла.

Повна тінь ‒ це область простору, у яку не потрапляє світло від джерела.

Якщо джерело світла є точковим, тінь від предмета буде чіткою. У цьому разі утворюється тільки повна тінь.

Якщо тіло освітлене протяжним джерелом світла, то утворюється тінь із нечіткими контурами, тобто утворюється не тільки повна тінь, а ще й півтінь.

Півтінь ‒ це область простору, освітлена деякими з наявних точкових джерел світла або частиною протяжного джерела.

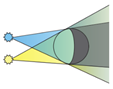
Повну тінь і півтінь пояснюють відповідно до закону прямолінійного поширення світла.

Отже, правильна відповідь ‒ Б.

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Кванти світла (фотони).

Завдання скеровано на перевірку знання і розуміння поняття імпульсу фотона.

Імпульс \(p\) фотона дорівнює відношенню його енергії \(E\) до швидкості руху \(c\) й обернено пропорційний довжині хвилі \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\) фотона: $$ p=\frac{E}{c}=\frac{h\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}}{c}=\frac{h}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}\) ‒ частота випромінювання, \(h\) ‒ стала Планка.

Модуль імпульсу фотона видимого світла $$ p_1=\frac{h}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_1}. $$

Модуль імпульсу фотона рентгенівського випромінювання $$ p_2=\frac{h}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2}. $$

Визначімо співвідношення \(p_1\) і \(p_2:\)

Відповідь: Г.

ТЕМА: Коливання і хвилі. Оптика. Закони відбивання заломлення світла.

Завдання скеровано на перевірку знання і розуміння законів поширення світла.

Кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) між променем, що падає, і перпендикуляром, проведеним із точки падіння, називають кутом падіння; кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) між відбитим променем і цим перпендикуляром називають кутом відбивання. А кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma},\) утворений заломленим променем і перпендикуляром до межі поділу двох середовищ, проведеним із точки падіння променя, називають кутом заломлення (див. рисунок).

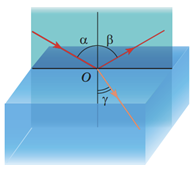
З огляду на визначення, кути \(1,\ 4,\ 7\) ‒ це кути падіння. А кути \(3,\ 6,\ 9\) ‒ це кути заломлення.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки й уміння застосовувати його до адіабатного та ізопроцесів.

Перший закон (начало) термодинаміки: кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

1. Ізотермічний процес. Під час цього процесу температура, а отже, і внутрішня енергія газу не змінюються \((\Delta U=0),\) тому рівняння першого закону термодинаміки має вигляд $$ Q=A. $$

Під час ізотермічного процесу вся передана газу кількість теплоти йде на виконання механічної роботи.

Варіант відповіді – Г.

2. Адіабатний процес. Це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти \(Q,\) передана системі, дорівнює нулю, тому перший закон термодинаміки має вигляд $$ \Delta U+A=0,\ \text{або}\ A=-\Delta U. $$

Під час адіабатного розширення газ виконує додатну роботу за рахунок зменшення внутрішньої енергії, а температура газу зменшується.

Відповідний варіант відповіді – В.

3. Ізохорний процес. Під час цього процесу об’єм газу не змінюється \((\Delta V=0)\) і газ роботу не виконує \((A=0),\) тому рівняння першого закону термодинаміки має вигляд \begin{gather*} Q=\Delta U. \end{gather*}

Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу.

Варіант відповіді – А.

4. Ізобарний процес. Під час цього процесу виконується робота і змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки має вигляд $$ Q=\Delta U+A. $$

Під час ізобарного процесу передана газу кількість теплоти йде і на збільшення внутрішньої енергії газу, і на виконання механічної роботи.

Варіант відповіді – Б.

Відповідь: 1Г, 2В, 3А, 4Б.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Ампера.

Завдання скеровано на перевірку знання і розуміння сили, що діє на провідник із струмом із боку магнітного поля – сили Ампера, уміння визначати її напрямок.

Сила Ампера − це сила, із якою магнітне поле діє на провідник зі струмом.

Напрямок сили Ампера визначають за правилом лівої руки (див. рисунок): якщо ліву руку розташувати так, щоб лінії магнітної індукції \(\overrightarrow{B}\) входили в долоню, а чотири витягнуті пальці вказували напрямок струму \(I\) в провіднику, то відігнутий на \(90^\circ\) великий палець укаже напрямок сили Ампера \(\overrightarrow{F}_A.\)

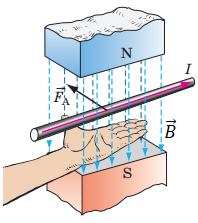
Розгляньмо кожний зображений варіант. Ліву руку орієнтуватимемо відносно сторінки з рисунком. Пригадаймо позначення:

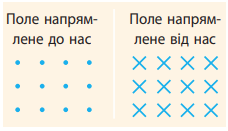
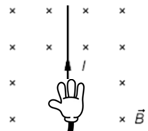
На рисунку 1 вектор магнітної індукції напрямлений перпендикулярно до площини рисунка від вас (позначено хрестиком). Отже, зорієнтуймо ліву руку долонею до себе (лінії магнітної індукції входять в долоню), чотири пальці напрямлені вертикально вгору за напрямком струму, тоді великий палець, відігнутий на \(90^\circ,\) буде напрямлений ліворуч у площині рисунка – варіант А.

На рисунку 2 вектор магнітної індукції напрямлений вертикально вниз, отже долоню зорієнтуймо торцем (перпендикулярно) до площини рисунка, а чотири пальці руки спрямуймо праворуч за напрямком сили струму. Тоді великий палець, відігнутий на \(90^\circ,\) буде напрямлений перпендикулярно до площини рисунка від вас – варіант В.

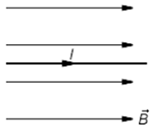
На рисунку 3 сила Ампера не діятиме, оскільки напрямок сили струму збігається з напрямком вектора магнітної індукції та неможливо зорієнтувати ліву руку відповідно до правила визначення сили Ампера. За формулою сила Ампера також дорівнює нулю. Оскільки кут \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) між напрямком струму в провіднику й вектором магнітної індукції дорівнює \(0^\circ,\) синус кута \(0^\circ\) дорівнює нулю, відповідно й сила Ампера дорівнює нулю: $$ F_A=BIl\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}, $$ де \(l\) – довжина провідника; $$ F_A=BIl\sin0^\circ=BIl\cdot 0=0. $$ Отже, сила Ампера не діятиме на провідник – варіант Д.

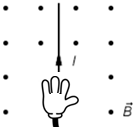
На рисунку 4 вектор магнітної індукції напрямлений перпендикулярно до площини рисунка до вас (позначено точками). Отже, зорієнтуймо ліву руку долонею від себе (лінії магнітної індукції входять в долоню), чотири пальці напрямлені вертикально вгору за напрямком струму, тоді великий палець, відігнутий на \(90^\circ,\) буде напрямлений праворуч у площині рисунка – варіант Б.

Відповідь: 1А, 2В, 3Д, 4Б.

ТЕМА: Коливання і хвилі. Оптика. Шкала електромагнітних хвиль. Властивості електромагнітного випромінювання різних діапазонів.

Завдання скеровано на перевірку знань про різні види електромагнітного випромінювання і їхні джерела.

Під час розпаду радіонуклідів у ядерному реакторі виникає радіоактивне випромінювання, один із видів якого – гамма-промені.

Будь-які тіла, температура яких вища від абсолютного нуля, випромінюють інфрачервоні промені. Саме на цьому ґрунтується застосування їх у тепловізорах – приладах нічного бачення. Тому гарячий чай є джерелом інфрачервоного (теплового) випромінювання.

Радіохвилі – від наддовгих із довжиною понад \(10\ \text{км}\) до ультракоротких і мікрохвиль із довжиною менш ніж \(0,1\ \text{мм}\) – породжує змінний електричний струм. Електромагнітні хвилі радіодіапазону породжені високочастотним змінним струмом, який створюють генератори високочастотних електромагнітних коливань. У цьому завданні джерелом радіохвиль є супутник зв’язку.

Люмінофор – речовина, яка здатна світитися за збудження, тобто люмінесціювати. Люмінофори широко використовують в електроніці, наприклад, ними вкривають екран телевізора, електропроменевої трубки, де їхнє світіння за бомбардування електронами формує зображення, у сцинтиляційних лічильниках тощо. Людське око сприймає це світіння, отже це діапазон видимого світла.

Відповідь: 1В, 2А, 3Г, 4Д.

ТЕМА: Квантова фізика. Елементи теорії відносності.

Завдання скеровано на перевірку знання і розуміння дослідів або спостережень, що сприяли відкриттям із розділів «Елементи теорії відносності», «Світлові кванти» й «Атом та атомне ядро».

1. Явище радіоактивності – засвічення фотопластинки солями Урану (Г).

Анрі Антуан Беккерель (1852–1908) − французький фізик, знаючи, що рентгенівські промені, на відміну від світлових, проходять крізь чорний папір, узяв загорнуту в чорний папір фотопластинку, поклав на неї крупинки уранової солі й на кілька годин виніс фотопластинку на яскраве сонячне світло. Після проявлення на фотопластинці виявилися темні плями саме в тих місцях, де лежала уранова сіль. Таким чином було з’ясовано, що уранова сіль дійсно випускає випромінювання, яке має велику проникну здатність і діє на фотопластинку. Беккерель вирішив продовжити дослідження і підготував дослід, який дещо відрізнявся від попереднього. Проте науковцю завадила похмура погода, і він із жалем поклав готову до досліду фотопластинку з урановою сіллю та мідним хрестом між ними в шухляду стола. Через кілька днів, так і не дочекавшись появи сонця, Беккерель вирішив про всяк випадок проявити фотопластинку. Результат був несподіваним: на пластинці з’явився контур хреста. Тож сонячне світло тут ні до чого, і сіль Урану сама, без впливу зовнішніх чинників, випускає невидиме випромінювання, якому не є перешкодою навіть шар міді! Пізніше таке випромінювання назвали радіоактивним випромінюванням (від латин. radio − випромінюю, activus − дієвий); здатність речовин до радіоактивного випромінювання – радіоактивністю. Це був 1896 рік.

2. Планетарна модель атома − бомбардування альфа-частинками золотої фольги (А).

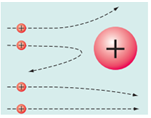
Вузький пучок \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\text{-частинок}\) зі свинцевого контейнера спрямовувався на тонку золоту фольгу, а далі потрапляв в екран, покритий шаром кристалів цинк сульфіду. Якщо в такий екран улучала \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\text{-частинка},\) то в місці її влучання відбувався слабкий спалах світла. Переважна більшість \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\text{-частинок}\) проходила крізь золоту фольгу, не змінюючи напрямку руху, деякі відхиляються від початкової траєкторії. Приблизно одна з \(20000\) частинок відскакувала від фольги, начебто натикаючись на якусь перешкоду. Після зазначених дослідів Ернест Резерфорд (1871–1937), видатний англійський фізик, у 1911 р. запропонував ядерну модель будови атома: атом складається з позитивно зарядженого ядра, оточеного негативно зарядженими частинками − електронами; саме в ядрі зосереджена мало не вся маса атома.

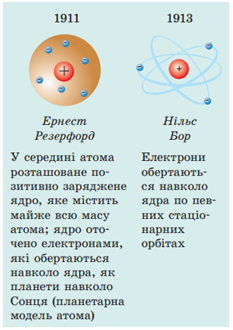
Ядерна (планетарна) модель атома, запропонована Резерфордом, була розвинена в роботах видатного данського фізика Нільса Бора (1885–1962). Саме на ядерній моделі ґрунтується сучасне уявлення про будову атома.

3. Закони фотоефекту – опромінювання металів світлом (В).

Розрізняють зовнішній фотоефект, за якого фотоелектрони вилітають за межі тіла, і внутрішній фотоефект, за якого електрони, «вирвані» світлом із молекул і атомів, залишаються всередині тіла.

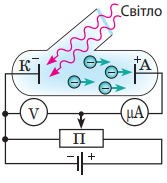
Зовнішній фотоефект відкрив німецький фізик Г. Герц 1887 р., а детально дослідив О. Столєтов (1839–1896) у 1888–1890 рр. Для вивчення фотоефекту О. Столєтов використав пристрій, сучасне зображення якого схематично наведено на рисунку. Усередині камери, з якої викачано повітря, розташовані два електроди (катод К і анод А), на які подається напруга від джерела постійного струму.

4. Три типи радіоактивних променів – дія магнітного поля на випромінювання урану (Б).

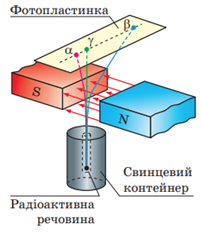
Досліди з вивчення природи радіоактивного випромінювання показали, що радіоактивні речовини можуть випромінювати промені трьох видів: позитивно заряджені частинки (\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\) (альфа)-випромінювання), негативно заряджені частинки (\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\) (бета)-випромінювання) і нейтральні промені (\(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\) (гамма)-випромінювання). На рисунку зображено схему одного з таких дослідів: пучок радіоактивного випромінювання потрапляє спочатку в сильне магнітне поле постійного магніту, а потім на фотопластинку. Після проявлення фотопластинки на ній чітко видно три темні плями. Найбільший внесок у вивчення \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\text{-випромінювання}\) зробив Е. Резерфорд. Він одним із перших з’ясував, що \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\text{-випромінювання}\) − це потік ядер атомів Гелію. \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\text{-випромінювання},\) як і \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}\text{-випромінювання},\) відхиляється магнітним полем, але в протилежний бік. Виявлено, що \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}\text{-випромінювання}\) − це потік електронів, які летять із величезною швидкістю (наближеною до швидкості поширення світла). Вивчення \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma}\text{-випромінювання}\) показало, що це електромагнітні хвилі надзвичайно високої частоти (понад \(10^{18}\) Гц).

Відповідь: 1Г, 2А, 3В, 4Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку знання і розуміння фізичних величин, що визначають прямолінійний рівноприскорений рух і вміння їх визначати.

1. В умові дано прискорення, отже, розглядається прямолінійний рівноприскорений рух.

З формули (записаної в проєкціях на горизонтальну вісь \(Ox\)) для прискорення \(a\) прямолінійного рівноприскореного руху визначімо час \(t,\) затрачений велосипедистом для досягнення вказаної швидкості \(v:\) $$ a=\frac{v-v_0}{t}, $$ де \(v_0=0\) (за умовою) − швидкість руху тіла в момент початку відліку часу (початкова швидкість); \(v\) − швидкість руху тіла через деякий інтервал часу \(t.\)

Відповідь: 5.

2. Для визначення шляху, подоланого велосипедистом за час \(t=5\ \text{с},\) скористаймося одним із рівнянь залежності проєкції переміщення \(s\) від часу для прямолінійного рівноприскореного руху (проєкції шляху і переміщення співпадають під час прямолінійного руху): \begin{gather*} s=v_0t+\frac{at^2}{2},\\[6pt] s=0\cdot 5\ \text{с}+\frac{1\ \text{м/с}^2\cdot (5\ \text{с})^2}{2}=12,5\ \text{м}. \end{gather*}

Відповідь: 12,5.

Відповідь: 1. 5. 2. 12,5.

ТЕМА: Механіка. Основи динаміки. Сила пружності. Закон Гука.

Завдання скеровано на перевірку знання і розуміння закону Гука.

1. Сила пружності \(\overrightarrow{F}_\text{пруж}\) − це сила, яка виникає під час деформації тіла і намагається повернути тіло в недеформований стан. За законом Гука в разі малих пружних деформацій розтягнення або стиснення сила пружності прямо пропорційна видовженню тіла: $$ \overrightarrow{F}_\text{пруж}=-k\overrightarrow{x}. $$

Знак мінус показує, що сила пружності напрямлена в бік, протилежний видовженню.

Запишімо закон Гука для модулів: $$ F_\text{пруж}=k|x|=k|\Delta l|, $$ де \(x=\Delta l\) – видовження, \(k\) – жорсткість пружини.

\begin{gather*} k=\frac{F_\text{пруж}}{|x|},\\[6pt] k=\frac{45\ \text{Н}}{0,15\ \text{м}}=300\frac{\text{Н}}{\text{м}}. \end{gather*}

Відповідь: 300.

2. Визначімо силу пружності \(F_\text{пруж1}\) у разі видовження тієї самої пружини \((k=300\ \text{Н/м})\) на \(|x_1|=10\ \text{см}=0,1\ \text{м}:\)

Відповідь: 30.

Відповідь: 1. 300. 2. 30.

ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умова плавання тіл.

Завдання скеровано на перевірку знання і розуміння повітроплавання тіл, уміння описувати його за допомогою формул.

Позначмо всі сили, що діють на систему тіл у повітрі: повітряна куля з гелієм ‒ вантаж. Це сила тяжіння \(m_\text{в}\overrightarrow{g},\) що діє на вантаж, сила тяжіння \((m_\text{об}+m_\text{He})\overrightarrow{g},\) що діє на повітряну кулю (оболонка плюс гелій), виштовхувальна сила (сила Архімеда) \(\overrightarrow{F}_A,\) що діє з боку повітря на цю систему тіл (див. рисунок).

За другим законом Ньютона векторна сума всіх сил дорівнюватиме нулю, оскільки в умові зазначено, що система не рухається: $$ m_\text{в}\overrightarrow{g}+(m_\text{об}+m_\text{He})\overrightarrow{g}+\overrightarrow{F}_A=0. $$

Запишімо це рівняння в проєкціях: $$ (m_\text{в}+m_\text{об}+m_\text{He})g=F_A. $$

Розпишімо силу Архімеда: $$ F_A=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{пов}gV, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{пов}\) ‒ густина повітря, \(g\) ‒ прискорення вільного падіння, \(V\) ‒ об’єм системи куля ‒ вантаж. В умові зазначено, що об’єм вантажу малий, тож ним можна знехтувати. Оболонка кулі є тонкою, тобто нехтуємо її товщиною, яка не впливатиме на шуканий об’єм. Також в умові відмічено, що газонепроникна оболонка кулі не чинить опору зміні об’єму кулі, тобто тиск \(p\) повітря ззовні кулі дорівнюватиме тиску, який чинить зсередини гелій. Отже, оскільки куля має неправильну форму, і ми не зможемо обчислити її об’єм, визначімо об’єм гелію \(V_\text{He}\) з рівняння стану ідеального газу ‒ рівняння Менделєєва ‒ Клапейрона (ідеальність гелію і повітря теж зазначено в умові): $$ pV_\text{He}=\frac{m_\text{He}}{M_\text{He}}RT, $$ де \(m_\text{He}\) ‒ маса гелію, \(M_\text{He}\) ‒ молярна маса гелію, \(R\) ‒ універсальна газова стала, \(T\) ‒ абсолютна температура.

Тобто $$ V_\text{He}=\frac{m_\text{He}\cdot RT}{p\cdot M_\text{He}}. $$

Запишімо рівняння Менделєєва ‒ Клапейрона для повітря: $$ pV_\text{пов}=\frac{m_\text{пов}}{M_\text{пов}}RT. $$

Звідси визначімо густину повітря: $$ \frac{pM_\text{пов}}{RT}=\frac{m_\text{пов}}{V_\text{пов}}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}_\text{пов}. $$

Підставімо вирази для густини повітря і для об’єму гелію у формулу виштовхувальної сили:

Повернімося до запису другого закону Ньютона в проєкціях і визначімо шукану величину ‒ масу гелію:

Відповідь: 100.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплової машини.

Завдання скеровано на перевірку знання і розуміння поняття коефіцієнта корисної дії.

З одного боку коефіцієнт корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) теплової машини − фізична величина, яка характеризує економічність теплової машини і дорівнює відношенню роботи \(A,\) виконуваної машиною за цикл, до кількості теплоти \(Q,\) одержуваної від нагрівника: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac AQ\cdot 100\ \text{%}. $$

З іншого боку коефіцієнт корисної дії ідеальної теплової машини дорівнює: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{T_\text{н}-T_\text{х}}{T_\text{н}}\cdot 100\ \text{%}, $$ де \(T_\text{н}\)− температура нагрівника; \(T_\text{х}\) − температура холодильника

Прирівняємо ці два вирази для коефіцієнта корисної дії: \begin{gather*} \frac AQ\cdot 100\ \text{%}=\frac{T_\text{н}-T_\text{х}}{T_\text{н}}\cdot 100\ \text{%}. \end{gather*}

Визначімо із цієї рівності кількість теплоти \(Q,\) яку має передати нагрівник робочому тілу \((T_\text{н}=527\ ^\circ\mathrm{C}+273=800\ \text{К},\) \(T_\text{х}=7\ ^\circ\mathrm{C}+273=280\ \text{К}):\)

Відповідь: 8.

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників. Послідовне і паралельне з’єднання провідників.

Завдання скеровано на перевірку знання і розуміння того, від яких параметрів провідника залежить його електричний опір, а також застосування правил визначення характеристик електричного струму під час послідовного і паралельного з’єднання провідників.

Опір \(R\) провідника (дротини), який має незмінний поперечний переріз, можна обчислити за формулою $$ R=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}l}{S}, $$ де \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\) − питомий опір речовини, з якої виготовлений провідник; \(l\) − довжина провідника; \(S\) − площа поперечного перерізу провідника.

Виразімо питомий опір: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}=\frac{RS}{l}. $$

Визначімо з умови опір \(R\) і площу поперечного перерізу \(S\) дротини (довжину \(l\) дротини дано в умові).

Покази вольтметра, що паралельно підключений до дротини (див. рисунок), становлять \(1\ \text{В}.\) Сила струму в колі дорівнює \(0,5\ \text{А}.\) Оскільки дротина й реостат з’єднані послідовно, сила струму, яку показує амперметр у колі, буде така сама і в дротині – \(0,5\ \text{А}.\)

Отже, можна визначити електричний опір дротини за законом Ома для ділянки кола: $$ R=\frac UI=\frac{1\ \text{В}}{0,5\ \text{А}}=2\ \text{Ом}. $$

Щоб визначити площу поперечного перерізу дротини, скористаймося методом рядів. На рисунку праворуч є ряд, утворений витками дротини. Довжина цього ряду \(L=12\ \text{мм}.\) Кількість витків у ряді \(N=24.\) Обчислімо діаметр \(d\) дротини: $$ d=\frac LN=\frac{12\ \text{мм}}{24}=0,5\ \text{мм}. $$

Ми свідомо не виразили значення діаметра дротини в метрах, оскільки вимога завдання – подати відповідь в \(\text{Ом}\cdot \text{мм}^2/\text{м}.\)

Тоді площу поперечного перерізу визначімо за формулою площі круга: $$ S=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}R^2=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}d^2}{4}. $$

Підставімо цей вираз для площі у формулу для питомого опору й обчислімо його:

Відповідь: 1,25.

ТЕМА: Електродинаміка. Основи електростатики. Електроємність. Конденсатори.

Завдання скеровано на перевірку знання і розуміння будови конденсатора та його технічних характеристик.

Годинник зможе працювати від цього конденсатора, поки напруга на ньому буде не нижчою за \(1,3\ \text{В}.\) На початку конденсатор був заряджений до напруги \(1,5\ \text{В}.\) Електроємність \(C\) конденсатора визначають за формулою \begin{gather*} C=\frac qU, \end{gather*} де \(q\) – заряд конденсатора, \(U\) − напруга між обкладками.

Отже, за певний час заряд конденсатора зменшиться на \(\Delta q:\)

Сила струму \(I\) зможе підтримуватися незмінною, як зазначено в умові, лише певний час \(\Delta t,\) поки зміна заряду конденсатора не приведе до падіння напруги від \(1,5\ \text{В}\) до \(1,3\ \text{В}:\) $$ I=\frac{\Delta q}{\Delta t} $$

За нижчої напруги годинник не працюватиме.

Визначімо проміжок часу, у який працюватиме годинник:

Відповідь: 25.

ТЕМА: Електродинаміка. Закони постійного струму. Коефіцієнт корисної дії.

Завдання скеровано на перевірку знання і розуміння змісту коефіцієнта корисної дії та вміння визначати його для різних пристроїв.

Коефіцієнт корисної дії \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}\) пристрою дорівнює відношенню роботи \(A,\) виконуваної пристроєм, до кількості теплоти \(Q,\) отриманої під час згоряння палива: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac AQ\cdot 100\ \text{%}. $$

Роботу струму визначімо як добуток потужності \(P\) струму й часу \(t\) роботи генератора: \begin{gather*} A=Pt. \end{gather*}

Кількість теплоти під час згоряння палива визначімо як добуток питомої теплоти згоряння \(q\) і маси палива \(m:\) $$ Q=qm. $$

Підставімо вирази для роботи і кількості теплоти у формулу для коефіцієнта корисної дії та обчислімо його:

Відповідь: 16.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Енергія магнітного поля.

Завдання скеровано на перевірку знання і розуміння того, якими величинами визначається енергія магнітного поля.

Енергія магнітного поля \(W_\text{м}\) провідника зі струмом дорівнює половині добутку індуктивності \(L\) провідника на квадрат сили струму \(I\) в провіднику: $$ W_\text{м}=\frac{LI^2}{2}. $$

Магнітний потік \(\textbf{Φ}\) прямо пропорційний силі струму в провіднику: $$ \textbf{Φ}=LI, $$ де індуктивність \(L\) є коефіцієнтом пропорційності.

Звідси $$ L=\frac{\textbf{Φ}}{I}. $$

Підставімо вираз для індуктивності у формулу енергії магнітного поля й обчислімо її:

Відповідь: 5.

ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла. Побудова зображень, які дає плоске дзеркало.

Завдання скеровано на перевірку знання і розуміння законів відбивання, правил побудови зображень, які дає плоске дзеркало.

За умовою промінь \(1,\) що падає на одне із дзеркал, є паралельним до променя \(2,\) що відбився від іншого дзеркала (див. рисунок).

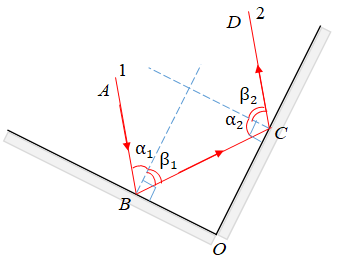
Отже, \(AB\) i \(CD\) паралельні (за умовою), а \(BC\) – січна (за побудовою). Тоді кути \(ABC\) і \(BCD\) – внутрішні односторонні, а їхня сума дорівнює \(180^\circ.\)

За законами відбивання кут падіння дорівнює куту відбивання, отже, \begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_1=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}_1,\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}_2. \end{gather*}

Знайдімо суму кутів \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}_1\) і \(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_2:\)

Тепер розгляньмо \(\Delta BOC.\) За побудовою кут \(CBO\) дорівнюватиме \((90^\circ−\style{font-style:normal;font-weight:bold;font-size:1.1em}{\beta}_1),\) а кут \(BCO\) – \((90^\circ−\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}_2).\) Тоді кут \(BOC\)

Отже, \(\Delta BOC\) – прямокутний. Кут між дзеркалами дорівнює \(90^\circ.\)

Відповідь: 90.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Тиск світла.

Завдання скеровано на перевірку знання і розуміння поняття тиску, законів відбивання світлового потоку від різних поверхонь.

Дзеркальна поверхня відбиває все електромагнітне випромінювання. Отже, світло, падаючи на дзеркальну поверхню, створюватиме на неї максимальний тиск.

Чорна поверхня поглинає все електромагнітне випромінювання, тому світло на неї чинить мінімальний тиск.

Тиск − це фізична величина, яка характеризує результат дії сили і дорівнює відношенню сили, яка діє перпендикулярно до поверхні, до площі цієї поверхні: $$ p=\frac FS, $$ де \(p\) − тиск; \(F\) − сила тиску − сила, що діє на поверхню перпендикулярно до неї; \(S\) − площа цієї поверхні.

Тиск світла на поверхню \(p_\text{пов}\) залежить від зміни імпульсу фотонів \(\Delta p_\text{ф},\) яку вони передають поверхні: $$ p_\text{пов}\sim N\cdot |\Delta p_\text{ф}|. $$

Помножмо чисельник і знаменник на час \(t:\) $$ p=\frac{Ft}{St}. $$

Величину \(\overrightarrow{F}t\) називають імпульсом сили. Отже, імпульс сили дорівнює зміні імпульсу тіла: $$ \overrightarrow{F}t=\Delta\overrightarrow{p}=\overrightarrow{p}_2-\overrightarrow{p}_1. $$

Щоб визначити модулі імпульсів початкового і кінцевого, виберімо уявну вісь \(Ox,\) напрямлену у бік відбитих від поверхні фотонів: $$ Ft=p_2-(-p_1). $$

Для дзеркальної поверхні

де \(N_\text{дз}=\frac 12 N_0\) (за умовою від дзеркальної поверхні відбилася половина світлового потоку) ‒ кількість відбитих фотонів, \(p_\text{ф}\) ‒ імпульс одного фотона, \(N_0\) ‒ загальна кількість фотонів, що впали на поверхню.

Для чорної (вкритої сажею) поверхні

де \(N_\text{ч}=0\) (як ми зазначили вище, чорна поверхня поглинає весь світловий потік, усі фотони) ‒ кількість відбитих фотонів, \(p_\text{ф}\) ‒ імпульс одного фотона, \(N_0\) ‒ загальна кількість фотонів, що впали на поверхню.

Порівняймо тиски:

Отже, світловий потік створює в \(1,5\) раза менший тиск на чорну поверхню, ніж на дзеркальну.

Відповідь: 1,5.