ЗНО онлайн 2013 року з фізики – пробний тест

12345678910111213141516171819202122232425262728293031323334

Зачекайте, йде розрахунок...

Завдання 1 з 34

Ціна поділки мірного циліндра, зображеного на рисунку, дорівнює 5 мл. Визначте об’єм рідини в циліндрі.

А10 мл

Б20 мл

В100 мл

Г200 мл

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

Тема: Фізичні величини. Вимірювання фізичних величин.

Завдання скеровано на перевірку розуміння побудови шкали приладів і вміння визначати за показами шкали приладів певні фізичні величини, зокрема об’єм.

Поділка ‒ це відстань між рисками (горизонтальними позначками, лініями) на вимірювальній шкалі.

Кількість поділок, на яку заповнено рідиною мірний циліндр, дорівнює $20.$ За умовою ціна поділки мірного циліндра – $5\ \text{мл}.$ Отже, об’єм рідини в циліндрі становитиме $$ 5\ \text{мл} \cdot 20=100\ \text{мл}. $$

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5526

Завдання 2 з 34

У якому із прикладів Місяць можна вважати матеріальною точкою?

Арозрахунок тривалості сонячного затемнення

Бвибір місця посадки на Місяць космічного корабля

Ввизначення гравітаційної сили, що діє між Місяцем і Сонцем

ГВизначення рельєфу поверхні Місяця

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Механіка. Основи кінематики. Матеріальна точка.

Завдання скеровано на перевірку знання і розуміння однієї з фізичних моделей ‒ матеріальної точки.

Матеріальна точка ‒ це фізична модель тіла, розмірами якого в умові задачі можна знехтувати. Те саме тіло в умовах однієї задачі можна вважати матеріальною точкою, а в умовах іншої ‒ ні.

Під час сонячного затемнення не можна нехтувати розмірами Місяця, оскільки від цього залежить тривалість затемнення і розміри тіні й півтіні, які спостерігають на поверхні Землі.

Напевне не можна вважати супутник Землі матеріальною точкою під час вибору місця посадки космічного корабля на Місяць, а також у ситуації вивчення рельєфу поверхні Місяця.

Добираючи місце посадки космічного корабля на Місяць, вибирають місцевість, задають певні координати на поверхні. Тому знехтувати розмірами Місяця і вважати його матеріальною точкою не можна.

Вивчаючи рельєф поверхні Місяця, описують просторові закономірності його будови й розвитку, нескінченні западини і височини, розмірами яких не можна знехтувати. Тобто вважати Місяць матеріальною точкою під час дослідження його рельєфу не можна.

Гравітаційну силу між Місяцем і Сонцем визначають за законом всесвітнього тяжіння, у якому йдеться про притягування будь-яких двох тіл одне до одного із силою, що прямо пропорційна добутку мас цих тіл й обернено пропорційна квадрату відстані між ними. Цей закон справджується, якщо обидва тіла є матеріальними точками (розмірами тіл нехтують, а маса матеріальної точки дорівнює масі того чи того тіла). Отже, у цій ситуації Місяць можна вважати матеріальною точкою.

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5527

Завдання 3 з 34

Визначте модуль рівнодійної всіх сил, що діють на автомобіль масою 800 кг, рівняння руху якого x=1+3t+2t².

А6400 Н

Б3200 Н

В2100 Н

Г800 Н

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

Тема: Механіка. Основи динаміки. Другий закон Ньютона.

Завдання скеровано на перевірку розуміння другого закону Ньютона й уміння читати кінематичні рівняння.

Відповідно до другого закону Ньютона тіло масою $m$ унаслідок дії сили набуває прискорення $a,$ модуль якого обчислімо за формулою $$ a=\frac Fm, $$ де $F$ ‒ це модуль рівнодійної всіх сил, що діють на тіло.

Для того щоб визначити модуль рівнодійної всіх сил, які діють на автомобіль, треба масу помножити на модуль прискорення: $$ F=ma. $$

Маса відома з умови. А прискорення визначімо з рівняння руху автомобіля, що наведене в умові.

Запишімо рівняння руху автомобіля в загальному вигляді: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де $x$ ‒ кінцева координата тіла, $x_0$ ‒ початкова координата тіла, $v_0$ ‒ модуль початкової швидкості руху тіла, $a$ ‒ модуль прискорення руху тіла, $t$ ‒ час руху тіла.

Значення прискорення ‒ це множник біля $\frac{t^2}{2}:$ $$ x=1+3t+2t^2=1+3t+\frac{4t^2}{2}, $$ отже, прискорення $a=4\ \text{м/с}^2.$

Обчислімо модуль рівнодійної: $$ F=800\ \text{кг}\cdot 4\ \text{м/с}^2=3200\ \text{Н}. $$

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5528

Завдання 4 з 34

Літак масою 20 т летів протягом 1 год горизонтально зі сталою швидкістю 360 км/год. Сила тяги двигунів дорівнює 10 кН. Визначте роботу, здійснену за цих умов силою тяжіння. Уважайте, що g=10 м/с².

А−3,6 ГДж

Б0 Дж

В3,6 ГДж

Г72 ГДж

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Механіка. Закони збереження в механіці. Механічна робота.

Завдання скеровано на перевірку розуміння поняття механічної роботи.

Механічна робота (робота сили) $A$ ‒ це фізична величина, якою характеризують зміну механічного стану тіла. Механічна робота дорівнює добутку модуля сили $F,$ модуля переміщення $s$ і косинуса кута $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}$ між вектором сили й вектором переміщення: $$ A=Fs\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}. $$

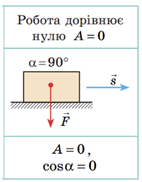
Сила тяжіння діє на літак і напрямлена вертикально вниз. Але переміщення літака по вертикалі немає. За умовою літак рухається горизонтально. Отже, кут між вектором сили тяжіння і вектором переміщення дорівнює $90^\circ.$ Косинус кута $90^\circ$ дорівнює нулю (див. рисунок). Відповідно робота сили тяжіння дорівнюватиме нулю, сила тяжіння не виконує роботу.

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5529

Завдання 5 з 34

Під час роботи ідеальної теплової машини від нагрівника отримано кількість теплоти, що дорівнює 300 кДж, а холодильнику передано кількість теплоти 100 кДж. Визначте температуру нагрівника, якщо температура холодильника дорівнює 250 К.

А300 К

Б450 К

В500 К

Г750 К

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

Тема: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплової машини.

Завдання скеровано на перевірку знання і розуміння поняття коефіцієнта корисної дії.

З одного боку коефіцієнт корисної дії $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}$ теплової машини − фізична величина, яка характеризує економічність теплової машини й дорівнює відношенню роботи $A,$ що виконує машина за цикл (корисної роботи), до кількості теплоти $Q,$ одержуваної від нагрівача: $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac AQ\cdot 100\ \text{%}. $$

З іншого боку коефіцієнт корисної дії ідеальної теплової машини $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\eta}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}\cdot 100\ \text{%}, $$ де $T_\text{Н}$ − температура нагрівача; $T_\text{Х}$ − температура холодильника.

Прирівняймо ці два вирази для коефіцієнта корисної дії: \begin{gather*} \frac AQ\cdot 100\ \text{%}=\frac{T_\text{Н}-T_\text{Х}}{T_\text{Н}}\cdot 100\ \text{%},\\[6pt] \frac AQ=1-\frac{T_\text{Х}}{T_\text{Н}}. \end{gather*}

Визначімо із цієї рівності температуру нагрівника: $$ T_\text{Н}=\frac{T_\text{Х}}{1-\frac AQ}. $$

Візьмемо до уваги, що $A$ ‒ це корисна робота, яка дорівнюватиме різниці кількості теплоти, отриманої від нагрівника, і кількості теплоти, яка була передана холодильнику:

$$ A=Q-Q_\text{Х}=300\ \text{кДж}-100\ \text{кДж}=200\ \text{кДж}. $$

Тепер можна обчислити температуру нагрівача:

$$ T_\text{Н}=\frac{250\ \text{К}}{1-\frac{200\ \text{кДж}}{300\ \text{кДж}}}=\frac{250}{1-\frac 23}\ \text{К}=750\ \text{К}. $$

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5530

Завдання 6 з 34

Під час якого з газових процесів концентрація молекул газу не може змінитися?

Алюдина набирає повітря в легені

Бповітря виходить із пробитої шини

Внасичену водяну пару охолоджують

Гкисень у закритому балоні остигає, коли вимикають опалення

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

Тема: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основне рівняння молекулярно-кінетичної теорії ідеального газу. Концентрація молекул газу.

Завдання скеровано на перевірку знання і розуміння поняття концентрації молекул газу й уміння аналізувати різні практичні ситуації, пов’язані з концентрацією газу.

Концентрація $n$ молекул газу ‒ це фізична величина, яка дорівнює кількості $N$ молекул в одиниці об’єму $V$ газу: $$ n=\frac NV. $$

Отже, якщо не змінюватимуться кількість молекул й об’єм, у якому ці молекули містяться, то концентрація залишиться тією самою. Проаналізуймо наведені ситуації.

Коли людина набирає повітря в легені, то об’єм легень збільшується, і кількість молекул повітря також збільшується. Тобто концентрація молекул у цьому разі змінюватиметься.

Об’єм пробитої шини, можливо, і не буде зменшуватися, а кількість молекул повітря, яке заповнювало шину, зменшуватиметься. Тому концентрація молекул у цій ситуації змінюватиметься.

Насиченою називають пару, яка перебуває в стані динамічної рівноваги зі своєю рідиною. Динамічна рівновага встановлюється між процесами конденсації і випаровування ‒ кількість молекул, які повертаються в рідину, дорівнюватиме кількості молекул, які за той самий час залишають рідину. Це можливо в закритій посудині, тобто об’єм пари між поверхнею рідини й кришкою посудини, залишатиметься сталим. Концентрація молекул насиченої пари ‒ найбільша можлива концентрація молекул пари за даної температури. Якщо ж насичену пару охолоджувати, то кількість молекул, що вилітатимуть з поверхні рідини, зменшуватиметься, а значить, концентрація вже ненасиченої пари теж стане меншою.

Говорячи про закритий балон, розуміємо, що об’єм, який займає кисень, залишається незмінним. Оскільки балон не відкривають, то кількість молекул кисню в ньому теж не змінюється, а отже, концентрація молекул не може змінитися. У результаті остигання кисню зменшиться швидкість руху молекул і, відповідно, тиск кисню в балоні.

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5531

Завдання 7 з 34

Тепловою рівновагою називають стан системи, за якого

Аробота, що виконує система, дорівнює отриманій кількості теплоти.

Бвсі параметри системи за відсутності зовнішніх впливів не змінюються.

Всистема здійснює роботу, а зміна внутрішньої енергії дорівнює нулю.

Гсистема отримує певну кількість теплоти, але не виконує роботу.

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Температура та її вимірювання.

Завдання скеровано на перевірку знання і розуміння поняття теплової рівноваги.

Досліди показують: коли більш нагріте тіло контактує з менш нагрітим, то більш нагріте тіло завжди охолоджується, а менш нагріте ‒ нагрівається. До того ж можуть змінюватися й інші властивості тіл: вони стають більшими або меншими за розмірами, можуть перейти в інший агрегатний стан, почати краще чи гірше проводити електричний струм, можуть почати випромінювати світло іншого кольору тощо. Натомість однаково нагріті тіла, контактуючи одне з одним, не змінюють своїх властивостей, і тоді кажуть, що ці тіла перебувають у стані теплової рівноваги.

Отже, стан теплової рівноваги ‒ це такий стан макроскопічної системи, коли всі макроскопічні параметри системи залишаються незмінними як завгодно довго.

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5532

Завдання 8 з 34

На рисунку зображено робочий цикл теплового двигуна. Визначте роботу, яку виконує газ за один цикл (p — тиск, V — об’єм).

А20 Дж

Б40 Дж

В20 МДж

Г40 МДж

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку розуміння, за яких умов виконується робота в термодинаміці, від яких фізичних величин вона залежить, а також на вміння читати графіки та брати з них необхідні для розв’язування задачі числові дані.

Повна робота за цикл дорівнює сумі робіт, виконаних під час кожного процесу циклу:

$$ A=A_{1-2}+A_{2-3}+A_{3-1}. $$

Запишімо формулу для визначення роботи газу в термодинаміці: $$ A=p\Delta V=p(V_2-V_1). $$

З формули бачимо: якщо не буде зміни об’єму, то робота не буде виконана й дорівнюватиме нулю.

Проаналізуймо кожну ділянку графіка.

Ділянка графіка 1‒2: з рівняння Клапейрона

$$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2},\ \text{тобто}\ \frac{pV}{T}=const $$

робимо висновок, що збільшуються всі три параметри газу ‒ й абсолютна температура $T,$ і тиск $p,$ й об’єм $V$ (довільний процес). Відповідно до першого закону термодинаміки ($Q=\Delta U+A$ ‒ кількість теплоти $Q,$ передана системі, йде на зміну внутрішньої енергії системи $\Delta U$ й на виконання системою роботи $A$ проти зовнішніх сил) у нас недостатньо даних із графіка, щоб визначити роботу, яку виконає газ на цій ділянці.

Ділянка графіка 2‒3 – ізохорне охолодження: $V=const,$ тиск $p$ зменшується. Отже, відповідно до рівняння Клапейрона для ізохорного процесу, температура $T$ теж знижуватиметься: $$ \frac pT=\mathrm{const}\Rightarrow \frac{p\downarrow}{T\downarrow}=\mathrm{const}. $$

Отже, під час цього процесу зміни об’єму не було $(\Delta V=0),$ отже, роботу газ не виконував: $$ A_{2-3}=0. $$

Ділянка графіка 3‒1 – ізобарне охолодження: $p=const.$ Під час цього процесу об’єм $V$ зменшується (див. рисунок). Відповідно до рівняння Клапейрона для ізобарного процесу температура $T$ теж буде зменшуватися: $$ \frac VT=\mathrm{const}\Rightarrow \frac{V\downarrow}{T\downarrow}=\mathrm{const}. $$

У цьому процесі можна визначити роботу на ділянці 3‒1:

\begin{gather*} A_{3-1}=p_1(V_1-V_3),\\[6pt] A_{3-1}=1\cdot 10^6\ \text{Па}\cdot (5\cdot 10^{-6}\ \text{м}^3-25\cdot 10^{-6}\ \text{м}^3)=-20\ \text{Дж}. \end{gather*}

Значення роботи на цій ділянці від’ємне, оскільки об’єм газу зменшується.

Зважаючи на те, що на ділянці 1‒2 неможливо визначити роботу через нестачу даних, не можна визначити й повну роботу, скористаймося графічним способом розв’язання. Геометричний зміст роботи під час довільного процесу: робота газу чисельно дорівнює площі криволінійної трапеції під графіком залежності $p(V).$

Згідно з її геометричним змістом робота газу в процесі 1–2 чисельно дорівнює площі прямокутної трапеції (добуток є половиною суми основ трапеції і її висоти), основи якої дорівнюють $p_1$ і $p_2,$ а висота ‒ $(V_2-V_1 ):$ $$ A_{1-2}=\frac{p_1+p_2}{2}\cdot (V_2-V_1). $$

Об’єм газу збільшується, тому ця робота додатна.

Робота газу в процесі 2–3 дорівнює нулю, оскільки цей процес ізохорний (див. пояснення вище).

Робота газу в процесі 3–1 $(V_3=V_2)$ чисельно дорівнює площі прямокутника зі сторонами $p_1$ і $(V_2-V_1):$ $$ A_{3-1}=p_1\cdot (V_2-V_1). $$

Об’єм газу зменшується, тому ця робота від’ємна (див. розрахунок вище).

Отже, для визначення роботи за весь цикл потрібно від площі трапеції відняти площу прямокутника. Тобто, як видно з рисунка, робота за цикл чисельно дорівнює площі прямокутного трикутника $1–2–3$ (половина добутку катетів): $$ A=\frac 12\cdot (p_2-p_1)\cdot (V_2-V_1). $$

Необхідні значення величин знайдімо з графіка:

$$ A=\frac 12\cdot (3\cdot 10^6\ \text{Па}-1\cdot 10^6\ \text{Па})\cdot (25\cdot 10^{-6}\ \text{м}^3-5\cdot 10^{-6}\ \text{м}^3)=20\ \text{Дж}. $$

Відповідь: A.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5533

Завдання 9 з 34

Плоский повітряний конденсатор зарядили та від’єднали від джерела струму. У конденсаторі установилася напруженість E₀. Яка буде напруженість електричного поля всередині конденсатора, якщо відстань між пластинами збільшити вдвічі?

АE₀

В(1/2)E₀

Г(1/4)E₀

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.

Завдання скеровано на перевірку знання і розуміння будови конденсатора, а також розуміння зв’язку його технічних характеристик.

Для зарядження конденсатора обидві його обкладки (пластини) з’єднують із полюсами джерела струму: на внутрішніх (унаслідок притягання різнойменних зарядів) поверхнях обкладок накопичуються рівні за модулем, але протилежні за знаком заряди.

За умовою конденсатор зарядили й від’єднали від джерела струму. Це означає, що незмінним залишиться накопичений заряд. Зарядом $q$ конденсатора називають модуль заряду однієї з його обкладок: $$ q=UC, $$ де $U$ ‒ напруга між обкладками, $C$ ‒ електроємність плоского конденсатора.

Електроємність плоского конденсатора обчислюють за формулою $$ C=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_0S}{d}, $$ де $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_0$ ‒ електрична стала; $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}$ ‒ діелектрична проникність діелектрика, яким заповнюють простір між обкладками конденсатора; $S$ ‒ площа обкладки конденсатора; $d$ ‒ відстань між обкладками.

Для однорідного електричного поля між обкладками плоского конденсатора зв’язок між напруженістю $E$ цього поля і напругою $U$ на обкладках конденсатора відображено формулою $$ U=Ed. $$

Запишімо тепер формулу для визначення заряду конденсатора:

$$ q=UC=Ed\cdot \frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_0S}{d}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_0SE, $$

звідки $$ E=\frac{q}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_0S}. $$

З формули випливає, що напруженість електричного поля всередині конденсатора не залежить від відстані між обкладками (пластинами) конденсатора. А всі інші фізичні величини $(q,\ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon},\ S),$ які могли би вплинути на зміну напруженості, за умовою залишаються незмінними. Тому за початкової напруженості $E_0$ в конденсаторі, яка встановилася згідно з умовою, після зміни відстані між обкладками (в умові завдання відстань збільшили вдвічі) напруженість не зміниться і становитиме $E_0.$

Відповідь: A.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5534

Завдання 10 з 34

На рисунку зображено взаємне розташування трьох однакових за модулем зарядів. Укажіть напрямок результуючої сили, що діє на другий заряд з боку першого та третього зарядів.

Анапрямок А

Бнапрямок Б

Внапрямок В

Гнапрямок Г

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона.

Завдання скеровано на перевірку знання і розуміння закону Кулона, а також вміння шукати рівнодійну сил.

Закон Кулона: сила $F$ взаємодії двох нерухомих точкових зарядів $q_1$ і $q_2$ прямо пропорційна добутку модулів цих зарядів й обернено пропорційна квадрату відстані $r$ між ними: $$ F=k\cdot \frac{|q_1|\cdot |q_2|}{r^2}, $$ де $k$ ‒ коефіцієнт пропорційності.

Сили, з якими взаємодіють точкові заряди, називають силами Кулона. Сили Кулона напрямлені вздовж умовної прямої, яка з’єднує точкові заряди, що взаємодіють.

З боку кульки $1$ на кульку $2$ діятиме сила відштовхування $\overrightarrow{F}_{12}$ (однойменні тіла відштовхуються).

З боку кульки $3$ на кульку $2$ діятиме сила притягання $\overrightarrow{F}_{32}$ (різнойменні тіла притягуються).

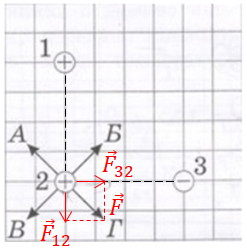
Парні сили взаємодії до вже позначених сил не позначено на рисунку, щоб його не захаращувати, але зрозуміло, що кулька $2$ теж діє з такими ж за модулями, але протилежними за напрямками відповідними силами на кульки $1$ і $3.$

Відповідно до закону Кулона сила, що діє з боку кульки $1$ буде тією самою за модулем, що й сила з боку кульки $3,$ оскільки за умовою всі заряди однакові за модулем, а відповідно до рисунку відстані між зарядами $1‒2$ і $3‒2$ теж однакові: $$ F_{12}=F_{32}. $$

Тож рівнодійну $$ \overrightarrow{F}=\overrightarrow{F}_{12}+\overrightarrow{F}_{32} $$ графічно можна побудувати за правилом паралелограма (див. рисунок). Напрямок рівнодійної $\overrightarrow{F}$ збігається з напрямком Г.

Відповідь: Г.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5535

Завдання 11 з 34

Спіраль електричного нагрівника вкоротили вдвічі. Визначте, як змінилася потужність цього нагрівника. Напругу в мережі вважайте сталою, залежність електричного опору від температури не враховуйте.

Азменшилася в 4 рази

Бзменшилася у 2 рази

Взбільшилася у 2 рази

Гзбільшилася в 4 рази

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.

Завдання скеровано на перевірку знання і розуміння потужності струму й параметрів, від яких вона залежить.

Потужність струму $P$ ‒ фізична величина, яка чисельно дорівнює роботі струму $A$ за одиницю часу $t:$ $$ P=\frac At. $$

Узявши до уваги, що $$ A=UIt, $$ маємо $$ P=UI, $$ де $U$ ‒ напруга на ділянці кола, на якій визначають потужність струму; $I$ ‒ сила струму в ділянці.

Фізична величина, що характеризує саме провідник (спіраль електричного нагрівника) ‒ це електричний опір. За допомогою закону Ома для ділянки кола покажемо, як залежить потужність від опору й, відповідно, від параметрів спіралі: \begin{gather*} I=\frac UR,\\[6pt] P=UI=U\cdot \frac UR=\frac{U^2}{R}. \end{gather*}

Опір провідника, який має незмінний поперечний переріз: $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS, $$ де $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}$ ‒ питомий опір речовини, з якої виготовлено провідник; $l$ ‒ довжина провідника; $S$ ‒ площа поперечного перерізу провідника: $$ P=\frac{U^2}{R}=\frac{U^2\cdot S}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}l}. $$

За умовою напруга в мережі стала, залежністю електричного опору від температури можна знехтувати. Отже, потужність нагрівача буде обернено пропорційна до його довжини: $$ P\sim \frac 1l. $$

Визначімо відношення потужності нагрівача після вкорочення його вдвічі до початкової його потужності: $$ \frac{P_2}{P_1}=\frac{1}{l_2}:\frac{1}{l_1}=\frac{l_1}{l_2}=\frac{l_1}{\frac 12 l_1}=2. $$

Отже, потужність $P_2$ нагрівника збільшилася вдвічі.

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5536

Завдання 12 з 34

У резисторі, через який тече постійний струм, за певний час виділяється кількість теплоти, що дорівнює Q. Визначте кількість теплоти, яка виділиться за вдвічі більший час у резисторі з удвічі більшим опором, за умови що величина сили струму залишається тією самою, як і в першому випадку.

А8Q

Б4Q

В2Q

ГQ

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля ‒ Ленца.

Завдання скеровано на перевірку знання і розуміння закону, що визначає кількість теплоти, яка виділяється в провіднику зі струмом і яку він віддає довкіллю ‒ закону Джоуля ‒ Ленца.

Кількість теплоти $Q,$ яка виділяється в провіднику зі струмом, прямо пропорційна квадрату сили струму $I,$ опору $R$ провідника й часу $t$ проходження струму: $$ Q=I^2Rt. $$

Цією формулою описують закон Джоуля ‒ Ленца. Запишімо його до і після змін параметрів (за умовою $I_1=I_2,$ $R_2=2R_1,$ $t_2=2t_1$):

\begin{gather*} Q_1=I^2R_1t_1=Q,\\[7pt] Q_2=I^2R_2t_2=I^2\cdot 2R_1\cdot 2t_1=4\cdot I^2R_1t_1=4Q. \end{gather*}

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5537

Завдання 13 з 34

У магнітне поле зі сталою магнітною індукцією влітає електрон. Як називають силу, що діє на електрон?

Асила Ампера

Бсила Лоренца

Всила Фарадея

Гсила Кулона

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку знання і розуміння сил електромагнітної природи.

Магнітне поле діє на провідник зі струмом із певною силою ‒ силою Ампера.

Оскільки електричний струм ‒ це напрямлений рух заряджених частинок, виникнення сили Ампера є результатом дії магнітного поля на окремі заряджені частинки, що рухаються в провіднику. Силу, з якою магнітне поле діє на одну рухому заряджену частинку, називають силою Лоренца. Тобто, на електрон, що влітає в магнітне поле, діятиме сила Лоренца.

Стала Фарадея ‒ фізична стала, заряд електронів кількістю речовини $1\ \text{моль}$ (але не сила Фарадея).

Сила Кулона ‒ це сила взаємодії між нерухомими точковими зарядами.

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5538

Завдання 14 з 34

Прикладом вільних коливань є коливання

Азанавіски біля прочиненого вікна під дією протягу.

Бгілочки, з якої тільки-но злетіла пташка.

Вголки працюючої швацької машинки.

Гбуйка під дією хвиль.

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Вільні механічні коливання.

Завдання скеровано на перевірку знання і розуміння видів механічних коливань, і вміння розпізнавати їх у конкретних прикладах.

Вільні коливання ‒ це коливання, які відбуваються під дією внутрішніх сил системи після того, як її було виведено з положення рівноваги. Щоб у коливальній системі виникли вільні коливання, необхідне виконання двох умов: 1) системі має бути передано надлишкову енергію; 2) тертя в системі має бути досить малим, інакше коливання швидко затухнуть або навіть не виникнуть. Оскільки під час вільних коливань система не отримує енергію ззовні, то вільні коливання ‒ це завжди згасні коливання.

З усіх наведених ситуацій прикладом вільних коливань є коливання гілочки, з якої щойно злетіла пташка ‒ пташка вивела гілочку із стану рівноваги, один раз штовхнувши її лапками (передала енергію), поступово ці коливання затухнуть унаслідок дії сил пружності і опору повітря.

Коливання занавіски біля прочиненого вікна під дією протягу й коливання буйка під дією хвиль можна вважати вимушеними: на занавіски діє зовнішня сила, що періодично змінюється, ‒ протяг, а буйок піднімається й опускається разом із хвилями на поверхні води. Такі коливання зазвичай незгасні, їхня частота дорівнює частоті зміни зовнішньої сили, що змушує тіло коливатися.

Коливання голки швацької машинки, що працює, ‒ це автоколивання. Ці коливання є незгасними й відбуваються внаслідок здатності системи самостійно регулювати надходження енергії від постійного джерела.

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5539

Завдання 15 з 34

На рисунку А зображено графік залежності координати x тіла від часу t при гармонічних коливаннях. Визначте, який із графіків на рисунку Б відображає залежність імпульсу p тіла, що коливається, від часу t.

А4

Б3

В2

Г1

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на перевірку знання і розуміння гармонічних коливань, а також уміння правильно їх описувати за допомогою графіків.

За умовою коливання є гармонічними, тож координата $x$ тіла, що коливається, змінюється з часом $t$ за законом косинуса (або синуса):

$$ x=A\cos(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0),\ \text{або}\ x=A\sin(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0) $$

де $A$ ‒ амплітуда коливань (найбільше зміщення тіла від положення рівноваги), $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}$ ‒ циклічна частота коливань, $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0$ ‒ початкова фаза коливань. Ці рівняння називають рівняннями гармонічних коливань.

Крива $x(t),$ зображена на рисунку $A,$ ‒ синусоїда; $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}_0=0$ (оскільки графік проходить через початок координат): $$ x=A\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t. $$

Імпульс тіла $\overrightarrow{p}$ ‒ це векторна фізична величина, яка дорівнює добутку маси $m$ тіла на швидкість $\overrightarrow{v}$ його руху: $$ \overrightarrow{p}=m\overrightarrow{v}. $$

Коли координата тіла змінюється за гармонічним законом (за законом косинуса або синуса), швидкість і прискорення руху тіла теж змінюються гармонічно. Швидкість руху тіла ‒ це похідна від зміщення тіла за часом:

$$ v(t)=x'(t)=(A\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t)'=A\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t. $$

Функція залежності модуля імпульсу тіла від часу матиме вигляд $$ p=mv=mA\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t. $$

Графіком такої функції $p(t)$ буде косинусоїда, тобто на рисунку Б це графік $2.$

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5540

Завдання 16 з 34

Коливальний контур складається з конденсатора ємністю 0,5 мкФ і котушки індуктивністю 0,5 Гн. Визначте, яка формула може описувати залежність напруги u на конденсаторі від часу t, коли в контурі відбуваються вільні електромагнітні коливання. Усі величини виражено в одиницях SI.

Аu=5cos1000t

Бu=0,5cos2000t

Вu=5cos1000πt

Гu=0,5cos2000πt

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Вільні електромагнітні коливання в коливальному контурі.

Завдання скеровано на перевірку знання суті і розуміння закономірностей коливального процесу в коливальному контурі, а також уміння описувати цей процес відповідним рівнянням.

Коливання (зміна значень напруги) у коливальному контурі відбуваються за гармонічним законом (законом косинуса або синуса): \begin{gather*} u=U_{max}\cos\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t,\\[7pt] \text{або}\\[7pt] u=U_{max}\sin\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}t, \end{gather*} де $u$ – миттєве значення напруги, $U_{max}$ – амплітудне значення напруги, $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}$ – циклічна частота напруги, $t$ – час.

В умові не задано амплітудне значення напруги, тож зосередимося на визначенні циклічної частоти $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}:$ $$ \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{T}, $$ де $T$ – період коливань.

Період власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}, $$ де $L$ – індуктивність котушки, $C$ – електроємність конденсатора.

\begin{gather*} \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}}{2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{LC}}=\frac{1}{\sqrt{LC}},\\[6pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\omega}=\frac{1}{\sqrt{0,5\ \text{Гн}\cdot 0,5\cdot 10^{-6}\ \text{Ф}}}=\frac{1}{0,5\cdot 10^{-3}}\frac{\text{рад}}{\text{с}}=2\cdot 10^3\frac{\text{рад}}{\text{с}}=2000\frac{\text{рад}}{\text{с}}. \end{gather*}

Отже, за цих умов єдиним рівнянням, що описує залежність напруги $u$ в котушці від часу $t,$ може бути рівняння $$ u=0,5\cos2000t. $$

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5541

Завдання 17 з 34

Під час незатухаючих електромагнітних коливань при розрядженні конденсатора коливального контуру зменшується

Амодуль магнітної індукції поля котушки.

Бенергія електричного поля.

Венергія магнітного поля.

Гсила струму в контурі.

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Електромагнітні коливання в коливальному контурі.

Завдання скеровано на перевірку знання і розуміння того, як змінюються фізичні величини під час електромагнітних коливань у коливальному контурі.

У коливальному контурі виникають електромагнітні коливання, якщо зарядити конденсатор. На обкладках конденсатора накопичиться деякий електричний заряд $q,$ а між обкладками виникне електричне поле, енергія $W_\text{ел}$ якого дорівнює ($C$ ‒ електроємність конденсатора): $$ W_\text{ел}=\frac{q^2}{2C}. $$

Якщо після зарядки конденсатор замкнути на котушку індуктивності, то під дією електричного поля конденсатора вільні заряджені частинки в контурі почнуть рухатися напрямлено. У контурі виникне електричний струм $i,$ а конденсатор почне розряджатися. Тобто заряд конденсатора зменшуватиметься, а отже й енергія електричного поля конденсатора меншатиме, оскільки вона прямо пропорційна квадрату заряду.

Під час того як конденсатор розряджатиметься, сила струму в контурі збільшуватиметься, а магнітне поле посилюватиметься, зростатиме його силова характеристика ‒ модуль магнітної індукції магнітного поля котушки. Оскільки енергія магнітного поля $W_\text{маг}$ котушки ($L$ ‒ індуктивність котушки) $$ W_\text{маг}=\frac{Li^2}{2} $$ прямо пропорційна силі струму $i$ в ній, збільшуватиметься й енергія магнітного поля.

Тож єдина з поданих фізична величина, яка зменшуватиметься під час розрядження конденсатора, ‒ це енергія електричного поля.

Відповідь: Б.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5542

Завдання 18 з 34

Світловий промінь переходить із середовища 1 у середовище 2 (див. рисунок). Укажіть правильне твердження.

Апромінь переходить із середовища 1 у середовище 2, не заломлюючись

Бкут падіння променя більший від кута заломлення

Вшвидкість світла в середовищі 1 менша, ніж у середовищі 2

Гдовжина світлової хвилі в середовищі 2 менша від довжини хвилі в середовищі 1

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Закони заломлення світла.

Завдання скеровано на перевірку знання і розуміння законів заломлення світла.

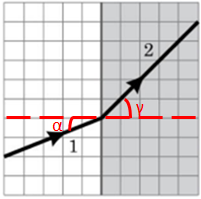
Світловий промінь $1$ проходить через межу в середовище $2,$ змінюючи, зазвичай, напрямок (див. рисунок). Отже, твердження А – неправильне.

Зміну напрямку поширення світла в разі його проходження через межу поділу двох середовищ називають заломленням світла. Промінь $2,$ який задає напрямок заломленого пучка світла, називають заломленим променем. Кут $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}$ між падаючим променем $1$ і перпендикуляром до межі поділу двох середовищ називають кутом падіння. Кут $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\gamma},$ утворений заломленим променем $2$ і перпендикуляром до межі поділу двох середовищ, проведеним із точки падіння променя, називають кутом заломлення. З рисунка видно, що кут падіння менший за кут заломлення, отже, твердження Б є неправильним.

Оскільки кут падіння менший за кут заломлення, то це означає, що промінь переходить з оптично густішого середовища в оптично менш густе. І тоді швидкість світла в середовищі $1$ менша, ніж у середовищі $2.$ Твердження В ‒ правильне.

Під час переходу з одного середовища в інше швидкість $v$ поширення світла змінюється, але частота $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu}$ світлової хвилі, і, відповідно, колір світла залишаються незмінними. За формулою хвилі $$ v=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}\style{font-style:normal;font-weight:bold;font-size:1.1em}{\nu} $$ змінюється довжина $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}$ світлової хвилі. Під час переходу в середовище $2$ з меншою оптичною густиною довжина хвилі, як і її швидкість, збільшується: $$ \frac{v_1}{v_2}=\frac{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_1}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\lambda}_2}. $$

Тобто твердження Г – неправильне.

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5543

Завдання 19 з 34

Яке перетворення енергії лежить в основі роботи фотоелемента?

Аенергія світла перетворюється в електричну енергію

Бенергія світла перетворюється в механічну енергію

Венергія світла перетворюється у внутрішню енергію

Гелектрична енергія перетворюється в енергію світла

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Застосування фотоефекту в техніці.

Завдання скеровано на перевірку розуміння суті фотоефекту й уміння застосовувати знання про це явище.

Супроводжувану випромінюванням (емісією) електронів взаємодію світла з речовиною називають фотоефектом.

Розрізняють зовнішній фотоефект, за якого фотоелектрони вилітають за межі тіла, і внутрішній фотоефект, за якого електрони, «вирвані» світлом із молекул й атомів, залишаються всередині тіла.

Фотоефект широко застосовують у пристроях для перетворення світлових сигналів на електричні або для безпосереднього перетворення світлової енергії на електричну.

Відповідь: A.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5544

Завдання 20 з 34

Укажіть фізичний процес, на якому ґрунтується робота камери Вільсона.

Айонізація молекул фотоемульсії

Бгазовий розряд унаслідок йонізації молекул газу

Вутворення центрів конденсації за рахунок йонізації молекул газу

Гвипромінювання квантів світла люмінофором, на який потрапляють частинки

Позначте відповіді:

А	Б	В	Г

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Методи реєстрації йонізувального випромінювання.

Завдання скеровано на перевірку знання і розуміння методів реєстрації йонізувального випромінювання.

Камера Вільсона ‒ це трековий детектор, ємність, заповнена парою спирту або ефіру. Коли поршень різко опускають, то внаслідок адіабатного розширення пара охолоджується і стає перенасиченою. Коли в перенасичену пару потрапляє заряджена частинка, на своєму шляху вона йонізує молекули пари ‒ отримані йони стають центрами конденсації. Ланцюжок крапель cконденсованої пари, який утворюється вздовж траєкторії руху частинки (трек частинки), знімають на камеру або фотографують (див. рисунок).

Загальний принцип реєстрації йонізувального випромінювання полягає в реєстрації дії, яку чинить це випромінювання:
‒ йонізація молекул фотоемульсії ‒ використовують шари фотоемульсій;
‒ газовий розряд унаслідок йонізації молекул газу ‒ газорозрядний лічильник;
‒ випромінювання квантів світла люмінофором, на який потрапляють частинки;
‒ сцинтиляційні лічильники.

Відповідь: B.

Вид завдання: Завдання з вибором однієї правильної відповіді
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5545

Завдання 21 з 34

Установіть відповідність між указаними діями і результатами — можливими змінами опору провідника.

1неізольований металевим дріт склали удвоє

2неізольований металевий дріт протягли через волочильний верстат: довжина дроту збільшилася у 2 рази, а маса не змінилася

3на неізольованому металевому дроті нарізали різьбу, унаслідок чого площа його поперечного перерізу зменшилася вдвічі по всій довжині

4неізольований металевий дріт укрили ізоляцією

Аопір провідника не змінився

Бопір провідника збільшився в 4 рази

Вопір провідника збільшився у 2 рази

Гопір провідника зменшився в 4 рази

Допір провідника зменшився до нуля

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Закони постійного струму. Опір провідників.

Завдання скеровано на перевірку знання і розуміння того, від яких параметрів залежить електричний опір провідника.

Опір провідника, який має незмінний поперечний переріз, обчислюють за формулою $$ R=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac lS, $$ де $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}$ ‒ питомий опір речовини, з якої виготовлено провідник; $l$ ‒ довжина провідника; $S$ ‒ площа поперечного перерізу провідника.

1. Неізольований металевий дріт склали вдвоє ‒ це означає, що довжина дроту зменшилася $(l_2=\frac 12 l_1),$ а площа поперечного перерізу збільшилася вдвічі $(S_2=2S_1).$

Визначімо, як змінився опір дроту після змін:

\begin{gather*} R_1=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_1}{S_1}\ -\ \text{початковий опір, до змін};\\[6pt] R_2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_2}{S_2}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{\frac 12 l_1}{2S_1}=\frac 14\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_1}{S_1}=\frac 14R_1. \end{gather*}

Отже, опір провідника зменшився вчетверо ‒ варіант відповіді Г.

2. Неізольований металевий дріт протягли через волочильний верстат: довжина дроту збільшилася вдвічі, а маса не змінилася: $l_2=2l_1,$ а якщо маса $m$ не змінилася, то змінилася площа поперечного перерізу:

\begin{gather*} m_1=m_2,\\[7pt] \style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}V_1=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}V_2\ \text{(тут }\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\ -\ \text{густина)},\\[7pt] S_1l_1=S_2l_2,\\[6pt] \frac{S_2}{S_1}=\frac{l_1}{l_2}=\frac{l_1}{2l_1}=\frac 12,\\[6pt] S_2=\frac 12S_1. \end{gather*}

Визначимо, як змінився опір дроту після змін:

\begin{gather*} R_1=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_1}{S_1}\ -\ \text{початковий опір, до змін};\\[6pt] R_2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_2}{S_2}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{2l_1}{\frac 12 S_1}=4\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_1}{S_1}=4R_1. \end{gather*}

Отже, опір провідника збільшився в $4$ рази ‒ Б.

3. На неізольованому металевому дроті нарізали різьбу, унаслідок чого площа його поперечного перерізу зменшилася вдвічі по всій довжині: тобто довжина залишилася тією самою $l_2=l_1,$ а $S_2=\frac 12 S_1.$

Визначимо, як змінився опір дроту після змін:

\begin{gather*} R_1=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_1}{S_1}\ -\ \text{початковий опір, до змін};\\[6pt] R_2=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_2}{S_2}=\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_1}{\frac 12 S_1}=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\rho}\frac{l_1}{S_1}=2R_1. \end{gather*}

Отже, опір провідника збільшився у $2$ рази ‒ B.

4. Неізольований металевий дріт укрили ізоляцією: довжина і площа поперечного перерізу залишилися ті самі, і матеріал дроту не змінився (питомий опір той самий).

Отже, ізоляція ніяк не впливає на опір дроту, його опір не змінився ‒ А.

Відповідь: 1Г, 2Б, 3В, 4А.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5546

Завдання 22 з 34

Установіть відповідність між фізичними величинами та математичними виразами, що їх описують.

1потенціальна енергія тіла, що здійснює горизонтальні коливання на пружині

2період коливань математичного маятник

3кінетична енергія тіла, що здійснює коливання

4період коливань тіла, що здійснює коливання на пружині

Аkx²/2

ВAsin(ωt+φ₀)

Гmυ²/2

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі.

Завдання скеровано на перевірку знання і розуміння формул розділу «Механічні коливання і хвилі».

1. Потенціальна енергія $E_p$ тіла, що здійснює горизонтальні коливання на пружині. Цю енергію має тіло внаслідок взаємодії з іншими тілами або внаслідок взаємодії частин тіла між собою (формула виводиться із геометричного змісту роботи сили пружності): $$ E_p=\frac{kx^2}{2}\ (\text{А}), $$ де $E_p$ ‒ потенціальна енергія, $k$ ‒ жорсткість пружини, $x$ ‒ видовження пружини.

2. Період $T$ коливань математичного маятника обчислюємо за формулою $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac lg}\ (\text{Д}), $$ де $l$ ‒ довжина маятника; $g$ ‒ прискорення вільного падіння.

3. Кінетична енергія $E_k$ тіла, що здійснює коливання, $$ E_k=\frac{mv^2}{2}\ (\text{Г}), $$ де $m$ ‒ маса тіла, $v$ ‒ швидкість руху тіла.

4. Період $T$ коливань тіла, що здійснює коливання на пружині, обчислюємо за формулою $$ T=2\style{font-style:normal;font-weight:bold;font-size:1.1em}{\pi}\sqrt{\frac mk}\ (\text{Б}), $$ де $m$ ‒ маса тіла, $k$ ‒ жорсткість пружини.

Відповідь: 1А, 2Д, 3Г, 4Б.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5547

Завдання 23 з 34

Установіть відповідність між назвами одиниць фізичних величин та фізичними величинами.

1генрі

2ват

3тесла

4фарад

Апотужність електричного струму

Бмагнітна індукція

Велектроємність

Гсила струму

Діндуктивність

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.

Завдання скеровано на перевірку знання одиниць фізичних величин із розділу «Магнітне поле, електромагнітна індукція».

1. Генрі (Гн) ‒ одиниця індуктивності $(L)$ в SI, названа на честь американського фізика Джозефа Генрі (1797–1878):

$$ L=\frac{|\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_{is}|}{|\Delta I|/\Delta t}\Rightarrow [L]=\frac{1\ \text{В}}{1\ \text{А}/1\ \text{с}}=1\ \text{Гн}. $$

Індуктивність провідника дорівнює $1$ генрі, якщо в ньому виникає ЕРС самоіндукції $(\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varepsilon}_{is})$ $1\ \text{В}$ у разі зміни сили струму $(\Delta I)$ на $1\ \text{А}$ за час $(\Delta t)$ $1\ \text{с}.$

Варіант відповіді ‒ Д.

2. Ват (Вт) ‒ одиниця потужності струму $(P)$ у Міжнародній системі одиниць SI, названа на честь шотландського винахідника-механіка Джеймса Ватта (1736‒1819):

$$ P=\frac At=UI\Rightarrow [P]=1\frac{\text{Дж}}{с}=1\ \text{А}\cdot \text{В}=1\ \text{Вт}. $$

$1$ Вт ‒ це потужність струму силою $1\ \text{А}$ на ділянці кола з напругою $1\ \text{В}.$

Варіант відповіді ‒ А.

3. Тесла (Тл) ‒ одиниця магнітної індукції $(B)$ у Міжнародній системі одиниць SI, названа на честь сербського фізика Ніколи Тесли (1856–1943):

$$ B=\frac{F_\text{Ампера}}{Il}\Rightarrow [B]=1\frac{\text{Н}}{\text{А}\cdot \text{м}}=1\ \text{Тл}. $$

$1$ тесла − це магнітна індукція такого однорідного магнітного поля, яке діє з максимальною силою $(F_\text{Ампера})$ $1\ \text{ньютон}$ на провідник завдовжки $(l)$ $1\ \text{метр},$ сила струму $(I)$ в якому $1\ \text{ампер}.$

Варіант відповіді ‒ Б.

4. Фарад (Ф) ‒ одиниця електроємності у Міжнародній системі одиниць SI, названа на честь англійського фізика і хіміка Майкла Фарадея (1791‒1867):

$$ C=\frac{q}{\style{font-style:normal;font-weight:bold;font-size:1.1em}{\varphi}}\Rightarrow [C]=1\frac{\text{Кл}}{\text{В}}=1\ \text{Ф}. $$

$1\ \text{Ф}$ ‒ це електроємність провідника, потенціал якого дорівнює $1\ \text{В},$ коли йому надають заряд $1\ \text{Кл}.$

Варіант відповіді ‒ В.

Відповідь: 1Д, 2А, 3Б, 4В.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5548

Завдання 24 з 34

Установіть відповідність між рівняннями ядерних реакцій та нуклідами, що беруть у них участь.

1⁷₃Li+⁴₂He→?+³₂He

2⁵⁵₂₅Mn+¹₁H→?+¹₀n

3¹⁰₅B+¹₀n→?+⁴₂He

4²₁H+²₁H→¹₀n+?

А¹₁H

Б³₂He

В⁵⁵₂₆Fe

Г⁷₃Li

Д⁸₃Li

Позначте відповіді:

	А	Б	В	Г	Д
1
2
3
4

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.

Завдання скеровано на перевірку вміння складати рівняння ядерних реакцій.

Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових.

Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.

1. Запишімо рівняння ядерної реакції відповідно до умови завдання: $$ \mathrm{_3^7Li+_2^4He\rightarrow\ _{Z}^{A}X+_3^2He}, $$ де $\mathrm{X}$ ‒ невідома частинка, що утворилася внаслідок реакції.

У лівій і правій частинах рівняння реакції суми зарядів, як і суми мас, мають збігатися. Із відповідних рівнянь дістанемо зарядове (протонне) $Z$ і масове (нуклонне) $A$ числа невідомого ядра елемента $\mathrm{X}.$

Запишімо суму мас і суму зарядів для обох частин рівняння реакції:

\begin{gather*} 7+4=A+3,\\[7pt] 3+2=Z+2. \end{gather*}

З одержаних рівнянь маємо: $$ A=8,\ Z=3. $$

Невідомий нуклід у рівнянні – Літій $\mathrm{_3^8Li}$ (Д).

2. Наступне рівняння $$ \mathrm{_{25}^{55}Mn+_1^1H\rightarrow\ _{Z}^{A}X+}_0^1n, $$ де $n$ ‒ нейтрон.

Запишімо суму мас і суму зарядів для обох частин рівняння реакції:

\begin{gather*} 55+1=A+1,\\[7pt] 25+1=Z+0. \end{gather*}

З одержаних рівнянь маємо: $$ A=55,\ \ Z=26. $$

Невідомий нуклід у рівнянні – Ферум $\mathrm{_{26}^{55}Fe}$ (В).

3. Наступне рівняння $$ \mathrm{_{\ 5}^{10}B+}_0^1n\rightarrow \mathrm{_Z^{A}X+_2^4He} $$

Запишімо суму мас і суму зарядів для обох частин рівняння реакції:

\begin{gather*} 10+1=A+4,\\[7pt] 5+0=Z+2. \end{gather*}

З одержаних рівнянь маємо: $$ A=7,\ \ Z=3. $$

Невідомий нуклід у рівнянні – Літій $\mathrm{_{3}^{7}Li}$ (Г).

4. Наступне рівняння $$ \mathrm{_{1}^{2}H+_1^2H}\rightarrow\ _0^1n+ \mathrm{_{Z}^{A}X} $$

Запишімо суму мас і суму зарядів для обох частин рівняння реакції:

\begin{gather*} 2+2=1+A,\\[7pt] 1+1=0+Z. \end{gather*}

З одержаних рівнянь маємо: $$ A=3,\ \ Z=2. $$

Невідомий нуклід у рівнянні – Гелій $\mathrm{_{2}^{3}He}$ (Б).

Відповідь: 1Д, 2В, 3Г, 4Б.

Вид завдання: Завдання на встановлення відповідності (логічні пари)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5549

Завдання 25 з 34

Камінець кинули горизонтально з високої скелі зі швидкістю 7,5 м/с. Визначте модуль переміщення камінця за 2 с. Опір повітря не враховуйте. Уважайте, що g=10 м/с². Відповідь запишіть у метрах.

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Механіка. Основи динаміки. Рух тіла під дією сили тяжіння.

Завдання скеровано на перевірку знання і розуміння руху тіла під дією сили тяжіння, кинутого горизонтально, і вміння застосовувати відповідні рисунки і формули.

Розглянемо рух камінця, кинутого горизонтально зі скелі, скориставшись принципом незалежності рухів. Опором повітря нехтуємо (за умовою), тобто рух відбувається лише під дією сили тяжіння з прискоренням $\overrightarrow{g}.$ Такий рух ‒ це результат додавання двох незалежних рухів: горизонтального ‒ рівномірного вздовж осі $Ox$ (оскільки $g_x=0$); вертикального ‒ рівноприскореного (з прискоренням $\overrightarrow{g}$) уздовж осі $Oy$ без початкової швидкості. Тобто камінець одночасно рухається горизонтально і падає.

Зобразімо схематично рух камінця. Нехай через $2\ \text{с}$ камінець, вилетівши з точки $A,$ опиниться в точці $B.$ Тоді модуль його переміщення дорівнюватиме довжині відрізка $AB.$ Відрізок $CB$ ‒ це дальність польоту, а відрізок $AC$ ‒ це висота. За $2\ \text{с}$ камінець може й не впасти на нульовий рівень (рівень основи скелі), тобто точка $B$ ‒ це якесь його проміжне положення.

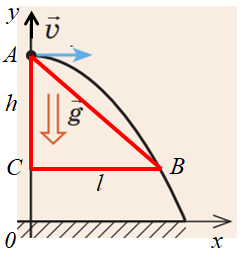
З рисунка бачимо, що переміщення $s=AB$ камінця можна визначити за теоремою Піфагора, обчисливши довжину гіпотенузи $AB$ з прямокутного трикутника $ABC,$ де $h=AC$ i $l=CB$ ‒ катети цього трикутника.

Дальність польоту $l=CB$ камінця можна визначити за формулою: \begin{gather*} l=v\cdot t,\\[7pt] l=7,5\ \text{м/с}\cdot 2\ \text{с}=15\ \text{м}, \end{gather*} де $v$ ‒ швидкість, з якою камінець кинули горизонтально, $t$ ‒ час руху.

Відстань $h,$ яку подолав би камінець, якщо б вільно падав вертикально, визначімо за формулою: \begin{gather*} h=\frac{gt^2}{2},\\[6pt] h=\frac{10\ \text{м/с}^2\cdot (2\ \text{с})^2}{2}=20\ \text{м}, \end{gather*} де $g$ ‒ прискорення вільного падіння.

Тепер за теоремою Піфагора визначімо модуль переміщення камінця:

\begin{gather*} s=\sqrt{l^2+h^2},\\[7pt] s=\sqrt{15^2+20^2}=\sqrt{225+400}=\sqrt{625}=25\ \text{м}. \end{gather*}

Відповідь: 25.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5550

Завдання 26 з 34

Під час ізобарного нагрівання гелій виконав роботу 30 Дж. Визначте зміну внутрішньої енергії гелію. Відповідь запишіть у джоулях.

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку знання, розуміння і застосування першого закону термодинаміки до ізопроцесів, а саме до ізобарного.

Під час ізобарного нагрівання передана газу кількість теплоти витрачається і на виконання механічної роботи, і на збільшення внутрішньої енергії газу. Якщо газ ідеальний одноатомний (гелій ‒ це одноатомний газ без запаху, кольору та смаку), то робота $A$ газу дорівнює $$ A=p\Delta V, $$ а зміна його внутрішньої енергії $$ \Delta U=\frac 32p\Delta V, $$ де $p$ ‒ тиск, $\Delta V$ ‒ зміна об’єму.

Отже, зміну внутрішньої енергії можна визначити за формулою:

\begin{gather*} \Delta U=\frac 32p\Delta V=\frac 32 A,\\[6pt] \Delta U=\frac 32\cdot 30\ \text{Дж}=45\ \text{Дж}. \end{gather*}

Відповідь: 45.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5551

Завдання 27 з 34

Амплітуда коливань тіла на пружині дорівнює 0,5 м. Визначте шлях, який пройшло це тіло за п’ять періодів коливань. Відповідь запишіть у метрах.

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.

Завдання скеровано на перевірку знання і розуміння поняття амплітуди, поняття одного повного коливання і шляху, що проходить тіло за один період коливання.

Амплітуда $A$ коливань ‒ це фізична величина, що дорівнює максимальній відстані, на яку відхиляється тіло від положення рівноваги під час коливань. За одне коливання тіло проходить шлях $l_0,$ який приблизно дорівнює чотирьом амплітудам: \begin{gather*} l_0=4A. \end{gather*}

Тоді за п’ять періодів коливань тіло, що здійснює коливання на пружині, пройде шлях

\begin{gather*} l=5l_0=5\cdot 4A=20A,\\[7pt] l=20\cdot 0,5\ \text{м}=10\ \text{м}. \end{gather*}

Відповідь: 10.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5552

Завдання 28 з 34

Якої мінімальної потужності нагрівник можна виготовити із двох спіралей опорами 200 і 284 Ом, розрахований на напругу 220 В? Відповідь запишіть у ватах.

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Закони постійного струму. Робота і потужність електричного струму.

Завдання скеровано на перевірку знання і розуміння потужності електричного струму.

Потужність електричного струму ‒ фізична величина, що характеризує швидкість виконання струмом роботи й дорівнює відношенню роботи струму до часу, за який цю роботу виконано: $$ P=\frac At, $$ де $P$ ‒ потужність електричного струму; $A$ ‒ робота струму за час $t.$

Оскільки

\begin{gather*} A=UIt,\ \text{то}\\[7pt] P=\frac At=\frac{UIt}{t}=UI. \end{gather*}

З умови відомі загальна напруга, на яку розрахований нагрівач, й опір кожної спіралі. Скориставшись законом Ома для ділянки кола, маємо формулу для визначення потужності відповідно до умови завдання:

$$ I=\frac UR\Rightarrow P=UI=U\cdot \frac UR=\frac{U^2}{R}. $$

Оскільки в умові завдання не вказано, як з’єднані спіралі ‒ послідовно чи паралельно, але треба виготовити нагрівач мінімальної потужності, то визначімо потужність для обох способів з’єднання і порівняємо.

Обчислімо загальний опір спіралей:
1) під час послідовного з’єднання:

\begin{gather*} R_\text{посл}=R_1+R_2,\\[7pt] R_\text{посл}=200\ \text{Ом}+248\ \text{Ом}=484\ \text{Ом}. \end{gather*}

2) під час паралельного з’єднання:

\begin{gather*} \frac{1}{R_\text{пар}}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{R_2+R_1}{R_1R_2},\\[6pt] R_\text{пар}=\frac{R_1R_2}{R_2+R_1},\\[6pt] R_\text{пар}=\frac{200\ \text{Ом}\cdot 284\ \text{Ом}}{284\ \text{Ом}+200\ \text{Ом}}=\frac{56800}{484}\ \text{Ом}=\frac{14200}{121}\ \text{Ом}\approx 117,4\ \text{Ом}. \end{gather*}

Тепер визначімо потужність:
1) під час послідовного з’єднання:

\begin{gather*} P_\text{посл}=\frac{U^2}{R_\text{посл}},\\[6pt] P_\text{посл}=\frac{(220\ \text{В})^2}{484\ \text{Ом}}=\frac{48400}{484}\ \text{Вт}=100\ \text{Вт}, \end{gather*}

2) під час паралельного з’єднання:

\begin{gather*} P_\text{пар}=\frac{U^2}{R_\text{пар}},\\[6pt] P_\text{пар}=\frac{(220\ \text{В})^2\cdot 121}{14200\ \text{Ом}}=\frac{48400\cdot 121}{14200}\ \text{Вт}\approx 412,4\ \text{Вт}. \end{gather*}

Отже, порівнявши значення потужностей $(P_\text{пар}\gt P_\text{посл}),$ ми бачимо, що під час послідовного з’єднання отримаємо нагрівач мінімальної потужності: $$ P_\text{посл}=100\ \text{Вт}. $$

Відповідь: 100.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5553

Завдання 29 з 34

Визначте кількість теплоти, яка виділиться під час перетворення водяної пари масою 10 г, що мала температуру 100 ^∘C, на воду з температурою 50 ^∘C. Питома теплота пароутворення води дорівнює 2300 кДж/кг, питома теплоємність води становить 4,2 кДж/(кг⋅К). Відповідь запишіть у кілоджоулях.

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Конденсація. Питома теплота пароутворення.

Завдання скеровано на перевірку знання і розуміння процесу фазового переходу з газуватого стану в рідкий, а також уміння визначати кількість теплоти під час фазового переходу й під час охолодження.

Для того щоб перетворити водяну пару на воду, треба спочатку її сконденсувати (за умовою водяна пара є за температури конденсації), а після фазового переходу пари в рідину потрібно рідину охолодити до температури $50\ ^\circ\mathrm{C}.$

Отже, кількість теплоти $Q,$ яка під час цього виділиться, складатиметься з двох порцій ‒ кількість теплоти $Q_1,$ що виділиться під час конденсації пари й кількість теплоти $Q_2,$ що виділиться під час охолодження води: \begin{gather*} Q=Q_1+Q_2,\\[7pt] Q_1=Lm_\text{пари}. \end{gather*} де $L$ ‒ питома теплота пароутворення (вона ж виділиться під час конденсації), $m_\text{пари}$ ‒ маса водяної пари. $$ Q_2=cm_\text{води}(t_1-t_2), $$ де $c$ ‒ питома теплоємність води, $m_\text{води}$ ‒ маса води, $t_1=100\ ^\circ\mathrm{C}$ ‒ початкова температура води, $t_2=50\ ^\circ\mathrm{C}$ ‒ кінцева температура води.

\begin{gather*} Q=Lm_\text{пари}+cm_\text{води}(t_1-t_2),\\[7pt] m_\text{пари}=m_\text{води}=m\\[7pt] Q=m(L+c(t_1-t_2)),\\[6pt] Q=10\cdot 10^{-3}\ \text{кг}\cdot (2300\cdot 10^3\frac{\text{Дж}}{\text{кг}}+4,2\cdot 10^3\frac{\text{Дж}}{\text{кг}\cdot\ ^\circ\mathrm{C}}\cdot (100\ ^\circ\mathrm{C}-50\ ^\circ\mathrm{C}))=\\[6pt] =10\cdot 10^{-3}\cdot 10^3(2300+4,2\cdot 50)\ \text{Дж}=10\cdot 2510\ \text{Дж}=25100\ \text{Дж}=25,1\ \text{кДж}. \end{gather*}

Відповідь: 25,1.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5554

Завдання 30 з 34

Електричний опір вольфрамового дроту за температури 0 ^∘C дорівнює 10 Ом. Дріт підключили до джерела струму, напруга на якому є постійною і дорівнює 5 В, у результаті температура дроту підвищилася до 200 ^∘C. Визначте потужність струму в дроті за цих умов. Температурний коефіцієнт опору вольфраму дорівнює 0,005 K⁻¹. Відповідь запишіть у ватах.

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Залежність опору металів від температури.

Завдання скеровано на перевірку знання і розуміння температурного коефіцієнта електричного опору й уміння застосовувати його у відповідних випадках.

Потужність електричного струму ‒ фізична величина, що характеризує швидкість виконання струмом роботи й дорівнює відношенню роботи струму до часу, за який цю роботу виконано: $$ P=\frac At, $$ де $P$ ‒ потужність електричного струму; $A$ ‒ робота струму за час $t.$

Оскільки \begin{gather*} A=UIt\\[6pt] \text{то}\ P=\frac At=\frac{UIt}{t}=UI. \end{gather*}

З умови відома напруга на джерелі струму й опір вольфрамового дроту, який залежить від температури. Скориставшись законом Ома для ділянки кола, маємо формулу для визначення потужності відповідно до даних умови:

$$ I=\frac UR\Rightarrow P=UI=U\cdot \frac UR=\frac{U^2}{R}. $$

Температурний коефіцієнт електричного опору ‒ це фізична величина, яка характеризує залежність опору (питомого опору) речовини від температури: \begin{gather*} R=R_0(1+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}t), \end{gather*} де $R_0$ ‒ опір провідника за температури $0\ ^\circ\mathrm{C};$ $R$ ‒ опір провідника за температури $t;$ $\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}$ ‒ температурний коефіцієнт електричного опору. Температура $t$ у формулі ‒ це фактично різниця температур $\Delta t=t-0\ ^\circ\mathrm{C}=t.$ А зміна температури за шкалою Цельсія дорівнює зміні температури за шкалою Кельвіна: $$ \Delta t=\Delta T, $$ тобто ціна поділки шкали Кельвіна дорівнює ціні поділки шкали Цельсія: $$ 1\ ^\circ\mathrm{C}=1\ \text{К}. $$

Отже, цей вираз для опору, який визначає залежність опору від температури, підставімо у формулу для обчислення потужності:

\begin{gather*} P=\frac{U^2}{R}=\frac{U^2}{R_0(1+\style{font-style:normal;font-weight:bold;font-size:1.1em}{\alpha}t)},\\[6pt] P=\frac{(5\ \text{В})^2}{10\ \text{Ом}(1+0,005\ \text{К}^{-1}\cdot 200\ ^\circ\mathrm{C})}=\frac{25}{10\cdot 2}\ \text{Вт}=1,25\ \text{Вт}. \end{gather*}

Відповідь: 1,25.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5555

Завдання 31 з 34

Збиральна лінза дає дійсне зображення предмета, розташованого на її головній оптичній осі. Розміри предмета та його зображення збігаються, відстань між предметом і зображенням становить 1,6 м. Визначте оптичну силу лінзи. Відповідь запишіть у діоптріях.

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Коливання і хвилі. Оптика. Оптична сила лінзи. Формула тонкої лінзи. Побудова зображень, які дає тонка лінза.

Завдання скеровано на перевірку знання і розуміння побудови зображень, які дає тонка лінза, уміння застосовувати формулу тонкої лінзи.

За умовою розміри предмета та його зображення збігаються. А це можливо тоді, коли предмет розташований у подвійному фокусі збиральної лінзи. Тоді зображення отримуємо теж у подвійному фокусі лінзи (за побудовою), дійсне, перевернуте, рівне за розмірами предмету (див. рисунок).

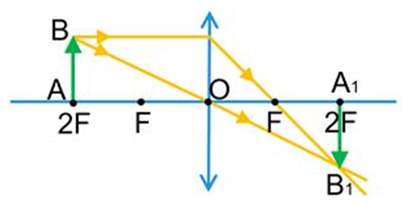
За умовою відома відстань між предметом $AB$ і його зображенням $A_1B_1$ ‒ це довжина відрізка $AA_1=1,6\ \text{м}.$

Скористаймося формулою тонкої лінзи, щоб визначити її оптичну силу $D:$ $$ D=\frac 1d+\frac 1f, $$ де $d$ ‒ відстань від предмета до лінзи ($d=AO=2F$ ‒ двом фокусним відстаням), $f$ ‒ відстань від лінзи до зображення ($f=A_1O=2F$ ‒ двом фокусним відстаням). Отже, $$ d=f=\frac 12AA_1=\frac 12\cdot 1,6\ \text{м}=0,8\ \text{м}. $$

Обчислімо оптичну силу лінзи:

\begin{gather*} D=\frac{1}{0,8\ \text{м}}+\frac{1}{0,8\ \text{м}}=\frac{2}{0,8\ \text{м}}=2,5\ \text{дптр}. \end{gather*}

Відповідь: 2,5.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5556

Завдання 32 з 34

Визначте енергетичний вихід ядерної реакції

якщо енергія зв'язку ядра нукліда берилію дорівнює 56,4 МеВ, нукліда літію — 39,2 МеВ, а нукліда дейтерію — 2,2 МеВ. Відповідь запишіть у мегаелектронвольтах (МеВ).

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Енергія зв’язку атомних ядер.

Завдання скеровано на перевірку знання і розуміння енергетичного виходу ядерних реакцій.

Енергетичний вихід ядерної реакції можна визначити як різницю енергії зв’язку ядер до реакції та енергії зв’язку ядер після реакції: $$ \Delta E=|E_\text{до}-E_\text{після}|. $$

Якщо $E_\text{до}\gt E_\text{після},$ то ядерна реакція ендотермічна (супроводжується поглинанням тепла), а якщо $E_\text{до}\lt E_\text{після},$ то ядерна реакція екзотермічна (супроводжується виділенням тепла).

\begin{gather*} \Delta E=|(39,2\ \text{МеВ}+2,2\ \text{МеВ})-(56,4\ \text{МеВ})|=|41,4-56,4|\ \text{МеВ}=15\ \text{МеВ}. \end{gather*}

Ця реакція екзотермічна.

Відповідь: 15.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5557

Завдання 33 з 34

Невеличке тіло ковзає зі швидкістю 8 м/с по горизонтальній площині, наближаючись до щілини. Щілина утворена двома вертикальними паралельними стінками, розташованими на відстані 0,4 м одна від одної. Напрямок швидкості руху тіла, що ковзає, перпендикулярний до стінок, які утворюють щілину. Тіло падає на дно щілини глибиною 20 м. Прискорення вільного падіння дорівнює 10 м/с². Визначте кількість ударів тіла об стінки щілини, доки воно досягне дна. Удари тіла об стінки щілини вважайте абсолютно пружними. Опором руху знехтуйте.

Впишіть відповідь:

Пропустити Відповісти Читати пояснення

Наступне Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Механіка. Основи динаміки. Рух тіла під дією сили тяжіння.

Завдання скеровано на перевірку знання і розуміння руху тіла під дією сили тяжіння, а також вміння застосувати їх до нестандартного руху тіла, описаного в завданні.

Зробимо схематичний рисунок.

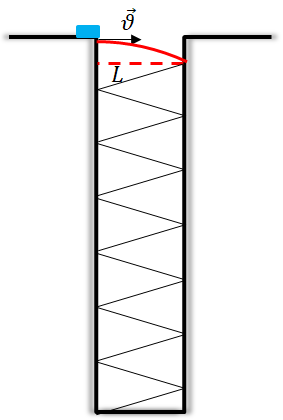
Діставшись краю щілини, тіло рухається далі, як ніби його кинули горизонтально зі швидкістю $\overrightarrow{v}.$ Дальність польоту дорівнюватиме ширині щілини $L.$

Визначімо спочатку час $t_1$ одного перельоту тіла від стінки до стінки:

\begin{gather*} L=v\cdot t_1,\\[6pt] t_1=\frac Lv,\\[6pt] t_1=\frac{0,4\ \text{м}}{8\ \text{м/с}}=0,05\ \text{с}. \end{gather*}

Під час такого руху швидкість зберігатиметься сталою, оскільки за умовою удари тіла об стінки щілини абсолютно пружні. Отже, і всі наступні проміжки часу між ударами зі стінками щілини будуть теж $0,05\ \text{с}.$

Одночасно з рівномірним прямолінійним рухом тіло падатиме вертикально рівноприскорено без початкової швидкості.

Тіло вдариться об стінки щілини $N$ разів, поки не впаде на дно щілини глибиною $H.$

Обчислімо час руху тіла від верхньої точки щілини до дна, якщо тіло падатиме вертикально рівноприскорено:

\begin{gather*} H=\frac{gt^2}{2},\\[6pt] t=\sqrt{\frac{2H}{g}},\\[6pt] t=\sqrt{\frac{2\cdot 20\ \text{м}}{10\ \text{м/с}^2}}=2\ \text{с}. \end{gather*}

Отже, якщо на один переліт від стінки до стінки витрачається $t_1=0,05\ \text{с},$ то можемо визначити кількість ударів: $$ N=\frac{t}{t_1}=\frac{2\ \text{с}}{0,05\ \text{с}}=40. $$

Відповідь: 40.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5558

Завдання 34 з 34

На скільки змістився у вертикальному напрямку електрон, що влетів горизонтально в плоский повітряний конденсатор з горизонтальним розташуванням пластин, на які подана напруга 9 В? Відстань між пластинами конденсатора дорівнює 1 см. Електрон влетів у конденсатор зі швидкістю 10⁷ м/с і пролетів у горизонтальному напрямку 10 см. Заряд електрона становить 1,6⋅10⁻¹⁹ Кл; маса електрона — 9⋅10⁻³¹ кг; прискорення вільного падіння дорівнює 10 м/с². Відповідь запишіть у міліметрах.

Впишіть відповідь:

Читати пояснення

Завершити тест

Коментарі доступні лише для зареєстрованих користувачів. Дивитись умови перегляду пояснень >>>.

Коментар

ТЕМА: Електродинаміка. Основи електростатики. Дія електричного поля на заряд.

Завдання скеровано на перевірку знання і розуміння руху зарядженої частинки (електрона) в однорідному електричному полі конденсатора.

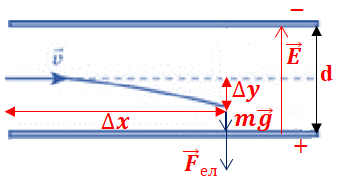
Електрон, який влітає між пластинами конденсатора, рухатиметься до позитивно зарядженої пластини. За час $t$ електрон пролетить відстань $\Delta x$ уздовж пластин і зміститься перпендикулярно до пластин, на відстань $\Delta y$ унаслідок дії на нього сили тяжіння $m\overrightarrow{g},$ а також дії електричного поля із силою $$ \overrightarrow{F}_\text{ел}=q\overrightarrow{E}=-e\overrightarrow{E} $$ (оскільки за умовою влітає електрон, заряд якого $e$), $$ \overrightarrow{F}_\text{ел} \uparrow\downarrow \overrightarrow{E}. $$

Електрон рухається горизонтально, відстань $\Delta x$ зі швидкістю $\overrightarrow{v}$ (електрон вважаємо нерелятивістським: $10^7\frac{\text{м}}{\text{с}}=\frac{1}{30}$ від швидкості світла). Можемо визначити час руху:

$$ t=\frac{\Delta x}{v}=\frac{10\cdot 10^{-2}\ \text{м}}{10^7\ \text{м/с}}=10^{-8}\ \text{с}. $$

Відстань $\Delta y,$ на яку зміститься електрон за цей самий час вертикально можна визначити за формулою (рух вертикальний рівноприскорений з прискоренням $\overrightarrow{a}$ без початкової швидкості): $$ \Delta y=\frac{at^2}{2}. $$

Щоб визначити прискорення, запишімо другий закон Ньютона для електрона, що рухається в однорідному електричному полі напруженістю $\overrightarrow{E}$ конденсатора: \begin{gather*} m\overrightarrow{a}=\overrightarrow{F}_\text{ел}+m\overrightarrow{g},\\[7pt] ma=F_\text{ел}+mg,\\[6pt] a=\frac{F_\text{ел}+mg}{m}=\frac{F_\text{ел}}{m}+g, \end{gather*} де $m$ ‒ маса електрона, $g$ ‒ прискорення вільного падіння, $F_\text{ел}=eE=e\frac Ud$ ($U$ ‒ напруга, подана на пластини конденсатора, $d$ ‒ відстань між пластинами).

\begin{gather*} a=\frac{eU}{dm}+g,\\[6pt] a=\frac{1,6\cdot 10^{-19}\ \text{Кл}\cdot 9\ \text{В}}{1\cdot 10^{-2}\ \text{м}\cdot 9\cdot 10^{-31}\ \text{кг}}+10\frac{\text{м}}{\text{с}^2}=1,6\cdot 10^{14}\frac{\text{м}}{\text{с}^2}+10\frac{\text{м}}{\text{с}^2}=1,6\cdot 10^{14}\frac{\text{м}}{\text{с}^2}, \end{gather*}

(прискоренням вільного падіння можна знехтувати ‒ сила тяжіння набагато менша за силу електричного поля).

Визначімо вертикальне зміщення електрона:

\begin{gather*} \Delta y=\frac{at^2}{2}=\frac{1,6\cdot 10^{14}\ \text{м/с}^2\cdot (10^{-8}\ \text{с})^2}{2}=0,8\cdot 10^{-2}\ \text{м}=8\ \text{мм}. \end{gather*}

Відповідь: 8.

Вид завдання: Завдання відкритої форми з короткою відповіддю (1 вид)
Знайшли помилку? Пишіть на

Тест 108. Запитання: 5559

Новини

У ВР пропонують законодавчо запустити систему освітніх грантів
Рейтинговий, конкурсний, мінімальний, прохідний бал: як розібратись вступнику
Відвідайте онлайн День відкритих дверей в Європейському університеті

Інформація

Усі завдання ЗНО з фізики за темами
Усі тести ЗНО з фізики онлайн
Завдання й відповіді ЗНО з фізики минулих років
Усе про тест ЗНО з фізики
Програма ЗНО з фізики
Тести ЗНО онлайн з інших предметів
Дорожня карта учасника ЗНО
Дорожня карта вступника на бакалавра

Facebook

Twitter