ЗНО онлайн 2012 року з фізики – пробний тест

ТЕМА: Механіка. Основи кінематики. Матеріальна точка.

Завдання скеровано на перевірку знання і розуміння фізичної моделі ‒ матеріальної точки.

Матеріальна точка ‒ це фізична модель тіла, розмірами якого в умові задачі можна знехтувати. Те саме тіло в умовах однієї задачі можна вважати матеріальною точкою, а в умовах іншої ‒ ні.

Це визначення можна застосувати до ведмедя і бджоли. Наприклад, розглядаючи будову тіла бджоли, не можна знехтувати розмірами її тіла. А під час вивчення її руху – можна.

Те саме стосується і ведмедя. Коли вивчають анатомію тварини, розміри важливі. Коли ж спостерігають за міграцією ведмедя, розмірами можна знехтувати.

Отже, чи можна знехтувати розмірами тіла, чи ні, визначають умови, за яких це тіло розглядаємо.

Відповідь: B.

ТЕМА: Механіка. Основи кінематики. Доцентрове прискорення.

Завдання скеровано на перевірку знання і розуміння, від яких фізичних величин і як залежить доцентрове прискорення.

У разі рівномірного руху тіла по колу вектор прискорення напрямлений до центра кола ‒ саме тому прискорення рівномірного руху тіла по колу називають доцентровим прискоренням \(\overrightarrow{a}_\text{дц}.\) Модуль доцентрового прискорення обчислюють за формулою $$ a_\text{дц}=\frac{v^2}{r}, $$ де \(v\) ‒ лінійна швидкість руху тіла; \(r\) ‒ радіус кола.

Позначмо на рисунку центри \(O_1\) і \(O_2\) кожної з двох дуг і радіуси кіл \(CO_1\) і \(AO_2=BO_2:\)

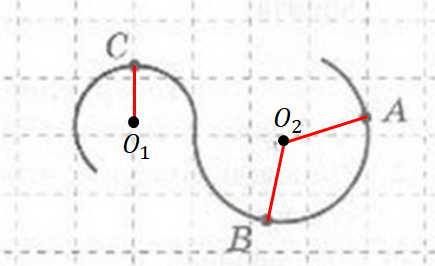
Запишімо формули для доцентрового прискорення в кожній точці: \begin{gather*} a_\mathrm{C}=\frac{v^2}{CO_1},\\[6pt] a_\mathrm{A}=\frac{v^2}{AO_2},\\[6pt] a_\mathrm{B}=\frac{v^2}{BO_2}. \end{gather*}

За умовою модуль швидкості тіла не змінюється. А за побудовою бачимо, що $$ AO_2=BO_2\gt CO_1. $$

Оскільки прискорення обернено пропорційне до радіуса кола $$ a_\text{дц}\sim \frac 1r, $$ то співвідношення між доцентровими прискореннями таке: $$ a_\mathrm{A}=a_\mathrm{B}\lt a_\mathrm{C}. $$

Відповідь: Б.

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу в рівномірному й рівноприскореному рухах.

Завдання скеровано на перевірку знання і розуміння кінематичних величин, уміння користуватися графіком.

Для рівноприскореного прямолінійного руху рівняння координати має вигляд: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) і \(x\) ‒ початкова і кінцева координата тіла відповідно через деякий інтервал часу \(t,\) \(v_0\) ‒ модуль швидкості руху тіла в момент початку відліку часу (початкова швидкість); \(a\) ‒ модуль прискорення руху тіла.

Із цього рівняння прискорення дорівнюватиме: $$ a=(x-x_0-v_0t)\cdot \frac{2}{t^2}. $$

Значення всіх величин візьмемо з графіка в умові: \begin{gather*} x_0=-10\ \text{м},\\[7pt] x=20\ \text{м},\\[7pt] t=2\ \text{с}. \end{gather*}

Початкова швидкість руху матеріальної точки дорівнює $$ v_0=3\ \text{м/c}. $$

Обчислімо прискорення цієї точки:

Відповідь: B.

ТЕМА: Механіка. Закони збереження в механіці. Імпульс тіла.

Завдання скеровано на перевірку знання і розуміння поняття імпульсу тіла, його напрямку й напрямку швидкості під час руху тіла, кинутого під кутом до горизонту.

Імпульс тіла \(\overrightarrow{p}\) ‒ це векторна фізична величина, яка дорівнює добутку маси \(m\) тіла на швидкість \(\overrightarrow{v}\) його руху: $$ \overrightarrow{p}=m\overrightarrow{v}. $$

У ході криволінійного руху напрямок швидкості руху весь час змінюється. Оскільки рівняння траєкторії руху тіла, кинутого з деякої висоти зі швидкістю під кутом до горизонту, має вигляд квадратичної функції (з виведенням формули можна ознайомитися в параграфах підручника з відповідної теми), то траєкторія руху тіла, якому поблизу поверхні Землі надано початкової швидкості, є параболічною (як в умові завдання).

Напрямок вектора імпульсу збігається з напрямком вектора швидкості: $$ \overrightarrow{p}\uparrow\uparrow \overrightarrow{v}. $$

У точці \(A,\) як і в будь-якій точці траєкторії будь-якого криволінійного руху тіла, швидкість напрямлена по дотичній.

Дотична ‒ це пряма, яка торкається кривої або поверхні в одній точці, не перетинаючи її. Якщо розглянути рисунок і візуально продовжити зображені промені в обидва боки, то дотична збігатиметься з напрямком \(2.\)

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Дифузія.

Завдання скеровано на перевірку знання і розуміння положень молекулярно-кінетичної теорії та явища дифузії, яке можна пояснити за цими положеннями.

Молекули, атоми, йони, між якими є проміжки, перебувають у безперервному хаотичному русі. Саме рухом частинок речовини можна пояснити таке явище, як дифузія.

Дифузія (від лат. diffusio ‒ поширення, розтікання) ‒ процес самовільного взаємного проникнення частинок однієї речовини у проміжки між частинками іншої (перемішування дотичних речовин), який відбувається внаслідок теплового руху цих частинок. Завдяки такому рухові речовини перемішуються без жодного зовнішнього втручання.

Пригадаймо, що молекули газів розташовані безладно й на відстанях, які в десятки разів більші за розміри самих молекул; молекули рідини розташовані хаотично, у розташуванні найближчих молекул зберігається певний (ближній) порядок, середня відстань між молекулами приблизно дорівнює розмірам самих молекул, кожна молекула час від часу перескакує з місця на місце; частинки твердих (кристалічних) тіл розташовані в певному порядку (утворюють кристалічні ґратки) на відстанях, що приблизно дорівнюють розмірам самих частинок, тому сили міжмолекулярної взаємодії (сили притягання між частинками) утримують їх біля положення рівноваги; на відміну від рідин, перескакування молекул у твердих тілах відбуваються дуже рідко.

Дифузія в рідині відбувається досить повільно (наприклад, сироп змішується з водою протягом доби), проте у твердих тілах дифузія повільніша в сотні й тисячі разів (дві відшліфовані та притиснуті одна до одної пластинки свинцю та золота «зростаються» на \(1\ \text{мм}\) протягом \(5\) років). У газах дифузія йде набагато швидше, ніж у рідинах, але все одно: якби не було конвекції (перенесення енергії потоками рідини або газу), запах парфумів поширювався би в кімнаті протягом годин.

Отже, як зазначено в умові, за інших однакових умов (як-от температура й тиск) найшвидше дифузія відбуватиметься в газах: у цьому завданні – між випарами ефіру й повітрям.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Стала Авогадро.

У будь-якій речовині кількістю \(1\ \text{моль}\) міститься однакова кількість атомів або молекул, ‒ стільки, скільки атомів Карбону міститься у вуглеці масою \(12\ \text{г}.\) Це стала Авогадро \(N_\mathrm{А},\) її одиниця – \(\text{моль}^{-1}.\)

Фізичну величину, яка дорівнює частці від ділення кількості структурних частинок речовини \(N\) до числа Авогадро, називають кількістю речовини \(\mathbf{\nu}:\) $$ \mathbf{\nu}=\frac{N(X)}{N_\mathrm{A}}, $$ де \(N(X)\) ‒ кількість структурних частинок речовини \(X.\)

Отже, щоб визначити кількість молекул \(N\) газу \(X\) у балоні, треба помножити одну порцію молекул \((N_\mathrm{А})\) на кількість цих порцій \((\mathbf{\nu}):\)

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.

Завдання скеровано на перевірку знання і розуміння ізопроцесів, а саме ізохорного.

Ізохорний процес ‒ це процес змінювання стану даного газу деякої маси, що відбувається за незмінного об’єму \((V=\mathrm{const}).\) Ділянки графіка \(2\rightarrow 3\) і \(4\rightarrow 1\) є ізохорами.

Що більшим є об’єм газу \((V_2\gt V_1),\) то менші концентрація цього газу й тиск, який він чинить. Ділянка графіка \(2\rightarrow 3\) (див. рисунок) відповідатиме ізохорному нагріванню, тому що температура підвищується, а ділянка графіка \(4\rightarrow 1\) ‒ це ізохорне охолодження.

Ділянки графіка \(1\rightarrow 2\) і \(3\rightarrow 4\) (див. рисунок) є ізобарами. Що більшим є тиск газу, за якого відбувається ізобарний процес \((p_2\gt p_1),\) то менший об’єм займає газ й то нижче розташована ізобара.

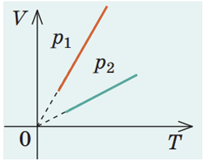
Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Середня квадратична швидкість теплового руху молекул.

Завдання скеровано на перевірку знання і розуміння зв’язку фізичних величин, що характеризують рух молекул ‒ середня квадратична швидкість руху молекул, середній квадрат швидкості, середня кінетична енергія поступального руху молекул ідеального газу.

Квадратний корінь із середнього квадрата швидкості називають середньою квадратичною швидкістю руху молекул \((\overrightarrow{v}_\text{кв}):\) $$ \overrightarrow{v}_\text{кв}=\sqrt{\overline{v^2}}. $$

(Середній квадрат швидкості \((\overline{v^2}):\) $$ \overline{v^2}=\frac{v_1^2+v_2^2+\text{...}+v_N^2}{N}, $$ де \(N\) ‒ кількість молекул; \(v_1, v_2, \text{...} v_N\) ‒ швидкості руху окремих молекул.)

Середній квадрат швидкості \(\overline{v^2}\) можна визначити з формули для середньої кінетичної енергії \(\overline{E}_\text{к}\) поступального руху молекул ідеального газу (кінетична енергія поступального руху, що в середньому припадає на одну молекулу масою \(m_0\)): $$ \overline{E}_\text{к}=\frac{m_0\overline{v^2}}{2}. $$

Залежність середньої кінетичної енергії поступального руху молекул ідеального газу від абсолютної температури \(T\) визначмо за формулою: $$ \overline{E}_\text{к}=\frac 32kT, $$ де \(k\) ‒ стала Больцмана.

Прирівняймо обидва вирази для визначення середньої кінетичної енергії поступального руху молекул ідеального газу: $$ \frac{m_0\overline{v^2}}{2}=\frac 32kT, $$ звідки $$ \overline{v^2}=\frac{3kT}{m_0}. $$

Отже, коли склянку заповнили снігом (див. рисунок 1), то температура становила \(t_1=-23\ ^\circ\mathrm{C}\) (абсолютна температура дорівнюватиме \(T_1=t_1+273=-23+273=250\ \text{K}\): $$ \overline{v}_\text{кв1}=\sqrt{\overline{v_1^2}}=\sqrt{\frac{3kT_1}{m_0}}. $$

Коли сніг у склянці розтанув, а вода нагрілася (див. рисунок 2), то температура \(t_2=87\ ^\circ\mathrm{C}\) (абсолютна температура дорівнюватиме \(T_2=t_2+273=87+273=360\ \text{K}\): $$ \overline{v}_\text{кв2}=\sqrt{\overline{v_2^2}}=\sqrt{\frac{3kT_2}{m_0}}. $$

Тепер визначимо, у скільки разів збільшилася середня квадратична швидкість руху молекул гелію в кульці:

Отже, середня квадратична швидкість руху молекул гелію в кульці збільшилася в \(1\mathord{,}2\) раза.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Кількість теплоти. Питома теплоємність речовини.

Завдання скеровано на перевірку знання і розуміння фізичного змісту питомої теплоємності речовини.

Питома теплоємність речовини \(c\) ‒ це фізична величина, що характеризує речовину й чисельно дорівнює кількості теплоти, яку необхідно передати речовині масою \(1\ \text{кг},\) щоб нагріти її на \(1\ ^\circ\mathrm{C}:\) $$ c=\frac{Q}{m\Delta t}. $$

За умовою маси тіл однакові. Узявши до уваги, що за той самий час тілам передавали однакову кількість теплоти, робимо висновок, що питома теплоємність обернено залежатиме лише від різниці температур (скористаємося графіком, проміжок часу візьмемо від \(0\) до \(2\mathord{,}5\) год):

Отже, запишімо співвідношення між питомими теплоємностями цих трьох тіл: $$ c_2\lt c_3\lt c_1. $$

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря та її вимірювання.

Завдання скеровано на перевірку знання і розуміння поняття вологості повітря.

Людина найкомфортніше почувається, коли температура повітря перебуває в межах від \(18\) до \(22\ ^\circ\mathrm{C},\) а рівень вологості ‒ від \(40\) до \(60\ \text{%}.\)

За високих температур краще, щоб була низька вологість, тобто щоб уміст водяної пари в повітрі був невеликий, тоді волога з поверхні людини випаровуватиметься інтенсивніше ‒ молекули води забиратимуть енергію, а тому температура тіла людини знижуватиметься, тіло охолоджуватиметься, тож людина легше переноситиме спеку.

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Електричний заряд.

Завдання скеровано на перевірку знання і розуміння основ утворення позитивно і негативно заряджених тіл.

Існують два роди електричних зарядів ‒ позитивні і негативні. Електричний заряд такого роду, як заряд, отриманий на бурштині або ебонітовій паличці, потертих об вовну, заведено називати негативним, а такого роду, як заряд, отриманий на паличці зі скла, потертій об шовк або папір, ‒ позитивним.

Вовна втримує свої електрони менш міцно, ніж ебоніт, тому під час контакту електрони переважно переходять із вовни на ебонітову паличку, а не навпаки. Отже, після роз’єднання паличка стає негативно зарядженим фізичним тілом, а вовна ‒ позитивно зарядженим.

Отже, електрони під час електризації тертям переходять із шерсті на ебонітову паличку.

Відповідь: B.

ТЕМА: Електродинаміка. Основи електростатики. Закон Кулона.

Завдання скеровано на перевірку знання і розуміння того, від яких фізичних величин і як залежить сила Кулона.

Закон Кулона: сила \(F\) взаємодії двох нерухомих точкових зарядів \(q_1\) і \(q_2\) прямо пропорційна добутку модулів цих зарядів й обернено пропорційна квадрату відстані \(r\) між ними: $$ F=k\frac{|q_1|\cdot |q_2|}{r^2}, $$ де \(k\) ‒ коефіцієнт пропорційності.

Отже, правильне твердження: «Сила кулонівської взаємодії двох нерухомих точкових заряджених тіл обернено пропорційна квадрату відстані між ними».

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики.

Завдання скеровано на перевірку знання і розуміння властивостей розміщення статичного заряду, принципу суперпозиції полів.

Електрон рухається рівномірно там, де електричне поле не діє. На інших ділянках швидкість електрона змінюватиметься. Рівномірно заряджена сфера, заряд якої дорівнює \(Q,\) створює ззовні таке електричне поле, як і точковий заряд \(Q,\) розташований у центрі сфери. Усередині ж сфери електричного поля немає. Увесь статичний заряд провідника зосереджений на його поверхні. Ця властивість є наслідком закону Кулона й властивості однойменних зарядів відштовхуватися.

У цій ситуації поля в точці немає, якщо сумарний заряд усіх внутрішніх для заданої точки сфер дорівнює нулю. Отже, електричного поля немає лише всередині найменшої сфери.

Ззовні найменшої сфери діє поле із зарядом \(+q.\) І воно накладається на поле найбільшої кулі із зарядом \(‒2q,\) тому ззовні всіх куль сумарний заряд дорівнюватиме \(‒q.\) Якщо подумки розбити траєкторію руху електрона на п᾽ять десятисантиметрових відрізків, то на двох останніх відрізках (тобто всередині найменшої кулі, \(20\ \text{см}\)) поля немає. А на трьох перших відрізках (тобто загалом \(30\ \text{см}\)) електрон рухатиметься під дією електричних полів, тобто його швидкість змінюватиметься.

Відповідь: B.

ТЕМА: Електродинаміка. Основи електростатики. Зв᾽язок між напругою і напруженістю однорідного електричного поля. Електроємність плоского конденсатора.

Завдання скеровано на перевірку знання і розуміння зв᾽язку електростатичних величин ‒ напруги, напруженості, електроємності і характеристик конденсатора.

Напруженість \(E\) електричного поля між пластинами плоского конденсатора можна визначити за формулою: $$ E=\frac Ud, $$ де \(U\) ‒ напруга, \(d\) ‒ відстань між пластинами плоского конденсатора.

Оскільки конденсатор зарядили і відключили від батарейки, то його заряд \(q\) не мінятиметься і дорівнюватиме: $$ q=UC,\ \text{звідки}\ U=\frac qC, $$ де \(C\) ‒ електроємність конденсатора.

Електроємність плоского конденсатора обчислюємо за формулою: $$ C=\frac{\mathbf{\varepsilon}\mathbf{\varepsilon}_0S}{d}, $$ де \(\mathbf{\varepsilon}_0=8\mathord{,}85\cdot 10^{-12}\ \text{Ф/м}\) ‒ електрична стала; \(\mathbf{\varepsilon}\) ‒ діелектрична проникність діелектрика; \(S\) ‒ площа пластини конденсатора; \(d\) ‒ відстань між пластинами.

Підставимо вирази для напруги і електроємності у формулу для напруженості: $$ E=\frac Ud=\frac{q\cdot d}{d\cdot \mathbf{\varepsilon}\mathbf{\varepsilon}_0S}=\frac{q}{\mathbf{\varepsilon}\mathbf{\varepsilon}_0S}. $$

Виходячи з даних умови, що діелектрична проникність слюди вшестеро більша за діелектричну проникність повітря, робимо висновок, що якщо у простір між пластинами конденсатора помістити слюдяну пластинку, то напруженість такого конденсатора зменшиться в \(6\) разів:

У другому ж випадку, коли пластини конденсатора розсовують, не заповнюючи простір між ними діелектриком, легко бачити, що напруженість залишиться незмінною, оскільки за формулою вона не залежить від відстані між пластинами: $$ E=\frac{q}{\mathbf{\varepsilon}\mathbf{\varepsilon}_0S},\ \ E=\mathrm{const}. $$

Відповідь: Г.

ТЕМА: Електродинаміка. Основи електростатики. Робота електричного поля при переміщеннi заряду. Потенціал і різниця потенціалу.

Завдання скеровано на перевірку знання і розуміння закону збереження енергії під час переміщення заряду електричним полем.

Найдоцільніше скористатися законом збереження енергії: $$ q\mathbf{\varphi}_1+\frac{mv_1^2}{2}=q\mathbf{\varphi}_2+\frac{mv_2^2}{2}, $$ де \(\mathbf{\varphi}_1\) і \(\mathbf{\varphi}_2\) ‒ потенціали у відповідних до умови завдання точках поля, \(v_1\) і \(v_2\) ‒ швидкості електрона у відповідних точках, \(q\) ‒ заряд електрона, \(m\) ‒ маса електрона.

Візьмімо до уваги, що за умовою \(v_2=0,\) а заряд електрона негативний \(q=-e.\) Отримаємо

Відповідь: B.

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.

Завдання скеровано на перевірку розуміння послідовного і паралельного з’єднань провідників і відповідних їм фізичних величин, уміння описувати аналітично схеми (ділянки схем) електричного кола й застосовувати закон Ома для ділянки кола.

Напруга на кінцях зображеної на рисунку ділянки електричного кола складається з напруги на першому резисторі й напруги на ділянці паралельно з’єднаних резисторів \(2\) і \(3,\) тому що резистор \(1\) і ділянка кола з резисторами \(2\) і \(3\) з’єднані послідовно. Обчислімо зазначені напруги, і тоді зможемо визначити загальну напругу на зображеній ділянці.

Почнімо з резистора \(3:\) відомий його опір і сила струму, яку показує амперметр. За законом Ома для ділянки кола зможемо обчислити напругу на цьому резисторі:

Напруга на кожному з паралельно з’єднаних провідників є однаковою: $$ U_3=U_2=4\ \text{В}. $$

За значеннями напруги на резисторі \(2\) та його опору зможемо обчислити силу струму, що проходить крізь резистор \(2:\) $$ I_2=\frac{U_2}{R_2}=\frac{4\ \text{В}}{5\ \text{Ом}}=0\mathord{,}8\ \text{А}. $$

(Дійсно, опори резисторів \(2\) і \(3\) відрізняються вчетверо, отже, і сили струму відрізнятимуться вчетверо ‒ обернена залежність).

Отже, загальний струм у ділянці кола \(I_1,\) тобто струм, що проходитиме крізь резистор \(1,\) дорівнюватиме сумі струмів \(I_2\) і \(I_3\) після розгалуження:

Визначмо напругу на резисторі \(1:\)

Обчислімо загальну напругу на зображеній ділянці електричного кола:

Відповідь: B.

ТЕМА: Електродинаміка. Закони постійного струму. Електровимірювальні прилади.

Завдання скеровано на перевірку знання і розуміння, що таке вольтметр і як його правильно підключати в електричне коло.

Вольтметр ‒ це прилад для вимірювання напруги. Його приєднують до електричного кола паралельно ділянці, на якій вимірюють напругу, щоб забезпечити мінімальний вплив високого опору вольтметра на вимірювані величини.

Отже, щоб виміряти напругу на джерелі струму, треба вольтметр підключити до точок \(A\) та \(E.\) Оскільки такої пари точок немає серед варіантів відповіді, то є варіант підключення вольтметра до точок \(B\) і \(E,\) це, власне, те саме.

Відповідь: Г.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на перевірку знання і розуміння принципу будови коливального контуру, і вміння проаналізувати перетворення енергії в цьому контурі.

Після замикання ключа конденсатор заряджатиметься. У той момент, коли його заряд стане максимальним, струм на цій ділянці припиниться. Отже, коли ключ замкнуто, то електричний струм тече через котушку й резистор, а на конденсаторі буде тільки спад напруги (струм крізь нього не тече). На котушці не буде спаду напруги, а струм, що тече через котушку, дорівнюватиме струму, що тече через резистор. Обчислімо силу струму \(I\) в колі з резистором і котушкою до розмикання ключа: $$ I=\frac{\mathbf{\varepsilon}}{R+r}, $$ де \(\mathbf{\varepsilon}\) ‒ електрорушійна сила джерела струму, \(R\) ‒ опір резистора, \(r\) ‒ внутрішній опір джерела струму. $$ I=\frac{10\mathord{,}01\ \text{В}}{1000\ \text{Ом}+1\ \text{Ом}}=0\mathord{,}01\ \text{А}. $$

Обчислімо спад напруги на конденсаторі до розмикання ключа: $$ U_C=U_R+U_L\approx U_R, $$ тому що в котушці протікає постійний струм. А тому індуктивний опір \(X_L\) її дорівнює: $$ X_L=\mathbf{\omega}L=0\cdot L=0, $$ де \(\mathbf{\omega}\) ‒ циклічна частота змінного струму, \(L\) ‒ індуктивність котушки.

Отже,

Після розмикання ключа конденсатор розряджатиметься на котушці й резисторі. Тобто виникнуть згасні (бо є резистор) електромагнітні коливання.

У початковий момент, після розмикання ключа, енергія коливань ‒ це накопичена енергія конденсатором і котушкою. Із закону збереження енергії очевидно, що вся енергія, яку має коливальний контур до розмикання ключа, перетвориться на тепло.

Визначмо кількість теплоти, яка виділяється на резисторі за час існування змінного струму в колі \(C-L-R\) (доки не згаснуть електромагнітні коливання в цьому коливальному контурі). У кінцевому випадку конденсатор після кількох заряджань і розряджань буде розрядженим, а в котушці струм зникне: \begin{gather*} W_\text{ел}+W_\text{маг}=Q,\\[6pt] Q=\frac{CU_C^2}{2}+\frac{LI^2}{2}. \end{gather*}

Обчислімо шукану кількість теплоти:

Відповідь: Б.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рух зарядженої частинки в магнітному полі.

Сила Лоренца завжди перпендикулярна до швидкості руху частинки, тому вона не виконує роботу і не змінює кінетичну енергію частинки, бо під дією сили Лоренца заряджена частинка рухається рівномірно. Проте траєкторія руху частинки буде різною ‒ залежно від того, під яким кутом частинка влетіла в магнітне поле і чи є магнітне поле однорідним.

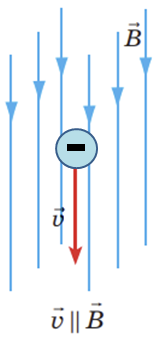
За умовою електрон влітає в однорідне магнітне поле зі швидкістю, паралельною до вектора магнітної індукції (див. рисунок).

У цьому разі кут \(\mathbf{\alpha}\) між вектором швидкості \(\overrightarrow{v}\) і вектором магнітної індукції \(\overrightarrow{B}\) дорівнює нулю (або \(180^\circ\)). Оскільки \(\sin \mathbf{\alpha}=0,\) то дорівнює нулю і сила Лоренца: $$ F_\text{Л}=|q|Bv\sin\mathbf{\alpha}=0. $$

Отже, магнітне поле не діє на електрон, тому, якщо немає інших сил, електрон рухатиметься рівномірно прямолінійно вздовж ліній магнітної індукції і траєкторією руху електрона буде пряма лінія.

Відповідь: A.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік. Закон електромагнітної індукції.

Завдання скеровано на перевірку знання і розуміння виникнення індукційного струму в рамці під дією магнітного поля, уміння чисельно його описати.

Під час обертання замкнутої рамки в магнітному полі у ній збуджується індукційне електричне поле, електрорушійна сила \(\mathbf{\varepsilon}\) якого згідно із законом електромагнітної індукції дорівнює: $$ \mathbf{\varepsilon}_i=-\frac{\Delta \text{Ф}}{\Delta t}. $$

Зміна магнітного потоку \(\Delta \text{Ф}\) за час \(\Delta t\) обертання рамки на кут \(180^\circ\) дорівнюватиме:

де \(B=\mathrm{const}\) ‒ магнітна індукція, магнітне поле однорідне; \(S=\mathrm{const}\) ‒ площа поверхні, обмежена рамкою, яка під час обертання не деформується; \(\mathbf{\alpha}\) ‒ кут між вектором нормалі \(\ \overrightarrow{n}\) до площини рамки й вектором магнітної індукції \(\overrightarrow{B}.\)

За умовою \(\mathbf{\alpha}_1=0\) (рамка лежить горизонтально, а магнітне поле вертикальне). Тоді

З іншого боку, сила індукційного струму \(I\) в рамці дорівнює: $$ I=\frac{\Delta q}{\Delta t}, $$ де \(\Delta q\) ‒ електричний заряд, що пройшов у рамці за проміжок часу \(\Delta t.\)

Звідси $$ \Delta q=I\Delta t. $$

Отже, зваживши ще й на закон Ома (\(I=\frac{\mathbf{\varepsilon}_i}{R},\ R\) ‒ опір рамки), отримаємо формулу для обчислення заряду в рамці, яку повернули на \(180^\circ\) навколо однієї сторони:

Відповідь: Г.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Перетворення енергії при гармонічних коливаннях.

Завдання скеровано на перевірку знання і розуміння перетворення енергії під час гармонічних коливань, а також уміння читати рівняння гармонічних коливань і брати з нього необхідні дані для розв’язання.

Потенціальна енергія \(E_p\) пружини маятника дорівнює: $$ E_p=\frac{kx^2}{2}, $$ де \(k\) ‒ жорсткість пружини, \(x\) ‒ видовження пружини.

Визначмо координату маятника в момент часу \(t_1=2\ \text{c}:\)

Підставмо цей вираз для координати у формулу для потенціальної енергії:

Запишімо закон збереження енергії для двох різних моментів часу ‒ для \(t_1=2\ \text{c}\) й для другого моменту часу \(t_2,\) коли тіло маятника зупинилося, а пружина розтягнулася на максимальну довжину \(A:\) $$ E_{k1}+E_{p1}=E_{k2}+E_{p2}, $$ де \(E_{k1}\) ‒ кінетична енергія в момент часу \(t_1=2\ \text{c},\) яку треба визначити; \(E_{p1}\) ‒ потенціальна енергія в момент часу \(t_1=2\ \text{c},\) значення якої дано в умові; \(E_{k2}=0\) ‒ ми наклали умову, що тіло маятника зупинилося; \(E_{p2}=\frac{kA^2}{2}\) ‒ максимальне значення потенціальної енергії за максимального розтягу пружини.

Отже,

Робімо висновок, що $$ E_{k1}=E_{p1}=10\ \text{мДж}. $$

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки.

Завдання скеровано на перевірку знання і розуміння будови дифракційної ґратки й уміння визначати її період.

Періодом ґратки або сталою ґратки називають загальну ширину \(d\) непрозорої \(b\) та прозорої \(a\) ділянок дифракційної ґратки: $$ d=b+a=\frac lN, $$ де \(N\) ‒ кількість штрихів на відрізку довжиною \(l\).

Визначмо загальну довжину \(l_0\) усіх ліній разом із проміжками між ними, які накреслили на аркуші паперу згідно з умовою завдання та пояснювальним рисунком до неї:

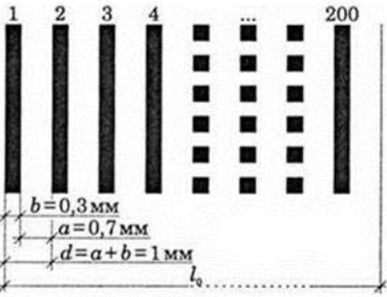
Відповідно до умови обчислімо довжину \(l\) дифракційної ґратки після зменшення зображення \(l_0\) у \(50\) разів: $$ l=\frac{l_0}{50}=\frac{0\mathord{,}2\ \text{м}}{50}=4\cdot 10^{-3}\ \text{м}. $$

Визначмо період дифракційної ґратки:

Відповідь: Г.

ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.

Завдання скеровано на перевірку знання і розуміння побудови зображень у різних оптичних пристроях.

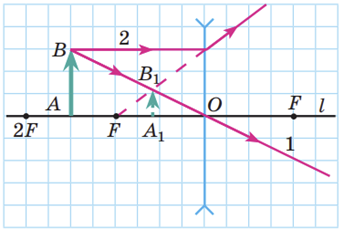
Побудова зображень, одержаних за допомогою розсіювальної лінзи, показує, що розсіювальна лінза завжди дає уявне, зменшене, пряме зображення предмета.

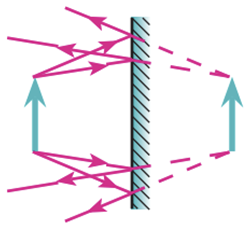
Зображення предмета в плоскому дзеркалі є уявним і прямим, дорівнює за розміром самому предмету й розташоване на тій самій відстані від дзеркала, що й предмет.

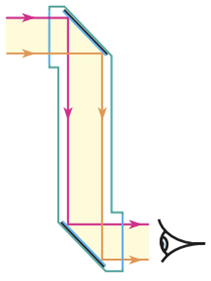
Перископ ‒ оптичний прилад, що дає змогу спостерігати за об’єктом, що перебуває в горизонтальній площині, яка не збігається з горизонтальною площиною ока спостерігача. Найпростіша конструкція пристрою ‒ це вертикальна труба з двома, нахиленими під кутом \(45^\circ\) дзеркалами або призмами з повним внутрішнім відбиванням, що розташовані паралельно одне одному в різних кінцях труби зі зверненими одна до одної поверхнями відбивання. Тобто уявне і пряме зображення дорівнює за розміром самому предмету.

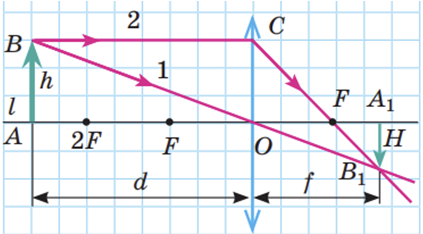
Якщо ж предмет розташований за подвійним фокусом збиральної лінзи, його зображення, одержане за допомогою лінзи, є дійсним, зменшеним, перевернутим. Таке зображення, наприклад, на сітківці ока або на матриці фотоапарата.

В усіх інших варіантах розташування предмета відносно лінзи орієнтуємося за таблицею.

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Фотоефект й експериментально встановлені його закони.

Завдання скеровано на перевірку знання і розуміння роботи виходу електрона.

Робота виходу \(A_\text{вих}\) ‒ це фізична величина, що характеризує метал і дорівнює енергії, яку треба передати електрону для того, щоб він зміг подолати сили, що втримують його на поверхні цього металу.

Для кожної речовини існує максимальна довжина світлової хвилі

за якої починається фотоефект. Опромінення речовини світловими хвилями, які мають більшу довжину, фотоефекту не викликає. Максимальна довжина світлової хвилі (мінімальна частота) відповідає мінімальній енергії фотона: якщо $$ h\mathbf{\nu}\lt A_\text{вих}, $$ то електрони не вилітатимуть із речовини. Умова $$ A_\text{вих}=h\mathbf{\nu}_\text{min}=\frac{hc}{\mathbf{\lambda}_\text{max}} $$ визначає червону межу фотоефекту.

Обчислімо роботу виходу електрона з деякого металу за даними завдання:

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Склад ядра атома.

Завдання скеровано на перевірку знання і розуміння будови атома.

Атом є електрично нейтральним: сумарний заряд протонів у ядрі дорівнює сумарному заряду електронів, що розташовані навколо ядра. Оскільки заряд протона за модулем дорівнює заряду електрона, то зрозуміло, що в атомі кількість протонів \(N_p\) дорівнює кількості електронів \(N_e.\) Кількість протонів \(N_p\) у ядрі називають зарядовим (протонним) числом і позначають символом \(Z.\) Порядковий номер елемента в системі хімічних елементів відповідає кількості протонів у ядрі (зарядовому числу).

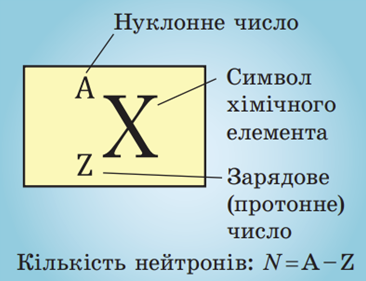
Отже, $$ N_e=N_p=Z=9\ \text{електронів}. $$

Відповідь: Г.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на перевірку знання і розуміння фізичних величин, що описують рух тіла по колу, і вміння їх визначати.

1. Модуль переміщення \(s\) дорівнюватиме довжині відрізка, що з’єднує початкову точку \(1\) з кінцевою точкою \(2.\) З рисунка бачимо, що відрізок \(1-2\) дорівнює довжині двох радіусів \(R\) кола: $$ s=2R - \text{вираз}\ \textbf{Г}. $$

2. Шлях \(l\) – це довжина траєкторії руху тіла, у цьому разі – довжина півкола: $$ l=\frac{2\mathbf{\pi}R}{2}=\mathbf{\pi}R - \text{вираз}\ \textbf{В}. $$

3. Швидкість руху \(v\) тіла по колу обчислімо за формулою $$ v=\frac{2\mathbf{\pi}R}{T}, $$ де \(T\) – період обертання. Оскільки тіло пройшло лише половину шляху (півкола), то за умовою завдання час руху тіла дорівнює \begin{gather*} t=\frac T2,\\[6pt] T=2t,\\[6pt] v=\frac{2\mathbf{\pi}R}{2t}=\frac{\mathbf{\pi}R}{t} - \text{вираз}\ \textbf{Б}. \end{gather*}

4. Кутову швидкість визначмо з формули, яка пов’язує кутову і лінійну швидкості: \begin{gather*} v=\mathbf{\omega}R,\\[6pt] \mathbf{\omega}=\frac vR=\frac{\mathbf{\pi}R}{t\cdot R}=\frac{\mathbf{\pi}}{t} - \text{вираз}\ \textbf{А}. \end{gather*}

Відповідь: 1Г, 2В, 3Б, 4А.

ТЕМА: Електродинаміка. Робота поля з переміщення заряду.

Завдання скеровано на перевірку знання і розуміння загального поняття роботи у фізиці, а також вміння визначати, від яких параметрів залежить робота різних полів.

Робота у фізиці – характеристика дії сили на тіло, що залежить від величини й напрямку цієї сили та переміщення точки її прикладання.

Запишімо загальну формулу роботи сили. Робота сили дорівнює добутку модуля сили \(F,\) модуля переміщення \(s\) і косинуса кута \(\mathbf{\alpha}\) між вектором сили й вектором переміщення: $$ A=Fs\cos\mathbf{\alpha}. $$

1. Вихрове електричне поле. Змінне магнітне поле завжди супроводжується появою вихрового електричного поля. Саме вихрове електричне поле діє на вільні заряджені частинки в провіднику й надає їм напрямленого руху, створюючи індукційний струм.

Робота вихрового електричного поля на замкненій траєкторії зазвичай не дорівнює нулю.

Робота вихрового електричного поля з переміщення одиничного позитивного заряду по замкнутому нерухомому провіднику чисельно дорівнює ЕРС індукції в цьому провіднику.

2. Електричне поле – форма матерії, яка існує навколо заряджених тіл і виявляється в дії з деякою силою на заряджене тіло, що перебуває в цьому полі.

Електричне поле є складником єдиного електромагнітного поля. Джерелами електричного поля можуть бути рухомі й нерухомі електричні заряди та змінні магнітні поля.

Електричне поле, створене лише нерухомими зарядами, є незмінним у часі (статичним). Таке поле називають електростатичним.

Нехай в однорідному електричному полі напруженістю \(\overrightarrow{E}\) позитивний точковий заряд \(q\) переміщується з точки \(1\) з координатою \(x_1\) у точку \(2\) з координатою \(x_2\) (див. рисунок). Обчислімо роботу \(A,\) яку виконує сила \(\overrightarrow{F},\) що діє на заряд з боку електростатичного поля.

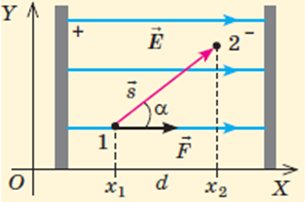
За означенням роботи: $$ A=Fs\cos\mathbf{\alpha}. $$

Поле однорідне, тому сила \(\overrightarrow{F}\) є незмінною, її модуль дорівнює: $$ F=qE, $$ а \(s\cos\mathbf{\alpha}=x_2-x_1\) є проєкцією вектора переміщення на напрямок силових ліній поля.

Отже, робота сил однорідного електростатичного поля в ході переміщення електричного заряду \(q\) із точки \(1\) у точку \(2\ (A_{1\rightarrow 2})\) дорівнює:

Формула \(A_{1\rightarrow 2}=qEd\) справджуватиметься у випадках руху заряду будь-якою траєкторією. Тобто однорідне електростатичне поле є потенціальним. Потенціальним є будь-яке електростатичне поле: робота електростатичних (кулонівських) сил (як і робота гравітаційних сил) не залежить від форми траєкторії, якою переміщується заряд, а визначається початковим і кінцевим положеннями заряду (Б). У випадку замкненої траєкторії руху заряду робота сил поля дорівнює нулю.

3. Гравітаційне поле існує навколо будь-якого тіла і виявляється у взаємному притяганні тіл одне до одного. Визначити силу \(F\) гравітаційної взаємодії можна за законом всесвітнього тяжіння: $$ F=G\frac{m_1m_2}{r^2}, $$ де \(m_1\) – маса одного тіла, \(m_2\) – маса другого тіла, \(r\) – відстань між тілами, \(G\) – гравітаційна стала.

Отже, сила, а значить, і робота гравітаційного поля залежатиме від маси частинки, не залежатиме від форми траєкторії, але від відстані (переміщення) залежатиме, тобто від положення початкової та кінцевої точок руху частинки (Г).

4. Магнітне поле – складник електромагнітного поля, основною властивістю якої є дія на рухомі заряджені частинки. Силова характеристика магнітного поля – вектор магнітної індукції \(\overrightarrow{B}.\) Сила, з якою магнітне поле діє на частинку (сила Лоренца \(F_\text{Л}\)), прямо пропорційна заряду \(q\) і швидкості \(v\) руху частинки: $$ F_\text{Л}=qBv\sin\mathbf{\alpha}, $$ де \(\mathbf{\alpha}\) – кут між напрямком руху частинки й напрямком магнітної індукції магнітного поля. Напрямок сили Лоренца визначають за правилом лівої руки: лінії магнітної індукції «ловимо» в долоню, чотири витягнуті пальці спрямовуємо за напрямком руху позитивно зарядженої частинки (або протилежно до руху негативно зарядженої), і тоді відігнутий на \(90^\circ\) великий палець укаже напрямок сили Лоренца (див. рисунок).

Тобто, ця сила напрямлена перпендикулярно до швидкості руху заряду й напрямку магнітного поля. А напрямок швидкості руху тіла збігається з напрямком його переміщення. Через це робота, що її виконує магнітне поле над частинкою, дорівнює нулю: $$ \cos90^\circ=0\Rightarrow A=Fs\cos\mathbf{\alpha}=0. $$

Відповідь: 1Д, 2Б, 3Г, 4А.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Поперечні та поздовжні хвилі.

Завдання скеровано на перевірку знання і розуміння руху точок хвилі.

Перш за все нагадаймо, що кожна точка шнура здійснює коливання. Коли зміщення від положення рівноваги максимальне за модулем, напрямок руху точки змінюється на протилежний, тобто в такі моменти швидкість руху точки дорівнює нулю. Але такі точки на шнурі не позначено.

На рисунку покажемо форму шнура через невеликий проміжок часу (точки на шнурі вже позначено штрихами).

Ми бачимо, що точки А та Г опустилися (найближчий гребінь хвилі віддалився від неї), а точки Б, В та Д піднялися (до кожної з них наблизився сусідній гребінь хвилі).

На кожну точку хвилі завжди діє сила, яка намагається повернути її до положення рівноваги, а згідно із другим законом Ньютона напрямок сили збігається з напрямком прискорення точки. Отже, прискорення кожної точки хвилі завжди напрямлене до положення рівноваги, коли шнур був у спокої.

Отже,
1 - швидкість напрямлена вниз, прискорення вгору ‒ точка Г,
2 - швидкість і прискорення напрямлені вгору ‒ точка В,
3 - швидкість і прискорення напрямлені вниз ‒ точка А,
4 - швидкість напрямлена вгору, прискорення вниз ‒ точка Д.

Відповідь: 1Г, 2В, 3А, 4Д.

ТЕМА: Коливання і хвилі. Оптика.

Завдання скеровано на перевірку знання і розуміння оптичних явищ геометричної і хвильової оптики.

1) Поширення світла в тумані ‒ А. Розсіювання світла туманом відбувається через взаємодію світлових променів з малими частинками води або інших речовин у тумані. Коли світло зустрічає ці частинки, воно розсіюється в усі напрямки, що дає змогу спостерігати туман як прозору або розсіяну масу, а не яскравий промінь.

2) Світіння ліхтаря ‒ Б. Ліхтар є джерелом світла, випромінювачем.

3) Проходження світла крізь вузький отвір ‒ Г. Дифракція ‒ явище обгинання хвилями перешкод або будь-яке інше відхилення поширення хвилі від законів геометричної оптики.

4) Поширення світла у світловоді ‒ В. Повіне відбивання світла ‒ явище, за якого заломлення світла відсутнє (світло повністю відбивається від середовища з меншою оптичною густиною).

Відповідь: 1А, 2Б, 3Г, 4В.

ТЕМА: Механіка. Основи динаміки. Рух тіла під дією кількох сил.

Завдання скеровано на перевірку знання і розуміння руху тіла під дією кількох сил, і вміння описати цей рух за допомогою другого закону Ньютона.

Позначимо на рисунку сили, які діють на важки до і після перепалювання нитки.

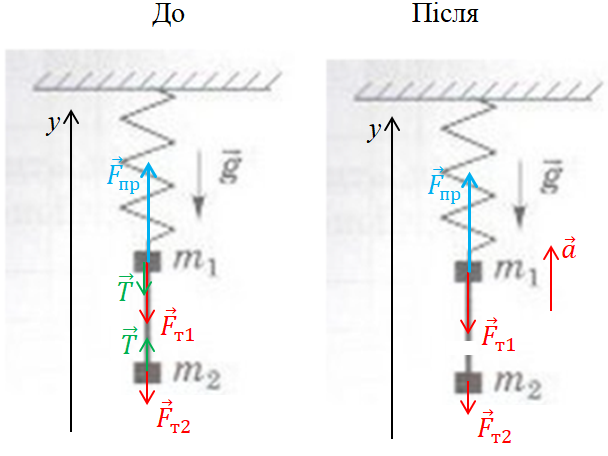
Запишімо другий закон Ньютона для обох випадків.

Підставмо вираз для сили пружності у формулу для прискорення і обчислимо його:

Відповідь: \(5.\)

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.

Завдання скеровано на перевірку знання і розуміння закону збереження імпульсу і руху під дією сили тяжіння.

У горизонтальному напрямку на систему осколків зовнішні сили не діють, хоча вертикально на них діє сила тяжіння (тобто система незамкнена). Отже, горизонтальна складова імпульсу не повинна змінюватися. Тому в горизонтальному напрямку виконуватиметься закон збереження імпульсу: $$ \overrightarrow{p}_\text{до розриву}=\overrightarrow{p}_\text{після розриву} $$

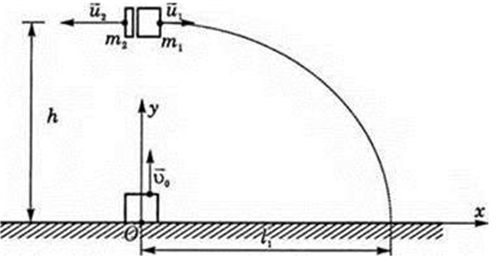
Запишемо проєкцію на вісь \(Ox:\)

Відстань \(l_1,\) яку пролетить більший осколок від точки пострілу до зіткнення з землею, дорівнюватиме: $$ l_1=u_1t_\text{п}, $$ де \(t_\text{п}\) ‒ час падіння (до речі пригадаємо, що під час руху під дією сили тяжіння час падіння дорівнює часу підйому \(t_\text{п}=t_\text{під}\)).

Визначмо час падіння, скориставшись тим, що з умови можна знайти час підйому. У верхній точці снаряд спочатку зупинився, а потім вже розірвався.

Запишімо рівняння для швидкості \(v\) руху снаряду спочатку у векторній формі, а потім у проєкції на вісь \(Oy:\) \begin{gather*} \overrightarrow{v}=\overrightarrow{v}_0+\overrightarrow{a}t,\\[7pt] 0=v_0-gt_\text{під}, \end{gather*} де \(v_0\) ‒ початкова швидкість снаряду, \(g\) ‒ прискорення вільного падіння.

Отже, $$ t_\text{п}=t_\text{під}=\frac{v_0}{g}. $$

Підставмо вирази для швидкості і часу у формулу для відстані, яку пролетить перший (більший) осколок (\(m_1=5m, m_2=m\) ‒ відповідно до умови): $$ l_1=u_1t_\text{п}=\frac{m_2u_2}{m_1}\cdot \frac{v_0}{g}. $$

Виконаймо обчислення: $$ l_1=\frac{m\cdot 20\ \text{м/с}\cdot 40\ \text{м/с}}{5m\cdot 10\ \text{м/с}^2}=16\ \text{м}. $$

Відповідь: \(16\).

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Внутрішня енергія та способи її зміни.

Завдання скеровано на перевірку знання і розуміння, що таке внутрішня енергія газу і які параметри впливають на її зміну.

Запишемо формулу для визначення внутрішньої енергії \(U\) для одноатомного ідеального газу: $$ U=\frac 32\mathbf{\nu}Rt, $$ де \(\mathbf{\nu}\) ‒ кількість речовини, \(R\) ‒ універсальна газова стала, \(T\) ‒ абсолютна температура газу.

Зміна внутрішньої енергії дорівнюватиме: \begin{gather*} \Delta U=U_2-U_1=\frac 32\mathbf{\nu}RT_2-\frac 32\mathbf{\nu}RT_1. \end{gather*}

Використавши рівняння Менделєєва ‒ Клапейрона, матимемо: $$ \mathbf{\nu}RT=pV, $$ де \(p\) ‒ тиск газу, \(V\) ‒ об’єм газу.

Тоді за незмінного об’єму \((V_1=V_2=V)\) матимемо: \begin{gather*} \mathbf{\nu}RT_1=p_1V,\\[7pt] \mathbf{\nu}RT_2=p_2V. \end{gather*}

Підставмо ці вирази у формули для визначення зміни внутрішньої енергії:

Отже, зміна внутрішньої енергії дорівнюватиме добутку зміни тиску і об’єму.

Обчислімо шукану величину:

Відповідь: \(4\mathord{,}5.\)

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на перевірку знання і розуміння перетворення енергії в коливальному контурі.

У той момент, коли конденсатор повністю розрядиться, енергія електричного поля дорівнюватиме нулю \(W_\text{ел}=0,\) сила струму сягне максимального значення \(I_\text{max},\) а повна енергія контуру становитиме:

За законом збереження енергії для ідеального коливального контуру максимальна енергія електричного поля дорівнює максимальній енергії магнітного поля: $$ W_\text{ел max}=W_\text{маг max}=45\ \text{мДж}. $$

Відповідь: \(45.\)

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення та періодом (частотою).

Завдання скеровано на перевірку знання і розуміння зв᾽язку між довжиною хвилі, швидкістю її поширення та періодом (частотою).

Відстань \(l,\) яку пройде звук, створений камертоном, можна визначити за формулою для прямолінійного рівномірного руху, знаючи час \(t\) і швидкість \(v_\text{зв}\) поширення звуку у повітрі: $$ l=v_\text{зв}\cdot t. $$

Довжину ж хвилі можна визначити за формулою хвилі ‒ це формула взаємозв’язку довжини \(\mathbf{\lambda},\) частоти ν та швидкості поширення хвилі:

Якщо поділимо відстань, яку пройде звук, на довжину хвилі, то дізнаємося, скільки довжин хвиль укладеться на цій відстані:

Відповідь: \(2040.\)

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Період піврозпаду.

Завдання скеровано на перевірку знання і розуміння закону періоду піврозпаду.Основний закон радіоактивного розпаду: $$ N=N_0\cdot 2^{-\frac tT}, $$ де \(N\) ‒ кількість ядер радіонукліда, що залишились у зразку через час \(t;\) \(N_0\) ‒ початкова кількість ядер; \(T\) ‒ період піврозпаду; \(t\) ‒ час розпаду.

Кількість \(N\) молекул речовини дорівнює: $$ N=\frac mM\cdot N_A, $$ де \(m\) ‒ маса молекул, \(M\) ‒ молярна маса речовини, \(N_А\) ‒ стала Авогадро.

Підставмо цей вираз у формулу для періоду піврозпаду: \begin{gather*} \frac mM\cdot N_A=\frac{m_0}{M}\cdot N_A\cdot 2^{-\frac tT},\\[6pt] m=m_0\cdot 2^{-\frac tT}, \end{gather*} де \(m\) ‒ маса молекул, що не розпалися; \(N_0\) ‒ початкова маса зразку.

Визначмо шукану величину \(t:\)

Відповідь: \(21.\)