ЗНО онлайн 2015 року з фізики – основна сесія
Тестові завдання основної сесії ЗНО 2015 року з фізики
ТЕМА: Механіка. Основи кінематики. Лінійна і кутова швидкості.
Завдання скеровано на перевірку знання і розуміння поступально-обертального руху.
Визначаючи лінійну швидкість верхнього кінця стержня, треба врахувати те, що сам стержень у той момент, коли його кінці ковзають із певними лінійними швидкостями відносно взаємно перпендикулярних поверхонь підлоги й стіни, здійснює обертальний рух із певною кутовою швидкістю.
Кутова швидкість
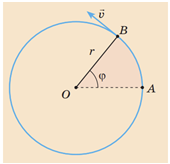
За час, що дорівнює періоду
Стержень довжиною
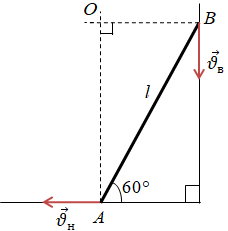
Лінійну швидкість
Кутова і лінійна швидкості пов’язані співвідношенням:
Кутова швидкість кожної точки стержня буде та сама. Тому виразімо кутову швидкість для верхнього і нижнього кінців стержня через їхні відповідні лінійні швидкості й радіуси та прирівняємо ці вирази:
Виразімо
Визначмо швидкість руху верхнього кінця стержня:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Шлях і переміщення.
Завдання скеровано на перевірку знання і розуміння фізичної величини переміщення.
Якщо спочатку турист рухався на захід, а потім ‒ на північ, це означає, що він, пройшовши
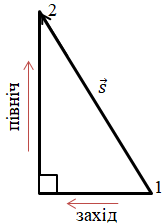
Якщо з’єднаємо початкову точку
Визначмо модуль цього переміщення ‒ довжину відрізка, що з’єднує точки
Отже, модуль переміщення дорівнюватиме
А можна без обчислень одразу сказати, чому дорівнюватиме гіпотенуза (модуль переміщення) цього прямокутного трикутника. Якщо сторони прямокутного трикутника співвідносяться як
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.
Завдання скеровано на перевірку знання і розуміння закону збереження імпульсу і вміння за його допомогою описувати конкретну систему тіл.
У замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії. Запишімо закон збереження імпульсу для системи тіл, як векторну суму імпульсів
Оскільки порожній вагон штовхне навантажений і вони разом, зчепившись, продовжать рух у тому самому напрямку, що й порожній, то можемо записати закон збереження імпульсу в проєкціях:
Навантажений вагон до зіткнення з порожнім стояв нерухомо, його швидкість дорівнювала нулю. Тож і його імпульс дорівнював нулю, оскільки імпульс тіла ‒ це добуток маси тіла на швидкість його руху:
З графіка залежності імпульсу порожнього вагона від часу можна визначити, що до зіткнення імпульс порожнього вагона
Отже, можемо визначити імпульс навантаженого вагона після поштовху порожнього вагона:
Запишімо формулу для імпульсу навантаженого вагона:
А швидкість руху
Визначмо тепер масу вантажу
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Потужність.
Завдання скеровано на перевірку уміння визначати потужність.
Потужність
Робота рівнодійної всіх сил, які діють на тіло, дорівнює зміні кінетичної енергії
У результаті дії сил опору автомобіль зупиниться, тобто через час
Тобто
За умовою завдання автомобіль змінює швидкість, сповільнюється. Тому середня потужність двигуна ‒ це середнє арифметичне потужностей у певні моменти часу (так би мовити миттєвих потужностей), що дорівнюють добутку модуля сили тяги двигуна на модуль його миттєвої швидкості.
Оскільки всю енергію двигуна буде витрачено на подолання сил опору, то середня потужність двигуна дорівнюватиме середній потужності сил опору.
Отже, визначмо середню потужність сил опору:
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Стала Авогадро.
Завдання скеровано на перевірку знання і розуміння кількості речовини й числа Авогадро.
У будь-якій речовині кількістю один моль міститься та сама кількість
За умовою завдання кількість речовини обох металів однакова –
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Елементи механіки рідин і газів. Атмосферний тиск. Тиск нерухомої рідини на дно та стінки посудини.
Завдання скеровано на перевірку знання і розуміння поняття тиску ‒ атмосферного й гідростатичного.
Тиск на поверхні води дорівнює атмосферному тиску ‒
А тиск
Запишімо відношення тисків:
Отже, тиск на глибині більший за тиск на поверхні води в
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря та її вимірювання.
Завдання скеровано на перевірку знання і розуміння поняття відносної вологості й уміння користуватися показами гігрометра й психрометричною таблицею.
Відносна вологість ‒ це фізична величина, яка показує, наскільки водяна пара близька до насичення.
Для прямого вимірювання вологості найчастіше використовують гігрометр психрометричний ‒ психрометр (його фрагмент зображено в умові завдання ліворуч від психрометричної таблиці). Дія цього приладу базується на двох фактах:
1) швидкість випаровування рідини то вища, що нижча відносна вологість повітря;
2) рідина під час випаровування охолоджується.
Складниками психрометра є два термометри ‒ сухий, яким вимірюють температуру довкілля, і вологий ‒ його колбу обгорнуто тканиною, кінчик якої опущено в посудину з водою (див. рисунок).
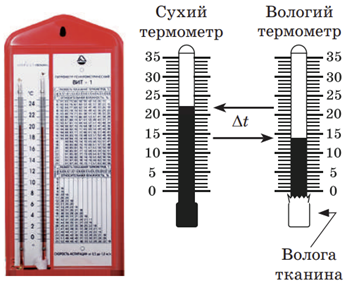
Вода з тканини випаровується, тому вологий термометр показує нижчу температуру, ніж сухий. Що нижча відносна вологість повітря, то швидше випаровується рідина й більша різниця показів сухого і вологого термометрів. Відносну вологість визначають за допомогою психрометричної таблиці (фрагмент такої таблиці подано в умові завдання).
Сухий термометр з умови (ліворуч) показує вищу температуру
Сухий термометр не може показувати меншу температуру, ніж вологий, це нереальна ситуація. Він може показувати таку саму температуру, як і вологий, у ситуації, коли відносна вологість дорівнює
Отже, різниця температур сухого і вологого термометрів
У психрометричній таблиці (верхній рядок) знаходимо різницю показів сухого і вологого термометрів
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти.
Завдання скеровано на перевірку знання і розуміння поняття кількості теплоти, а також вміння здобувати інформацію з графіків.
Кількість теплоти, яка поглинається внаслідок нагрівання речовини (або виділяється внаслідок її охолодження), обчислюють за формулою
Скористаймося графіками з умови завдання, щоб визначити відношення мас двох порцій води.
Загальна формула для визначення маси така:
Питома теплоємність води однакова в обох її порціях. Зручно взяти також однакову кількість теплоти ‒
Графік 1: зважаючи на те, що одиничний відрізок по вертикальній осі температур становить
Після отримання теплоти
Тоді різниця температур
Графік 2: початкова температура
Після отримання теплоти
Тоді різниця температур
Запишімо формули для визначення мас й обчислімо відношення їх:
Отже, маса порції води
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.
Завдання скеровано на перевірку вміння визначати загальний опір послідовного, паралельного й мішаного з’єднання провідників.
Загальний опір послідовно з’єднаних провідників
Це значення загального опору ділянки електричного кола набагато більше за
Коли всі резистори з’єднано паралельно (варіант відповіді Г), загальний опір
У разі однакового опору резисторів (як в умові завдання) формулу можна спростити:
Це значення загального опору ділянки електричного кола набагато менше за
Розгляньмо мішане з’єднання резисторів (варіанти відповіді А і Б).
У варіанті А два резистори з’єднано послідовно:
Паралельно до цих двох резисторів приєднано третій такий самий резистор опором
У варіанті Б два резистори з’єднано паралельно:
Послідовно до цих двох резисторів приєднано третій такий самий резистор опором
Отже, щоб отримати ділянку електричного кола з опором 6 Ом, потрібно з’єднати два резистори паралельно, а третій приєднати послідовно до них (за умови, що всі резистори однакові).
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля. Принцип суперпозиції полів.
Завдання скеровано на перевірку розуміння напруженості електричного поля, уміння застосовувати принцип суперпозиції електричних полів.
Напруженість електричного поля
За напрямок вектора напруженості в точці електричного поля беруть напрямок сили, яка діяла б на пробний позитивний заряд, якби він був поміщений у цю точку поля. На рисунку це точка C: поле створив позитивний точковий заряд
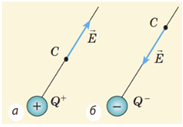
Якщо ж поле утворено кількома зарядами, то результувальна сила, яка діє на пробний заряд із боку системи зарядів, є геометричною сумою сил, із якими діють ці заряди на пробний заряд:
Звідси випливає принцип суперпозиції (накладання) електричних полів: напруженість електричного поля системи зарядів у певній точці простору дорівнює векторній сумі напруженостей полів, створених цими зарядами в цій точці:
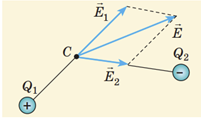
Якщо ж точка

За умовою заряд рівномірно розподілений по всій довжині дротин, із яких виготовлені рамки. Дротяні фігури є симетричними, тому можна в кожній із них знайти симетричні пари точок, відносно яких за принципом суперпозиції електричних полів напруженість дорівнюватиме нулю. І таких пар точок нескінченно багато.
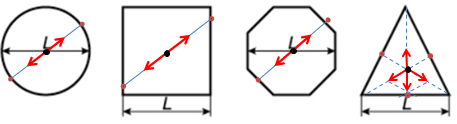
У рівносторонньому трикутнику, наприклад, три рівновіддалені від його центра точки. Центр рівностороннього трикутника є центром описаного і вписаного кіл. Визначаємо геометрично за правилом паралелограма суму двох векторів напруженостей (на рисунку ‒ вектор, що позначає їхню суму, напрямлений вертикально вниз). Якщо додати геометрично вектори, що на рисунку напрямлені вертикально, їхня сума дорівнюватиме нулю. І так для безлічі рівновіддалених точок.
Отже, напруженість дорівнюватиме нулю в геометричному центрі кожної дротяної фігури, про яку йдеться в умові.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання і розуміння параметрів, від яких залежить електроємність конденсатора.
Електроємність
Виразімо з формули шукану величину – діелектричну проникність
Площу пластини конденсатора визначимо за формулою
Обчислімо діелектричну проникність текстоліту:
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Правило Ленца.
Завдання скеровано на перевірку розуміння індукційного струму, взаємодії створеного ним магнітного поля з магнітним полем, що викликало цей струм.
Модель із кільцями, використана в завданні, дуже схожа на пристрій, сконструйований Емілем Ленцем для демонстрації однойменного правила. Але в пристрої «Кільця Ленца» одне кільце розрізане.
Якщо наближати магніт до суцільного кільця, то в кільці виникне індукційний струм
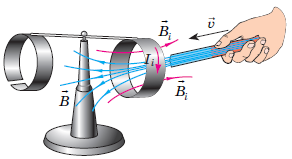
Якщо магніт віддаляти від суцільного кільця, то кільце притягуватиметься до магніту.
У розрізаному кільці індукційний струм не міг виникнути, бо кільце не замкнене. А в моделі, про яку йдеться в умові завдання, друге кільце суцільне. Але в ньому також не може виникнути індукційний струм. Адже до другого кільця магніт не наближають, із першим кільцем воно з’єднане дерев’яним стержнем, а дерево – це діелектрик.
Отже, унаслідок унесення в кільце штабового магніту (тобто наближення магніту) кільце рухатиметься за напрямком стрілки – відштовхуватиметься від магніту.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у напівпровідниках.
Завдання скеровано на перевірку знання і розуміння протікання електричного струму в напівпровідниках.
Розгляньмо пряме підключення кристала зі сформованим у ньому
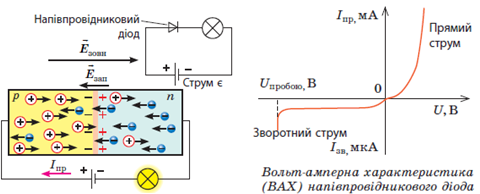
Електрони почнуть рух до позитивного полюса джерела струму, а дірки − до негативного. Запірний шар поповниться вільними електронами й дірками, тому його опір зменшиться. Оскільки через місце контакту рухаються основні носії струму (електрони з
Отже, з усіх залежностей сили струму від напруги, зображених на рисунках у варіантах відповіді, вольт-амперній характеристиці напівпровідникового діода, підключеного в прямому напрямку, відповідає лише графік А.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.
Завдання скеровано на перевірку вміння визначати фізичні величини, які характеризують гармонічні коливання.
Гармонічними називають коливання, під час яких координата
Перша похідна від координати за часом
А друга похідна від координати за часом або перша похідна від швидкості ‒ це прискорення
Зробимо заміну в рівнянні для прискорення, скориставшись першим загальним рівнянням:
У будь-який момент часу руху тіла його прискорення прямо пропорційне зміщенню і напрямлене в бік, протилежний зміщенню (тому знак «мінус»).
Визначмо циклічну частоту коливань:
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.
Завдання скеровано на перевірку знання і розуміння перетворення механічної енергії під час коливального руху пружинного маятника.
У завданні описана ситуація, коли тягарець проходить якесь проміжне положення і не перебуває ні в положенні рівноваги, ні на максимальній відстані від нього, яку називають амплітудою.
Під час коливального руху тягарця потенціальна енергія деформованої пружини перетворюватиметься на кінетичну енергію руху тягарця, і навпаки. Тобто виконуватиметься закон збереження механічної енергії.
Запишімо розподіл енергії в цьому проміжному положенні. Тягарець володітиме кінетичною енергією
У крайньому положенні, тобто коли тягарець віддалений від положення рівноваги на максимальну відстань, його кінетична енергія дорівнюватиме нулю, тому що він на мить зупиняється, тобто швидкість його руху дорівнює нулю.
А потенціальна енергія розтягнутої пружини буде максимальною
Запишімо закон збереження механічної енергії:
Помножимо ліву і праву частини рівності на
Обчислимо значення амплітуди:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки й використання їх для визначення довжини світлової хвилі.
Завдання скеровано на перевірку розуміння поняття дифракційної ґратки й утворення спектрів різних порядків.
Скористаймося формулою дифракційної ґратки
Вимірюючи кут
Ось приклад зображення дифракційного спектру. Інтерференційні максимуми

Запишімо формули для визначення довжин хвиль для максимумів
Дифракційна ґратка та сама, тож період однаковий. Оскільки спектри перекриваються, то
Поділимо ліві і праві частини формул:
Звідси визначмо довжину хвилі в спектрі
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона.
Завдання скеровано на перевірку знання і розуміння формули Томсона ‒ формули для визначення періоду власних коливань контуру.
Період
Запишімо формулу для визначення періоду до змін і після них:
Отже, після змін параметрів котушки і конденсатора період власних коливань контуру збільшиться вдвічі.
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність. Період піврозпаду.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Скористаймося основним законом радіоактивного розпаду:
Тоді кількість ядер радіонукліда, що розпадеться за час, зазначений в умові, становитиме
Запишімо це відношення відповідно до умови завдання:
Отже, розпадеться
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Релятивістський закон додавання швидкостей.
Завдання скеровано на перевірку розуміння релятивістського закону додавання швидкостей та умов його застосування.
Можна одразу відкинути варіанти відповіді Б і Г як неможливі. Адже в них швидкість електрона або досягла максимального значення ‒ швидкості світла у вакуумі, або перевищила його.
У завданні необхідно визначити максимально можливу швидкість руху електрона відносно Землі. Ідеться про ситуацію, коли ядро й електрон, який з нього вилітає, рухатимуться в одному напрямку.
Оскільки йдеться про швидкості руху порядку швидкості світла, то треба скористатися релятивістським законом додавання швидкостей:
де
Отже,
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.
Завдання скеровано на перевірку вміння застосовувати формулу тонкої лінзи.
Зробимо схематичний збільшений рисунок відповідно до фотографії в умові завдання.
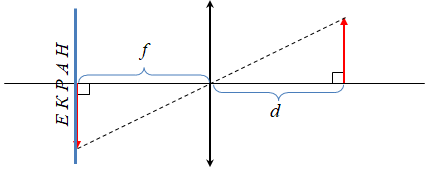
Лінза є збиральною, оскільки дає дійсне зображення: на екрані з іншого від предмета (нитки розжарення) боку лінзи зображення утворюють саме заломлені промені, що пройшли крізь лінзу, а не їхні продовження з того самого боку лінзи, що й предмет.
З фото видно, що відстань від предмета до лінзи
Зваживши на це, запишімо формулу тонкої лінзи:
де
Фізичну величину, яка характеризує заломні властивості лінзи й обернена до її фокусної відстані, називають оптичною силою
Отже, дістанемо формулу для визначення оптичної сили лінзи відповідно до умов завдання:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах.
Завдання скеровано на перевірку знання різних середовищ і вільних носіїв електричного заряду в них.
Метал: вільними носіями електричного заряду в ньому є вільні електрони.
Розчин електроліту: провідність такого розчину йонна, тобто носіями електричного заряду в ньому є лише позитивні і негативні йони.
Напівпровідник: його електричні властивості істотно залежать від домішок, тому основними носіями заряду в ньому можуть бути і умовні частинки, що мають позитивний заряд – «дірки», і електрони.
Плазма: носіями електричного заряду є і вільні електрони, і переважно позитивні йони.
Відповідь: 1В, 2Д, 3А, 4Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Вага тіла.
Завдання скеровано на перевірку розуміння ваги тіла й уміння визначати її в різних ситуаціях.
Усі тіла внаслідок гравітаційного притягання стискають або прогинають опору або розтягують підвіс. Силу, яка характеризує таку дію тіл, називають вагою і позначають символом
1) Тіло перебуває в ліфті, що рухається вниз із прискоренням
Вага тіла, яке рухається з прискоренням, напрямленим вертикально вниз, менша, ніж вага
2) Тіло вільно падає біля поверхні Землі. Це означає, що на нього діє лише сила тяжіння, а тіло не діє на опору чи підвіс, тобто воно перебуває в стані невагомості. Тобто вага тіла дорівнює нулю:
3) Тіло зважують на поверхні Місяця, тож вага тіла за модулем дорівнюватиме силі тяжіння:
Але це сила тяжіння, з якою Місяць притягуватиме тіло, а прискорення вільного падіння
Отже, на Місяці вага тіла
4) Тіло рухається в міжпланетному кораблі, тобто далеко від планет. Тому на нього не діє жодна сила тяжіння. За другим законом Ньютона
Вага за модулем дорівнюватиме силі нормальної реакції опори згідно з третім законом Ньютона:
Відповідь: 1Г, 2А, 3Б, 4В.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.
Завдання скеровано на перевірку знання і розуміння процесів, що відбуваються з парою і рідиною, застосування цих процесів у приладах.
1) Пару, яка перебуває зі своєю рідиною в стані динамічної рівноваги (тобто кількість молекул, які повертаються в рідину, дорівнює кількості молекул, які за той самий час залишають рідину), називають насиченою.
Перенасиченою є пара, тиск якої перевищує тиск насиченої пари за певної температури. Перенасичена пара утворюється внаслідок збільшення тиску пари в об’ємі, вільному від центрів конденсації (пилинок, йонів, краплинок рідини малих розмірів тощо). Інший спосіб отримання ‒ охолодження насиченої пари за тих же умов. Саме цей спосіб використовують у камері Вільсона.
Камера Вільсона ‒ це трековий детектор. Камеру заповнено парою спирту або медичного ефіру. Коли поршень різко опускають, то внаслідок адіабатного розширення пара охолоджується і стає перенасиченою. Коли в перенасичену пару потрапляє заряджена частинка, на своєму шляху вона йонізує молекули пари. Йони, що утворилися, стають центрами конденсації. Ланцюжок крапель cконденсованої пари, який утворюється вздовж траєкторії руху частинки (трек частинки), знімають на камеру або фотографують: 1 ‒ Г.
2) Властивість рідини розширюватися під час нагрівання використовують у медичному термометрі: 2 ‒ Д. Причина теплового розширення полягає в тому, що зі збільшенням температури збільшується швидкість руху частинок речовини (атомів, молекул, йонів), унаслідок чого збільшується середня відстань між частинками. Медичний термометр складається зі скляного резервуара, наповненого ртуттю, який переходить у капіляр, скляної шкали з поділками та скляної захисної трубки. Ртуть ‒ це єдиний метал, який за кімнатної температури є рідиною. Об’єм рідини є мірою температури: що вища температура тіла, то більшим є об’єм рідини й вищим стовпчик рідини в термометрі.
3) Якщо з рідини видалити розчинене повітря (наприклад, багатократним кип’ятінням) і можливі центри пароутворення (пилинки, йони тощо), то можна нагріти рідину до температури, дещо вищої від температури кипіння. Такий стан називають перегрітою рідиною. Стан перегрітої рідини також можна одержати й унаслідок зниження зовнішнього тиску до рівня, нижчого за тиск насиченої пари рідини за цієї температури.
Саме цей процес лежить в основі роботи бульбашкової камери. Вона також є трековим детектором, як і камера Вільсона. І принцип роботи бульбашкової камери подібний до принципу роботи камери Вільсона. А відмінність полягає в тому, що робочим тілом у бульбашковій камері є перегріта рідина: йони, які виникають уздовж траєкторії руху частинки, стають центрами кипіння ‒ утворюється ланцюжок бульбашок: 3 ‒ А.
4) У рідині завжди є молекули, які рухаються досить швидко, а тому випаровування рідин відбувається за будь-якої температури. Оскільки під час випаровування рідину залишають найшвидші молекули, то середня кінетична енергія решти молекул зменшується. Тому, якщо рідина не отримує енергії ззовні, вона охолоджується.
Саме цей принцип використовують у психрометрах (гігрометрах психрометричних ‒ приладах для прямого вимірювання вологості повітря), а ще той факт, що швидкість випаровування рідини то вища, що нижча відносна вологість повітря: 4 ‒ В.
Манометр ‒ це прилад для вимірювання тиску рідин і газів. Рідинним манометром вимірюють різницю рівнів рідини в колінах U-подібної трубки. Тобто визначають, на скільки тиск газу в груші, закріпленій на одному з отворів трубки, відрізняється від атмосферного. Є також металеві деформаційні манометри.
Відповідь: 1Г, 2Д, 3А, 4В.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти. Коефіцієнт корисної дії нагрівника.
Завдання скеровано на перевірку розуміння того, що є корисною, а що – повною кількістю теплоти, уміння застосовувати формули для обчислення кількості теплоти під час нагрівання речовини і коефіцієнта корисної дії нагрівника.
1. Кількість теплоти
Обчислимо кількість теплоти, необхідної для нагрівання порції води до кипіння відповідно до умови завдання:
Відповідь: 672.
2. Коефіцієнт корисної дії
Відповідно до умови завдання корисно спожита кількість теплоти ‒ це та кількість теплоти, яку поглинула вода під час нагрівання її до кипіння:
Під час проходження струму в електричному чайнику протягом
Обчислімо коефіцієнт корисної дії чайника:
Відповідь: 1. 672. 2. 56.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Прямолінійний рівноприскорений рух.
Завдання скеровано на перевірку вміння застосовувати кінематичні рівняння для прямолінійного рівноприскореного руху.
1. Векторну фізичну величину, яка характеризує швидкість зміни швидкості руху тіла й дорівнює відношенню зміни швидкості руху тіла до інтервалу часу, за який ця зміна відбулася, називають прискоренням руху тіла.
Користуючись тим, що в умові дана відстань
За умовою початкова швидкість руху кульки дорівнює нулю
Учень п’ять разів виміряв час, тому необхідно визначити середнє значення часу як середнє арифметичне значення:
Виразімо й обчислимо прискорення:
Відповідь: 2.
2. Формула для визначення модуля прискорення така:
Тож для рівноприскореного прямолінійного руху маємо рівняння, із якого можна визначити швидкість кульки в нижній точці
Відповідь: 2.
Відповідь: 1. 2. 2. 2.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота. Потенціальна енергія.
Завдання скеровано на перевірку розуміння закону збереження механічної енергії, уміння описати аналітично рух тіла під дією кількох сил.
Перед початком руху тіло масою
Отже,
Ковзаючи по похилій площині довжиною
Сила тертя ковзання напрямлена проти руху тіла, а переміщається воно вздовж похилої площини, то ж зазначений кут становитиме
Схематично зобразимо на похилій площині й позначимо всі сили, що діють на тіло. Сила тяжіння
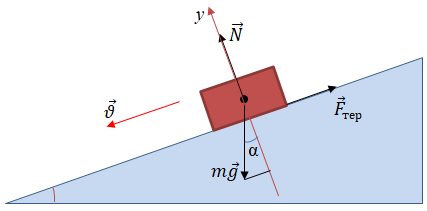
Запишімо другий закон Ньютона у векторній формі:
Сила тертя ковзання
Для того, щоб визначити
Отже,
Виразимо модуль переміщення тіла (довжину похилої площини) через дані в умові завдання:
Отже, остаточна формула для визначення роботи сили тертя ковзання набуває такого вигляду:
Відповідь: 2.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Додавання швидкостей.
Завдання скеровано на перевірку знання і розуміння закону додавання швидкостей у класичній механіці.
Для визначення часу, який знадобиться автомобілю, щоб проїхати від останнього до першого вагона, необхідно знати швидкість руху автомобіля відносно поїзда. Відстань, яку треба проїхати автомобілю, ‒ це довжина
де
Тепер можна обчислити час
Відповідь: 20.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.
Завдання скеровано на перевірку знання і розуміння закону Ома для повного кола і послідовного з’єднання гальванічних елементів.
Запишімо закон Ома для повного кола:
Джерелом струму в колі є батарея з трьох з’єднаних послідовно гальванічних елементів опором
Електричний опір
Гальванічні елементи однакові й з’єднані послідовно, то ж електрорушійну силу
Підставимо вирази для внутрішнього опору, електрорушійної сили батареї елементів й опору лампи у формулу, що відображає закон Ома для повного кола:
Виразімо звідси силу струму:
Помножмо ліву і праву частини рівняння на
Підставимо числові значення відомих в умові величин:
Ми отримали квадратне рівняння
Обчислимо корені рівняння:
Меншим є значення сили струму
Відповідь: 0,5.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля ‒ Ленца.
Завдання скеровано на перевірку вміння застосовувати закон Джоуля ‒ Ленца й тлумачити показання приладів за певної послідовності підключення їх.
Кількість теплоти
Електричний опір резистора і час протікання струму відомі, а силу струму в резисторі можна визначити за законом Ома для повного кола:
Фотоелемент є джерелом струму. Коли до полюсів фотоелемента приєднали вольтметр (ще без навантаження ‒ резистора), вольтметр показав електрорушійну силу
Коли ж до полюсів приєднали замість вольтметра амперметр, який за умовою є ідеальним, тобто його опір
Звідси визначмо внутрішній опір фотоелемента, необхідний для визначення сили струму в резисторі:
Обчислімо силу струму в резисторі:
Визначимо кількість теплоти, яка виділиться в резисторі:
Відповідь: 125.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна та його максимальне значення.
Завдання скеровано на перевірку знання і розуміння формул для визначення коефіцієнта корисної дії теплового двигуна.
Коефіцієнт корисної дії
За умовою нагрівником є резервуар із водою, яка кипить. Температура кипіння дорівнює
Холодильником є ємність із льодом, який тане. Температура танення льоду
З іншого боку коефіцієнт корисної дії теплової машини дорівнює відношенню корисної роботи
Частина теплоти
Прирівняймо ці два вирази для визначення коефіцієнта корисної дії:
Порція теплоти, яка буде передана холодильнику, може розплавити лід масою
Тобто
Підставимо числові значення величин з умови завдання і визначимо масу льоду:
Відповідь: 910.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Повне відбивання.
Завдання скеровано на перевірку знання і розуміння оптичного явища ‒ повного внутрішнього відбивання.
Явище, коли заломлення світла немає, тобто світло повністю відбивається від межі поділу із середовищем меншої оптичної густини, називають явищем повного внутрішнього відбивання.
Найменший кут падіння, починаючи з якого вся світлова енергія повністю відбивається від межі поділу двох прозорих середовищ, називають граничним кутом повного внутрішнього відбивання
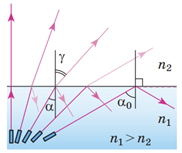
За умовою завдання світло переходитиме з речовини, яка оптично густіша за повітря. На рисунку нижче зображена ситуація, коли промінь йде по межі двох середовищ. Якщо далі збільшувати кут падіння, то промінь повністю відбиватиметься в речовині, не заломлюватиметься і не виходитиме в повітря.
Оскільки промені від точкового джерела розходяться в усі боки, то виберемо з них ті, які падають під кутом
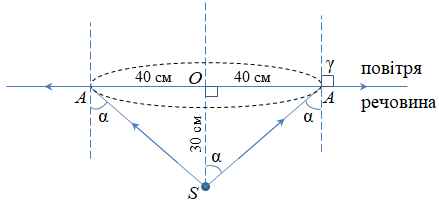
Для двох середовищ відношення синуса кута падіння
Показник заломлення повітря дорівнює
Щоб визначити
Якщо один катет
Тоді
Підставимо це значення в формулу для показника заломлення і обчислимо його:
Відповідь: 1,25.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.
Завдання скеровано на перевірку розуміння будови трансформатора й уміння описувати його роботу аналітично, через відношення фізичних величин.
Первинна обмотка трансформатора підключена до джерела змінного струму, напруга на виході якого
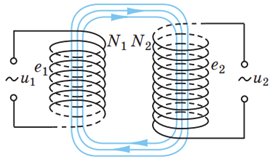
У вторинній обмотці струм не йде (вона розімкнена), тому напруга на кінцях вторинної обмотки за модулем дорівнює ЕРС індукції, отже, відповідно маємо рівність:
Отже, у режимі холостого ходу справджується рівність
У разі підключення обмоток першим способом ЕРС індукції в першій обмотці дорівнює фактично напрузі на джерелі:
А ЕРС індукції у вторинній обмотці за умовою дорівнює
Якщо ж поміняти місцями обмотки й підключити вторинну обмотку до джерела, то
А ЕРС індукції в первинній обмотці, яка тепер стала вторинною, за умовою дорівнює
Коефіцієнт трансформації для першого способу підключення
А для другого способу з’єднання коефіцієнт трансформації буде такий самий:
Прирівняємо праві частини цих рівностей:
Обчислимо напругу джерела:
Відповідь: 8.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Фотоефект і його експериментально встановлені закони. Рівняння Ейнштейна для фотоефекту.
Завдання скеровано на перевірку знання, розуміння і застосування фізичних характеристик, рівняння Ейнштейна для фотоефекту, його законів.
Унаслідок поглинання фотона металом енергія фотона
Запишімо рівняння Ейнштейна для фотоефекту за початкових умов (до зміни довжини хвилі
Тоді рівняння для фотоефекту таке:
Запишімо рівняння Ейнштейна для фотоефекту, якщо довжина хвилі світла збільшиться у
За умовою завдання
Розв’яжімо систему рівнянь, поділивши рівняння одне на одне:
Підставимо числові значення й обчислимо затримувальну різницю потенціалів, зваживши на те, що
Відповідь: 0,5.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність. Період піврозпаду.
Завдання скеровано на перевірку знання і застосування основного закону радіоактивного розпаду.
Період піврозпаду
Фізичну величину, яка чисельно дорівнює кількості розпадів, що відбуваються в певному радіоактивному джерелі за одиницю часу, називають активністю радіоактивного джерела.
Нехай
Це означає, що відбулося три піврозпади: унаслідок першого розпаду кількість ядер зменшилася у
Отже, за час
Отже, період піврозпаду радіоактивного елемента становить
Відповідь: 5.
Знайшли помилку? Пишіть на




