ЗНО онлайн 2015 року з фізики – додаткова сесія

ТЕМА: Механіка. Основи динаміки. Сили пружності. Закон Гука.

Завдання скеровано на перевірку розуміння дії тіла на підвіс і застосування знань про з’єднання пружин.

На нижній динамометр діє сила тяжіння, а він підвішений до двох верхніх динамометрів за допомогою гачка, з’єднаного з його пружиною. Отже, у підвісі (тобто в пружині) сила пружності виникає завдяки силі, яку називають вагою. Нижній динамометр покаже значення сили тяжіння, яка за модулем дорівнює силі пружності і протилежно до неї напрямлена, а оскільки динамометр перебуває в стані спокою, то вага дорівнюватиме за модулем силі тяжіння.

Вагу нижнього динамометра розподілено порівну між верхніми динамометрами, оскільки динамометри за умовою однакові. Унаслідок дії нижнього динамометра пружини верхніх динамометрів однаково розтягуються. Отже, верхні динамометри показують значення сил пружності: $$ F_\text{пруж1}=F_\text{пруж2}=4\ \text{Н}. $$

Оскільки пружини верхніх динамометрів з’єднані паралельно стержнем, до якого підвішений нижній динамометр, то жорсткості цих пружин додають: $$ k=k_1+k_2. $$

Отже, та сила пружності, що виникає в нижньому динамометрі, дорівнюватиме сумі сил пружності, що виникають у верхніх динамометрах: $$ F_\text{пруж}=F_\text{пруж1}+F_\text{пруж2}=8\ \text{Н}. $$

А нижній динамометр покаже значення сили тяжіння, яка за модулем дорівнює силі пружності: $$ F_\text{тяж}=F_\text{пруж}=8\ \text{Н}. $$

Відповідь: A.

ТЕМА: Механіка. Основи динаміки. Рух тіл під дією кількох сил.

Завдання скеровано на перевірку знання і розуміння дії простого механізму ‒ нерухомого блоку, і вміння аналітично описувати рух зв’язаних тіл за допомогою другого закону динаміки Ньютона.

Схематично зобразімо на рисунку сили тяжіння \(\overrightarrow{F}_\text{т1}\) і \(\overrightarrow{F}_\text{т2}\) й сили натягу нитки \(\overrightarrow{T},\) що діють на кожний зі шматків жерсті масами \(m_1\) і \(m_2,\) а також напрямки прискорень \(\overrightarrow{a}_1\) і \(\overrightarrow{a}_2\) й вибраний напрямок осі координат \(Oy.\)

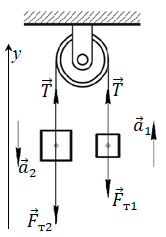
Запишімо для обох предметів другий закон динаміки Ньютона у векторному вигляді:

Запишімо систему рівнянь у проєкціях на вісь \(Oy:\) $$ \left\{ \begin{array}{l} m_1a_1=-F_\text{т1}+T\\ -m_2a_2=-F_\text{т2}+T \end{array} \right. $$

Пояснімо, чому за модулем $$ a_1=a_2=a $$ й сила натягу нитки за модулем однакова.

Відповідно до умови кінематичного зв’язку, що випливає з нерозтяжності нитки, за будь-який інтервал часу ліва ділянка нитки подовжується саме на стільки, на скільки скорочується права. Таким чином, переміщення обох шматків жерсті весь час однакові за модулем. Звідси випливає, що в шматків однакові й модулі швидкостей, і модулі прискорень, тому $$ a_1=a_2=a. $$

Якщо масами нитки та блока, а також тертям в осі блока можна знехтувати (а це можна зробити, тому що в умові завдання даних про це немає), то сила натягу нитки \(\overrightarrow{T}\) в усіх її перерізах однакова. Отже, нитка діє на обидва тягарці з однаковою силою \(\overrightarrow{T},\) напрямленою вгору (див. рисунок).

Узявши до уваги попередні пояснення

і віднявши від першого рівняння системи друге, дістанемо: \begin{gather*} m_1a_1+m_2a_2=-m_1g+m_2g,\\[6pt] a=\frac{g(m_2-m_1)}{m_2+m_1}. \end{gather*}

В умові є інформація про матеріал і розміри шматків жерсті, тож виразімо їхні маси через густину \(\mathbf{\rho}\) й об’єм \(V:\)

Шматки жерсті виготовлено з однакового матеріалу, тому $$ \mathbf{\rho}_1=\mathbf{\rho}_2=\mathbf{\rho}. $$

Товщина \(h\) шматків однакова, а сторона \(a\) квадратного шматка жерсті вдвічі більша за сторону іншого:

Отже,

Підставимо отримані вирази для мас у формулу для прискорення:

Відповідь: Г.

ТЕМА: Механіка. Елементи механіки рідин і газів. Сполучені посудини.

Завдання скеровано на перевірку знання, розуміння і вміння застосовувати властивості сполучених посудин.

Відповідно до основної властивості сполучених посудин у відкритих сполучених посудинах вільні поверхні однорідної нерухомої рідини (за умовою – води) встановлюються на одному рівні. Тож поки в посудинах була лише вода, її рівень в обох посудинах однаковий.

Після того, як обережно (не змішуючи) в одну з посудин (праворуч) долили важчу за воду рідину (густина \(\mathbf{\rho}_\text{рідини}\) за умовою більша за густину \(\mathbf{\rho}_\text{води}),\) рівень води в другій посудині (ліворуч) підвищився, а в посудині, що праворуч, знизився (див. рисунок). Різниця рівнів води в правій і лівій посудинах становить \(\Delta h.\)

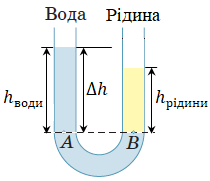
В однорідній рідині (тут – у воді) тиск на одному горизонтальному рівні є однаковим. На рівні \(AB\) в обох колінах міститься вода, тому на цьому рівні тиски, створені атмосферою \(p_\text{атм}\) і рідинами, однакові. Для визначення гідростатичних тисків води \(p_\text{води}\) і рідини \(p_\text{рідини}\) треба знати їхні густини \(\mathbf{\rho}_\text{води}\) і \(\mathbf{\rho}_\text{рідини}.\)

Визначімо висоту стовпчика води \(h_\text{води}.\) Для цього дізнаємося тиск у точках \(A\) і \(B:\)

Оскільки \(p_A=p_B,\) маємо:

або $$ \mathbf{\rho}_\text{води}gh_\text{води}=\mathbf{\rho}_\text{рідини}gh_\text{рідини}. $$

Звідси дізнаймося висоту стовпчика води:

Якщо нульовим рівнем уважати рівень води в посудині праворуч, різниця рівнів води дорівнюватиме висоті стовпчика води в посудині ліворуч:

Відповідь: Г.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах.

Завдання скеровано на перевірку знання і розуміння закону збереження повної механічної енергії, а також залежності в цьому законі величин, які описують тіло або систему тіл, від часу.

Тіло, кинуте під кутом до горизонту, рухається по параболі, тож кінетична енергія тіла переходить у потенціальну, а потім, під час падіння, навпаки – потенціальна в кінетичну.

У замкненій системі тіл, які взаємодіють тільки консервативними силами, повна механічна енергія залишається незмінною (зберігається).

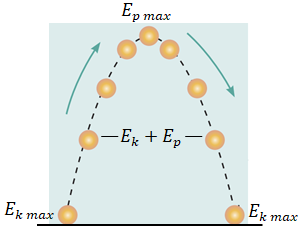
Закон збереження повної механічної енергії виконується тільки в тому разі, якщо в системі немає тертя.

За умовою на опір повітря не зважаємо, тому закон збереження повної механічної енергії справедливий.

Якщо повна механічна енергія \(E\) із часом залишається сталою, то графіком її залежності від часу \(t\) буде пряма, паралельна до осі часу ‒ варіант В:

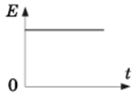
Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку розуміння рівняння стану ідеального газу та вміння за його допомогою визначати макроскопічні параметри газу.

За допомогою рівняння стану ідеального газу (рівняння Менделєєва – Клапейрона) $$ pV=\frac mM RT $$ можна встановити зв’язок між макроскопічними параметрами газу (\(p\) – тиск, \(V\) − обʼєм, \(T\) – абсолютна температура) у разі його переходу з одного стану в інший. Тобто якщо газ тієї ж маси \(m\) і молярної маси \(M,\) то можемо скористатися рівнянням Клапейрона: $$ \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}, $$ тобто для газу деякої маси відношення добутку тиску на об’єм до температури газу є незмінним: $$ \frac{pV}{T}=\text{const.} $$

Запишімо рівняння Клапейрона для кожної ділянки циклу.

Процес \(1−2\) відбувається за незмінного об’єму (відповідно до графіка), тобто \begin{gather*} V=\text{const},\\[6pt] \frac{p_1}{T_1}=\frac{p_2}{T_2},\\[6pt] \frac{p}{T_1}=\frac{2p}{T_2}, \end{gather*} \(T_2=2T_1\) – температура під час процесу \(1−2\) підвищилася в \(2\) рази порівняно з початковою температурою \(T_1.\)

Процес \(2−3\) відбувається за незмінного тиску (див. графік), тобто \begin{gather*} p=\text{const},\\[6pt] \frac{V_2}{T_2}=\frac{V_3}{T_3},\\[6pt] \frac{V}{T_2}=\frac{2V}{T_3}, \end{gather*} \(T_3=2T_2=4T_1\) – температура під час процесу \(2−3\) підвищилася в \(4\) рази порівняно з початковою температурою \(T_1.\)

Процес \(3−4\) відбувається за незмінного об’єму (відповідно до графіка), тобто \begin{gather*} V=\text{const},\\[6pt] \frac{p_3}{T_3}=\frac{p_4}{T_4},\\[6pt] \frac{2p}{T_3}=\frac{p}{T_4}, \end{gather*} \(T_4=\frac 12 T_3=\frac 12\cdot 4T_1=2T_1\) – температура під час процесу \(3−4\) підвищилася в \(2\) рази порівняно з початковою температурою \(T_1.\)

Процес \(4−1\) відбувається за незмінного тиску (відповідно до графіка), тобто \begin{gather*} p=\text{const},\\[6pt] \frac{V_4}{T_4}=\frac{V_1}{T_1},\\[6pt] \frac{2V}{T_4}=\frac{V}{T_1}, \end{gather*} \(T_4=2T_1\) – температура під час процесу \(4−1\) дійсно підвищилася в \(2\) рази порівняно з початковою температурою \(T_1,\) що вже було математично доведено на ділянці циклу \(3−4.\)

Отже, температура підвищилася найбільше під час процесу \(2−3\) – у \(4\) рази.

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку знання і застосування рівняння стану ідеального газу.

Запишімо рівняння стану ідеального газу (рівняння Менделєєва – Клапейрона): $$ pV=\frac mM RT, $$ де \(p\) – тиск, \(V\) − обʼєм, \(m\) – маса газу, \(M\) – молярна маса газу, \(R\) – універсальна газова стала, \(T\) – абсолютна температура.

Перетворімо це рівняння, щоб можна було визначити густину \(\mathbf{\rho}\) газу в балоні: \begin{gather*} \mathbf{\rho}=\frac mV,\\[6pt] \mathbf{\rho}=\frac mV=\frac{pM}{RT}. \end{gather*}

Запишімо температуру в градусах Кельвіна й обчислімо густину газу:

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.

Завдання скеровано на перевірку знання і розуміння поняття силової характеристики електричного поля ‒ напруженості.

Розгляньмо поле зарядженої сфери за умови рівномірного розподілу заряду \(q\) по її поверхні. Із симетрії системи випливає, що всі силові лінії напрямлені радіально (див. рисунок). Вочевидь поле не відрізняється від поля точкового заряду \(q,\) розташованого в центрі сфери. Отже, якщо заряд розподілений по поверхні сфери, то всередині сфери електричного поля немає, тобто напруженість поля дорівнюватиме нулю, як на рисунку Г.

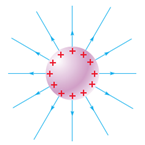
Біля поверхні сфери напруженість буде максимальною (на відстані радіуса R від центру сфери), про що говорить стрибок значення напруженості на графіку \(E(r)\) варіанта відповіді Г.

Залишається визначити поле ззовні від сфери.

Напруженість є силовою характеристикою електричного поля. Напруженість \(\overrightarrow{E}\) електричного поля чисельно дорівнює силі \(\overrightarrow{F},\) з якою поле в даній точці діє на одиничний позитивний заряд \(q_1:\) $$ \overrightarrow{E}=\frac{\overrightarrow{F}}{q_1}. $$

За законом Кулона модуль сили дорівнює $$ F=k\frac{|q|\cdot |q_1|}{r^2}. $$ де \(k\) – коефіцієнт пропорційності, \(q\) – нерухомий точковий позитивний заряд, що є джерелом електричного поля, \(r\) – відстань між зарядами.

Маємо $$ E=k\frac{|q|}{r^2}. $$

Тобто напруженість поля точкового заряду \(q\) спадає нелінійно, обернено пропорційно квадрату відстані від джерела поля до заряду \(q_1,\) поміщеного в поле. Що далі від поверхні сфери, то слабша дія електричного поля сфери.

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Капілярні явища.

Завдання скеровано на перевірку знання і використання формули для визначення підняття рідини в капілярі.

Висота \(h\) підняття рідини в капілярі прямо пропорційна поверхневому натягу \(\mathbf{\sigma}\) рідини й обернено пропорційна густині \(\mathbf{\rho}\) рідини, прискоренню вільного падіння \(g\) й радіусу капіляра \(r:\) $$ h=\frac{2\mathbf{\sigma}}{\mathbf{\rho}gr}. $$

Обчислімо висоту стовпчика води в капілярній трубці за даних в умові температур:

Тепер визначмо, на скільки зменшиться висота стовпчика води в капілярній трубці:

Відповідь: A.

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.

Завдання скеровано на перевірку вміння тлумачити електричну схему, еквівалентно її перетворювати й застосовувати відношення фізичних величин, що характеризують послідовне і паралельне з’єднання провідників.

Перебудуємо еквівалентно ділянку електричного кола, про яку йдеться в умові.

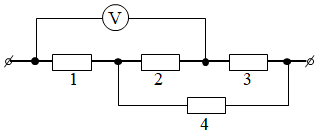
Вольтметр показує напругу на резисторах \(1\) і \(2,\) які з’єднано послідовно, отже, напруга \(U_V\) на них дорівнюватиме сумі напруг \(U_1\) і \(U_2:\) $$ U_V=U_1+U_2. $$

Обчислімо напругу на першому резисторі: $$ U_1=I_1R=IR, $$ де \(I\) – загальний струм у ділянці кола, \(R\) – опір резистора.

Напруга на другому резисторі становитиме: $$ U_2=I_2R. $$

Опір усіх резисторів за умовою однаковий. Сила струму у вітці, де резистори \(2\) і \(3\) з’єднані послідовно, буде у \(2\) рази меншою за силу струму в резисторі \(4,\) що приєднаний до них паралельно, тому що загальний опір резисторів \(2\) і \(3\) вдвічі більший за опір резистора \(4.\)

Силу струму \(I_2\) визначімо зі співвідношення: $$ I_2=I_3:I_4=1:2. $$

Отже,

Тоді $$ U_2=I_2R=\frac 13IR, $$

А сумарна напруга на резисторах \(1\) і \(2\) $$ U_V=U_1+U_2=IR+\frac 13 IR=\frac 43 IR. $$

Виразімо добуток \(IR\) через напругу на ділянці кола: $$ U=IR_\text{заг}. $$

Визначімо загальний опір ділянки кола:

Підставімо цей вираз для загального опору у формулу для напруги на ділянці кола: $$ U=IR_\text{заг}=I\cdot\frac 53R=\frac 53 IR. $$

Звідси $$ IR=\frac 35U. $$

Отже, дізнаймося значення напруги, яке показує вольтметр: \begin{gather*} U_V=\frac 43IR=\frac 43\cdot \frac 35U=\frac 45U,\\[6pt] U_V=\frac 45\cdot 100\ \text{В}=80\ \text{В}. \end{gather*}

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Потенціал і різниця потенціалів.

Завдання скеровано на перевірку знання і розуміння потенціалу.

Потенціал \(\mathbf{\varphi}\) поля, створеного точковим зарядом \(Q,\) у точках, які розташовані на відстані \(r\) від цього заряду, можна розрахувати за формулою $$ \mathbf{\varphi}_1=k\frac Qr. $$

Ця формула справджується і для потенціалу поля рівномірно зарядженої сфери (або кулі) на відстанях, які більші за її радіус або дорівнюють йому.

Обчислімо загальний заряд восьми крапель ртуті відповідно до закону збереження заряду:

Обчислімо об’єм однієї краплі ртуті:

Загальний об’єм великої краплі дорівнюватиме

Тоді радіус утвореної великої краплі становитиме

Визначімо загальний потенціал краплі, утвореної з восьми крапель ртуті, підставивши визначені значення загального заряду \(Q\) великої краплі та її радіуса \(R:\)

Відповідь: Б.

ТЕМА: Електромагнетизм. Магнітне поле, електромагнітна індукція. Магнітний потік.

Завдання скеровано на перевірку знання і розуміння фізичного змісту магнітного потоку і фізичних величин, від яких він залежить.

Потік магнітної індукції (магнітний потік) \(\textbf{Ф}\) ‒ це фізична величина, яка дорівнює добуткові магнітної індукції \(B\) на площу \(S\) поверхні та на косинус кута \(\mathbf{\alpha}\) між вектором магнітної індукції і нормаллю до поверхні: $$ \textbf{Ф}=BS\cos \mathbf{\alpha}. $$

За умовою магнітне поле є однорідним і незмінним, тому його силова характеристика магнітна індукція також залишається незмінною під час повороту контуру навколо його сторони. І площа поверхні, обмежена контуром, також не змінюється під час повороту.

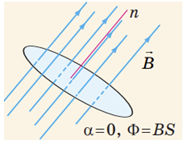
Магнітний потік буде максимальним, якщо поверхня перпендикулярна до ліній магнітної індукції:

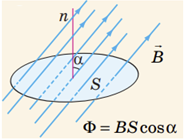
Нормаль \(n,\) проведена до поверхні, що обмежує контур, утворює кут \(\mathbf{\alpha}\) з вектором магнітної індукції \(\overrightarrow{B}:\)

Отже, для того, щоб магнітний потік зменшився вдвоє, треба контур повернути навколо його сторони на кут \(60^\circ.\)

Відповідь: B.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у напівпровідниках.

Завдання скеровано на перевірку знання і розуміння ввімкнення напівпровідникового діода в електричне коло.

Пряме включення: підключімо кристал зі сформованим у ньому \(p\text{-}n\textbf{-переходом}\) до джерела струму так, щоб \(p\text{-ділянка}\) була з’єднана з позитивним полюсом джерела, а \(n\text{-ділянка}\) ‒ з негативним.

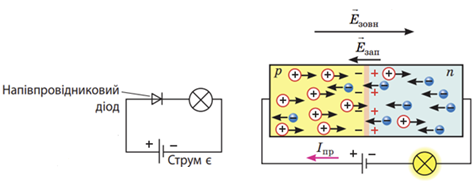
Електрони почнуть рух до позитивного полюса джерела струму, а дірки − до негативного. Запірний шар поповниться вільними електронами й дірками, тому його опір зменшиться. Оскільки через місце контакту рухаються основні носії струму (електрони з \(n\text{-ділянки}\), дірки з \(p\text{-ділянки}\)), яких багато, то в колі існує помітний електричний струм.

У варіантах відповіді А і Г неправильно позначено ділянку \(n\text{-типу}.\) А у варіанті відповіді Б зображене зворотне підключення ‒ коли електрони почнуть рух до позитивного полюса джерела струму, дірки ‒ до негативного. Запірний шар розшириться, його опір збільшиться. Через місце контакту рухаються тільки неосновні носії струму (вільні електрони з \(p\text{-ділянки},\) дірки з \(n\text{-ділянки}\)), яких дуже мало, тому сила зворотного струму незрівнянно менша від прямого.

Отже, правильна відповідь ‒ варіант В.

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.

Завдання скеровано на перевірку знання і розуміння того, від яких величин залежить період коливань тіла на пружині.

Застосуймо формулу для обчислення періоду \(T\) коливань пружинного маятника: $$ T=2\mathbf{\pi}\sqrt{\frac mk}, $$ де \(m\) ‒ маса тіла, яке підвішене до пружини, \(k\) ‒ жорсткість пружини.

Зазначмо, що період коливань пружинного маятника не залежить ні від амплітуди коливань, ні від того, де відбуваються ці коливання (на поверхні Землі, у космічному кораблі чи на поверхні Місяця), ‒ він визначений тільки власними характеристиками коливальної системи «тіло ‒ пружина».

Відповідно до умови важок перебуває в спокої, отже, сила тяжіння і сила пружності зрівноважують одна одну: \begin{gather*} \overrightarrow{F}_\text{тяж}=\overrightarrow{F}_\text{пруж},\\[6pt] mg=k|\Delta x|,\\[6pt] \frac mk=\frac{|\Delta x|}{g}, \end{gather*} де \(g\) ‒ прискорення вільного падіння, що дорівнює \(10\ \text{м/с}^2.\)

Замінимо відношення величин \(\frac mk\) у формулі для визначення періоду на отримане відношення інших величин, які наведено в умові завдання: $$ T=2\mathbf{\pi}\sqrt{\frac mk}=2\mathbf{\pi}\sqrt{\frac{|\Delta x|}{g}}. $$

Обчислімо період вертикальних коливань важка на пружині:

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Перетворення енергії у гармонічних коливаннях.

Завдання скеровано на перевірку знання і розуміння закону збереження механічної енергії на прикладі математичного маятника.

Повна механічна енергія кульки, яка складається з кінетичної і потенціальної енергій, зберігатиметься: уважаємо, що опір повітря нехтовно малий, а сили, що діють у системі, є консервативними. Якщо значення одного виду енергії зменшується, то відповідно, значення іншого виду енергії збільшується.

За умовою завдання маятник рухається в бік положення рівноваги (вертикального положення). Це означає, що висота підняття кульки під час здійснення коливання зменшуватиметься, а швидкість руху кульки у напрямку положення рівноваги збільшуватиметься (див. рисунок).

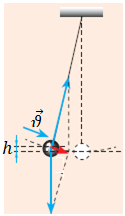
Потенціальна енергія \(W_p\) кульки прямо пропорційна висоті \(h\) підняття кульки відносно нульового рівня (коли кулька перебуває в положенні рівноваги): $$ W_p=mgh, $$ де \(m\) ‒ маса кульки, \(g\) ‒ прискорення вільного падіння.

Отже, якщо висота зменшується, то потенціальна енергія теж зменшується.

Кінетична енергія \(W_k\) прямо пропорційна квадрату швидкості руху \(v\) кульки: $$ W_k=\frac{mv^2}{2}. $$

Отже, у разі збільшення швидкості руху кінетична енергія кульки теж збільшуватиметься.

Відповідь: Г.

ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки та використання їх для визначення довжини світлової хвилі.

Завдання скеровано на перевірку розуміння будови дифракційної ґратки.

Скористаймося формулою дифракційної ґратки $$ d\sin\mathbf{\varphi}=k\mathbf{\lambda}, $$ де \(k\) ‒ ціле число: \(k=0\) ‒ відповідає центральному (нульовому) максимуму, \(k=\pm 1\) ‒ відповідає максимумам першого порядку тощо. Максимуми одного порядку розташовані симетрично з обох боків від центрального максимуму.

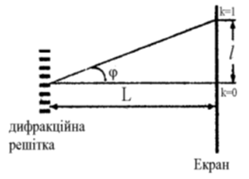
Скористаймося малокутовим наближенням (апроксимація малих кутів): $$ \mathbf{\varphi}\approx \operatorname{tg}\mathbf{\varphi}=\frac lL. $$ де \(l\) ‒ відстань від центрального максимуму до максимуму \(k\text{-го}\) порядку.

Отримаємо формулу для визначення \(l:\)

Відповідь: A.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання. Власна частота й період електромагнітних коливань. Формула Томсона.

Завдання скеровано на перевірку знання формули Томсона й розуміння її фізичного змісту.

Період \(T\) власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$ T=2\mathbf{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки, \(C\) ‒ електроємність конденсатора.

Коливання в ідеальній коливальній системі називають власними коливаннями, період власних коливань визначений параметрами коливальної системи і не залежить від амплітуди коливань, тобто від енергії, яку передано системі під час виведення її з положення рівноваги. Оскільки конденсатор і котушка після зміни сили струму залишилися ті самі, то і період коливань контуру не зміниться.

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на перевірку розуміння наслідків постулатів теорії відносності.

Оскільки в умові завдання йдеться про релятивістський ефект скорочення довжини тіла, а це стає помітним тільки в разі руху тіла зі швидкістю \(v,\) яка порівнянна зі швидкістю поширення світла \(c,\) тож скористаймося наслідком постулатів теорії відносності: $$ l=l_0\sqrt{1-\frac{v^2}{c^2}}, $$ де \(l_0\) ‒ довжина тіла в системі відліку, відносно якої тіло перебуває у спокої; \(l\) ‒ довжина тіла в системі відліку, відносно якої тіло рухається (відносно спостерігача в лабораторії).

Якщо за умовою поздовжні розміри тіла зменшилися на \(20\ \text{%},\) то $$ l=0,8l_0. $$

Підставімо це відношення у формулу й визначмо швидкість руху тіла:

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом й атомне ядро. Ядерні реакції.

Завдання скеровано на перевірку вміння складати рівняння ядерних реакцій.

Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових.

Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.

Запишімо рівняння ядерної реакції відповідно до умови завдання:

де \(\mathrm{X}\) ‒ невідома частинка, що утворилася внаслідок реакції.

У лівій і правій частинах рівняння реакції суми зарядів, як і суми мас, мають збігатися. Із відповідних рівнянь дістанемо зарядове (протонне) \(Z\) та масове (нуклонне) \(A\) числа невідомого ядра елемента \(\mathrm{X}.\)

Запишімо суму мас і суму зарядів для обох частин рівняння реакції:

З одержаних рівнянь маємо: $$ A=24,\ \ Z=11. $$

Невідоме в рівнянні – нуклід \(^{24}_{11}\mathrm{Na}.\)

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Абсолютний і відносний показники заломлення.

Завдання скеровано на перевірку знання і розуміння фізичного змісту відносного показника заломлення.

$$ n_{21}=\frac{n_2}{n_1}, $$ де \(n_{21}\) ‒ це фізична величина, яку називають відносним показником заломлення середовища \(2\) (середовища, в якому світло поширюється після заломлення) відносно середовища \(1\) (середовища, із якого світло падає).

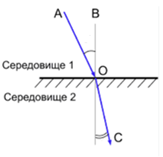
Відносний показник заломлення \(n_{21}\) показує, у скільки разів швидкість \(v_1\) поширення світла в середовищі \(1\) більша (або менша), ніж швидкість \(v_2\) поширення світла в середовищі \(2:\) $$ n_{21}=\frac{v_1}{v_2}. $$

Отже, обчислімо відношення швидкостей світла в середовищах з різними показниками заломлення відповідно до умови: $$ \frac{v_1}{v_2}=\frac{n_2}{n_1}=\frac{1,65}{1,5}=1,1. $$

Відповідь: Г.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.

Завдання скеровано на перевірку знання і розуміння фізичних величин, що характеризують магнітне поле.

1. За визначенням кількість ліній магнітної індукції, що пронизують виділену в магнітному полі рамку, характеризує фізична величина, яку називають потік магнітної індукції або магнітний потік − В.

2. Фізичну величину, яка характеризує магнітні властивості середовища і дорівнює відношенню магнітної індукції магнітного поля в середовищі до магнітної індукції магнітного поля у вакуумі, називають відносною магнітною проникністю середовища – Г.

3. Фізична величина, яка характеризує провідник і чисельно дорівнює ЕРС (електрорушійній силі) самоіндукції, що виникає в провіднику в разі зміни сили струму на \(1\ \text{А}\) за \(1\ \text{с},\) називається індуктивністю − А.

4. Моментом сили, яка діє на рамку площею \(1\ \text{м}^2\) під час проходження в ній струму \(1\ \text{А}\) визначена магнітна індукція – Б.

Відповідь: 1В, 2Г, 3А, 4Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку знання і розуміння кінематичних характеристик прямолінійного рівномірного і рівноприскореного рухів, що є складниками рівняння руху.

1. Рівнянням координати \(x\) $$ x=5+2t $$ описують прямолінійний рівномірний рух: $$ x=x_0+vt, $$ де \(x_0\) – початкова координата, \(v\) – проєкція швидкості руху, \(t\) – час спостереження.

Відповідно до цього рівняння початкова координата \(x_0=5\ \text{м},\) швидкість руху тіла \(v=2\ \text{м/с},\) а прискорення \(a=0\ \text{м/с}^2,\) оскільки рух рівномірний – варіант відповіді Г.

2. Рівнянням координати \(x\) $$ x=5t+2t^2 $$ описують прямолінійний рівноприскорений рух: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) – початкова координата, \(v_0\) – проєкція початкової швидкості руху, \(t\) – час спостереження, \(a\) – проєкція прискорення.

Відповідно до цього рівняння початкова координата \(x_0=0\ \text{м},\) початкова швидкість руху тіла \(v_0=5\ \text{м/с},\) а прискорення \(a=4\ \text{м/с}^2\) – варіант відповіді А.

3. Рівнянням координати \(x\) $$ x=2t+5t^2 $$ описують прямолінійний рівноприскорений рух: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) – початкова координата, \(v_0\) – проєкція початкової швидкості руху, \(t\) – час спостереження, \(a\) – проєкція прискорення.

Відповідно до цього рівняння початкова координата \(x_0=0\ \text{м},\) початкова швидкість руху тіла \(v_0=2\ \text{м/с},\) а прискорення \(a=10\ \text{м/с}^2\) – варіант відповіді Б.

4. Рівнянням координати \(x\) $$ x=5+t^2 $$ описують прямолінійний рівноприскорений рух: $$ x=x_0+v_0t+\frac{at^2}{2}, $$ де \(x_0\) – початкова координата, \(v_0\) – проєкція початкової швидкості руху, \(t\) – час спостереження, \(a\) – проєкція прискорення.

Відповідно до цього рівняння початкова координата \(x_0=5\ \text{м},\) початкова швидкість руху тіла \(v_0=0\ \text{м/с},\) а прискорення \(a=2\ \text{м/с}^2\) – варіант відповіді Д.

Відповідь: 1Г, 2А, 3Б, 4Д.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.

Завдання скеровано на перевірку знання і розуміння понять і фізичних величин, які стосуються властивостей газів і рідин.

1. Абсолютна вологість − фізична величина, якою характеризують уміст водяної пари в повітрі. Абсолютна вологість чисельно дорівнює масі водяної пари, що міститься в повітрі об’ємом \(1\ \text{м}^3\) – Б.

2. Відносна вологість − фізична величина, яка показує, наскільки водяна пара близька до насичення. Відносна вологість дорівнює поданому у відсотках відношенню абсолютної вологості до густини насиченої водяної пари за певної температури. Оскільки густина водяної пари прямо пропорційна її парціальному тиску і концентрації молекул пари, то можна сказати, що відносна вологість – це відношення парціального тиску водяної пари, що є в повітрі за певної температури, до тиску насиченої пари за цієї температури – А.

3. Конденсація – це процес переходу речовини з газуватого стану в рідкий – В.

4. Точка роси – це температура, за якої водяна пара, що міститься в повітрі, стає насиченою – Д.

Відповідь: 1Б, 2А, 3В, 4Д.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Основні положення молекулярно-кінетичної теорії. Основи термодинаміки. Внутрішня енергія.

Завдання скеровано на перевірку знання і розуміння основних понять молекулярно-кінетичної теорії та їхнього зв’язку між собою.

1. Гелій – одноатомний газ. Атоми такого газу рухаються лише поступально, тому, щоб визначити його внутрішню енергію \(U,\) треба середню кінетичну енергію \(\overline{E}_k\) поступального руху атомів $$ \overline{E}_k=\frac{m_0\overline{v}^2_\text{кв}}{2} $$ помножити на кількість атомів \(N:\) $$ N=\frac mM N_A. $$

Тобто \begin{gather*} U=\overline{E}_k\cdot N,\\[6pt] U=\frac{m_0\overline{v}^2_\text{кв}}{2}\cdot \frac mM N_A,\\[6pt] U=M\cdot\frac{\overline{v}^2_\text{кв}}{2}\mathbf{\nu}, \end{gather*} де \(M=m_0\cdot N_А\) (\(M\) – молярна маса, \(m_0\) – маса молекули (атома) цієї речовини, \(N_А\) – стала Авогадро), \(\mathbf{\nu}=\frac mM\) (\(\mathbf{\nu}\) – кількість речовини, \(m\) – маса речовини).

Відповідь: 18.

2. Середню кінетичну енергію поступального руху молекул ідеального газу (кінетична енергія поступального руху, що в середньому припадає на одну молекулу) обчислюють за формулою $$ \overline{E}_k=\frac{m_0\overline{v}^2_\text{кв}}{2}. $$

З іншого боку середня кінетична енергія поступального руху молекул ідеального газу прямо пропорційна абсолютній температурі \(T:\) $$ \overline{E}_k=\frac 32 kT, $$ де \(k\) – стала Больцмана.

Прирівняймо праві частини цих формул: $$ \frac{m_0\overline{v}^2_\text{кв}}{2}=\frac 32 kT. $$

Перетворімо отриману рівність так, щоб можна було визначити температуру газу, використовуючи фізичні величини з умови завдання: \begin{gather*} m_0=\frac{M}{N_A},\\[6pt] \frac{M}{N_A}\cdot \frac{\overline{v}^2_\text{кв}}{2}=\frac 32 kT,\\[6pt] \frac{M\overline{v}^2_\text{кв}}{2}=\frac 32 kN_AT, \end{gather*} де добуток сталої Больцмана і сталої Авогадро дорівнює універсальній газовій сталій \(R:\)

Відповідь: 1500.

Відповідь: 1. 18. 2. 1500.

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.

Завдання скеровано на перевірку знання і розуміння фізичних характеристик рівномірного руху по колу – доцентрового прискорення, лінійної швидкості, кутової швидкості.

1. Запишімо формулу для визначення доцентрового прискорення \(a_\text{дц}:\) $$ a_\text{дц}=\mathbf{\omega}^2r, $$ де \(\mathbf{\omega}\) – кутова швидкість, \(r\) – радіус кола.

За умовою кутова швидкість для всіх точок стала й однакова, а модуль доцентрового прискорення прямо пропорційний радіусу кола. Отже, модуль доцентрового прискорення \(a_1\) буде найменшим для точок диска, що перебувають на найменшій відстані від центра диска – це точки на внутрішньому отворі диска діаметром \(d_1=1,5\ \text{см}.\) Тоді найбільшим буде модуль доцентрового прискорення \(a_3\) для точок на зовнішньому краю диска – це коло діаметром \(d_3=12\ \text{см}:\) \begin{gather*} a_1=\mathbf{\omega}^2r_1=\mathbf{\omega}^2\cdot \frac{d_1}{2},\\[6pt] a_3=\mathbf{\omega}^2r_3=\mathbf{\omega}^2\cdot \frac{d_3}{2}. \end{gather*}

Визначімо відношення максимального і мінімального модулів доцентрових прискорень: \begin{gather*} \frac{a_3}{a_1}=\frac{\mathbf{\omega}^2\cdot d_3\cdot 2}{2\mathbf{\omega}^2\cdot d_1}=\frac{d_3}{d_1},\\[6pt] \frac{a_3}{a_1}=\frac{12\ \text{см}}{1,5\ \text{см}}=8. \end{gather*}

Відповідь: 8.

2. Формула для визначення лінійної швидкості ϑ рівномірного руху тіла по колу: \begin{gather*} v=\mathbf{\omega}R. \end{gather*}

За умовою кутова швидкість для всіх точок стала й однакова, а лінійна швидкість прямо пропорційна радіусу кола. Отже, найбільшою буде лінійна швидкість \(v_3\) зовнішнього краю диска \(R_3=6\ \text{см},\) а найменшою \(v_2\) – внутрішнього краю області диска, на якому вже можна записувати / зчитувати інформацію – \(R_2=2\ \text{см:}\) \begin{gather*} v_3=\mathbf{\omega}R_3,\\[7pt] v_2=\mathbf{\omega}R_2. \end{gather*}

Визначімо, у скільки разів максимальна швидкість записування / зчитування інформації більша за мінімальну: \begin{gather*} \frac{v_3}{v_2}=\frac{\mathbf{\omega}R_3}{\mathbf{\omega}R_2}=\frac{R_3}{R_2},\\[6pt] \frac{v_3}{v_2}=\frac{6\ \text{см}}{2\ \text{см}}=3. \end{gather*}

Відповідь: 3.

Відповідь: 1. 8. 2. 3.

ТЕМА: Механіка. Основи кінематики. Прямолінійний рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку розуміння закономірностей прямолінійного рівномірного й рівноприскореного рухів.

Розгляньмо рух парашутиста й монети.

Парашутист за умовою опускається зі сталою швидкістю \(v=5\ \text{м/с},\) оскільки дія сили тяжіння скомпенсована дією сили опору повітря. Отже, відстань \(h=10\ \text{м}\) він пройде за \(2\ \text{с}:\) $$ t_\text{пар}=\frac hv=\frac{10}{5}=2\ \text{с}. $$

Монета пройде той самий шлях \(h=10\ \text{м},\) але рухатиметься рівноприскорено. Власна початкова швидкість монети дорівнює нулю, оскільки вона просто випала з кишені. Але ж вона випала з кишені парашутиста, який рухався зі швидкістю \(v=5\ \text{м/с},\) тому початкова швидкість монети $$ v_0=5\ \text{м/с}. $$

Вплив опору повітря на монету за умовою до уваги не беремо, тож знайдемо час її падіння з кінематичного рівняння: $$ h=v_0t+\frac{>^2}{2}, $$ де \(g\) ‒ прискорення вільного падіння; усі векторні величини записано в проєкціях на вісь \(Oy,\) що, як і вектор прискорення вільного падіння, напрямлена вертикально вниз.

Підставімо значення величин у рівняння: $$ h=v_0t+\frac{>^2}{2}\Rightarrow 10=5t+\frac{10t^2}{2}. $$

Поділімо ліву і праву частину рівняння на \(5\) й дістанемо зведене квадратне рівняння: $$ t^2+t-2=0. $$

За теоремою Вієтта знайдімо корені рівняння: $$ t_1=-2,\ \ t_2=1. $$

Час не може бути від’ємним, тому умову задовольняє корінь \(t_2=1\ \text{с},\) тобто монета впала за \(1\ \text{с},\) а парашутист приземлився на \(1\ \text{с}\) пізніше: $$ \Delta t=t_\text{пар}-t_2=2\ \text{с}-1\ \text{с}=1\ \text{с}. $$

Відповідь: 1.

ТЕМА: Механіка. Основи динаміки. Рух тіл під дією кількох сил.

Завдання скеровано на перевірку вміння розв’язувати задачі на рух тіла під дією кількох сил.

Запишімо рівняння другого закону Ньютона у векторному вигляді та в проєкціях на осі координат

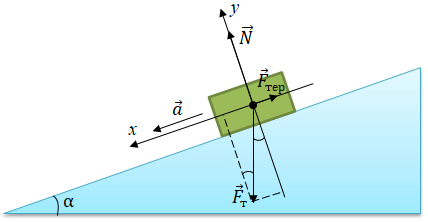
де \(m\) – маса тіла, \(g\) – прискорення вільного падіння, \(\overrightarrow{a}\) – прискорення, з яким зісковзує тіло з похилої площини, \(\overrightarrow{F}_\text{Т}\) – сила тяжіння, \(\overrightarrow{N}\) – сила нормальної реакції опори, \(\overrightarrow{F}_\text{тер}\) – сила тертя ковзання, \(\mathbf{\mu}\) – коефіцієнт тертя ковзання.

Виразімо силу нормальної реакції опори з рівняння (2) і підставимо в рівняння (1):

Обидві частини отриманого рівняння скоротімо на масу \(m\) тіла: $$ a=g\sin\mathbf{\alpha}-\mathbf{\mu}g\cos\mathbf{\alpha}. $$

Виразімо й обчислімо коефіцієнт тертя ковзання: $$ \mathbf{\mu}=\frac{g\sin\mathbf{\alpha}-a}{g\cos\mathbf{\alpha}}. $$

За умовою $$ \mathbf{\alpha}=\arcsin\mathbf{\alpha}. $$

Відповідно

Відповідь: 0,5.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.

Завдання скеровано на перевірку вміння застосовувати закон Ома для повного кола.

Запишімо закон Ома для повного кола: $$ I=\frac{\mathbf{\varepsilon}}{R+r}, $$ де \(I\) ‒ сила струму, \(\mathbf{\varepsilon}\) ‒ електрорушійна сила джерела струму, \(R\) – опір резистора, \(r\) – внутрішній опір джерела струму.

Коли вимикач розімкнутий, то вольтметр показує значення електрорушійної сили джерела струму: $$ \mathbf{\varepsilon}=12\ \text{В}. $$

Перетворімо цю формулу закону й визначмо внутрішній опір джерела струму: \begin{gather*} \mathbf{\varepsilon}=IR+Ir. \end{gather*}

За законом Ома для ділянки кола $$ IR=U, $$ це напруга на резисторі.

Отже, $$ \mathbf{\varepsilon}=IR+Ir=U+Ir, $$ звідки

Відповідь: 2,5.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.

Завдання скеровано на перевірку вміння застосовувати перший закон термодинаміки до ізопроцесів, зокрема до ізобарного.

За умовою ідеальному одноатомному газу передали енергію кількістю \(Q\) за сталого тиску – процес ізобарний. У ході цього процесу виконується робота \(A\) і змінюється внутрішня енергія \(\Delta U\) газу, тому рівняння першого закону термодинаміки має вигляд: $$ Q=\Delta U + A. $$

За умовою газ ідеальний одноатомний, то робота газу дорівнює $$ A=p\Delta V, $$ де \(p\) – тиск, \(\Delta V\) – зміна об’єму.

А зміна його внутрішньої енергії $$ \Delta U=\frac 32p\Delta V. $$

Тоді кількість енергії, передана газу, дорівнює: $$ Q=\frac 32p\Delta V+p\Delta V=\frac 52p\Delta V. $$

Використавши рівняння Менделєєва – Клапейрона $$ p\Delta V=\frac mM R\Delta T=\mathbf{\nu}R\Delta T, $$ де \(\mathbf{\nu}=\frac mM\) – кількість речовини, що дорівнює відношенню маси газу до його молярної маси, \(R\) – універсальна газова стала, \(\Delta T\) – зміна температури, вираз для переданої ідеальному одноатомному газу енергії можна подати так: $$ Q=\frac 52p\Delta V=\frac{5}{2}\frac mM R\Delta T=\frac 52\mathbf{\nu}R\Delta T. $$

Виразімо і обчислімо зміну температури газу:

(Зміна температури за шкалою Кельвіна дорівнює зміні температури за шкалою Цельсія: \(\Delta T=\Delta t,\) тобто ціна поділки шкали Кельвіна дорівнює ціні поділки шкали Цельсія: \(1\ ^\circ\mathrm{C}=1\ \text{K}.\))

Відповідь: 40.

ТЕМА: Електродинаміка. Основи електростатики. Енергія електричного поля.

Завдання скеровано на перевірку вміння визначати характеристики батарей конденсаторів у разі їхнього паралельного і послідовного з’єднання, а також уміння визначати енергію електричного поля конденсаторів.

Енергію електричного поля \(W_1\) конденсатора \(1\) обчислюємо так: \begin{gather*} W_1=\frac{q^2_1}{2C}, \end{gather*} де \(q_1\) ‒ заряд конденсатора \(1,\ C\) ‒ електроємність конденсатора \(1\) (за умовою всі три конденсатори мають однакову електроємність).

Конденсатор \(1\) з’єднаний послідовно з ділянкою кола, де конденсатори \(2\) і \(3\) з’єднані паралельно. У цьому разі заряд конденсатора \(1\) дорівнює заряду послідовно з’єднаної з ним ділянки кола: $$ q_1=q_2+q_3. $$

Оскільки в разі паралельного з’єднання конденсаторів напруга на них однакова й за умовою електроємність конденсаторів однакова, то й заряди конденсаторів \(2\) і \(3\) будуть однакові: \begin{gather*} q=UC,\\[7pt] q_2=q_3. \end{gather*}

Отже, \begin{gather*} q_1=2q_2,\\[6pt] q_2=\frac{q_1}{2}. \end{gather*}

Запишімо формулу для енергії електричного поля конденсатора \(2:\) $$ W_2=\frac{q^2_2}{2C}=\frac{q^2_1}{8C}. $$

Визначімо, у скільки разів енергія електричного поля конденсатора \(1\) більша за енергію електричного поля конденсатора \(2:\)

Відповідь: 4.

ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.

Завдання скеровано на перевірку вміння застосовувати формулу тонкої лінзи.

Якщо лінза дає дійсне зображення, то це збиральна лінза.

Запишімо формулу тонкої лінзи: $$ \frac 1F=\frac 1d+\frac 1f, $$ де \(F\) ‒ фокусна відстань лінзи, \(d\) ‒ відстань від предмета до лінзи, \(f\) ‒ відстань від лінзи до предмета. Тоді за умовою відстань між предметом і його зображенням дорівнює $$ d+f=80\ \text{см}=0,8\ \text{м}. $$

Скористаймося ще відношенням розмірів і відстаней. Відношення лінійного розміру \(H\) зображення предмета до розміру \(h\) самого предмета називають лінійним збільшенням \(\textbf{Г}\) лінзи: $$ \textbf{Г}=\frac Hh=\frac fd. $$

За умовою зображення предмета втричі більше за предмет: \begin{gather*} \frac Hh=\frac{3h}{h}=3,\\[6pt] d=0,8\ \text{м}-f. \end{gather*}

Отже, $$ \frac Hh=\frac fd\Rightarrow 3=\frac{f}{0,8-f}. $$

Визначімо відстань \(f\) від лінзи до зображення:

Тоді відстань \(d\) від предмета до лінзи дорівнюватиме:

Обчислімо фокусну відстань цієї лінзи:

Відповідь: 15.

ТЕМА: Коливання і хвилі. Механічні коливання і хвилі. Коливання вантажу на пружині.

Завдання скеровано на перевірку знання і розуміння механічних коливань тіла на пружині.

Запишімо формулу для визначення періоду \(T\) пружинного маятника: $$ T=2\mathbf{\pi}\sqrt{\frac mk}, $$ де \(m\) ‒ маса тіла (дана в умові), \(k\) ‒ жорсткість пружини (необхідно визначити).

Під час максимальної деформації пружини на тіло, прикріплене до неї, діятиме максимальна сила пружності \(F_\text{пр max}\) з боку пружини: $$ F_\text{пр max}=kA, $$ де \(A\) ‒ максимальне відхилення тіла від положення рівноваги ‒ амплітуда.

Отже, \begin{gather*} k=\frac{F_\text{пр max}}{A}. \end{gather*}

Амплітудне значення відхилення тіла можна визначити, скориставшись повною енергією тіла. Оскільки в крайній точці тіло не рухатиметься, тобто кінетична енергія дорівнюватиме нулю, то повна (максимальна) енергія тіла ‒ це потенціальна енергія \(E_p\) пружно деформованого тіла: \begin{gather*} E_p=\frac{kA^2}{2}. \end{gather*}

Визначімо амплітуду \(A,\) скориставшись для цього методом підстановки: \begin{gather*} E_p=\frac{kA\cdot A}{2}=\frac{F_\text{пр max}\cdot A}{2},\\[6pt] A=\frac{2E_p}{F_\text{пр max}},\\[6pt] A=\frac{2\cdot 60\cdot 10^{-6}\ \text{Дж}}{3\cdot 10^{-3}\ \text{Н}}=40\cdot 10^{-3}\ \text{м}. \end{gather*}

Тепер можемо визначити жорсткість пружини \(k:\) \begin{gather*} k=\frac{F_\text{пр max}}{A}=\frac{3\cdot 10^{-3}\ \text{Н}}{40\cdot 10^{-3}\ \text{м}}=\frac{3}{40}\ \text{Н/м}. \end{gather*}

Обчислімо період коливань тіла \(T:\)

Результат округлімо до сотих: $$ T=1,256\ \text{с}\approx 1,26\ \text{с}. $$

Відповідь: 1,26.

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Фотоефект.

Завдання скеровано на перевірку знання і розуміння, що таке фотострум, і фізичного змісту сили струму.

Фотоефектом називають явище взаємодії світла з речовиною, яке супроводжується випромінюванням (емісією) електронів.

Запишімо формулу для визначення сили струму \(I:\) \begin{gather*} I=\frac Qt=\frac{e\cdot N_S}{t}, \end{gather*} де \(Q\) ‒ загальний заряд електронів, що вилетіли з поверхні за час \(t,\ e\) ‒ елементарний заряд, \(N_S\) ‒ кількість електронів, що вилетіли з поверхні площею \(S.\)

Обчислімо кількість електронів, що вилетіли з поверхні площею \(S=1\ \text{м}^2:\) \begin{gather*} N_S=\frac{It}{e},\\[6pt] N_S=\frac{2\cdot 10^{-5}\ \text{А}\cdot 1\ \text{с}}{1,6\cdot 10^{-19}\ \text{Кл}}=1,25\cdot 10^{14}. \end{gather*}

В \(1\ \text{м}^2\) міститься \(10^{6}\ \text{мм}^2.\) Отже, поділімо кількість електронів \(N_S\) на кількість міліметрів квадратних і визначмо кількість електронів, що вилітають з поверхні площею \(1\ \text{мм}^2:\)

Відповідь: 125.

ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси та енергії.

Завдання скеровано на перевірку знання і розуміння зв’язку маси та енергії як важливого результату спеціальної теорії відносності, коли тіла (частинки) рухаються зі швидкістю порядку швидкості світла у вакуумі.

З погляду спеціальної теорії відносності, якщо тіло масою \(m\) рухається зі швидкістю \(v\) відносно якоїсь системи відліку, то енергія \(E\) тіла в цій системі відліку становить: $$ E=\frac{mc^2}{\sqrt{1-\frac{v^2}{c^2}}}, $$ де \(c\) ‒ швидкість світла у вакуумі.

Будь-яке тіло (будь-яка частинка), що має масу, несе із собою запас енергії. Дійсно, навіть якщо швидкість руху тіла (частинки) зменшується до нуля \((v=0),\) то згідно із цією формулою тіло все одно має енергію \(E_0:\) $$ E_0=mc^2. $$

Цю енергію називають енергією спокою.

Тоді формула для повної енергії матиме такий вигляд: $$ E=\frac{E_0}{\sqrt{1-\frac{v^2}{c^2}}}. $$

Підставімо значення відповідних величин з умови завдання й обчислімо повну енергію електрона:

Відповідь: 136.