ЗНО онлайн 2014 року з фізики – основна сесія
Тестові завдання основної сесії ЗНО 2014 року з фізики
ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу під час рівномірного і рівноприскореного руху.
Завдання скеровано на перевірку вміння читати графіки залежності кінематичних величин від часу під час рівномірного і рівноприскореного рухів.
Залежність проєкції швидкості
Що більше прискорення руху тіла, то більший кут нахилу графіка проєкції швидкості до осі часу.
Розгляньмо рисунок. Найменший кут нахилу графіка ‒ на ділянці від
Перевірити правильність відповіді можна за допомогою розрахунків, скориставшись формулою для прискорення
Інтервал часу від
Інтервал часу від від
Інтервал часу від від
Інтервал часу від від
Як бачимо, мінімальне прискорення відповідає інтервалу часу від
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Умови рівноваги.
Завдання скеровано на перевірку знання і розуміння умов рівноваги тіла, а також вміння застосовувати правило моментів.
За умовою важіль
Момент сили
У цьому разі на важки і на вантаж діють сили тяжіння
Плече
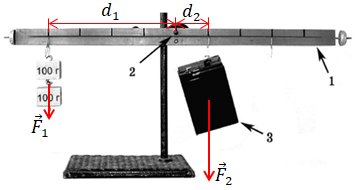
Визначимо масу вантажу
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи динаміки. Додавання сил. Другий закон Ньютона.
Завдання скеровано на перевірку вміння описати систему зв’язаних тіл за допомогою другого закону Ньютона.
Зробимо схематичний рисунок, який ілюструватиме умову цього завдання. І на рисунку позначимо всі сили, що діють на обидва тіла.
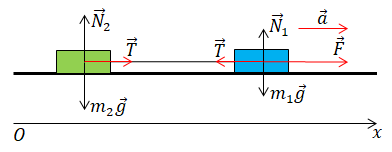
І на перше, і на друге тіло діятимуть сила тяжіння
Запишімо рівняння другого закону Ньютона для кожного з тіл у проєкціях на горизонтальну вісь
Обчислімо горизонтальну силу
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Закон збереження енергії в механічних процесах. Закон збереження імпульсу.
Завдання скеровано на перевірку знання і розуміння законів збереження в механіці й уміння їх застосовувати.
Кульку, що нерухомо висить на нитці, позначмо
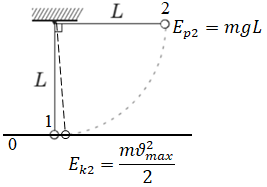
Після того як кульку
Відповідно до умови зіткнення кульок
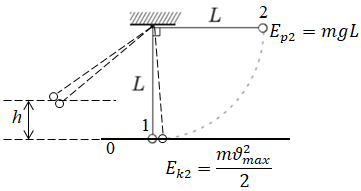
Опишімо взаємодію двох кульок законом збереження імпульсу:
Знову запишімо закон збереження енергії для кульок, які рухаються разом:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Елементи механіки рідин та газів. Закон Паскаля для рідин та газів. Атмосферний тиск. Тиск нерухомої рідини на дно і стінки посудини.
Завдання скеровано на перевірку знання і розуміння атмосферного і гідростатичного тисків, а також вміння визначати тиск у будь-якій точці сполучених посудин.
У точці
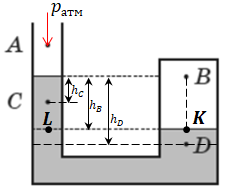
Точка
У точці
У точці
Найменшим буде тиск у точці
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Ізопроцеси в газах.
Завдання скеровано на перевірку вміння описати стан газу за допомогою рівняння стану газу (Менделєєва ‒ Клапейрона).
Запишімо рівняння Менделєєва ‒ Клапейрона для стану
Права частина однакова, оскільки записуємо рівняння для того самого ідеального газу масою
Уважатимемо сторону клітинки за одиничний відрізок:
Запишімо рівняння Клапейрона:
Рівність виконуватиметься, якщо
Процес змінювання стану даного газу деякої маси, що відбувається за незмінного об’єму, називають ізохорним процесом:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів.
Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки і вміння застосовувати його до ізопроцесів.
Під час ізобарного процесу виконується робота і змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки має вигляд:
Під час ізобарного процесу передана газу кількість теплоти
Визначімо зміну внутрішньої енергії:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці
Завдання скеровано на перевірку розуміння роботи в термодинаміці і вміння визначати її під час різних ізопроцесів.
Розгляньмо окремо кожну ділянку графіка. З’ясуємо, чому дорівнюватиме загальна робота
Процес
Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу.
Процес
Отже, робота виконуватиметься лише під час ізобарного процесу:
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля.
Завдання скеровано на перевірку знання і розуміння напруженості електричного поля.
Напруженість електричного поля
Визначмо модуль сили, з якою діє електричне поле Землі на краплю води:
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Електроємність плоского конденсатора.
Завдання скеровано на перевірку знання і розуміння характеристики конденсатора ‒ електроємності, а також від яких параметрів і як вона залежить.
Електроємність
З формули видно, що електроємність прямо пропорційна діелектричній проникності діелектрика:
Оскільки в умові питають, як зміниться електроємність системи конденсаторів, то йдеться про загальну електроємність. Отже, після того, як повітряні конденсатори (діелектрична проникність повітря дорівнює практично
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Залежність опору металів від температури.
Завдання скеровано на перевірку знання і розуміння електричного опору в металевих провідниках і їхньої залежності від температури.
Опір металевого провідника залежить не тільки від його геометричних розмірів і речовини, з якої він виготовлений, а й від температури: якщо температура
Як видно з формули, із підвищенням температури опір металу збільшується, і навпаки, зі зниженням температури опір металу зменшується. Отже, графік Г неправильний ‒ він відображає зменшення опору зі зростанням температури.
Розкриймо у формулі дужки:
Отже, за температури
Якщо температура металу знижується, наближаючись до абсолютного нуля
Отже, графік В задовольняє всім вищезазначеним умовам залежності електричного опору металу від температури.
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля‒Ленца.
Завдання скеровано на перевірку знання і розуміння залежності кількості теплоти від характеристик електричного струму і часу.
Закон Джоуля ‒ Ленца: кількість теплоти
До зміни сили струму кількість теплоти становила:
Після збільшення сили струму в
Визначмо, у скільки разів змінилася кількість теплоти:
Отже, після збільшення сили струму в
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Індуктивність.
Завдання скеровано на перевірку знання і розуміння фізичного змісту індуктивності.
Індуктивність
Одиниця індуктивності в SІ ‒ генрі:
Одиниця сили струму ампер (А) і одиниця часу секунда (с) є одиницями SI.
Розпишімо одиницю електрорушійної сили самоіндукції ‒ вольт (В) ‒ через одиниці SI:
Виразимо одиницю індуктивності через основні одиниці SI:
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання. Зміщення, амплітуда, період, частота і фаза гармонічних коливань.
Завдання скеровано на перевірку знання і розуміння періоду коливань.
За умовою завдання зміщення тіла фіксували протягом половини періоду:
Із наведених варіантів відповіді єдиний, який задовольняє умову, це варіант Б ‒ послідовність моментів часу від
Усі інші числові дані в завданні є зайвими за поданого формулювання умови.
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Звукові хвилі. Висота тону і тембр звуку.
Завдання скеровано на перевірку знання і розуміння суб’єктивних (фізіологічних) характеристик звуку.
Висоту звуку визначає, переважно, частота звукової хвилі: що більша її частота, то вищий тон звуку. Наприклад, ноті ля першої октави відповідає частота
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.
Завдання скеровано на перевірку знання і розуміння закону збереження енергії під час електромагнітних коливань в коливальному контурі і вміння його застосовувати.
Під час електромагнітних коливань в коливальному контурі відбувається періодичне перетворення енергії: енергія електричного поля конденсатора переходить в енергію магнітного поля, і навпаки.
Запишімо закон збереження енергії для ідеального (вважаємо, що енергія не витрачається на нагрівання підвідних проводів, обмотки котушки, на поляризацію діелектрика, тощо) коливального контуру відповідно до умови завдання:
Помножмо цю рівність на
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Оптика. Закони відбивання світла. Побудова зображень, які дає плоске дзеркало.
Завдання скеровано на перевірку знання і розуміння закону відбивання світла і вміння застосовувати його до побудови зображення світлового променя, які дає плоске дзеркало.
Закони відбивання світла:
1. Промінь, що падає, промінь відбитий і перпендикуляр до поверхні відбивання, проведений із точки падіння променя, лежать в одній площині.
2. Кут відбивання дорівнює куту падіння:
Як бачимо з рисунка, даного в умові, кут
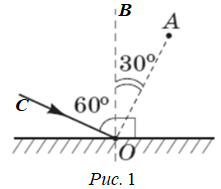
За другим законом кут відбивання
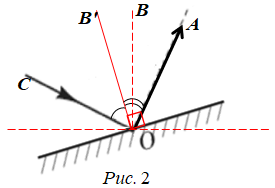
За означенням променя, що падає, і за першим законом відбивання
Відповідь: A.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Шкала електромагнітних хвиль.
Завдання скеровано на перевірку знання і розуміння видів електромагнітного випромінювання.
Шкала (спектр) електромагнітних хвиль ‒ безперервна послідовність частот і довжин електромагнітних хвиль, що існують у природі.
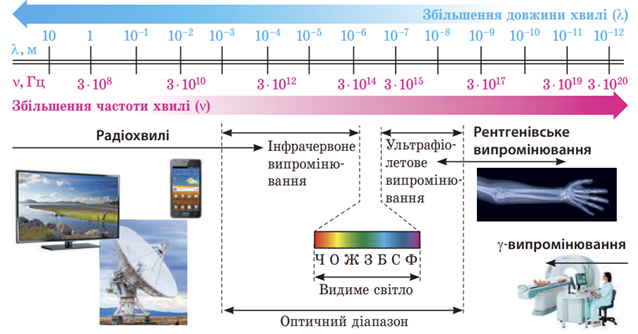
Довжина хвилі й частота випромінювання пов’язані формулою:
Залежність між довжиною хвилі і частотою є оберненою: що більша частота, то менша довжина хвилі, і навпаки, що менша частота, то більша довжина хвилі (див. рисунок).
Найбільші довжини хвиль відповідають радіохвилям ‒ електромагнітним хвилям довжиною від
Оптичний діапазон включає в себе інфрачервоне (теплове, довжина хвилі від
‒ інфрачервоне ‒ порядку
‒ видиме ‒ порядку
‒ ультрафіолетове ‒ порядку
Рентгенівське випромінювання (
Гамма
Отже, з названих у варіантах відповіді видів електромагнітного випромінювання найбільшу частоту мають рентгенівські хвилі.
Відповідь: Г.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Гіпотеза Планка. Стала Планка. Кванти світла (фотони).
Завдання скеровано на перевірку знання і розуміння гіпотези Планка.
Гіпотеза Планка: випромінювання електромагнітних хвиль атомами і молекулами речовини відбувається не безперервно, а дискретно, тобто окремими порціями, енергія
Згодом порції енергії стали називати квантами енергії, а сталу
Відповідь: Б.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Склад ядра атома. Ізотопи.
Завдання скеровано на перевірку знання і розуміння складу ядра атома та їхніх різновидів.
Різновиди атомів того самого хімічного елемента, ядра яких містять однакову кількість протонів, але різну кількість нейтронів, називають ізотопами («однакові за місцем»). Кожний хімічний елемент має декілька ізотопів. Наприклад, ізотопи Гідрогену, які існують у природі:
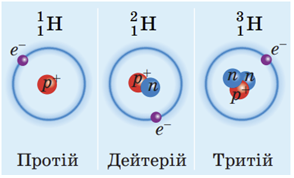
Відповідь: B.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу.
Завдання скеровано на перевірку знання і розуміння фізичних величин, що описують рух тіла по колу, і вміння їх визначати.
1. Модуль переміщення
2. Шлях
3. Швидкість руху
4. Кутову швидкість визначмо з формули, яка зв’язує кутову швидкість і швидкість:
Відповідь: 1Г, 2В, 3Б, 4А.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.
Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки і вміння застосовувати його до адіабатного та ізопроцесів.
Перший закон (начало) термодинаміки: кількість теплоти
1. Ізотермічний процес. Під час цього процесу температура, а отже, і внутрішня енергія газу не змінюються
Під час ізотермічного процесу вся передана газу кількість теплоти йде на виконання механічної роботи.
Відповідний варіант відповіді – В.
2. Ізобарний процес. Під час цього процесу виконується робота і змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки має вигляд:
Під час ізобарного процесу передана газу кількість теплоти йде і на збільшення внутрішньої енергії газу, і на виконання механічної роботи.
Відповідний варіант відповіді – А.
3. Ізохорний процес. Під час цього процесу об’єм газу не змінюється
Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу.
Відповідний варіант відповіді – Д.
4. Адіабатний процес. Це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти
Під час адіабатного розширення газ виконує додатну роботу за рахунок зменшення внутрішньої енергії, а температура газу зменшується.
Відповідний варіант відповіді – Г.
Відповідь: 1В, 2А, 3Д, 4Г.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики.
Завдання скеровано на перевірку знання і розуміння основних фізичних величин електростатики.
1. Потенціал
Варіант відповіді – Г.
2. Напруженість електричного поля
Варіант відповіді – А.
3. Електроємність – це характеристика конденсатора, яку визначають як відношення заряду
Варіант відповіді – Д.
4. Густина енергії − енергія речовини або поля віднесена до одиниці об’єму. Густину енергії електричного поля визначмо за формулою
Варіант відповіді – Б.
Відповідь: 1Г, 2А, 3Д, 4Б.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.
Завдання скеровано на перевірку вміння складати рівняння ядерних реакцій.
Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових.
Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.
1. Запишімо рівняння ядерної реакції відповідно до умови завдання:
У лівій і правій частинах рівняння реакції суми зарядів, як і суми мас, мають збігатися. Із відповідних рівнянь дістанемо зарядове (протонне)
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідома частинка в рівнянні – позитрон
2. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідома частинка в рівнянні – електрон
3. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідома частинка в рівнянні – протон
4. Наступне рівняння
Запишімо суму мас і суму зарядів для обох частин рівняння реакції:
З одержаних рівнянь маємо:
Невідома частинка в рівнянні – нейтрон
Відповідь: 1Б, 2А, 3В, 4Г.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.
Завдання скеровано на перевірку знання і розуміння рівноприскореного руху і вміння застосовувати кінематичні рівняння для його описання.
1. Кінематичне рівняння, що описує прямолінійний рівноприскорений рух,
Початкова координата тіла дорівнювала
Визначмо, через скільки секунд тіло опиниться в початку координат ‒
За теоремою Вієта для зведеного рівняння (коефіцієнт біля
Отже, через
Відповідь: 2.
2. Рівняння проєкції швидкості для прямолінійного рівноприскореного руху має вигляд
З рівняння
‒ початкової швидкості
Час, через який тіло опиниться в початку координат, ми визначили, відповідаючи на перше питання:
Обчислімо значення швидкості руху тіла під час проходження точки з координатою
Отже, в початку координат тіло зупиниться.
Відповідь: 0.
Відповідь: 1. 2. 2. 0.
Знайшли помилку? Пишіть на
ТЕМА: Механіка. Закони збереження в механіці. Механічна робота. Потужність.
Завдання скеровано на перевірку знання і розуміння механічної роботи і потужності і вміння їх визначати за заданих умов.
1. Роботу
Це математичний запис теореми про потенціальну енергію: робота всіх консервативних сил (що не залежать від траєкторії руху тіла), які діють на тіло, дорівнює зміні потенціальної енергії
Потенціальна енергія піднятого тіла залежить від висоти, на якій перебуває тіло, тобто залежить від вибору нульового рівня, ‒ рівня, від якого буде відлічуватися висота. Нульовий рівень вибирають з міркувань зручності. А зміна потенціальної енергії, а отже, і робота сили тяжіння від вибору нульового рівня не залежать.
Отже, за нульовий рівень візьмемо підніжжя гори, де потенціальна енергія
Потенціальна енергія
Визначимо корисну роботу, яку виконує підйомник:
Відповідь: 63.
2. Потужність
Обчислимо потужність двигуна підйомника:
Відповідь: 52,5.
Відповідь: 1. 63. 2. 52,5.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря та її вимірювання.
Завдання скеровано на перевірку знання і розуміння абсолютної і відносної вологості, і вміння обчислювати величини, які визначають поняття вологості.
Відносна вологість
Абсолютна вологість
Зробимо підстановку виразу для абсолютної вологості у формулу для відносної вологості:
Обчислімо масу водяної пари в повітрі кімнати:
Відповідь: 600.
Знайшли помилку? Пишіть на
ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Кількість теплоти. Закон збереження енергії в теплових процесах (перший закон термодинаміки).
Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки і вміння його застосовувати до різних процесів.
Загальна кількість теплоти
Визначимо кількість теплоти окремо для кожного процесу.
Згідно з першим законом термодинаміки кількість теплоти
Розгляньмо процес 1‒2. Графік цього процесу не відповідає жодному з графіків ізопроцесів, які можуть відбуватися з ідеальним газом. Під час цього процесу зростають об’єм, тиск і температура. Запишімо перший закон термодинаміки для процесу 1‒2:
відповідно до рівняння стану газу Менделєєва – Клапейрона
Робота
Визначмо
Розгляньмо процес 2‒3. З рисунка видно, що об’єм залишається сталим
Під час цього процесу об’єм газу не змінюється:
Під час ізохорного процесу вся передана газу кількість теплоти витрачається на збільшення внутрішньої енергії газу. Якщо газ ідеальний одноатомний як в умові, то кількість теплоти, передана газу, дорівнює:
Значення кількості теплоти в процесі 2‒3 від’ємне. Це означає, що газ під час цього процесу віддав певну кількість теплоти.
Визначмо, на скільки збільшиться кількість теплоти
Але в завданні питають, яку кількість теплоти газ отримав. Отримання відбувалося лише під час процесу 1‒2:
У цьому завданні обидві відповіді зараховані як правильні.
Відповідь: 1,6 і 4,3.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Закони постійного струму. Паралельне і послідовне з’єднання провідників.
Завдання скеровано на перевірку знання і розуміння послідовного і паралельного з’єднання провідників і відповідно змінювання фізичних величин, які характеризують електричний струм під час цих з’єднань.
У разі застосування шунта струм
Дізнаймося, який шунт треба приєднати паралельно амперметру, щоб збільшити верхню межу вимірювання амперметра в
Оскільки
Напруга на шунті й амперметрі однакова, тому відповідно до закону Ома маємо:
Отже, необхідний опір шунта визначаємо за формулою:
Визначмо, у скільки разів може збільшитися верхня межа вимірювання сили струму, якщо
Обчислімо опір шунта:
Відповідь: 101.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Основи електростатики. Напруженість електричного поля. Магнітне поле, електромагнітна індукція. Сила Лоренца.
Завдання скеровано на перевірку знання і розуміння руху зарядженої частинки в електромагнітному полі і вміння застосувати відповідні формули.
На частинку, яка має заряд
За умовою електрон рухається прямолінійно рівномірно. Це відбудеться у разі, коли сили, що діють на частинку, будуть скомпенсовані (
Зобразімо електрон і позначмо сили, що діють на нього.
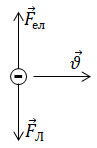
Тепер впевнімося, що електричне і магнітне поля дійсно взаємно перпендикулярні. Поля характеризує вектор напруженості
Якщо ми зобразили вектор сили Лоренца
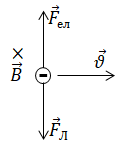
Сила
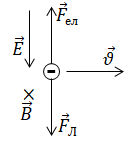
Отже, вектори полів дійсно взаємно перпендикулярні:
Повернімося до рівності сил:
Виразімо й обчислімо шукану величину ‒ швидкість руху електрона:
Відповідь: 1000.
Знайшли помилку? Пишіть на
ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Закони електролізу.
Завдання скеровано на перевірку знання і розуміння законів Фарадея для електролізу і вміння їх застосовувати.
Запишімо закони Фарадея для електролізу.
1. Маса
2. Електрохімічний еквівалент
Тобто стала Фарадея дорівнює модулю заряду електронів кількістю
Підставімо вирази для
Звідси
Вираз
Тобто
За умовою електролізом добули молекулярний водень. Його хімічна формула
Кількість речовини
Атомів Гідрогену вдвічі більше, ніж молекул водню, тому і кількість речовини атомарного водню вдвічі більша за кількість речовини молекулярного водню:
Підставімо вираз для кількості речовини атомарного водню у формулу для визначення заряду й обчислімо його:
Є ще один спосіб визначити кількість речовини за допомогою рівняння стану газу ‒ рівняння Менделєєва ‒ Клапейрона:
В умові зазначено, що водень добуто за нормальних умов (н. у.). Нормальні умови у фізиці ‒ це: тиск
Як бачимо, використавши цей спосіб, маємо приблизно те саме значення для кількості речовини молекулярного водню.
Обчислення в першому способі були без наближень і їх можна виконати без калькулятора. Також, в умові не зазначено, які точно числові дані брати для фізичних величин, що визначають нормальні умови, і для констант. Зваживши на це, зупинімося на відповіді, отриманій першим способом ‒
Відповідь: 96.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Власна частота і період електромагнітних коливань. Формула Томсона. Електричний резонанс.
Завдання скеровано на перевірку знання і розуміння власної частоти, періоду коливань коливального контуру і поняття електричного резонансу.
Електромагнітні хвилі, досягши приймальної антени, збуджують у ній коливання тієї самої частоти, що й частота хвиль.
Частота зовнішньої хвилі
Але в антену надходять коливання від різних радіостанцій, і кожна радіостанція працює на своїй частоті. Щоб із безлічі коливань виділити коливання потрібної частоти, використовують електричний резонанс. Для цього індуктивно з антеною пов’язують коливальний контур (див. рисунок). Змінюючи електроємність конденсатора (настроюючи радіоприймач), змінюють власну частоту
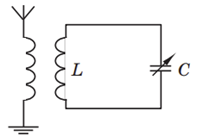
Коли власна частота коливань коливального контуру збігається із частотою електромагнітної хвилі, на яку настроєно радіоприймач, настає резонанс: амплітуда вимушених коливань сили струму в контурі різко збільшується. Отже, з безлічі сигналів, що збуджують коливання в приймальній антені, виділений один високочастотний модульований сигнал.
Прирівняємо вирази для частоти:
Виразімо й обчислімо шукану величину ‒ електроємність конденсатора:
Відповідь: 2.
Знайшли помилку? Пишіть на
ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.
Завдання скеровано на перевірку знання і розуміння формули для періоду математичного маятника і вміння її застосовувати.
Фізична величина довжина
Виразімо
Період
Обчислімо довжину маятника:
Відповідь: 6,25.
Знайшли помилку? Пишіть на
ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Кванти світла (фотони).
Завдання скеровано на перевірку знання і розуміння імпульсу тіла та імпульсу фотона.
Імпульс тіла
Отже, в проєкціях на вісь
Імпульс фотона
За умовою імпульс електрона дорівнює імпульсу фотона:
З цієї рівності виразімо й обчислімо шукану величину ‒ швидкість руху електрона:
Відповідь: 1,1.
Знайшли помилку? Пишіть на




