ЗНО онлайн 2015 року з фізики – пробний тест

ТЕМА: Механіка. Основи кінематики. Рівномірний рух по колу. Лінійна і кутова швидкості.

Завдання скеровано на перевірку знання і розуміння характеристик рівномірного руху по колу.

За періодом \(T\) обертання та радіусом \(R\) колової траєкторії легко визначити лінійну швидкість \(v\) рівномірного руху тіла по колу. Дійсно, за час \(t\) одного оберту \((t=T)\) тіло долає відстань, що дорівнює довжині кола \(l\): $$ l=2\mathbf{\pi}R. $$

Оскільки \(v=\frac <,\) маємо: $$ v=\frac{2\mathbf{\pi}R}{T}. $$

Запишімо відповідні формули для визначення лінійних швидкостей стрілок годинника:

За умовою хвилинна стрілка вдвічі довша за годинну. Оскільки йдеться про рух кінців цих стрілок, то довжини стрілок – це радіуси обертання кінців стрілок – хвилинної \(R_\text{хв}\) і годинної \(R_\text{год}:\) $$ R_\text{хв}=2R_\text{год}. $$

Тоді період обертання хвилинної стрілки становитиме \(1\) годину: $$ T_\text{хв}=60\ \text{хв}=1\ \text{год}. $$

А період обертання годинної стрілки – \(12\) годин: $$ T_\text{год}=12\ \text{год}. $$

Запишімо відношення лінійних швидкостей стрілок годинника і обчислімо його:

Отже, лінійна швидкість хвилинної стрілки \(v_\text{хв}\) більша за лінійну швидкість годинної стрілки \(v_\text{год}\) у \(24\) рази.

Відповідь: Г.

ТЕМА: Механіка. Основи динаміки. Другий закон Ньютона.

Завдання скеровано на перевірку другого закону Ньютона.

Відповідно до другого закону Ньютона тіло масою \(m\) внаслідок дії сили набуває прискорення, модуль якого обчислімо за формулою:

Отже, під дією сили тіло буде рухатися рівноприскорено, із прискоренням \(2\ \text{м/с}^2.\)

Відповідь: Б.

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження імпульсу.

Завдання скеровано на перевірку знання і вміння застосовувати закон збереження імпульсу.

Скористаймося законом збереження імпульсу для системи тіл криголам ‒крижина: $$ \overrightarrow{p}_1+\overrightarrow{p}_2=\overrightarrow{p'}_1+\overrightarrow{p'}_2, $$ де \(\overrightarrow{p}_1\) і \(\overrightarrow{p}_2\) ‒ імпульси криголама і крижини до зіткнення, \(\overrightarrow{p'}_1\) і \(\overrightarrow{p'}_2\) ‒ імпульси криголама і крижини після зіткнення відповідно.

Спроєктуймо вектори імпульсів цього рівняння на горизонтальну вісь, що напрямлена вздовж напрямку руху криголама й, відповідно, руху криголама разом із крижиною після зіткнення: $$ p_1=p'_1+p'_2, $$ \(p_2=0,\) оскільки до зіткнення крижина була нерухома за умовою.

Візьмімо до уваги, що після зіткнення криголам масою \(m_1\) і крижина масою \(m_2\) рухатимуться разом, тобто з однаковою швидкістю \(v':\)

Відповідь: A.

ТЕМА: Механіка. Елементи механіки рідин та газів. Гідростатичний тиск. Атмосферний тиск.

Завдання скеровано на перевірку знання і розуміння атмосферного і гідростатичного тисків та їхніх властивостей.

На повітря під ртуттю тисне повітря (позначмо цей тиск як \(p_\text{атм}\)), що заходить через відкритий верхній кінець, і стовпчик ртуті, гідростатичний тиск якого позначмо \(p_\text{гідр1}.\) Тиск повітря під ртуттю позначмо \(p_\text{п1}.\) Прирівняймо ці тиски: $$ p_\text{п1}=p_\text{атм}+p_\text{гідр1}=p_\text{атм}+\mathbf{\rho}gh_1, $$ де \(\mathbf{\rho}\) ‒ густина ртуті, \(g\) ‒ прискорення вільного падіння, \(h_1\) ‒ висота стовпчика ртуті.

Повітря під ртуттю за умовою має надлишковий тиск \(p_\text{надл}.\) Можемо зробити висновок, що надлишковий тиск повітря під ртуттю дорівнюватиме гідростатичному тиску стовпчика ртуті: $$ p_\text{надл}=p_\text{гідр1}. $$

Обчислімо тиск повітря під ртуттю: $$ p_\text{п1}=1\ \text{атм}+0,2\ \text{атм}=1,2\ \text{атм}. $$

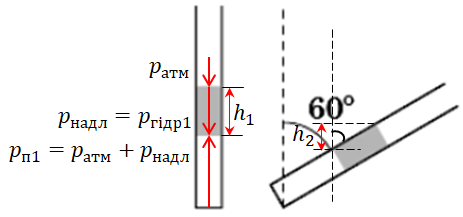
Коли ж нахилити трубку, зміниться гідростатичний тиск ртуті, який залежить від висоти (див. рисунок) стовпчика рідини в посудині: $$ p_\text{гідр2}=\mathbf{\rho}gh_2=\mathbf{\rho}gh_1\cos 60^\circ. $$

Тоді тиск повітря під стовпчиком ртуті дорівнюватиме:

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Середня квадратична швидкість теплового руху молекул.

Завдання скеровано на перевірку знання і розуміння поняття середньої квадратичної швидкості руху молекул.

Запишімо основне рівняння молекулярно-кінетичної теорії, яке показує залежність тиску \(p\) ідеального газу від маси \(m_0\) його молекул і середнього квадрата швидкості \(\overline{v^2}\) їхнього руху: $$ p=\frac 13m_0n\overline{v^2}. $$

Зауважмо, що \(m_0\) ‒ це маса однієї молекули, а \(n\) ‒ це концентрація молекул газу, що дорівнює кількості \(N\) молекул в одиниці об’єму \(V:\) $$ n=\frac NV. $$

Отже, \begin{gather*} p=\frac 13m_0\cdot \frac NV\cdot \overline{v^2}=\frac{m\cdot \overline{v^2}}{3V}, \end{gather*} де \(m=m_0\cdot N\) ‒ маса газу.

Середня квадратична швидкість пов’язана із середнім квадратом швидкості таким співвідношенням: \begin{gather*} \overline{v}_\text{кв}=\sqrt{\overline{v^2}}. \end{gather*}

Звідси \begin{gather*} \overline{v^2}=(\overline{v}_\text{кв})^2. \end{gather*}

Підставімо цей вираз для середнього квадрату швидкості в основне рівняння молекулярно-кінетичної теорії і визначімо середню квадратичну швидкість:

Відповідь: Г.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Закон збереження енергії в теплових процесах (перший закон термодинаміки).

Завдання скеровано на перевірку знання і розуміння першого закону термодинаміки й уміння застосовувати його в конкретних ситуаціях.

У термодинаміці розглядають системи, механічна енергія яких під час переходу з одного термодинамічного стану в інший не змінюється. У такому разі, якщо зовнішні сили виконали роботу \(A'\) й водночас системі передано певну кількість теплоти \(Q,\) то вся енергія йде на зміну внутрішньої енергії системи \(\Delta U.\)

Закон збереження та перетворення енергії в такому разі називають першим законом (началом) термодинаміки.

На практиці частіше розглядають не роботу зовнішніх сил \(A',\) а роботу \(A,\) яку виконує дана система проти зовнішніх сил.

З огляду на те, що $$ A'=-A, $$ перший закон (начало) термодинаміки можна сформулювати так:
кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

Якщо система одержує певну кількість теплоти, то в наведеній формулі \(Q\) беремо зі знаком + (плюс), якщо внутрішня енергія системи зменшилася, то записуємо \(\Delta U\) зі знаком – (мінус): $$ Q=-\Delta U+A. $$

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Сила поверхневого натягу.

Завдання скеровано на перевірку знання і розуміння поняття поверхневого натягу й чинників, які на нього впливають.

Сили поверхневого натягу намагаються ніби стягнути поверхню. Якщо по один бік від соломинки налили мильного розчину, то цим послабили силу поверхневого натягу, як порівняти із чистою водою. Отже, рівнодійна \(F\) дорівнюватиме різниці сил поверхневого натягу чистої води \(F_\text{пн води}\) і мильного розчину \(F_\text{пн розчину}\). І напрямлена буде в бік чистої води:

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду.

Завдання скеровано на перевірку вміння застосовувати закон збереження електричного заряду.

Закон збереження електричного заряду: повний заряд електрично замкненої системи тіл залишається незмінним під час усіх взаємодій, які відбуваються в цій системі: $$ q_1+q_2+\cdots +q_n=\mathrm{const}, $$ де \(q_1,\ q_2,\ \cdots ,\ q_n\) ‒ заряди тіл, які утворюють систему; \(n\) ‒ кількість тіл.

За умовою \begin{gather*} q_1=-q.\\[7pt] q_2=+3q, \end{gather*} Отже, після дотику заряд перерозподілиться порівну між кульками, і заряд кульки \(1\) дорівнюватиме заряду кульки \(2:\)

Відповідь: A.

ТЕМА: Електродинаміка. Основи електростатики. Конденсатори.

Завдання скеровано на перевірку знання і розуміння залежності між зарядом конденсатора й напругою на його обкладках.

Зарядом конденсатора називають модуль заряду однієї з його обкладок. Відношення заряду q конденсатора до різниці потенціалів \((\mathbf{\varphi_1}-\mathbf{\varphi_2})\) між його обкладками не залежить ані від \(q,\) ані від \((\mathbf{\varphi_1}-\mathbf{\varphi_2}),\) тож може слугувати характеристикою конденсатора. Таку характеристику називають електроємністю конденсатора \(C.\)

Електроємність конденсатора визначають за формулами: \begin{gather*} C=\frac{q}{\mathbf{\varphi_1}-\mathbf{\varphi_2}},\\[6pt] \text{або}\ C=\frac{q}{U}, \end{gather*} де \(U\) ‒ напруга між обкладками, яка тут дорівнює різниці потенціалів між ними.

Отже, заряд конденсатора прямо пропорційний напрузі, прикладеній до його пластин: $$ q=C\cdot U\Rightarrow q\sim U. $$

Графіком такої залежності є пряма ‒ графік А.

Наприклад, під час розряджання конденсатора напруга між його обкладками спадатиме прямо пропорційно заряду \(q\) від первинного значення \(U\) до \(0.\)

Відповідь: A.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для повного кола.

Завдання скеровано на перевірку знання і застосування закону Ома для повного кола.

Скористаймося законом Ома для повного кола: сила струму \(I\) в повному електричному колі дорівнює відношенню електрорушійної сили \(\mathbf{\varepsilon}\) (ЕРС) джерела струму до повного опору кола \((R+r):\) $$ I=\frac{\mathbf{\varepsilon}}{R+r}, $$ де \(R\) ‒ активний опір зовнішнього кола (опір резистора), \(r\) ‒ внутрішній опір джерела.

Виразімо з формули шукану величину й обчислімо її:

Відповідь: B.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах.

Завдання скеровано на перевірку розуміння фізичної природи електричного струму в різних середовищах, а також залежності сили струму від температури.

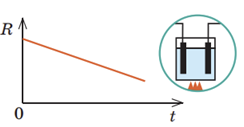
Згідно з класичною електронною теорією модель внутрішньої будови металу – це утворена позитивно зарядженими йонами кристалічна ґратка, яка перебуває в «газі» вільних електронів. Якщо в металевому провіднику створити електричне поле, то на хаотичний рух електронів накладеться дрейф електронів у напрямку сили, що діє на електрони з боку електричного поля. Цей дрейф електронів і є електричним струмом у металах. Якщо підвищувати температуру металевого провідника, то йони у вузлах кристалічної ґратки коливатимуться з більшою амплітудою, хаотичність руху електронів збільшиться, і вони частіше зіштовхуватимуться з йонами. Відповідно опір (питомий опір) збільшуватиметься (див. графік), а сила струму зменшуватиметься за законом Ома для ділянки кола: $$ I=\frac UR, $$ де \(I\sim \frac 1R\) ‒ сила струму \(I,\) що обернено пропорційна до електричного опору \(R.\)

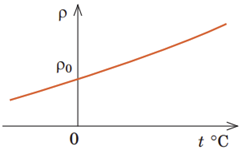
Електроліти ‒ тверді або рідкі речовини, які мають йонну провідність. Якщо в розчин або розплав помістити електроди, приєднані до різнойменних полюсів джерела струму, то, подібно до вільних електронів у металах, йони дрейфуватимуть у певному напрямку: позитивні йони (катіони) ‒ до негативного електрода (катода); негативні йони (аніони) ‒ до позитивного електрода (анода). Тобто в розчині виникне електричний струм. З підвищенням температури кількість йонів в електроліті значно збільшується, тому, незважаючи на збільшення кількості ефективних зіткнень, опір електроліту зменшується (див. графік), відповідно сила струму збільшується.

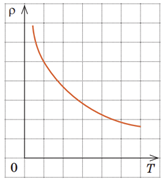
Напівпровідники, як це випливає з їхньої назви, за своєю провідністю посідають проміжне місце між провідниками й діелектриками. Серед валентних електронів обов’язково є електрони, кінетична енергія яких є достатньою, щоб покинути зв’язки і стати вільними. Якщо напівпровідниковий кристал помістити в електричне поле, то вільні електрони почнуть рухатися до позитивного полюса джерела струму й у напівпровіднику виникне електричний струм. Якщо напівпровідник нагріти або опромінити світлом, кількість вільних електронів і дірок збільшиться, відповідно збільшиться і провідність напівпровідника. На відміну від металевих провідників питомий опір напівпровідників зазвичай зменшується з підвищенням температури (див. графік), а отже, сила струму збільшується.

Відповідь: Б.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку знання і розуміння дії магнітного поля на рух зарядженої частинки в магнітному полі.

Сила Лоренца завжди перпендикулярна до швидкості руху частинки, тому вона не виконує роботу і не змінює кінетичну енергію частинки, бо під дією сили Лоренца заряджена частинка рухається рівномірно. Проте траєкторія руху частинки буде різною ‒ залежно від того, під яким кутом частинка влетіла в магнітне поле і чи є магнітне поле однорідним.

За умовою електрон влітає в однорідне магнітне поле зі швидкістю, паралельною до вектора магнітної індукції (див. рисунок).

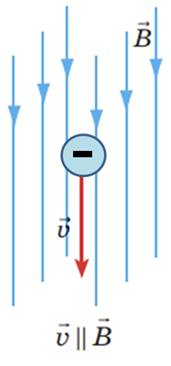
У цьому разі кут \(\mathbf{\alpha}\) між вектором швидкості \(\overrightarrow{v}\) і вектором магнітної індукції \(\overrightarrow{B}\) дорівнює нулю \((\text{або}\ 180^\circ).\) Оскільки \(\sin\mathbf{\alpha}=0,\) то дорівнює нулю і сила Лоренца: $$ F_\text{Л}=|q|Bv\sin\mathbf{\alpha}=0. $$

Отже, магнітне поле не діє на електрон, тому, якщо немає інших сил, електрон рухатиметься рівномірно прямолінійно вздовж ліній магнітної індукції і траєкторією руху електрона буде пряма лінія.

Відповідь: A.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Нитяний маятник, період коливань нитяного маятника.

Завдання скеровано на перевірку вміння застосовувати формули періоду коливань нитяного маятника, розуміння того, від яких фізичних величин залежить період коливань цього маятника.

Маленька мавпочка на довгій, нерозтяжній і невагомій ліані є фізичною моделлю нитяного маятника.

Період \(T_1\) коливань нитяного маятника, коли мавпочка гойдалася на ліані довжиною \(L,\) обчислімо за формулою: $$ T_1=2\mathbf{\pi}\sqrt{\frac Lg}, $$ де \(L\) ‒ довжина маятника; \(g\) ‒ прискорення вільного падіння.

Коли ж мавпочка піднялася по ліані вгору на відстань \(l,\) то період коливань \(T_2\) змінився: \begin{gather*} T_2=2\mathbf{\pi}\sqrt{\frac {L-l}{g}}, \end{gather*} а саме зменшився пропорційно до \(\sqrt{L-l}:\) $$ T_2\sim\sqrt{L-l}. $$

Відповідь: A.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Формула Томсона.

Завдання скеровано на перевірку вміння застосовувати формули для визначення довжини хвилі й періоду коливань коливального контуру.

Довжину \(\mathbf{\lambda}\) радіохвилі визначімо за формулою $$ \mathbf{\lambda}=c\cdot T, $$ де \(c\) ‒ швидкість поширення світла у вакуумі (також швидкість поширення всіх електромагнітних хвиль, якими є радіохвилі), \(T\) ‒ період поширення хвилі.

Період поширення електромагнітної хвилі визначімо за формулою Томсона: $$ T=2\mathbf{\pi}\sqrt{LC}, $$ де \(L\) ‒ індуктивність котушки коливального контуру, що є джерелом електромагнітних хвиль, \(C\) ‒ електроємність конденсатора, що також є складником коливального контуру.

Запишімо формули для обчислення обох зазначених в умові довжин радіохвиль:

Поділімо ліві і праві частини цих формул і визначімо шукану величину:

Отже, електроємність конденсатора \(C_2\) треба збільшити в \(9\) разів, щоб налаштувати радіоприймач на довжину хвилі, утричі більшу за початкову.

Відповідь: B.

ТЕМА: Коливання і хвилі. Електромагнітні коливання і хвилі. Змінний електричний струм.

Завдання скеровано на перевірку розуміння виникнення змінного електричного струму й законів, яким він підпорядкований.

У рамці, яка обертається в магнітному полі зі сталою кутовою швидкістю, індукуватиметься змінна електрорушійна сила (ЕРС), що змінюватиметься за гармонічним законом – за законом синуса або косинуса. Кут \(\mathbf{\alpha}\) між нормаллю до площини рамки й вектором магнітної індукції під час обертання змінюватиметься за законом $$ \mathbf{\alpha}=\mathbf{\omega}\cdot t. $$

Тому й магнітний потік через площину рамки змінюватиметься: $$ \mathrm{Ф}=BS\cos\mathbf{\omega}t. $$

Відповідно ЕРС індукції, що виникає в рамці за законом Фарадея, змінюватиметься за законом $$ e(t)=\mathbf{\varepsilon}_{max}\sin\mathbf{\omega}t, $$ оскільки $$ e(t)=-\mathrm{Ф}'(t), $$ де \(\mathrm{Ф}'(t)\) – похідна магнітного потоку за часом.

Сила струму в рамці, згідно із законом Ома, змінюватиметься так:

Отже, сила струму пропорційна часу, але під тригонометричною функцією. Тому із часом сила струму, як і ЕРС індукції, змінюватиметься за законом синуса (або косинуса за певних умов).

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Оптика. Побудова зображень, які дає тонка лінза.

Завдання скеровано на перевірку вміння застосовувати знання про побудову зображень, які дає тонка лінза.

Розгляньмо спочатку побудову зображення предмета \(AB,\) який розташовано на подвійній фокусній відстані від збиральної лінзи. З рисунка бачимо, що зображення отримали на тій самій відстані від лінзи, що й предмет, тобто на подвійній фокусній відстані: $$ OA=OA_1=2F. $$

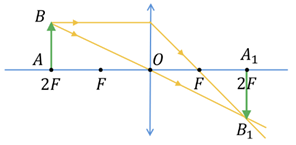
На рисунку в умові завдання бачимо, що промінь, який пройшов крізь лінзу, перетинає головну оптичну вісь на такій самій відстані, що й промінь, який падає на лінзу. Тобто, можна зробити висновок, що це подвійна фокусна відстань.

Підтвердьмо це побудовою точки \(A.\) На рисунку вище фактично зображена побудова лише точки \(B,\) отримали її зображення ‒ точку \(B_1\) і з неї опустили перпендикуляр на головну оптичну вісь. Тобто отримали зображення точки \(A\) ‒ точку \(A_1.\)

А тепер побудуймо зображення точки \(A,\) накресливши додатковий довільний промінь із точки \(A\) (див. рисунок).

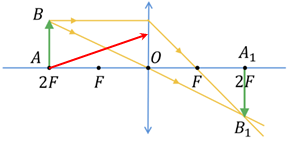
Далі через оптичний центр лінзи (точку \(O\)) проведімо додаткову оптичну вісь, паралельну до цього променя, а через фокус побудуймо фокальну площину, яка є перпендикуляром до головної оптичної осі. На перетині додаткової оптичної осі і фокальної площини отримаємо побічний фокус \(F_1\) (див. рисунок).

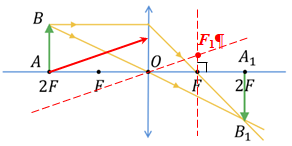
Після проходження крізь лінзу промінь пройде через побічний фокус \(F_1.\) На перетині з другим, необхідним для побудови зображення точки, променем, який проходить без заломлення крізь оптичний центр лінзи й у цій ситуації збігається з головною оптичною віссю, отримаємо зображення точки \(A\) ‒ точку \(A_1.\)

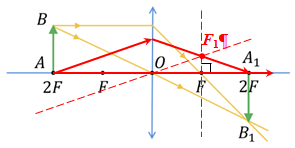
На рисунку в умові завдання зображено саме цей випадок побудови. Отже, відстань від лінзи до точок перетину променів з головною оптичною віссю ‒ це подвійна фокусна відстань \(2F:\)

Оптична сила лінзи ‒ це фізична величина, яка характеризує лінзу та є оберненою до фокусної відстані лінзи:

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Оптика. Абсолютний і відносний показники заломлення.

Завдання скеровано на перевірку знання і застосування законів заломлення геометричної оптики.

Закони заломлення світла:

1. Промінь, що падає, промінь заломлений і перпендикуляр до межі поділу двох середовищ, установлений із точки падіння променя, лежать в одній площині.

2. Відношення синуса кута падіння до синуса кута заломлення для двох даних середовищ є величиною незмінною: $$ n_{21}=\frac{\sin\mathbf{\alpha}}{\sin\mathbf{\gamma}}, $$ де \(n_{21}\) ‒ фізична величина, яку називають відносним показником заломлення середовища \(2\) (середовища, у якому світло поширюється після заломлення ‒ рідина) відносно середовища \(1\) (середовища, із якого світло падає ‒ повітря).

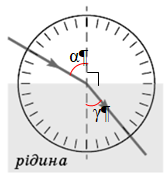
Повне коло становить \(360^\circ.\) Поділок усього ‒ \(36.\) Отже, ціна поділки становить \(10^\circ.\) Тоді кут падіння \(\sin\mathbf{\alpha}\) і кут заломлення \(\sin\mathbf{\gamma}\) дорівнюватимуть відповідно:

Показнику заломлення рідини дорівнюватиме значення виразу $$ \frac{\sin 60^\circ}{\sin 40^\circ}. $$

Відповідь: B.

ТЕМА: Квантова фізика. Елементи теорії відносності. Елементи теорії відносності. Принципи (постулати) теорії відносності Ейнштейна.

Завдання скеровано на перевірку знання і розуміння постулатів теорії відносності.

Перший постулат спеціальної теорії відносності (СТВ): в інерціальних системах відліку (СВ) усі закони природи однакові.

Другий постулат СТВ: швидкість поширення світла у вакуумі однакова в усіх інерціальних СВ.

Це означає, що швидкість поширення світла у вакуумі інваріантна ‒ вона не залежить від швидкості руху джерела або приймача світла. Відповідно до цього постулату швидкість поширення світла ‒ максимально можлива швидкість поширення будь-якої взаємодії.

Отже, варіанти відповіді А і В суперечать другому постулату СТВ.

У релятивістській механіці час залежить від вибору СВ. Події, що відбулися в одній СВ одночасно, в іншій СВ можуть бути розділені часовим проміжком. Одночасність двох подій відносна: події, одночасні в одній інерціальній СВ, не є одночасними в інерціальних СВ, що рухаються відносно першої СВ. Математично це підтверджено формулою: \begin{gather*} \mathbf{\tau}=\frac{\mathbf{\tau}_0}{\sqrt{1-\frac{v^2}{c^2}}} \end{gather*} (якщо поділити значення часу на десятковий дріб із-під кореня квадратного, то отримаємо більше значення часу).

Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Склад ядра атома.

Завдання скеровано на перевірку знання будови атома і його ядра.

Атомне ядро складається із частинок двох видів: протонів, які мають позитивний електричний заряд, і нейтронів, які не мають заряду.

Сумарну кількість протонів і нейтронів в атомі називають нуклонним (масовим) числом і позначають символом \(\mathrm{A}.\)

Атом є електрично нейтральним: сумарний заряд протонів у ядрі дорівнює сумарному заряду електронів, що розташовані навколо ядра. Оскільки заряд протона за модулем дорівнює заряду електрона, то зрозуміло, що в атомі кількість протонів дорівнює кількості електронів.

Кількість протонів у ядрі називають зарядовим (протонним) числом і позначають символом \(\mathrm{Z}.\)

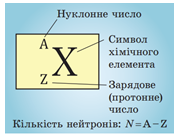
Порядковий номер хімічного елемента в періодичній системі відповідає кількості протонів у ядрі (зарядовому числу).

Отже, у ядрі атома Урану \(^{235}_{\ \ 92}\mathrm{U}\) кількість протонів і нейтронів разом становить \(235:\) $$ \mathrm{A}=235. $$

А зарядове (протонне) число, тобто кількість протонів – \(92:\) $$ \mathrm{Z}=92. $$

Тоді кількість нейтронів \((n)\) дорівнює різниці між нуклонним і протонним числами: \begin{gather*} N_n=\mathrm{A-Z};\\[7pt] N_n=235-92=143. \end{gather*}

Обчислімо, на скільки кількість нейтронів \((n)\) більша за кількість протонів \((p):\) $$ N_n-N_p=143-92=51. $$

Відповідь: B.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Механічні властивості твердих тіл.

Завдання скеровано на перевірку знання і розуміння залежності механічних властивостей твердих тіл від навантаження.

Розгляньмо діаграму напруг в умові завдання.

За невеликих деформацій після припинення дії навантаження тіло повертається в початковий стан (точка \(K\)) – прямо пропорційна залежність видовження дроту від прикладеної сили. У цьому випадку деформацію вважають пружною, закон Гука виконується – варіант відповіді Г.

Тільки-но навантаження стане таким, що механічна напруга в мідному дроті сягне межі пружності \(\mathbf{\sigma}_\text{пр},\) залежність \(\mathbf{\sigma}(\mathbf{\varepsilon})\) стає нелінійною. Проте якщо зняти навантаження, то зразок відновить свої форму та розміри, тобто точка \(L\) відповідає найбільшій напрузі, за якої деформація залишається пружною, але закон Гука вже не виконується (немає лінійної залежності видовження дроту від прикладеної сили) – варіант відповіді Б.

Якщо збільшувати навантаження далі, то після досягнення межі пружності деформація починає швидко зростати і стає пластичною, а після досягнення межі плинності (точка \(M\)) мідний дріт взагалі деякий час подовжується без збільшення навантаження. Деформація непружна, є текучість (плинність) – варіант відповіді А.

Якщо навантаження знову збільшити, дріт ще трохи видовжиться, напруга в зразку сягне межі міцності (точка \(N\)), після чого зразок розірветься. Деформація непружна, відповідає межі міцності – варіант відповіді Д.

Відповідь: 1Г, 2Б, 3А, 4Д.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.

Завдання скеровано на перевірку знання одиниць фізичних величин із розділу «Магнітне поле, електромагнітна індукція».

Одиниця магнітної індукції \((B)\) у Міжнародній системі одиниць SI − тесла (Тл), названа на честь сербського фізика Ніколи Тесли (1856–1943): $$ B=\frac{F_\text{Ампера}}{Il}\Rightarrow [B]=1\frac{\text{Н}}{\text{А}\cdot \text{м}}=1\ \text{Тл}. $$

1 тесла − це магнітна індукція такого однорідного магнітного поля, яке діє з максимальною силою \((F_\text{Ампера})\) \(1\) ньютон на провідник завдовжки \((l)\) \(1\) метр, сила струму \((I)\) в якому \(1\) ампер.

Одиниця магнітного потоку \((\text{Ф})\) у SI − вебер (Вб), названа на честь німецького фізика В. Вебера (1864−1920):

1 вебер − це максимальний магнітний потік, який створюється магнітним полем індукцією \((B)\) \(1\) тесла через поверхню площею \((S)\) \(1\) метр квадратний.

Одиниця індуктивності \((L)\) в SI – генрі (Гн), названа на честь американського фізика Джозефа Генрі (1797–1878):

Індуктивність провідника дорівнює 1 генрі, якщо в ньому виникає ЕРС самоіндукції \(\mathbf{\varepsilon}_{\text{is}}\) \(1\) В у разі зміни сили струму \((\Delta I)\) на \(1\) А за час \((\Delta t)\) \(1\) с.

Одиниця електрорушійної сили (ЕРС) індукції \((\mathbf{\varepsilon}_i)\) в SI – вольт (В), названа на честь італійського фізика Алессандро Вольта (1745–1827): $$ \mathbf{\varepsilon}_i=\frac{\mathrm{A}_\text{ст}}{q}\Rightarrow [\mathbf{\varepsilon}_i]=1\ \frac{\text{Дж}}{Кл}=1\ \text{В}. $$

Електрорушійна сила індукції (ЕРС індукції) дорівнює \(1\) вольт, якщо сторонніми силами виконана робота \((\mathrm{A}_\text{ст})\) \(1\) Дж із переміщення одиничного позитивного заряду \((q)\) \(1\) Кл.

Відповідь: 1Б, 2В, 3Д, 4Г.

ТЕМА: Коливання і хвилі. Оптика. ‒ Механічні коливання і хвилі. Зв’язок між довжиною хвилі, швидкістю її поширення і періодом (частотою).

Завдання скеровано на перевірку знання і розуміння характеристик механічної хвилі.

1. Довжина хвилі \(\mathbf{\lambda}\) ‒ це відстань між двома найближчими точками, які коливаються синхронно, в однаковій фазі. Наприклад, візьмемо відстань між сусідніми верхніми піками. Ці точки рухатимуться синхронно. Відстань між ними становить \(20\) клітинок. За умовою довжина бічної сторони кожної клітинки дорівнює \(5\ \text{см.}\)

Довжина хвилі \(\mathbf{\lambda}=5\ \text{см}\cdot 20\ \text{клітинок}=100\ \text{см}=1\ \text{м}\) ‒ варіант відповіді Г.

2. Період \(T\) ‒ це час, за який хвиля поширюється на відстань, що дорівнює довжині хвилі. Також період ‒ це величина, взаємно обернена до частоти \(\mathbf{\nu}.\) За умовою частота дорівнює \(2\ \text{Гц.}\)

Період \(T=\frac{1}{\mathbf{\nu}}=\frac{1}{2\ \text{Гц}}=0,5\ \text{с}\) ‒ варіант відповіді В.

3. Амплітуда \(A\) ‒ це максимальне відхилення від положення рівноваги. На рисунку бачимо, що максимально шнур відхиляється від положення рівноваги (штрихової лінії) на пів клітинки.

4. Швидкістю поширення хвилі називають швидкість переміщення точок із однаковою фазою коливань (наприклад, швидкість переміщення гребеня хвилі). Швидкість поширення хвилі не збігається зі швидкістю руху частинок середовища: частинки коливаються біля положень рівноваги, а хвиля поширюється в певному напрямку.

Із означення довжини хвилі \(\mathbf{\lambda}\) ‒ відстань, на яку поширюється хвиля зі швидкістю \(v\) за час, що дорівнює періоду \(T\) ‒ маємо формулу для визначення швидкості поширення хвилі:

Відповідь: 1Г, 2В, 3А, 4Б.

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку розуміння і вміння описувати рух тіл за допомогою кінематичних рівнянь, знаходити потрібні фізичні величини.

1). Опишімо рух кота і мишеняти за допомогою кінематичних рівнянь координат (у проєкціях на вісь \(Ox\)).

Для кота ‒ прямолінійний рівноприскорений рух: \begin{gather*} X=x_\text{0к}+v_\text{0к}t+\frac{at^2}{2},\\[6pt] X=x_\text{0к}+\frac{at^2}{2}, \end{gather*} де \(X\) ‒ кінцева координата кота (точка \(X,\) у якій кіт наздожене мишеня (див. рисунок)), \(x_\text{0к}=-4,5\ \text{м}\) ‒ початкова координата кота, \(v_\text{0к}=0\) (за умовою) ‒ проєкція початкової швидкості руху кота, \(t\) ‒ час руху кота (поки наздожене мишеня), \(a=2\ \text{м/с}^2\) ‒ проєкція прискорення руху кота.

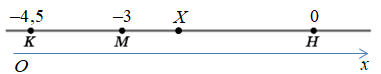
Для мишеняти ‒ прямолінійний рівномірний рух: $$ X=x_\text{0м}+v_\text{м}t, $$ де \(X\) ‒ кінцева координата мишеняти (співпадає з кінцевою координатою кота (див. рисунок)), \(x_\text{0м}=-3\ \text{м}\) ‒ початкова координата мишеняти, \(v_\text{м}=0,5\ \text{м/с}\) (за умовою) ‒ проєкція швидкості руху мишеняти, \(t\) ‒ час руху мишеняти (такий самий, як для кота).

Оскільки час руху кота і мишеняти однаковий, прирівняймо його, щоб визначити спільну кінцеву координату \(X:\)

Підставімо числові значення величин (в умові всі значення величин подано в системі SI):

Координата \(X_2=-3,5\) не задовольняє умову завдання, оскільки мишеня біжить до нірки і його кінцева координата має бути більша за \(‒3\) (див. рисунок).

Отже, координата точки, у якій кіт наздожене мишеня, дорівнює $$ X=-2,25\ \text{м}, $$ тобто кіт упіймає мишеня на відстані \(2,25\ \text{м}\) від нори.

Відповідь: 2,25.

2). Для визначення часу, за який кіт наздожене мишеня скористаймося формулами, отриманими у першій частині завдання: \begin{gather*} t^2=\frac{2(X-x_\text{0к})}{a},\\[6pt] t=\frac{X-x_\text{0м}}{v_\text{м}}. \end{gather*}

Можна підставити значення в одну із формул і обчислити час:

Перевірка за іншою формулою:

Відповідь: 1,5.

Відповідь: 1. 2,25. 2. 1,5.

ТЕМА: Механіка. Основи динаміки. Умови рівноваги тіла.

Завдання скеровано на перевірку розуміння шарнірного з’єднання стержнів і скомпенсованості сил, уміння позначати сили, що діють, шукати їхні проєкції.

За умовою стержні невагомі, один на одного не діють.

У точці \(C\) підвішено тіло, на яке діє сила тяжіння. У стержні \(AC\) виникає деформація розтягу, а у стержні \(BC\) ‒ деформація стиску. Сили пружності \(\overrightarrow{F}_{AC}\ \text{i}\ \overrightarrow{F}_{BC}\) будуть направлені, як на рисунку:

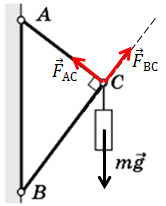
Побудуймо рівнодійну цих сил пружності. Вона буде компенсувати дію сили тяжіння.

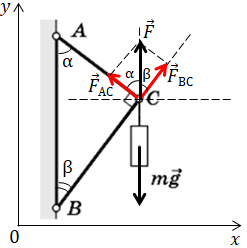
За другим законом Ньютона

Спроєктуймо вектори сил на вісь \(Ox\) і \(Oy.\)

Визначімо з прямокутного трикутника \(ABC\) тригонометричні функції:

Розв’яжімо систему рівнянь:

1) З другого рівняння системи визначімо силу пружності в стержні \(AC:\)

Відповідь: 15.

2) Підставімо в перше рівняння системи значення сили пружності \(F_{AC}\) й обчислімо силу пружності в стержні \(BC:\) \begin{gather*} F_{BC}=\frac{0,8F_{AC}}{0,6}=\frac{0,8\cdot 15\ \text{Н}}{0,6}=20\ \text{Н}. \end{gather*}

Відповідь: 20.

Відповідь: 1. 15. 2. 20.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку розуміння і вміння застосовувати рівняння стану газу.

Запишімо рівняння стану газу до накачування і після: \begin{gather*} p_1V=\frac{m_1}{M}RT,\\[6pt] p_2V=\frac{m_2}{M}RT, \end{gather*} де \(p_1\) і \(p_2\) ‒ початковий тиск і тиск повітря після накачування відповідно, \(m_1\) і \(m_2\) ‒ маса повітря в м’ячі до і після накачування. Середня молярна маса повітря \(M,\) універсальна газова стала \(R,\) абсолютна температура повітря \(T\) й об’єм \(V,\) який займає повітря в м’ячі, ‒ ці величини залишаються незмінними для обох станів повітря в м’ячі.

Запишімо формули для маси повітря як добуток густини \(\mathbf{\rho}\) і відповідного об’єму повітря в м’ячі \(V_1\) або \(V_2,\) зважаючи на кількість накачувань \(N\) (\(V_0\) ‒ об’єм повітря за одне накачування): \begin{gather*} m_1=\mathbf{\rho}\cdot V_1,\\[7pt] m_2=\mathbf{\rho}\cdot V_2=\mathbf{\rho}\cdot (V_1+N\cdot V_0). \end{gather*}

Підставімо в рівняння стану газу замість мас відповідні вирази й поділімо ліві і праві частини цих рівнянь:

Обчислімо шукану величину ‒ кількість накачувань:

Відповідь: 10.

ТЕМА: Тема: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку розуміння і вміння застосовувати рівняння теплового балансу.

Запишімо рівняння теплового балансу: з одного боку льоду треба надати кількість теплоти \(Q_\text{л},\) щоб він нагрівся до температури плавлення, і ще порцію кількості теплоти \(Q_\text{пл},\) щоб лід повністю розтанув, з іншого боку ця кількість теплоти \(Q_\text{в}\) буде передаватися льоду від теплої води, яку доливатимуть у посудину: \begin{gather*} Q_\text{л}+Q_\text{пл}=Q_\text{в},\\[7pt] Q_\text{л}=c_\text{л}m_\text{л}(t_\text{пл}-t_\text{л}), \end{gather*} де \(c_\text{л}\) ‒ питома теплоємність льоду, \(m_\text{л}\) ‒ маса льоду, \(t_\text{пл}=0\ ^\circ\mathrm{C}\) ‒ температура плавлення льоду, \(t_\text{л}\) ‒ початкова температура льоду. $$ Q_\text{пл}=\mathbf{\lambda}m_\text{л}, $$ де \(\mathbf{\lambda}\) ‒ питома теплота плавлення льоду (під час плавлення ‒ зміни агрегатного стану льоду з твердого на рідкий ‒ температура залишиться сталою, уся енергія ітиме на руйнування кристалічних ґраток). $$ Q_\text{в}=c_\text{в}m_\text{в}(t_\text{в}-t_\text{пл}), $$ де \(c_\text{в}\) ‒ питома теплоємність води, \(m_\text{в}\) ‒ маса води, \(t_\text{в}\) ‒ початкова температура води, \(t_\text{пл}=0\ ^\circ\mathrm{C}\) ‒ температура, до якої охолоне вода.

Підставімо усі вирази для кількості теплоти в рівняння теплового балансу:

Виразімо і обчислімо масу води:

Відповідь: 8,5.

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у металах.

Завдання скеровано на перевірку знання і розуміння середньої швидкості поступального руху електронів.

За інтервал часу \(t\) через переріз площею \(S\) провідника проходить \(N\) електронів: $$ N=nS\overline{v}t, $$ де \(n\) ‒ концентрація вільних електронів у провіднику.

де \(V\) ‒ об’єм провідника довжиною \(l\) (\(l=\overline{v}t\) під час рівномірного руху електронів по провіднику, де \(\overline{v}\) - середня швидкість поступального руху електронів).

При цьому переноситься заряд \(q:\) \begin{gather*} q=N|e|, \end{gather*} де \(e\) ‒ електричний заряд одного електрона.

За означенням сила струму \(I\) в провіднику дорівнює заряду \(q,\) що проходить через поперечний переріз провідника за одиницю часу \(t:\) $$ I=\frac qt. $$

Отже, маємо:

Обчислімо шукану величину ‒ середню швидкість поступального руху електронів:

Відповідь: 0,25.

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне та паралельне з’єднання провідників.

Завдання скеровано на перевірку вміння читати електричні схеми й визначати за їхньою допомогою потрібні величини.

Запишімо закон Ома для повного кола: $$ I=\frac{\mathbf{\varepsilon}}{R+r}, $$ де \(I\) ‒ сила струму в колі, \(\mathbf{\varepsilon}\) ‒ електрорушійна сила джерела струму, \(R\) ‒ активний опір зовнішнього кола, \(r\) ‒ внутрішній опір джерела струму.

За умовою внутрішнім опором джерела струму можна знехтувати, тож формула матиме вигляд: $$ I=\frac{\mathbf{\varepsilon}}{R}. $$

Запишімо, чому дорівнюватиме сила струму до замикання ключа \(I_1\) і після замикання \(I_2:\) $$ I_1=\frac{\mathbf{\varepsilon}}{R_\text{заг1}}=\frac{\mathbf{\varepsilon}}{3R}, $$ де загальний опір \(R_\text{заг1}=3R,\ R\) ‒ опір кожного з трьох послідовно з’єднаних резисторів.

$$ I_2=\frac{\mathbf{\varepsilon}}{R_\text{заг2}}. $$ Якщо замкнути ключ, то до двох послідовно з’єднаних резисторів паралельно буде приєднаний ще один резистор.

Опір двох послідовно з’єднаних резисторів \(R_\text{посл}\) дорівнюватиме $$ R_\text{посл}=R+R=2R. $$

Опір розгалуженої ділянки \(R_\text{д}\) дорівнюватиме:

Визначімо загальний опір \(R_\text{заг2}:\) $$ R_\text{заг2}=R+\frac{2R}{3}=\frac{3R}{3}+\frac{2R}{3}=\frac{5R}{3}. $$

Тоді сила струму за замкненого ключа дорівнюватиме: $$ I_2=\frac{\mathbf{\varepsilon}}{5R/3}=\frac{3\mathbf{\varepsilon}}{5R}. $$

Визначімо, у скільки разів сила струму \(I_2\) більша за силу струму \(I_1:\) $$ \frac{I_2}{I_1}=\frac{3\mathbf{\varepsilon}\cdot 3R}{5R\cdot \mathbf{\varepsilon}}=\frac 95=1,8. $$

Відповідь: 1,8.

ТЕМА: Молярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку вміння визначати кількість теплоти, що віддають і поглинають тіла, а також уміння складати рівняння теплового балансу.

Кількість теплоти \(Q_\text{к},\) яку віддасть кип’ятильник, становитиме: \begin{gather*} Q_\text{к}=I^2R\mathbf{\tau} - \text{закон Джоуля ‒ Ленца}, \end{gather*} де \(I\) ‒ сила струму, \(R\) ‒ опір кип’ятильника, \(\mathbf{\tau}\) ‒ час.

Оскільки в умові дано напругу, а не силу струму, то, скориставшись законом Ома для ділянки кола $$ I=\frac UR, $$ отримаємо формулу для кількості теплоти кип’ятильника: $$ Q_\text{к}=\frac{U^2}{R^2}\cdot R\mathbf{\tau}=\frac{U^2\mathbf{\tau}}{R}. $$

Кількість теплоти \(Q_\text{в},\) необхідну для кип’ятіння води, визначімо за формулою \begin{gather*} Q_\text{в}=cm(t_2-t_1), \end{gather*} де \(c\) ‒ питома теплоємність води, \(m\) ‒ маса води, \((t_2-t_1)\) ‒ різниця температур води.

Тоді кількість теплоти, що витрачається під час цього на теплообмін із навколишнім середовищем, є різницею енергії, яку дає кип’ятильник, й енергії, потрібної для того, щоб закип’ятити воду: \begin{gather*} \Delta Q=Q_\text{к}-Q_\text{в}. \end{gather*}

Виконаймо розрахунки:

де \(m=\mathbf{\rho}\cdot V\) (\(\mathbf{\rho}\) ‒ густина води, \(V\) ‒ об’єм води в одиницях SI).

Відповідь: 390.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на перевірку знання і розуміння перетворення енергії в коливальному контурі.

Коли конденсатор максимально заряджений, то на обкладках конденсатора накопичений максимальний електричний заряд \(q_\text{max},\) а між обкладками виникне електричне поле, енергія якого дорівнює \(W_\text{ел. max}:\) $$ W_\text{ел. max}=\frac{q^2_\text{max}}{2C}, $$ де \(C\) ‒ електроємність конденсатора, його незмінна характеристика.

У той момент, коли конденсатор повністю розрядиться, енергія електричного поля дорівнюватиме нулю, сила струму сягне максимального значення \(I_\text{max},\) а повна енергія контуру дорівнюватиме максимальній енергії магнітного поля \(W_\text{маг. max}:\) $$ W_\text{маг. max}=\frac{LI^2_\text{max}}{2}, $$ де \(L\) ‒ індуктивність котушки, її незмінна характеристика.

Запишімо закон збереження енергії контуру: $$ W_\text{ел. max}=W_\text{ел.}+W_\text{маг.}=W_\text{маг. max}. $$

Якщо за умовою струм, що проходить крізь котушку, становить \(80\ \text{%}\) від максимально можливого, то формула для визначення енергії магнітного поля матиме вигляд:

Тоді енергія електричного поля конденсатора становитиме

Відповідно до закону збереження енергії

Відповідь: 0,6.

ТЕМА: Коливання і хвилі. Оптика. Закони відбивання світла.

Завдання скеровано на перевірку розуміння законів відбивання світла й уміння будувати промені, які падають і відбиваються від плоского дзеркала.

Закони відбивання світла:

1. Промінь, що падає, промінь відбитий і перпендикуляр до поверхні відбивання, проведений із точки падіння променя, лежать в одній площині.

2. Кут відбивання дорівнює куту падіння.

Зробімо додаткові побудови ‒ перпендикуляри в точках падіння променів на обох дзеркалах.

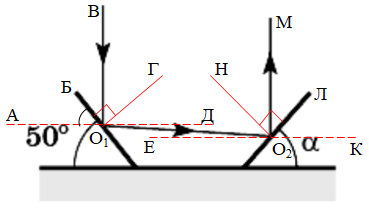
Перенесемо паралельним переносом горизонтальну поверхню в точки падіння променів \(О_1\) і \(О_2.\) Тоді перше дзеркало розташоване під \(\angle АО_1Б=50^\circ.\) \(\angle АО_1В=\angle ВО_1Д=90^\circ\) за умовою, бо промінь \(О_1Б\) напрямлений вертикально вниз.

Тоді \(\angle БО_1В=40^\circ.\) Відповідно \(\angle ВО_1Г=90^\circ‒40^\circ=50^\circ.\) Це кут падіння променя на перше дзеркало. Отже, кут відбивання буде таким самим: \(\angle ВО_1Г=\angle ГО_1О_2=50^\circ.\)

Розгляньмо дві паралельні прямі \(АД\) і \(ЕК\) й січну \(О_1О_2.\)

Тоді й \(\angle О_1О_2Е=10^\circ\) як внутрішній різносторонній до \(\angle ДО_1О_2.\)

Перейдімо до другого дзеркала й розгляньмо кут падіння \(О_1О_2Н\) і кут відбивання \(НО_2М:\)

Тоді обчислімо кут \(МО_2Л:\) $$ \angle МО_2Л=90^\circ-40^\circ=50^\circ. $$

Промінь \(О_2М\) відбився вертикально вгору від другого дзеркала, отже, $$ \angle МО_2К=90^\circ. $$

Тоді

Тобто друге дзеркало розташоване до поверхні столу під кутом \(40^\circ.\)

Відповідь: 40.

ТЕМА: Коливання і хвилі. Оптика. Дифракційні ґратки й використання їх для визначення довжини світлової хвилі.

Завдання скеровано на перевірку розуміння будови дифракційної ґратки.

Скористаймося формулою дифракційної ґратки (\(d\) ‒ період дифракційної ґратки, \(\mathbf{\lambda}\) ‒ довжина хвилі світла): $$ d\sin\mathbf{\varphi}=k\mathbf{\lambda}, $$ де \(k\) ‒ ціле число: \(k=0\) ‒ відповідає центральному (нульовому) максимуму, \(k=\pm 1\) ‒ відповідає максимумам першого порядку тощо. Максимуми одного порядку розташовані симетрично з обох боків від центрального максимуму.

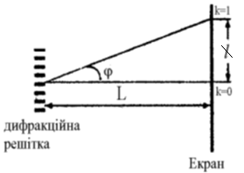
Скористаймося малокутовим наближенням (апроксимація малих кутів), яке зазначено в умові: \begin{gather*} \sin\mathbf{\varphi}=\operatorname{tg}\mathbf{\varphi}=\frac xL, \end{gather*} де \(x\) ‒ відстань від центрального максимуму до максимуму \(k\text{-го}\) порядку.

Отримаємо формулу для визначення \(d:\)

Відповідь: 30.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Альфа-, бета- і гамма-випромінювання.

Завдання скеровано на перевірку знання і застосування правил альфа- і бета-розпадів.

Запишімо реакцію розпаду ядра атома \(\mathrm{^{A}_{Z}X}\) де \(A\) ‒ нуклонне (масове) число, \(Z\) ‒ протонне (зарядове) число: $$ \mathrm{^{A}_{Z}X\rightarrow ^{A'}_{Z'}Y}+N_{\mathbf{\alpha}}\cdot \mathrm{^4_2He}+N_{\mathbf{\beta}}\cdot ^{\ \ \ 0}_{-1}e. $$

Унаслідок реакції отримали інше ядро атома \(\mathrm{^{A'}_{Z'}Y},\) невідому кількість \(N_{\mathbf{\alpha}}\) \(\mathbf{\alpha}\text{-частинок} \ \mathrm{^4_2He}\) і невідому кількість \(N_{\mathbf{\beta}}\) \(\mathbf{\beta}\text{-частинок} \ ^{\ \ \ 0}_{-1}e.\)

Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.

Відповідно до цих законів запишімо рівності:

За умовою масове число зменшилося на \(12:\) $$ \mathrm{A'=A-12.} $$

Водночас заряд ядра атома зменшився на \(4:\) $$ \mathrm{Z'=Z-4}. $$

Підставімо ці вирази:

Отримуємо

Отже, відбулися два \(\mathbf{\beta}\text{-розпади.}\)

Відповідь: 2.