ЗНО онлайн 2016 року з фізики – пробний тест

Пояснення

ТЕМА: Механіка. Основи динаміки. Інерціальні системи відліку.

Завдання скеровано на перевірку розуміння руху тіла за інерцією і вміння читати графіки.

Тіло, на яке не діють інші тіла й поля, називають ізольованим (вільним), а рух ізольованого тіла – рухом за інерцією. У реальності практично неможливо створити умови, коли на тіло нічого не діє, тому рухом за інерцією називають рівномірний прямолінійний рух за відсутності або скомпенсованості дії на тіло інших тіл і полів.

Єдиний графік, який відповідає прямолінійному рівномірному руху ‒ це графік залежності координати \(x\) від часу \(t\) на рисунку A (із часом координата тіла зменшується, оскільки тіло рухається вздовж осі \(Ox,\) але в протилежному напрямку).

На рисунку Б зображено графік залежності прискорення \(a\) від часу \(t.\) Прискорення із часом зростає, отже, це рух із прискоренням, яке рівномірно зростає, а не прямолінійний рівноприскорений рух.

На рисунках В і Г зображено графіки прямолінійного рівноприскореного руху: графік залежності швидкості \(v\) від часу \(t\) і графік залежності координати \(x\) від часу \(t.\) Швидкість рівномірно зростає із часом, а не є сталою, як для рівномірного руху. Графіком залежності координати від часу є вітка параболи, тобто це квадратична, а не пряма залежність величин \(x\) від \(t\) як під час рівномірного руху.

Отже, правильна відповідь ‒ графік на рисунку А.

Відповідь: A.

Пояснення

ТЕМА: Механіка. Закони збереження в механіці. Кінетична і потенціальна енергія.

Завдання скеровано на перевірку розуміння зв’язку між імпульсом тіла і його кінетичною енергією.

Кінетична енергія \(E_k\) ‒ це фізична величина, яка характеризує механічний стан рухомого тіла й дорівнює половині добутку маси \(m\) тіла на квадрат швидкості \(v\) його руху: $$ E_k=\frac{mv^2}{2}. $$

На зміну кінетичної енергії м’яча після зіткнення зі стінкою вплине зміна його швидкості, маса ж залишиться незмінною.

Визначiмо зміну швидкості через зміну імпульсу \(p\) м’яча.

Імпульс тіла \(\overrightarrow{p}\) ‒ це векторна фізична величина, яка дорівнює добутку маси \(m\) тіла на швидкість \(\overrightarrow{v}\) його руху: $$ \overrightarrow{p}=m\overrightarrow{v}. $$

За умовою м’яч до зіткнення зі стінкою мав імпульс $$ p_1=p_0=mv_0. $$

Після зіткнення зі стінкою величина імпульсу м’яча становить $$ p_2=\frac{p_0}{2}=\frac{mv_0}{2}. $$

Отже, швидкість зменшилася вдвічі. Порівняймо, як змінилася кінетична енергія:

Отже, кінетична енергія м’яча внаслідок зіткнення зі стінкою зменшилася вчетверо.

Відповідь: Б.

Пояснення

ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила. Умова плавання тіл.

Завдання скеровано на перевірку знання і розуміння умови плавання тіл і закону Архімеда.

Прирівняймо сили, що діють на кубик: $$ F_\text{т}=F_\text{А}, $$ де \(F_\text{т}\) ‒ сила тяжіння, яка діє на все тіло й напрямлена вертикально вниз, \(F_\text{А}\) ‒ сила Архімеда, що діє лише на занурену частину тіла й напрямлена вертикально вгору.

Розпишімо ці сили: $$ mg=\mathbf{\rho}_\text{Hg}gV_\text{зан}, $$ де \(m\) ‒ маса тіла (кубика), \(g\) ‒ прискорення вільного падіння, \(\mathbf{\rho}_\text{Hg}\) ‒ густина рідини (ртуті), у яку занурено тіло, \(V_\text{зан}\) ‒ об’єм зануреної частини тіла.

Маса тіла дорівнює добутку густини й об’єму тіла: $$ \mathbf{\rho}_\text{т}Vg=\mathbf{\rho}_\text{Hg}gV_\text{зан}. $$

Кубик лише на \(\frac 15\) свого об’єму занурений у ртуть, тому

Відповідно до таблиці, у якій наведено густини металів, кубик виготовлено з алюмінію \(\mathrm{Al},\) отже, правильна відповідь ‒ Б.

Відповідь: Б.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Адіабатний процес.

Завдання скеровано на перевірку розуміння адіабатного процесу й уміння обчислювати роботу під час цього процесу.

Без теплообміну з навколишнім середовищем відбувається адіабатний процес. Під час адіабатного процесу кількість теплоти \(Q,\) передана системі, дорівнює нулю, тому перший закон термодинаміки має вигляд: $$ \Delta U+A=0\ \text{або}\ A=-\Delta U. $$

Під час адіабатного розширення газ виконує додатну роботу \(A\) за рахунок зменшення внутрішньої енергії \(\Delta U,\) а температура газу зменшується.

Якщо газ ідеальний одноатомний, то робота газу дорівнює добутку тиску \(p\) і зміни об’єму \(\Delta V\) газу: $$ A=p\Delta V, $$ а зміна його внутрішньої енергії $$ \Delta U=\frac 32p\Delta V. $$

Використаймо рівняння Менделєєва ‒ Клапейрона $$ p\Delta V=\frac mM R\Delta T=\mathbf{\nu}R\Delta T, $$ де \(\frac mM=\mathbf{\nu}:\ m\) ‒ маса газу, \(M\) ‒ молярна маса газу, \(\mathbf{\nu}\) ‒ кількість речовини, \(R\) ‒ універсальна газова стала, \(\Delta T\) ‒ зміна абсолютної температури.

Отже, внутрішню енергію ідеального одноатомного газу можна обчислити за формулою $$ \Delta U=\frac 32p\Delta V=\frac 32\mathbf{\nu}R\Delta T. $$

Пам’ятаймо, що зміна температури за шкалою Кельвіна дорівнює зміні температури за шкалою Цельсія: \begin{gather*} \Delta T=\Delta t, \end{gather*} де \(T\) ‒ абсолютна температура за шкалою Кельвіна, тобто ціна поділки шкали Кельвіна дорівнює ціні поділки шкали Цельсія:

Відповідь: A.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку розуміння переходу кількості теплоти під час теплових процесів.

Запишімо рівняння теплового балансу для процесу, описаного в умові завдання: $$ Q_1=Q_2, $$ де \(Q_1\) ‒ це кількість теплоти, яку гарячіша вода віддасть, \(Q_2\) ‒ кількість теплоти, яку холодніша вода отримає.

Запишімо відповідні формули: $$ Q_1=c_\text{в}m_1(t_1-t_\text{к}), $$ де \(c_\text{в}\) ‒ питома теплоємність води, \(m_1\) ‒ маса гарячішої води, \(t_1\) ‒ початкова температура гарячішої води, \(t_\text{к}\) ‒ кінцева температура суміші; $$ Q_2=c_\text{в}m_2(t_\text{к}-t_2), $$ де \(m_2\) ‒ маса холоднішої води, \(t_2\) ‒ початкова температура холоднішої води.

Підставімо всі вирази для кількості теплоти в рівняння теплового балансу й визначімо відношення мас води \(\frac{m_2}{m_1}:\)

Зміна температури за шкалою Кельвіна дорівнює зміні температури за шкалою Цельсія: $$ \Delta T=\Delta t, $$ де \(T\) ‒ абсолютна температура за шкалою Кельвіна, тобто ціна поділки шкали Кельвіна дорівнює ціні поділки шкали Цельсія: $$ 1\ ^\circ{\mathrm{C}}=1\ \text{K}. $$

Обчислімо відношення мас води \(\frac{m_2}{m_1}:\) $$ \frac{m_2}{m_1}=\frac{(80-40)\ ^\circ{\mathrm{C}}}{(40-20)\ ^\circ{\mathrm{C}}}=2. $$

Відповідь: B.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Відносна вологість повітря і вимірювання її.

Завдання скеровано на перевірку розуміння відносної вологості й параметрів, від яких вона залежить.

Відносна вологість \(\mathbf{\varphi}\) ‒ фізична величина, яка показує, наскільки водяна пара близька до насичення, і дорівнює поданому у відсотках відношенню абсолютної вологості до густини насиченої водяної пари за даної температури:

\(\mathbf{\rho}_{a}\) ‒ це абсолютна вологість ‒ фізична величина, яка характеризує вміст водяної пари в повітрі та чисельно дорівнює масі \(m_\text{в}\) водяної пари в об’ємі \(V=1\ \text{м}^3\) повітря:

Тепер запишімо формулу для відносної вологості після того, як у посудину додали ще воду, а температура залишилася незмінною, що означає, що густина насиченої пари для цієї ж температури теж залишилася незмінною:

де \(m_\text{в}\) ‒ маса води, яку додали в посудину.

Перед тим, як обчислити, якою ж стала відносна вологість через деякий час, знайдімо масу \(m_\text{в1}\) води, яка була в посудині на початку:

А тепер обчислімо \(\mathbf{\varphi}_2:\)

Відповідь: B.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Внутрішня енергія і способи зміни її.

Завдання скеровано на перевірку розуміння поняття внутрішньої енергії і знання чинників, від яких вона залежить.

Внутрішню енергію в термодинаміці визначають як суму кінетичних енергій хаотичного (теплового) руху частинок речовини (атомів, молекул, йонів), із яких складається тіло, і потенціальних енергій їхньої взаємодії.

Отже, внутрішня енергія \(U\) тіла змінюється зі зміною його температури \(T\) і під час зміни агрегатного стану речовини, з якої це тіло складається: $$ U\sim T. $$

Якщо підняти тіло на певну висоту, то зміниться його механічна енергія, зокрема потенціальна.

Якщо надати тілу швидкості, то теж зміниться його механічна енергія, зокрема кінетична.

Якщо сховати тіло до теплоізолювальної шафи, то тіло не отримуватиме або не віддаватиме тепло, не змінюватиметься його температура, а отже, не змінюватиметься його внутрішня енергія.

А от якщо нагріти тіло, то його внутрішня енергія збільшиться. Отже, правильна відповідь ‒ В.

Відповідь: B.

Пояснення

ТЕМА: Електродинаміка. Основи електростатики. Електроємність.

Завдання скеровано на перевірку розуміння поняття електроємності провідника.

Електроємність характеризує здатність провідників або системи з кількох провідників накопичувати електричний заряд.

Електроємність провідника – це властивість провідного тіла, яка залежить від його розмірів, форми, навколишнього середовища, розташування інших провідників і характеризує пряму пропорційну залежність між зарядом тіла та потенціалом його поверхні.

Отже, правильна відповідь ‒ А.

Відповідь: A.

Пояснення

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.

Завдання скеровано на перевірку знання і розуміння послідовного і паралельного з’єднання провідників, а також уміння читати електричні схеми.

Перерисуймо цю ділянку кола й пронумеруймо резистори:

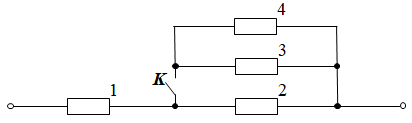
Коли вимикач \(K\) було замкнено, резистор 1 був послідовно з’єднаний із резисторами 2, 3 й 4, які між собою з’єднані паралельно. Загальний опір за такого підключення становив за умовою \(16\ \text{Ом.}\) Знайдімо опір одного резистора, оскільки за умовою вони всі однакові: \begin{gather*} R_\text{заг1}=R_1+R_{234},\\[6pt] R_{234}=\frac R3, \end{gather*} де \(R\) ‒ опір одного резистора. \begin{gather*} R_\text{заг1}=R+\frac R3=\frac{4R}{3},\\[6pt] 16\ \text{Ом}=\frac{4R}{3},\\[6pt] R=\frac{16\ \text{Ом}\cdot 3}{4}=12\ \text{Ом}. \end{gather*}

Після розмикання вимикача \(K\) струм іде крізь резистори 1 і 2. Крізь розгалуження ділянки кола, де підключені резистори 3 і 4, струм не піде (див. рисунок).

Якщо резистори 1 і 2 з’єднано послідовно, загальний опір \(R_\text{заг2}\) дорівнюватиме сумі опорів резисторів 1 і 2:

Відповідь: B.

Пояснення

ТЕМА: Електродинаміка. Закони постійного струму. Сила струму.

Завдання скеровано на перевірку знання і розуміння поняття сили струму.

Сила струму \(I\) в провіднику ‒ фізична величина, яка характеризує електричний струм і чисельно дорівнює заряду \(q,\) що проходить через поперечний переріз провідника за одиницю часу \(t:\) $$ I=\frac qt. $$

Відповідно до системи SI виразімо час у секундах: $$ t=1\ \text{хв}=60\ \text{с}. $$

Загальний заряд усіх електронів, що проходять через поперечний переріз провідника, дорівнює \(q=N\cdot e,\) де \(N\) ‒ кількість електронів, \(e\) ‒ елементарний електричний заряд, заряд електрона за модулем дорівнює елементарному заряду.

Отже, визначімо шукану силу струму:

Відповідь: B.

Пояснення

ТЕМА: Електродинаміка. Електричний струм у різних середовищах. Електричний струм у газах. Несамостійні і самостійні розряди.

Завдання скеровано на перевірку розуміння несамостійного і самостійного газового розряду й уміння читати графіки.

Газовий розряд, який відбувається без дії зовнішнього йонізатора, називають самостійним газовим розрядом, а газовий розряд, який відбувається тільки під час дії зовнішнього йонізатора, називають несамостійним газовим розрядом.

Розгляньмо детальніше вольт-амперну характеристику (ВАХ) газового розряду. Закон Ома, що передбачає лінійну залежність струму \(I\) від напруги \(U,\) часто не виконуваний для газів. Пояснити особливості кривої можна зміною концентрації носіїв струму залежно від напруги.

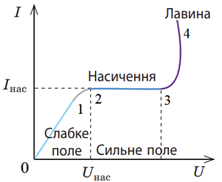
Ділянці графіка 0‒1 відповідає залежність сили струму від напруги, яка підпорядкована закону Ома, ‒ пряма залежність.

На ділянці 1‒2 пряму залежність порушено. Напруга збільшується, а сила струму зростає повільніше ‒ усі носії швидко потрапляють на електроди й концентрація їх у розряді зменшується.

На ділянці 2‒3 збільшення напруги триває, а сила струму залишається незмінною. У сильному електричному полі всі заряджені частинки, які створює йонізатор, долітають до електродів. Найбільшу силу струму, що є можливою внаслідок дії даного йонізатора, називають струмом насичення \(I_\text{нас.}\)

На ділянці 3‒4 сила струму різко зростає за незначного збільшення напруги. Це відбувається завдяки йонізації газу електронним ударом, унаслідок чого кількість вільних заряджених частинок лавиноподібно або каскадно збільшується ‒ зростає концентрація носіїв струму в розряді (див. рисунок ‒ схему розвитку електронної лавини). Кількість їх зумовлена тепер не йонізатором, а дією самого поля, і провідність з несамостійної стає самостійною (відбувається пробій). Напругу, за якої запалюється самостійний розряд, називають напругою пробою.

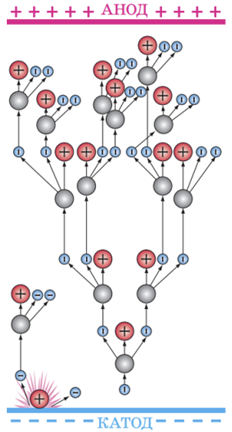
Отже, самостійному газовому розряду відповідає ділянка 3‒4 графіка.

Відповідь: Г.

Пояснення

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік.

Завдання скеровано на перевірку знання і розуміння фізичного змісту фізичних величин, які визначають магнітний потік.

Потік магнітної індукції (магнітний потік) \(\text{Ф}\) ‒ це фізична величина, яка дорівнює добуткові магнітної індукції \(B\) на площу \(S\) поверхні та на косинус кута \(\mathbf{\alpha}\) між вектором магнітної індукції і нормаллю до поверхні: $$ \text{Ф}=BS\cos\mathbf{\alpha}. $$

Одиниця магнітного потоку в SІ ‒ вебер (названо на честь В. Вебера (1804‒1891), німецького фізика): $$ [\text{Ф}]=1\ \text{Вб (Wb)}. $$

\(1\) вебер ‒ це максимальний магнітний потік, який створюється магнітним полем індукцією \(1\) тесла через поверхню площею \(1\) метр квадратний: $$ 1\ \text{Вб}=1\ \text{Тл}\cdot \ \text{м}^2. $$

Одиниця магнітної індукції в SІ ‒ тесла (названо на честь Ніколи Тесли (1856–1943), сербського фізика).

\(1\) тесла ‒ це магнітна індукція \((B)\) такого однорідного магнітного поля, яке діє з максимальною силою \((F_\text{Amax})\ 1\) ньютон на провідник завдовжки \((l)\ 1\) метр, сила струму \((I)\) в якому \(1\) ампер: \begin{gather*} B=\frac{F_\text{Amax}}{Il},\\[6pt] [B]=1\ \text{Тл}=1\frac{\text{Н}}{\text{А}\cdot\text{м}}. \end{gather*}

Отже,

Метр і ампер ‒ це основні одиниці SI. Виразімо ще ньютон через основні одиниці SI.

Ньютон ‒ одиниця сили в SІ: \(1\) ньютон \((\text{Н})\) дорівнює силі, яка, діючи на тіло масою \(1\ \text{кг,}\) надає йому прискорення \(1\ \text{м/с}^2:\) $$ 1\ \text{Н}=1\ \text{кг}\cdot 1\ \text{м/с}^2. $$

Кілограм і секунда ‒ теж основні одиниці SI. Тож тепер остаточно запишімо одиницю магнітного потоку через основні одиниці SI:

Відповідь: Б.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.

Завдання скеровано на перевірку знання і застосування формули періоду коливань на пружині.

Формула для обчислення періоду \(T\) коливань пружинного маятника: $$ T=2\mathbf{\pi}\sqrt{\frac mk}, $$ де \(m\) ‒ маса тіла на пружині, \(k\) ‒ жорсткість пружини.

Маса тіла дорівнює добутку густини \(\mathbf{\rho}\) матеріалу тіла і його об’єму \(V:\) $$ m=\mathbf{\rho}V. $$

До пружин підвішено кулі, об’єм кулі обчислюють за формулою $$ V=\frac 43\mathbf{\pi}R^3. $$

Запишімо формули періодів малих вертикальних коливань обох куль на пружинах, зваживши на те, що за умовою радіуси куль однакові, однакові й пружини, тобто однакова жорсткість пружин:

Визначімо співвідношення періодів:

Тобто \(T_2=4T_1\) ‒ це правильне співвідношення періодів.

Відповідь: Г.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливальний рух.

Завдання скеровано на перевірку знання і розуміння частоти коливань.

Частота коливань \(\mathbf{\nu}\) ‒ це кількість \(N\) коливань за одиницю часу \(t:\) $$ \mathbf{\nu}=\frac Nt. $$

Звідси знайдімо формулу для визначення кількості коливань: \begin{gather*} N=\mathbf{\nu}t,\\[6pt] N=2\ \text{Гц}\cdot 10\ \text{с}=20. \end{gather*}

Відповідь: Г.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Трансформатор.

Завдання скеровано на перевірку знання і розуміння будови й роботи трансформатора.

У режимі холостого ходу трансформатора (в умові йдеться про розімкнену вторинну обмотку, тобто трансформатор не навантажений) справджується рівність: $$ \frac{U_1}{U_2}\approx\frac{\mathbf{\varepsilon}_1}{\mathbf{\varepsilon}_2}=\frac{N_1}{N_2}=k. $$

Відношення значень ЕРС \((\mathbf{\varepsilon}_1\ \text{i}\ \mathbf{\varepsilon}_2)\) у дії, індукованих у первинній і вторинній обмотках трансформатора, дорівнює відношенню кількості витків \((N_1\ \text{i}\ N_2)\) в обмотках. Величину \(k\) називають коефіцієнтом трансформації. Первинна обмотка трансформатора підключена до джерела змінного струму, напруга на виході якого \(U_1.\) У вторинній обмотці струм не йде (вона розімкнена), тому напруга на кінцях вторинної обмотки за модулем дорівнює ЕРС індукції \((N_2=\mathbf{\varepsilon}_2).\)

За умовою кількість витків первинної обмотки не змінювалася, і змінний струм у первинній обмотці протікав той самий. На кінцях вторинної обмотки напруга підвищилася, тож і кількість витків у ній збільшилася. Визначімо, на скільки збільшилася кількість витків у вторинній обмотці:

Отже, \(N_2-N_1=120-80=40\) ‒ кількість витків у вторинній обмотці трансформатора збільшилася на \(40\) витків, щоб напруга підвищилася до \(9\ \text{В}.\)

Відповідь: Г.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.

Завдання скеровано на перевірку знання і застосування правил побудови зображень, які дає розсіювальна і збиральна лінзи.

Уявне зображення ‒ це оптичне зображення, утворене променями, які насправді не перетинаються, а перетинаються тільки їхні уявні продовження.

Розсіювальна лінза завжди дає уявне, зменшене, пряме зображення предмета.

А збиральна лінза дає уявне зображення лише в разі розміщення предмета між лінзою і фокусом.

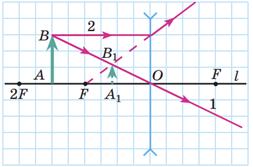
Приклад побудови зображення в розсіювальній лінзі

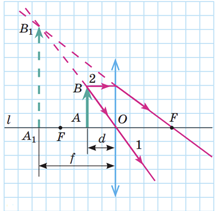
Приклад побудови уявного зображення в збиральній лінзі

Отже, обидві лінзи, і розсіювальна, і збиральна, можуть давати уявне зображення.

Відповідь: B.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Інтерференція світла, її практичне застосування.

Завдання скеровано на перевірку знання і розуміння явища інтерференції.

Хвилі, які відповідають умовам когерентності, називають когерентними хвилями.

Умови когерентності хвиль:
1) хвилі повинні мати однакову частоту (відповідно й довжину);
2) різниця \(\Delta \mathbf{\varphi}\) початкових фаз хвиль має бути незмінною (хвилі, що накладаються, повинні мати незмінний у часі зсув фаз).

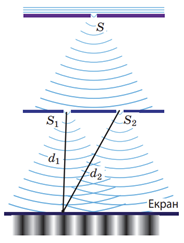
Ідеальними джерелами когерентних світлових хвиль є лазери ‒ оптичні квантові генератори.

Коли хвилі надходять у точку \(P\) в протилежних фазах, вони гаситимуть одна одну (див. рисунок) ‒ у точці \(P\) спостерігають інтерференційний мінімум.

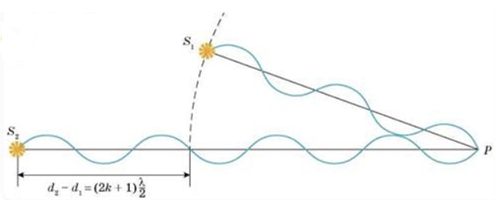
Це відбудеться за умови, що на відрізку \(\Delta d\) укладатиметься непарна кількість півхвиль. Умова інтерференційного мінімуму: у точці простору відбувається послаблення результувальних світлових коливань, якщо різниця ходу двох світлових хвиль, що надходять у цю точку, дорівнює непарному числу півхвиль: \begin{gather*} \Delta d=d_2-d_1=(2k+1)\frac{\mathbf{\lambda}}{2}\\[6pt] \text{або}\\[6pt] \Delta d=k\mathbf{\lambda}+\frac{\mathbf{\lambda}}{2}, \end{gather*} де \(\mathbf{\lambda}\) ‒ довжина хвилі; \(k\) ‒ ціле число.

За умовою довжина хвилі випромінювання \(\mathbf{\lambda}=600\ \text{нм.}\) Розгляньмо кожен із запропонованих варіантів відповіді.

A \(\Delta d=400\ \text{нм}=\frac 23\mathbf{\lambda}=\frac 16\mathbf{\lambda}+\frac{\mathbf{\lambda}}{2}\) – за умовою \(k\) ‒ ціле число, а за такої різниці ходу \(k=\frac 16;\)

Б \(\Delta d=600\ \text{нм}=\mathbf{\lambda}=\frac 12\mathbf{\lambda}+\frac{\mathbf{\lambda}}{2}\) – знову отримали \(k=\frac 12\) ‒ дробове число;

B \(\Delta d=1200\ \text{нм}=2\mathbf{\lambda}=\frac 32\mathbf{\lambda}+\frac{\mathbf{\lambda}}{2}-k=\frac 32\) – дробове число;

Г \(\Delta d=1500\ \text{нм}=2\mathbf{\lambda}+\frac{\mathbf{\lambda}}{2}-k=2\) – ціле число, що задовольняє умову інтерференційного мінімуму.

Отже, правильна відповідь Г ‒ \(1500\ \text{нм:}\) це дві цілі довжини хвилі і ще пів хвилі ‒ непарне число півхвиль ‒ п᾽ять.

Відповідь: Г.

Пояснення

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом й атомне ядро. Період піврозпаду.

Завдання скеровано на перевірку розуміння закону радіоактивного розпаду й уміння застосовувати формулу, якою описують цей закон.

Період піврозпаду \(T\) ‒ це фізична величина, що дорівнює часу, протягом якого розпадається половина наявної кількості ядер певного радіонукліда.

Основний закон радіоактивного розпаду описують формулою \begin{gather*} N=N_0\cdot 2^{-\frac tT}, \end{gather*} де \(N\) ‒ кількість ядер радіонукліда, що залишились у зразку через час \(t;\ N_0\) ‒ початкова кількість ядер; \(T\) ‒ період піврозпаду; \(t\) ‒ час розпаду.

Визначімо, у скільки разів було більше атомів Урану, ніж їх залишилося після розпаду за зазначений період розпаду:

Отже, кількість атомів Урану зменшиться в \(\sqrt[{3}]{4}\) разів.

Відповідь: B.

Пояснення

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.

Завдання скеровано на перевірку знання і вміння складати рівняння ядерних реакцій.

Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових. Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.

Запишімо рівняння ядерної реакції відповідно до умови завдання: $$ \mathrm{^{19}_{\ \ 9}F+X\ \rightarrow\ ^{16}_{\ \ 8}O\ +\ ^{4}_{2}He}, $$ де \(X\) ‒ шукана частинка.

Відповідно до закону збереження електричного заряду і закону збереження енергії-маси визначімо \(\mathrm{A}\) ‒ нуклонне (масове) і \(\mathrm{Z}\) ‒ протонне (зарядове) числа частинки: \begin{gather*} \mathrm{A}=16+4-19=1,\\[7pt] \mathrm{Z}=8+2-9=1. \end{gather*}

Отже, частинка з таким нуклонним і протонним числами ‒ це протон \(^1_1\mathrm{p}.\) Тоді остаточно рівняння реакції матиме такий вигляд: $$ \mathrm{^{19}_{\ \ 9}F+\ ^1_1p\ \rightarrow\ ^{16}_{\ \ 8}O\ +\ ^{4}_{2}He}. $$

Відповідь: A.

Пояснення

ТЕМА: Механіка. Основи динаміки (закон всесвітнього тяжіння.). Закони збереження в механіці (прості механізми, закон збереження імпульсу). Коливання і хвилі. Оптика. Механічні коливання і хвилі. Коливання вантажу на пружині.

Завдання скеровано на перевірку знання і розуміння механічних процесів, уміння описати їх за допомогою формул і законів.

Взаємодію Землі і Місяця описуємо за допомогою закону всесвітнього тяжіння: будь-які два тіла притягуються одне до одного із силою \(F,\) яка прямо пропорційна добутку мас \(m_1\) і \(m_2\) цих тіл й обернено пропорційна квадрату відстані \(R\) між ними: $$ F=G\frac{m_1m_2}{R^2}. $$

Відкручування гайки за допомогою гайкового ключа є прикладом застосування простого механізму ‒ важеля ‒ на практиці. Чим довшою буде ручка гайкового ключа, тим легше ми відкрутимо або сильніше закрутимо гайку, прикладаючи меншу силу. Описати цей процес можна відповідно до правила моментів: $$ F_1l_1=F_2l_2, $$ де сила \(\overrightarrow{F}_1\) повертає важіль за ходом годинникової стрілки, сила \(\overrightarrow{F}_2\) ‒ проти ходу годинникової стрілки, а \(l_1\) і \(l_2\) ‒ плечі цих сил відповідно.

Коливання тіла масою \(m\) на пружині жорсткістю \(k\) можна описати за допомогою формули для обчислення періоду \(T\) коливань пружинного маятника: $$ T=2\mathbf{\pi}\sqrt{\frac mk}. $$

Зіткнення більярдних куль, як приклад абсолютно пружного удару, опишімо за допомогою закону збереження імпульсу: у замкненій системі тіл векторна сума імпульсів тіл до взаємодії дорівнює векторній сумі імпульсів тіл після взаємодії. Зваживши на те, що імпульс тіла дорівнює добутку маси \(m\) і швидкості \(\overrightarrow{v}\) до взаємодії (або \(\overrightarrow{u}\) після взаємодії) руху тіла, закон збереження імпульсу для зіткнення більярдних куль матиме такий вигляд: $$ m_1\overrightarrow{v}_1+m_2\overrightarrow{v}_2=m_1\overrightarrow{u}_1+m_2\overrightarrow{u}_2. $$

Відповідь: 1Д, 2Б, 3В, 4Г.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку розуміння і застосування першого закону термодинаміки до ізопроцесів і адіабатного процесу.

Перший закон (начало) термодинаміки: кількість теплоти \(Q,\) передана системі, йде на зміну внутрішньої енергії системи \(\Delta U\) та на виконання системою роботи \(A\) проти зовнішніх сил: $$ Q=\Delta U+A. $$

Запишімо перший закон термодинаміки для ізопроцесів й адіабатного процесу.

Адіабатний процес ‒ це процес, який відбувається без теплообміну з навколишнім середовищем. Під час адіабатного процесу кількість теплоти \(Q,\) передана системі, дорівнює нулю, тому запис першого закону термодинаміки такий: $$ \Delta U+A=0\ \text{або}\ A=-\Delta U. $$

Під час адіабатного розширення газ виконує додатну роботу за рахунок зменшення внутрішньої енергії, а температура газу зменшується. Тому під опис адіабатного розширення підходять числові значення фізичних величин, зазначених у варіанті A: \(Q=0,\ A=12\ \text{кДж},\ \Delta U=-12\ \text{кДж}.\)

Ізохорне охолодження. Під час цього процесу об’єм газу не змінюється \((\Delta V = 0)\) і газ роботу не виконує \((A=0),\) тому рівняння першого закону термодинаміки має вигляд: $$ Q=\Delta U. $$

Газ під час ізохорного охолодження віддасть певну кількість теплоти, на стільки само зменшиться його внутрішня енергія. Тому ізохорному охолодженню відповідають числові значення фізичних величин, зазначені у варіанті Г: \(Q=-18\ \text{кДж},\ A=0,\ \Delta U=-18\ \text{кДж}.\)

Ізотермічне розширення. Під час цього процесу температура, а отже, і внутрішня енергія газу не змінюються \((\Delta U=0),\) тому рівняння першого закону термодинаміки таке: $$ Q=A. $$

Під час ізотермічного розширення вся передана газу кількість теплоти йде на виконання механічної роботи. Тому процесу ізотермічного розширення ставімо у відповідність варіант В: \(Q=24\ \text{кДж},\ A=24\ \text{кДж},\ \Delta U=0.\)

Ізобарне нагрівання. Під час цього процесу виконується робота й змінюється внутрішня енергія газу, тому рівняння першого закону термодинаміки таке: $$ Q=\Delta U+A. $$

Під час ізобарного нагрівання передана газу кількість теплоти йде і на збільшення внутрішньої енергії газу, і на виконання механічної роботи. Отже, підійде той варіант, у якому сума значень внутрішньої енергії і роботи дорівнюватиме значенню отриманої кількості теплоти ‒ це варіант Б: \(Q=5\ \text{кДж},\ A=2\ \text{кДж},\ \Delta U=3\ \text{кДж}.\)

У варіанті Д сума значень внутрішньої енергії і роботи також дорівнює значенню отриманої кількості теплоти, але значення кількості теплоти від’ємне, як і значення внутрішньої енергії і роботи. Це означає, що газ не нагрівається, не отримує кількість теплоти, а навпаки віддає її.

Відповідь: 1А, 2Г, 3В, 4Б.

Пояснення

ТЕМА: Електродинаміка. Основи електростатики. Зв’язок між напругою і напруженістю однорідного електричного поля.

Завдання скеровано на перевірку розуміння зв’язку між напругою і напруженістю однорідного електричного поля, уміння визначати напругу між точками поля.

Картину силових ліній електричного поля, створеного системою двох пластин, заряди яких рівні за модулем і протилежні за знаком, зображено на рисунку. Синіми стрілками позначено напрямки векторів напруженості. Між пластинами поле однорідне, тому що вектори напруженості між ними однакові.

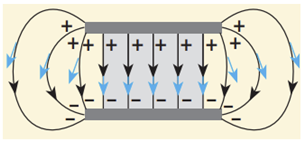
Повернімо на \(90^\circ\) проти годинникової стрілки систему пластин. Скористаймося формулою, що пов’язує напругу \(U,\) напруженість \(E\) і проєкцією \(d\) вектора, який з’єднує точки поля 1 і 2, на напрямок силових ліній поля (див. рисунок): $$ U=Ed. $$

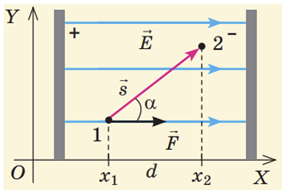
За умовою напруга між пластинами дорівнює \(40\ \text{В}.\) В умові завдання на рисунку чотири клітинки між пластинами, отже, сторону однієї клітинки вважатимемо одиничним відрізком, який відповідає \(10\ \text{В}.\)

Якщо з’єднати букву Б з буквою А вектором й визначити в уяві його проєкцію на вертикально напрямлену вниз силову лінію, то проєкція дорівнюватиме стороні однієї клітинки, отже, напруга між точками Б і А становитиме \(10\ \text{В:}\) $$ U_\text{БА}=10\ \text{В}. $$

Точки А і Г лежать на одній горизонтальній прямій, тому вектор, яким можна з’єднати їх, проєктується в точку, тобто його проєкція дорівнює нулю. Тому, з огляду на формулу, напруга між точками А і Г теж дорівнюватиме нулю: $$ U_\text{АГ}=0. $$

Проєкція вектора, яким можна з’єднати точки Б і В, відповідає трьом одиничним відрізкам, тож напруга між цими точками дорівнює \(30\ \text{В:}\) $$ U_\text{БВ}=30\ \text{В}. $$

Проєкція вектора, яким можна з’єднати точки Г і В, відповідає двом одиничним відрізкам, тож напруга між цими точками дорівнює \(20\ \text{В:}\) $$ U_\text{ГВ}=20\ \text{В}. $$

Відповідь: 1Б, 2А, 3Г, 4В.

Пояснення

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Ядерні реакції.

Завдання скеровано на перевірку знання і вміння складати рівняння ядерних реакцій.

Ядерною реакцією називають взаємодію ядер або елементарних частинок із ядром, яка відбувається з утворенням частинок, відмінних від початкових. Під час ядерних реакцій, як і під час будь-яких явищ, що відбуваються у Всесвіті, справджуються закони збереження: закон збереження електричного заряду, закон збереження імпульсу, закон збереження енергії-маси.

Запишімо рівняння ядерної реакції відповідно до умови завдання для кожного випадку 1‒4 і відповідно до закону збереження електричного заряду і закону збереження енергії-маси визначімо \(\mathrm{A}\) ‒ нуклонне (масове) і \(\mathrm{Z}\) ‒ протонне (зарядове) числа відповідного нукліда Нітрогену, позначеного в рівнянні \(\mathrm{X}\):

У реакції 1 бере участь нуклід Нітрогену \(^{12}_{\ \ 7}\mathrm{N}\) ‒ варіант відповіді A.

У реакції 2 бере участь нуклід Нітрогену \(^{13}_{\ \ 7}\mathrm{N}\) ‒ варіант відповіді Б.

У реакції 3 бере участь нуклід Нітрогену \(^{17}_{\ \ 7}\mathrm{N}\) ‒ варіант відповіді Д.

У реакції 4 бере участь нуклід Нітрогену \(^{16}_{\ \ 7}\mathrm{N}\) ‒ варіант відповіді Г.

Відповідь: 1А, 2Б, 3Д, 4Г.

Пояснення

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рух.

Завдання скеровано на перевірку знання і вміння застосовувати кінематичні характеристики прямолінійного рівномірного руху.

Проаналізуймо наведені в умові кінематичні рівняння руху велосипедиста і мотоцикліста. Як бачимо, це залежність координати \(x\) від часу \(t\) в першому степені. Загальний вигляд рівняння координати для прямолінійного рівномірного руху такий: $$ x=x_0+vt, $$ де \(x_0\) ‒ початкова координата; \(v\) ‒ проєкція швидкості на горизонтальну вісь \(Ox,\) уздовж якої рухається тіло.

Для велосипедиста: початкова координата \(x_{01}=150\ \text{м,}\) проєкція швидкості \(v_1=-5\ \text{м/с.}\) Знак мінус означає, що велосипедист рухається в протилежному до вибраного напрямку горизонтальної осі \(Ox\) (див. рисунок).

Для мотоцикліста: початкова координата \(x_{02}=-50\ \text{м,}\) проєкція швидкості \(v_2=20\ \text{м/с.}\) Початкова координата зі знаком мінус означає, що мотоцикліст на початку руху перебував лівіше від початку відліку, вибраного на осі \(Ox\) (див. рисунок).

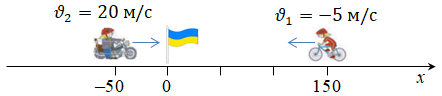
1. Час, через який зустрінуться велосипедист і мотоцикліст, однаковий для них, бо час плине однаково для всіх. Велосипедист зустрінеться з мотоциклістом ‒ це означає, що вони перебуватимуть у точці з однаковою координатою. Тож прирівняймо їхні координати \(x_1=x_2:\)

Велосипедист і мотоцикліст зустрінуться через \(8\ \text{с.}\)

Відповідь: 8.

2. Оскільки до зустрічі велосипедист рухався \(8\ \text{с}\) зі швидкістю \(5\ \text{м/с,}\) шлях визначімо за формулою: \begin{gather*} s_1=v_1t,\\[6pt] s_1=5\ \frac{\text{м}}{\text{с}}\cdot 8\ \text{с}=40\ \text{м}. \end{gather*}

Можна визначити координату велосипедиста через \(8\ \text{с}\) руху й обчислити його шлях до зустрічі з мотоциклістом, як різницю між початковою і кінцевою координатами велосипедиста:

Відповідь: 40.

Відповідь: 1. 8. 2. 40.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку знання рівняння стану ідеального газу і вміння за допомогою його описувати стан газу.

1. За умовою випарувалася половина зрідженого гелію, тобто

Відповідно можна обчислити кількість речовини \(\mathbf{\nu}\) гелію: $$ \mathbf{\nu}=\frac mM=\frac{\mathbf{\rho}V}{M}. $$

Попередньо виразімо значення густини \(\mathbf{\rho}\) гелію в одиницях SI ‒ у кілограмах на метр кубічний \((\text{кг/м}^3):\)

Обчислімо кількість речовини \(\mathbf{\nu}\) гелію, що випарувався:

Опишімо рівнянням стану ідеального газу (рівняння Менделєєва ‒ Клапейрона) стан гелію в резервуарі до того, як туди закачали гелій, що випарувався: $$ p_1V_1=\mathbf{\nu}_1RT_1, $$ де \(p_1\) ‒ початковий тиск газу в резервуарі, \(V_1\) ‒ об’єм гелію, який вже міститься в резервуарі (це і є об’єм резервуара), \(\mathbf{\nu}_1\) ‒ кількість речовини в резервуарі, \(R\) ‒ універсальна газова стала, \(T_1\) ‒ температура гелію в резервуарі.

Знайдімо із цього рівняння, початкову кількість речовини \(\mathbf{\nu}\) гелію в резервуарі:

Тепер можна визначити кількість речовини газу в резервуарі після того, як у нього закачали гелій, зібраний після випаровування:

Відповідь: 1062,5.

2. Опишімо стан газу в резервуарі після закачування гелію ‒ зміниться кількість речовини \(\mathbf{\nu}_2\) (збільшиться), отже, збільшиться тиск \(p_2,\) абсолютна температура гелію в резервуарі залишиться сталою \((T_2=T_1=const),\) об’єм, який займатиме гелій, теж не зміниться \((V_2=V_1):\) $$ p_2V_2=\mathbf{\nu}_2RT_2. $$

Обчислімо тиск, який установиться в резервуарі:

Щоб визначити зміну тиску в резервуарі у відсотках, складімо пропорцію:

Отже, \(\Delta p\ (\text{%})=106,25\ \text{%}-100\ \text{%}=6,25\ \text{%}.\)

Відповідь: 6,25.

Відповідь: 1. 1062,5. 2. 6,25.

Пояснення

ТЕМА: Механіка. Основи кінематики. Рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку знання і розуміння кінематичних рівнянь, що описують прямолінійний рівноприскорений рух і вміння застосовувати їх.

Обчислімо модуль переміщення \(s:\) $$ s=\frac{v^2-v^2_0}{2g}, $$ де \(v_0\) ‒ проєкція початкової швидкості в момент початку відліку часу \(t,\ v\) ‒ проєкція кінцевої швидкості через деякий інтервал часу \(t,\ g\) ‒ прискорення вільного падіння;

Можна також спочатку визначити проміжок часу, за який швидкість руху зміниться від \(v_0=6\ \text{м/с}\) до \(v=24\ \text{м/с}\) за формулою для визначення проєкції швидкості руху на вертикальну вісь \(Oy,\) напрямлену вниз (вектори початкової, кінцевої швидкостей і вектор прискорення вільного падіння будуть напрямлені вниз уздовж осі \(Oy\)):

Знаючи проміжок часу, за який відбулася зазначена в умові зміна швидкості, можна визначити модуль переміщення:

Відповідь: 27.

Пояснення

ТЕМА: Механіка. Закони збереження в механіці. Закон збереження механічної енергії.

Завдання скеровано на перевірку вміння застосовувати закони збереження імпульсу й енергії під час непружного удару тіл.

Якщо після зіткнення частина кінетичної енергії перетворюється на внутрішню енергію (витрачається на деформацію та нагрівання тіл), таке зіткнення називають непружним. Після такого удару тіла рухаються як єдине ціле (див. рисунок).

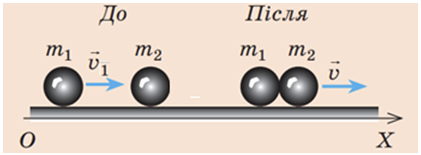
Опишімо рух куль до і після удару за допомогою закону збереження імпульсу у векторному вигляді та в проєкціях на вісь \(Ox:\) \begin{gather*} m_1\overrightarrow{v}_1=(m_1+m_2)\overrightarrow{v},\\[7pt] m_1v_1=(m_1+m_2)v, \end{gather*} де \(m_1\) ‒ маса пластилінової кульки, що рухалася зі швидкістю \(\overrightarrow{v}_1,\ m_2\) ‒ маса нерухомої до удару кульки, \(\overrightarrow{v}\) ‒ швидкість руху обох кульок після удару.

Обчислімо швидкість руху куль після удару:

Запишімо закон збереження енергії для цієї умови: $$ \frac{m_1v^2_1}{2}=\frac{(m_1+m_2)v^2}{2}+Q, $$ де \(Q\) ‒ утрачена кінетична енергія після удару кульок.

Обчислімо її:

Відповідь: 22.

Пояснення

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії (рівняння стану ідеального газу). Властивості газів, рідин і твердих тіл (теплота згоряння палива).

Завдання скеровано на перевірку вміння описувати стан газу за допомогою рівняння стану ідеального газу, визначати кількість теплоти згоряння палива.

Кількість теплоти \(Q,\) що виділиться внаслідок згоряння всього метану, який міститься в автомобільному газовому балоні, можна обчислити за формулою $$ Q=\mathbf{\lambda}m, $$ де \(\mathbf{\lambda}\) ‒ питома теплота згоряння палива, \(m\) ‒ маса метану.

Визначімо масу метану в балоні. Для цього опишімо за допомогою рівняння стану ідеального газу (рівняння Менделєєва ‒ Клапейрона) стан метану в балоні: $$ pV=\frac mMRT, $$ де \(p\) ‒ тиск газу в балоні, \(V\) ‒ об’єм метану в балоні (а це і є об’єм балона), \(m\) ‒ маса метану, \(M\) ‒ молярна маса метану, \(R\) ‒ універсальна газова стала, \(T\) ‒ температура метану в балоні.

Виразімо з рівняння стану масу: $$ m=\frac{pVM}{RT}. $$

Переведімо значення всіх величин у систему SI:

Підставимо ці значення у формулу для обчислення маси:

Підставимо значення маси у формулу для визначення кількості теплоти згоряння метану:

Відповідь: 400.

Пояснення

ТЕМА: Електродинаміка. Закони постійного струму. Закон Ома для ділянки кола. Послідовне і паралельне з’єднання провідників. Закон Ома для повного кола.

Завдання скеровано на перевірку знання і розуміння послідовного з’єднання провідників, а також уміння визначати характеристики елементів електричного кола.

Для визначення опору \(R_\text{р}\) резистора необхідно використати формулу закону Ома для ділянки кола: \begin{gather*} I_\text{p}=\frac{U_\text{p}}{R_\text{p}},\\[6pt] \text{звідки}\ R_\text{p}=\frac{U_\text{p}}{I_\text{p}}, \end{gather*} де \(I_\text{p}\) ‒ сила струму, що проходить крізь резистор, \(U_\text{p}\) ‒ напруга на резисторі.

Крізь резистор проходитиме така сама сила струму, як і крізь світлодіоди, оскільки вони за схемою з’єднані послідовно, тобто $$ I_\text{p}=20\ \text{мА}=20\cdot 10^{-3}\ \text{А}. $$

Для визначення спаду напруги на резисторі скористаймося законом Ома для повного кола: $$ I=\frac{\mathbf{\varepsilon}}{R+r}. $$

Сила струму \(I\) в повному електричному колі дорівнює відношенню електрорушійної сили \(\mathbf{\varepsilon}\) (ЕРС) джерела струму до повного опору кола \((R+r),\) де \(R\) ‒ загальний опір навантаження, підключеного до джерела струму, \(r\) ‒ внутрішній опір джерела струму (тут – батареї гальванічних елементів).

За умовою внутрішнім опором батареї можна знехтувати, а резистор і світлодіоди з’єднані послідовно (їхні напруги додають). Тому електрорушійна сила дорівнюватиме сумі спадів напруги на резисторі \(U_\text{p}\) і світлодіодах \((U_1=U_2=U_3\ -\ \text{за умовою):}\)

Звідси обчислімо напругу на резисторі:

Отже, тепер можна визначити опір резистора:

Відповідь: 30.

Пояснення

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік. Закон електромагнітної індукції.

Завдання скеровано на перевірку знання і розуміння поняття індукційного струму, електрорушійної сили (ЕРС) індукції, магнітного потоку й уміння застосувати аналітичні зв'язки між цими поняттями.

Силу індукційного струму \(I_\text{i}\) в контурі опором \(R\) визначають за законом Ома: $$ I_\text{i}=\frac{\mathbf{\varepsilon}_\text{i}}{R}. $$

За законом електромагнітної індукції визначімо електрорушійну силу (ЕРС) індукції \(\mathbf{\varepsilon}_\text{i}.\) ЕРС індукції дорівнює швидкості зміни магнітного потоку \(\text{Ф},\) який пронизує поверхню, обмежену контуром: $$ \mathbf{\varepsilon}_\text{i}=-\frac{\Delta \text{Ф}}{\Delta t}. $$

Знак мінус відображає правило Ленца: індукційний струм, який виникає в замкненому провідному контурі, має такий напрямок, що створений цим струмом магнітний потік перешкоджає зміні магнітного потоку, який спричинив появу індукційного струму.

Потік магнітної індукції (магнітний потік) \(\text{Ф}\) ‒ це фізична величина, яка дорівнює добуткові магнітної індукції \(B\) на площу \(S\) поверхні та на косинус кута \(\mathbf{\alpha}\) між вектором магнітної індукції і нормаллю \(n\) до поверхні: $$ \text{Ф}=BS\cos\mathbf{\alpha}. $$

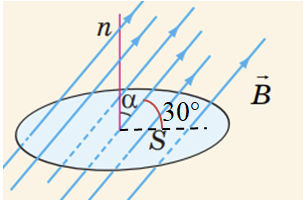
В умові кут між вектором магнітної індукції й горизонтом \(\mathbf{\varphi}=30^\circ .\) Тоді кут $$ \mathbf{\alpha}=90^\circ-\mathbf{\varphi}=90^\circ-30^\circ=60^\circ, $$ оскільки нормаль \(n\) ‒ це перпендикуляр до поверхні.

За умовою завдання магнітне поле, у якому перебуває контур (горизонтальне кільце), змінюється, тому маємо: $$ \mathbf{\varepsilon}_\text{i}=\frac{\Delta BS\cos\mathbf{\alpha}}{\Delta t}. $$

Тоді силу індукційного струму \(I_\text{i}\) в контурі можна визначити за формулою

Відповідь: 0,6.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Гармонічні коливання.

Завдання скеровано на перевірку знання і розуміння характеристик механічних коливань, уміння читати рівняння гармонічних коливань і брати з них потрібну інформацію.

Кількість \(N\) коливань за одиницю часу \(t\) ‒ це частота коливань \(\mathbf{\nu}:\) \begin{gather*} \mathbf{\nu}=\frac Nt,\ \text{звідки}\ N=\mathbf{\nu}t. \end{gather*}

Частоту \(\mathbf{\nu}\) можна визначити з рівняння гармонічних коливань. Коливання, під час яких координата \(x\) тіла, що коливається, змінюється із часом \(t\) за законом косинуса (або синуса), називають гармонічними коливаннями: \begin{gather*} x=A\cos(\mathbf{\omega}t+\mathbf{\varphi}_0), \end{gather*} де \(A\) ‒ амплітуда коливань, \(\mathbf{\omega}\) ‒ циклічна частота, \(\mathbf{\varphi}_0\) ‒ початкова фаза; $$ \mathbf{\omega}=\frac{2\mathbf{\pi}}{T}=2\mathbf{\pi}\mathbf{\nu}, $$ де \(T\) ‒ період коливань, звідки $$ \mathbf{\nu}=\frac{\mathbf{\omega}}{2\mathbf{\pi}}. $$

Циклічну частоту визначімо з рівняння в умові завдання ‒ це множник перед \(t:\) \begin{gather*} x=0,06\cos 4\mathbf{\pi}t,\\[7pt] \mathbf{\omega}=4\mathbf{\pi}. \end{gather*}

Отже,

Визначімо тепер кількість коливань за \(10\ \text{с:}\) $$ N=\mathbf{\nu}t=2\ \text{Гц}\cdot 10\ \text{с}=20. $$

Відповідь: 20.

Пояснення

ТЕМА: Коливання і хвилі. Оптика. Формула тонкої лінзи.

Завдання скеровано на перевірку знання і розуміння формули тонкої лінзи й побудови зображень у тонкій лінзі.

Оптичну силу \(D\) лінзи (об’єктива) ‒ фізичну величину, яка характеризує заломні властивості лінзи й обернена до її фокусної відстані \(F\) можна визначити за формулою: $$ D=\frac 1F. $$

Математична залежність між відстанню d від предмета до лінзи, відстанню f від зображення предмета до лінзи і фокусною відстанню F лінзи представлена формулою тонкої лінзи: \begin{gather*} \frac 1F=\frac 1d+\frac 1f. \end{gather*}

Розгляньмо схематичну побудову зображення \(A_1B_1\) дерева \(AB\) в збиральній лінзі об’єктива фотоапарата: дерево \(AB\) розташоване за подвійним фокусом об’єктива, тому зображення \(A_1B_1\) виходить дійсним, зменшеним, перевернутим.

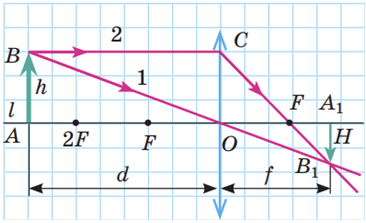
За умовою об᾽єктив фотоапарата дає зображення дерева, зменшене в \(600\) разів, тобто (див. рисунок) $$ \frac{A_1B_1}{AB}=\frac Hh=\frac{1}{600}. $$

Відношення лінійного розміру \(H\) зображення предмета до розміру \(h\) самого предмета називають лінійним збільшенням \(\text{Г}\) лінзи: $$ \text{Г}=\frac Hh=\frac fd $$ (це співвідношення можна отримати з подібних трикутників \(OAB\) і \(OA_1B_1).\)

Відстань \(d\) від дерева до лінзи дано в умові ‒ \(15\ \text{м.}\) А відстань \(f\) від зображення дерева до лінзи можна визначити із співвідношення

Тепер можна визначити оптичну силу об᾽єктива фотоапарата:

Відповідь треба округлити до цілого числа (до одиниць), отже, $$ D=40,0(6)\ \text{м}\approx 40\ \text{м}. $$

Відповідь: 40.

Пояснення

ТЕМА: Квантова фізика. Елементи теорії відносності. Світлові кванти. Рівняння Ейнштейна для фотоефекту.

Завдання скеровано на перевірку знання і розуміння рівняння Ейнштейна для фотоефекту.

Для описання фотоефекту скористаймося рівнянням Ейнштейна: $$ h\mathbf{\nu}=A_\text{вих}+E_{kmax}. $$

Унаслідок поглинання фотона металом енергія фотона $$ E_\text{ф}=h\mathbf{\nu}, $$ де \(h\) ‒ стала Планка, \(\mathbf{\nu}\) ‒ частота випромінювання може бути повністю передана електрону й витратитися на здійснення роботи виходу \(A_\text{вих}\) й надання електрону кінетичної енергії \(E_{kmax}.\)

Запишімо рівняння до підвищення частоти за умови, що \(E_{k1max}=\frac 12A_\text{вих}:\)

Після підвищення частоти випромінювання максимальна кінетична енергія фотоелектронів збільшилася в \(7\) разів:

Визначімо, у скільки разів збільшилася частота випромінювання:

Отже, частота випромінювання збільшилася в \(3\) рази.

Відповідь: 3.