ЗНО онлайн 2017 року з фізики – пробний тест

ТЕМА: Механіка. Основи кінематики. Графіки залежності кінематичних величин від часу за рівномірного й рівноприскореного рухів.

Завдання скеровано на перевірку вміння інтерпретувати графіки, переходити від однієї до другої залежності величин.

Розгляньмо щосекунди наведений в умові завдання графік залежності координати $x$ тіла від часу $t.$

Ділянка графіка від початку відліку часу до першої секунди: це графік прямолінійного рівноприскореного руху. Адже графіком є частина параболи (вітки вниз), початкова координата $x_0=0,$ кінцева координата $x=-2\text{м}.$ На графіку точка початку відліку є вершиною параболи ‒ точкою розвороту. Тож до початку відліку часу тіло рухалося вздовж осі $Ox.$ Із початком відліку часу тіло розвернулося (початкова швидкість $v_0=0)$ і протягом $1\text{с}$ прискорювало свій рух, рухаючись у протилежному до осі $Ox$ напрямку. Запишімо рівняння координати й визначмо прискорення руху тіла: $$x=x_0+v_{0}t+\frac{a{t}^2}{2}.$$

Оскільки $x_0=0$ і $v_0=0,$ то $x=\frac{a{t}^2}{2}.$ Звідси $$a=\frac{2x}{t^2}=\frac{2\cdot (-2)\text{м}}{1{\text{с}}^2}=-4{\text{м/с}}^2.$$

Знаючи прискорення руху тіла, знайдімо кінцеву швидкість руху тіла наприкінці першої секунди: $$v=v_0+at=-4{\text{м/с}}^2\cdot 1\text{с}=-4\text{м/с}.$$

Знак «мінус» указує на те, що тіло рухалося в напрямку, протилежному до напрямку осі $Ox.$

Значення початкової і кінцевої швидкості руху тіла за першу секунду відповідають лише варіанту відповіді A. Щоб упевнитися в правильності варіанта відповіді A, проаналізуймо рух тіла в наступні секунди.

Від 1-ї до 2-ї секунди: ділянка графіка залежності координати тіла від часу прямолінійна, отже, рух рівномірний, швидкість стала.

Від 2-ї до 3-ї секунди: це графік прямолінійного рівноприскореного руху, оскільки графіком є частина параболи (вітки вгору), тіло гальмує, швидкість руху тіла зменшується до нуля, тіло зупиняється.

Від 3-ї до 4-ї секунди: координата тіла не змінюється, отже, швидкість тіла дорівнює нулю ‒ тіло не рухається.

Відповідь: A.

ТЕМА: Механіка. Основи кінематики. Прямолінійний рівномірний і рівноприскорений рухи.

Завдання скеровано на перевірку розуміння закономірностей прямолінійного рівномірного і рівноприскореного рухів.

Розгляньмо рух парашутиста і рух монети.

За умовою завдання парашутист опускався зі сталою швидкістю $v=5\text{м/с,}$ оскільки дія сили тяжіння була скомпенсована дією сили опору повітря. Отже, відстань $h=100\text{м}$ він подолав за $20\text{с:}$ $$t_{\text{пар}}=\frac{h}{v}=\frac{100\text{м}}{5\text{м/с}}=20\text{с}.$$

Монета пройшла той самий шлях $h=100\text{м},$ але рухалася рівноприскорено. Власна початкова швидкість монети, що просто випала з кишені, дорівнювала нулю. Але до того монета була в кишені парашутиста, який рухався зі швидкістю $5\text{м/с},$ тому початкова швидкість монети $v_0$ становила $5\text{м/с}.$ За умовою впливом опору повітря на монету нехтуємо, тож можемо визначити час її падіння з кінематичного рівняння: $$h=v_{0}t+\frac{g{t}^2}{2},$$ де $g$ ‒ прискорення вільного падіння (усі векторні величини записано в проєкціях на вісь $Oy,$ напрямлену вертикально вниз, так само, як і вектор прискорення вільного падіння).

Підставмо значення величин у рівняння: $$h=v_{0}t+\frac{g{t}^2}{2}\Rightarrow 100=5t+\frac{10t^2}{2}.$$

Поділімо ліву і праву частину рівняння на $5$ і дістанемо зведене квадратне рівняння: $$t^2+t-20=0.$$

За теоремою Вієта визначмо корені рівняння: $$t_1=-5,t_2=4.$$

Час не може бути від’ємним, тому умову задовольняє корінь $t_2=4\text{с},$ тобто монета впала за $4\text{с},$ а парашутист, відповідно, приземлився на $16\text{с}$ пізніше: $$\mathrm{\Delta }t=t_{\text{пар}}-t_2=20\text{с}-4\text{с}=16\text{с}.$$

Відповідь: Г.

ТЕМА: Механіка. Закони збереження в механіці. Імпульс тіла. Кінетична енергія.

Завдання скеровано на перевірку знання формул для визначення імпульсу й кінетичної енергії тіла.

Імпульс тіла $\overrightarrow{p}$ – це векторна фізична величина, яка дорівнює добутку маси $m$ тіла на швидкість $\overrightarrow{v}$ його руху: $$\overrightarrow{p}=m\overrightarrow{v}.$$

Обчислімо значення імпульсу автомобіля: $$p=1000\text{кг}\cdot 10\text{м/с}={10}^4\text{кг}\cdot \text{м/с}.$$

Кінетична енергія $E_k$ ‒ це фізична величина, якою характеризують механічний стан рухомого тіла. Кінетична енергія дорівнює половині добутку маси $m$ тіла на квадрат швидкості $v$ його руху: $$\begin{array}{c}{E}_k=\frac{m{v}^2}{2}.\end{array}$$

Обчислімо значення кінетичної енергії автомобіля: $$E_k=\frac{1000\text{кг}\cdot (10\text{м/с}{)}^2}{2}=5\cdot {10}^4\text{Дж}.$$

Відповідь: Б.

ТЕМА: Механіка. Елементи механіки рідин і газів. Умови плавання тіл.

Завдання скеровано на перевірку розуміння умов плавання тіл.

Розгляньмо два варіанти плавання бруска: у гасі й у воді. Силу тяжіння $F_{\text{тяж}},$ що діє на брусок, урівноважує сила Архімеда $F_{А}$ (за модулем).

Варіант перший – брусок плаває у гасі: $$\begin{array}{c}{F}_{\text{тяж}}=F_{\text{АГ}},\\ mg={\rho }_{\text{Г}}g{V}_{\text{Гзан}},\end{array}$$ де $m$ ‒ маса бруска, $g$ ‒ прискорення вільного падіння, ${\rho }_{\text{Г}}$ ‒ густина гасу, $V_{\text{Гзан}}$ ‒ об’єм зануреної в гас частини бруска.

Після перетворень дістанемо вираз: $$m={\rho }_{\text{Г}}S{h}_{\text{Г}},$$ де $S$ ‒ площа основи (нижньої грані) бруска, $h_{\text{Г}}$ ‒ глибина занурення бруска в гас.

Варіант другий – брусок плаває у воді: $$\begin{array}{c}{F}_{\text{тяж}}=F_{\text{АВ}},\\ mg={\rho }_{\text{В}}g{V}_{\text{Взан}},\end{array}$$ де ${\rho }_{\text{В}}$ ‒ густина води, $V_{\text{Взан}}$ ‒ об’єм зануреної у воду частини бруска.

Після перетворень дістанемо вираз: $$\begin{array}{c}m={\rho }_{\text{В}}S{h}_{\text{В}},\end{array}$$ де $h_{\text{В}}$ – глибина занурення бруска у воду.

Прирівняймо вирази для визначення маси $m$ бруска: $$\begin{array}{c}{\rho }_{\text{В}}S{h}_{\text{В}}={\rho }_{\text{Г}}S{h}_{\text{Г}}.\end{array}$$

Визначмо й обчислімо шукану величину $h_{\text{В}}$ ‒ глибину занурення бруска у воду: $$\begin{array}{c}{h}_{\text{В}}=\frac{{\rho }_{\text{Г}}{h}_{\text{Г}}}{{\rho }_{\text{В}}},\\ h_{\text{В}}=\frac{800{\text{кг/м}}^3\cdot 60\text{мм}}{1000{\text{кг/м}}^3}=48\text{мм}.\end{array}$$

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Кількість речовини.

Завдання скеровано на перевірку розуміння основних понять молекулярно-кінетичної теорії (кількість речовини, стала Авогадро, а також на перевірку вміння обчислювати кількість молекул газу).

Кількість структурних частинок у макроскопічних тілах величезна. Структурними частинками можуть бути атоми, молекули, йони, електрони або інші частинки чи певні групи частинок.

Для зручності обчислень використовують одиницю кількості речовини – моль. Будь-яка речовина кількістю $1\text{моль}$ містить $6\cdot {10}^{23}$ (число Авогадро) структурних частинок.

Стала Авогадро $N_A\approx 6\cdot {10}^{23}{\text{моль}}^{‒1}$ – кількість структурних частинок $N$ у речовині кількістю $1\text{моль}.$ Кількість речовини позначають буквою $\nu$ грецької абетки й обчислюють за формулою: $$\nu =\frac{N}{N_A}.$$

Відповідно

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Застосування першого закону термодинаміки до ізопроцесів. Адіабатний процес.

Завдання скеровано на перевірку розуміння змін макроскопічних фізичних параметрів газу під час адіабатного процесу.

Адіабатний процес відбувається без теплообміну з навколишнім середовищем. За адіабатного процесу кількість теплоти, передана системі, дорівнює нулю. Тож умову завдання не задовольняють варіанти відповіді, у яких зазначено, що газ отримує тепло.

Перший закон термодинаміки для адіабатного процесу запишімо так: $$\begin{array}{c}\mathrm{\Delta }U+A=0,\\ A=-\mathrm{\Delta }U.\end{array}$$

Це означає, що під час адіабатного розширення газ виконує додатну роботу $A$ за рахунок зменшення внутрішньої енергії $\mathrm{\Delta }U,$ одночасно температура й тиск газу зменшуються, а об’єм збільшується.

Тобто за адіабатного розширення газ не отримує тепла, а його внутрішня енергія зменшується.

Відповідь: Б.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Робота в термодинаміці.

Завдання скеровано на перевірку вміння обчислювати термодинамічну роботу.

За ізобарного процесу передана газу кількість теплоти йде як на збільшення внутрішньої енергії газу, так і на виконання механічної роботи. За умовою азот розріджений, тобто відстань між молекулами набагато більша за розміри самих молекул, тому ці молекули можна вважати матеріальними точками, а їхньою взаємодією, окрім моментів зіткнення, можна знехтувати. Тобто азот можна вважати ідеальним газом, а роботу газу $A$ визначити за формулою $$A=p\mathrm{\Delta }V,$$ де $p$ ‒ тиск газу, $\mathrm{\Delta }V$ ‒ зміна об’єму газу.

Для визначення виконаної азотом роботи скористаймося рівнянням стану ідеального газу (рівнянням Менделєєва – Клапейрона): $$\begin{array}{c}p\mathrm{\Delta }V=\frac{m}{M}R\mathrm{\Delta }T,\\ A=\frac{m}{M}R\mathrm{\Delta }T,\end{array}$$ де $m$ ‒ маса газу, $M$ ‒ молярна маса газу, $R$ ‒ універсальна газова стала, $\mathrm{\Delta }T$ ‒ зміна температури газу.

Обчислімо шукану величину:

Відповідь: В.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл. Рівняння теплового балансу для найпростіших теплових процесів.

Завдання скеровано на перевірку розуміння теплових процесів і вміння складати рівняння теплового балансу.

Під час згоряння паливо віддаватиме тепло, яке потрібне, щоб розтопити лід.

В ізольованій системі тіл, у якій внутрішня енергія тіл змінюється лише внаслідок теплопередачі, загальна кількість теплоти, віддана одними тілами системи, дорівнює загальній кількості теплоти, одержаної іншими тілами цієї системи.

Загальний вигляд рівняння теплового балансу такий:

Запишімо рівняння теплового балансу відповідно до умови завдання: $$\begin{array}{c}{Q}_{\text{згоряння}}^{-}=Q_{\text{плавлення}}^{+};\\ q{m}_{\text{п}}=\lambda m_{\text{л}},\end{array}$$ де $q$ ‒ питома теплота згоряння палива, $m_{\text{п}}$ ‒ маса палива, $\lambda$ ‒ питома теплота плавлення льоду, $m_{\text{л}}$ ‒ маса льоду.

В умові йдеться про лід за температури його плавлення – $0{}^{\circ }\mathrm{C}.$ Тож уся отримана від згоряння палива кількість теплоти буде витрачена на зміну агрегатного стану льоду з твердого на рідкий.

Обчислімо необхідну масу палива:

Відповідь: Б.

ТЕМА: Електродинаміка. Основи електростатики. Закон збереження електричного заряду. Напруженість електричного поля.

Завдання скеровано на перевірку розуміння закону збереження електричного заряду й силової характеристики електричного поля ‒ напруженості.

Модуль напруженості $\overrightarrow{E}$ електричного поля, створеного точковим зарядом $Q$ на відстані $r$ від цього заряду, обчислюють за формулою $$E=k\frac{|Q|}{r^2},$$ де $k$ ‒ коефіцієнт пропорційності.

Запишімо формулу для визначення модуля напруженості електричного поля дощової краплі із зарядом $q_1=+1,5\text{нКл}$ на відстані $10\text{см}$ від неї: $$E_1=k\frac{|q_1|}{r^2}=\frac{1,5k}{r_2}.$$

Визначмо заряд $Q_2$ краплі, якого вона набуде після злиття з краплею, заряд $q_2$ якої становив $-0,5\text{нКл.}$

За законом збереження електричного заряду повний заряд електрично замкненої системи тіл залишається незмінним під час усіх узаємодій, які відбуваються в цій системі: $$q_1+q_2+\cdots +q_n=const,$$ де $q_1,q_2,...,q_n$ ‒ заряди тіл, що створюють електрично замкнену систему ($n$ ‒ кількість таких тіл).

Тобто

Запишімо формулу для визначення модуля напруженості електричного поля на тій самій відстані $10\text{см}$ після того, як краплі злилися: $$E_2=k\frac{|Q_2|}{r^2}=\frac{k}{r^2}.$$

Визначмо відношення модулів напруженості: $$\frac{E_2}{E_1}=\frac{k{r}^2}{1,5k{r}^2}=\frac{1}{1,5}.$$

Отже, напруженість $E_2$ зменшиться в $1,5$ раза.

Відповідь: Г.

ТЕМА: Електродинаміка. Закони постійного струму. Умови існування електричного струму.

Завдання скеровано на перевірку розуміння існування і протікання електричного струму в колі.

Для виникнення та існування електричного струму необхідні дві умови:

1) вільні заряджені частинки ‒ носії струму;

2) електричне поле, дія якого створює і підтримує напрямлений рух вільних заряджених частинок.

За створення електричного поля «відповідають» джерела струму ‒ пристрої, які перетворюють різні види енергії на електричну енергію. У джерелах струму виконується робота з розділення різнойменних електричних зарядів, у результаті чого один полюс джерела набуває позитивного заряду, а другий ‒ негативного; у такий спосіб створюється електричне поле.

За напрямок струму в електричному колі прийнято напрямок, у якому рухалися б цим колом позитивно заряджені частинки, тобто напрямок від позитивного полюса джерела струму до негативного. В умовному позначенні гальванічного елемента довга риска позначає позитивний, а коротка ‒ негативний полюс джерела.

На схемі ж в умові завдання гальванічні елементи або акумулятори підключені між собою однойменними полюсами, позитивними, тому струму за такого підключення в колі не буде.

Щоб амперметр показав наявність струму в колі, треба підключити додатковий опір паралельно до одного із джерел струму, щоб заряджені частинки змогли в обхід одного джерела дістатися від позитивного полюса до негативного полюса другого джерела струму.

Із запропонованих пар точок умову завдання задовольняє пара 2 та 3.

Відповідь: Б.

ТЕМА: Електродинаміка. Закони постійного струму. Закон Джоуля – Ленца.

Завдання скеровано на перевірку вміння застосувати закон Джоуля – Ленца.

За законом Джоуля – Ленца визначають кількість теплоти $Q,$ яка виділяється в провіднику зі струмом. Вона прямо пропорційна квадрату сили струму $I,$ опору $R$ провідника та часу $t$ проходження струму: $$Q=I^{2}Rt.$$

Запишімо закон Джоуля – Ленца для зовнішнього і для повного кіл:

Обчислімо частку кількості теплоти, що виділилася на резисторі, від загальної кількості теплоти, що виділилася в електричному колі: $$\frac{Q_{\text{зовн}}}{Q_{\text{повн}}}=\frac{I^{2}4rt}{I^{2}5rt}=\frac{4}{5}=0,8\text{або}80\text{\%}.$$

Відповідь: B.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Сила Лоренца.

Завдання скеровано на перевірку розуміння руху зарядженої частинки під дією магнітного поля.

Силу, з якою магнітне поле діє на рухому заряджену частинку, називають силою Лоренца ${\overrightarrow{F}}_{\text{Л}}.$ Сила Лоренца завжди перпендикулярна до швидкості руху частинки, тому вона не виконує роботу і не змінює кінетичну енергію частинки. Тобто під дією сили Лоренца заряджена частинка рухається рівномірно. Траєкторія руху частинки залежить від величини кута, під яким частинка влетіла в магнітне поле. Також на траєкторію руху частинки впливає однорідність магнітного поля.

За умовою магнітне поле є однорідним. Частинка влітає в магнітне поле під деяким кутом $\alpha$ до ліній магнітної індукції $\overrightarrow{B},$ а саме під кутом ${30}^{\circ }.$

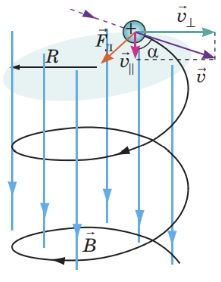
У цьому разі швидкість $\overrightarrow{v}$ руху частинки можна розкласти на два складники. Перший – швидкість ${\overrightarrow{v}}_{||}$ паралельна лініям магнітної індукції поля, вона забезпечує рух частинки вздовж цих ліній. Другий складник – перпендикулярна до ліній магнітної індукції поля швидкість ${\overrightarrow{v}}_{\perp },$ поле змушує частинку рухатися по колу. Тому траєкторія руху частинки – гвинтова лінія.

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Механічні коливання і хвилі. Звукові хвилі.

Завдання скеровано на перевірку вміння визначати довжину хвилі через інші її характеристики.

Довжину хвилі $\lambda$ можна визначити за формулою $$\lambda =\frac{v}{\nu },$$ де $v$ ‒ швидкість звуку в повітрі, $\nu$ ‒ частота звукових хвиль.

Оскільки в умові дано діапазон частот звукових хвиль у повітрі, можна обчислити діапазон відповідних їм довжин хвиль:

Тобто діапазон довжини хвиль такий: $$17\text{мм}<\lambda <17\text{м}.$$

Із наведених у варіантах відповіді у цей діапазон потрапляє лише хвиля довжиною $3,4\text{м.}$

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на перевірку розуміння перетворення енергії в коливальному контурі.

Коливальний контур – фізичний пристрій, який є коливальною системою, тобто в ньому можуть виникати вільні електромагнітні коливання. Коливальний контур можна створити, послідовно з’єднавши конденсатор і котушку індуктивності.

Якщо після зарядження конденсатор замкнути на котушку індуктивності, то під дією електричного поля конденсатора вільні заряджені частинки в контурі почнуть рухатися напрямлено. У контурі виникне електричний струм, а конденсатор почне розряджатися.

Заряд на обкладках конденсатора поступово зменшується, а сила струму в котушці зростає, тому магнітна індукція створеного струмом магнітного поля зростає теж. Отже, протягом першої чверті періоду енергія електричного поля $W_{\text{ел}}$ конденсатора перетворюється на енергію магнітного поля котушки.

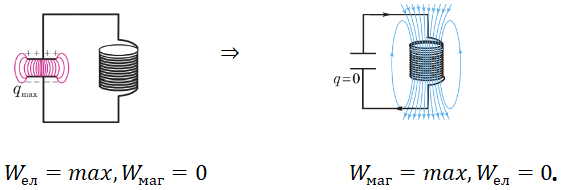
Конденсатор перезаряджається – заряд на його обкладках змінюється на протилежний. Отже, протягом другої чверті періоду енергія магнітного поля котушки перетворюється на енергію електричного поля конденсатора.

Наступну половину періоду характер зміни електричного заряду на обкладках конденсатора й характер зміни сили струму в контурі будуть такими самими, тільки у зворотному напрямку. Коли заряд на обкладках конденсатора досягне максимального значення, то завершиться одне повне коливання.

Час одного повного коливання ‒ це період. Період власних електромагнітних коливань у коливальному контурі визначають за формулою Томсона: $$T=2\pi \sqrt{LC},$$ де $L$ ‒ індуктивність котушки, $C$ ‒ електроємність конденсатора.

Тоді можна визначити чверть періоду: $$\frac{1}{4}T=\frac{2\pi \sqrt{LC}}{4}=\frac{\pi }{2}\sqrt{LC}.$$

Відповідь: Б.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Електромагнітні хвилі та швидкість поширення їх.

Завдання скеровано на перевірку вміння визначати довжину електромагнітної хвилі через характеристики коливального контуру.

Довжину електромагнітної хвилі $\lambda$ можна визначити за формулою $$\lambda =cT,$$ де $c$ ‒ швидкість світла у вакуумі, $T$ ‒ період поширення електромагнітної хвилі.

Світло є електромагнітною хвилею, тож швидкість поширення електромагнітної хвилі також дорівнює $3\cdot {10}^8\text{м/с.}$

Період поширення електромагнітної хвилі визначають за формулою Томсона: $$T=2\pi \sqrt{LC},$$ де $L$ ‒ індуктивність котушки, $C$ ‒ електроємність конденсатора.

Обчислімо довжину електромагнітної хвилі:

Відповідь: B.

ТЕМА: Коливання і хвилі. Оптика. Побудова зображень, які дає тонка лінза.

Завдання скеровано на перевірку вміння будувати зображення в тонкій лінзі.

На рисунку зображено розсіювальну лінзу (зверніть увагу на позначення її кінців). Через оптичний центр лінзи точку $O$ горизонтально проходить головна оптична вісь. За правилами побудови промінь, що падає на лінзу паралельно головній оптичній осі, після проходження крізь лінзу розсіюється, а його уявне продовження повинно обов’язково пройти через фокус $F$ лінзи з того ж боку, із якого падає промінь (див. рисунок):

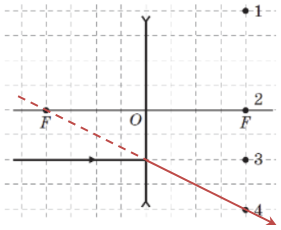
Відповідь: Г.

ТЕМА: Квантова фізика. Елементи теорії відносності. Взаємозв’язок маси й енергії.

Завдання скеровано на перевірку вміння визначати потужність випромінювання.

Потужність випромінювання $P$ – це повна енергія $E,$ яку переносить світло за одиницю часу $t:$ $$P=\frac{E}{t}.$$

Енергію світлових променів, про які йдеться, визначають за формулою $E=m{c}^2.$ Запишімо формулу для визначення маси:

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності. Рівняння Ейнштейна для фотоефекту.

Завдання скеровано на перевірку розуміння фотоефекту й застосування щодо нього рівняння Ейнштейна.

Запишімо рівняння Ейнштейна для зовнішнього фотоефекту: $$E_{\text{Ф}}=A_{\text{вих}}+E_{kmax}.$$

Унаслідок поглинання фотона металом енергія фотона $E_{\text{Ф}}$ може бути повністю передана електрону й витрачена на здійснення роботи виходу $A_{\text{вих}}$ та надання електрону кінетичної енергії $E_{kmax}.$

Обчислімо роботу виходу електрона з металу: $$\begin{array}{c}{A}_{\text{вих}}=E_{\text{Ф}}-E_{kmax},\\ A_{\text{вих}}=4,5\text{еВ}-1,5\text{еВ}=3\text{еВ}.\end{array}$$

Відповідь: Б.

ТЕМА: Квантова фізика. Елементи теорії відносності.

Завдання скеровано на перевірку знання і розуміння основних фундаментальних дослідів квантової і ядерної фізики.

Золоту фольгу бомбардували альфа-частинками для дослідження внутрішньої структури атома і доведення існування ядра.

За пропускання білого світла крізь газ спостерігають темні лінії на тлі неперервного спектра. Сукупність цих ліній називають лінійчастим спектром поглинання.

Опромінювання металів світлом дало змогу відкрити й дослідити фотоефект.

Засвітивши закриту фотопластинку сіллю Урану, з’ясували, що ця сіль дійсно висилає випромінювання з великою проникною здатністю ‒ радіоактивне.

Відповідь: Г.

ТЕМА: Механіка. Коливання і хвилі.

Завдання скеровано на перевірку розуміння фізичних процесів механіки і знання формул, якими описують ці процеси.

Усім тілам у Всесвіті властива гравітаційна взаємодія, виявом якої є їхнє взаємне притягання. Відповідно до закону всесвітнього тяжіння планети Венера й Марс притягуються одна до одної із силою $F,$ яка прямо пропорційна добутку їхніх мас $m_1$ і $m_2$ й обернено пропорційна квадрату відстані $r$ між ними: $$F=G\frac{m_1\cdot m_2}{r^2},$$ де $G$ ‒ гравітаційна стала (коефіцієнт пропорційності, однаковий для всіх тіл у Всесвіті).

Якщо розтягнуту гумову нитку відпустити, то, скорочуючись, вона виконає роботу. Робота сили пружності визначена лише початковим і кінцевим станами гумової нитки, тобто сила пружності ‒ консервативна або потенціальна сила. Величину $$E=\frac{k{x}^2}{2}$$ називають потенціальною енергією $E$ пружно деформованого тіла, де $x$ ‒ видовження пружного тіла, $k$ ‒ жорсткість.

Між дотичними поверхнями стрічки транспортера й цеглини діє сила тертя спокою, яка перешкоджає виникненню відносного руху їх. Сила тертя спокою завжди дорівнює за модулем і протилежна за напрямком рівнодійній зовнішніх сил, які намагаються зрушити тіло з місця. Після того як рівнодійна зовнішніх сил зрівняється з максимальною силою тертя спокою, тіло починає ковзання, тобто починає діяти сила тертя ковзання. Отже, максимальна сила тертя спокою дорівнює силі тертя ковзання: $$F_{\max }=\mu N,$$ де $F_{\max }$ ‒ максимальна сила тертя спокою, $\mu$ ‒ коефіцієнт тертя, $N$ ‒ сила нормальної реакції опори.

Маленька сталева кулька коливається на довгій нерозтяжній нитці ‒ це модель нитяного (математичного) маятника. Період коливань $T$ нитяного маятника обчислюють за формулою $$T=2\pi \sqrt{\frac{l}{g}},$$ де $l$ ‒ довжина маятника; $g$ ‒ прискорення вільного падіння.

Відповідь: 1А, 2Г, 3Д, 4Б.

ТЕМА: Молекулярна фізика і термодинаміка. Властивості газів, рідин і твердих тіл.

Завдання скеровано на перевірку знання і розуміння станів речовини та їхніх властивостей.

Рідина ‒ один із фазових (агрегатних) станів речовини. Молекули рідини в цілому розташовані хаотично, однак у розташуванні найближчих молекул зберігається певний (ближній) порядок. Під дією зовнішніх сил рідина набуває форми посудини, у якій міститься, одночасно об’єм рідини залишається незмінним.

Ідеальний газ ‒ це фізична модель газу, молекули якого вважають матеріальними точками, що не взаємодіють одна з одною на відстані та пружно взаємодіють у моменти зіткнення. Стан ідеального газу описують рівнянням Менделєєва ‒ Клапейрона: $$pV=\frac{m}{M}RT,$$ де $p$ ‒ тиск газу, $V$ ‒ об’єм газу, $m$ ‒ маса газу, $M$ ‒ молярна маса газу, $R$ ‒ універсальна газова стала, $T$ ‒ температура газу. За умовою $T=const,$ отже, у правій частині рівняння всі величини сталі. Залишімо в лівій частині рівняння лише тиск $p:$ $$p=\frac{mRT}{MV}\Rightarrow p\sim \frac{1}{V}.$$

Після перетворення рівняння можна дійти висновку, що тиск газу обернено пропорційний об’єму.

Монокристал ‒ тверде тіло, частинки якого утворюють єдину кристалічну ґратку. Упорядковане розташування частинок у монокристалі є причиною того, що монокристали мають плоскі грані й незмінні кути між гранями. Фізичні властивості монокристалів залежать від вибраного в них напрямку.

Залежність фізичних властивостей кристала від вибраного в ньому напрямку називають анізотропією (від грец. anisos ‒ нерівний і tropos ‒ напрямок, властивість). Тобто монокристали є анізотропними.

Насиченою парою називають пару, яка перебуває в динамічній рівновазі зі своєю рідиною, тобто кількість молекул, які повертаються в рідину, дорівнюватиме кількості молекул, які за той самий час залишають рідину. Концентрація молекул насиченої пари ‒ найбільша можлива концентрація молекул пари за певної температури. Тиск, створюваний насиченою парою, є найбільшим тиском, який може створити пара рідини за певної температури.

Якщо зменшити об’єм, який займає насичена пара, то на короткий проміжок часу концентрація молекул пари збільшиться, динамічна рівновага порушиться і кількість молекул, що надходять у рідину, перевищить кількість молекул, які залишають її поверхню. Конденсація буде більшою за випаровування доти, доки концентрація молекул пари не знизиться до концентрації молекул насиченої пари, а тиск не дорівнюватиме тиску насиченої пари.

Зі збільшенням об’єму насиченої пари переважатиме випаровування, унаслідок чого знову встановиться початковий тиск. Отже, на відміну від ідеального газу, тиск насиченої пари не залежить від її об’єму.

Відповідь: 1Д, 2Г, 3В, 4Б.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція.

Завдання скеровано на перевірку знання формул, за якими визначають фізичні величини.

Електрорушійну силу індукції, що виникає в провіднику внаслідок зміни його власного магнітного поля, називають ектрорушійною силою (ЕРС) самоіндукції ${\epsilon }_{is}.$

ЕРС самоіндукції ${\epsilon }_{is}$ прямо пропорційна швидкості зміни сили струму $I$ в провіднику за час $t:$ $${\epsilon }_{is}=-L\frac{\mathrm{\Delta }I}{\mathrm{\Delta }t}.$$

Коефіцієнт пропорційності $L$ називають індуктивністю провідника.

Потік магнітної індукції (магнітний потік) $\mathbf{Ф}$ ‒ це фізична величина, яка дорівнює добуткові магнітної індукції $B,$ площі $S$ поверхні й косинуса кута $\alpha$ між вектором магнітної індукції та нормаллю до поверхні: $$\mathbf{Ф}=BS\cos \alpha .$$

Силу, із якою магнітне поле діє на рухому заряджену частинку, називають силою Лоренца: $$F_{\text{Л}}=Bv|q|\sin \alpha ,$$ де $F_{\text{Л}}$ ‒ модуль сили Лоренца, $q$ ‒ заряд частинки, $B$ ‒ магнітна індукція поля, $v$ ‒ швидкість руху частинки, $\alpha$ ‒ кут між напрямками руху частинки й магнітної індукції магнітного поля.

Сила Ампера $F_{\text{А}}$ ‒ це сила, із якою магнітне поле діє на провідник зі струмом. Якщо провідник прямолінійний, а магнітне поле, у якому він перебуває, однорідне, то модуль сили Ампера визначають за формулою $$F_{\text{А}}=BIl\sin \alpha ,$$ де $B$ ‒ магнітна індукція поля, у якому перебуває провідник; $I$ ‒ сила струму в провіднику; $l$ ‒ довжина активної частини провідника; $\alpha$ ‒ кут між вектором магнітної індукції та напрямком струму.

Відповідь: 1Г, 2А, 3Д, 4В.

ТЕМА: Коливання і хвилі. Оптика.

Завдання скеровано на перевірку розуміння і застосування механічних й електромагнітних явищ.

Виникнення вихрового електричного поля або електричної поляризації провідника під час зміни магнітного поля або під час руху провідника в магнітному полі називають електромагнітною індукцією. Важливим наслідком електромагнітної індукції для генерування електричного струму є виникнення електрорушійної сили в провідному контурі, магнітний потік через який змінюється.

Період $T$ коливань математичного маятника не залежить від маси маятника, а лише від довжини $l$ нитки та прискорення $g$ вільного падіння в тому місці, де розташований цей маятник: $$T=2\pi =\sqrt{\frac{l}{g}}.$$

Тому, вимірявши довжину нитки й період коливань маятника, можна визначити прискорення вільного падіння в певній місцевості.

У радіолокації використовують ультракороткі електромагнітні хвилі частотою від $100$ до $1000\text{МГц}.$ У радіолокаційному пристрої радарі є передавальна та приймальна частини. Імпульс гостронапрямленої радіохвилі від потужного радіопередавача пересилають за допомогою параболічної антени. Досягнувши цілі, радіохвиля відбивається від неї та повертається назад. Відбиту хвилю, уловлену тією самою антеною, реєструє приймач.

Просвітлення оптики ‒ збільшення прозорості деталей оптичних систем (лінз, оптичних призм) нанесенням на їхні поверхні тонкого шару діелектрика (або кількох шарів) із показником заломлення, меншим, ніж у матеріалу оптичної деталі. Просвітлення оптики ‒ результат інтерференції світла, яке відбивається від передньої та задньої границь цього шару (просвітлювальної плівки). За належного добору речовини й товщини плівки для певного кута падіння відбиті світлові хвилі певної довжини можуть повністю погасити одна одну.

Відповідь: 1В, 2Б, 3Д, 4Г.

ТЕМА: Механіка. Елементи механіки рідин і газів. Архімедова сила.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з визначення маси тіла й виштовхувальної сили.

1. На рисунку 1 зображено тіло в повітрі, підвішене до динамометра. Динамометр показує значення ваги тіла в повітрі $P_{\text{повітря}}$ ‒ сили, із якою тіло діє на опору чи підвіс, у цій ситуації ‒ на пружину динамометра. Вага виникає внаслідок дії сили тяжіння. У повітрі вага тіла у спокої або прямолінійному рівномірному русі збігається за напрямком із силою тяжіння і дорівнює їй за значенням: $$P_{\text{повітря}}=F_{\text{тяж}}=30\text{Н}.$$

З формули для визначення сили тяжіння визначмо масу $m$ тіла: $$F_{\text{тяж}}=mg,$$ де $g$ ‒ прискорення вільного падіння.

Відповідно $$m=\frac{F_{\text{тяж}}}{g}=\frac{30\text{Н}}{10{\text{м/с}}^2}=3\text{кг}.$$

Відповідь: 3.

2. На рисунку 2 динамометр показує вагу тіла в рідині: $$P_{\text{рідина}}=20\text{Н}.$$

На тіло, занурене в рідину, діє виштовхувальна сила (сила Архімеда). У цій ситуації виштовхувальна сила дорівнюватиме різниці ваги тіла в повітрі й ваги тіла в рідині: $$\begin{array}{c}{F}_{\text{А}}=P_{\text{повітря}}-P_{\text{рідина}}=30\text{Н}-20\text{Н}=10\text{Н}.\end{array}$$

Відповідь: 10.

Відповідь: 1. 3. 2. 10.

ТЕМА: Електродинаміка. Магнітне поле, електромагнітна індукція. Магнітний потік. Закон електромагнітної індукції.

Завдання скеровано на перевірку вміння розв’язувати розрахункові задачі з визначення магнітного потоку й електрорушійної сили індукції.

1. Зміна потоку магнітної індукції (магнітного потоку) $\text{Φ}$ дорівнює добутку зміни магнітної індукції $B,$ площі $S$ поверхні й косинуса кута $\alpha$ між вектором магнітної індукції і нормаллю $n$ до поверхні, обмеженої контуром, тобто до площини, яку обмежує квадратна рамка: $$\mathrm{\Delta }\text{Φ}=\mathrm{\Delta }BS\cos \alpha .$$

За умовою вектор магнітної індукції перпендикулярний до площини рамки $\overrightarrow{B}\perp S,$ тож кут $\alpha$ між вектором магнітної індукції та нормаллю (перпендикуляром) до площини рамки дорівнює $0^{\circ }(\overrightarrow{B}||n),\cos \alpha =\cos 0^{\circ }=1.$

Обчислімо зміну магнітного потоку:

Відповідь: 0,1.

2. За законом електромагнітної індукції електрорушійна сила індукції ${\epsilon }_i$ дорівнює швидкості зміни магнітного потоку $\mathrm{\Delta }\text{Φ},$ який пронизує поверхню, обмежену контуром $(\mathrm{\Delta }t‒\text{проміжок часу}):$ $${\epsilon }_i=|-\frac{\mathrm{\Delta }\text{Φ}}{\mathrm{\Delta }t}|.$$

(Знак «мінус» відображає правило Ленца для визначення напрямку індукційного струму.)

Обчислімо ЕРС індукції: $${\epsilon }_i=\frac{0,1\cdot {10}^{-3}\text{Вб}}{2\cdot {10}^{-3}\text{с}}=0,05\text{В}.$$

Відповідь: $0,05.$

Відповідь: 1. 0,1. 2. 0,05.

ТЕМА: Механіка. Основи динаміки. Сила тертя.

Завдання скеровано на перевірку вміння визначати сили тертя і рівнодійну сил, прикладених до тіл.

Щоб натягнути нитку, якою зв’язано бруски, треба зрушити з місця другий брусок, подолати максимальну силу тертя спокою, протилежно напрямлену до прикладеної горизонтальної сили $\overrightarrow{F}.$ Обчислімо максимальну силу тертя спокою, яка діє на другий брусок:

Обчислімо силу натягу нитки $T:$ $$\begin{array}{c}T=F-F_{2\max \text{тер. спокою}}=8\text{Н}-6\text{Н}=2\text{Н}.\end{array}$$

Перевірімо, чи рухатиметься за таких умов перший брусок і, відповідно, уся система тіл. Для цього обчислімо максимальну силу тертя спокою, яка мала б діяти на перший брусок, якби він зрушив із місця:

Нитку натягнуто із силою $2\text{Н},$ тож перший брусок залишиться на місці. Для того, щоб зрушити обидва зв’язані бруски, треба було б прикласти силу, що дорівнює сумі максимальних сил тертя спокою обох брусків, тобто $11\text{Н}.$

Відповідь: 2.

ТЕМА: Молекулярна фізика і термодинаміка. Основи молекулярно-кінетичної теорії. Рівняння стану ідеального газу.

Завдання скеровано на перевірку вміння описати стан газів рівнянням Менделєєва ‒ Клапейрона й обчислити необхідну величину.

Запишімо рівняння стану для гелію $(\mathrm{He})$ і для азоту $({\mathrm{N}}_2):$ $$\begin{array}{c}p(\mathrm{He})V(\mathrm{He})=\frac{m(\mathrm{He})}{M(\mathrm{He})}RT(\mathrm{He}),\\ p({\mathrm{N}}_2)V({\mathrm{N}}_2)=\frac{m({\mathrm{N}}_2)}{M({\mathrm{N}}_2)}RT({\mathrm{N}}_2),\end{array}$$ де $p$ ‒ тиск газу, $V$ ‒ об’єм газу, $m$ ‒ маса газу, $M$ ‒ молярна маса газу, $R$ ‒ універсальна газова стала, $T$ ‒ температура газу.

Поршень встановиться нерухомо на певній висоті за однакового тиску на поршень зверху й знизу: $$p(\mathrm{He})=p({\mathrm{N}}_2).$$

За умовою і температура, і маса газів однакові в обох частинах посудини. Поділімо ліві і праві частини рівнянь, щоб скоротити однакові величини:

Відношення висот тих частин циліндричної посудини, які займає кожен газ, становить $7$ до $1.$ Одну частину висоти посудини позначмо $x.$ Тоді $$\begin{array}{c}h(\mathrm{He})=7x,\\ h({\mathrm{N}}_2)=x;\\ h(\mathrm{He})+h({\mathrm{N}}_2)=1,2\text{м},\\ 7x+x=1,2\text{м},\\ 8x=1,2\text{м},\\ x=\frac{1,2\text{м}}{8}=0,15\text{м}.\end{array}$$

За умовою в нижній частині посудини міститься азот, $$\begin{array}{c}h({\mathrm{N}}_2)=x=0,15\text{м},\end{array}$$ тож поршень встановиться на висоті $0,15\text{м}.$

Відповідь: 0,15.

ТЕМА: Молекулярна фізика і термодинаміка. Основи термодинаміки. Коефіцієнт корисної дії теплового двигуна та його максимальне значення.

Завдання скеровано на перевірку розуміння коефіцієнта корисної дії (ККД) й уміння обчислити температуру нагрівача.

Аналізуючи роботу теплових двигунів, французький інженер Саді Карно (1796–1832) 1824 р. дійшов висновку, що найефективнішим (із максимально можливим ККД ${\eta }_{\max }$ є так званий ідеальний тепловий двигун, який працює за циклом із двох ізотермічних і двох адіабатних процесів. Карно довів, що ККД такого двигуна можна обчислити за формулою $$\eta =\frac{T_{\text{н}}-T_{\text{х}}}{T_{\text{н}}}\cdot 100\text{\%}=(1-\frac{T_{\text{х}}}{T_{\text{н}}})\cdot 100\text{\%},$$ де $T_{\text{н}}$ ‒ температура нагрівника; $T_{\text{х}}$ ‒ температура холодильника.

Переведімо температуру холодильника в кельвіни: $$T_{\text{х}}=(21+273)\text{К}=294\text{К}.$$

Обчислімо температуру нагрівача:

$$\begin{array}{c}30\text{\%}=(1-\frac{294\text{К}}{T_{\text{н}}})\cdot 100\text{\%},\\ \frac{294\text{К}}{T_{\text{н}}}=1-0,3,\\ T_{\text{н}}=\frac{294\text{К}}{0,7}=420\text{К}.\end{array}$$

Відповідь: 420.

ТЕМА: Електродинаміка. Закони постійного струму. Послідовне і паралельне з’єднання провідників.

Завдання скеровано на перевірку вміння еквівалентно перетворювати схеми й розв’язувати розрахункові задачі, у яких ідеться про послідовне і паралельне з’єднання провідників.

Спочатку еквівалентно перебудуємо електричну схему з умови завдання, щоб було чітко видно, які з резисторів з’єднані паралельно, які ‒ послідовно, на яких саме резисторах вольтметром вимірюють напругу.

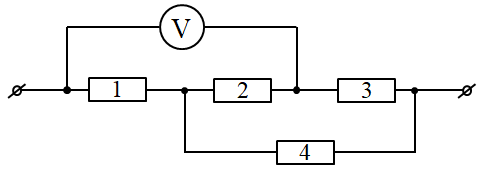
Вольтметр покаже суму напруг на послідовно з’єднаних резисторах 1 і 2. Визначмо їх.

Запишімо вирази для напруги $U$ на ділянці кола: $$U=U_1+U_{23}\text{або}U=U_1+U_4,$$ оскільки за паралельного з’єднання провідників $U_{23}=U_4.$

Резистори 2 та 3 з’єднано послідовно, тому $$U_{23}=U_2+U_3.$$

Визначмо загальну силу струму на ділянці кола: $$I=I_1=\frac{U_1}{R}\Rightarrow U_1=IR.$$

Резистор 4 приєднаний паралельно до резисторів 2 та 3. Тому струм розділиться на частини $I_{23}$ і $I_4$ так: загальний опір вітки з резисторами 2 та 3 вдвічі перевищуватиме опір резистора 4 (за послідовного з’єднання о́пори додають: $R_{23}=R+R=2R,R_4=R;$ пам’ятаймо, що за умовою всі резистори однакові, тобто з однаковим опором).

Віткою 23 пройде струм удвічі менший за струм, який пройде через резистор 4 (із закону Ома для ділянки кола $I=\frac{U}{R}$ сила струму обернено пропорційна опору провідника).

Запишімо, з огляду на це й закон Ома для ділянки кола, вирази для напруги на резисторах 2, 3 й 4: $$\begin{array}{c}{U}_{23}=U_2+U_3=\frac{1}{3}IR+\frac{1}{3}IR=\frac{2}{3}IR,\\ U_4=\frac{2}{3}IR.\end{array}$$

Підставивши вирази для напруг на окремих резисторах у формулу для напруги на ділянці кола, маємо: $$U=U_1+U_{23}=IR+\frac{2}{3}IR=\frac{5}{3}IR.$$

Розв’яжімо системи рівнянь:

Поділімо ліві і праві частини рівнянь:

Визначмо із цих відношень величини $U_1$ і $U_2:$ $$\begin{array}{c}{U}_1=\frac{3U}{5}=\frac{3\cdot 100\text{В}}{5}=60\text{В},\\ U_2=\frac{U}{5}=\frac{100\text{В}}{5}=20\text{В}.\end{array}$$

Отже, вольтметр покаже напругу на резисторах 1 і 2: $$U_{12}=U_1+U_2=60\text{В}+20\text{В}=80\text{В}.$$

Відповідь: 80.

Електродинаміка. Магнітне поле, електромагнітна індукція. Енергія магнітного поля.

Завдання скеровано на перевірку вміння розрахувати енергію магнітного поля.

Енергію $W_{\text{маг}}$ магнітного поля можна обчислити за формулою $$W_{\text{маг}}=\frac{L{I}^2}{2},$$ де $L$ – індуктивність котушки, $I$ ‒ сила струму.

$$W_{\text{маг}}=\frac{3\text{Гн}\cdot 0,5^2{\text{А}}^2}{2}=0,375\text{Дж}.$$

Відповідь: 0,375.

ТЕМА: Коливання і хвилі. Оптика. Електромагнітні коливання і хвилі. Перетворення енергії в коливальному контурі.

Завдання скеровано на перевірку розуміння перетворення енергії в коливальному контурі, уміння обчислювати необхідну фізичну характеристику електромагнітних коливань у будь-який момент часу.

Якщо на обкладках конденсатора накопичиться максимальний електричний заряд $q_{\max },$ то повна енергія $W$ коливального контуру дорівнюватиме максимальній енергії електричного поля $W_{\text{ел}}$ між обкладками конденсатора: $$W=W_{\text{ел}\max }=\frac{q_{\max }^2}{2C},$$ де $C$ ‒ електроємність конденсатора.

У той момент, коли конденсатор повністю розрядиться, енергія електричного поля дорівнюватиме нулю $(W_{\text{ел}}=0),$ сила струму сягне максимального значення $I_{\max },$ а повна енергія $W$ коливального контуру дорівнюватиме максимальній енергії $W_{\text{маг}}$ магнітного поля: $$\begin{array}{c}W=W_{\text{маг.}\max }=\frac{L{I}_{\max }^2}{2},\end{array}$$ де $L$ ‒ індуктивність котушки.

Повну енергію $W$ коливального контуру в довільний момент часу $t$ можна обчислити за формулою $$W=W_{\text{ел}}+W_{\text{маг}}=\frac{q^2}{2C}+\frac{L{I}^2}{2}.$$

Виконаймо необхідні математичні перетворення, щоб визначити шукану силу струму: $$\frac{q_{\max }^2}{2C}=\frac{L{I}_{\max }^2}{2}=\frac{q^2}{2C}+\frac{L{I}^2}{2}.$$

Помножмо всі вирази на $2$ й поділімо на $L:$ $$\frac{q_{\max }^2}{LC}=I_{\max }^2=\frac{q^2}{LC}+I^2.$$

Обчислімо добуток $LC$ в одиницях СІ:

Підставмо це значення добутку $LC$ у формулу із шуканою величиною:

Відповідь: 4.

ТЕМА: Коливання і хвилі. Оптика. Лінза. Оптична сила лінзи. Формула тонкої лінзи.

Завдання скеровано на перевірку вміння розрахувати оптичну силу лінзи, виконавши необхідні геометричні побудови.

Оберненою до фокусної відстані лінзи фізичну величину, якою характеризують лінзу, називають оптичною силою лінзи. Оптичну силу лінзи позначають символом $D$ й обчислюють за формулою $$D=\frac{1}{F},$$ де $F$ ‒ фокусна відстань.

Отримане зображення (див. рисунок в умові) дійсне, зменшене й перевернуте. Таке зображення могла дати лише збиральна лінза. Оптична сила збиральної лінзи є додатною. Тому формула тонкої лінзи така: $$D=\frac{1}{F}=\frac{1}{d}+\frac{1}{f},$$ де $d$ ‒ відстань від предмета до лінзи, $f$ ‒ відстань від лінзи до зображення.

Отже, потрібно дізнатися місцеположення лінзи. За правилами побудови зображень у тонкій лінзі з’єднаймо точку $A$ з її зображенням – точкою $A_1.$ Промінь $A{A}_1$ проходить без заломлення через оптичний центр лінзи.

З’єднаймо точку $B$ з її зображенням точку $B_1.$ Промінь $B{B}_1$ є горизонтальним, теж без заломлення проходить через оптичний центр лінзи й збігається з головною оптичною віссю лінзи.

Отже, на перетині променів $A{A}_1$ і $B{B}_1$ лежить оптичний центр лінзи – точка $O$ (див. рисунок).

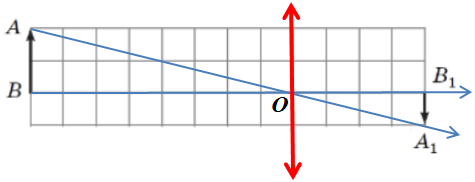
За рисунком можна визначити відстань $d$ від предмета до лінзи:

Визначмо відстань $f$ від лінзи до зображення:

Обчислімо оптичну силу лінзи:

Відповідь: 6,25.

ТЕМА: Квантова фізика. Елементи теорії відносності. Атом та атомне ядро. Радіоактивність.

Завдання скеровано на перевірку розуміння закону радіоактивного розпаду й уміння працювати з формулою, якою описано цей закон.

Період піврозпаду $T$ ‒ це фізична величина, якою характеризують радіонуклід. Період піврозпаду дорівнює часу, протягом якого розпадається половина наявної кількості ядер певного радіонукліда.

Основний закон радіоактивного розпаду: $$\begin{array}{c}N=N_0\cdot 2^{-\frac{t}{T}},\end{array}$$ де $N$ ‒ кількість ядер радіонукліда, що залишились у зразку через час $t;$ $N_0$ ‒ початкова кількість ядер; $T$ ‒ період піврозпаду; $t$ ‒ час розпаду.

Виразимо кількість $N$ ядер речовини через фізичні величини, дані в умові завдання ‒ масу $m$ нукліда і його молярну масу $M.$

Початкова кількість $N_0$ ядер нукліда Натрію: $$N_0(\mathrm{Na})=\frac{m_1(\mathrm{Na})}{M(\mathrm{Na})}{N}_A;$$ кінцева кількість $N$ ядер нукліда Натрію: $$N(\mathrm{Na})=\frac{m_2(\mathrm{Na})}{M(\mathrm{Na})}{N}_A,$$ де $N_A$ ‒ стала Авоґадро.

Підставмо ці вирази у формулу закону радіоактивного розпаду:

Підставмо числові дані з умови й обчислімо шуканий проміжок часу $t:$

Відповідь: 13.